引 言

电流体动力学(electro-hydrodynamics, EHD)属于电磁学和流体动力学等多学科交叉领域, 它描述了带电粒子在库仑力驱动下引起的电对流^[1]. 作为EHD的基本课题之一, 电热对流(electro-thermo convection, ETC)考虑电场、流场和温度场等多个物理场耦合及带电粒子与流体介质之间的相互作用, 也是EHD的重要研究课题之一^[2-3]. 近年来, 随着能源问题的日益突出, 节能环保等相关问题越来越受到广泛的关注, 科研人员对于电热对流强化传热应用逐渐重视^[4-5]. ETC与许多其他传统强化传热方法相比, 具有节约资源、提高传热效率、结构简单和安全等优点, 在强化传热领域受到许多研究人员的关注^[6].

近年来众多****对ETC问题开展了相关研究, 早期对ETC的研究主要是对简化的理论模型和实验数据进行分析. Atten^[7]的研究结果表明电热对流可以显著提高传热效率, 传热效率提升了15倍. Mccluskey和Atten^[8]的研究结果显示, 电热对流对传热的影响比纯自然对流要高一个数量级. Wu等^[9]研究了电热对流中亚临界或超临界的分叉类型和有限幅度稳定性标准, 并发现了超临界点和亚临界点的取值很大程度上取决于普朗特数$ Pr $和无量纲离子迁移率$ M $. 随后, Traore等^[10]提出一种求解ETC控制方程的数值模拟方案, 该方案能够很好解决ETC问题的多物理场耦合问题, 基于该模型, 作者还对二维腔体中的ETC进行了数值研究. Dantchi等^[11]采用有限体积法求解ETC方程, 模拟中考虑了二维腔体内从下壁面电极和从侧壁面电极注入电荷两种情况, 结合相关无量纲参数进行分析, 研究结果表明电场增强了传热, 对于足够大的$ T $值, 努塞特数与瑞利数无关. Luo等^[12]设计了格子Boltzmann模型来求解ETC方程, 使用4个不同的分布函数分别计算流场、电势、电荷密度分布和温度场, 还进行了多尺度分析来将离散的格子Boltzmann方程恢复到宏观控制方程, 并通过对几种问题进行验证, 最后得到的结果与解析解等其他数值结果一致. 除此之外, Lu等^[13]采用了高分辨率逆风方案(high resolution upwind scheme)探究了方腔内介电液体中电热对流的流动结构和传热现象, 通过研究相关无量纲参数如热瑞利数、无量纲离子迁移率以及普朗特数, 最后发现了多种流动结构以及传热规律. Hu等^[14]采用了格子Boltzamnn方法研究了不同几何结构下的二维电热对流问题, 探讨了瑞利数、电瑞利数、长宽比和普朗特数等无量纲参数对流场流线、等温线、电荷密度分布和界面的平均努塞特数的影响, 结果表明增加电瑞利数可以提升传热效率并改变了流场的结构. Wang等^[15]提出了一种谱元法(spectral element method)的新型数值方法, 在验证该数值方法能有效的解决电热对流问题后, 又模拟了正弦温度边界方腔内的二维电热对流问题, 研究结果表明, 与均匀温度边界相比, 正弦温度边界能提高传热效率. 还有一些关于电热对流的拓展研究. Chand等^[16]研究了两平行电极板之间的纳米流体在电场影响下的热不稳定性. Srivastava^[17]对多孔介质中的二元流体电热对流进行了稳定性分析.

上述研究在很大程度上加深了人们对电热对流在传热过程中的内在机理. 但是应当指出的是, 上述研究, 模型大多数是水平放置的两平行电极板^{[7, 9, 12, 18]}或者是局部单极注入电荷^[19-20], 这些研究中较少考虑温度分布不均匀的情况, 实际上在许多研究领域如对自然对流的研究, 非均匀温度边界问题一直是热门的研究课题. Poulikakos^[21]研究了二维方腔左侧壁面上半部分加热, 下半部分冷却, 其他壁面隔热的情况, 结果表明, 当加热区域位于冷却区域下方时, 整体的传热增强. Sathiyamoorthy等^[22]研究了二维方腔两侧壁面的温度是具有线性变化的情况, 结果表明, 当壁面两侧的温度呈线性变化时, 方腔底部的努塞特数会变得十分不稳定. 此外, Bilgen和Yedder^[23]研究了二维矩形腔体垂直壁面的温度呈正弦分布而其他壁面绝热的情况. 另外, 考虑加热器长度和位置的情况, Oztop和Abu-Nada^[24]研究了部分加热的二维腔体中纳米流体的自然对流, 发现了加热器的位置会影响流线结构和温度分布. 最近, Wang等^[25]研究了局部加热的二维方腔中纳米流体的自然对流, 结果表明传热效率随着加热器的长度增加而降低. 从这些文献中不难看出, 不论是在电热对流中考虑局部单极注入电荷还是在自然对流中考虑非均匀温度边界情况下, 都会对传热效率产生影响, 并产生复杂的流动结构. 而电热对流本质是电对流和自然对流耦合的问题, 因此对于局部单极注入电荷和局部加热相结合的机制需要进行更深入的研究, 以便于理解非均匀温度边界的电热对流的流体流动和传热特性.

本文采用了格子Boltzmann方法(LBM)求解控制方程组, 其中包括Navier?Stokes方程, 电荷密度守恒方程, 电势的泊松方程以及温度方程, 另外, 为了减少计算时间以及提升计算效率, 本文使用NVIDIA 图形处理平台, 编写计算统一设备架构程序. 研究了在局部受热条件下, 方腔内流体流动和系统传热效率的变化情况, 并为研究其他非均匀温度边界的电热对流问题提供参考数据.

1.
问题描述

1.1
物理模型和控制方程

如图1所示, 介电液体被限制在长度为$ H $的二维方腔中. 左侧壁面是加热的电极板, 温度值固定为$ theta_{0} $, 电势保持为$ phi_{0} $, 长度为$ h $, 电极板的中心点到下壁面的距离用$ delta $来表示. 右壁面温度固定为$ theta_{1} $, 电势保持为$ phi_{1} $, 且$ theta_{0} > theta_{1} $, $ phi_{0} > phi_{1} $, 上下壁面是绝热且绝缘的. 为方便模拟, 假设方腔中的流体是不可压缩的牛顿流体, 流体的密度变化是满足标准的Boussinesq假设的, 自由电荷的产生只发生在介电液体与电极界面之间的电化学反应, 并且注入的电荷密度取恒定值为$ q_{0} $. 另外, 忽略了黏性热耗散以及焦耳热的影响^[26].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
物理模型示意图



Figure
1.
Schematic diagram of the physical model



下载:
全尺寸图片
幻灯片


基于上述假设, 二维局部受热腔体内电热对流问题可以通过连续方程、动量方程、电势的泊松方程、电场的定义方程、电荷密度守恒方程和温度方程共同描述^[27]

$$ nabla cdot {{boldsymbol{u}}} = 0 $$

(1)

$$ begin{split}&frac{{partial {{boldsymbol{u}}}}}{{partial t}} + nabla cdot left({{boldsymbol{uu}}} ight) = - nabla {p} + nabla cdot left{ {{upsilon}left[ {nabla {{boldsymbol{u}}} + {{left( {nabla {{boldsymbol{u}}}} ight)}^{ m{T}}}} ight]} ight} +&qquadq{{boldsymbol{E}}} + {{boldsymbol{g}}}[1-beta(theta-theta_{{ m{ref}}})] end{split} $$

(2)

$$ nabla^{2}phi = -frac{q}{varepsilon} $$

(3)

$$ {{boldsymbol{E}}} = - {nabla {phi}} $$

(4)

$$ frac {partial {q}}{partial t}+nabla cdot left[{q left( {K{{boldsymbol{E}}} } + {{boldsymbol{u}}} ight)} ight] = nabla cdot left(Dnabla q ight) $$

(5)

$$ frac{partial theta}{partial t}+nabla cdot ({{boldsymbol{u}}}theta) = nabla cdot (chi nabla theta) $$

(6)

在上述方程组中, $ {{boldsymbol{u}}} $, $ {{boldsymbol{E}}} $, $ {{boldsymbol{g}}} $, $ q $, $ theta $, $theta_{{
m{ref}}}$, $ phi $分别为流体速度、电场强度、重力加速度、电荷密度、温度、参考温度、电势. $ p $, $ upsilon $, $ beta $, $ varepsilon $, $ K $, $ D $, $ chi $分别代表压力、运动学黏性、热膨胀系数、介电常数、离子迁移率、电荷扩散系数以及热扩散系数. 为了更方便的研究电热对流问题, 引入以下无量纲参数^[28]

$$ left.begin{array}{l} Ra = dfrac{g betaleft(theta_{0}-theta_{1} ight) H^{3}}{upsilon chi}, quad T = dfrac{varepsilonleft(phi_{0}-phi_{1} ight)}{mu K} Pr = dfrac{upsilon}{chi}, quad M = dfrac{1}{K}left(dfrac{varepsilon}{ ho_{0}} ight)^{1 / 2} alpha = dfrac{D}{Kleft(phi_{0}-phi_{1} ight)}, quad C = dfrac{q_{0} H^{2}}{varepsilonleft(phi_{0}-phi_{1} ight)} end{array} ight} $$

(7)

其中, $ Ra $为热瑞利数, 表示浮升力与黏性力的比值. $ T $为电瑞利数, 表示库仑力与黏性力的比值. 对于热瑞利数$ Ra $以及电瑞利数$ T $而言, 在实际实验中可依据温度差和电压差灵活设置^[29], 为了系统探究其影响, 本文将之分别约束在$ 0leqslant Tleqslant 1200 $, $ 1.0times10^{4}leqslant Raleqslant $$ 1.0times10^{5} $区间. $ C $为电荷注入强度, 罗康^[30]的理论研究和数值模拟研究中, 一般取$ C = 10.0 $作为其强注入的代表性值, 为此本文中所涉及的电荷注入强度$ C $在未加强调的情况下, 其值均为10.0. 无量纲离子迁移率$ M $是所谓的水动力学迁移率与真实迁移率的比值. 对于带有注入粒子的介电液体而言, 实验显示其值一般大于等于3^[3], 例如甲醇(${
m{H}}^{+}$, $ M = 4.1 $)、氯苯(${
m{Cl}}^{-}$, $ M = 4.9 $)、乙醇(${
m{H}}^{+}$, $ M = 8.8 $; ${
m{ Cl}}^{-}$, $ M = 26.5 $)、硝基苯(${
m{Cl}}^{-}$, $ M = 22 $)、碳酸丙烯(${
m{Cl}}^{-}$, $ M = 51 $), 鉴于此, 为了更加清晰地认识无量纲离子迁移率$ M $对于电热对流的影响, 本文所考察的无量纲离子迁移率$ M $介于5.0和50.0之间. $ alpha $为无量纲电荷扩散系数, 其值一般介于$ 10^{-3} $和$ 10^{-4} $之间^[28], 在本文中参考了文献[31], 将其值固定为$ 1.0times 10^{-4} $. $ Pr $为动量边界层与热边界层之比, 反映了流体物理性质对热传递的影响, 本文重点关注一类液体形态的介电介质^[3], 因此将其值设置在5.0和50.0之间. 另外, 还考虑了电极板的长度$ h $和电极板的中心点到下壁面的距离$ delta $, 分别取值为$0.5Hleqslant hleqslant H$, $ 0.25Hleqslantdeltaleqslant 0.75H $. 对于温度边界、电势边界、电荷密度边界以及速度边界, 它们的数学描述如下, 左侧壁面电极板边界条件如下

$$ theta = theta_{0}, ;;phi = phi_{0},;; q = q_{0} $$

(8)

左侧壁面除电极板外的边界条件如下

$$ theta = {partial theta}/{partial{x}},;; phi = {partial phi}/{partial{x}}, ;;q = {partial q}/{partial{x}} $$

(9)

右侧壁面边界条件如下

$$ theta = theta_{1}, ;;phi = phi_{1},;; q = {partial q}/{partial{x}} $$

(10)

上下壁面的温度、电势、电荷密度的边界条件如下

$$ {partial theta}/{partial{y}} = 0,;; {partial phi}/{partial{y}} = 0,;; {partial q}/{partial{y}} = 0 $$

(11)

而对于速度边界而言, 方腔的4个壁面均为无滑移边界

$$ {{boldsymbol{u}}} = {boldsymbol{0}} $$

(12)

2.
数值方法

在数值方法选择上, 本文采用LBM进行模拟, 与有限体积法和有限元方法等传统方法不同, LBM在处理复杂边界问题时具有高效和简单的优点^[32], 又因为LBM具有天然并行性^[33], 所以使得并行计算成为可能^[34-35]. 经过数十年的发展, LBM的应用领域从单相问题延伸到多相流^[36]、多孔介质^[37-38]、在电流体动力学^{[9, 12, 30]}等诸多领域, 并受到了许多研究人员的广泛关注. 在本文中, 拟并采用4个演化方程分别求解Navier?Stokes方程, 电势的泊松方程, 电荷密度守恒方程和温度方程. 接下来将依次介绍.

2.1
流场格子Boltzmann模型

在假设流体为不可压牛顿流体的前提下, 采用的是Guo等^[39]提出的格子Boltzmann模型进行求解, 该模型的演化方程可以表示如下

$$ begin{split}& {f_i}left( {{{boldsymbol{x}}} + {{{boldsymbol{c}}}_i}Delta t,t + Delta t} ight) - {f_i}left( {{{boldsymbol{x}}},t} ight) = - frac{1}{{{tau _{ m{f}}}}}Bigr[ {{f_i}left( {{{boldsymbol{x}}},t} ight) }-& qquad { f_i^{ m{eq}}left( {{{boldsymbol{x}}},t} ight)} Bigr] + Delta t{F_i} end{split} $$

(13)

其中$ {f_i}left( {{{boldsymbol{x}}},t}
ight) $为分布函数, 表示$ t $时刻$ i $方向的流体微团在$ {{boldsymbol{x}}} $处的信息, 平衡态分布函数$ f_i^{
m{eq}}({boldsymbol{x}},t) $计算如下

$$ f_i^{ m{eq}}({{boldsymbol{x}}},t) = {eta _i}p + {omega _i}left[ {frac{{{{{boldsymbol{c}}}_i} cdot {{boldsymbol{u}}}}}{{c_{ m{s}}^2}} + frac{{{{boldsymbol{uu}}}:({{{boldsymbol{c}}}_i}{{{boldsymbol{c}}}_i} - c_{ m{s}}^2{{boldsymbol{I}}})}}{{2c_{ m{s}}^4}}} ight] $$

(14)

其中参数$ {eta _i} $满足${eta _0} = 1+(omega _0-1)/{c_{
m{s}}^2}$, $ {eta _i} = omega _i/{c_{
m{s}}^2} (ineq 0) $, $
ho_0 $为流体平均密度, $ {{boldsymbol{c}}}_{i} $为离散速度, 对于本文考虑的二维问题采用D2Q9模型中的速度离散方案, 其定义如下

$$ begin{array}{l} {{boldsymbol{c}}}_{i} = left{ begin{array}{ll} (0,0), & i = 0 cleft{cos left[(i-1) dfrac{{text{π}}}{2} ight], sin left[(i-1) dfrac{{text{π}}}{2} ight] ight}, & i = 1,2,3,4 sqrt{2} cleft{cos left[(2 i-1) dfrac{{text{π}}}{4} ight], sin left[(2 i-1) dfrac{{text{π}}}{4} ight] ight}, & i = 5,6,7,8 end{array} ight. end{array} $$

(15)

其中, $c_{
m{s}} = c/sqrt 3$为格子声速, $ c $为离散速度, 且$ c = Delta x/Delta t $, $ Delta x $为网格步长, $ Delta t $为时间步长. 权重$ omega_{i} $定义如下

$$ begin{array}{l} {omega}_{i} = left{ begin{array}{ll} 4/9, & i = 0 1/9, & i = 1,2,3,4 1/36, & i = 5,6,7,8 end{array} ight. end{array} $$

(16)

另一方面, $ F_{i}({boldsymbol{x}},t) $为外力项, 其表达式如下^[40]

$$ begin{array}{l} {F_i}({{boldsymbol{x}}},t) = {omega _i}left( {1 - dfrac{1}{{2{tau _f}}}} ight)left[ {dfrac{{{{{boldsymbol{c}}}_i} cdot {{boldsymbol{F}}}}}{{c_{ m{s}}^2}}} ight. left.{+ dfrac{ {left({{boldsymbol{Fu}}} + {{boldsymbol{uF}}} ight):left( {{{{boldsymbol{c}}}_i}{{{boldsymbol{c}}}_i} - c_{ m{s}}^2{{boldsymbol{I}}}} ight)}}{{2c_{ m{s}}^4}}} ight] end{array} $$

(17)

其中外力${{boldsymbol{F}}} = q{{boldsymbol{E}}}+{{boldsymbol{g}}}beta left(theta-theta_{{
m{ref}}}
ight)$. $ {tau _{
m{f}}} $为流场的无量纲松弛时间, 它与$ upsilon $的关系如下

$$ upsilon = c_{ m{s}}^2 (tau_ { m{f}}-0.5)Delta t $$

(18)

最后计算宏观速度$ {{boldsymbol{u}}} $以及压力项$ p $, 由以下公式计算得到

$$ {{boldsymbol{u}}} = sumlimits_i {{{{boldsymbol{c}}}_i}{f_i}} + frac{{Delta t}}{2}{{boldsymbol{F}}} $$

(19)

$$p = frac{{c_s^2}}{{1 - {omega _0}}}left( {sumlimits_{i ne 0} {{f_i}} - {omega _0}frac{{{{left| {{boldsymbol{u}}} ight|}^2}}}{{2c_{ m{s}}^2}}} ight) $$

(20)

2.2
电势场格子Boltzmann模型

本质上而言, 电势控制方程(3)为一类典型的泊松方程. 在这里采用下述演化方程^[41]

$$ begin{split}& {g_i}left( {{{boldsymbol{x}}} + {{{boldsymbol{c}}}_i}Delta t,t + Delta t} ight) - {g_i}left( {{{boldsymbol{x}}},t} ight) = & qquad- dfrac{1}{{{tau _{{ m{g}}}}}}left[ {{g_i}left( {{{boldsymbol{x}}},t} ight) }{- g_i^{ m{eq}}left( {{{boldsymbol{x}}},t} ight)} ight] + Delta t {widetilde{omega}}_{i} zeta R end{split} $$

(21)

其中, $ zeta $为扩散系数, 取$ zeta $等于0.5以保持数值的稳定性. 此外, 源项$ R = q/varepsilon $. 平衡态分布函数$ g_i^{
m{eq}}({{boldsymbol{x}}},t) $定义如下

$$ begin{array}{l} g_i^{ m{eq}}({{boldsymbol{x}}},t) = left{ begin{array}{ll} left({{widetilde{{omega}} _0}-1} ight){phi}, & i = 0 {widetilde{{omega}} _i}phi, & i = 1,2,3,4end{array} ight. end{array} $$

(22)

因为电势的平衡态分布函数为线性的平衡态形式, 为加快运算效率, 采用D2Q5的格子模型^[41], 该模型的权系数$ widetilde{omega_{i}} $取值如下

$$ begin{array}{l} widetilde{omega} _i = left{ begin{array}{ll} 0, & i = 0 1/4, & i = 1,2,3,4 end{array} ight. end{array} $$

(23)

其中格子声速$ {widetilde {c}}_{
m{s}}^2 = c^2/2 $, 松弛时间$ tau_{{
m{g}}} $通过如下关系式得到

$$ tau_{{ m{g}}} = 0.5+zeta/(widetilde{c_{ m{s}}}^{2}Delta t) $$

(24)

最后, 电势$ phi $则通过下式计算得到

$$ {phi} = frac {1}{1-{widetilde{omega} _0}} { sumlimits_{i} g_{i}}$$

(25)

而电场$ {{boldsymbol{E}}} $则可以通过式(4)和电势的一阶分布函数计算得到^[12], 具体计算表达式如下

$$ {{boldsymbol{E}}} = frac{1}{{tau _{{ m{g}}}}{widetilde {c}}_{ m{s}}^2}sumlimits_{i}{boldsymbol{c}}_{i}{g_i} $$

(26)

2.3
电荷密度的格子Boltzmann模型

从文献[30]中可知电荷的传输机制有三种, 第一种是在电场作用下, 电荷会发生漂移; 第二种是电荷在流体速度的影响下运动; 第三种则是电荷的扩散. 而电荷密度守恒方程属于强对流方程, 对于该方程的求解在算法中起着重要作用, 因此为了能很好的求解该方程, 使用罗康^[30]提出的格子Boltzmann模型来求解, 其演化方程表示如下

$$ begin{split}& {h_i}left( {{{boldsymbol{x}}} + {{{boldsymbol{c}}}_i}Delta t,t + Delta t} ight) - {h_i}left( {{{boldsymbol{x}}},t} ight) =&qquad - frac{1}{{{tau _{ m{h}}}}}left[ {{h_i}left( {{{boldsymbol{x}}},t} ight) }{- h_i^{ m{eq}}left( {{{boldsymbol{x}}},t} ight)} ight] end{split} $$

(27)

其中, $ h_i^{
m{eq}}left( {{{boldsymbol{x}}},t}
ight) $为平衡态分布函数, 具体表达如下

$$ begin{split}&h_i^{ m{eq}}({{boldsymbol{x}}},t) = {q{omega _i}} left{ 1+frac{ {{{{boldsymbol{c}}}_i} cdot left( {K{boldsymbol{E}}} +{{boldsymbol{u}}} ight) } } {{c_{ m{s}}^2}} ight. + &qquadleft. frac{ left[ {{boldsymbol{c}}}_i cdot left(K{{boldsymbol{E}}}+{bf{u}} ight) ight]^{2} - c_{ m{s}}^2 left| K{{boldsymbol{E}}}+{{boldsymbol{u}}} ight|^{2} } {{2c_{ m{s}}^4}} ight} end{split} $$

(28)

松弛时间$ tau_{{
m{h}}} $通过如下关系式得到

$$ tau _{ m{h}} = 0.5+D/({c_{ m{s}}^{2}}Delta t) $$

(29)

最后, 计算电荷密度$ q $的宏观量

$$ q = sumlimits_{i} h_{i} $$

(30)

上述等式中的权重$ omega_{i} $, 离散速度$ {{boldsymbol{c}}}_{i} $都与流场相同.

2.4
温度场格子Boltzmann模型

本文中的温度方程是忽略了黏性热耗散和焦耳热后的简化方程, 从实现的角度和精度的满足两个方面, 简化的温度方程能很好地应用于各种传热问题中^[42]. 因此采用文献[12]中的方法, 温度的演化方程如下

$$ begin{split}& {l_i}left( {{{boldsymbol{x}}} + {{{boldsymbol{c}}}_i}Delta t,t + Delta t} ight) - {l_i}left( {{{boldsymbol{x}}},t} ight) =& qquad- frac{1}{{{tau _{ m{l}}}}}left[ {{l_i}left( {{{boldsymbol{x}}},t} ight)}{ - l_i^{ m{eq}}left( {{{boldsymbol{x}}},t} ight)} ight] end{split} $$

(31)

温度的平衡态分布函数$ l_i^{
m{eq}}({{boldsymbol{x}}},t) $如下

$$ l_i^{ m{eq}}({{boldsymbol{x}}},t) = hat{omega}_{i}theta left(1+dfrac{{boldsymbol{c}}_{i} cdot {boldsymbol{u}}}{hat{c}_{ m{s}}^{2}} ight) $$

(32)

其中松弛时间$ tau_{{
m{l}}} $与热扩散系数$ chi $的关系如下

$$ tau_{ m{l}} = 0.5+chi/(hat{c}_{ m{s}}^{2}Delta t) $$

(33)

与电势场一样, 鉴于温度场的平衡态分布函数$ l_i^{
m{eq}}left({{{boldsymbol{x}}},t}
ight) $也是线性平衡态形式, 这里也采用D2Q5的格子模型模型^[43], 其中$ hat{c}_{
m{s}}^{2} = 2c^2/5 $, 权系数$ hat{omega}_{i} = 1/5 $. 最后, 温度$ theta $由下式计算可得

$$ theta = sumlimits_{i} l_{i} $$

(34)

3.
边界处理和程序流程

在格子Boltzmann方法中, 边界条件的处理一般采用Guo等^[44]提出的非平衡态外推格式, 所得的分布函数精度为二阶, 具有很好的数值稳定性. 另外, 程序的具体步骤为: (1)初始化为系统平衡态, 此时电荷运输和温度传递处于平衡状态, 流场处于静止状态; (2)进行碰撞流动, 并通过式(19)计算速度$ {boldsymbol{u}} $; (3)计算电势的演化方程(21), 结合式(25)和式(26)得到电势$ phi $和电场强度$ {boldsymbol{E}} $; (4)计算电荷密度分布的演化方程(27), 通过式(30)得到电荷密度$ q $; (5)计算温度的演化方程(31), 并计算式(34)得到温度$ theta $; (6)计算式(17)得到结果并代入流场的演化方程(13)中, 依次重复步骤(2) ~ 步骤(6)直到系统稳定并收敛为止. 最后, 定义二维问题中的局部努塞特数$ Nu_{y} $和平均努塞特数$Nu_{{
m{av}}}$^[34]以及最大的流体速度$ V_{max} $分别用来表示传热效率和流动强度, 通过如下公式计算得到

$$left. {begin{array}{*{20}{l}}{N{u_y} = {{left. {dfrac{{partial theta }}{{partial x}}} ight|}_{x = 0}},quad N{u_{{ m{av}}}} = dfrac{1}{h}displaystyleint_0^h N {u_y}{ m{d}}y}{{V_{{ m{max}}}} = max {sqrt {u_x^2 + u_y^2} } }end{array}} ight}$$

(35)

4.
数值验证

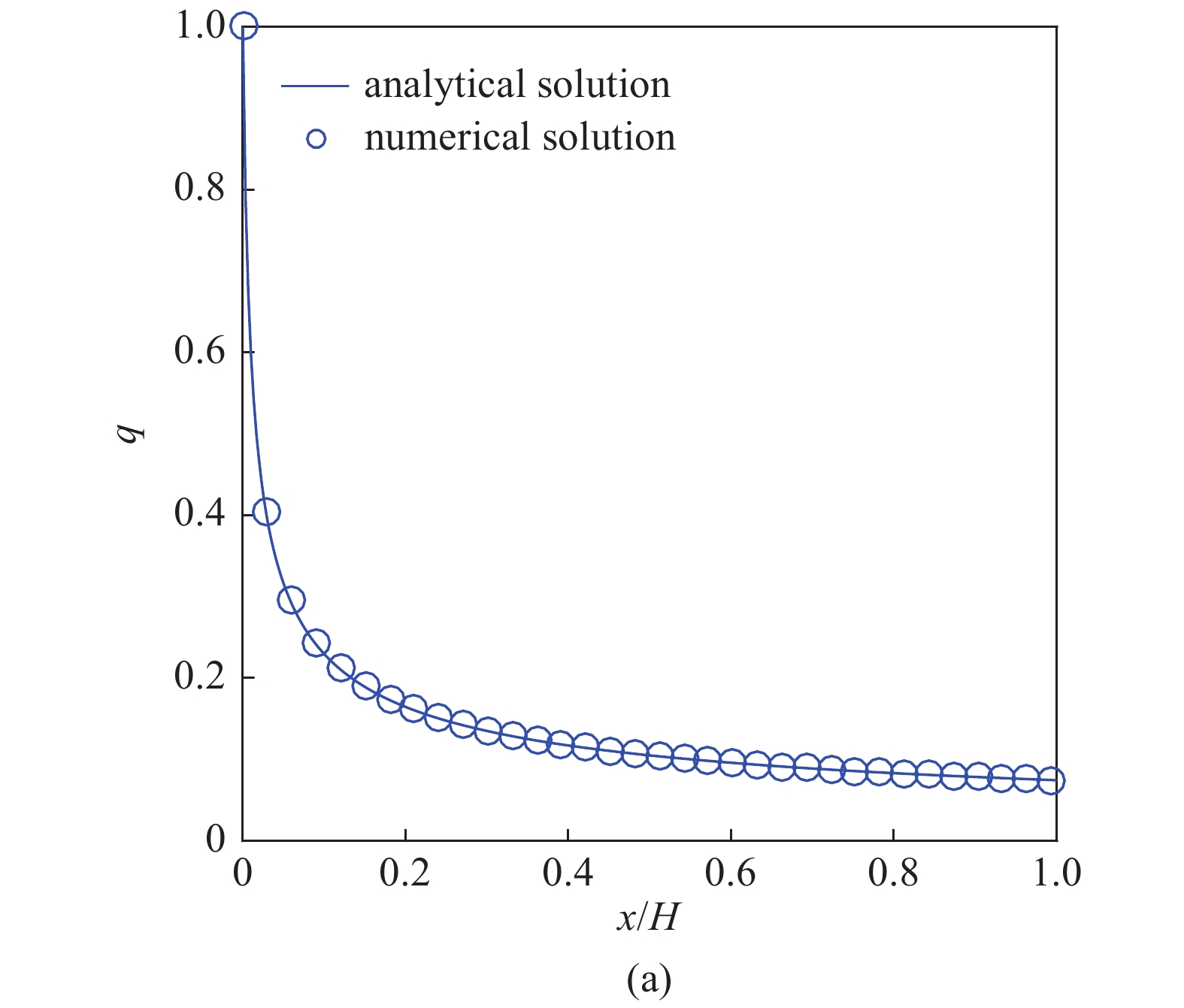
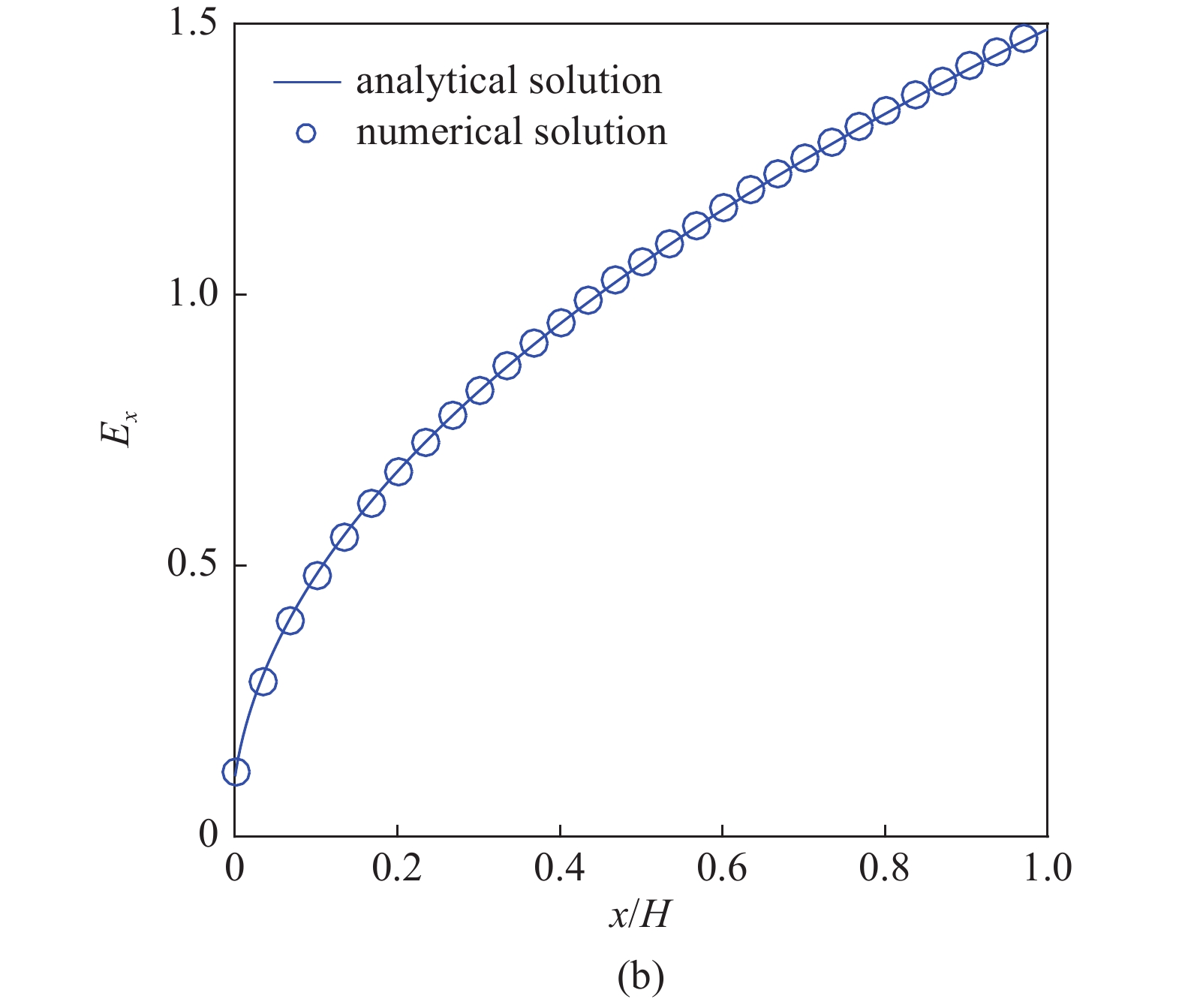
如图2所示, 对系统处于平衡态时的电荷密度$ q $和$ x $方向的电场强度$ E_{x} $的数值解与解析解进行了比较. 其中, 平衡态电荷密度$ q $和电场强度$ E_{x} $的解析解表示如下



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-2-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
电荷密度$ q $, 水平方向电场强度$ E_{x} $的数值解与解析解对比



Figure
2.
Comparisons of the charge density q and horizontal electric field strength $ E_{x} $ between the analytical solutions and numerical solutions



下载:
全尺寸图片
幻灯片

$$q= frac{a}{2Csqrt{x+b}},;; E_{x} = asqrt{x+b} $$

(36)

上式中的参数$ a $和$ b $的取值与电荷注入强度$ C $有关^[12], 在验证中取$ C = 10 $.

结果表明, 通过当前LBM代码计算得到的数值解与解析解吻合较好.

5.
数值模拟结果与讨论

5.1
库仑力和浮升力作用下的电热对流问题探究

本节中, 对二维局部受热腔体结构中的电热对流问题进行了模拟, 并初步对该结构下系统的传热效率、流体流动以及电热对流的分岔结构进行了分析. 实验中将采用$ 300times300 $的网格分辨率, 其可满足网格无关性验证. 如图3(a)所示, 首先观察了在热对流很弱时(热瑞利数$ Ra = 400 $), 电对流主导流体流动的情况, 其他参数分别为$ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $. 图3(a)中描述了随着电瑞利数$ T $的增加和降低, 相应传热效率$ Nu_{{
m{av}}} $的变化情况, 图3(a)中还给出了相关分岔点处的电荷密度分布图. 对于电瑞利数$ T $的值逐渐增加的情况, 当电瑞利数$ T $低于临界值^[45]($ T_{{
m{c}}}approx174 $, $Pr = 10,; M = 10$)时, $ Nu_{{
m{av}}} $的变化不是很大, 在前半段几乎保持水平状态, 并且电荷密度分布比较均匀, 这都表明流体没有形成强烈的对流, 库仑力无法有效的激发流体流动, 因此传热效率变化速度缓慢. 然而当电瑞利数$ T $超过临界值$T_{{
m{c}}}$以后, $Nu_{{
m{av}}}$的值会突然向上跳跃式增加, 并且电荷分布图中会出现空电荷区, 空电荷区的形成与电荷运输过程中的漂移和对流机制之间的竞争有关^{[7, 9, 12, 46]}. 从电荷密度守恒方程(5)中的对流速度$(K{boldsymbol{E}} + {{boldsymbol{u}}})$可以知道, 一旦该区域的最大速度超过了电荷的漂移速度$ K{boldsymbol{E}} $, 强对流结构就会阻碍扩散到这些区域的电荷, 结果就出现了空电荷区, 并且会发生传热增强的现象. 对于逐渐减少电瑞利数$ T $的情况, 当从电瑞利数$ T = 300 $开始逐渐减少时, $Nu_{{
m{av}}}$并不能沿着增长时的曲线完全返回, 这意味着强大的对流可以维持很大范围内的电瑞利数$ T $值. 但是当电瑞利数$ T $接近148附近时, $ Nu_{{
m{av}}} $会突然下降, 可以观察到电瑞利数$ T = 148 $和$ T = 174 $之间会形成所谓的回滞区, 并且如预期中那样, 空电荷区消失, $Nu_{{
m{av}}}$会沿着曲线原路返回. 接着观察在电对流很弱时(电瑞利数$ T = 80 $), 热对流主导流体流动的情况, 图3(b)中随着$ Ra $的增加和降低, 往返的$Nu_{{
m{av}}}$共用相同的演化曲线, 表现出超临界特征($Pr = 10, ;M = 10$). 另外, $Nu_{{
m{av}}}$变化过程中并没有出现回滞区, 这说明流体流动表现出规律且单一的机制. 在图3(b)中, 还插入了热瑞利数$ Ra = 800 $时的电荷密度分布和温度分布图, 通过观察发现它们并没有形成空电荷区, 电荷密度分布与温度分布相似, 说明了流体运动十分弱, 速度无法超过电荷的漂移速度. 这也说明当电瑞利数$ T $的取值很低时, 只凭借浮升力的作用无法产生电热对流中分岔结构. 通过对两种不同情况下的电热对流的稳定性分析, 能够对电热对流中许多现象的产生有一定的初步认识, 接下来会探讨在库仑力和浮升力共同作用下的电热对流问题.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
(a) 热瑞利数 Ra = 400, 变化电瑞利数 T 的分岔结构和(b) 电瑞利数T = 80, 变化热瑞利数Ra 的分岔结构 ($ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



Figure
3.
(a) The distributions of the maximum speed $ V_{{
m{max}}} $ vs. electric Rayleigh number $ T $. (b) The distributions of the maximum speed $ V_{{
m{max}}} $ vs. Rayleigh number $ Ra $ ($ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片


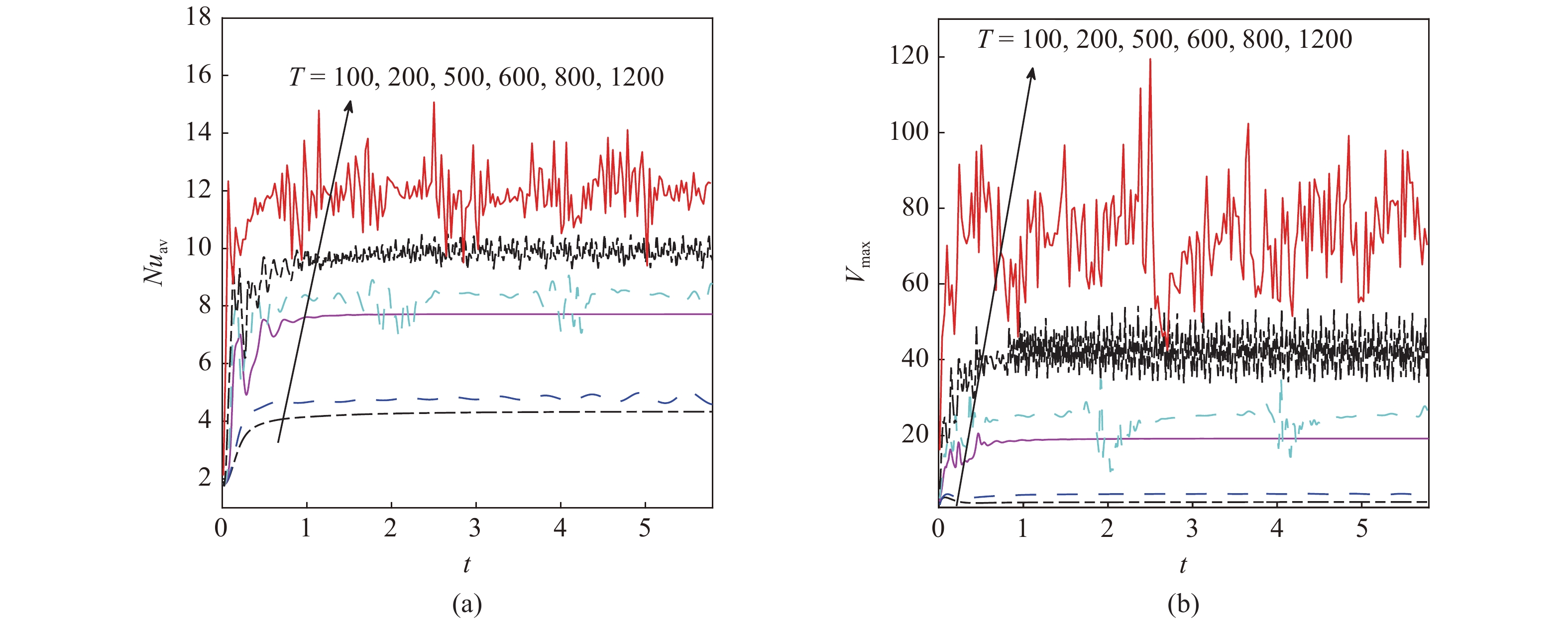
固定参数$ Ra = 1times10^{4} $, $ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $, 图4描绘了电瑞利数T在100 ~ 1200范围内, 不同强度的库仑力作用下的系统传热效率和流体流动的变化情况. 可以看出, 由于库仑力和浮升力之间的相互竞争, 每条曲线都对应着不同的流动状态. 随着电瑞利数T的增加, 库仑力变大, $Nu_{{
m{av}}}$和$V_{{
m{max}}}$显著增加, 系统的传热效率和流动强度都会变大. 值得注意的是, 当电瑞利数$ T $较小(例如电瑞利数$ T = 100 $)时, 系统始终处于稳定的对流状态, 此时的传热效率和流动强度的增强是有限的. 接着当$ T $增加时, 则会在演化的最后出现一种不稳定的对流状态($ T = 200 $), 并且$ Nu_{{
m{av}}} $会围绕某一值波动. 但是当电瑞利数$ T $的值增大时($500leqslant Tleqslant 800$), 系统再次出现稳定的对流状态(电瑞利数$ T = 500 $)以及周期性流动状态(电瑞利数$ T = 600, T = 800 $时), 主要原因是库仑力逐渐增大后, 会在对流中占据主导地位. 随着电瑞利数$ T $的增加(当电瑞利数$ T = 1200 $时), 流动变得十分不稳定, 此时的库仑力急剧增加并由稳定或周期性的对流状态变成混沌状.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
在不同电瑞利数T下, (a) 平均努塞特数$Nu_{{
m{av}}}$和(b) 最大速度$V_{{
m{max}}}$随时间变化的曲线 ($ Ra = 1times10^{4} $, $ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



Figure
4.
The distributions of (a) the average Nusselt number $Nu_{{
m{av}}}$ vs. time and (b) the maximum speed $V_{{
m{max}}}$ vs. ${
m{time}}$ under different electric Rayleigh number $ T $ ($ Ra = 1times10^{4} $, $ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片


为了直观地理解电瑞利数$ T $对电热对流的影响, 如图5所示, 给出了稳定和非稳定情况下的电荷密度分布、温度分布和流线分布图. 图5(a) ~ 图5(e)分别为电瑞利数$ T = 0 $, $200$, $500$, $800$, $1200$时, 其余无量纲参数为$ Ra = 1times10^{4} $, $ C = 10 $, $M = $$ 10$, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $. 可以看到, 当电瑞利数$ T = 0 $时, 表示为纯自然对流的情况, 方腔内只有一个沿顺时针方向旋转的漩涡, 且上下对称. 当电瑞利数$ T = 200 $时, 流线分布图与电瑞利数$ T = 0 $时相似, 都出现了一个漩涡, 虽然在方腔顶部出现了两个次级涡, 但是库仑力还比较弱, 对流动和传热产生的贡献很小, 电荷只能在浮升力的影响下朝方腔顶部移动, 下方的电荷密度则会变小. 当电瑞利数$ T = 500 $时, 流线变得十分复杂, 不仅由一个漩涡分裂成两个漩涡, 而且方腔的4个角落均出现了4个小涡, 此时的库仑力急剧增加, 对流动和传热效率的影响大于浮升力, 因此引导电荷逐渐摆脱浮升力的束缚, 进而形成了上下对称的空电荷区, 此时温度的分布受到了库仑力的影响, 温度的热羽流与空电荷区形状相似. 当电瑞利数T继续增加到800和1200时, 流线中的上下两个漩涡都分别超过了分界线, 流体流动的平衡再次被打破, 由于强大的库伦力导致了对流变得十分不稳定, 空电荷区变大, 传热效率显而易见的增加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
电瑞利数(a) $ T = 0 $, (b) $ T = 200 $, (c) $ T = 500 $, (d) $ T = 800 $, (e) $ T = 1200 $时的电荷密度分布(上)、温度分布(中)和流线分布(下)图($ Ra = 1times10^{4} $, $ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



Figure
5.
The distributions of the charge density (top), temperature (middle) and streamlines (bottom) under different electrical Rayleigh number T. (a) $ T = 0 $, (b) $ T = 200 $, (c) $ T = 500 $, (d) $ T = 800 $, (e) $ T = 1200 $ ($ Ra = 1times10^{4} $, $ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片


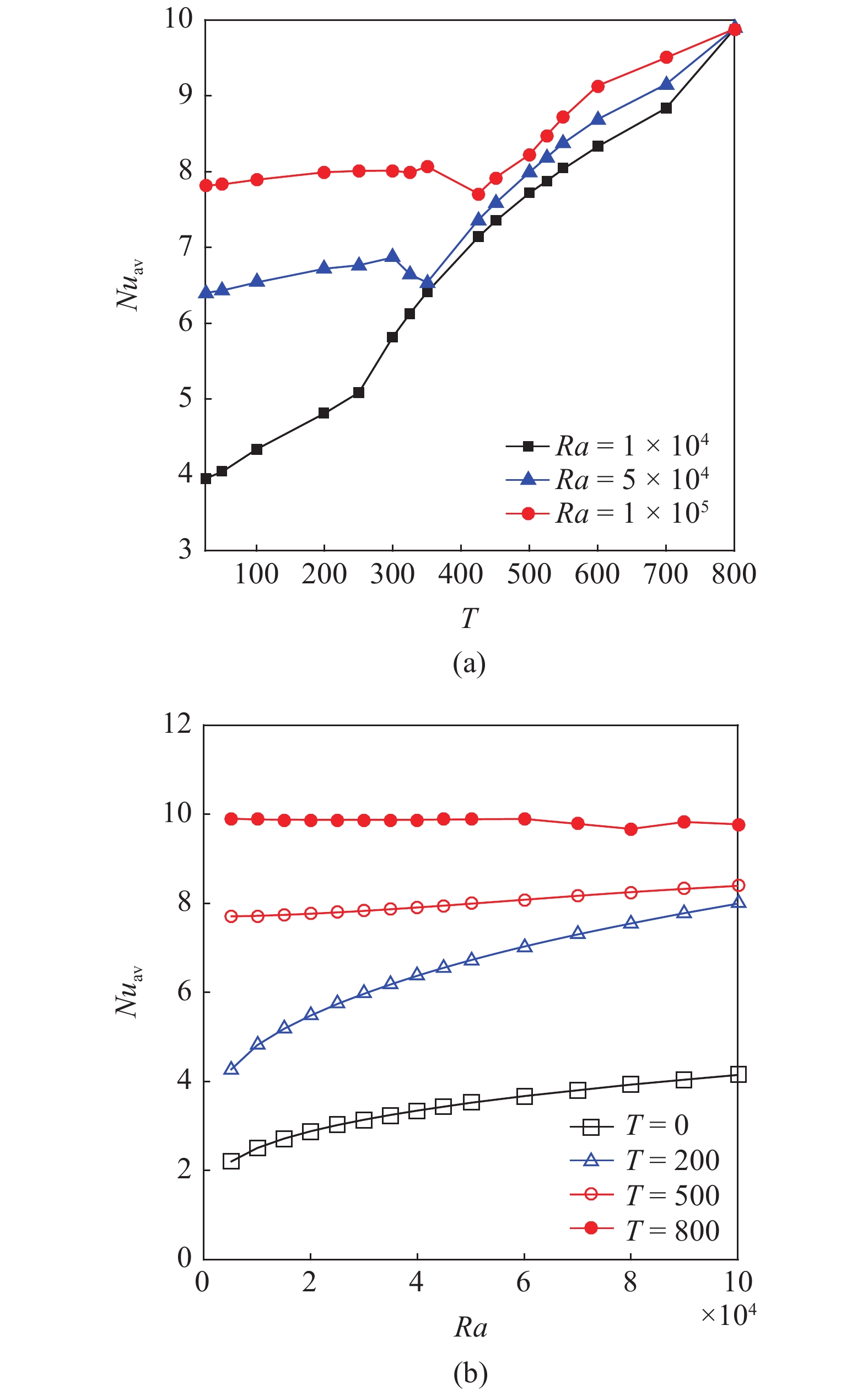
最后, 在图6(a)中, 给出了在热瑞利数$ Ra = $$ 1times 10^{4} $, $ 5times 10^{4} $, $ 1times 10^{5} $情况下的平均努塞特数$ Nu_{{
m{av}}} $随电瑞利数$ T $变化的曲线, 并固定其他无量纲参数$ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $. 通过上述分析, 知道电瑞利数$ T $是存在一个临界阈值$T_{{
m{c}}}$, 当电瑞利数$ T $超过该值时, $ Nu_{{
m{av}}} $会急剧增加. 在图6(a)中, 可以发现类似的现象, 热瑞利数$ Ra = 1times 10^{5} $时, 此时电瑞利数$ T $的临界阈值在400 ~ 500之间, 电瑞利数$ T $的取值超过500以后, $ Nu_{{
m{av}}} $会发生明显的变化.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
(a) 探究不同电瑞利数T下的平均努塞特数$Nu_{{
m{av}}}$的变化过程和(b) 探究不同热瑞利数$ Ra $下的平均努塞特数$Nu_{{
m{av}}}$的变化过程($ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



Figure
6.
(a) The distributions of the average Nusselt number $Nu_{{
m{av}}}$ vs. electrical Rayleigh number T under different Rayleigh number $ Ra $.(b) The distributions of the average Nusselt number $Nu_{{
m{av}}}$ vs. Rayleigh number $ Ra $ under different electrical Rayleigh number T ($ C = 10 $, $ M = 10 $, $ Pr = 10 $, $ h = 0.5H $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片


需要指出的是, 热瑞利数$ Ra = 5times 10^{4} $时, 电瑞利数$ T $在$ 300sim400 $之间出现的凹点是因为此区间内的库仑力和浮升力对腔体下半区域的对流影响相当, 加之二者所致的涡流方向在此区域又相反^[27], 如此二者相互竞争尤为激烈, 腔体内的总体能量减少(主要体现在动能上), 进而导致传热效率相对电瑞利数$Tleqslant 300$时略有降低, 从而出现凹点. 而当热瑞利数$ Ra = 10^4 $, 电瑞利数$ T = 300sim400 $时, 因此时浮升力相对库仑力的影响较小, 系统内库仑力影响绝对占优, 因此方腔内的传热效率随着电瑞利数$ T $的增加而增加, 从而也不会出现上述凹点. 当电瑞利数$ T $小于临界阈值$T_{{
m{c}}}$时, 浮升力的作用会增强系统的传热效率, 但是当电瑞利数$ T $大于临界阈值$T_{{
m{c}}}$以后, $Nu_{{
m{av}}}$的上升是由于库仑力增强导致的. 当电瑞利数$ T $足够大时, 因为库仑力在流动中发挥主导作用, 反观浮升力的影响可以忽略, 所以传热增强不再取决于热瑞利数$ Ra $, 可以看到3条曲线最后收敛为一个点. 在图6(b)中, 探究了不同电瑞利数$ T $值情况下, $Nu_{{
m{av}}}$随着热瑞利数$ Ra $的演化曲线, 当电瑞利数$ T $的取值大于500以后, 曲线的斜率是逐渐下降的, 这是库仑力在主导热传递引起的, 浮升力的影响在逐渐减弱, 特别是当电瑞利数$ T = 800 $时, 曲线几乎是水平的, $ Nu_{{
m{av}}} $的变化与热瑞利数$ Ra $的取值无关. 可以注意到, 与纯自然对流问题(电瑞利数$ T = 0 $)情况相比, $ Nu_{{
m{av}}} $显著增加, 当热瑞利数$ Ra = 1times10^{4} $时, 在电瑞利数$ T $的取值为500的情况下, 较于纯自然对流传热大约增强了$ 84.31% $, 说明加入电场后会强化传热. 在本节中, 探究了电热对流中的基本特征, 并加深了对电热对流中库仑力和浮升力共同作用下流体流动结构、温度分布以及电荷的运输机制的理解. 接下来, 会对其他无量纲参数进行研究.

5.2
电极板位置影响探究

本节中, 研究了电极板位置的影响. 图7描绘了电极板位置对在不同电瑞利数$ T $下的传热效率的影响, 其余各无量纲参数为$ Ra = 1times10^{4}$, $ C = 10$, $ Pr = $$ 10$, $ M = 10 $, $ h = 0.5H $. 其中, 当电瑞利数$ T = 800 $, 热瑞利数$ Ra = 1times10^{4} $时, 相比于浮升力, 库仑力影响绝对占优; 将加热壁面从下半区域$ (delta = 0.25H )$更改为上半区域$ (delta = 0.75H) $后, 浮升力变化带来的影响基本可以忽略, 此时系统传热效率主要由库仑力决定, 又因两种情况下流动结构以及库仑力分布等基本镜面对称, 从而$ T = 800 $时, 上下两种位置对应的传热效率基本重合. 另外, 当加热壁面处于中间位置($ delta = 0.5H $)时, 上下两部分的速度分布相对更加均匀, 流体流动速度比另外两个位置下的要大, 对流强度相对更强, 温度边界层也相对更薄, 因而此位置下的传热效率一般优于另外两种情况. 另外, 在$0leqslant $$ Tleqslant 225$区间, 电极板在上半区域时$( delta = 0.75H) $的$Nu_{{
m{av}}}$小于在下半区域时$( delta = 0.25H )$的$Nu_{{
m{av}}}$. 在图7中画出了电瑞利数$ T = 200 $时, $ A $和$ B $两点处的平均努塞特数变化曲线图, 可以看出$ B $点处的对流十分不稳定, 这也说明库仑力和浮升力竞争相较于A点处更加激烈, 并在极大程度上影响了系统的传热效率, 因此$ delta = 0.75H $时的传热效率低于$ delta = 0.25H $时的传热效率, 但是随着电瑞利数$ T $的取值继续增加, 库仑力在对流中的影响增强, 当电瑞利数$ T = 800 $时, 库仑力占据绝对优势, 此时系统的传热效率与热瑞利数$ Ra $无关, 所以两个位置重合. 最后, 在电瑞利数$ T = 200 $到$ T = 300 $之间, 3条曲线分别出现了一个临界阈值, 这与图6(a)中热瑞利数$ Ra = 1times 10^{4} $时出现的临界阈值范围相同.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
电极板在不同位置下, 随着电瑞利数$ T $增加, 平均努塞特数$Nu_{{
m{av}}}$的变化曲线 ($ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



Figure
7.
The distributions of the average Nusselt number $Nu_{{
m{av}}}$ vs. electrical Rayleigh number $ T $ under different heating locations $ delta $ ($ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



下载:
全尺寸图片
幻灯片


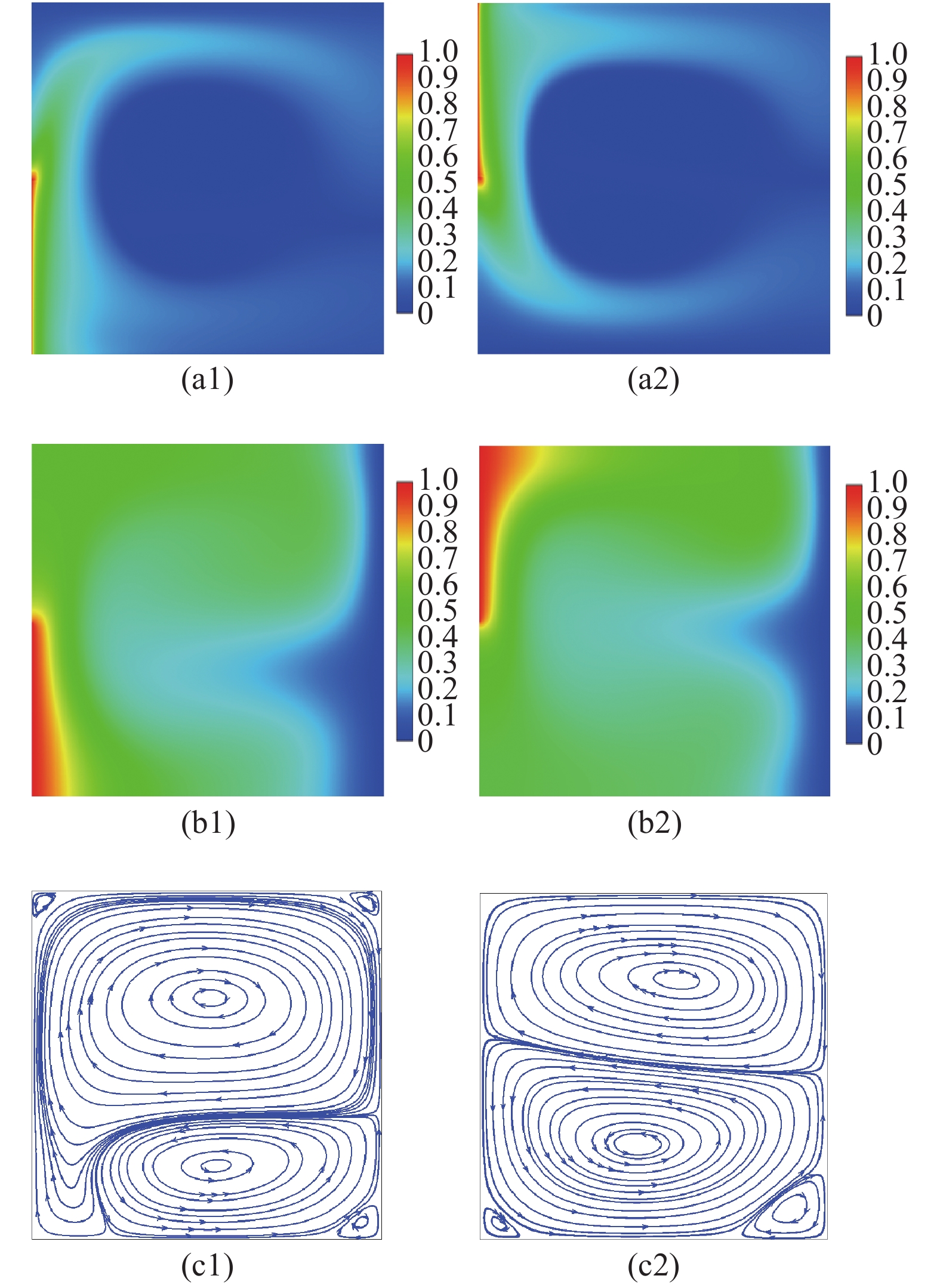
如图8所示, 画出了当电瑞利数$ T = 250 $时, $ delta = 0.25H $和$ delta = 0.75H $时的电荷密度分布、温度分布和流线分布图. 在这两种情况下, 电荷密度分布图中都出现了空电荷区, 根据在5.1节中的分析, 可以知道, 此时的库仑力增大并与浮升力相互竞争, 通过观察和分析两种情况下的流线分布(图8(c1)和图8(c2)), 当电极板在下半区域时, 由于库仑力增强, 导致了下部分对流减弱, 并且图8(c1)下部分的漩涡比图8(c2)的漩涡小, 因此系统的传热效率也降低了. 所以从图7中可以发现电极板在上半区域的$ Nu_{{
m{av}}} $高于在下半区域时的$ Nu_{{
m{av}}} $, 并且在之后的发展中一直保持(即使差异会越来越小).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
电极板在上半区域和下半区域时的电荷密度分布图(上)、温度分布图(中)和流线分布图(下) ($ T = 250 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



Figure
8.
The distributions of the charge density (top), temperature (middle) and streamlines (bottom) as the electrode plate is at the top and bottom positions ($ T = 250 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



下载:
全尺寸图片
幻灯片


图9给出了电瑞利数$ T = 800 $时, 电极板在下半区域图9(a), 中间图9(b), 上半区域图9(c)位置时的电荷密度分布、温度分布和流线分布图. 可以看到在电荷分布图中都形成了一个很明显的空电荷区, 此时的库仑力在流动过程中占据主导地位. 当电极板在上半区域和下半区域时, 库仑力分布不均匀, 从而导致速度大小分布不均匀. 电极板在下半区域时, 下半部分的速度大小会比上半部分的小, 因此方腔下半部分的热量转移相比上半部分的热量转移要少, 从温度分布图中的热羽的形状也可以发现靠近壁面的温度边界层变厚. 无论是电极板在上半区域还是在下半区域, 与电极板在中间时相比, 都会使得靠近壁面一侧的温度梯度降低, 从而传热效率变低. 通过以上分析说明了当电极板放在中间位置时, 传热效率最佳. 另外, 电极板在上半区域和下半区域时的漩涡结构类似, 这也说明了为什么传热效率会随着电瑞利数$ T $的取值增加而最终接近. 通过对比图8和图9中的电荷密度分布, 可以发现电荷分布会受到库仑力和浮升力的影响, 当电瑞利数$ T $的取值很小时, 库仑力较弱, 左壁面的电荷会由于浮升力作用向上壁面运动, 而在右壁面一定范围内的电荷向下运动后, 接着会沿着下壁面向左壁面流动, 从而形成一个顺时针的对流. 虽然库仑力始终向右并会对下部分一定区域的对流造成阻碍, 但是电瑞利数$ T $的取值很小, 浮升力大于库仑力, 因此流动的方向仍然和在浮升力影响下的方向一致. 但是随着电瑞利数$ T $的取值增加, 库仑力逐渐增加, 流动的方向逐渐受到库仑力的影响, 最终的对流方向会被库仑力主导, 这也可以从图9中的温度分布图中的热羽形状和电荷分布形状相似看出.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
电极板在(a)下半区域, (b)中间, (c)上半区域, 电荷密度分布(左)、温度分布(中)和流线分布(右)图 ($ T = 800 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



Figure
9.
The distributions of the charge density (left), temperature (middle) and streamlines (right) as the electrode plate is at the top, middle and bottom positions ($ T = 800 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ h = 0.5H $)



下载:
全尺寸图片
幻灯片

5.3
电极板长度影响探究

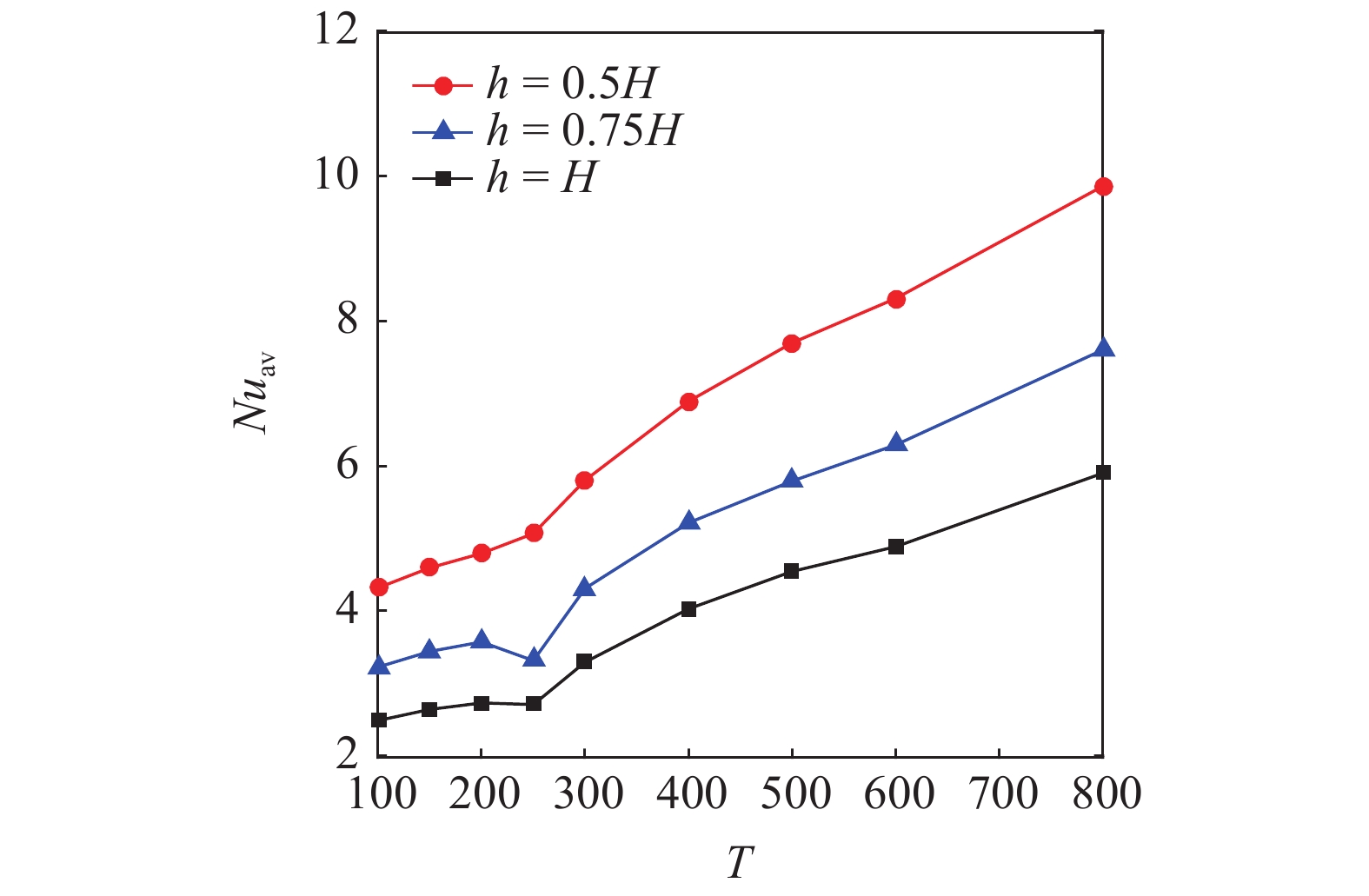
本节中, 考虑了电极板长度$ h $对传热的影响, 相应的数据结果如图10所示, 其余各无量纲参数为$ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $. 从图10中可以看出, 对于给定的电瑞利数$ T $, 传热效率会随着电极板的长度增加而降低, 并且3种情况下电瑞利数$ T $的临界阈值都在$ 200sim300 $之间, 在大于临界阈值以后, 它们的变化趋势十分相似, 再结合上一节中的临界阈值, 发现电极板长度$ h $和位置$ delta $对临界阈值的范围影响不大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
电极板长度不同时, 随着电瑞利数$ T $增加, 平均努塞特数$Nu_{{
m{av}}}$的变化曲线 ($ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



Figure
10.
The distributions of the average Nusselt number $Nu_{{
m{av}}}$ vs. electrical Rayleigh number $ T $ under different length of electrode plate $ h $ ($ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片


分别画出了电瑞利数$ T = 250 $(图11)和电瑞利数$ T = 300 $(图12)时的电荷密度分布、温度分布和流线分布图. 在图11中, 随着电极板的长度增加, 温度分布图中的热羽流变小至一半并类似于纯自然对流(电瑞利数$ T = 0 $), 空电荷区向下移动并逐渐远离电极板, 从流线分布图中可以看出下方的一级漩涡最终退化为次级漩涡, 下方的对流由有序逐渐变为无序, 从而整体的传热效率逐渐下降. 又如图12所示, 当电瑞利数$ T = 300 $时, 此时的库仑力在与浮升力的竞争中占据了优势, 并且在方腔的中心区域形成了空电荷区. 但是随着电极板两端的增加, 电场力减弱, 热壁面的速度下降, 无法将更多的热量转移到介电液体中, 同时热壁面的温度边界层变厚, 温度梯度降低, 因此传热效率会随着电极板的长度增加而降低.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
不同长度下, (a) $ h = 0.5H $, (b) $ h = 0.75H $, (c) $ h = H $, 电荷密度分布图(左)、温度分布图(中)和流线分布图(右) ($ T = 250 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



Figure
11.
The distributions of the charge density (left), temperature (middle) and streamlines (right) under different length of electrode plate. (a) $ h = 0.5H $, (b) $ h = 0.75H $, (c) $ h = H $ ($ T = 250 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-12.jpg'"
class="figure_img
figure_type2 ccc " id="Figure12" />



图
12
不同长度下, (a) $ h = 0.5H $, (b) $ h = 0.75H $, (c) $ h = H $, 电荷密度分布图(左)、温度分布图(中)和流线分布图(右) ($ T = 300 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



Figure
12.
The distributions of the charge density (left), temperature (middle) and streamlines (right) under different length of electrode plate. (a) $ h = 0.5H $, (b) $ h = 0.75H $, (c) $ h = H $ ($ T = 300 $, $ Ra = 1times10^{4} $, $ C = 10 $, $ Pr = 10 $, $ M = 10 $, $ delta = 0.5H $)



下载:
全尺寸图片
幻灯片

5.4
无量纲离子迁移率和普朗特数的联合影响

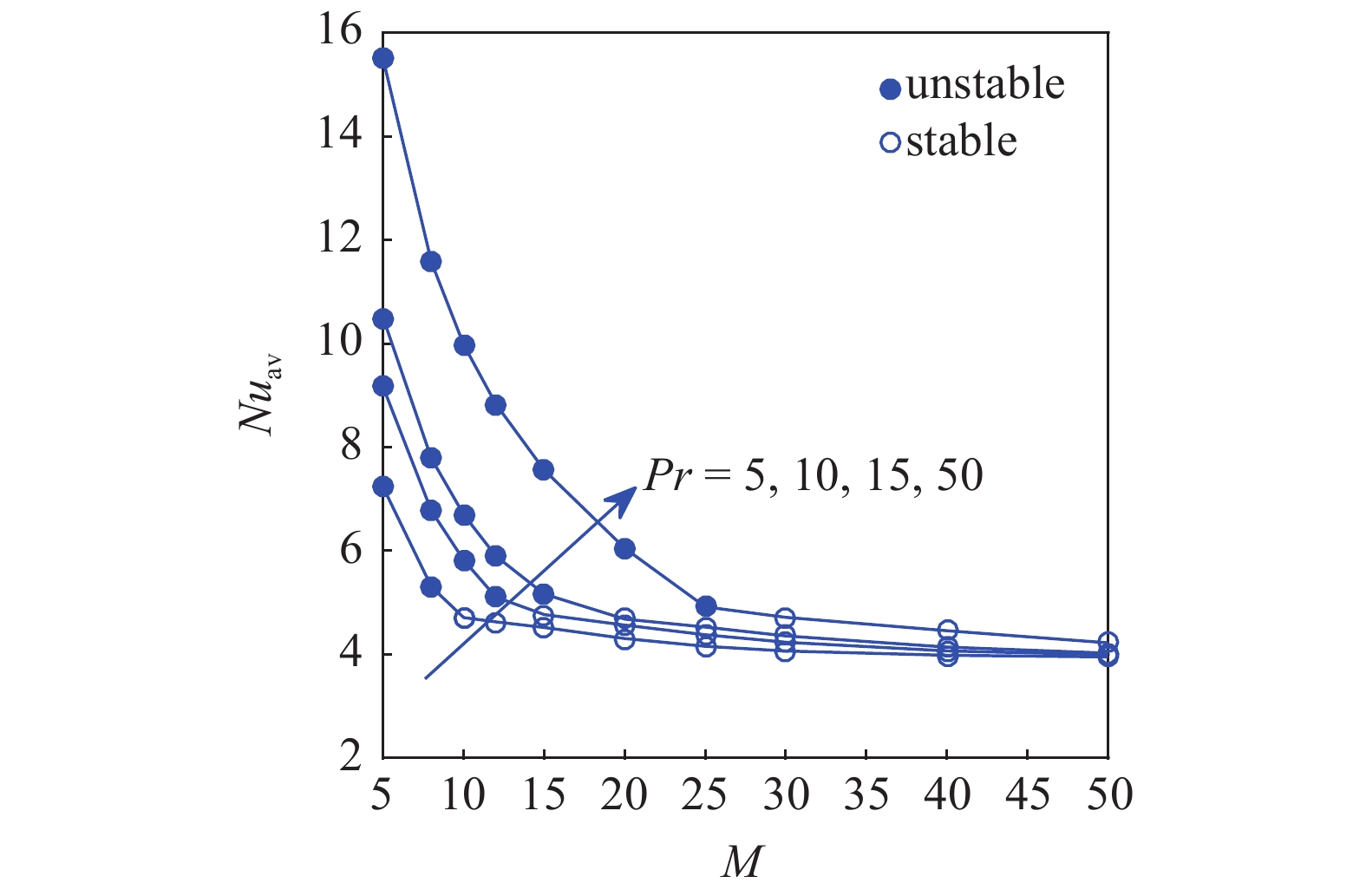
如图13所示, 还研究了无量纲离子迁移率$ M $和普朗特数$ Pr $的联合影响, 其余无量纲参数为$ Ra = 1times10^{4} $, $ T = 300 $, $ C = 10 $, $ delta = 0.5H $, $ h = 0.5H $. 从图13可以看出在给定$ Pr $的情况下, 随着$ M $的增加, 平均努塞特数$ Nu_{{
m{av}}} $会从一开始的急剧下降转变为趋势平缓的情况. $ M $越小, $ Nu_{{
m{av}}} $会随着$ Pr $增加而增加, 当$ M $很大时($ M = 50 $), $ Nu_{{
m{av}}} $几乎保持不变. 事实上, 如文献[9]指出, $ M $的大小决定了静电方程组与Navier–Stokes方程组的耦合紧密程度, $ M $越大, 两个方程组的耦合程度越弱, 进而库仑力对流场的作用减弱. 另外, 不同的$ M $和$ Pr $数的流体流动状态也存在一定差异, 主要分为稳态和非稳态, 具体可见图13中的标记.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
固定普朗特数Pr, 在不同无量纲离子迁移率M下, 平均努塞特数$ Nu_{{
m{av}}} $的变化曲线 ($ Ra = 1times10^{4} $, $ T = 300 $, $ C = 10 $, $ delta = 0.5H $, $ h = 0.5H $)



Figure
13.
The distributions of the average Nusselt number $ Nu_{{
m{av}}} $ vs. dimensionless ion mobility $ M $ under different Prandtl number $ Pr $ ($ Ra = 1times10^{4} $, $ T = 300 $, $ C = 10 $, $ delta = 0.5H $, $ h = 0.5H $)



下载:
全尺寸图片
幻灯片


最后, 取图13中$ Pr = 50 $的曲线肘部处和端点处的值即$ M = 25 $, $ M = 30 $和$ M = 50 $, 画出这3点处的电荷密度分布、温度分布和流线分布图, 如图14所示, 当$ M = 25 $和$ M = 30 $时, 空电荷区会变得不明显, 还会偏移中心向下且远离电极板, 这都说明库仑力的影响在减弱, 而且流线分布图中的漩涡结构的差异更加明显, 由两个反向旋转的漩涡变成了一个漩涡结构, 这不仅减弱了对流而且破坏了有序的对流结构, 因此降低了系统的传热效率. 当$ M = 50 $时, 差异会变得十分明显, 虽然离子迁移率增加导致大量电荷注入到方腔中, 但是两方程组的耦合程度减弱, 库仑力减弱导致系统的对流减弱. 所以当$ M $越大时, 系统的传热效率反而会减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-205-14.jpg'"
class="figure_img
figure_type2 ccc " id="Figure14" />



图
14
不同M值下的电荷密度分布(左)、温度分布(中)和流线分布(右)图. (a) $ M = 25 $, (b) $ M = 30 $, (c) $ M = 50 $ ($ Pr = 50 $,$ Ra = 1times10^{4} $, $ T = 300 $, $ C = 10 $, $ delta = 0.5H $, $ h = 0.5H $)



Figure
14.
The distributions of the charge density (left), temperature (middle) and streamlines (right) under different dimensionless ion mobility $ M$. (a) $ M = 25 $, (b) $ M = 30 $, (c) $ M = 50 $ ($ Pr = 50 $,$ Ra = 1times10^{4} $, $ T = 300 $, $ C = 10 $, $ delta = 0.5H $, $ h = 0.5H $)



下载:
全尺寸图片
幻灯片

6.
结 论

本文采用了格子Boltzmann方法对二维局部受热腔体结构中电热对流问题进行模拟, 首先对系统的传热效率、流体流动以及电热对流的分岔结构进行了分析, 对在库仑力和浮升力共同作用下流体的流动、温度的分布以及电荷的运输机制有了初步理解, 然后探究了电极板的位置和长度的影响, 最后探讨了无量纲离子迁移率$ M $和普朗特数$ Pr $的联合影响. 根据以上研究中呈现的数值结果, 主要结论如下:

(1) 固定热瑞利数$ Ra $, 平均努塞特数$ Nu_{{
m{av}}} $会随着电瑞利数T的增加而增加, 这主要是由于库仑力增强导致的. 当电瑞利数$ T $超过临界阈值($T_{{
m{c}}}$, $Pr = $$ 10$, $M = 10$)后, $ Nu_{{
m{av}}} $会急剧增加, 并且热瑞利数$ Ra $越大, 临界阈值也会增加. 通过稳定性分析可以发现, 电瑞利数$ T $会存在一个亚临界点$T_{{
m{f}}}$, 然而热瑞利数$ Ra $不会出现分岔结构, 会表现为超临界特征. 另外, 当电瑞利数$ T $足够大时, 库仑力占据绝对优势, 浮升力对传热的影响减弱, $ Nu_{{
m{av}}} $的值不再依赖于热瑞利数$ Ra $.

(2) 传热效率很大程度上受到电极板位置的影响, 并且在中间位置时的传热效率最佳, 这主要是由于电极板在中间位置时的对流最强导致的.

(3) 传热效率会随着电极板的长度增加而降低, 这主要是由于电极板长度增加以后, 方腔底部的对流减弱, 从而导致传热效率降低.

(4) 当$ M $越大时, 系统的传热效率越低, 这是因为随着$ M $的增加, 库仑力会对流场的影响减弱, 从而导致对流减弱和传热效率降低.