引言

作为泡沫金属的典型代表, 闭孔泡沫铝具有轻质、高比刚度、高比强度等优良特性^[1], 是一种理想的减重、吸能材料, 在航空航天、交通运输、建筑工程、机械制造等领域展现出巨大的应用潜力. 因此, 研究闭孔泡沫铝的压缩变形机理、能量吸收特性等具有十分重要的工程意义.

在闭孔泡沫铝的有限元数值分析中, ****们提出了多种代表性体积单元(representative volume element, RVE)^[2], 用以表征闭孔泡沫铝复杂胞孔结构的细观构型. 总体上, 现有的细观模型可以分为3类, 球体几何模型(geometric model)^[2-3]、结构模型(structural model)^{[2, 4-5]}和离散模型(discrete model, 也称逆向重构模型)^{[2, 6]}. 作为结构模型的代表, 3D-Voronoi随机模型既可以反映低相对密度闭孔泡沫铝内部的复杂构造, 又具有较高的计算效率, 因此被广泛应用于闭孔泡沫铝的有限元仿真分析中^[7-13].

在闭孔泡沫铝的唯象本构模型中, 泊松比是一个非常关键的参数. 有限元软件LS-DYNA 内置的154#模型^[14-16], 有限元软件ABAQUS内置的各向同性强化可压缩模型(crushable foam model with isotropic hardening)^[17], Deshpande和Fleck^[18]提出的自相似模型(self-similar model), Miller模型^[19]和Chen-Lu模型^[20]均涉及此参数. 然而, 在应用中上述模型均假定闭孔泡沫铝压缩过程中泊松比为一个常数. 实际泊松比的取值是否可以假设为一个常数, 这个常数怎样取值仍是有待研究的课题. Bi^[21]、张健等^[6]、张乐等^[22]及Fang等^[23]均对闭孔泡沫铝泊松比的变化规律、取值方式及其对本构模型的影响进行了研究.

已有的研究中, 对于闭孔泡沫铝的泊松比变化规律, 存在两种观点: (1)随着轴向压缩应变的增大, 泊松比呈现出“增高?降低?再增高”的“S”型变化过程, 且再增高阶段起始于闭孔泡沫铝密实阶段的起始应变; (2)随着轴向压缩应变的增大, 泊松比呈现出先增高, 再降低的变化过程, 并逐渐趋近于0. 这两种观点的分歧在于闭孔泡沫铝进入致密化阶段后泊松比的变化情况. 张建等^[6]基于逆向重构模型的研究, 张乐等^[22]基于实体单元Kelvin模型的研究, 均支持观点(1); 王长峰等^[24]、Zhu等^[25]基于3D-Voronoi模型的研究则支持观点(2). 此外, 对于闭孔泡沫铝泊松比变化规律中特征点(极大值点)的物理意义尚不明确.

毋庸置疑, 探究闭孔泡沫铝泊松比变化规律的分歧, 认识闭孔泡沫铝泊松比变化规律中特征点的物理意义, 是进一步研究闭孔泡沫铝本构关系的重要切入点, 对完善闭孔泡沫铝本构体系至关重要. 为了明确闭孔泡沫铝泊松比的变化规律及特征点(极大值)的物理意义, 研究闭孔泡沫铝三轴压缩应力状态下的变形模式, 本文采用数值分析方法, 利用表征闭孔泡沫铝细观结构的2D-Voronoi模型及3D-Voronoi模型, 对其进行侧面位移耦合单轴压缩及侧面位移受限轴向压缩分析. 研究结果明确了闭孔泡沫铝的泊松比变化规律及特征点物理意义, 确定了闭孔泡沫铝三轴压缩应力状态下的变形模式, 对后续闭孔泡沫铝唯象本构模型的研究具有重要意义.

1.
有限元模型与边界条件

借助开源软件Neper^[26]及有限元软件ANSYS, 构建闭孔泡沫铝3D-Voronoi及2D-Voronoi的几何模型, 将几何模型导入有限元软件ABAQUS/Explicit中, 赋予材料参数, 进行仿真分析.

1.1
闭孔泡沫铝的建模

闭孔泡沫铝的3D-Voronoi几何模型如图1所示, 模型尺寸为20 mm × 20 mm × 20 mm, 包含343个(7³)胞孔.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
3D-Voronoi几何模型



Figure
1.
3D-Voronoi geometrical model



下载:
全尺寸图片
幻灯片


闭孔泡沫铝的2D-Voronoi几何模型如图2所示, 模型尺寸为20 mm × 20 mm × 0.10 mm, 包含92个(介于9²与10²)胞孔. 2D-Voronoi模型相当于3D-Voronoi模型的断层扫描切片.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
2D-Voronoi几何模型



Figure
2.
2D-Voronoi geometrical model



下载:
全尺寸图片
幻灯片


基于相关的研究结论^{[4, 10-11, 13, 27]}及课题组已有的工作^{[5, 7, 22]}, 所构建的3D-Voronoi模型及2D-Voronoi模型的宏观几何尺寸及各方向上的胞孔数目均满足代表性体积单元(RVE)的要求^[2].

假定闭孔泡沫铝孔壁厚度均匀, 其相对密度${
ho _{
m{r}}}$可表示为

$$ { ho }_{ m{r}}=frac{ ho }{{ ho }_{ m{s}}}={h {displaystyle sum _{i=1}^{n}{A}_{i}}}Biggr/{V}$$

(1)

式中, ${
ho _s}$为泡沫铝孔壁材料的密度; $
ho $为泡沫铝密度; $V$为模型体积; ${A_i}$为第i个孔壁的面积; h为孔壁的厚度.

模型的相对密度均取值0.2, 依据式(1)计算各模型的孔壁厚度. 壳单元3D-Voronoi模型(仅使用壳单元, 后文简称3D-Voronoi模型)及壳单元2D-Voronoi模型的孔壁厚度在截面属性中设置, 实体单元2D-Voronoi模型的孔壁厚度在几何建模时考虑. 为了控制变量, 几何建模过程中已经适当调整模型的胞孔数目, 使所有模型的孔壁厚度取值相同.

3D-Voronoi模型及壳单元2D-Voronoi模型均采用壳单元中的S3R单元及S4R单元, 实体单元2D-Voronoi模型采用实体单元中的C3D8R单元及C3D6单元. 结合课题组已有工作经验及网格敏感性分析, 发现3D-Voronio模型、壳单元2D-Voronoi模型及实体单元2D-Voronoi模型的单元特征长度依次取值0.14 mm, 0.10 mm及0.10 mm时, 仿真结果已经具有较好的收敛性, 进一步细分网格所得到的结果变化甚微, 此时模型的单元数目依次为402 271个, 3431个及7022个.

接触设置均采取通用接触, 摩擦系数0.02.

1.2
模型边界条件设置及对应问题

研究采用两种边界条件: 侧面位移耦合单轴压缩和侧面位移受限轴向压缩.

1.2.1
侧面位移耦合单轴压缩

图3为3D-Voronoi模型的侧面位移耦合单轴压缩示意图. 模型被放置在两块平行的解析刚性板之间, 底部刚性板固定, 顶部刚性板沿Y轴负方向以恒定速度对模型进行准静态压缩. 分别耦合4个侧面的法向位移, 保证模型每个侧面节点的法向位移相等. 这种边界条件相当于对无限大的平板进行压缩, 可以消除模型的边界效应. 3D-Voronoi模型的侧面位移耦合单轴压缩用于分析闭孔泡沫铝泊松比变化规律特征点(极大值点)的物理意义.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
3D-Voronoi模型侧面位移耦合单轴压缩示意图



Figure
3.
Lateral displacement coupled uniaxial compression of 3D-Voronoi model



下载:
全尺寸图片
幻灯片


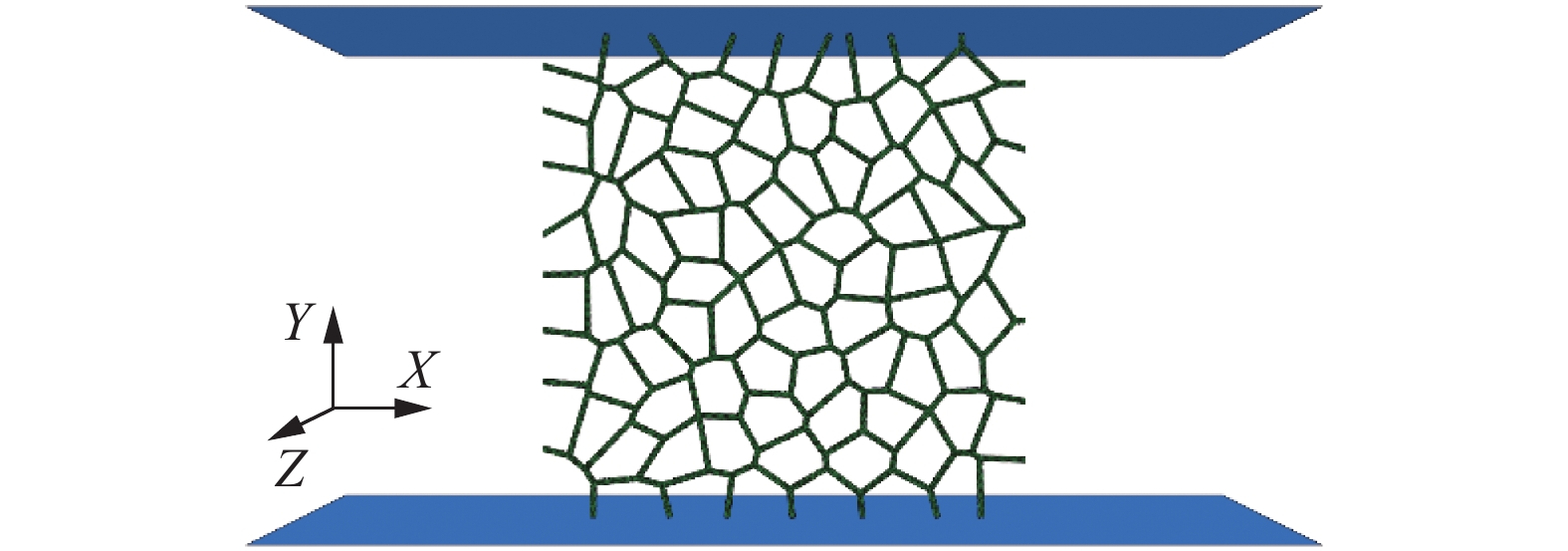
壳单元2D-Voronoi模型与实体单元2D-Voronoi模型的边界条件相同. 图4所示为2D-Voronoi模型的侧面位移耦合单轴压缩示意图. 2D-Voronoi模型可以看作3D-Voronoi模型的断层扫描切片, 其边界条件设置与3D-Voronoi模型相似. 耦合左、右两个侧面沿X轴方向的位移, 并通过约束, 使模型在Z轴方向的位移与应变均为零. 壳单元2D-Voronoi模型及实体单元2D-Voronoi模型的侧面位移耦合单轴压缩用于分析闭孔泡沫铝致密化阶段泊松比变化趋势.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
2D-Voronoi模型侧面位移耦合单轴压缩示意图



Figure
4.
Lateral displacement coupled uniaxial compression of 2D-Voronoi model



下载:
全尺寸图片
幻灯片

1.2.2
侧面位移受限轴向压缩

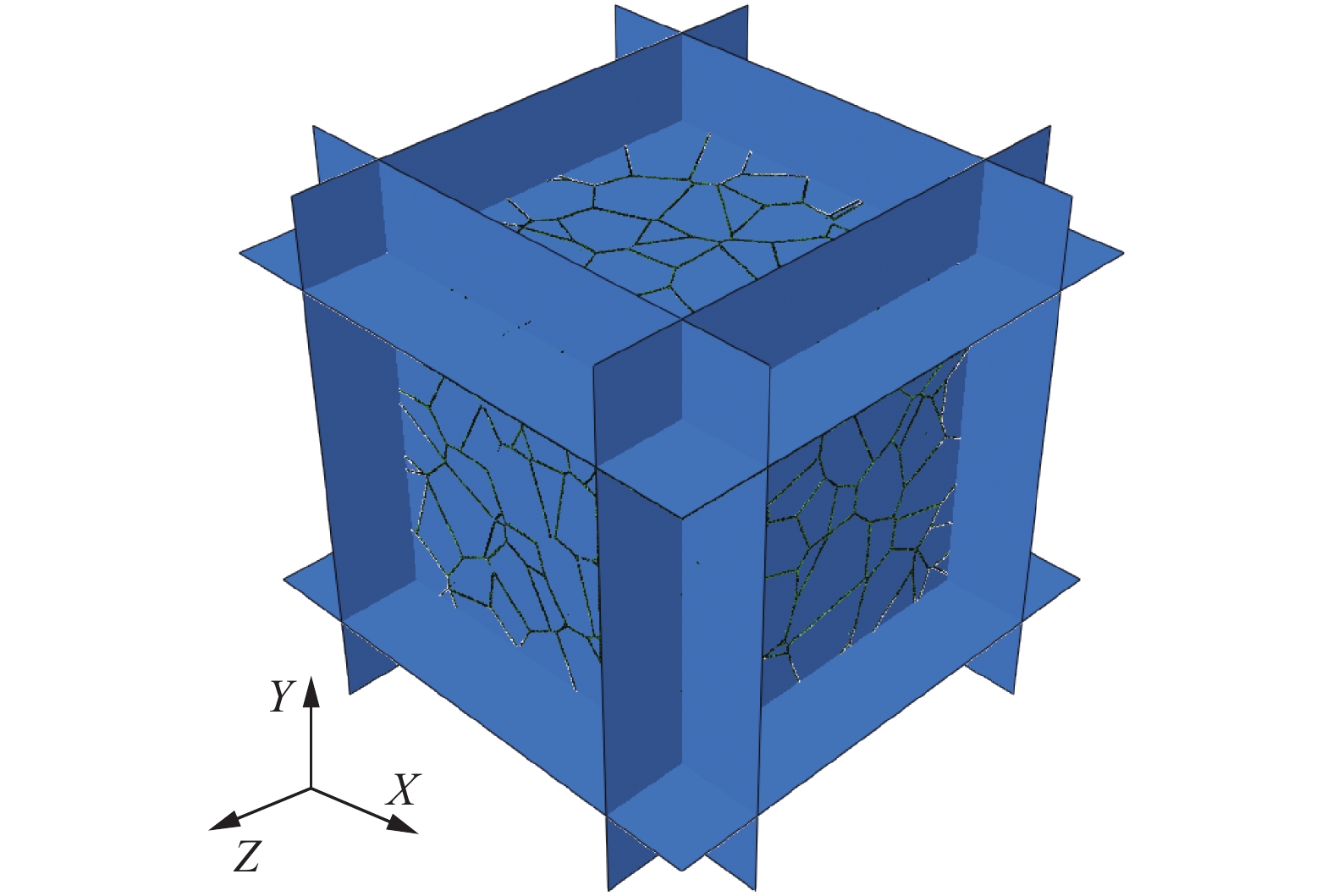
图5 为3D-Voronoi模型的侧面位移受限轴向压缩示意图. 在此边界条件下, 模型被6个垂直于坐标轴的解析刚性板包裹, 顶部刚性板沿Y轴负方向以恒定速度对模型进行准静态压缩, 其余5个刚性板固定. 侧面位移受限轴向压缩时, 第二主应力${sigma _2}$与第三主应力${sigma _3}$近似相等. 此边界条件是闭孔泡沫铝这类体积可压缩材料独有的一种应力状态. 3D-Voronoi模型的侧面位移受限轴向压缩用于分析闭孔泡沫铝三轴等比压缩下的变形模式.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
3D-Voronoi模型侧面位移受限轴向压缩示意图



Figure
5.
Lateral displacement limited axial compression of 3D-Voronoi model



下载:
全尺寸图片
幻灯片

2.
数值计算结果分析

2.1
泡沫铝致密化阶段泊松比变化规律

2D-Voronoi模型相当于3D-Voronoi模型的断层扫描切片, 便于观察胞孔结构的变形, 因此选用2D-Voronoi模型研究闭孔泡沫铝致密化阶段的泊松比变化规律. 2D-Voronoi模型闭孔泡沫铝泊松比的表达式如下

$$nu = - frac{{{varepsilon _x}}}{{{varepsilon _y}}}$$

(2)

式中, ${varepsilon _x}$, ${varepsilon _y}$依次为模型X轴与Y轴方向的真实应变.

闭孔泡沫铝致密化阶段的起始应变通过吸能效率(energy absorption efficiency)${eta _{
m{E}}}$确定^[28], 即吸能效率曲线极值点所对应的应变为闭孔泡沫铝压缩致密化的起始应变(onset of densification)^[28], 用符号$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$表示. 吸能效率的表达式如下

$${eta _{ m{E}}}left( varepsilon ight) = {{displaystyleint_0^varepsilon {sigma left( varepsilon ight){ m{d}}varepsilon } }}Bigr/{{sigma left( varepsilon ight)}}$$

(3)

研究结果^{[7, 29-31]}发现, 常规的壳单元(也称薄壳单元)接触过程中具有厚度减薄(thickness reduction)的特性, 不能反映较大压缩量时材料孔壁厚度上的堆叠^[29-30], 由此推测常规壳单元接触过程中的厚度减薄特性是研究人员对闭孔泡沫铝致密化阶段的泊松比变化规律结论存在分歧的原因.

壳单元2D-Voronoi模型、实体单元2D-Voronoi模型的仿真结果验证了这一推测.

基于泊松比变化规律分歧, 针对性地选取致密化起始应变$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$邻域内的泊松比曲线进行分析.

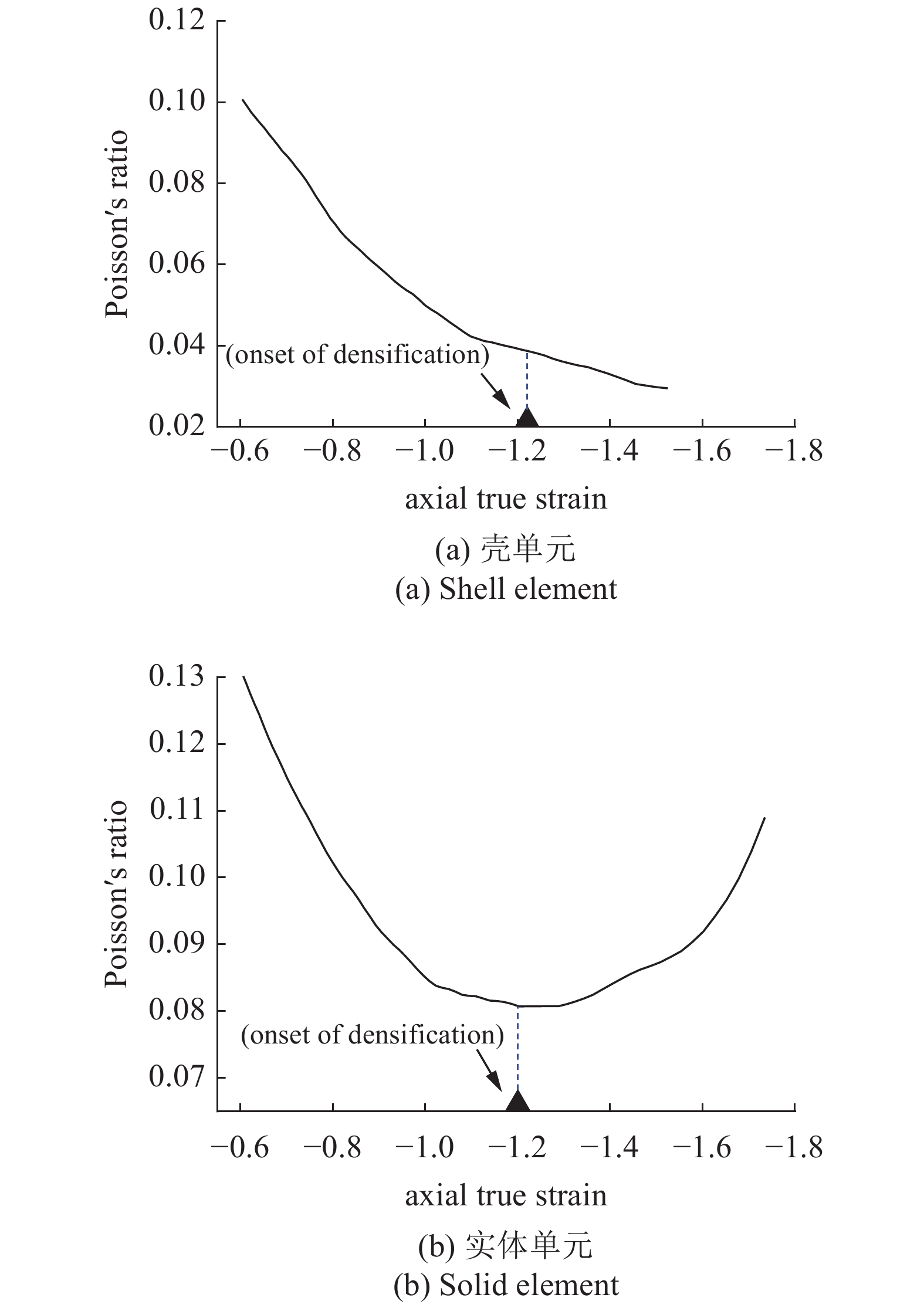
图6为壳单元2D-Voronoi模型与实体单元2D-Voronoi模型致密化的起始应变邻域内的泊松比-轴向真实应变曲线, 并于应变轴上标注由${eta _E}$确定的致密阶段起始应变. 如图6(a)所示, 壳单元2D-Voronoi模型得出观点(1)所表述的规律; 如图6(b)所示, 实体单元2D-Voronoi模型得出观点(2)所表述的规律.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
2D-Voronoi模型致密起始应变邻域内泊松比曲线



Figure
6.
Poisson’s ratio curves in neighborhood of onset of densification of 2D-Voronoi model



下载:
全尺寸图片
幻灯片


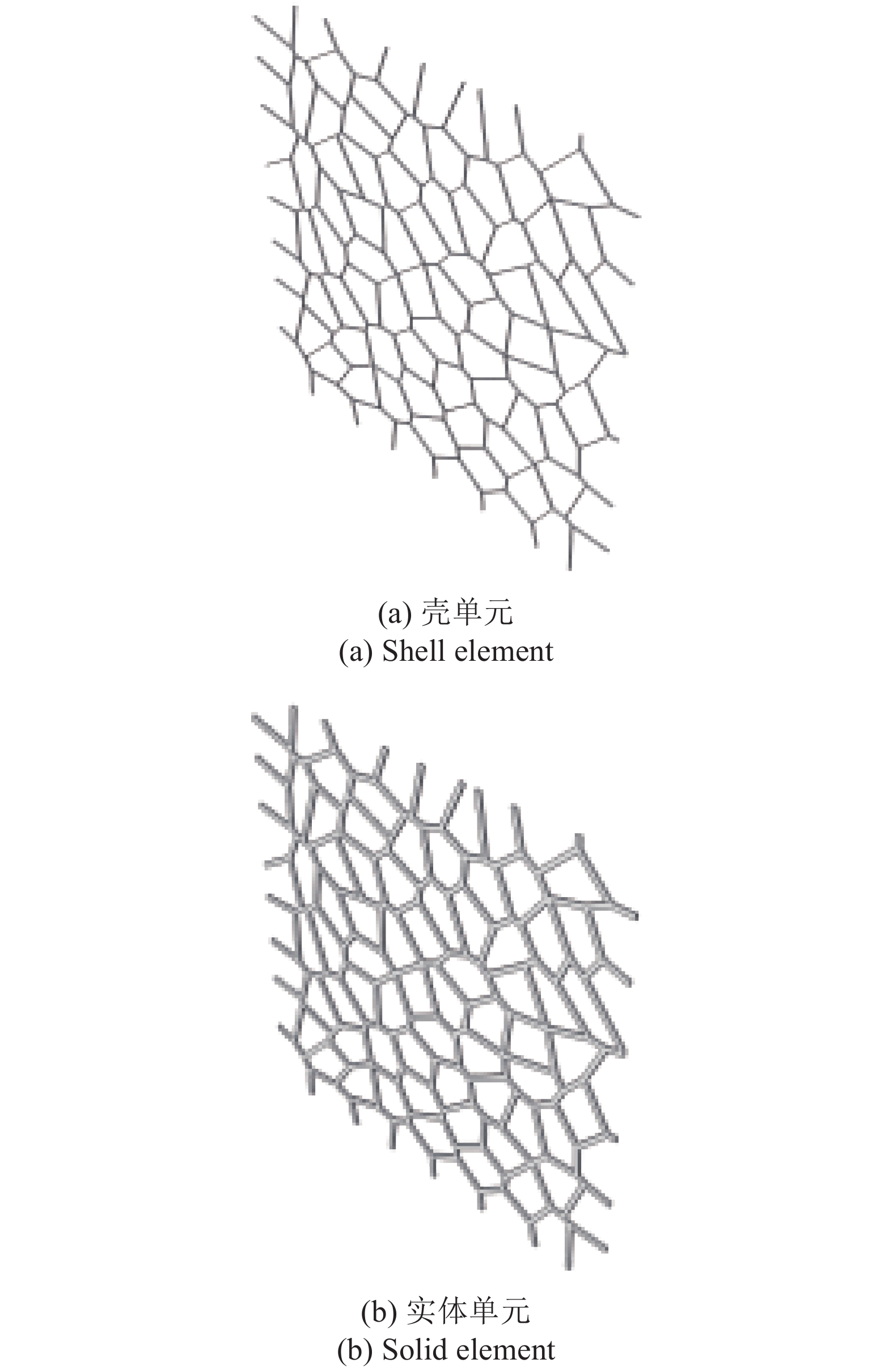
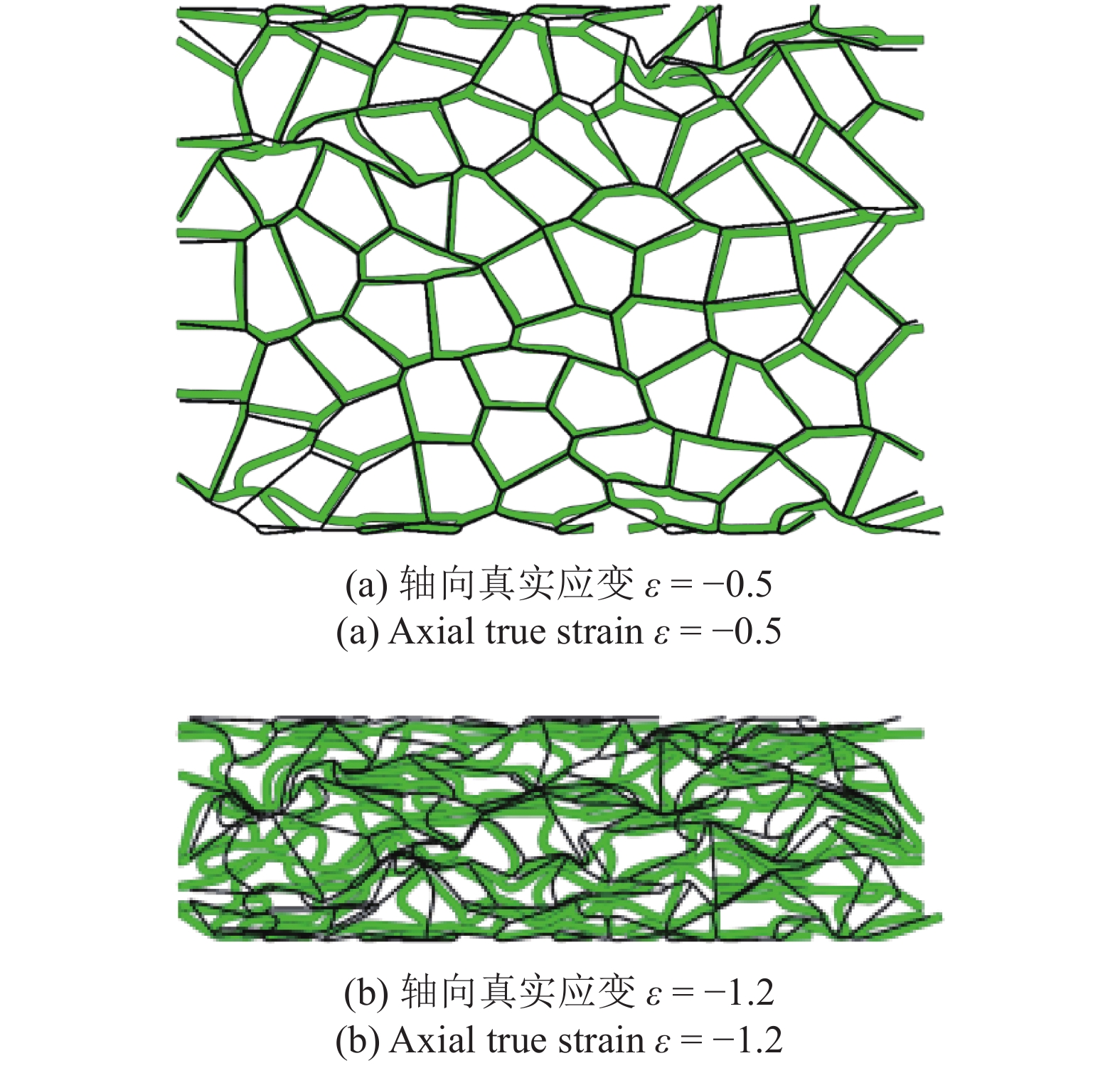
图7为2D-Voronoi模型的胞孔结构变形图, 其中, 黑色线框表示壳单元2D-Voronoi模型的胞孔变形情况, 绿色截面表示实体单元2D-Voronoi模型的胞孔变形情况. 由图7(a)可知, 模型致密化之前, 孔壁厚度方向上的堆叠并不显著, 因此壳单元2D-Voronoi模型与实体单元2D-Voronoi模型的胞孔结构变形基本是一致的; 但是, 当应变达到致密化起始应变点时, 如图7(b)所示, 孔壁厚度方向上堆叠明显, 二者胞孔结构变形产生巨大的差异. 显然, 实体单元2D-Voronoi模型能准确反映闭孔泡沫铝致密化阶段胞孔充分坍塌造成的孔壁堆叠.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
2D-Voronoi模型胞孔结构变形图



Figure
7.
Cellular structure deformation of 2D-Voronoi model



下载:
全尺寸图片
幻灯片


由图6及图7可知, 壳单元Voronoi模型致密化起始应变$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$之后的泊松比数据是无效的, 因此, 对应变区间$left( {0,varepsilon _{{
m{E - max}}}^{{
m{uni}}}}
ight]$内的数据进行误差分析, 以量化壳单元厚度减薄对误差的影响, 修正误差$delta ({varepsilon _y})$的表达式如下

$$delta ({varepsilon _y}) = alphafrac{{{nu _{{ m{Solid}}}} - {nu _{{ m{Shell}}}}}}{{{nu _{{ m{Solid}}}}}} times 100% $$

(4)

式中, ${nu _{{
m{Solid}}}}$为实体单元2D-Voronoi模型的泊松比, ${nu _{{
m{Shell}}}}$为壳单元2D-Voronoi模型的泊松比, $alpha $为修正系数.

闭孔泡沫铝是一种各向同性材料^[7], 2D模型Z轴方向的位移及应变约束为零, 使得本应均分在${nu _{{{XY}}}}$(X轴?Y轴的泊松比)及${nu _{{{ZY}}}}$(Z轴?Y轴的泊松比)的误差, 均累积于${nu _{{{ZY}}}}$, 因此修正系数$alpha $取值0.5.

对修正误差进行非线性函数拟合, 得到如下表达式

$$ delta ({varepsilon }_y)=0.04 {{ m{e}}}^{1.50 left|{varepsilon }_y ight|}$$

(5)

式(5)的残差平方和RSS/SSR (residual sum of squares/sum squared residual)为3.080 × 10^?5, 调整R方(adjusted R-square)为0.989, 并满足$mathop {lim }limits_{left| {{varepsilon _y}}
ight| to 0} delta ({varepsilon _y}) = $$ 0.04 approx 0$.

结合图6、图7及误差分析可知, 在应变区间$left( {0,varepsilon _{{
m{E - max}}}^{{
m{uni}}}}
ight]$内, 壳单元的厚度减薄所造成的误差会随着轴向(Y轴)压缩而不断累积, 但不会影响胞孔的结构变形; 当应变大于$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$后, 厚度减薄所造成的误差已经明显影响胞孔厚度上的堆叠、胞孔的结构变形.

已有的研究结果表明, 在壳单元接触过程中, 厚度减薄不会干扰截面参数中壳厚度改变对应力计算的影响^[29-31], 即使不同****选取的模型不同, 应变区间$left( {0,varepsilon _{{
m{E - max}}}^{{
m{uni}}}}
ight]$内的有限元仿真研究的结论并无明显分歧, 壳单元Voronoi模型受到众多研究人员的青睐^[7-13].

由以上分析可知: 常规壳单元接触过程中的厚度减薄特性是研究人员对闭孔泡沫铝致密化阶段的泊松比变化规律结论存在分歧的原因; 闭孔泡沫铝的泊松比变化规律为“增高?降低?再增高”的“S”型变化过程; 壳单元Voronoi模型致密化起始应变$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$之后的数据无效.

2.2
泊松比特征点(极大值)物理意义

闭孔泡沫铝压缩过程中泊松比有极大值、极小值两个特征点^{[6, 22]}, 后者的物理意义已明确, 即泊松比极小值对应闭孔泡沫铝单轴压缩吸能效率的极大值, 即泡沫铝致密化阶段的起点^[28], 本节针对前者的物理意义进行探究.

相较于2D-Voronoi模型, 3D-Voronoi模型可以更加精准地体现闭孔泡沫铝材料胞孔结构在三维空间的压缩变形, 因此选用壳单元3D-Voronoi模型研究闭孔泡沫铝泊松比“S”型变化规律极大值的物理意义, 此时, 闭孔泡沫铝的泊松比的表达式如下

$$nu = - frac{{{varepsilon _x} + {varepsilon _z}}}{{2{varepsilon _y}}}$$

(6)

式中, ${varepsilon _x}$, ${varepsilon _y}$, ${varepsilon _z}$依次为模型X轴、Y轴、Z轴方向的真实应变.

由2.1节可知, 壳单元Voronoi模型致密化起始应变$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$之后的数据不可采信, 因此仅分析3D-Voronoi模型$varepsilon _{{
m{E - max}}}^{{
m{uni}}}$之前的数据.

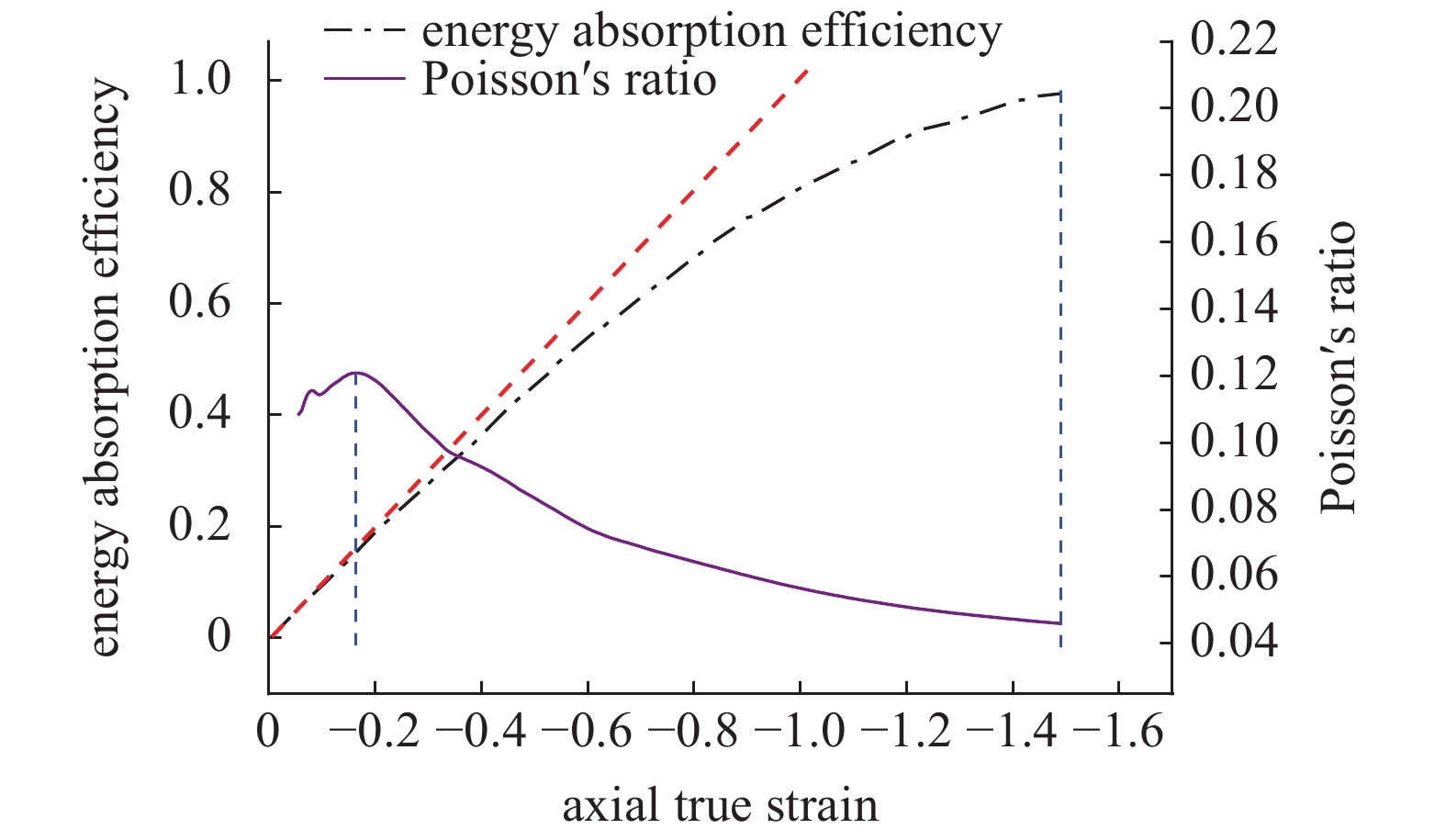
3D-Voronoi模型侧面耦合单轴压缩的仿真结果如图8所示, 泊松比曲线的起点应变为$varepsilon $= ?0.057, 以消除外部不完整胞孔孔壁受压失稳的干扰, 泊松比曲线的截止点应变为$varepsilon = varepsilon _{{
m{E - max}}}^{{
m{uni}}} = $ ?1.489.

由图8可知, 泊松比曲线达到极大值(图8左侧竖直虚线标注处)之前, 吸能效率与轴向真实应变大致呈线性关系, 泊松比达到极大值后, 吸能效率增速开始显著下降.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
3D-Voronoi模型泊松比及吸能效率曲线



Figure
8.
Curves of Poisson’s ratio and energy absorption efficiency of 3D-Voronoi model



下载:
全尺寸图片
幻灯片


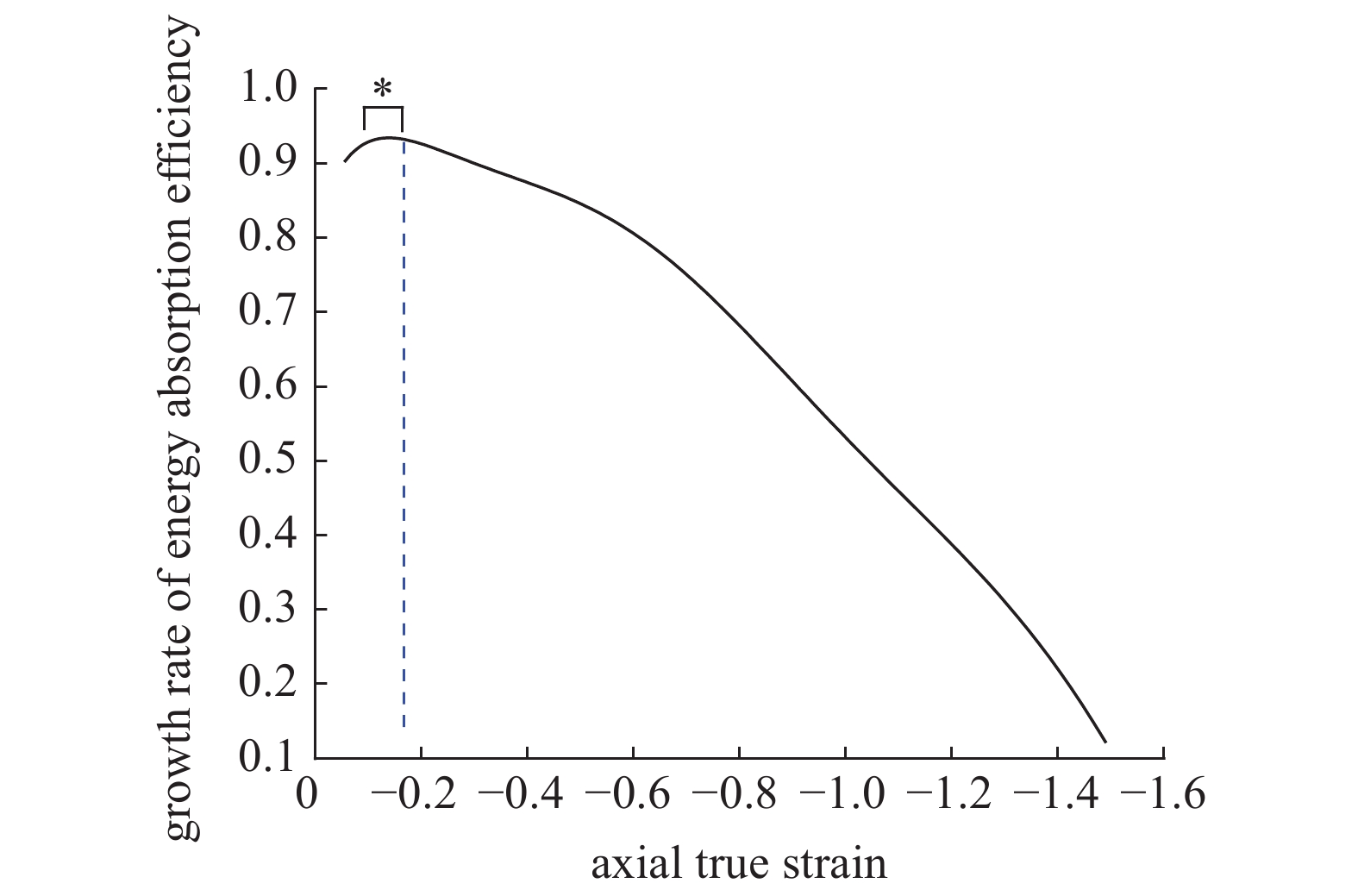
为进一步明确吸能效率的变化情况, 计算吸能效率曲线的斜率, 得到吸能效率增速?轴向真实应变曲线, 如图9所示(左侧竖直虚线标注处为泊松比极大值所对应的应变).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
3D-Voronoi模型吸能效率增速曲线



Figure
9.
Growth rate of energy absorption efficiency of 3D-Voronoi model



下载:
全尺寸图片
幻灯片


由于图9中“*”所示的区域, 吸能效率的增速近乎恒定, “*”所示区域之前的增速上升阶段很短, 因此已有的研究结果^{[7, 22, 28]}及本文得到的吸能效率曲线均有一段近乎线性的增长区域. 当泊松比达到极大值之后, 吸能效率的增速开始下降.

综上可知, 泊松比曲线极大值对应闭孔泡沫铝吸能效率的增速下降点, 此即闭孔泡沫铝泊松比曲线极大值点的物理意义.

2.3
压缩应力路径与变形模式

基于闭孔泡沫铝本构模型的唯象特性, 对其压缩变形机理的研究显得尤为重要. 为区分不同的压缩应力状态, 引入加载路径比例系数(the proportional stress path^[18]或stress ratio^[20])的概念, 用符号${eta _{
m{L}}}$表示

$${eta _{ m{L}}} = left| {frac{{{sigma _{ m{m}}}}}{{{sigma _{ m{e}}}}}} ight|$$

(7)

式中, ${sigma _{
m{m}}}$为平均应力, ${sigma _{
m{e}}}$为Mises有效应力. 由此, 泡沫铝的压缩应力状态可划分为: 单轴压缩(${eta _{
m{L}}}$= $1/3$), 静水压缩(${eta _{
m{L}}}$= $infty $)及等比压缩$Big(dfrac{{{sigma _2}left( varepsilon
ight)}}{{{sigma _1}left( varepsilon
ight)}} equiv dfrac{{{sigma _3}left( varepsilon
ight)}}{{{sigma _1}left( varepsilon
ight)}} equiv $$ C in left( {0,1}
ight)$, $1/3 < {eta _{
m{L}}} < infty Big)$.

上述划分方式无法体现泡沫铝三轴压缩(主要为等比压缩)应力状态下的变形模式, 为从变形层面对已有划分方式进行补充, 并探究泡沫铝三轴压缩应力状态下的变形模式, 引入临界应力路径(critical stress path)的概念, 用符号$eta _{
m{L}}^{
m{0}}$表示.

临界应力路径, 即当沿此路径进行三轴等比压缩时, 仅最大主应力方向表现出压缩变形, 第二及第三主应力方向应变为0 (侧面位移受限轴向压缩边界条件下得到的加载路径比例系数).

临界应力路径$eta _{
m{L}}^{
m{0}}$与轴向真实应变${varepsilon _y}$(等效于真实体积应变${varepsilon _{
m{V}}}$)的关系曲线由闭孔泡沫铝侧面位移受限轴向压缩得到. 闭孔泡沫铝侧面位移受限时轴向压缩的临界应力路径$eta _{
m{L}}^{
m{0}}$及吸能效率${eta _{
m{E}}}$的曲线如图10所示, 参照泊松比的研究结果, 吸能效率极大值为临界应力路径曲线的截止点, 用符号$eta _{{
m{L - cutoff}}}^{
m{0}}$表示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-173-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
临界应力路径及吸能效率曲线



Figure
10.
Curves of critical stress path and energy absorption efficiency



下载:
全尺寸图片
幻灯片


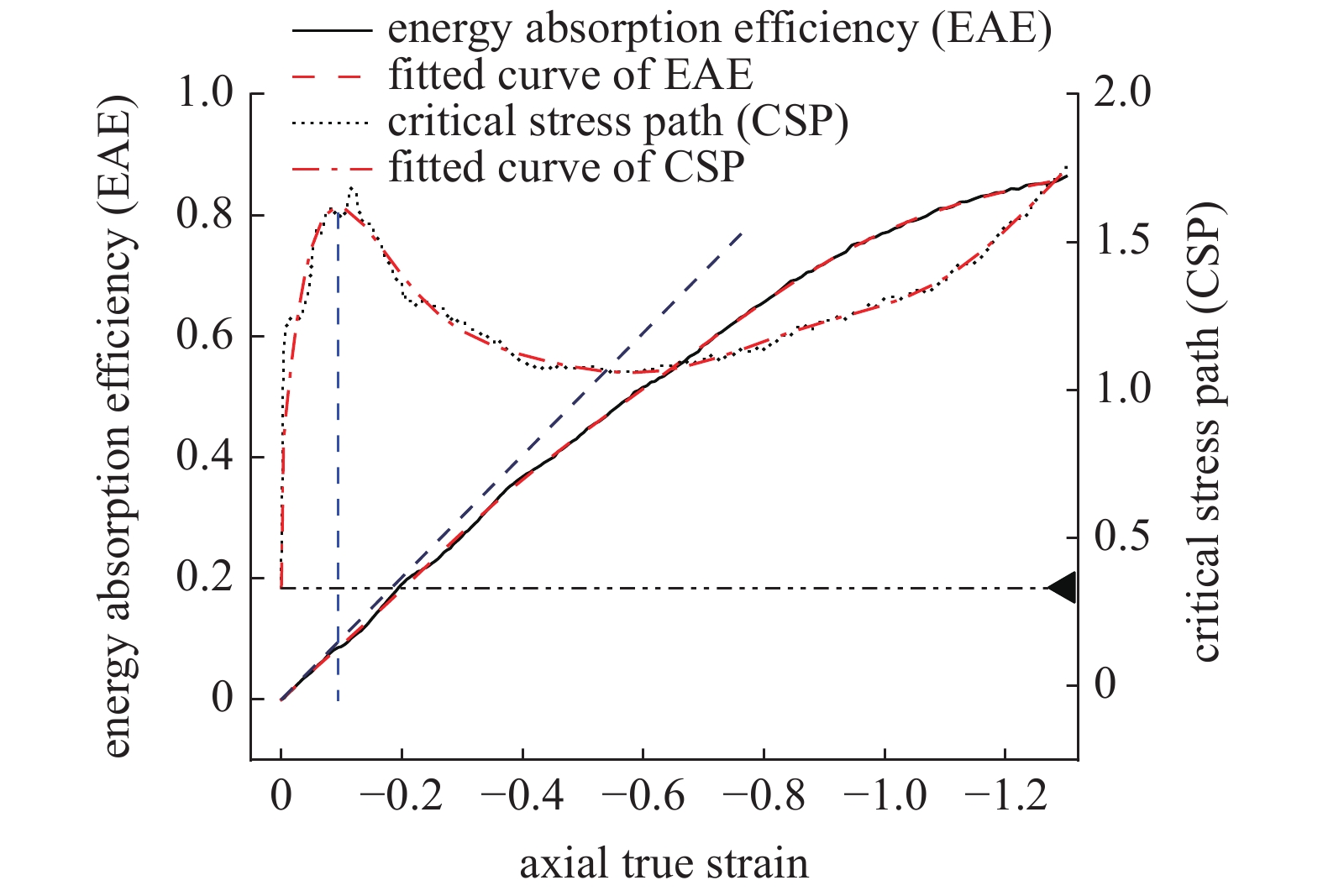
由图10可知, 临界应力路径$eta _{
m{L}}^{
m{0}}$同样呈现出“增高?降低?再增高”的“S”型变化过程, 存在极大值($eta _{{
m{L - max}}}^{
m{0}}$)、极小值($eta _{{
m{L - min}}}^{
m{0}}$)两个特征点, 且临界应力路径$eta _{
m{L}}^{
m{0}}$的极大值对应闭孔泡沫铝吸能效率的增速下降点, 这与闭孔泡沫铝泊松比的规律相似.

闭孔泡沫铝等比压缩边界条件的实现, 无论是试验还是仿真分析, 均存在较大困难, 尤其是等比压缩下的大变形研究, 试验或仿真分析均未得到实现^[7]. 借助临界应力路径曲线, 不但可以从变形层面进一步细化闭孔泡沫铝的等比压缩应力状态, 而且可以预测闭孔泡沫铝等比压缩应力状态整个变形过程(尤其是大变形)的变形模式.

等比压缩时, 若1/3 < ${eta _{
m{L}}}left( {{varepsilon _{
m{V}}}}
ight)$ < $eta _{
m{L}}^{
m{0}}left( {{varepsilon _{
m{V}}}}
ight)$, 此时闭孔泡沫铝虽然三轴受压, 但是仅第一主应力方向的变形表现为向内压缩, 第二及第三主应力方向(下文简称侧面)均表现为向外膨胀, 此时的胞孔变形状态更加接近单轴压缩; 若${eta _{
m{L}}}left( {{varepsilon _{
m{V}}}}
ight)$ > $eta _{
m{L}}^{
m{0}}left( {{varepsilon _{
m{V}}}}
ight)$, 此时闭孔泡沫铝各个方向的变形均表现为向内压缩.

由图10可知, 随着${eta _{
m{L}}}$的逐渐增大, 可以发现, 闭孔泡沫铝等比压缩应力状态下存在4种变形模式:

(1)当1/3 < ${eta _{
m{L}}}$ < $eta _{{
m{L - min}}}^{
m{0}}$时, 闭孔泡沫铝的侧面变形过程为“(短期)压缩变形→膨胀变形”;

(2)当$eta _{{
m{L - min}}}^{
m{0}}$ < ${eta _{
m{L}}}$ < $eta _{{
m{L - max}}}^{
m{0}}$时, 闭孔泡沫铝的侧面变形过程为“压缩变形→膨胀变形→压缩变形→膨胀变形”;

(3)当$eta _{{
m{L - max}}}^{
m{0}}$ < ${eta _{
m{L}}}$ < $eta _{{
m{L - cutoff}}}^{
m{0}}$时, 闭孔泡沫铝的侧面变形过程为“压缩变形→(短期)膨胀变形”;

(4)当${eta _{
m{L}}}$ > $eta _{{
m{L - cutoff}}}^{
m{0}}$时, 闭孔泡沫铝的侧面变形过程为“压缩变形”.

3.
结论

建立闭孔泡沫铝的3D-Voronoi模型及2D-Voronoi模型, 通过有限元软件ABAQUS/Explicit对其进行侧面耦合单轴压缩及侧面位移受限轴向压缩边界条件下的数值模拟分析. 根据计算结果, 讨论了Voronoi模型的特点, 阐明了对闭孔泡沫铝泊松比变化规律的研究结果存在分歧的原因, 明确了闭孔泡沫铝泊松比的变化规律及特征点的物理意义, 发现了闭孔泡沫铝等比压缩应力状态下的4种变形模式. 研究结果发现:

(1)常规壳单元接触中的厚度减薄特性是导致闭孔泡沫铝泊松比变化规律的研究结果存在分歧的原因, 但是, 厚度减薄不会影响泡沫铝模型致密前胞孔结构的变形模式, 保证了壳单元Voronoi模型弹性阶段与平台阶段应力、应变结果的准确性.

(2)闭孔泡沫铝泊松比的变化规律为“增高?降低?再增高”的“S”型曲线, 泊松比曲线极大值对应闭孔泡沫铝吸能效率的增速下降点, 曲线极小值对应闭孔泡沫铝吸能效率的极大值(即闭孔泡沫铝致密化阶段的起点).

(3)以侧面变形模式为判别标准, 闭孔泡沫铝等比压缩应力状态下, 随着加载路径比例系数的取值不同存在4种变形模式, 分别为, 侧面变形过程“(短期)压缩变形→膨胀变形”、“压缩变形→膨胀变形→压缩变形→膨胀变形”、“压缩变形→(短期)膨胀变形”及“压缩变形”.