引言
地下流体在多孔介质中的流动往往涉及多尺度、多变量、多物理场的耦合. 现有的产量预测方法包括经验曲线法[1-3]、(半)解析方法[4-6]及数值模拟法[7-11]. 因为模型的假设条件及方程的局限性, 无法真实准确地刻画实际油藏生产过程, 从而造成了产量预测结果不确定性. 尽管低渗, 特低渗及非常规油气资源的开发已成为当前研究热点问题, 人们对地下复杂的油气渗流机理的认识仍不完善[12-15], 这也限制了这些传统方法的适用性. 此外, 综合考虑多种力学问题的耦合渗流问题存在机理表征困难, 模型求解难度大, 计算不收敛等问题. 因此, 实际油田中的多变量, 多尺度和非线性数据给传统产量预测模型带来了巨大的挑战[16-18].
近年来, 人工智能技术, 大数据分析方法由于其强大的学习及预测能力在工业界得到了广泛应用. 同时, 油田中存在的地质?油藏?流体?工艺数据给数据建模技术应用在石油行业提供了可能性. 吴新根等[19]应用BP神经网络预测罗马什金油田年产量, 与Weng旋回模型预测结果相比, 人工神经网络是一种可行的石油产量外推预测方法. 李留仁等[20]采用3层BP神经网络预测了12个月的月产油量, 预测月产油量误差在10%以内. 邢明海等[21]以多层前馈神经网络和函数连接神经网络为基础, 研究了5种不同的组合方式下的油田总产量. Chithra等[22]利用高阶神经网络模型预测10个月的累积产量, 误差在5%以内. 高阶神经网络包含传统神经网络的线性相关项(突触操作)及神经输入与突触权重的高阶相关项(n阶相关项). 马林茂等[23]利用遗传算法优化BP神经网络连接权值和阈值, 并将该算法用于预测大庆油田BED试验区高含水阶段的油田产量预测. 李彦尊等[24]基于静态地质, 油藏及工程参数, 利用人工神经网络方法预测页岩油气的投产5年内的产量. 神经网络强大的预测能力往往依赖于大量样本数据库, 对于小样本数据(数据量小于1000)的训练, 容易出现明显的过拟合现象. 而实际油田开发过程中由于区块限制, 记录不全, 操作不当等因素难以获取较为准确的大量样本数据. 近年来, 众多****探索了机器学习算法在产量预测中的应用, 并取得了一定的效果. Bhattacharya等[25] 和Wang等[26]等综合多类型油藏数据, 建立机器学习模型, 预测页岩气单井日产量. 宋宣毅等[27]利用随机森林方法确定了影响产能的主控因素. Xue等[28]以页岩气藏的多段压裂水平井为例, 综合影响页岩气产量的9个主控参数及生产动态中的最大产气量数据, 对比多目标随机森林回归和多输出回归链算法对日产气量进行预测.
针对地下流体在多孔介质中的渗流机理复杂, 渗流模型求解难度大, 产量预测结果不确定性强等问题, 本文以特低渗透油藏开发过程中搜集到的小样本数据为例(样本量 < 1000), 探究一种适用于预测产量的数据代理模型, 它可以省去复杂物理建模过程, 简化模型求解问题, 兼顾计算效率与预测精度. 此外, 给出了数据代理模型预测产量的详细流程, 并对比分析三种代理模型在产量预测中应用效果. 最后, 针对小样本多变量产量预测问题, 给出能有效提高模型预测效果的针对性建议, 为渗流代理模型在石油行业的应用提供了理论指导.
1.
数据建模预测产量流程
渗流代理模型能否准确预测油气产量往往取决于可靠的油田数据. 而真实的油田数据资料往往存在数据跳跃, 数据缺失等问题. 因此, 数据预处理, 作为建立代理模型的第一步, 能将原始油田数据进行加工、降噪、归一化等一系列处理形成产量预测数据库. 为了保证计算精度的前提下尽可能节省代理模型的计算时间, 模型的超参数优化在数据建模中也至关重要. 最后, 经过训练后的最优代理模型能用于油气产量预测. 本文将数据建模技术预测油气产量的一般流程划分为数据采集, 数据预处理, 代理模型建立与优化三个部分, 如图1所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
数据建模技术预测油气产量的一般流程
Figure
1.
A general flow of data modeling techniques for predicting oil and gas production
下载: 全尺寸图片
幻灯片
1.1
数据采集
为了获得准确可靠的产量预测结果, 应尽可能广泛地收集影响油气产量的油田数据. 本文结合地质背景, 在充分理解油藏开发规律和生产工艺的基础上, 将影响产量预测的实际油田数据归为以下八类(如图2所示). 针对产量预测这类回归问题, 类别数据需通过独热编码技术, 图像数据通过卷积神经网络转化后便于代理提取和学习.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
油田数据库的建立
Figure
2.
Establishment of oilfield database
下载: 全尺寸图片
幻灯片
1.2
数据预处理
为了使机器学习算法具有更好的预测能力, 需要有足够数量和质量的训练数据. 实际油田数据存在着记录不完整、数据噪声大等问题. 这些实际数据在输入机器学习模型进行训练之前需要进行预处理. 本文将数据预处理的过程分为四个部分: 数据清理、数据标准化、相关性分析和数据集劈分. 数据清理是数据预处理的第一步, 其中包括删除或填充丢失的记录和异常值, 对分类数据进行编码和对数据集进行平滑处理等. 此外, 对输入数据进行标准化是获得可靠的训练模型所必不可少的步骤, 它可以消除不同维度的变量之间的差异. 在训练渗流代理模型之前, 通过均值和方差对数据进行归一化. 特征工程是构建渗流代理模型的基础, 应基于影响石油生产的理论知识和现场专业知识进行初步提取. 此外, 低相关性的变量会降低模型的准确性, 而高相关性的变量会大大降低模型的复杂度并提高预测准确率. 因此, 变量间的相关性分析和重要性排序对油气产量预测具有重要意义, 可用于主成分分析, 灰色关联分析, 随机森林进行分析. 数据劈分是防止模型过拟合并提高模型泛化能力的方法之一. 通过从产量预测模型数据集中随机抽取训练数据, 然后将训练, 测试和验证数据集通过交叉验证进行划分, 交叉验证可用于评估和预测油井的性能.
1.3
代理模型建立与优化
建立数据库后, 将训练数据输入到数据驱动的模型中进行训练, 通过优化算法对超参数进行优化. 当训练误差达到期望值或没有减少时, 可以通过验证集验证训练模型. 最后, 通过随机选择测试数据对模型进行盲测. 在本文中, 均方误差(mean square error) Ems和准确率R2被用来评估代理模型, 其具体表达式如下
$$ {{E}}_{ m{ms}} = frac{1}{n}sumlimits_{i = 1}^n {{{left( {{y_i} - {{hat y}_i}} ight)}^2}} $$  | (1) |
$${R^2}{ m{ = }}1 - frac{{displaystylesum {{{left( {{y_i} - {{hat y}_i}} ight)}^2}} }}{{displaystylesum {{{left( {{y_i} - bar y} ight)}^2}} }};;$$  | (2) |
式中,
2.
理论基础
2.1
随机森林(random forest)
决策树(decision tree)通过拆分预测变量并递归划分数据集来描述因变量与一个或多个自变量之间的关系[29]. 在决策树的每个分支上, 观察数据通过自变量的阈值分配给左右路径. 在回归树中, 通过最小化误差指标劈分数据集并在叶子节点上获得预测值. 基于CART树和装袋法的随机森林, 通过聚集大量决策树来近似表征任意复杂的非线性曲面, 这使得它成为一个强大的预测工具[30-31], 能用于解决复杂的非线性回归和分类问题. 它能从训练数据集中获得预定数量的小样本用于并行估计, 通过简单的参数优化, 便可获得较高的预测精度. 如图3所示, 通过分割每个节点并随机选择给定节点的子集来构建随机森林模型进行训练, 并且未经过剪枝的树在每个节点处随机增长. 这种随机化特征使得模型能够避免过拟合问题. 最终预测值是RF算法中每个决策树的平均值. 此外, 随机森林方法也可以对变量的重要性进行排序, 便于抽提产量主控因素, 有助于分析油田生产动态分析.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
随机森林预测产量示意图
Figure
3.
Schematic diagram of random forest forecast oil production
下载: 全尺寸图片
幻灯片
2.2
极限梯度提升树(extreme gradient boosting)
梯度提升树(gradient boosting decision tree, GBDT)通过多轮迭代, 每轮迭代产生一个弱学习器(CART回归树), 每个学习器通过降低上一轮的残差进行训练[32-33]. 最终的预测结果通过将每轮训练得到的弱学习器进行加权求和得到, 这种通过集合多个弱学习器形成一个强化模型的集成学习方法能大大减少模型的训练时间, 同时可以有效避免过拟合问题. 近年来, 由陈天奇等[34-35]提出的极限梯度爬升算法(extreme gradient boosting, XGBoost)对GBDT进行了优化, 进一步提升了算法的计算速度和预测性能, 成为了当前数据挖掘算法中的热点. 其主要优点如下[36-37].
(1)目标函数优化利用了损失函数关于待求函数的二阶导数, 加快优化进程, 增加模型准确性.
(2)支持并行化, 对于某个节点, 节点内选择最佳分裂点, 候选分裂点计算增益用多线程并行. 训练速度快.
(3)通过引入正则化项, 增加模型的泛化能力, 能有效防止过拟合问题.
2.3
人工神经网络
人工神经网络 (artificial neural network), 作为功能强大的机器学习算法, 可以充分挖掘隐藏在数据背后的非线性关系. 多个相互连接的并行神经元组成的人工神经网络系统一般包括输入层, 隐藏层和输出层. 仅包含输入和输出层的神经网络也称为单层感知器, 通常用于解决线性问题. 多层感知器可能包含多个隐藏层, 用来探索因变量和自变量之间复杂非线性关系[38-39]. 神经元之间的连接可以用等式(3)表示, 当输入信号通过时, 神经元根据其权重交换消息. 每个神经元的输入信息通过线性加权组合在一起, 通过不断调整权重和偏差以使输出与输入变量相关. 最后, 通过激活函数获得计算结果的输出
$${y_i} = fleft( {sumlimits_{j = 1}^m {{w_{ij}}} {x_j} + {b_i}} ight)$$  | (3) |
式中yi是神经元i的输出; f(·)是激活函数, 可用于控制神经元的状态(兴奋或抑制); wij是后一层的神经元j和当前层的神经元i之间的连接权重; xj表示上一层神经元j的输出值; bi是神经元i的偏差.
神经网络的训练过程包括两个阶段: 信号的前馈传输和误差的反向传播[40-41]. 在第一阶段, 信号从输入层传递到隐藏层或输出层. 在第二阶段, 将从预测值和实际值计算出的误差信号传播回输入层, 并更新输入层中神经元之间的连接权重和偏差. 最后, 需要一个具有滤波器功能的传递函数来激活该单元并产生输出. 人工神经网络中的常用激活函数包括Sigmoid函数, tanh函数和ReLU函数. 为了节省模型优化时间, 本文采用文献报道中普遍适用的ReLU函数作为产量预测的激活函数[42-44].
3.
实例分析
3.1
产量预测数据库建立
本文以国内某特低渗透油田为例, 尽可能地搜集了该油田242口压裂水平井的6个月累积产油量及影响产量的地质?油藏?工艺变量, 主要包括孔隙度(φ), 渗透率(K), 含水饱和度(Sw), 泥质含量(Sh), 电阻率(R), 射孔厚度(hperf), 有效厚度(h), 井底流压(pwf), 生产压差(ΔP), 油藏位置(边部), 入地总液量(Vfrac)及六个月的平均产量(Q6?m). 为了准确评估压后效果及训练模型, 选取6个月平均月产量作为预测指标, 通过函数插值填补缺失值、降噪、类别数据独热编码等技术手段对数据进行预处理, 获得了12个变量的统计分析结果, 主要包括均值(mean), 标准差(std), 最小值(min), 第一四分位数(25%), 中位数(50%), 第三四分位数(75%), 最大值(max), 具体结果如表1所示.
表
1
产量数据库统计分析
Table
1.
Statistical analysis of oilfield database
table_type1 ">
| Statistics | φ | K (10?3μm3) | Sw | Sh |
| mean | 11.8 | 5.1 | 48.7 | 25.7 |
| std | 2.8 | 9.0 | 8.0 | 8.4 |
| min | 5.2 | 0.0 | 0.0 | 7.4 |
| 25% | 10.6 | 1.0 | 45.0 | 19.3 |
| 50% | 11.5 | 2.9 | 48.9 | 24.9 |
| 75% | 12.7 | 5.8 | 52.6 | 30.4 |
| max | 47.0 | 74.6 | 73.8 | 54.0 |
| Statistics | R | hperf/m | h/m | pwf |
| mean | 20.0 | 3.4 | 12.4 | 7.3 |
| std | 7.3 | 1.2 | 5.5 | 2.4 |
| min | 6.1 | 1.1 | 4.1 | 1.3 |
| 25% | 14.3 | 2.9 | 8.5 | 5.3 |
| 50% | 20.1 | 3.3 | 10.7 | 6.5 |
| 75% | 24.7 | 4.0 | 15.7 | 9.3 |
| max | 45.3 | 10.0 | 27.1 | 15.0 |
| Statistics | ΔP/MPa | Position | Vfrac/m3 | Q6?m/(t·d?1) |
| mean | 10.7 | 0.3 | 62.4 | 3273 |
| std | 5.2 | 0.5 | 32.5 | 2190 |
| min | 2.0 | 0 | 5.3 | 0 |
| 25% | 6.3 | 0 | 40.7 | 2019 |
| 50% | 10.0 | 0 | 57.6 | 3102 |
| 75% | 14.3 | 1.0 | 78.0 | 4095 |
| max | 23.7 | 1.0 | 178.9 | 16 146 |
下载: 导出CSV
|显示表格
针对油田所搜集到的242口压裂水平井数据的产量预测问题, 本文的工作流程如下.
(1)首先通过填补缺失值, 类别数据(如油藏位置)进行独热编码进行数据预处理;
(2)为了获得较为可靠的预测结果, 在数据预处理的基础上先对数化处理再进行数据标准化, 获得符合高斯分布特征的无量纲数据, 形成产量预测数据库;
(3)为了对比验证三种代理模型的预测效果, 利用随机劈分方法将数据切分为训练集和测试集;
(4)经过模型训练后的数据, 为了减少模型训练过程中预测结果的差异性, 采用十折交叉验证方法评估三种代理模型(随机森林、XGBoost、人工神经网络)的预测效果.
(5)为了评估小样本数据下数据预处理对模型预测效果的影响, 考虑经过数据对数化处理和不经过对数化处理两种条件下评估代理模型的预测效果.
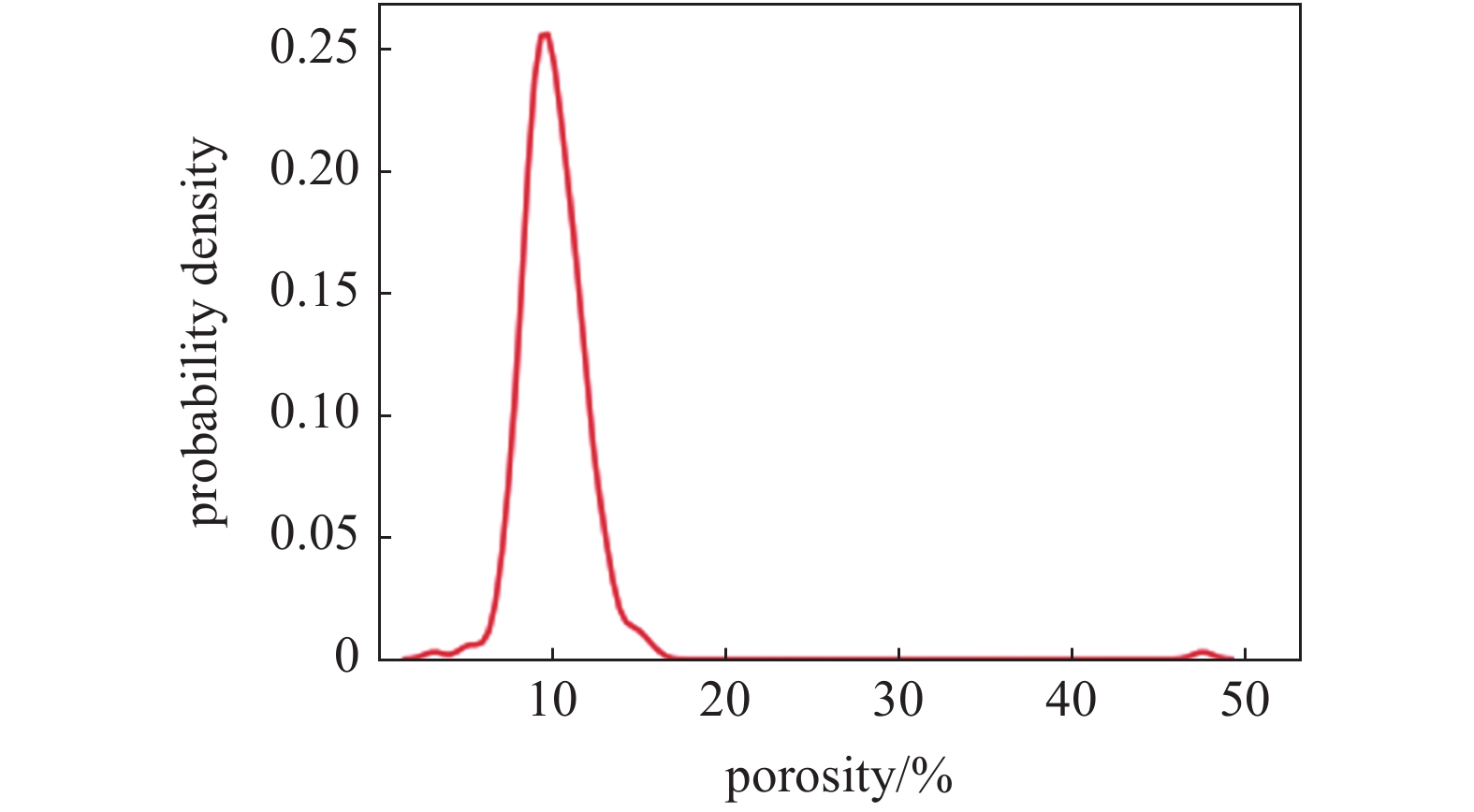
数据预处理是获得准确可靠的预测结果的关键, 针对本案例中偏度较大的变量, 本文采用对数函数进行转化, 利用核密度估计方法获取转换前后的概率密度分布
$${hat f_{ m{h}}}(x) = frac{1}{n}sumlimits_{i = 1}^n {{K_{ m{h}}}} left( {x - {x_i}} ight) = frac{1}{{nh}}sumlimits_{i = 1}^n K left( {frac{{x - {x_i}}}{h}} ight)$$  | (4) |
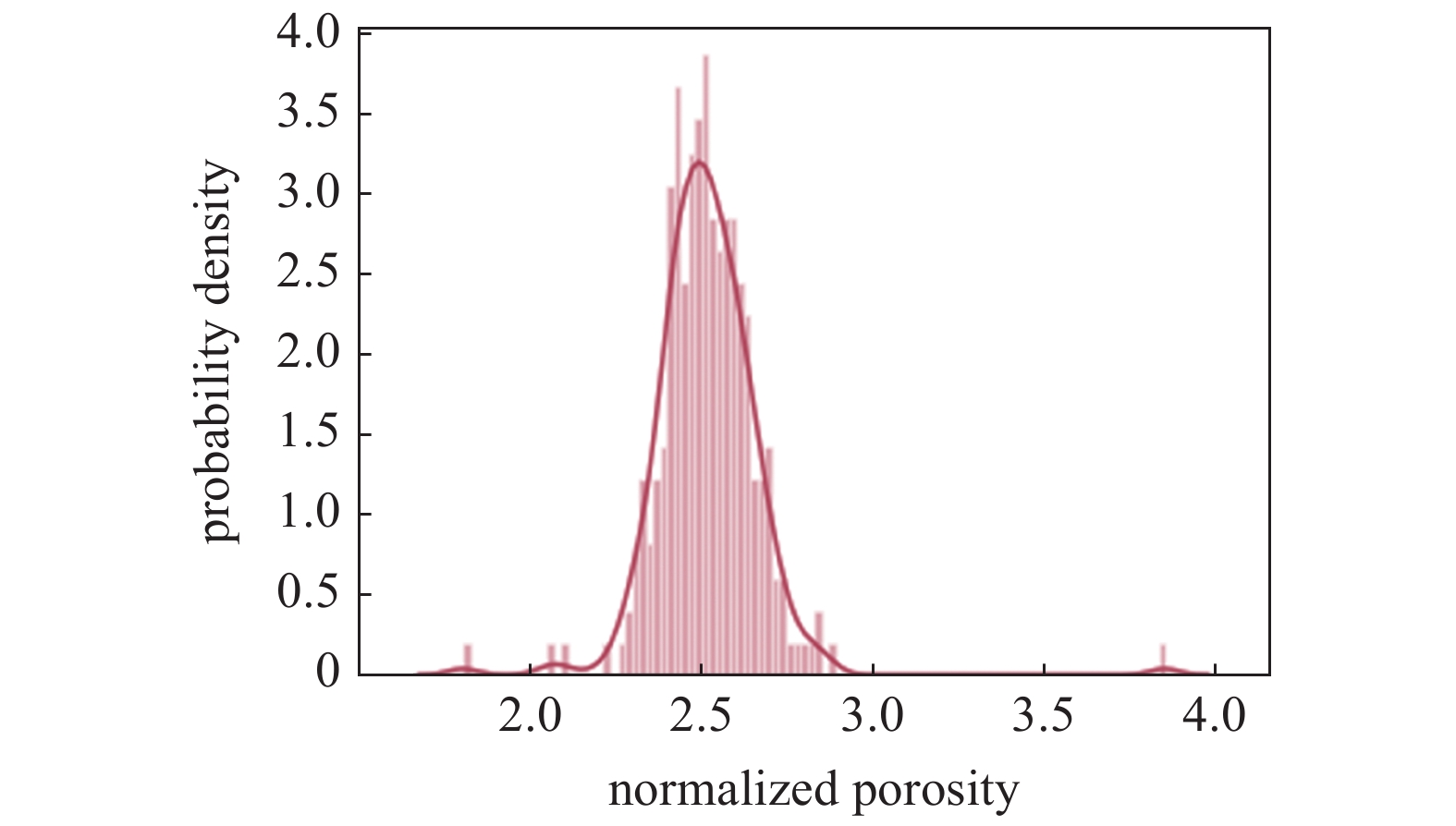
式中, f为概率密度函数, K(·)为核函数(非负、积分为1, 符合概率密度性质, 并且均值为0), h > 0为一个平滑参数, 称作带宽. 结果表明, 对数化处理后的数据更加服从高斯分布(见图4, 图5所示).
为了消除不同变量之间的量纲影响, 采用基于原始数据的均值和标准差进行数据标准化处理, 其表达为
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
转换前数据分布(以孔隙度为例)
Figure
4.
Data distribution before transformation (taking porosity as an example)
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
转换后数据分布(以孔隙度为例)
Figure
5.
Data distribution after transformation (taking porosity as an example)
下载: 全尺寸图片
幻灯片
$${x^*} = frac{{x - mu }}{sigma }$$  | (5) |
式中, x表示原始数据, μ表示数据的均值, σ表示数据的标准差, x*为标准化后的数据.
经过预处理的数据可输入到机器学习算法中进行训练, 为了评估模型效果并对比分析随机森林、XGBoost、人工神经网络之间的差异, 本文采用随机劈分方法将产量预测数据库划分为训练集(70% 数据集)和测试集(30% 数据集), 通过十折交叉验证的均方误差和准确率来评估模型的预测效果.
3.2
模型结构
正如前文所述, 本文采用适用于小样本的集成学习模型(随机森林及XGBoost)进行训练, 并与人工神经网络模型进行对比. 为了获取高效准确的优化模型, 通过十折交叉验证对渗流代理模型进行超参数优化, 优化后的模型结构如表2所示.
表
2
模型参数优化结果
Table
2.
Model parameter optimization results
table_type1 ">
| Seepage proxy model | Optimal model structure |
| random forest | number of estimators =150 |
| min samples split = 2 | |
| XGBoost | number of estimators = 120 |
| learning rate = 0.05 | |
| subsample = 0.8 | |
| max depth = 5 | |
| artificial neural networks | hidden layers = 2 |
| first layer = 200 neurons | |
| second layer = 10 neurons | |
| activation function = ReLU |
下载: 导出CSV
|显示表格
4.
结果与讨论
4.1
产量主控因素排序
产量主控因素分析及排序是油井性能评估的一个重要步骤, 本文基于数据建模技术及前文建立的产量模型数据库, 采用皮尔逊相关系数分析各个变量对6个月累积产油量的影响. 皮尔逊相关系数能定量分析不同自变量与因变量之间的相关程度并排序, 其值越接近1, 相关性越强; 其值越接近0, 相关性越弱. 皮尔逊相关系数的表达式为
$${ ho _{X,Y}} = frac{{{ m{cov}} (X,Y)}}{{{sigma _X}{sigma _Y}}} = frac{{Eleft[ {left( {X - {mu _X}} ight)left( {Y - {mu _Y}} ight)} ight]}}{{{sigma _X}{sigma _Y}}}$$  | (6) |
式中,
ho _{X,Y}}$
m{cov}} (X,Y)$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-6.jpg'" class="figure_img
figure_type2 ccc " id="Figure6" />
图
6
产量影响因素分析
Figure
6.
Analysis of factors affecting oil production
下载: 全尺寸图片
幻灯片
4.2
数据标准化对预测效果影响
此外, 为了说明数据预处理步骤在数据驱动预测产量过程中的重要性, 本文对比了三种渗流代理模型在经过数据预处理(标准化)和不经过数据标准化的两种场景下的预测效果, 如图7 ~ 图9所示.
从图7 ~ 图9可以看出, 未经过标准化的数据直接输入到模型中会产量较大误差, 严重影响模型预测效果. 对比三种渗流代理模型来看, 数据标准化对神经网络模型影响最大; 而对于集成学习模型, 未进行标准化也能取得一定的效果. 因此, 利用渗流代理模型进行回归预测时, 数据标准化是模型取得较高准确率的关键, 尤其是对于神经网络, 未经数据标准化的数据会模型会严重影响产量预测效果.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
随机森林模型标准化对比
Figure
7.
Standardization comparison of random forest models
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
XGBoost模型标准化对比
Figure
8.
Standardization comparison of XGBoost models
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
人工神经网络模型标准化对比
Figure
9.
Standardization comparison of artificial neural network models
下载: 全尺寸图片
幻灯片
4.3
三种渗流代理模型对比
将随机劈分的产量预测数据库分别输入到优化的随机森林、XGBoost回归树及人工神经网络模型中, 通过指数化及反归一化可以得到产量模型的预测结果. 所得训练集, 测试集及整个数据集的均方误差及准确率结果如表3所示. 为了更加直观对比三种机器学习算法的预测性能, 绘制了目标值与模型值的交会图如图10 ~ 图12所示.
表
3
渗流代理模型结果对比
Table
3.
Comparison of results of seepage proxy model
table_type1 ">
| Seepage proxy model | Dataset | Ems | R2 |
| random forest | train (70%) | 0.07 | 0.93 |
| test (30%) | 0.28 | 0.71 | |
| total | 0.12 | 0.87 | |
| XGBoost | train (70%) | 0.11 | 0.70 |
| test (30%) | 0.30 | 0.89 | |
| total | 0.17 | 0.83 | |
| artificial neural networks | train (70%) | 0.08 | 0.92 |
| test (30%) | 0.45 | 0.54 | |
| total | 0.20 | 0.80 |
下载: 导出CSV
|显示表格
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
随机森林目标值与预测值交会图
Figure
10.
Cross plot of target and predicted values of random forest
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
XGBoost目标值与预测值交会图
Figure
11.
Cross plot of target and predicted values of XGBoost
下载: 全尺寸图片
幻灯片
结合两种模型评估指标(均方误差, Ems、准确率, R2)来看, 总体而言三种渗流代理模型均能取得较好的预测效果(R2 > 0.8, Ems < 0.2), 这说明渗流代理模型能被用来挖掘多变量油田数据之间复杂非线性关系. 从测试集的均方误差结果可以看出, 人工神经网络针对小样本数据的预测的过拟合现象十分严重(Ems = 0.45, R2 = 0.54), 不太适合小样本数据的预测, 而随机森林算法和极限梯度提升数的预测效果明显优于神经网络, 进一步说明集成学习算法在处理小样本数据时表现出来的优越性, 对比随机森林和极限梯度提升树来看, 随机森林在测试集上略低于极限梯度提升树, 而在总体预测结果来看, 随机森林算法仍具有明显的优势, 因此, 随机森林算法能较好地用于小样本多变量的油田数据分析.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-155-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
人工神经网络目标值与预测值交会图
Figure
12.
Cross plot of target and predicted values of artificial neural networks
下载: 全尺寸图片
幻灯片
5.
结论
本文针对地下多孔介质渗流过程中存在的非线性、多尺度、多物理场等耦合渗流机理难以准确刻画与表征, 考虑多机理耦合的渗流模型求解难度大, 计算效率低等渗流力学发展面临的瓶颈问题, 探索了一种利用大数据分析方法建立渗流代理模型预测石油产量的方法与流程, 所得结论如下.
(1)本文建立的三种渗流代理模型不需要建立复杂的物理模型及假设便能挖掘油田数据之间复杂的非线性关系, 高效准确地预测产量, 兼顾计算效率的同时能实现产量的准确预测.
(2)渗流代理模型预测石油产量包括油田数据收集、数据清洗(缺失值填充、数据标准化与对数化等)、产量预测数据库建立、代理模型优化、产量预测等步骤. 针对油田开发过程中的多变量小样本问题, 在模型开始训练前, 数据对数化及归一化处理能明显提升模型的预测效果.
(3)代理模型能快速分析多变量之间的相关性, 抽提影响产量的主控因素. 相比于神经网络模型, 随机森林具有更好的泛化性能, 能更好地适用于小样本多变量的产量预测问题.
