 ,*,2), 姚永芳*,?, 郭迪龙*, 杨国伟
,*,2), 姚永芳*,?, 郭迪龙*, 杨国伟 ,3),*, 姚拴宝**, 张业**, 陈大伟**, 李桂波*,*, 尚克明**, 贾玲**
,3),*, 姚拴宝**, 张业**, 陈大伟**, 李桂波*,*, 尚克明**, 贾玲** ?
**
RESEARCH PROGRESS IN AERODYNAMIC OPTIMIZATION OF HIGH-SPEED TRAINS 1)
Sun Zhenxu ,*,2), Yao Yongfang*,?, Guo Dilong*, Yang Guowei
,*,2), Yao Yongfang*,?, Guo Dilong*, Yang Guowei ,3),*, Yao Shuanbao**, Zhang Ye**, Chen Dawei**, Li Guibo*,*, Shang Keming**, Jia Ling**
,3),*, Yao Shuanbao**, Zhang Ye**, Chen Dawei**, Li Guibo*,*, Shang Keming**, Jia Ling** ?
**
通讯作者: 2)孙振旭, 副研究员, 主要研究方向: 高速列车气动特性与气动优化. E-mail:sunzhenxu@imech.ac.cn3) 杨国伟, 研究员, 主要研究方向: 计算流体力学、气动优化设计、气动弹性. E-mail:gwyang@imech.ac.cn
收稿日期:2020-06-17接受日期:2020-10-12网络出版日期:2021-12-31
| 基金资助: |
Received:2020-06-17Accepted:2020-10-12Online:2021-12-31
作者简介 About authors

摘要
随着运行速度的提升, 高速列车对气动外形的要求也越来越高, 追求性能优异、美观大方的气动外形是新型高速列车研发的一个重要方向. 基于当前高速列车外形研发的思路, 可以将气动外形优化概括为基于流场机理的改型优化和基于优化算法的外形优化两类. 本文简要回顾了当前国内外在这两类优化途径上的系列工作, 着重介绍了作者所在团队近年来做过的一系列气动外形优化工作. 在基于流场机理的改型优化上, 着重从"和谐号"和"复兴号"这两款主力车型的外形研发上探讨其改型优化的思路, 主要探讨了空调导流罩、受电弓平台、风挡和转向架裙板几类对列车阻力影响较为明显的部件的优化设计,并介绍了其相对于上一代车型在气动性能上的提升. 基于优化算法的外形优化方法,则因循气动外形优化流程, 在列车外形已经具有较好性能的基础上,以高速列车头型流线型为主要优化对象,分别从高速列车参数化方法、替代模型开发以及优化算法改进三个方面进行介绍.其中,高速列车参数化方法主要介绍了局部型函数法、修正车辆造型函数法和类别/形状函数法三类;替代模型开发介绍了最优化替代模型和基于交叉验证的Kriging模型; 在优化算法的改进上介绍了改进的非劣分类多目标粒子群算法和连续域混沌蚁群算法两方面的内容.基于上述三个方面介绍了气动外形优化策略在典型工程上的应用案例.
关键词:
Abstract
With the increase of running speed, high-speed trains have higher requirement for aerodynamic shape. The pursuit of excellent performance and beautiful aerodynamic shape tends to be an important direction in the development of new high-speed trains. Based on the current aerodynamic study of high-speed trains, aerodynamic shape optimization can be divided into two categories: shape modification optimization based on flow mechanism and shape optimization based on optimization algorithms. After a brief review of the current domestic and foreign work on these two optimization approaches, this paper focuses on a series of aerodynamic shape optimization work done by the author's team in recent years. In terms of the modification optimization based on the flow field mechanism, this paper focuses on the research and development of the appearance of the two main models, namely "CRH" and "Fuxing" , to discuss the idea of the modification optimization. It mainly discusses the optimization design of air conditioning cover, pantograph installation platform, windshield and bogie apron, which have obvious influence on the train resistance, and introduces the improvement of aerodynamic performance of these components compared with the previous models. In the shape optimization method based on an optimization algorithm, according to the aerodynamic shape optimization process, taking the streamline of high-speed train head as the main optimization object, we introduce our series of work from three aspects: high-speed train parameterization method, surrogate model development and the improvement of the optimization algorithm. Among them, high-speed train parameterization methods mainly include local function method, modified vehicle modeling function method, and category/shape function method; in the development of the alternative model, the optimization alternative model and Kriging model based on cross-validation are introduced; on the improvement of the optimization algorithm, the improved non-inferior classification multi-objective particle swarm optimization algorithm and continuous domain chaotic ant colony algorithm are introduced. Based on the improvement of the above three aspects, the application cases of the developed aerodynamic shape optimization strategy in typical engineering are further introduced.
Keywords:
PDF (17927KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
孙振旭, 姚永芳, 郭迪龙, 杨国伟, 姚拴宝, 张业, 陈大伟, 李桂波, 尚克明, 贾玲. 高速列车气动外形优化研究进展 1). 力学学报[J], 2021, 53(1): 51-74 DOI:10.6052/0459-1879-20-205
Sun Zhenxu, Yao Yongfang, Guo Dilong, Yang Guowei, Yao Shuanbao, Zhang Ye, Chen Dawei, Li Guibo, Shang Keming, Jia Ling.
引言
高速铁路的发展对我国国民经济发展和社会进步起着至关重要的作用. 至2019年底,中国高速铁路营业总里程达到3.5万千米, 居世界第一."复兴号"列车在京沪高速铁路上运营速度实现350 km/h.高速列车运行时的稳定性、舒适性以及环境友好性等与高速列车的空气动力学性能紧密相关.列车外形流线型直接影响列车空气动力性能[1-2].列车的阻力特性与列车提速和节能环保能力密切相关, 头部长度在10 m左右,流线型程度非常高的动车组, 在 300 km/h的时速下, 空气阻力占总阻力的75%左右[3]. 随着列车运行速度的提高, 列车的空气动力学问题变得越来越显著,严重影响列车运行安全性和乘坐舒适性[4-6]. 列车的气动性能优化有着重要意义.国内外****也在高速列车的气动性能优化上做了大量探索,主要优化策略可以概括为两方面的内容:基于流场机理的改型优化和基于优化算法的外形优化.基于流场机理的高速列车局部外形快速设计和基于优化算法的列车外形优化,尤其是对列车头型进行优化,成为了高速列车气动外形优化设计中两种相辅相成的重要方法.在基于流场机理的高速列车的局部改型优化上, 国内外****相关的探索工作,主要包括实验和数值模拟两方面. 在实验方面, 通过对日本新干线几种模型的研究,得到了转向架整流装置的安装对动车组周围流场空气动力学的影响[7].文献[8]通过风洞试验对ETR500列车运行参数进行了检测,得出转向架整流装置可以降低高速列车运行的气动阻力. I Do等[9]通过风洞试验发现列车底部气流对底部形状非常敏感.文献[10,11]对不同头型的高速列车模型进行了风洞试验研究,给出了列车减阻的措施. 在数值分析方面, 针对CRH380型列车,部分****也在局部构型优化上做了相关研究.杨加寿等[12]以3节车厢组成的CRH380型列车简化模型为基础,研究7种风挡形式对各车厢和车厢连接处气动性能的影响.研究结果发现采用全风挡车厢连接处的气动阻力最小;仅有内风挡车厢连接处气动阻力最大; 采用上下和两侧闭式风挡阻力介于其中,且更具工程易实现性.兰州交通大学的杨恩宇[13]以CRH380A外形为基础建立3编组列车模型,对5种不同风挡类型的气动特性进行了对比分析, 其气动阻力表现排序为:全封闭外风挡>闭合式半风挡>带缝式半风挡>内偏置式半风挡>内风挡,全封闭外风挡气动阻力系数比仅有内风挡时的降低了约20%,内风挡的减阻效果最差.Kaltenbach等[14]的研究表明转向架装置显著改变车底流量.郑循皓等[15]分析头尾车末端裙板和导流结构, 对转向架阻力的影响,指出适当改进车底结构有利于减小转向架气动阻力.杨志刚等[16]通过分析国外某型号高速列车转向架及周边裙板对整车气动性能的影响,表明在车底安装裙板有利于减小列车气动阻力. Wang等[17]的研究表明,转向架整流罩对高速列车的滑流和尾流有影响.全包整流罩覆盖的转向架显著降低了列车的滑流速度,削弱了高速列车尤其是转向架附近的压力波动.较大尺寸的整流罩可以减小尾流区纵向涡的尺度, 降低尾流速度分布.建议采用较大的转向架整流罩来改善列车的气动性能,提高轨旁作业人员和站台乘客的安全性. Wang等[18]对350 km/h动车组明线运行进行了数值分析,得出通过添加侧向裙板的措施可降低列车的运行阻力,并描述了添加裙板后转向架底部空间的流场分布特征.
基于优化算法的外形优化, 国内外****也进行了大量的研究,大多数的研究成果是运用于头部形状的设计.该方法主要是通过数学方法在一定约束范围内对设计变量进行自动寻优,对设计者的工程经验要求较低.Krajnovi[19]以径向基神经网络和多项式函数为组合代理模型,对列车的气动特性进行了优化.熊骏[20]基于多目标遗传算法NSGA-II和近似模型方法,以明线列车气动阻力和侧风下头车倾覆力矩为优化目标,对列车三维外形进行气动优化设计. 结果表明: 优化后的列车外形向着头型更尖扁,横断面积更小, 车身侧壁弧度增大的方向变化. 刘加利等[21],以气动阻力和偶极子噪声源为优化目标,对高速列车流线型头型进行减阻降噪的多目标优化设计, 利用多目标遗传算法NSGA-II对优化设计变量进行更新, 实现高速列车流线型头型的多目标自动寻优设计.优化后的流线型头型最大可使高速列车的气动阻力降低 4.54%,偶极子噪声源减小4.95 dB. 李明等[22]采用 CATIA软件对列车模型进行参数化,并通过 Insight 优化软件对优化过程进行集成,提出了一种参数化驱动的优化设计方法.文献[23]采用遗传算法对高速列车进隧道时的鼻部形状进行了优化.孙振旭等[24]采用直接网格变形技术, 省去了几何重构和网格划分时间,对高速列车鼻部形状和司机室上壁高度进行减阻优化设计,优化后列车气动阻力减小1.85%.于梦阁等[25]对高速列车的流线型头型进行多目标优化设计,优化后的列车阻力减小4.15%, 轮重减载率减小1.72%,该作者还对横风下高速列车流线型头型进行多目标自动优化设计[26],以高速列车的侧力和升力为优化目标, 结合多目标遗传算法对气动性能进行了优化.翟建平[27]也做了横风载荷作用下列车头型优化的探究.姚拴宝等[28]通过对CRH3型动车组阻力分布特性进行研究,表明头车一位端转向架比其他转向架的气动阻力明显偏大,因此在头型优化时考虑了转向架,在自由曲面变形法FFD的基础上采用局部形状函数LSF参数化方法,对高速列车鼻部外形进行优化, 该方法可以在少量设计参数的情况下控制大变形,保证变形区的平滑和不同变形区的平滑过渡, 在寻找全局最优解上有优势[29].以头+一节车厢+尾列车简化外形为例, 气动阻力降低了8.7%.该作者后期以CRH380A高速列车流线型为基础,以尾车气动升力和流线型头部体积为目标, 建立了基于响应面的多目标优化过程,优化后的高速列车运行安全性和舒适性有很大提高[30].在姚栓宝研究工作的基础上, 龚明等[31]以3辆编组高速列车为例,以整车气动阻力系数、流线型部分容积、尾车气动侧向力系数和尾车倾覆力矩系数为优化目标,以鼻锥厚度、鼻锥引流、鼻锥高度、车体宽度、司机室视角和排障器形状为设计参数利用多目标优化算法得到满足约束条件的Pareto最优解集, 利用测试函数验证优化设计方法的可靠性,进行横风环境下高速列车的外形优化.He等[32]为提高无侧风条件下高速列车空气动力性能优化的精度,提出了一种基于混合代理模型方法和基于竞争机制的多目标粒子群优化算法的全局优化策略.混合代理模型和基于竞争机制的多目标粒子群优化算法的使用极大地提高了优化效率.Munoz Paniagua和Garc$\acute{i}$a[33]研究了高速列车在零偏航角条件下,最大限度地减小阻力系数的车头形状优化问题. 以列车气动模型为参考几何模型,采用遗传算法进行优化. 优化设计使阻力系数降低到参考几何形状的32.5%.张亮等[6]基于伴随方法和径向基函数网格变形技术,选取整车气动阻力和尾车气动升力为优化目标,对高速列车头型进行多目标气动优化设计. 优化后, 在满足约束条件的情况下,列车的整车气动阻力减小2.83%, 尾车气动升力减小25.86%.
可以看到,国内外****基于流场机理的改型优化和基于优化算法的外形优化在高速列车气动外形优化设计中都积累了一定的研究成果.在基于流场机理的改型优化上主要研究工作包括:转向架整流装置、不同形式的车底导板、转向架舱导流结构、风挡和转向架及周边裙板设计几个方面,发现在高速列车的减阻上全封闭外风挡的减阻效果最好,在车底安装裙板有利于减小列车气动阻力,适当改进车底结构有利于减小转向架气动阻力. 在基于优化算法的外形优化上,大多数工作主要针对高速列车车头流线型进行优化设计,部分****也对进隧道时的鼻部形状进行了优化以及对横风下高速列车流线型头型进行了优化.在优化方法上主要有基于CATIA 软件对列车模型进行参数化驱动的优化设计方法,局部形状函数参数化方法, 多目标遗传算法 NSGA-II.不同的改型方法和优化方法在选定的优化目标上都取得了一定的效果.本文将系统总结近年来我们在高速列车气动外形优化设计上进行的一系列工作,基于与工程部门紧密结合的优势,分析运用的不同优化策略进行气动外形优化的优缺点,并结合典型工程实际展示优化效果.
1 基于流场机理的改型优化
近年来, 随着计算流体力学的发展以及计算能力的提升,已经可以通过精细CFD数值模拟来完成高速列车的气动特性分析,获取高速列车的尾涡特性, 底部流场特性, 横风特性,以及各种运行场景下的流场特性, 进而获得典型流场结构对宏观气动力的作用机理.这使得基于高速列车的复杂流场机理进行列车结构的改型优化成为可能,也是当前进行高速列车气动优化的一个最直接可行的方法.由于有限工况的数值模拟计算代价较小, 且极易给出相对于原始设计更优的气动外形,因而这方面的研究相对来讲比较充裕, 成果也比较丰富,许多研究成果已经成功地应用在新型高速列车的外形研制上.下面将结合不同高速列车的外形研制, 介绍我们在其中做过的气动外形优化工作.
1.1 和谐号局部结构改型优化
和谐号高速列车, 也称为新一代高速列车, 主流车型包括CRH380A和CRH380B等.在外形设计时, 多基于原有的引进高速列车, 在其外形基础上做改型优化.本节重点讨论针对CRH380B列车进行的改型优化. 精确地气动分析是改型优化的前提,在对CRH380B进行优化改型之前首先对原型车做了详尽的气动分析[30].以便于更有针对性的对其外形进行合理设计. 作为原型车,图1为CRH3型车的8编组实车外形.图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1CRH3的8编组实车外形方案
Fig.1Real CRH3 model with 8 carriages
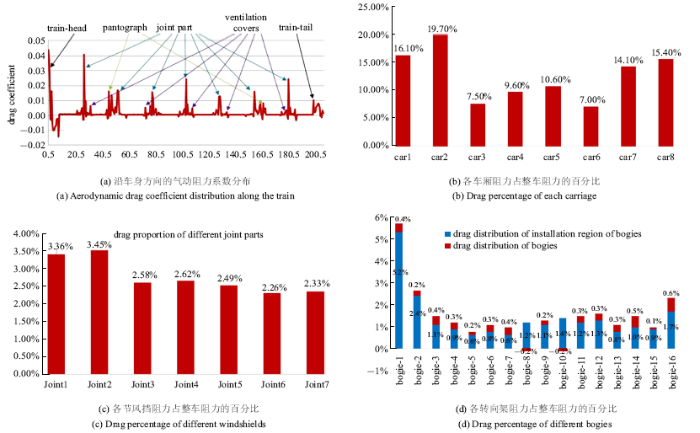
如图2所示对其进行气动特性分析.图2(a)为沿车身方向整车不同位置的气动阻力系数分布,图2(b)为各车厢阻力占整车阻力的百分比. 可以看到, 在整车气动阻力上,头车与尾车阻力占总阻力的31.5%, 第二节车厢与第七节车厢占总阻力的33.8%,其余中间四节车厢占总阻力的34.7%. 整体来说, 第二节车厢的阻力最大,头车和尾车次之, 主要是因为靠前的车厢与来流的作用相对于靠后车厢更为强烈,存在较大的压差阻力. 随着来流向后移动, 流场与车厢作用后边界层逐渐增厚,所以靠后的车厢压差阻力相对减小, 摩擦阻力的作用增大,但总体来看中间车厢的阻力仍然较小. 对于尾车而言,由于尾车和头车一样都是流线型过渡外形, 流速发生快速变化,且流场在尾部还存在涡脱落等尾涡效应, 使得尾车处的压差阻力也较大,因而尾车整体阻力也较大. 对于靠前的第一、第二节车厢, 由于CRH3的8编组车型,受电弓安装于第二节和第七节车厢, 受电弓也是列车上重要的阻力来源之一,使得第二节车厢上的阻力增大并超过了头车阻力.
从图2(c)对风挡的气动阻力情况进行分析,发现风挡带来的阻力占整车阻力的19.1%, 其中第一个与第二个风挡占6.81%; 在图2(d)中对转向架阻力情况分析上可以看到, 转向架阻力约占整车阻力的27.4%,其第一个与第十六个转向架占7.9%;从受电弓的分析上发现受电弓阻力约为整体阻力的12%, 空调整流罩占到7.6%.
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2CRH380B的8编组气动力分析结果
Fig.2Aerodynamic performance of CRH380B
可以看到,对整车气动阻力影响较大的区域主要集中在风挡、空调导流罩、受电弓导流罩和转向架处等外形复杂或直接大面积裸露于列车外部的部分.这些部件对流场的干扰较大, 也较容易产生流动分离等情况. 基于空气动力学原理,减少流动分离, 使气流更加光顺地流经车体, 可以适当进行改型优化. 如图3所示,针对CRH380B列车, 进行了改型优化. 保持基础外形不变,头车、尾车、受电弓、转向架外形不动,将风挡由原来的开口式设计为半包和全包方式;将空调整流罩与车体连接处设计为过渡更好的流线型;将受电弓导流罩外形设计为流线型过渡; 将转向架区域设计为全/半包裙板.
将改型设计的风挡、空调导流罩、受电弓导流罩和裙板的新方案减阻情况与原设计方案相比,如表1所示, 可以看到, 风挡的半包和全包形式都使列车阻力有所降低,且减阻效果相当. 该结论与杨加寿等[12]和杨恩宇[13]对于风挡结构的研究结论相一致.将空调导流罩流线化, 裙板向下延伸也都起到了一定的减阻效果. 同时,可以明显看到转向架延伸至与设备舱平齐有较好的减阻效果. 在实车设计中,考虑到实际生产和维修等后期问题, 建议设计方案为外风挡采用半包形式;空调整流罩采用流线型; 头车转向架裙板下延至转向架轴心高度, 同时向外圆滑过渡;其他转向架裙板下沿80 mm, 对该设计方案进行分析可以看到其综合减阻效果明显,减阻率为8.9%.
1.2 复兴号局部结构改型优化
作为和谐号之后的下一代主力高速列车车型,复兴号高速列车在气动性能又有了进一步的提升,这主要得益于更深入的局部结构改型优化.尽管和谐号列车阻力特性相对于引进的CRH2和CRH3型列车等有了较大提升,但是其在受电弓区域、风挡区域、转向架区域等均有进一步优化的空间,本节将介绍我们在这些部位改型优化取得的成果.图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3CRH380B的局部外形优化方案
Fig.3Partial shape optimization scheme of CRH380B
Table 1
Table 1Comparison of drag reduction in different design schemes
 |
新窗口打开|下载CSV
1.2.1 受电弓平台设计
相对于"和谐号", "复兴号"最突出的改变就在受电弓平台上."和谐号"列车受电弓直接裸露于车体之上, 以CRH380A为例,尽管在受电弓左右两侧增设挡板, 但其作用主要体现在降低噪声向两侧的辐射上,但同时又作为阻力源给整车带来了额外的阻力. 因此在新列车的设计时,摒弃掉导流板以及受电弓裸露的方案, 而采用受电弓平台使其下沉一定高度,将受电弓的大部置于车身速度边界层内, 从而降低受电弓阻力和远场噪声辐射.
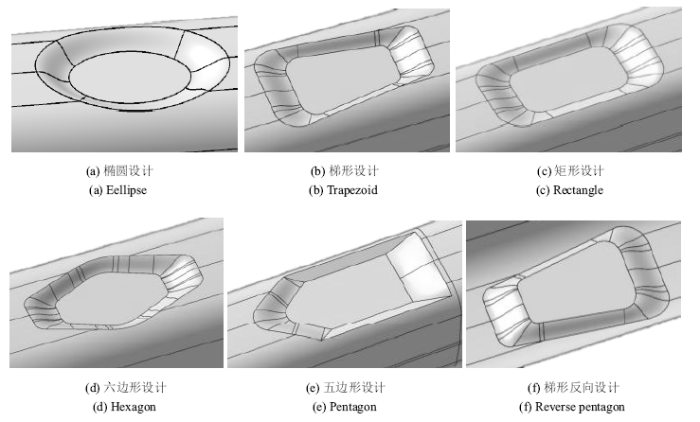
在平台设计时, 存在以下关键问题: 平台轮廓、平台深度以及平台侧边设计等.平台轮廓即平台外形, 在设计时需要综合考察流体力学效果以及美学效果,在外形设计时引入椭圆设计、梯形设计、矩形设计、六边形设计、五边形设计几种不同的设计方案,研究其气动阻力特性差异, 这几种外形如图4所示.其中原平台为水平光滑未做任何处理, 受电弓直接裸露于车体上的结构,在该处没有展示其几何形状.
数值仿真均为置于8编组列车之上, 计算来流速度为350 km/h, 密度为1.225 kg/m$^{3}$,参考面积为11.942 m$^{2}$. 如无特殊说明, 以后各节分析均同.几种方案的受力统计如表2所示.
Table 2
Table 2Force statistics of six pantograph platform schemes
 |
新窗口打开|下载CSV
可以发现, 梯形方案(前宽后窄)对应列车整车气动阻力最低,是所有外形设计中的最佳方案. 然而, 在所有外形对比中发现,最优与最差方案相差很小, 最差与最优之间相差仅为1%, 这说明,受电弓平台的外形对气动力的影响可以忽略. 在外形设计时可以不用从气动角度考虑,相反可以从美学、工程加工等角度进行考虑.
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图46种不同的受电弓平台外形
Fig.4Six different shapes of pantograph platform
气动阻力可以分为压差阻力和摩擦阻力,而在平台高度设计时则需要重点考察由于高度变化引起的受电弓、受电弓平台以及受电弓下游车体的阻力变化,最佳高度需要在这三者的总体阻力变化中寻求最优.尽管受电弓下沉会降低受电弓本身承受阻力, 但由于受电弓区域整体高度降低,其下游车体因为边界层变薄, 其承受的摩擦阻力又会有一定提升, 另外,平台深度增大也会增大平台本身的压差阻力. 通过分析不同平台深度发现,当深度为380 mm时列车整体阻力最优.
在平台侧边设计上, 需要重点考察侧边导流与全凹腔设计两种思路.侧边是否如空调导流罩一样进行大的导流设计主要基于由于平台本身带来的额外气动阻力.然而当进行大导流设计时, 尽管会一定程度上降低平台本身的阻力,但是导流会引导气流高速冲向腔内撞击到受电弓底座, 导致受电弓压差阻力剧增.当进行凹腔设计时, 平台本身的阻力会有一定幅值增大, 但是气流在流经凹腔平台时,会在凹腔前壁面下游产生流动分离, 形成大尺度涡,这样使得受电弓底部受到来流的冲击大大变小. 整体来看,侧边设计也需要综合考察受电弓及受电弓平台的整体受力.
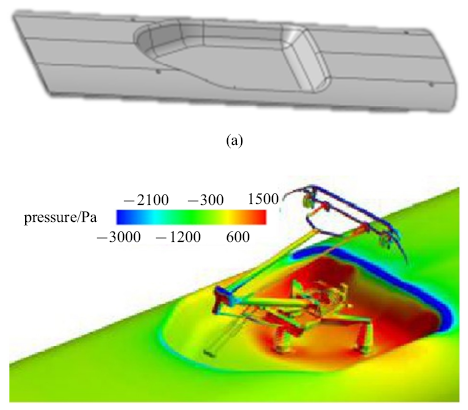
通过一系列轮廓及倒角分析, 并基于客室空间考虑, 最终确立平台方案如图5(a)所示.图5(b)给出了受电弓平台的表面压力分布云图, 可以看到,尽管在平台内下游区域存在局部高压, 但由于受电弓底座整体落于平台内,其承受的压力阻力获得大幅降低. 整体来看,相对于完全裸露于车体表面的原始设计方案, 新的平台方案减阻约4%.
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5最终平台设计方案及表面压力分布
Fig.5Final platform design scheme and the pressure contour around it
1.2.2 风挡外形优化设计
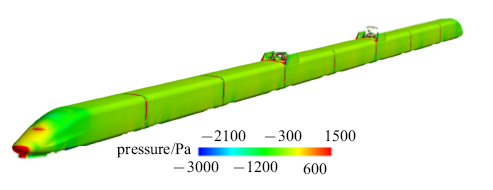
不同风挡形式的设计都有可能引起列车阻力性能的变化,进而会对列车运行的安全性、舒适性和能耗产生影响.如2.1节CRH3型高速列车气动分析可见,无外风挡情况下所有风挡承受阻力可以达到整体阻力的19.1%,具有较大的优化空间. 在新一代高速列车设计时, 对风挡区域进行了一定优化,增设了外风挡, 但是该外风挡并非全封闭风挡, 高速气流仍然可以流入风挡内部,形成较大阻力. 图6给出了典型的CRH380A高速列车的整车表面压力分布云图.可以看到, 在各个风挡部位均存在非常明显的高压区域, 从数值分析上来看,风挡承受阻力占总体阻力约11.7%, 可见风挡部位减阻依然存在较大空间.
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6CRH380A高速列车的整车表面压力分布云图
Fig.6Pressure contour of CRH380A
尽量少的控制气流流入到风挡内部可以大幅降低风挡部位阻力,新的设计方案即从该方向展开, 确立全包外风挡设计方案.典型的全包方案及压力分布云图如图7所示.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7典型风挡全包方案及压力分布云图
Fig.7Typical windshield full package schemes and pressure contour on corresponding scheme
从研究结果上看, 对于全密封风挡, 假如风挡部位几何过渡不够光滑,在这些位置将会产生涡旋, 从而影响风挡气动力.现实设计中在考虑列车转弯特性以及风挡材料属性的基础上, 尽量保持光顺化,CR400AF采用了方案三设计, 八编组真实列车外形中风挡在总体阻力中占比约5.5%,气动性能获得了大幅提升.
1.2.3 转向架舱外形优化设计
在对CRH3列车的研究中已经发现转向架是高速列车气动阻力的一个重要来源.突出于列车车体的部位会受到来流的冲击, 会产生较大阻力,这部分阻力是不可避免的, 除非改变车体高度等硬性参数.而隐藏于列车车体部分的转向架, 其阻力大小主要由转向架舱的外形设计来决定的.合理的转向架舱外形可以有效引导来流进入舱内的方向,使得冲击到转向架上的冲击力大幅降低, 从而可以有效降低阻力.在对复兴号转向架舱设计上重点研究了开舱大小以及舱口倒角对列车气动性能的影响.
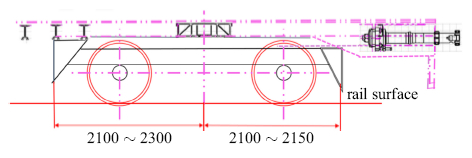
对转向架舱进行外形设计, 考察转向架舱的前后倾角等对列车整体性能的影响.其前倾角下缘边线移动范围为2100~2300 mm,后倾角下缘边线移动范围为2100~2150 mm,转向架截面变化范围如图8所示.
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8转向架舱横截面尺寸
Fig.8Cross sectional dimension of bogie cabin
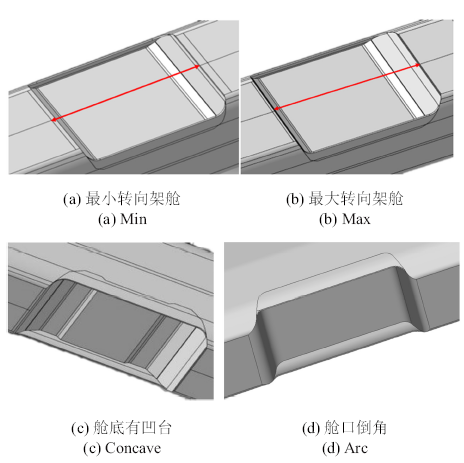
变化转向架舱前缘和尾缘, 交叉组合可以形成以下4种工况: 最小转向架舱,最大转向架舱, 前倾角最大+后倾角最小, 前倾角最小+后倾角最大.为了考察舱底平面外形的影响, 在最大转向架舱基础上加算平面存在凹台工况.为了考察转向架舱下缘倒角对整车气动力的影响, 在最小距离基础上加算大倒角工况,因而共计有6个工况.在6种工况中选取代表性的最小转向架舱、最大转向架舱、舱底有凹台以及舱口倒角四种外形进行详细探究,外形设计如图9所示.
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9四种转向架舱示意
Fig.9Four kinds of bogie cabins
4个工况的受力情况如表3所示.
Table 3
Table 3Relative aerodynamic drag values of four shapes
 |
新窗口打开|下载CSV
研究发现转向架舱最小方案使得舱内空间狭小, 较少气流可以直接流入舱内,转向架承受的压差阻力大幅降低. 在开舱口较大时, 气流极易流入舱内冲击转向架,从而带来高阻力. 针对舱口倒角的研究发现, 大导角会使气流流入舱内更加方便,从而导致列车气动力整体大幅提升.
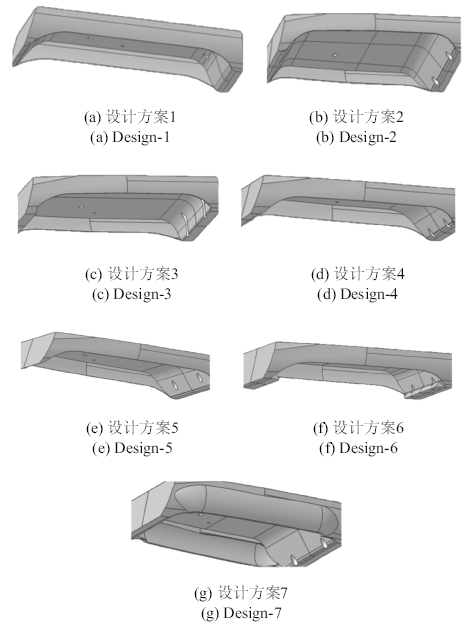
基于以上分析, 在最终确认CR400AF的转向架舱气动外形设计前,备选最终外形设计方案包括7个, 基本外形如图10所示.
图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10转向架舱的最终7个设计外形方案
Fig.10Seven design schemes of bogie cabins
对其进行气动特性分析, 整体气动阻力如表4所示.
Table 4
Table 4Comparison of drag coefficients of seven design schemes
 |
新窗口打开|下载CSV
可以看到气动阻力最小的模型为design-6, 而阻力最大的模型为design-7.从外形设计来看, 设计7由于两侧分别存在一个凸起,这个凸起会给列车带来额外的气动阻力. 此外,转向架舱下侧是否存在比较大的倒角是阻力效果差异的一个重要因素.设计1和设计5的倒角效果最明显, 设计3不存在倒角,而设计6则将原来的倒角设计取消掉, 采用了两个棱柱块挡住倒角区域,同时也限制住了转向架舱的空间大小. 从效果上来看, 这种设计阻力降幅最为明显.当存在大的倒角时, 气流会更易沿着倒角方向流向转向架舱,使得舱内转向架承受了更大的阻力. 而回避掉这个倒角后,若转向架舱边缘更贴近于转向架, 使得转向架舱的凹腔效果不明显,从而有效降低了转向架承受的阻力.
1.2.4 复兴号局部改性优化小结
针对受电弓平台的研究发现, 平台高度对气动阻力的影响并不是线性的,主要表现在两个方面: 随着平台深度增大, 列车车体的摩擦阻力会逐渐变大;而随着平台深度增大, 由于裸露于车体上的受电弓迎风面逐渐变小,因而其压差阻力也在逐渐变小.列车整体受力需要同时考察这两个变化方向相反的力的作用.针对凹腔类型的受电弓平台, 由于漩涡的存在, 会加大平台本身承受的气动阻力.同时由于漩涡的存在, 直接冲向受电弓气流的流速会大大降低,因而受电弓本身的受力会得到有效降低. 列车整体的阻力效果是这两个作用的叠加.
针对风挡设计的研究表明, 风挡部位的表面平整度是影响风挡气动性能的关键因素,全封闭风挡由于不会导致气流向车厢间流动, 整体上气动性能都要优于半封闭风挡.半封闭风挡部位形成三维涡的强度要远大于全封闭风挡.在风挡设计时应该尽可能的使用全封闭风挡, 且风挡外侧应该尽可能地采用平整设计,以有效降低风挡本身产生的阻力.
针对转向架舱的研究发现, 转向架舱开舱口越小, 由转向架区域带来的阻力就越小.这是因为开舱口小导致舱内空间狭小, 较少气流可以直接流入舱内,当多数气流可以沿舱外侧直接流走. 在开舱口较大时, 气流极易流入舱内冲击转向架,从而带来高阻力. 针对舱口倒角的研究发现, 大导角会使气流流入舱内更加方便,从而导致列车气动力整体大幅提升.因而转向架舱舱口的设计已经尽量避免使得气流流向舱内,相反应该尽可能地将气流导流到舱外.
通过搭载所有部件较优设计方案的CR400AF与CRH380A的比较分析可以发现,相对CRH380A, 标准动车组的气动性能具有大幅提升.通过针对列车各个部件的详细统计可以发现,气动性能提升的主要部位在受电弓区域以及风挡区域. 两者在设计上的区别表现为:CR400AF列车受电弓两侧无立板, 受电弓下沉在平台内, 高压设备无裸露;而CRH380A立车受电弓两侧有立板, 无受电弓平台降阻,高压设备完全裸露于受电弓下游. CR400AF列车采用了全封闭风挡,而CRH380A采用了半封闭风挡. 不同设计方案最大减阻情况对比如表5所示.
Table 5
Table 5Comparison of maximum drag reduction in different design schemes
 |
新窗口打开|下载CSV
2 基于优化算法的外形优化
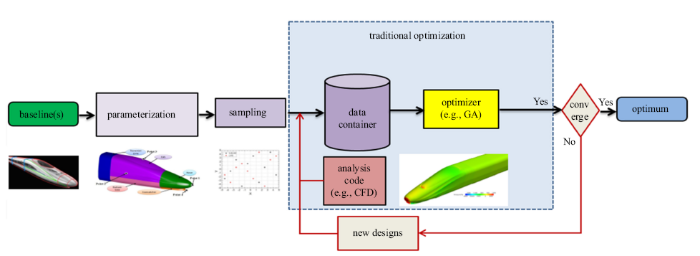
基于流场机理进行高速列车的气动外形优化,很大程度上依赖于****的空气动力学理论认知以及工程师的工程经验, 二者相互结合,可以高效地给出一个更优的优化外形, 相对于原始方案,该优化外形通常会有大幅的性能提升. 然而,当针对各个特殊部件都进行了基于流场机理的优化之后,这类优化方式已经达到了其性能提升的极限. 譬如, 针对空调导流罩的平顺处理,到底该采用多大的导流角度才能达到最优; 针对转向架裙板的高度设置,到底该采用多大的高度才能阻力最小. 传统的工程师经验在此已经失效,这时必须要采用优化算法, 细化需要进行气动优化的具体设计变量,基于优化算法寻优获得最佳参数组合. 采用数学方法获取最佳外形,同时还可以获得各个具体变量对优化目标的影响规律, 而这些规律通常是非线性的,可以给列车设计者们带来更加细化的设计经验. 基于优化算法的高速列车外形优化,通常是在列车外形已经具有较好性能的基础上进行的, 因而其优化收益可能会比直接细部结构改型设计要小一些.但是由于该设计过程依赖于严谨的数学理论, 又可以额外提供各类设计变量影响规律,因而基于优化算法的外形优化是非常有必要的.气动外形优化设计, 从流程上来讲可以分为3大部分,即参数化设计、性能评估和优化算法3类. 传统气动外形优化流程如图11所示.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图11传统气动外形优化流程
Fig.11Traditional aerodynamic shape optimization process
为了有效提升气动外形优化的精度和效率, 自然可以在以上3个部分展开详细研究.而针对高速列车气动外形优化而言,首先要面对的问题就是第二个问题——性能评估.当前性能评估主要是采用CFD进行分析, 获得具体的气动性能参数.性能评估的难度限制了高速列车气动外形优化的实际应用.高速列车复杂的几何外形给气动分析带来了极高的计算代价,从而影响了气动外形优化的效率.针对长大编组真实外形的高速列车进行常规的气动分析已经难度较大,更不用说在优化问题上需要针对每一个设计点重复进行一系列的气动分析.这是高速列车气动外形优化难以展开的一个重要原因. 然而,针对气动外形的优化需求是真实存在的,这也促使科研工作者们通过各种方法来解决这个问题. 当前主要的开展思路有两种:(1)弱化模型复杂度. 即在不影响分析问题的前提下, 简化列车模型.例如在开展列车头型优化的时候, 可以简化列车的编组数,由常规线路运行的八编组或者十六编组简化为三编组, 即包含首尾车和一节中间车,这样既包含了首尾车带流线头型的关键车厢和一个典型的中间车厢. 另外,还可以简化掉受电弓、中间车的转向架等细部结构,由此使计算模型获得进一步的简化. (2)发展精度较高的替代模型.传统的气动外形优化, 若采用梯度算法等尽管可以提升优化速度,但极易陷入局部最优, 得不到全局最优解. 然而,若采用遗传算法、粒子群算法等全局优化算法, 优化效率则会受到较大制约.为了解决这个问题, 当前一个比较有效的方法是开展基于替代模型的优化研究,即基于已有设计点数据构建精确的设计变量与优化目标之间的非线性映射,并不断精确化该替代模型. 在满足精度要求的前提下,则可以在该替代模型上采用全局优化算法进行寻优,而此时寻优不需要针对设计点进行额外的气动计算. 可以看到,基于替代模型进行寻优, 仅需要在替代模型的构建中进行有限次数的CFD计算,远远小于直接采用优化算法进行优化时的CFD计算次数. 因此,优化效率可以获得可观提升. 具体优化流程如图12所示.
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图12基于替代模型的气动外形优化流程
Fig.12Aerodynamic shape optimization process based on surrogate model
此外, 参数化设计是整个优化的基础. 参数化对应优化设计过程中设计变量的个数,而设计变量的个数与优化设计需要进行性能评估的次数成幂指数关系.多一维设计变量就会给性能评估次数多增大一个维度. 合理的参数化方法,需要采用尽量少的设计变量有效描述气动外形的变化.发展小样本量的参数化方法也是影响高速列车气动外形优化设计的一个关键因素.
基于以上分析,本节拟从参数化方法、替代模型开发以及优化算法改进等方面概述当前高速列车外形优化的现状以及我们在其中开展的一系列工作,最后给出两个典型的气动外形优化算例.
2.1 参数化方法
高速列车几何外形的参数化是优化设计的基础. 高速列车头型的长细比较大,其几何外形由复杂的自由曲面组成, 在设计过程中曲面变形非常大,甚至会出现类型完全不同的曲面形状, 因此,发展专门针对高速列车头型的参数化设计方法显得十分必要.目前常用的曲面参数化方法有:解析法、网格点法、样条曲面法、基于曲面的自由变形法等.解析法则直接建立二维或三维控制面的控制方程,通过修正控制方程的参数来控制变形, 但是这类方法多针对简化外形,实际应用性不强[34-36]. Iida等[35]直接给出了二维头型的参数化表达式,通过修改形状控制参数来获得不同的头型方法.Kwon等[37]则在Iida的基础上增大了Hicks-Henne外形函数,研究表明由此可以获得更好的几何外形.而Lorriaux和Valta则将二维列车头型简化为由5个参数控制的两段椭圆弧,分别控制了流线型长度、鼻锥高度和头型角度等变量, 以此实现更为精细化的变形.二维方法是面向高速列车头型参数化的简单尝试,为后续三维的参数化研究奠定了基础. 从二维方法拓展到三维,在欧洲开始设计了完全由简单方程控制的简化列车外形.该头型由Sima等[38]在2011年提出, Paniagua等[23]针对上述车型选取了l1, l2, R1作为基本优化变量, 分别控制了头车平整段长度、鼻锥钝度和底部圆弧过渡.由于外形的构建极其简单, 可以直接在Catia中参数化构建而成.因而其外形的参数化可以由Catia完成, 生成新的设计外形.此外形也经常被后续研究者采纳用作外形优化研究.网格点法虽然可以描述任意外形, 但较容易产生非光滑病态型面,对设计变量的数量和网格点梯度求解要求苛刻,但这类方法在实际列车流线头型参数化中应用较多;自由变形法和样条曲面法是性能良好的曲面参数化方法,能够使用较少的控制点控制较大的变形区域, 而且能够保证曲面的光顺性.基于样条曲面法的研究, 当前主要借助于造型软件Catia,其主要思想为通过若干个控制点建立B样条控制线,而若干条控制线可以形成特定B样条曲面, 通过控制点坐标的变化驱动控制线,进而控制列车曲面变形. 国内主要由西南交通大学团队,包括刘加利、张亮等广泛使用.
接下来将简要介绍本团队在高速列车头型参数化中做过的一系列工作,主要包含以下几类参数化方法,分别为局部型函数法、修正车辆造型函数法和类别/形状函数法、自由变形法等,本节重点介绍前三类参数化方法. 按照参数化实现方法的区别,可以概述为扰动类和描型类参数化方法. 扰动类参数化方法即针对已有的外形,通过设置不同的设计变量, 在原始外形上产生一定的增量变化,而新的外形则由原始外形叠加扰动产生的增量变化形成.这类参数化方法通常具有变形直观、快捷方便等特征.而描型类参数化方法需要综合分析高速列车流线头型的特点,确立关键的型线特征或者曲面特征, 进而确立恰当的型线方程或者曲面方程,能够描述关键型线/曲面的特征. 在此基础上,关键型线可以进行空间插值形成基本的流线头型, 曲面方程则可以直接形成流线头型,曲面的参数化则可以通过型线方程/曲面方程的系数来定义. 本团队发展的几类方法中,其中局部型函数法和自由变形法属于扰动类参数化方法,而修正车辆造型函数法和类别/形状函数法则属于描型类参数化方法.
2.1.1 局部型函数法
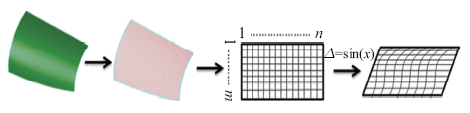
局部型函数法由我们首次提出[39-42], 其具体实现步骤为:(1)对于给定的几何外形, 根据具体的优化问题, 划分出需要局部变形的区域,为了更加容易实现几何曲面光滑变形, 在不影响整体变形的情况下,选取的变形区域应尽可能的保证边界坐标值一致,即同一边界的某个方向的坐标值相等. (2)对划分的区域进行网格离散,得到所有区域的离散网格点的坐标值, 为使变形曲面更为光顺,网格离散使用结构网格离散方法, 如图13所示. (3)设计每个区域的变形函数,变形函数的选择具有一定的任意性, 但需要保证每个区域边界处的光滑过渡. 为此,对于规则边界(沿某一方向的离散点坐标值不变),可以使用离散点的坐标值作为变形函数的自变量;对于不规则边界(沿任意方向曲面的离散点坐标值均不同),需要使用离散点的拓扑编号作为变形函数的自变量, 由此, 将不规则曲面投影到平面,并成为一个规则的长方形区域, 如图13所示.(4)为每个型函数设置一个权重因子$w_{i} $, $w_{i}$的代数和决定变形曲面的最大变形量.(5)根据每个区域所选择的型函数和权重因子计算出所有离散网格点的坐标增量值$\varDelta$. (6)将得到坐标增量值$\varDelta$与原始离散网格点的坐标值代数相加,得到变形后外形网格点的坐标值.(7)根据变形后外形网格点的坐标值重新拟合出变形后的曲面, 完成一次变形.
图13
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图13局部型函数曲面变形示意图
Fig.13Surface deformation diagram of local function
步骤(3)是参数化过程的关键, 不同的变形函数会产生完全不同的曲面变形,选择不合适函数容易导致病态变形,常用的变形函数有三角函数、指数函数、对数函数等,较为复杂的有多项式函数、样条函数等.
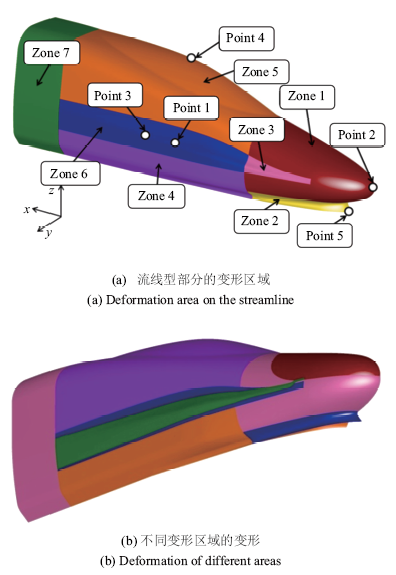
以CRH380A流线型为例介绍局部型函数法的具体应用.将参数化部分分隔为7个变形区域, 如图14(a)所示.变形区域4~7共同控制车体宽度, 提取一个设计参数$w_{1}$为控制点Point3沿$y$方向的坐标值; 变形区域5和6控制司机室的视角,提取一个设计参数$w_{2} $为控制点Point4沿$z$方向的坐标;变形区域1和3控制鼻锥高度, 设置一个控制点Point2,提取其$z$方向坐标为设计参数$w_{3} $; 变形区域3和6控制鼻锥处的引流,设置一个控制点Point1, 提取其$y$方向坐标为设计参数$w_{4} $.在不影响设计空间内几何曲面任意变形的情况下, 为便于操作,所有变形区域均使用三角函数作为变形函数, 图14(b)给出了鼻锥处和排障器的变形,可以看出, 变形区域能够保证曲面的光顺性,而且不同变形区域之间能够实现光滑过渡.
图14
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图14流线型部分的变形曲面
Fig.14Deformation surface of streamline region
2.1.2 修正车辆造型函数法
高速列车头型的细长比较大, 其几何外形由复杂的自由曲面组成,在设计过程中曲面变形非常大, 甚至会出现类型完全不同的曲面形状, 因此,发展专门针对高速列车头型的参数化设计方法显得十分必要.图15给出了高速列车鼻锥几何外形的关键控制型线, 纵剖面的外形由$L1$控制,排障器区域的外形由$L2$控制, 水平剖面和底部剖面的外形分别由$L3$和$L4$控制,最大横截面的外形由$L5$控制. 对于工程设计, 为了与已有的车厢相匹配,通常情况下最大横截面的形状是给定的, 因此, $L5$将是一个确定的外形,以CRH380A的最大横截面外形为原型. $L3$和$L4$的曲线外形是相似的,可以使用形式相同的数学表达式描述.$L1$和$L2$的形状对整个鼻锥的外形有很大影响, 通过改变这两条型线的外形,可以得到形状完全不同的头型, 尤其是$L2$, 其外形不仅对头型的美学效果有很大影响,而且对列车的气动性能影响很大.
图15
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图15鼻锥外形关键控制型线
Fig.15Key control profiles of the nose
VMF参数化方法是Rho等[43]通过对Bernstein多项式进行改进,针对汽车外形设计时存在许多小曲率半径的型线,为减少设计变量个数而提出的一种参数化设计方法. 相比于NURBS方法,该方法可以大大减少设计变量的个数, 有效提高汽车外形设计及优化的效率. Ku等[44]将VMF参数化方法引入到了高速列车头型优化设计研究中,提取了4个设计变量控制头型的几何形状,虽然如此少的设计变量难以考虑列车最大横截面形状、设备仓及司机室的容积,也无法得到可以用于工程设计的头型,但其设计思想可以为高速列车头型设计提供较好的参考和借鉴.我们基于以上研究成果, 并对其控制方程做进一步发展,使之更适合于高速列车的流线外形, 具体控制方程可以参考文献[45].
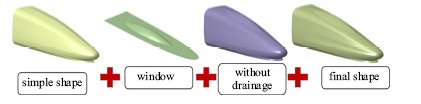
确定了各个关键型线的控制方程后,接着通过关键二维控制型线拟合出基本的曲面外形,使用拉普拉斯方法对不同曲面块之间连接不光顺的区域进行光顺处理.为了使曲面外形与实际流线头型尽量一致, 还需要将司机室玻璃叠加到基本曲面上,最后在鼻锥两侧添加鼻锥引流方式, 从而得到完整的流线外形,由此构成了MVMF方法的流线型参数化过程, 如图16所示.
图16
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图16MVMF方法的流线型参数化过程
Fig.16Streamline parameterization process of MVMF method
图17给出了不同的高速列车头型, 可以看出, 通过调整设计参数的值,能够得到完全不同的头部外形. 控制鼻锥外形的3条剖面型线决定了头型的基本轮廓,排障器区域型线的变化极大的丰富了头型的形状.司机室玻璃的形状和鼻锥引流方式的变化能够进一步调整头型的细微轮廓.
图17
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图17不同高速列车头型
Fig.17The streamlined shapes obtained by MVMF
2.1.3 类别/形状函数变换法
类别/形状函数变换CST方法最早应用于航空航天飞行器的参数化中,现有文献很难看到该参数化方法在高速列车流线型参数化中的应用.我们基于流线头型的特点, 对CST方法进行了算法实现,确立了形状函数和类别函数中的几个关键设计参数值,为了使由CST方法拟合出来的头型更接近于实际列车头型, 还基于优化拟合的思路,建立了基于优化的CST方法[42]. 在三维CST建模方法中,首先确定基于Bernstein多项式形状函数建立的CST截面表达式
$\begin{eqnarray*} \zeta \left( \psi \right)=C_{N2}^{N1} \left( \psi \right)\Sigma b_{i} N_{k}^{i} \left( \psi \right)+\Delta \zeta_{N} \left( \psi \right) \end{eqnarray*}$
三维外形可以看作一系列平行截面沿着轴线方向的组合.通过在不同的轴向位置处利用形状函数来描述不同的截面形状,确定出一个解析形状函数面, 从而得到整个三维外形的解析描述形式.在这里采用同样的CST参数化方法来表征截面形状沿轴向的变化, 定义
$\begin{eqnarray*} &&b_{i} =C_{M2}^{M1} \left( \eta \right)+\Delta \zeta_{M} \left( \eta \right)\\ &&s\left( \eta \right)=\mathop \Sigma\limits_{j=0}^{m} b_{j} N_{k}^{j} \left( \eta \right) \end{eqnarray*}$
其中, $\eta =x/L$为归一化的轴线坐标, $L$为几何外形轴向总长. 代入上式并展开
$\begin{eqnarray*} &&\zeta \left( {\psi ,\eta } \right)=C_{N2}^{N1} \left( \psi \right)C_{M2}^{M1} \left( \eta \right)\mathop \Sigma\limits_{i=0}^{n} \mathop \Sigma\limits_{j=0}^{m} b_{i,j} N_{k}^{i} \left( \psi \right)N_{k}^{j} \left( \eta \right)+ \Delta \zeta_{M,N} \left( {\psi ,\eta } \right) \end{eqnarray*}$
因此, 还需要参数化整个二维网格点阵的边界轮廓, 对$Z$引入同样的CST控制方式
$\begin{eqnarray*} Z\left( \eta \right)=C_{T2}^{T1} \left( \eta \right)\sum {_{i=0}^{w} b_{t} } N_{k}^{it} \left( \psi \right) \end{eqnarray*}$
以上定义了完整的三维参数化几何曲面的解析描述规则,将上述定义转换到具有物理意义的笛卡尔全局坐标系中, 即可得到归一化的三维 CST曲面表达式. 结合真实列车流线头型后部完全开口的特点,类函数的指数中$M2$和$T2$应该为0; 另外, 真实列车头型是沿中间对称面左右对称的,所以指数$N1$与$N2$应该相等, 权重系数矩阵$b_{w} $的各行元素也是对称的. 同时,为了进一步减少设计变量的数量,在参数化过程中指定3个维度的形函数的阶数都为3阶.
基于优化的CST方法还需要针对初始的外形进行拟合以更好的贴近真实流线头型.其具体实现过程为: 在真实列车头型几何文件的基础上,利用网格软件生成结构化的面网格. 调整网格的节点分布, 将网格$i$,$j$方向型线的节点调整为等距分布. 以调整好的真实列车头型面网格为拟合目标,对三维CST方法中的参数进行优化,得到能够使三维CST方法建模结果与真实列车头型最接近的一组参数.为了更好拟合真实列车头型, 在对三维CST方法参数优化的过程中引入两个约束条件:将$yz$平面和$xy$平面内参数化的截面型线与真实列车头型截面型线的距离和作为罚函数,并引入适应度函数中.这样在参数优化同时能够尽可能地减小参数化曲线与真实列车头型$yz$平面和$xy$平面内截面型线间的偏差.
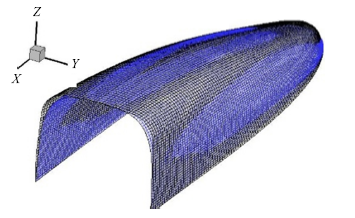
图18给出了经过参数优化后的CST参数化曲面和真实列车头型曲面的对比情况.可以看出, 优化以后, 三维CST曲面与真实列车流线型在大多数区域重合,在局部略有差别, 能够基本满足工程反设计的要求.
综合来看,局部型函数方法可以在流线型感兴趣部位直接设置设计变量实现光滑连续变形,具有设计变量易于控制、算法上较易实现等优点, 具有非常高的通用性.
图18
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图18CST曲面与真实列车外形设计对比
Fig.18Comparison between the CST surface and the real train shape design
修正车辆造型函数参数化方法为型线方程驱动的参数化方法,结合空间插值后可以细致的描述高速列车头型的三维外形,能够用于头型的概念设计和头型的优化设计, 有利于提高头型的设计效率. 但是,该方法也具有其固有的缺点, 即其对应的各个参数均为关键型线控制方程的系数,与实际外形的物理意义对应关系较差.
而类别/形状函数方法同样属于曲面方程驱动的参数化方法,既能够从无到有地构建列车的流线型外形, 也能够用于已有外形的参数化建模,该方法的缺点与VMF类似, 即其设计变量与流线头型的物理意义缺少一一对应的关系.
2.2 替代模型开发
在基于替代模型的优化设计过程中,需要耗费大量时间和计算资源的数值仿真计算由近似预测模型所替代, 因此,替代模型的精度、效率直接影响整个优化设计的准确性与成本控制.从20世纪70年代多项式替代模型被应用于结构优化设计至今,国内外****在优化设计领域发展和应用了多种代理模型方法. 其中,神经网络、Kriging模型、支持向量机回归、径向基函数替代模型等已经在航空航天中获得了大幅应用,在高速列车气动外形优化中也逐渐开始流行起来.本节将介绍我们在其中做过的一系列工作, 将按照发展替代模型的种类分别介绍.2.2.1 最优化替代模型
所谓最优化替代模型, 是指将优化算法和替代模型结合起来,通过优化算法确认构建替代模型的参数, 通常来讲,最优化替代模型会比传统的替代模型具有更高的预测精度. 基于这种方法,我们发展了传统的广义回归神经网络模型、最小二乘支持向量机模型和Kriging模型.
经典广义回归神经网络GRNN是径向基神经网络的一种, 建立在数理统计的基础上,不需要事先确定方程形式, 以概率密度函数替代固有的方程形式,具有很强的非线性映射能力以及高度的容错性和鲁棒性, 即使样本数量稀少,网络的输出结果也能收敛于最优回归面, 适用于解决非线性问题.GRNN将各个神经元的光滑因子设置为同一个值,网络的训练过程是对光滑因子的单值寻优过程,没有考虑不同光滑因子对输出结果的影响, 在一定程度上降低了网络的预测精度.所谓最优化神经网络模型, 可以将每个神经元的光滑因子作为一个独立的变量,根据不同神经元对输出结果的影响程度不同,使用遗传算法寻找每个神经元对应的最优光滑因子值, 构造出GA-GRNN模型,消除了使用同一个光滑因子对网络预测精度的影响.
支持向量机建立在统计学习理论的基础之上,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷.通过引入不敏感损失函数, Vapnik等[46]将SVM推广到非线性系统的回归估计,建立了支持向量机回归(support vector regression, SVR),并展现了极好的学习能力. 对于非线性回归问题,SVR首先使用一个非线性映射将数据映射到高维特征空间,然后在高维特征空间进行线性回归, 从而取得在原空间非线性回归的效果,为了解决在低维输入空间向高维特征空间映射过程中空间维数的急剧增长而难以直接计算最优超平面的问题,SVR引入了核函数, 从而将该问题转化到输入空间进行计算.最小二乘支持向量机LSSVR采用等式约束最小化目标函数,并引入平方和误差项代替原有的线性项, 避免了求解耗时的二次规划问题, Suykens等[47]又提出了修剪算法, 以解决最小二乘支持向量机带来的稀疏性问题.对于简单函数基于高斯径向基核函数的LSSVR能够表现出良好的泛化能力和回归精度,对于更为复杂的测试函数, 往往需要不断调整参数以及核函数指数来提高预测能力,而且实际工程问题往往复杂性、非线性、噪声影响更加突出,通过经验分析和调试合理的参数值需要花费大量的时间,对于回归精度的提高也收效甚微. 因此我们发展了最优化LSSVR代理模型.以LSSVR的关键参数以及核函数指数为设计变量, 以回归精度作为目标函数,通过数值优化算法求解最优的参数值.以最优参数值构建LSSVR模型作为最终的代理模型.
Kriging模型包含回归模型和相关模型, 回归模型是空间上的全局近似,相关模型反映空间分布结构, 对Kriging模型的预测能力有重要影响.Kriging模型的构建过程即为相关模型参数的寻优过程.相关模型参数为设计变量的影响权重, 当其值相同时, 相关函数各向同性, 此时,模型的预测精度较低, 因此, 为提高Kriging模型的预测精度,可以通过最大化响应值的似然估计将相关模型参数的求解过程转化为一个非线性无约束的最大化优化问题.
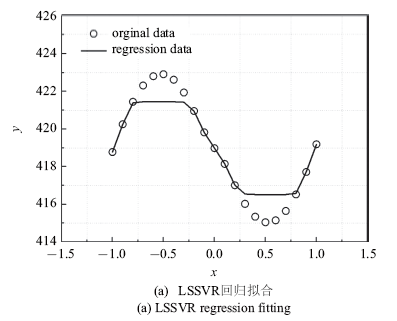
接下来以最优化支持向量机回归模型为例,讨论最优化替代模型与传统替代模型的精度差异.本节选用优化算法中常用的测试函数Schwefel函数
$\begin{eqnarray*} f(x)=418.9829-x\sin \left( {\sqrt {\left| x \right|} } \right) \end{eqnarray*}$
初始参数值$\left( {c,\varepsilon ,\gamma } \right)$设为(2.2, 0.01, 2.8),样本点统一设置为20个, 利用LSSVR和OPT-LSSVR进行回归拟合. 如图19所示, 可以看出,对于非线性较强的测试函数, 尤其在梯度较大的极值点附近,LSSVR的回归精度显著下降. 而针对最优参数模型拟合结果,回归曲线能够精确捕捉样本数据点的变化规律,在梯度较大的极值点附近也能够良好地拟合. 基于优化算法,最小化目标函数设为均方误差MSE, 得到每个测试函数对应的最优参数值.利用最优参数进行建模, 得到的拟合结果如表6所示. 从表6中对比数据可以看出,最优参数构建的LSSVR模型均方误差MSE\vspace{-3mm}\linebreak
图19
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图19初始参数模型拟合效果
Fig.19Fitting effect of initial parameter model
图19
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图19初始参数模型拟合效果(续)
Fig.19Fitting effect of initial parameter model (continued)
Table 6
Table 6Comparison of regression accuracy between initial parameters and optimal parameters
 |
新窗口打开|下载CSV
明显减小, 初始参数模型MSE均在$10^{-1}\sim 10^{-2}$左右, 优化后减小至$10^{-4}\sim 10^{-5}$;决定系数$R^{2}$提高至0.999以上,因此利用优化算法构建的LSSVR模型具有更高的回归精度.
2.2.2 基于交叉验证的Kriging模型
交叉验证方法属于统计分析方法的一种, 基本思想是将已知的样本点分组,用其中一部分作为训练代理模型的样本, 其他部分作为验证代理模型精度的测试样本.根据分组策略的不同, 交叉验证方法又可以分为K折交叉验证、留一交叉验证,留P交叉验证, 蒙特卡洛交叉验证等. 为提升Kriging模型的预测精度和效率,我们也构建了基于交叉验证的Kriging模型. 其具体构建思路可以概况如下:(1)根据目标函数值的变化范围确定主目标;(2)根据设计参数值对目标函数值的影响确定其对应的相关模型参数的取值范围;(3)给定遗传算法所需的初始参数值,包括种群规模、选择概率、交叉概率、变异概率、初始种群、最大进化代数等;(4)对训练样本点随机分为$N$组, 为提高样本点信息的利用率,每组样本点的个数不宜过多;(5)选取其中$N-1$组样本点构建一个子Kriging模型(相关参数即为种群个体的值),剩余的1组样本点作为检验样本点, 保持值不变,顺序使每组样本点都做一次检验样本点;(6)对$N$组检验样本点的预测误差的绝对值求和后取平均值, 作为遗传算法的目标函数;(7)使用遗传算法寻优, 得到平均绝对误差最小时的值,并将$N$组样本点构建的$N$个子Kriging模型中预测误差最小的模型作为最终模型;
可以看出, 基于交叉验证算法的构建方法的计算量比传统的构建方法增大很多,但相对于训练样本点的流场计算量可以忽略不计, 因此,对于需要大计算量的气动外形优化设计, 这种构建方法的优点可以得到充分体现.
2.3 优化算法改进
作为高速列车气动外形优化的关键一环, 优化算法直接影响了最终的优化结果,我们需要同时兼顾优化算法的效率和精度.从20世纪50年代开始优化算法逐渐发展起来,早期梯度型算法如最速下降法、牛顿法、拟牛顿法等属于局部优化算法,可以迅速有效地找到问题的局部最优解. 随着问题复杂度的提升,许多新问题呈现出高非线性、复杂性以及约束多、建模难等特点, 因此,适合于大规模并行、并且具有智能特性的随机型全局优化算法应运而生,如遗传算法、粒子群算法、蚁群算法、模拟退火算法等. 不同的算法各有优缺点,为了提升算法的全局寻优能力、鲁棒性和寻优效率,对上述不同算法进行改进可以衍生出许多更多子类型的优化算法,下面简要介绍一下我们的一些研究进展.2.3.1 改进的非劣分类多目标粒子群算法
基本粒子群算法是通过种群的历史最优粒子$g_{best}$和个体的历史最优粒子$p_{best}$不断更新粒子的位置和飞行速度,引导粒子向$g_{best}$和$p_{best}$附近移动, 多目标粒子群算法与单目标粒子群算法相比,最大的不同点在于如何确定种群的历史最优粒子.由于多目标问题得到的是一组最优解集, 其中的每个解不分优劣,如何从这组解集中选取种群的历史最优粒子成为算法性能优劣的关键.为保证种群多样性,选取的最优粒子应该能够充分引导其他粒子在整个设计空间内向最优解集附近移动.因此, 历史最优粒子应该为种群种历次迭代时得到的Pareto最优解集中的一个解,并且应该尽量存在于设计空间内粒子较为稀疏的区域.
随着目标数量的增多, Pareto最优解的数量将急剧增大,导致种群内部的选择压力减小,仅以Pareto非劣关系作为优化准则的多目标粒子群算法难以从众多的非劣解中选择出合适的种群历史最优粒子,影响到粒子的寻优轨迹和种群多样性, 进而影响到算法的收敛性.为保证种群内部适当的选择压力和种群的多样性, 我们借助外部文件,根据小生境粒子数和拥挤距离的大小选取种群的历史最优粒子和个体的历史最优粒子.
外部文件用来存放粒子搜索过程中寻找到的Pareto最优解,也即每次迭代得到的第一非劣前沿解集. 外部文件中的所有粒子应有非支配关系,因此, 每次迭代之后都需要对外部文件中的粒子重新进行非劣等级的排序,只保留第一非劣前沿解集.种群的历史最优粒子将根据第一非劣前沿解集中粒子的小生境数和拥挤距离的大小确定.
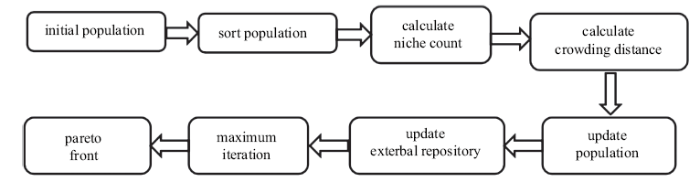
图20给出了多目标粒子群算法MPSO的基本算法流程: 首先对粒子种群进行初始化,得到初始种群的粒子位置和速度,并将初始种群的粒子位置作为个体历史最优粒子$p_{best}$的初始值,然后根据粒子的适应度函数对种群进行非劣等级的排序,并计算出每个粒子的小生境数和拥挤距离,根据小生境数和拥挤距离对种群历史最优粒子$g_{best}$进行初始化,并且初始化外部文件; 根据得到$p_{best}$和$g_{best}$对种群进行更新, 得到子代种群;对子代种群进行非劣等级排序, 将第一非劣前沿解添加到外部文档,并对外部文档中的粒子进行非劣等级排序, 只保留第一非劣前沿解,而将其他粒子删除, 并根据小生境数和拥挤距离得到种群历史最优粒子;如果迭代步数达到最大迭代步数, 输出外部文档中的Pareto最优解集, 算法结束,否则进行下一次迭代. 为了验证该多目标优化算法的精度,我们采用了4个测试函数进行校验, 具体校验过程可以参考文献[48]. 研究发现,分别使用小生境粒子数和拥挤距离的大小在外部文件中确定种群历史最优粒子,与基于实数编码和二进制编码的非劣分类多目标自适应遗传算法进行了对比分析,发现基于拥挤距离的概念构造的算法具有较强的寻优能力,尤其是对于高维设计空间、Pareto最优解集非连续问题, 表现更为突出.
2.3.2 连续域混沌蚁群算法
基本蚁群算法通过模拟蚂蚁寻找食物的过程来寻找最优解.蚂蚁个体之间是通过一种称之为信息素的物质进行信息传递,蚂蚁会在它所经过的路径上留下该种物质,而且蚂蚁在运动过程中能够感知周围环境中信息素的存在及其强度,并以此指导自己的运动方向, 蚂蚁倾向于朝着信息素强度高的方向移动. 因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多, 则后来者选择该路径的概率就越大.蚂蚁个体之间就是通过这种信息的交流达到搜索食物的目的.基本蚁群算法在离散优化领域取得了广泛的成功,为了将蚁群算法应用于连续域寻优问题, 国内外****进行了大量的研究.按照改进方式的不同, 目前的连续域蚁群算法可以分为两大类:一类是保持基本蚁群算法数学模型不变, 将连续问题转化为离散问题进行求解;另一类较为成功的连续域蚁群算法为Marco Dorigo及其合作者于2008年提出、2014年改进的基于高斯分布概率函数的蚁群算法.
蚁群算法ACO$_{R}$能够良好地解决大部分连续域数值优化问题, 且优化效率高.但是由于在构建的过程中, 对于每次迭代过程中得到的最优个体$S_{guide}$缺乏变异机制, 这就导致对于存在多峰值且局部极值特性明显的优化问题,ACO$_{R}$容易陷入局部极值. 另外, 目前大多只应用于单目标优化,针对多目标优化问题的改进仍然较少. 通过引入混沌变异机制,改进和发展了连续域混沌蚁群算法,同时利用小生境共享+外部存档技术发展了多目标混沌蚁群算法.混沌现象现在还没有严格的定义, 一般指无固定周期的具有渐进的自相似性的现象.混沌现象具有随机性、遍历性、规律性等特殊性质,目前数值优化领域已利用这些特点, 发展了混沌优化算法.混沌用于优化设计的根本点在于混沌的一个轨道能以任意精度逼近吸引子中的任意点,同时混沌的遍历性特点可以作为寻优过程中避免陷入局部极小的一种优化机制.
图20
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图20MPSO的基本算法流程
Fig.20Basic algorithm flow of MPSO
利用上述混沌模型对蚁群算法进行改进: 种群初始化阶段利用混沌模型进行初始化;信息素更新时利用混沌模型产生随机扰动.混沌蚁群算法(CACO$_{R})$具体构建流程如下.
(1) 种群初始化
$\begin{eqnarray*} {Ant}\ j:\ \left\{\begin{array}{l} X_{n+1} =\mu X_{n} (1-X_{n} ),n=0,1,2,\cdots \\ S_{j}^{i} =(b_{i} -a_{i} )X_{i} +a_{i} ,i=1,2,\cdots ,D\\ \end{array}\right. \end{eqnarray*}$
其中, $S_{j}^{i}$是个体$S_{j} $的分量, 其定义域为[$a_{i}$, $b_{i}$].
(2) 求解个体的目标值, 排序, 求解$\omega_{j} $及$P_{j} $, 选择$S_{{guide}} $. 在优先解附近产生$N_{new}$个新个体并移除最差的$N_{new} $个个体, 计算当前最优值$J_{best}$.
(3) 引入混沌扰动
重新计算目标值并排序, 更新$S_{{guide}} $及$J_{best}$.
\begin{eqnarray*} S_{j}^{i} (t+\Delta t)=\rho \cdot S_{j}^{i} (t)+\lambda X_{i} \end{eqnarray*}
(4) 计算相邻两代最优值的差, 如果不满足终止条件, 循环(2)(3).
(5) 计算终止, 输出最优值$J_{best} $及最优个体$S_{{guide}} $.
验证函数的验证表明[49], 该算法以高斯分布函数作为转移概率,
减小了每个个体向最优值收敛的时间, 提高了效率,
混沌模型带来的扰动避免其陷入局部最优, 具有良好的寻优能力.
2.4 典型工程应用算例
基于发展的参数化方法、替代模型和优化算法,可以完美解决实际工程中的优化效率问题, 使得针对实际外形进行优化成为可能.本节将简要介绍两个经典应用案例,分别对应当前实际线路上运行的CRH380A和CR400AF列车.2.4.1 CRH380A多目标优化
本节优化以CRH380A高速列车的尾车气动升力和车体容积为优化目标,参数化方法采用增量叠加法, 替代模型采用基于交叉验证的Kriging模型,而优化算法则采用基于实数编码的非劣分类多目标遗传算法,将以上方法叠加形成最终气动外形优化策略完成优化.
根据CRH380A的具体外形, 将其分为了5个变形区域, 如图21所示, 对每个变形区域,进行网格离散, 得到各区域的离散网格点坐标及拓扑结构, 保证拓扑结构不变,使用不同的变形函数对网格点坐标值进行扰动, 获取变形曲面.各区域的变形按顺序依次完成, 得到所有变形区域的坐标增量之后,将坐标增量与原始坐标值代数相加, 得到变形后的曲面. 在优化分析时,共设计了5个优化变量.
图21
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图21变形区域的划分示意图
Fig.21Division of deformation area
优化得到的Pareto最优解集如图22所示, 可以看出, Pareto解集的分布均匀,车体容积Vol的变化范围较小, 而升力$C_{l}$的变化范围比较大,说明$C_{l}$对头型气动外形的改变比较敏感.由于最终得到的优化头型的容积不能小于原型车头型的容积,且尾车的气动升力要小于原型车,为获取气动性能较好但流线型部分容积满足要求的列车头型,选取Case4作为最终的优化外形, 与原始外形进行气动性能的对比分析.表7给出了原始外形与典型设计点对应的Case4外形的气动力和流线型部分的容积,可以看出, 优化后, 设计点的气动性能都有了不同程度的提高, Case4 的流线型部分的容积与原始外形一致, 但其尾车气动升力减小了25.46%,整车气动阻力减小了5.73%.
图22
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图22基于Kriging替代模型得到的Pareto最优解集
Fig.22Pareto optimal solution set based on Kriging model
Table 7
Table 7Volume and aerodynamic force before and after optimization
 |
新窗口打开|下载CSV
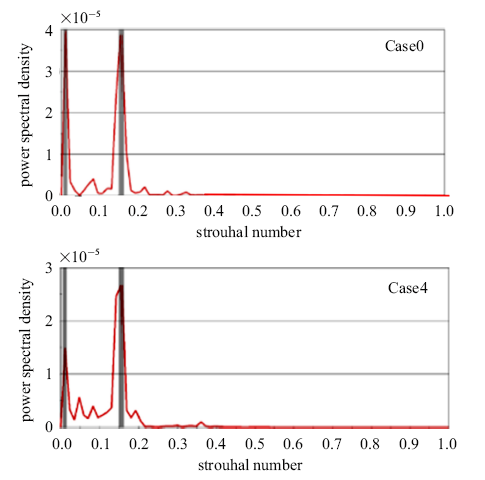
图23给出了优化前后尾车升力的功率谱密度图, 可以看出, 原始外形存在一个主频,位于: $St=0.012$处, 对应的频率分别为1 Hz, 在$St=0.157$处存在一个次频,对应的频率为13.1 Hz; 优化外形存在一个主频, 位于$St=0.156$处,对应的频率为13 Hz, 在$St=0.011$处存在一个次频, 对应的频率为0.92 Hz, 可见,优化后尾车气动升力的振动频率有所变大,说明优化后由气动升力引起的尾车振动频率变大,但优化后尾车气动升力的波动幅值减小, 因此,优化后由气动升力引起的尾车振动对列车乘坐舒适性的影响并不是很大,而列车的运行安全性有所提高.
列车的气动外形对尾涡结构的形成和发展有很大的影响,不同的头型可能会导致尾涡不同的脱落方式.
图23
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图23优化前后尾车升力的功率谱密度
Fig.23Power spectral density of the lift of the tail car before and after optimization
图24给出了优化前后尾流场的纵剖面速度云图和涡量云图, 可以看出,气流通过转向架区域的干扰, 在地面效应的作用下,在尾锥处与从尾锥上部的来流相遇, 形成强度较大的旋涡; 优化后,排障器后移幅度很大, 此处的流动方式发生了较大的变化, 低速区的范围更大,相应的高压区域和涡的强度也更大, 从而使该区域内的车体受到的向外的拉力更大,一定程度上使尾车的正升力减小; 随着尾涡向后的发展,优化外形的尾涡强度迅速减弱, 涡核迅速较小,而原始外形的尾涡强度和涡核的尺度仍然较大, 对列车周围设施的危险性比较大.
从研究结果上可以看到, 在基本不影响空间体积的情况下,尾车气动升力获得了大幅改善, 达到了多目标优化的目的,表明我们发展的气动外形优化策略可以有效地应用于真实外形高速列车气动外形优化上去,可以较好地指导工程外形设计.
图24
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图24优化前后尾流场纵剖面瞬时速度云图和涡量云图($t=1.5$ s)
Fig.24Instantaneous velocity and vorticity contour of longitudinal section of wake field before and after optimization ($t=1.5$ s)
2.4.2 CR400AF多目标优化
CR400AF即当前线路运行的复兴号, 设计运行速度为350km/h, 针对该型高速列车,以整车阻力和尾车升力为优化目标, 通过自由曲面变形法FFD进行流线型参数化,共设计16个设计变量, 以发展的多目标粒子群算法为优化算法,在基于交叉验证的Kriging替代模型上完成优化.
优化前后的外形比对如图25所示. 可以看出, 优化以后鼻锥高度下降,鼻锥长度略有增大; 司机室高度降低, 流线型前半部分宽度变窄,后半部分宽度略有增大,采用基于平行控制体的FFD参数化方法使得优化后的外形并不改变原有列车外形的拓扑结构及形貌的大致特征,一定程度上保持了原始设计的美观及其设计内涵.优化后列车的气动性能有了明显提高, 其中整车气动阻力减小3.13%,尾车升力减小16.46%. 列车所受到的气动阻力可分为压差阻力和摩擦阻力,其中压差阻力系数减小6.30%, 摩擦阻力系数在优化前后变化不大.
图25
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图25优化前后效果对比: 绿色, 优化前; 橙色, 优化后
Fig.25Shape comparison before (green color) and after optimization (orange color)
图26给出了优化前后列车头部表面压力分布云图及尾车等$Q$图($Q=100$),从图中可以看出, 主要有3个位置的表面压力发生了变化, 一是鼻锥前端长度增大,高度下降后, 对应的鼻锥下半部分压力减小, 如A1所示;二是由于在导流槽对应的侧面位置形状改变,引起导流槽下方区域接近底部长条形区域压力减小, 如图A2所示;三是列车鼻锥后半部分宽度改变, 对应于A3区域的压力减小. 从尾车等$Q$图可以看出,从尾迹区发展出的尾涡主要有4个: V1, V2, V3, V4, 其中V1和V4是主涡.优化后的外形V1的强度明显减小, 同时在鼻锥末端底部T1区域的涡的强度也有所减小,V4的强度略有增大, 综合作用下, 优化后的外形在减小尾涡方面更具有优势,因而尾车升力要明显小于优化前的外形.
图26
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图26优化前后列车头部表面压力分布云图及尾车等$Q$图
Fig.26Pressure contour on the head of train and iso-surface of $Q$ of tail train before and after optimization
从研究结果上看, 我们发展的气动外形优化策略可以极好地应用于实际外形优化,对于已有的流线化程度较高的列车外形, 提出的方法能够明显提高其气动性能.
3 结论
基于高速列车气动外形优化策略的不同,本文分别从基于流场机理的改型优化以及基于优化算法的外形优化两个方面介绍了我们在其中做过的一系列工作,主要结论如下:(1) 在基于流场机理的改型优化方面, 主要结合和谐号以及复兴号两款主力车型的气动外形研发, 介绍其局部结构改型优化的过程及效应. CRH380B重点在风挡、空调导流罩、受电弓导流罩和转向架区域进行了优化改进, 按照空气动力学原理, 减少流动分离, 使气流更加光顺地流经车体. 结合风挡、空调导流以及转向架区域的优化构型, CRH380B相对于原型车在气动阻力上能够减少约8.9%. 复兴号则在改型优化上走得更深入, 在受电弓区域没有采用和谐号的直接裸放于车体上的设计, 而是采用了受电弓平台, 通过研究发现受电弓平台的外形轮廓对整体阻力影响较小, 而平台深度在380 mm时阻力最优; 在风挡设计上采用了全封闭风挡, 减少气流在风挡部位形成的涡旋强度; 在转向架舱设计上, 重点研究了开舱口的大小、舱口倾角、裙板高度等影响规律, 研究发现在舱口进行舱外引流对减阻具有重要影响. 汇总各部件最优方案的CR400AF相对于CRH380A在气动阻力性能上获得了大幅提升, 整体减阻约13.27%.
(2) 在基于优化算法的外形优化上, 则从整体优化流程出发, 介绍了基于替代模型进行外形优化的快速高效策略. 从优化流程的具体步骤上, 简要介绍了我们在参数化方法、替代模型开发以及优化算法改进方面进行的工作. 参数化方法上, 局部型函数方法可以在流线型感兴趣部位直接设置设计变量实现光滑连续变形, 具有设计变量易于控制、算法上较易实现等优点, 具有非常高的通用性. 修正车辆造型函数参数化方法为型线方程驱动的参数化方法, 结合空间插值后可以细致的描述高速列车头型的三维外形, 能够用于头型的概念设计和头型的优化设计, 有利于提高头型的设计效率. 而类别/形状函数方法同样属于曲面方程驱动的参数化方法, 既能够从无到有地构建列车的流线型外形, 也能够用于已有外形的参数化建模. 替代模型开发上, 最优化替代模型重点从替代模型的参数确定上, 摒弃原有的指定参数, 采用优化的方法确定最优参数, 一般而言, 最优化替代模型相对于传统模型具有更高的精度. 而交叉验证的替代模型, 则无论在模型构建效率还是精度上, 均相对于原有模型有了大幅提升. 在优化算法改进上, 则引入了外部文件记录拥挤距离等, 发展了改进的非劣分类多目标粒子群算法和连续域混沌蚁群算法, 具有更强的寻优能力, 尤其是对于高维设计空间、Pareto最优解集非连续问题, 表现更为突出.
(3) 将发展的快速气动外形优化策略应用于CRH380A和CR400AF上, 充分验证了参数化方法的有效性、替代模型的准确性和改进算法的寻优能力, 两个工程算例均取得了良好的优化效果.
本文用到的两类气动外形优化方法中,基于流场机理的改型优化是当前进行高速列车气动优化最直接可行的方法,该方法一般只需要进行有限工况的数值模拟, 计算代价较小,易给出相对于原始设计更优的气动外形. 但基于流场机理的高速列车的气动外形优化,很大程度上依赖于****的空气动力学理论认知以及工程师的工程经验.基于优化算法的外形优化常常运用于针对各特殊部件已进行基于流场机理优化达到其性能提升的极限之后.该方法进一步细化气动优化的具体变量的设计,得到最佳参数组合和各个具体变量对优化目标的影响规律.两类设计方法在列车气动优化设计中都有其重要意义. 未来,基于流场机理的改型优化随着CFD数值模拟精细程度的不断提升,对流场特性的把握更加精准, 将能更有针对性的运用于高速列车的气动外形优化.基于优化算法的外形优化在优化方法的选择和优化效率的提升上通过进一步探索,对于缩短列车气动外形优化周期有积极意义.
本文中我们主要运用上述两类方法在高速列车气动外形优化方面做了相关一系列工作,相对于原始车型, 经过外形优化后的车型在气动性能上均有了大幅提升. 可以看到,当前的研究多集中在形状的改变上, 这是当前研究的局限.在未来气动外形的优化改进上, 仍然可以借鉴航空业里面发展的先进技术,如针对边界层的主/被动流场控制技术、仿生表面控制技术等.这些方法在航空业中业已获得大幅应用, 相信在高铁的气动优化中也会大有用武之地.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
URL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
URL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[J].
[本文引用: 1]
[本文引用: 1]
URL [本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
