张慧萍
1 , 王淑月
1 , 欧忠辉
, , 1 , 2 , * 1 福建师范大学数学与信息学院, 福州 350117 2 福建省分析数学及其应用重点实验室, 福州 350117 Approximate analytical solutions of root surface nutrient uptake flux and rhizosphere solute concentrations ZHANG Hui-Ping
1 , WANG Shu-Yue
1 , OU Zhong-Hui
, , 1 , 2 , * 1 College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350117, China 2 Fujian Key Laboratory of Mathematical Analysis and Applications, Fuzhou 350117, China 通讯作者: * 欧忠辉 ORCID: 0000-0002-9661-7798 (
zhou@fjnu.edu.cn )
编委: 周广胜
责任编辑: 李敏
收稿日期: 2018-05-17
网络出版日期: 2018-10-20
基金资助: 国家自然科学基金 .11671085 国家自然科学基金 .11771082 福建省引导性项目 .2015Y0054
Received: 2018-05-17
Online: 2018-10-20
Fund supported: Supported by the National Natural Science Foundation of China .11671085 Supported by the National Natural Science Foundation of China .11771082 the Fujian Province Guiding Project .2015Y0054
摘要 该文用Nye-Tinker-Barber模型来研究植物根系表面的养分吸收通量和根围溶质浓度的近似解析解。将根围区域分为远场区域和近场区域, 在远场用相似变量, 在近场用尺度变换, 将远场解在根表面展开并与近场解进行待定函数的匹配, 从而获得对流扩散方程根表面通量和浓度的一阶近似解析解, 该解能够简化到扩散方程的解的形式。对氮、钾、硫、磷、镁、钙的养分吸收通量和氮、钾的浓度分别进行数值模拟, 比较模型的数值解、Roose的近似解析解和该文的近似解析解。结果表明: 在扩散方程中, 6种元素通量的解析解与Roose解析解相近, 但均高于数值解, 钾和磷的通量在短时间内迅速衰减; 钾和氮浓度的全局近似解析解与Roose解析解接近, 并与数值解的变化趋势一致。在对流扩散方程中, 除氮外的5种元素通量的近似解较Roose的解析解更接近于数值解, 且没有奇性。
关键词: 解析解 ;
养分吸收通量 ;
Nye-Tinker-Barber模型 ;
溶质浓度全局解 Abstract Aims We use the Nye-Tinker-Barber model to obtain approximate analytical solutions of the root surface nutrient uptake flux and the rhizosphere solute concentrations.
Methods The rhizosphere is divided into the distant field and the close-range field. The outer solution is obtained by the similarity variable method, and the inner solution is obtained by the rescaling method. Expanding the outer solution from root surface and matching it with the inner solution, we finally obtain the approximate analytical solutions of the root surface nutrient uptake flux and rhizosphere solute concentrations based on Nye-Tinker-Barber model. Numerical simulations are performed on the uptake fluxes of six elements (N, K, P, Mg, S and Ca) and the solute concentrations of two elements (N and K). Comparisons are made among the Nye- Tinker-Barber model approximate analytical solutions, Roose’s analytical solutions and the numerical solutions.
Important findings The approximate analytical solutions of the root surface uptake fluxes based on the diffusion Nye-Tinker-Barber model are similar to those of the Roose's analytical solutions; both approaches produced higher values than the numerical solutions. The approximate analytical solutions of the rhizosphere N and K concentrations based on the diffusion Nye-Tinker-Barber model are similar to the Roose’s analytical solutions and coincide with the trend of changes in the numerical solutions. The approximate analytical solutions of all elements but N, of the root surface, uptake fluxes based on the convection-diffusion Nye-Tinker-Barber model are more similar to the numerical solutions than the Roose’s analytical solutions, and the approximate analytical solutions of the rhizosphere N and K concentrations are coincide with the trend of changes in the numerical solutions.
Keywords: analytical solution ;
nutrient absorption flux ;
the Nye-Tinker-Barber model ;
global solution of solute concentration PDF (1090KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 本文引用格式 张慧萍, 王淑月, 欧忠辉. 根表面养分吸收通量和根围溶质浓度的近似解析解.
植物生态学报 [J], 2018, 42(10): 1043-1049 DOI:
10.17521/cjpe.2018.0117 ZHANG Hui-Ping, WANG Shu-Yue, OU Zhong-Hui.
Approximate analytical solutions of root surface nutrient uptake flux and rhizosphere solute concentrations .
Chinese Journal of Plant Ecology [J], 2018, 42(10): 1043-1049 DOI:
10.17521/cjpe.2018.0117 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 )。目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取。养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 )。早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究。
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型。 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子。
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型。因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的。Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 )。在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项。
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性。
Roose等在Nye-Tinker-Barber模型基础上考虑土壤颗粒表面的吸附和解析与浓度的关系, 通过尺度变换、渐近展开、匹配的方法得到对流扩散方程和扩散方程单根、根表面和根系统养分吸收通量的近似解析解(
Roose et al ., 2001 ;
Roose & Kirk, 2009 )。随后
Nowack等(2006) 用3种地球化学计算工具(ORCHESTRA、MIN3P和PHREEQC)检验解的合理性。我们发现Roose的工作还有以下几个方面需要改进和完善: 扩散方程求得的根表面养分通量的解析解存在奇异性, 需要对时间进行平移; 没有给出扩散方程和对流扩散方程根围区域浓度的解, 因此我们不知道整个根围区域溶质浓度的变化; 没有将对流扩散方程和扩散方程的通量解析解给出统一的形式。本文在Roose工作的基础上试图解决以上问题, 并与数值模拟结果进行比较。
1 Nye-Tinker-Barber模型 20世纪70年代Nye、Tinker与Barber考虑土壤中固态和液态养分的守恒, 提出的养分吸收模型(Nye-Tinker-Barber模型)是较为经典的单根养分吸收模型(
Nye & Tinker, 1977 ;
Barber, 1984 )。
(1) $\frac{\partial {{C}_{S}}}{\partial {{t}^{*}}}={{d}_{S}}$ (2) $\frac{\partial }{\partial {{t}^{*}}}\left( \phi C \right)+\nabla \cdot \left( CU \right)=\nabla \cdot \left[ \phi D\nabla C \right]-{{d}_{S}}$ C 是土壤中液态养分浓度,
C S 是土壤中固态养分浓度, $\phi $是液体饱和度,
U 是水流达西通量,
D 是扩散系数,
d S 是解析出被吸附离子的量。假设离子在土壤颗粒表面的吸附和解吸与浓度成比例, 从而可以写出吸附率、解吸率和固态、液态离子浓度的线性关系表达式, 即:
(3) ${{d}_{\text{S}}}={{k}_{\text{a}}}C-{{k}_{\text{b}}}{{C}_{\text{S}}}$ K a 是养分吸收速率,
K b 是养分离子解吸率。由于土壤颗粒附着的离子解析时间较长, 因此,
(4) ${{C}_{\text{S}}}=bC$ 其中:$b={{{K}_{\text{a}}}}/{{{K}_{\text{b}}}}\;$为土壤缓冲率, 方程(1)和(2)可以通过方程(3)和(4)变为:
$\left( \phi +\text{b} \right)\frac{\partial C}{\partial {{t}^{*}}}+\nabla \cdot \left( CU \right)=\phi D{{\nabla }^{2}}C$
根表面的养分吸收遵循Michaelis-Menton动力学原理,
$\phi D\frac{\partial C}{\partial n}-\left( C{{U}_{\text{n}}} \right)=\frac{{{F}_{m}}C}{{{K}_{m}}+C},{{r}^{*}}=a$
在植物学中,
F m 和
K m 分别是所考虑植物的生长速率和酶促反应速度达最大值一半时的底物浓度。
n 是根表面指向土壤的单位矢量。
达西通量为$U={aV}/{{{r}^{*}}}\;$,
V 是水进入根部的达西通量,
r 是根半径,
a 是径向距离且满足$\nabla \cdot U=0$。因此在圆柱坐标里Nye-Tinker-Barber模型极坐标形式为:
(5) $\left\{ \begin{matrix} & \left( \phi +\text{b} \right)\frac{\partial C}{\partial t*}-\frac{aV}{r*}\frac{\partial C}{\partial r*}=\frac{\phi D}{r*}\frac{\partial }{\partial r*}\left( r*\frac{\partial C}{\partial r*} \right) \\ & \phi D\frac{\partial C}{\partial n}+VC=\frac{{{F}_{\text{m}}}C}{{{K}_{\text{m}}}+C},r*=a \\ & C\to {{C}_{0}},r*\to \infty ,t*\to 0 \\ \end{matrix} \right.$ 引入量纲$C={{K}_{\text{m}}}c,$$r*=ar,$$t*={\left( \phi +D \right){{a}^{2}}t}/{\phi D}\;,$对模型(5)进行无量纲化处理变为:
(6) $\frac{\partial c}{\partial t}-Pe\frac{1}{r}\frac{\partial c}{\partial r}=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial c}{\partial r} \right)$ (7) $\frac{\partial c}{\partial r}+Pec=\frac{\lambda c}{1+c},r=1$ (8) $c={{c}_{\infty }},r={{r}_{\infty }}$ (9) $c={{c}_{\infty }},t\to 0$ 其中, 无量纲参数
pecelet 数(对流速率与扩散速率之比)$Pe={aV}/{\phi D}\;\text{,}$养分吸收通量系数$\lambda \text{=}\frac{{{F}_{\text{m}}}a}{\phi D{{K}_{\text{m}}}},$ 无量纲远场区域液态养分浓度和初始浓度${{c}_{\infty }}={{C}_{0}}/$ ${{K}_{\text{m}}}$。
由左边界条件(7)可知, 根表面的无量纲养分吸收通量
F tot (
t )为:
${{F}_{tot}}\left( t \right)={{\left. \frac{\lambda c}{1+c} \right|}_{r=1}}$
2 模型求解 本文将整个根区分为远场区域和近场区域, 在远场区域对方程和右边界条件进行尺度变换, 并引入相似变量进行求解。在近场区域对方程和左边界条件进行尺度变换, 进行求解。对远场解和近场解中的常数项及一次项进行匹配, 从而获得根表面的养分吸收通量近似解析解和溶质浓度的全局近似解析解。
2.1 远场区域 对模型中的时间变量
t 和空间变量
r 进行尺度变换, 并引入相似变量
η 。
(10) $t=\frac{\tau }{{{\sigma }^{2}}},r=\frac{R}{\sigma },\eta =\frac{{{R}^{2}}}{\tau }$ $c\left( r,t \right)$可以写为关于$\eta $的函数, $c\left( r,t \right)={{c}_{\infty }}f\left( r,t \right)=$ ${{c}_{\infty }}f\left( \eta \right)$
(11) $\left\{ \begin{matrix} & \frac{\partial c}{\partial t}\text{=}-{{c}_{\infty }}{f}'\left( \eta \right)\frac{{{r}^{2}}}{{{\tau }^{2}}} \\ & \frac{\partial c}{\partial r}=-{{c}_{\infty }}{f}'\left( \eta \right)\frac{2r}{\tau } \\ & \frac{{{\partial }^{2}}c}{\partial {{t}^{2}}}=\frac{4}{r}{{c}_{\infty }}{f}'\left( \eta \right)+{{c}_{\infty }}{f}''\left( \eta \right)\frac{4{{r}^{2}}}{{{\tau }^{2}}} \\ \end{matrix} \right.$ 将方程(11)代入方程(6)中, 可以得到:
(12) $-\eta {f}'\left( \eta \right)=2\left( Pe+2 \right){f}'\left( \eta \right)+{f}''\left( \eta \right)\eta$ 联立方程(12)和右边界条件(8)求解, 可得远场区域的养分浓度:
(13) $c\left( r,t \right)={{c}_{\infty }}-{{2}^{-Pe}}BGamma\left[ -\frac{Pe}{2},\frac{{{r}^{2}}}{4t} \right]$ 在
r = 1处把方程(13)渐近展开到一阶:
(14) $\begin{matrix} & c\left( r,t \right)={{c}_{\infty }}-{{2}^{-Pe}}BGamma\left[ -\frac{Pe}{2},\frac{1}{4t} \right]+ \\ & \ \ \ \ 2B{{e}^{-\frac{1}{4t}}}{{t}^{\frac{Pe}{2}}}\left( r-1 \right)+O{{\left( r-1 \right)}^{2}} \\ \end{matrix}$ 2.2 近场区域 对模型中的时间尺度
t 进行尺度变换:
(15) $t=\frac{\tau }{{{\sigma }^{2}}}$ 将方程(15)代入方程(6)得到:
(16) ${{\sigma }^{2}}\frac{\partial c}{\partial \tau }=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial c}{\partial r} \right)+Pe\frac{1}{r}\frac{\partial c}{\partial r}$ 如果$\sigma <<1$, 方程(16)可以简化为:
(17) $0=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial c}{\partial r} \right)+Pe\frac{1}{r}\frac{\partial c}{\partial r}$ 通解为: $c\left( r,t \right)={{c}_{1}}-\frac{{{c}_{0}}}{Pe}{{r}^{-Pe}}$, 其中
c 1 和
c 0 是关于
t 的函数, 根据模型的边界条件$\left( F={{\left. \frac{\partial c}{\partial r} \right|}_{r=1}}={{c}_{0}} \right)$, 可得$F={{\left. \frac{{{c}_{0}}}{r} \right|}_{r=1}}={{c}_{0}}$, 所以根表面附近的养分浓度为:
(18) $c\left( r,t \right)={{c}_{1}}-\frac{F}{Pe}{{r}^{-Pe}}$ 在
r = 1处把方程(18)渐近展开到二阶,
(19) $c\left( r,t \right)={{c}_{1}}-\frac{F}{Pe}+\left( r-1 \right)F+O{{\left( r-1 \right)}^{3}}$ 2.3 解的匹配 方程(14)和方程(19)是关于
r = 1的级数形式, 匹配它们的常数项和一次项, 进行待定函数求解:
${{c}_{1}}-\frac{F}{Pe}={{c}_{\infty }}-{{2}^{-Pe}}BGamma\left[ -\frac{Pe}{2},\frac{1}{4t} \right]$
$F=2B{{e}^{-\frac{1}{4t}}}{{t}^{\frac{Pe}{2}}}$
(20) $F=\frac{2{{c}_{\infty }}\left[ \lambda -Pe\left( 1+{{c}_{\infty }} \right) \right]}{h\left( \lambda -Pe{{c}_{\infty }} \right)+\left( 1-Peh \right)\left( 1+{{c}_{\infty }} \right)+\sqrt{{{\left( 1+{{c}_{\infty }} \right)}^{2}}+{{h}^{2}}{{\left( \lambda -Pe \right)}^{2}}-2h\left[ \lambda \left( -1+{{c}_{\infty }} \right)+Pe\left( 1+{{c}_{\infty }} \right) \right]}}$ (21) ${{F}_{tot}}=F+Pe\left( {{c}_{\infty }}-hF \right)=\frac{2\lambda {{c}_{\infty }}}{\left( 1+{{c}_{\infty }} \right)+\left( \lambda -Pe \right)h+\sqrt{{{\left( 1+{{c}_{\infty }} \right)}^{2}}+{{h}^{2}}{{\left( \lambda -Pe \right)}^{2}}-2h\left[ \lambda \left( -1+{{c}_{\infty }} \right)+Pe\left( 1+{{c}_{\infty }} \right) \right]}}$ (22) $c\left( r,t \right)={{c}_{\infty }}+\frac{{{2}^{-Pe}}{{c}_{\infty }}{{t}^{-\frac{Pe}{2}}}{{e}^{\frac{1}{4t}}}\left[ Pe\left( 1+{{c}_{\infty }} \right)-\lambda \right]Gamma\left[ {-Pe}/{2}\;,{1}/{4t}\; \right]}{h\left( \lambda -Pe{{c}_{\infty }} \right)+\left( 1-Peh \right)\left( 1+{{c}_{\infty }} \right)+\sqrt{{{\left( 1+{{c}_{\infty }} \right)}^{2}}+{{h}^{2}}{{\left( \lambda -Pe \right)}^{2}}-2h\left[ \lambda \left( {{c}_{\infty }}-1 \right)+Pe\left( 1+{{c}_{\infty }} \right) \right]}}$ (23) ${{F}_{tot}}\left( t \right)=\frac{2\lambda {{c}_{\infty }}}{1+{{c}_{\infty }}-\lambda l+\sqrt{{{\left( 1+{{c}_{\infty }}-\lambda l \right)}^{2}}+4\lambda l{{c}_{\infty }}}}$ (24) $c\left( r,t \right)={{c}_{\infty }}+\frac{\lambda {{c}_{\infty }}{{e}^{\frac{1}{4t}}}ExpIntergralEi\left[ -{1}/{4t}\; \right]}{-l\lambda +\left( 1+{{c}_{\infty }} \right)+\sqrt{{{\left( 1+{{c}_{\infty }} \right)}^{2}}+{{\left( \lambda l \right)}^{2}}+2l\lambda \left( {{c}_{\infty }}-1 \right)}}$ 由边界条件(7)解得方程(20)。根据模型的边界条件(7), 得到土壤中根表面的无量纲养分吸收通量为方程(21)。由方程(14)得到土壤中根围区域无量纲液态养分浓度的全局近似解析解为方程(22), 其中:
${h=1}/{{{2}^{^{1+Pe}}}}\;{{e}^{\frac{1}{4\text{t}}}}{{t}^{-\frac{Pe}{2}}}Gamma\left[ {-Pe}/{2}\;,{1}/{4t}\; \right]$
通常情况下, 土壤里面的对流项很小, 一般认为是
Pe = 0, 由方程(21)和(22)我们推出
Pe = 0时, 土壤中根表面的无量纲养分吸收通量
F tot (
t )和液态养分浓度的全局近似解析解
c (
r, t )分别为方程(23)和(24), 其中: $l=\frac{1}{2}{{e}^{\frac{1}{4t}}}ExpIntergralEi\left[ -{1}/{4t}\; \right]$。
Roose等在2001求解扩散方程的吸收通量的近似解析解为:
${{F}_{tot}}\left( t \right)=\frac{\lambda \left[ {{c}_{\infty }}+{F\left( \gamma -\ln 4t \right)}/{2}\; \right]}{1+{{c}_{\infty }}+{F\left( \gamma -\ln 4t \right)}/{2}\;}$
当
t = 0时
F tot = 0或$\lambda $
, 并不满足边界${{F}_{tot}}=\frac{\lambda {{c}_{\infty }}}{\left( 1+{{c}_{\infty }} \right)}$, 需要时间的平移解决奇性, $\ln 4t$应变成$\ln (4t+{{\text{e}}^{\gamma }})$。
在$Pe\text{=}0$的情况下, 我们使用方程(14)和(7), 得出
(25) ${{F}_{tot}}=\frac{\lambda \left( {{c}_{\infty }}-{{e}^{\frac{1}{4t}}}ExpIntergralEi\left[ -\frac{1}{4t} \right]F \right)}{1+{{c}_{\infty }}-{{e}^{\frac{1}{4t}}}ExpIntergralEi\left[ -\frac{1}{4t} \right]F}$ 由于: $\underset{t\to 0}{\mathop{\lim }}\,{{e}^{\frac{1}{4t}}}ExpIntergralEi\left[ -{1}/{4t}\; \right]=0$ 因此方程(25)满足边界条件${{F}_{tot}}={\lambda {{c}_{\infty }}}/{\left( 1+{{c}_{\infty }} \right)}\;$ 且没有奇性。
方程(22)和(24)是对流扩散方程和扩散方程根围区域溶质浓度的全局近似解析解, 方程(21)和(23)是对流扩散方程和扩散方程根表面养分吸收通量的近似解析解。由于
Gamma [0,1/4
t ]
= -ExpIntergralEi [1/4
t ], 因此方程(21)、(22)、(23)、(24)具有统一的形式。
3 数值模拟 在方程(6)中, 我们选取一般土壤特征参数值(扩散系数
D = 0.3 × 10
-5 cm
2 ·s
-1 , 土壤含水量$\phi \text{=}0.3$, 水分通量
V = 10
-7 cm
2 ·s
-1 )植物(玉米)相关的参数(根半径
a = 0.02 cm, 根围
r max = 3 cm)。我们对方程(6)采取迎风差分格式进行数值模拟, 其中时间步长为0.004, 靠近根表面的空间步长为0.4, 远离根表面的空间步长为4。模拟不同元素(钾、氮、硫、磷、镁、钙)通量随时间变化情况和不同养分元素(钾和氮)浓度在不同时间(1天、7天、13天、19天)的变化情况。
如
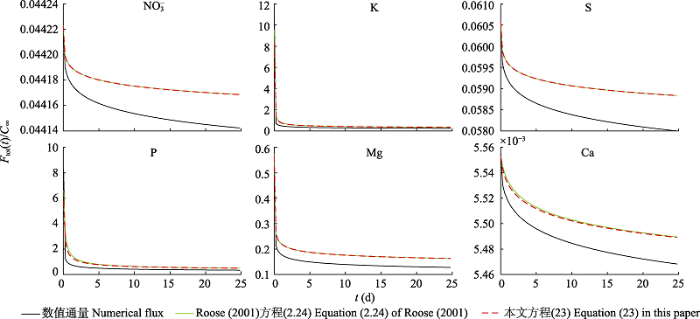
图1 所示, 在扩散方程中, 6种元素的通量呈现两种衰减趋势, 其中钾、磷、镁通量在短时间内迅速减少, 氮、硫、钙的通量则随时间的变化而缓慢下降。根表面养分通量的近似解析解方程(23) 和
Roose等(2001) 的解析解(2.24)接近, 但均高于数值解。
图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1扩散方程中6种元素通量随时间的变化趋势。c ∝ 是初始浓度, 6种元素的初始浓度分别为5、0.046、0.1、0.0029、0.001、0.008 μmol·cm-3 ; F tot (t )是养分吸收通量; t 是时间, 以25天为例。 Fig. 1Changes in the fluxes of six elements with time in diffusion Nye-Tinker-Barber model. c ∝ is the initial concentration, with given values of 5, 0.046, 0.1, 0.0029, 0.001, 0.008 μmol·cm-3 for the six elements; F tot (t ) is the element uptake flux; t is time, with a duration of 25 days as an example. 如
图2 所示, 在对流扩散方程中, 镁的通量呈现不同的变化趋势。在根表面
Roose等(2001) 的解析解要比数值解大很多, 但本文养分通量的近似解析解方程(21)较
Roose等(2001) 的近似解析解更接近于数值解。
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2对流扩散方程中6种元素通量随时间的变化趋势。c ∝ 是初始浓度, 6种元素的初始浓度分别为5、0.046、0.1、0.0029、0.001、0.008 μmol·cm-3 ; F tot (t )是养分吸收通量; t 是时间, 以25天为例。 Fig. 2Changes in the fluxes of six elements with time in convection-diffusion Nye-Tinker-Barber model. c ∝ is the initial concentration, with given values of 5, 0.046, 0.1, 0.0029, 0.001, 0.008 μmol·cm-3 for the six elements; F tot (t ) is the element uptake flux; t is time, with a duration of 25 days as an example. 如
图3 所示, 在扩散方程中, 在不同时间钾在根表面的浓度随距离的变化被快速吸收。在近场区域,
Roose等(2001) 的解析解(2.21)与本文的近似解析解方程(24)接近但均高于数值解, 但随后与数值解重合。
图3 新窗口打开 |
下载原图ZIP |
生成PPT 图3扩散方程中1、7、13、19天钾浓度随距离的变化趋势。c (t )是养分浓度; c ∝ 是养分初始浓度, 钾的初始浓度为0.046 μmol·cm-3 ; r 是到根表面的距离。 Fig. 3Changes in potassium concentration with distance for 1, 7, 13 and 19 in diffusion Nye-Tinker- Barber model. c (t ) is the nutrient concentration; c ∝ is the initial concentration, with a given value of 0.046 μmol·cm-3 for potassium, r is the distance to the root surface. 如
图4 所示, 在对流扩散方程中, 在近场区域, 本文的近似解析解方程(22)接近于数值解, 随后与数值解重合(
Roose等(2001 )没有给出对流扩散方程根围的溶质浓度)。
图4 新窗口打开 |
下载原图ZIP |
生成PPT 图4对流扩散方程中1、7、13、19天钾液态浓度随距离的变化趋势。c (t )是养分浓度; c ∝ 是养分初始浓度, 钾的初始浓度为0.046 μmol·cm-3 ; r 是到根表面的距离。 Fig. 4Changes in potassium concentration with distance for 1, 7, 13 and 19 in convection-diffusion Nye-Tinker- Barber model. c (t ) is the nutrient concentration; c ∝ is the initial concentration, with a given value of 0.046 μmol·cm-3 for potassium; r is the distance to the root surface. 在
图5 中, 在扩散方程中, 在同一时刻氮在根表面的浓度随距离的变化而缓慢变化。在近场区域,
Roose等(2001) 的解析解(2.21)与本文的近似解析解方程(24)重合, 在根表面与数值解接近, 随后与数值解重合。
图5 新窗口打开 |
下载原图ZIP |
生成PPT 图5扩散方程中1、7、13、19天氮浓度随距离的变化趋势。c (t )是养分浓度; c ∝ 是养分初始浓度, 氮的初始浓度为5 μmol·cm-3 ; r 是根表面的距离。 Fig. 5Changes in nitrogen concentration with distance for 1, 7, 13 and 19 d in diffusion Nye-Tinker- Barber model. c (t ) is the nutrient concentration; c ∝ is the initial concentration, with a given value of 5 μmol·cm-3 for nitrogen; r is the distance to the root surface. 在
图6 中, 在对流扩散方程中, 在近场区域, 本文的近似解析解方程(22)接近于数值解, 随后与数值解重合(
Roose等(2001) 没有给出对流扩散方程根围的溶质浓度)。
图6 新窗口打开 |
下载原图ZIP |
生成PPT 图6对流扩散方程中1、7、13、19天氮液态浓度随距离的变化趋势。c (t )是养分浓度; c ∝ 是养分初始浓度, 氮的初始浓度为5 μmol·cm-3 ; r 是根表面的距离。 Fig. 6Changes in nitrogen concentration with distance for 1, 7, 13 and 19 d in convection-diffusion Nye- Tinker-Barber model. c (t ) is the nutrient concentration; c ∝ is the initial concentration, with a given value of 5 μmol·cm-3 ; r is the distance to the root surface. 4 结论 本文用Nye-Tinker-Barber模型来求解植物根系表面的养分吸收通量和根围溶质浓度的近似解析解。通过把远场解在根表面展开并与近场解匹配, 不仅获得根表面的养分吸收通量近似解析解, 还求解出根际周围溶质浓度的全局近似解析解, 从而解决了Roose解中的奇性问题, 并且本文给出了对流扩散方程和扩散方程根表面养分通量和溶质浓度全局近似解析解的统一形式。
通过数值模拟对比, 在扩散模型和对流扩散模型中, 我们都发现6种元素的通量随时间的增加而衰减, 且呈现两种变化趋势, 其中钾、磷、镁通量在短时间内迅速减少, 镁通量在扩散方程和对流扩散方程呈现不同变化趋势, 氮、硫、钙的通量则随时间的变化而缓慢下降, 在对流扩散方程中本文的解析解较Roose的解析解更接近于数值解; 近场区域对流扩散模型和扩散模型中, 两种元素浓度全局解析解的变化趋势与数值解一致, 先高于数值解, 随后与数值解重合。
致谢 感谢福建师范大学创新团队项目(19120/ Z1607219016和IRTL1206)和分析数学及应用重点实验室项目(ZGD1707233和ZGD1707222711)资助。感谢穆怡教授、沈建和教授和陈建清教授的指导和帮助。
[1] Barber SA 1984 ). Soil nutrient bioavailability: A mechanistic approachQuarterly Review of Biology , 161, 140 -141 . [本文引用: 2] [2] Badge R Adlakha N 2017 ). Two-dimensional finite element model to study the effect of water flux on the nitrate dynamics in the rhizosphere of a maize rootInternational Journal of Biomathematics , 10, 333 -351 . [本文引用: 1] [3] Bouldin DR 1961 ). Mathematical description of diffusion processes in the soil-plant systemSoil Science Society of America Journal , 25, 476 -480 . DOI URL [本文引用: 1] [4] Chen H Feng Y Zhou JM Xu ZG Lian C Guo QR 2013 ). Research advance of plant root biologyWorld Forestry Research , 26(5 ), 25 -29 . [本文引用: 1] [ 陈红 , 冯云 , 周建梅 , 徐振国 , 廉超 , 郭起荣 ( 2013 ). 植物根系生物学研究进展世界林业研究 , 26(5 ), 25 -29 .] [本文引用: 1] [5] Epstein E 1972 ). Mineral Nutrition of Plants: Principles and Perspectives [本文引用: 1] [6] Kumar A Hafiz A 2011 ). A mathematical description of pollutant uptake in plants by single cylindrical rootAmerican Journal of Experimental Agriculture , 1, 265 -280 . DOI URL [本文引用: 1] [7] Meng HS Feng JY Hu DD Qin WM Yan L 2017 ). Root system development and nutrient absorption in plantJournal of Shanxi Agricultural Sciences , 45, 1048 -1052 . [本文引用: 1] [ 蒙好生 , 冯娇银 , 胡冬冬 , 秦武明 , 严理 ( 2017 ). 植物根系发育与养分的吸收山西农业科学 , 45, 1048 -1052 .] [本文引用: 1] [8] Nowack B Mayer KU Oswald SE van Beinum W Appelo CAJ Jacques D Seuntjens P Gérard F Jaillard B Schnepf A Roose T 2006 ). Verification and intercomparison of reactive transport codes to describe root-uptakePlant and soil , 285, 305 -321 . DOI URL [本文引用: 1] [9] Nye PH Spiers JA 1964 ). Simultaneous diffusion and mass flow to plant rootsProceedings of the 8th International Congress of Soil Science. Rompresfilatelia, Bucharest, Hungary . 535 -544 . [本文引用: 1] [10] Nye PH Tinker PB 1977 ). Solute Movement in the Soil-Root System [本文引用: 2] [11] Olsen SR Kemper WD Jackson RD 1962 ). Phosphate diffusion to plant rootsSoil Science Society of America Journal , 26, 222 -227 . DOI URL [本文引用: 1] [12] Picart D Ozier-Lafontaine H Omrane A Louison L 2017 ). Modeling plant nutrient uptake: Mathematical analysis and optimal controlEvolution Equations and Control Theory , 4, 193 -203 . [本文引用: 1] [13] Roose T Fowler AC 2004 ). A mathematical model for water and nutrient uptake by plant root systemsJournal of Theoretical Biology , 228, 173 -184 . DOI URL [本文引用: 1] [14] Roose T Fowler AC Darrah PR 2001 ). A mathematical model of plant nutrient uptakeJournal of Mathematical Biology , 42, 347 -360 . DOI URL [本文引用: 8] [15] Roose T Kirk DJD 2009 ). The solution of convection-diffusion equations for solute transport to plant rootsPlant and Soil , 316, 257 -264 . DOI URL [本文引用: 1] [16] Schnepf A Jones D Roose T 2011 ). Modelling nutrient uptake by individual hyphae of arbuscular mycorrhizal fungi: Temporal and spatial scales for an experimental designBulletin of Mathematical Biology , 73, 2175 -2200 . DOI URL [本文引用: 1] [17] Schnepf A Roose T 2006 ). Modeling the contribution of arbuscular mycorrhizal fungi to plant phosphate uptakeNew Phytologist , 171, 669 -682 . [本文引用: 1] [18] Zygalakis KC Kirk GJ Jones DL Wissuwa M Roose T 2011 ). A dual porosity model of nutrient uptake by root hairsNew Phytologist , 192, 676 -688 . DOI URL [本文引用: 1] [19] Zygalakis KC Roose T 2012 ). A mathematical model for investigating the effect of cluster roots on plant nutrient uptakeThe European Physical Journal Special Topics , 204, 103 -118 . DOI URL [本文引用: 1] Soil nutrient bioavailability: A mechanistic approach
2
1984
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
... 20世纪70年代Nye、Tinker与Barber考虑土壤中固态和液态养分的守恒, 提出的养分吸收模型(Nye-Tinker-Barber模型)是较为经典的单根养分吸收模型(
Nye & Tinker, 1977 ;
Barber, 1984 ). ...
Two-dimensional finite element model to study the effect of water flux on the nitrate dynamics in the rhizosphere of a maize root
1
2017
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
Mathematical description of diffusion processes in the soil-plant system
1
1961
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
植物根系生物学研究进展
1
2013
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
植物根系生物学研究进展
1
2013
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
1
1972
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
A mathematical description of pollutant uptake in plants by single cylindrical root
1
2011
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
植物根系发育与养分的吸收
1
2017
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
植物根系发育与养分的吸收
1
2017
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
Verification and intercomparison of reactive transport codes to describe root-uptake
1
2006
... Roose等在Nye-Tinker-Barber模型基础上考虑土壤颗粒表面的吸附和解析与浓度的关系, 通过尺度变换、渐近展开、匹配的方法得到对流扩散方程和扩散方程单根、根表面和根系统养分吸收通量的近似解析解(
Roose et al ., 2001 ;
Roose & Kirk, 2009 ).随后
Nowack等(2006) 用3种地球化学计算工具(ORCHESTRA、MIN3P和PHREEQC)检验解的合理性.我们发现Roose的工作还有以下几个方面需要改进和完善: 扩散方程求得的根表面养分通量的解析解存在奇异性, 需要对时间进行平移; 没有给出扩散方程和对流扩散方程根围区域浓度的解, 因此我们不知道整个根围区域溶质浓度的变化; 没有将对流扩散方程和扩散方程的通量解析解给出统一的形式.本文在Roose工作的基础上试图解决以上问题, 并与数值模拟结果进行比较. ...
Simultaneous diffusion and mass flow to plant roots
1
1964
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
2
1977
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
... 20世纪70年代Nye、Tinker与Barber考虑土壤中固态和液态养分的守恒, 提出的养分吸收模型(Nye-Tinker-Barber模型)是较为经典的单根养分吸收模型(
Nye & Tinker, 1977 ;
Barber, 1984 ). ...
Phosphate diffusion to plant roots
1
1962
... 植物根系具有固定植物、吸收养分、储存水分、合成运输有机物等众多重要功能(
陈红等, 2013 ).目前已知高等植物需要的16-18种营养元素除碳、氢、氧可以从大气中获取外, 其余如氮、磷、钾、钙、镁、硫、铁、锰、锌、铜等都必须依靠根系从土壤中汲取.养分一般以截取、离子扩散、质流这三种方式向根表面迁移, 但由于土壤颗粒与根的接触面积有限, 因此截取量很少(仅为植物需要量的5%), 远远不能满足植物的生长需要, 还必须通过扩散和质流获取更多的养分(
蒙好生等, 2017 ).早在20世纪60年代植物学家就开始了对根部吸收养分过程的研究.
Bouldin (1961) 假设根的养分吸收通量与养分浓度成正比关系, 建立了土壤养分扩散模型. 随后
Olsen等(1962) 通过假设恒定的养分吸收通量或者养分浓度, 建立了类似的模型, 但是这类模型只适用于像磷和钾这样以扩散为主要的迁移方式的养分离子, 不适合像氮、硫、钠等以对流为主的养分离子. ...
Modeling plant nutrient uptake: Mathematical analysis and optimal control
1
2017
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
A mathematical model for water and nutrient uptake by plant root systems
1
2004
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
A mathematical model of plant nutrient uptake
8
2001
... Roose等在Nye-Tinker-Barber模型基础上考虑土壤颗粒表面的吸附和解析与浓度的关系, 通过尺度变换、渐近展开、匹配的方法得到对流扩散方程和扩散方程单根、根表面和根系统养分吸收通量的近似解析解(
Roose et al ., 2001 ;
Roose & Kirk, 2009 ).随后
Nowack等(2006) 用3种地球化学计算工具(ORCHESTRA、MIN3P和PHREEQC)检验解的合理性.我们发现Roose的工作还有以下几个方面需要改进和完善: 扩散方程求得的根表面养分通量的解析解存在奇异性, 需要对时间进行平移; 没有给出扩散方程和对流扩散方程根围区域浓度的解, 因此我们不知道整个根围区域溶质浓度的变化; 没有将对流扩散方程和扩散方程的通量解析解给出统一的形式.本文在Roose工作的基础上试图解决以上问题, 并与数值模拟结果进行比较. ...
... 如
图1 所示, 在扩散方程中, 6种元素的通量呈现两种衰减趋势, 其中钾、磷、镁通量在短时间内迅速减少, 氮、硫、钙的通量则随时间的变化而缓慢下降.根表面养分通量的近似解析解方程(23) 和
Roose等(2001) 的解析解(2.24)接近, 但均高于数值解. ...
... 如
图2 所示, 在对流扩散方程中, 镁的通量呈现不同的变化趋势.在根表面
Roose等(2001) 的解析解要比数值解大很多, 但本文养分通量的近似解析解方程(21)较
Roose等(2001) 的近似解析解更接近于数值解. ...
... 的解析解要比数值解大很多, 但本文养分通量的近似解析解方程(21)较
Roose等(2001) 的近似解析解更接近于数值解. ...
... 如
图3 所示, 在扩散方程中, 在不同时间钾在根表面的浓度随距离的变化被快速吸收.在近场区域,
Roose等(2001) 的解析解(2.21)与本文的近似解析解方程(24)接近但均高于数值解, 但随后与数值解重合. ...
... 如
图4 所示, 在对流扩散方程中, 在近场区域, 本文的近似解析解方程(22)接近于数值解, 随后与数值解重合(
Roose等(2001 )没有给出对流扩散方程根围的溶质浓度). ...
... 在
图5 中, 在扩散方程中, 在同一时刻氮在根表面的浓度随距离的变化而缓慢变化.在近场区域,
Roose等(2001) 的解析解(2.21)与本文的近似解析解方程(24)重合, 在根表面与数值解接近, 随后与数值解重合. ...
... 在
图6 中, 在对流扩散方程中, 在近场区域, 本文的近似解析解方程(22)接近于数值解, 随后与数值解重合(
Roose等(2001) 没有给出对流扩散方程根围的溶质浓度). ...
The solution of convection-diffusion equations for solute transport to plant roots
1
2009
... Roose等在Nye-Tinker-Barber模型基础上考虑土壤颗粒表面的吸附和解析与浓度的关系, 通过尺度变换、渐近展开、匹配的方法得到对流扩散方程和扩散方程单根、根表面和根系统养分吸收通量的近似解析解(
Roose et al ., 2001 ;
Roose & Kirk, 2009 ).随后
Nowack等(2006) 用3种地球化学计算工具(ORCHESTRA、MIN3P和PHREEQC)检验解的合理性.我们发现Roose的工作还有以下几个方面需要改进和完善: 扩散方程求得的根表面养分通量的解析解存在奇异性, 需要对时间进行平移; 没有给出扩散方程和对流扩散方程根围区域浓度的解, 因此我们不知道整个根围区域溶质浓度的变化; 没有将对流扩散方程和扩散方程的通量解析解给出统一的形式.本文在Roose工作的基础上试图解决以上问题, 并与数值模拟结果进行比较. ...
Modelling nutrient uptake by individual hyphae of arbuscular mycorrhizal fungi: Temporal and spatial scales for an experimental design
1
2011
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
Modeling the contribution of arbuscular mycorrhizal fungi to plant phosphate uptake
1
2006
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
A dual porosity model of nutrient uptake by root hairs
1
2011
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
A mathematical model for investigating the effect of cluster roots on plant nutrient uptake
1
2012
...
Nye和Spiers (1964) 建立了一个同时考虑对流和扩散的模型.因为养分和水分向根表面移动的动力是根表面对养分吸收后形成的浓度差, 所以
Epstein (1972) 提出用米氏动力学方程作为养分吸收模型的边界条件来描述根表面的养分吸收, 该边界条件是非线性的.Nye, Tinker和Barber等研究者, 在Nye和Spiers的模型基础上, 同时考虑对流和扩散过程, 建立了大范围内养分向根部迁移的圆柱形单根养分吸收模型, 简称Nye-Tinker-Barber模型(
Nye & Tinker, 1977 ;
Barber, 1984 ).在此模型的基础上使用平均化方法修正根对土壤养分扩散吸收或者在对流扩散方程中增加源汇项.
Roose和Fowler (2004) 建立了植物根系同时吸收水分和养分的模型;
Schnepf和Roose (2006) 建立了菌丝体养分吸收模型;
Schnepf等(2011) 建立了单个菌丝养分吸收模型;
Zygalakis等(2011) 建立了根毛的养分吸收的双重孔隙模型;
Zygalakis和Roose (2012) 建立了主根和排根分泌柠檬酸盐对根系吸收养分影响的模型;
Badge和Adlakha (2017) 建立了水通量对玉米根基硝酸盐动态影响的二维有限元模型;
Kumar和Hafiz (2011) 用此模型研究植物根部的污染物的吸收;
Picart等(2017) 对此模型进行数学分析和最优控制并证明溶质浓度的存在性及唯一性. ...
 ,
, ,1,2,*
,1,2,* ,
, ,1,2,*
,1,2,*
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT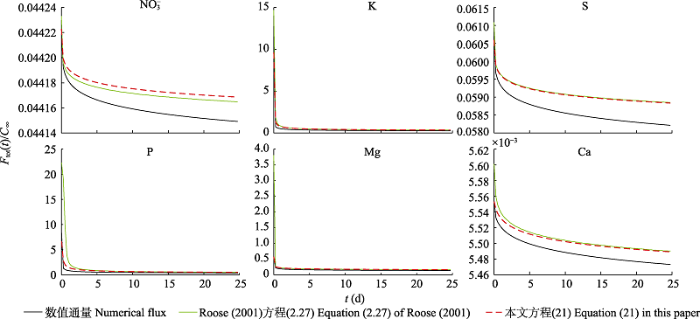 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT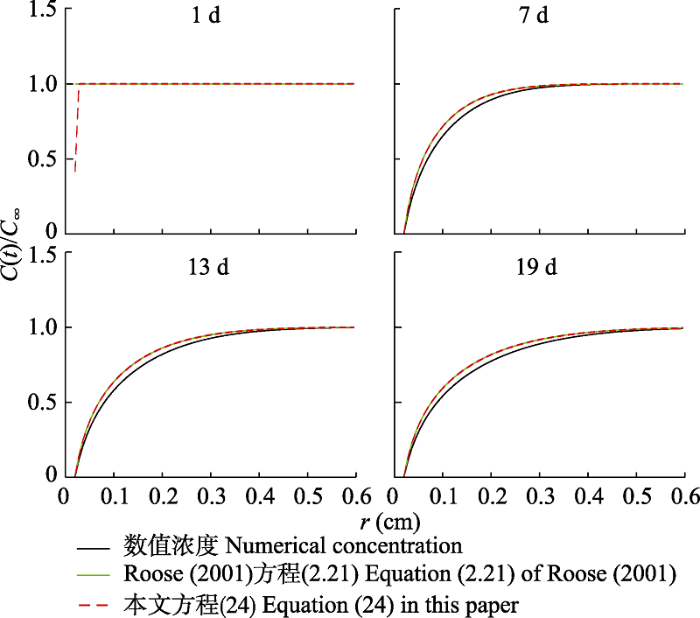 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT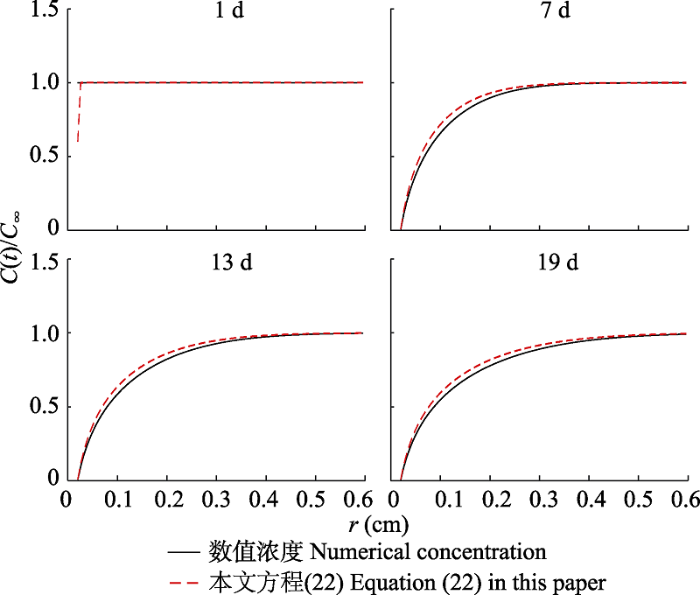 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT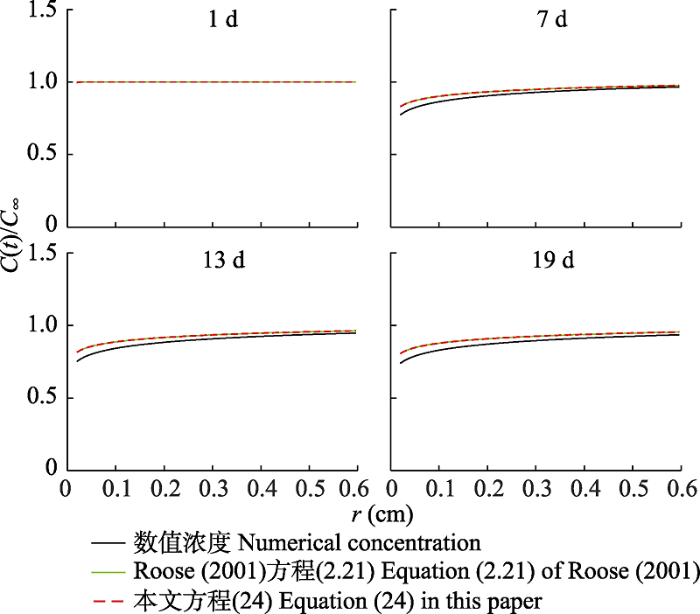 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT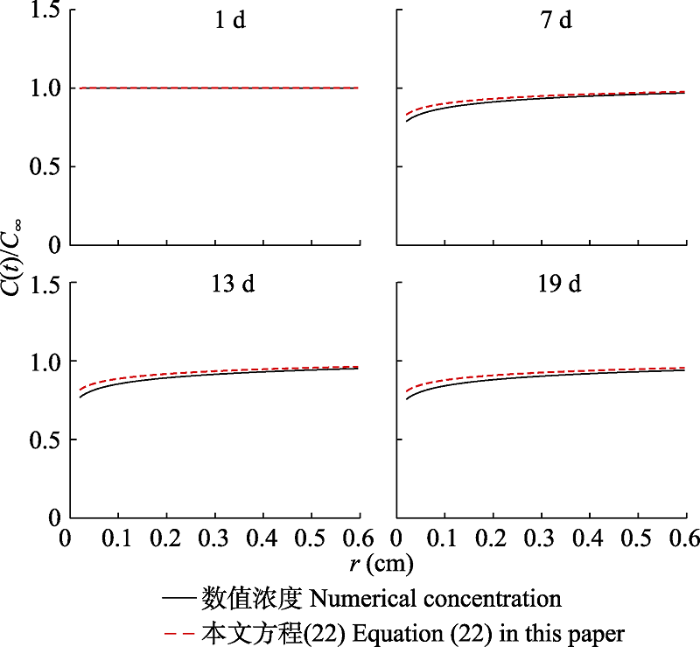 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
