大部分电子设备,尤其是机载或车载电子设备经常处于各种振动的服役环境中,振动成了影响焊点可靠性的重要环境因素。统计数据表明[4-5],振动载荷下焊点的失效率高达20%,因此针对电子封装的微互连焊点在振动条件下的可靠性研究具有重要的意义。
在往复振动载荷下,电子组件基板和印刷电路板(Printed Circuit Board,PCB)在振动载荷下产生翘曲效应,互联结构受到交变应力,其内部应力集中的部位会首先出现微小的损伤并不断累积,当前,确定互联结构损伤的方法主要基于电参数和应变参数。Kwon等[6]研究发现焊点发生损伤的时刻电阻信号会产生剧烈变化;Tang等[7]依据试验监测的电阻信号,提出振动载荷下焊点的失效过程可以分为健康状态、轻度失效、中度失效及彻底失效;陈垚君等[8]依据BGA(Ball Grid Array)焊点在正弦振动下的电阻数据,建立了单个BGA焊点的退化模型;王文等[9]根据无铅BGA焊点在随机振动下的全寿命电阻监测数据,利用比例风险模型对焊点剩余寿命进行了预测。
上述研究虽然进行了特征提取、退化建模、寿命预测的系统研究,但主要针对单个焊点开展。然而,对整个芯片而言,是多焊点组成的复杂系统,芯片内不同位置的焊点受到的应力大不相同,因此不能用简单地针对单焊点的研究方法来研究整个芯片焊点的可靠性。焊点全寿命周期内的电参数数据庞大繁杂、失效时间长、难以获得其寿命数据,为了获取较多寿命数据以建立更精确的寿命分布模型需要进行大量试验获得更多样本,时间耗费长、经济性差,而针对退化量分布建立寿命分布模型却能较好的克服这些缺点。退化量分布建模的关键是如何确定退化量分布的类型,余荣斌等[10]用β分布作为退化量分布,进行了光伏组件的退化建模;王立等[11]结合退化量分布参数估计的平稳时序类型给出了基于退化量分布的寿命预测方法。
鉴于此,本文选取BGA封装的菊花链测试芯片为试验对象,搭建了电子芯片可靠性试验台,获取多组随机振动条件下电子芯片全寿命周期内的电阻退化数据寿命的时间数据;依据断裂力学理论,推导了BGA封装芯片服从两参数威布尔分布的理论依据,建立了基于寿命数据的电子芯片寿命分布函数;接着利用退化量分布建立了基于退化量分布的寿命分布函数。通过比较发现,2种统计建模方法结果具有一致性,都可用于具体的工程实践,从而为实现电子芯片剩余使用寿命评估提供重要依据。
1 随机振动载荷下电子芯片环境应力试验 1.1 试验件设计 试验选用具有菊花链连接的测试芯片作为被测对象,其内部所有的BGA焊球都被串联起来形成了一个完整的回路,如图 1所示。
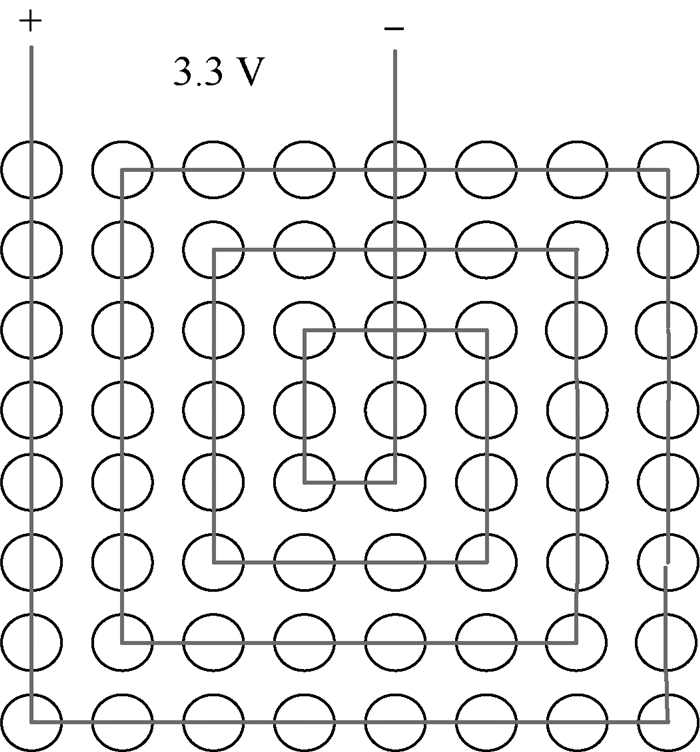 |
| 图 1 菊花链测试芯片互联结构连接图 Fig. 1 Connection diagram of interconnected structure of daisy-chain test chip |
| 图选项 |
这样,只要有一个焊球产生断裂,整个芯片都会对外表现出失效。测试芯片的尺寸为8 mm×8 mm, 厚度为0.97 mm,焊球直径0.4 mm,焊球间距0.8 mm,通过钎料锡铅焊料焊接在一块尺寸为180 mm×90 mm,厚度为0.7 mm的PCB板上,且将测试芯片置于PCB板中央,如图 2所示,能确保对称位置的焊点承受一致的应力载荷。
 |
| 图 2 随机振动试验件 Fig. 2 Test piece for random vibration |
| 图选项 |
同时,为了找到试验件的最初共振点和振动特性,采用正弦振动扫频试验法。首先将应变片置于试验件中央靠近芯片处,设置振动台采用正弦扫频振动方式,频率在20~1 000 Hz,功率谱密度设置为0.5 g2/Hz(g为重力加速度),得到的应变响应经过傅里叶变换后结果如图 3所示(只列举了前三阶固有频率)可以发现,试验件的一阶固有频率在300 Hz附近。
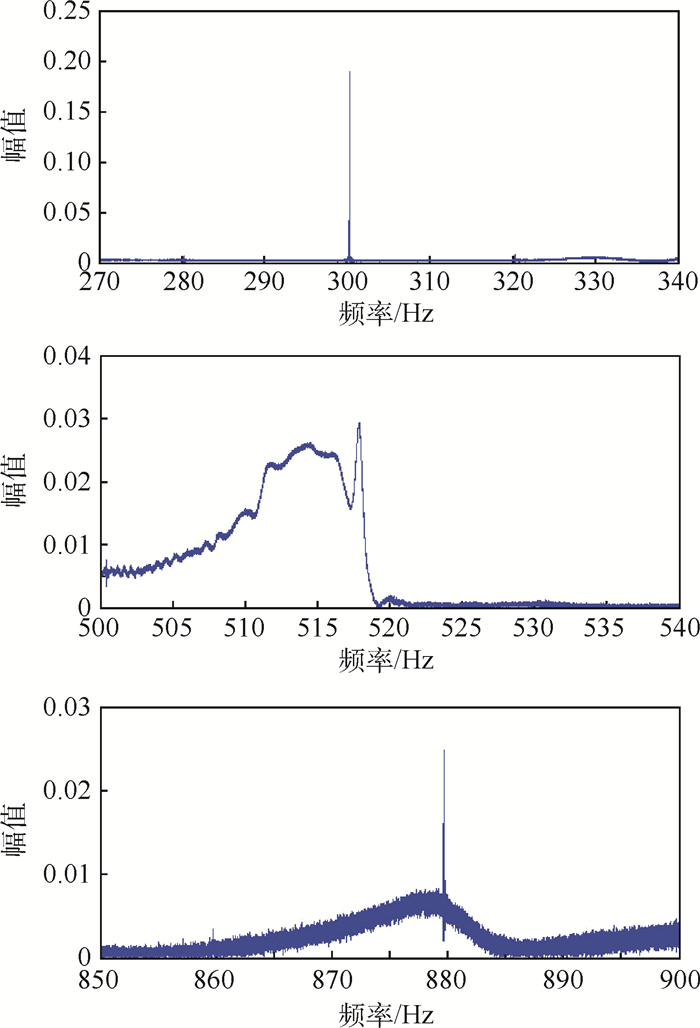 |
| 图 3 试验件的振动特性 Fig. 3 Vibration characteristics of test piece |
| 图选项 |
1.2 随机振动试验方法
1.2.1 随机振动载荷谱的确定 机载平台和装备用途的不同,会导致电子装备处在不同的振动环境中,因此,对于不同用途的电子设备,在试验中选择的振动量级也不尽相同。以喷气式飞机机载航电设备中仪表设备为例,发动机噪声对飞机结构的激励、飞机外部结构上的气动湍流、对外部气流敞开的空舱中气动湍流共振以及机动飞行、滑行等都会使电子设备处于振动环境中。其中,仪表板及机身、发动机舱等区域的振动环境均为随机振动[12],因此本文选择GJB 150.16A—2009[13]提供的仪表设备参考振动谱型来设置振动试验的载荷谱。其中,加速度功率谱密度w0一般取值为0.01、0.02、0.04、0.06、0.08 g2/Hz,但这些功率谱密度值较小,得到完整的全寿命退化数据会耗费大量的时间,因此本文以w0=0.8 g2/Hz设计加速度功率谱进行试验。同时该标准还指出,仪表设备处于30~1 000 Hz的振动频率之间,为了达到最大振动激励并同时更真实的模拟仪表设备服役环境,将载荷谱设置为一阶固有频率处,即290~310 Hz。功率谱密度值±3 dB设置警戒线,±6 dB设置中断线,当试验振动参数出现异常,会发出警告直至自行中断试验,确保整个试验过程中振动参数控制在规定值±3 dB以内。
1.2.2 随机振动试验步骤 在菊花链芯片的2个端点引出测试线,接入串联分压电路,菊花链两端的分压便能够反映菊花链内各个焊球的退化状态,这是因为,焊球内的裂纹会随着振动逐渐增大,增大的裂纹导致焊球电阻增大,进而菊花链两端的电压升高。并且只要有一个焊点出现失效,那么整个回路都会被置于高电平,从而反映出芯片的失效。将测试线从芯片引出至PCB板并利用ECONMI-7016型16通道数据采集仪采集测试芯片两端的电压退化数据。
2 电子芯片焊点失效机理及统计建模 2.1 电子芯片焊点失效机理 通过随机振动试验,可以得到连接成菊花链的芯片内互联结构由健康到完全失效的等效电阻分压的动态趋势,以其中的一个试验件的退化过程为例,如图 4所示。给定的供电电压为3.3 V,当菊花链测试芯片内的互联结构都完好时,等效电阻很小,分压接近于0V,当菊花链内任意一个焊球产生裂纹,整个回路的等效电阻增大,分压随之增大,当有任意一个焊点完全失效时,整个菊花链回路变为开路状态,电阻变为无穷大,分压达到3.3 V,电子芯片完全失效。
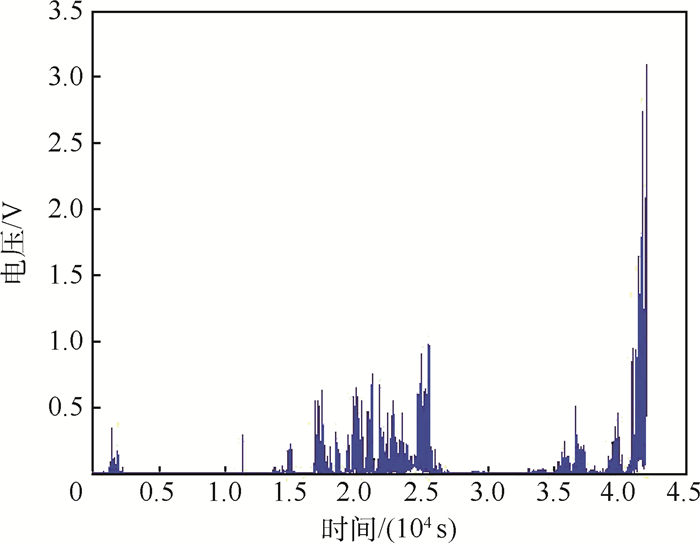 |
| 图 4 菊花链测试芯片互联结构的退化过程 Fig. 4 Degradation process of interconnected structure of daisy-chain test chip |
| 图选项 |
由图 4还可以看出,电压测值虽然已经达到3.3 V,但却出现了高低反复振荡,而不是稳定在较高水平,这反映了芯片内失效焊点随着振动出现了反复开合的现象,即焊点在拉力作用下出现开裂、导电面积减小、电阻增大、分压增大的现象;当振动台向反方向运动时,焊点受压,出现了闭合、导电面积增大、电阻减小、分压减小的现象。
2.2 基于寿命数据的电子芯片失效统计建模 随着振动时间的增加,焊球内裂纹的长度也在逐渐增大,令δi为第i次振动循环后的裂纹长度,则一定有δ1 < δ2 < … < δn。当裂纹长度达到δm时,焊点失效,假设δ0为初始裂纹,其存在且极其微小可视为0。则在第j个循环下,焊球内部裂纹的增量为δj-δj-1。依据断裂力学中裂纹长度计算公式Paris公式:
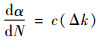 | (1) |
式中:k为应力强度因子,Δk为k的增量;α为裂纹长度;N为振动循环次数;c为常数。根据美国国家航空航天局(NASA)[14]给出的圆截面在拉压弯曲组合作用下圆弧裂纹扩展模型的应力强度因子为
 | (2) |
式中:a为裂纹的深度;F0=G(0.752+1.286β+0.37Y3),G=0.92(2/π)sec β((tanβ)/β)1/2,Y=1-sinβ,β=πa/(4R), R为焊球半径; σ0为受到的正应力。
将式(2)代入式(1),可知应力强度因子正比于裂纹长度,即裂纹的增量正比于裂纹长度,因此有理由假定裂纹扩展按照比例效应增长,即
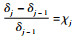
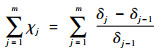 | (3) |
同时,当每次振动循环下裂纹的增量是微量的情况下有
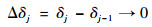 | (4) |
那么
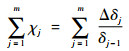 | (5) |
当振动循环充分大时,依据微积分定义可知
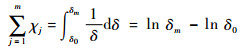 | (6) |
移项得
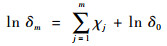 | (7) |
由中心极限定理可得
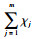
假设一个芯片有n个焊点,第i个焊点的寿命为Ti(i=1, 2…n),则每个焊点的寿命分布即为Fi(t)。对于一个具有完整功能的电子芯片而言,每一个引脚都需要实现特定的功能,因此如果假设只要有一个焊点出现失效,那么整个芯片就会失效。设芯片的寿命分布为F(t),则芯片的寿命分布就是所有焊点寿命的极小值分布。即令N=min(T1, T2, …, Tn),令焊点的失效阈值为z,则有
 | (8) |
每个焊点的失效状态互不影响,故可以认为Ti相互独立,则有
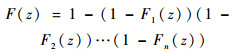 | (9) |
另外,在振动载荷下,芯片不同位置的焊球所受到的应力不是均匀的,文献[15]表明,位于芯片边角处的焊点受应力更为集中,会优先失效,故Fi(t)虽然均服从对数正态分布,但参数却会随着焊球的位置变化而有所不同。定义位置参数P,对不同位置焊球的尺度参数进行归一化,则不同位置焊球的寿命分布Fi(t)可以归一化为FP(t)。因此有
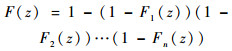 | (10) |
可化为
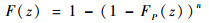 | (11) |
文献[16]表明,当FP(t)服从对数正态分布且n充分大时,F(z)=1-(1-FP(z))n的渐进分布为两参数威布尔分布,其概率密度函数为
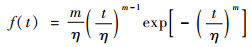 | (12) |
式中:m为形状参数; η为尺度参数。由此给出了BGA封装形式的电子芯片互联结构失效寿命服从威布尔分布的理论依据。
3 基于退化量分布的电子芯片失效统计建模 3.1 基于退化量分布的寿命分布模型 如果把电子芯片的互联结构的退化看作一随时间变化的随机过程x(t),同一批产品虽然总体来说具有同一种退化规律,但是对于不同的个体而言,在t时刻的退化量x(t)又会具有较大的差异,但如果在某一时刻t确定了x(t)在不同个体中的形式G(x, t),并且能通过试验数据统计出G(x, t)随时间变化的规律,就确定了G(x, t),从而能推导出寿命的累积分布函数F(t)。
由于产生了裂纹的BGA焊点在振动过程中出现的开开合合的间歇性失效现象,为了增加数据的单调性,消除间歇性失效的影响,对数据进行进行累加生成,即由原始的退化量数据x1, x2, …, xn变化为x1, x1+x2, …, x1+x2+…+xn。收集试验产品在t1, t2, …, tM时刻的性能退化数据,依据中心极限定理,可以导出,经过逐步累加的退化数据在ti(i=1, 2, …, M)时刻不同样品的退化量的渐进分布为均值为μ(t),标准差为σ(t)的正态分布。
对它们进行标准化可以得到
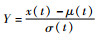
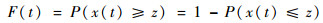 | (13) |
有
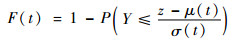 | (14) |
可得
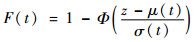 | (15) |
3.2 基于退化量分布的电子芯片焊点失效数据统计建模 将得到的原始电压数据进行累加生成,得到的退化轨迹如图 5所示(以5个样本中的某一样本为例),累计退化量变成了单调增函数。
 |
| 图 5 菊花链测试芯片互联结构累计退化量 Fig. 5 Accumulated degradation of interconnected structure of daisy-chain test chip |
| 图选项 |
取时间t的初始值为5 000 s,每间隔5 000 s取5个试验样本对应时间下的累计退化量,为一组,共取20组,取它们的累加退化量的均值μ和标准差σ,其随时间的分布具有较好的线性度,如图 6所示。
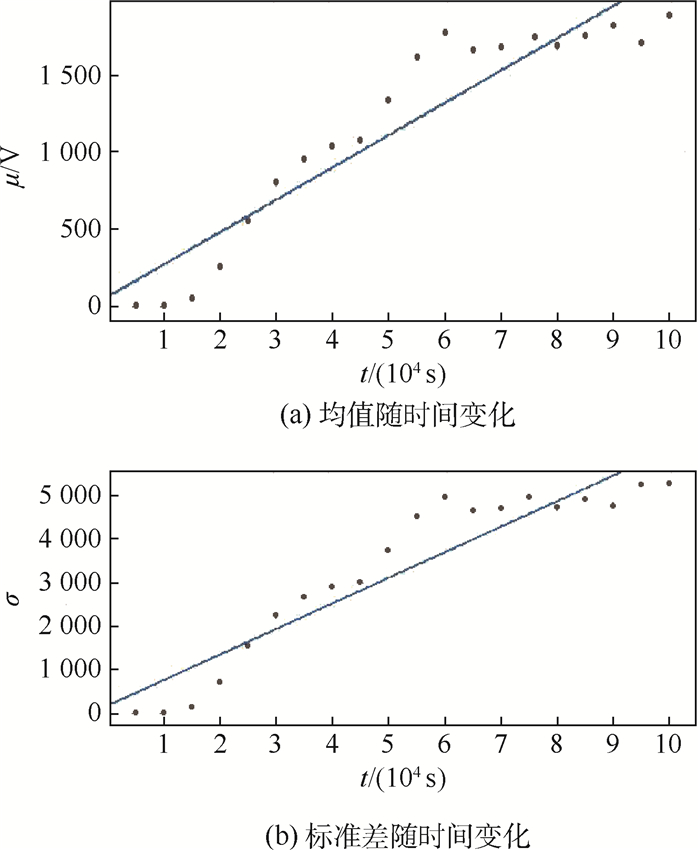 |
| 图 6 互联结构累计退化量的均值和标准差随时间变化 Fig. 6 Variation of mean value and standard deviation of accumulated degradation of interconnected structure with time |
| 图选项 |
对均值和标准差进行最小二乘拟合,得到了均值随和标准差随时间的表达式分别为
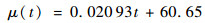 | (16) |
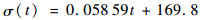 | (17) |
选择完全断裂时芯片两端的分压3.3 V为失效阈值,对5组试验数据失效的首达时间下的累计退化量做平均值作为累计退化量的经验阈值,经计算得到阈值为3 749 V,将该经验值和式(16)、式(17)代入式(15)得到了芯片的寿命的累积分布函数。
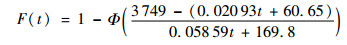 | (18) |
同时,试验件的5组累计失效时间如表 1所示。
表 1 各组试验件的累计失效时间 Table 1 Accumulative failure time for each group of test piece
| 试验组 | 累积失效时间/s |
| 1 | 60 627 |
| 2 | 118 618 |
| 3 | 42 017 |
| 4 | 165 376 |
| 5 | 26 115 |
表选项
3.3 对比分析 利用极大似然估计得到了二参数威布尔分布的形状参数和寿命参数如表 2所示。
表 2 两参数威布尔分布的参数估计 Table 2 Parameter estimation of two-parameter Weibull distribution
| 参数 | 数值 |
| 形状参数m | 1.667 |
| 尺度参数η | 93 002 |
表选项
基于退化量数据的电子芯片寿命的累积分布函数和基于寿命数据的电子芯片寿命的累计分布函数如图 7所示。
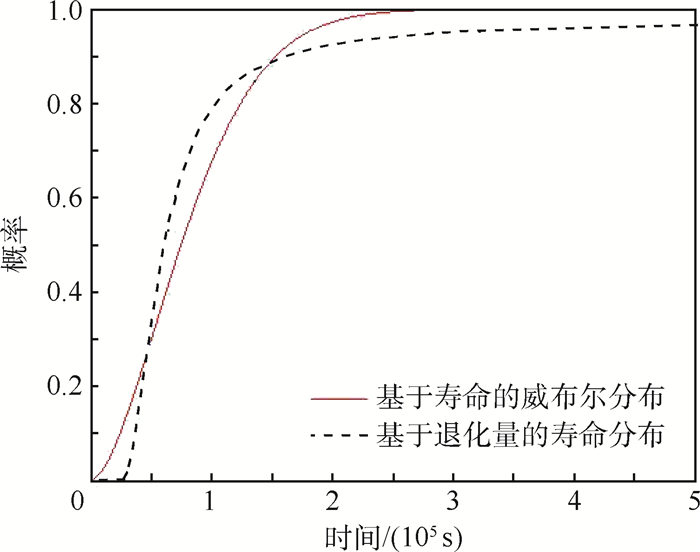 |
| 图 7 菊花链测试芯片互联结构的寿命分布 Fig. 7 Lifetime distribution of interconnected structure of daisy-chain test chip |
| 图选项 |
对比分析发现,2种寿命分布建模方法得到的累积分布函数具有较高一致性,基于退化量数据进行统计建模可以大幅缩短试验时间,但因需要引入经验值导致精度上会有所缺失。基于寿命数据的统计建模方法具有较高的精度,但因失效时间长而导致寿命数据难以获取。
4 结论 本文针对电子芯片互联结构失效机理复杂、寿命数据难以获取且缺乏具有理论依据支撑的寿命分布模型等问题,开展了电子芯片互联结构的可靠性试验。结合断裂力学理论,推导了电子芯片互联结构寿命分布服从两参数威布尔分布的理论依据,并建立了基于寿命数据的电子芯片失效的统计模型。利用退化数据,建立了基于退化数据的电子芯片失效统计模型。2种模型结果均以电子芯片寿命的累计分布函数给出。由此得到了以下结论:
1) 电子芯片互联结构的寿命分布的渐进分布服从两参数威布尔分布,利用其分布能够建立基于寿命数据的电子芯片失效统计模型。
2) 基于退化数据的电子芯片统计模型与基于寿命数据的电子芯片统计模型结果互相吻合,具有较高的一致性。
3) 基于退化量数据进行统计建模可以大幅缩短试验时间,但因需要引入经验值导致精度上会有所缺失。基于寿命数据的统计建模方法具有较高的精度,但因寿命数据难以获取会给建模带来困难。
参考文献
| [1] | 胡家兴, 景博, 汤巍, 等. 电子设备无铅焊点的热疲劳评估进展与展望[J]. 空军工程大学学报(自然科学版), 2016, 17(6): 7-12. HU J X, JING B, TANG W, et al. Evaluation and prospect of thermal fatigue on lead-free solder joints in electronic equipment[J]. Journal of Air Force Engineering University(Natural Science Edition), 2016, 17(6): 7-12. (in Chinese) |
| [2] | 周德俭. 电子制造中的电器互连技术[M]. 北京: 电子工业出版社, 2010: 1-5. ZHOU D J. Manufacturing technology for electronics[M]. Beijing: Electronic Industry Press, 2010: 1-5. (in Chinese) |
| [3] | GUO Q, ZHAO M, WANG H F. SMT solder joint's semi-experimental fatigue model[J]. Mechanics Research Communications, 2005, 32(3): 351-358. DOI:10.1016/j.mechrescom.2004.03.011 |
| [4] | 胡家兴, 景博, 汤巍, 等. 无铅微焊点的热效应仿真及可靠性分析[J]. 电子元件与材料, 2016, 32(3): 81-84. HU J X, JING B, TANG W, et al. Thermo effect simulation and reliability analysis of lead-free micro solder joints[J]. Electronic Compoents and Materials, 2016, 32(3): 81-84. (in Chinese) |
| [5] | PANG J H L, WONG F L, HENG K T, et al.Combined vibration and thermal cycling fatigue analysis for SAC305 lead free solder assemblies[C]//2013 IEEE 63rd Electronic Components and Technology Conference.Piscataway, NJ: IEEE Press, 2013: 1300-1307. |
| [6] | KWON D, AZARIAN M H, PECHT M. Remaining-life prediction of solder joints using RF impedance analysis and Gaussian process regression[J]. IEEE Transactions on Components Packaging & Manufacturing Technology, 2015, 5(11): 1602-1609. |
| [7] | TANG W, JING B, HUANG Y F, et al. Multistate degradation model for prognostics of solder joints under vibration conditions[J]. Chinese Journal of Electronics, 2016, 25(4): 779-785. |
| [8] | 陈垚君, 景博, 常雅男, 等. 振动载荷下板级焊点退化状态表征与分析[J]. 微电子学, 2017, 47(6): 866-871. CHEN Y J, JING B, CHANG Y N, et al. Failure characterization and analysis of board level solder interconnects under vibration load[J]. Microelectronics, 2017, 47(6): 866-871. (in Chinese) |
| [9] | 王文, 孟光, 刘芳, 等. 基于比例风险模型的板级无铅焊点跌落寿命分析[J]. 振动与冲击, 2011, 30(3): 124-128. WANG W, MENG G, LIU F, et al. Lifetime analysis of lead-free solder joints under drop impact using proportional hazards model[J]. Journal of Vibration and Shock, 2011, 30(3): 124-128. DOI:10.3969/j.issn.1000-3835.2011.03.025 (in Chinese) |
| [10] | 余荣斌, 刘桂雄, 徐欢. 基于β分布统示法的光伏组件性能退化可靠度估算[J]. 仪器仪表学报, 2015, 36(11): 2586-2593. YU R B, LIU G X, XU H. β distribution uniform expression based photovoltaic modules reliability evaluation with degradation data distribution[J]. Chinese Journal of Scientific Instrument, 2015, 36(11): 2586-2593. DOI:10.3969/j.issn.0254-3087.2015.11.024 (in Chinese) |
| [11] | 王立, 李晓阳, 姜同敏. 基于退化量分布时序分析的产品寿命预测[J]. 北京航空航天大学学报, 2011, 37(4): 492-498. WANG L, LI X Y, JIANG T M. Life prediction of product based on degradation amount distribution time series analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 492-498. (in Chinese) |
| [12] | 祝耀昌, 李韵, 徐俊, 等. 民用飞机机载设备振动实验要求和应用分析(一)[J]. 装备环境工程, 2016, 13(4): 54-61. ZHU Y C, LI Y, XU J, et al. Vibration test requirements and application analysis of civil aircraft equipment(1)[J]. Equipment Environmental Engineering, 2016, 13(4): 54-61. (in Chinese) |
| [13] | 军用装备实验室环境试验方法: 第16部分: 振动实验: GJB 150.16A-2009[S].北京: 中国人民解放军总装备部. Military equipment laboratory environmental methods: Part 16 vibration experiment: GJB 150.16A-2009[S].Beijing: PLA General Armament Department(in Chinese). |
| [14] | FORMAN R G, SHIVAKUMAR V.Growth behavior of surface crack in the circumferential plane of solid and hollow cylinders[M]//UNDERWOOD J, CHAIT R, WILHEM D, et al.Frac-ture Mechanics: Seventeenth Volume.West Conshohoken: ASTM International, 1986: 59-74. |
| [15] | KIM Y K, HWANG D S. PBGA packaging reliability assessments under random vibrations for space applications[J]. Microelectronics Reliability, 2015, 55(1): 172-179. |
| [16] | 钱萍.航天电连接器综合应力加速寿命试验与统计分析的研究[D].杭州: 浙江大学, 2009. QIAN P.Research on multiple stresses accelerated life test and statistical analysis of aerospace electronic connecter[D].Hangzhou: Zhejiang University, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10335-2010055978.htm |
