对于承力结构的隔振设计,一般是在结构与基础间施加质量、弹性及阻尼元件,通过转移和消耗振动能量使振动传递率达到最小[2]。根据隔离对象的不同可分为:减小振源对基础力的传递与减小基础振动对附着结构的运动传递,即力隔振与运动隔振[3-4]。在此方面,王祖华等[5]应用阻振质量对振动波传递的阻抑特性,通过构造阻抗失配结构,为舰船舱壁进行了隔振优化设计。况成玉[6]利用周期结构对弹性波传播的抑制效果,设计出船体隔振浮筏,并研究了其隔振特性。姜洪源等[7]通过对航空发动机用金属橡胶隔振器的实验研究,验证了其较橡胶更优异的隔振性能。考虑航空发动机承力结构作为板壳组合结构系统,采用通常方法很难使得各位置都达到理想效果。近年来,国内外****提出利用时滞反馈等主动或半主动介入方式[8],即在系统中引入外界能量产生与主振源相抵消的振动,实现对振动的有效隔离[9-10]。在此方面,Nagai等[11]应用神经网络控制方法对列车悬挂系统进行了振动主动控制的研究。梅德庆和陈子辰[12]为微制造平台设计了基于磁致伸缩作动器的二维模糊主动隔振系统。但主动隔振器存在输出力与响应时间的限制、信号在传输过程中的迟滞等问题[13-14],还会对承力结构产生附加质量,影响发动机工作可靠性的同时也不利于结构减重。马艳红等[15]针对涡轴发动机涡轮级间支承结构隔振设计问题,初步提出相邻部件之间刚度/质量分布差异加大可有效避免耦合振动的设计思想,但缺少相关理论分析及试验的验证。
本文在对先进航空发动机涡轮承力框架结构及其隔振特性分析的基础上,进一步总结提出了通过承力结构几何构形的变化改变其力学特征,利用结构间刚度/质量分布的差异和阶跃,提高结构系统在宽频域内的机械阻抗,实现高隔振性的设计方法。在研究中建立了承力结构隔振特性分析力学模型,并通过转子-承力框架试验系统进行了试验验证。本文研究对于航空发动机承力结构的自主设计与高隔振性改进具有指导意义。
1 承力框架结构及力学特征 1.1 结构特征 典型涡轮承力框架是由具有板/壳等不同几何构形的部件组成的复杂结构系统。不同部件的受力形式及振动模态都具有局部特征,并表现出一定的正交性。因此,以各部件间连接处为节点,根据不同结构特征,将整个系统离散化为不同的结构单元。图 1为先进涡轮级间共用承力框架的结构示意图,其主要由涡轮机匣、导流器组件、承力鼓筒、共用轴承座等组成。
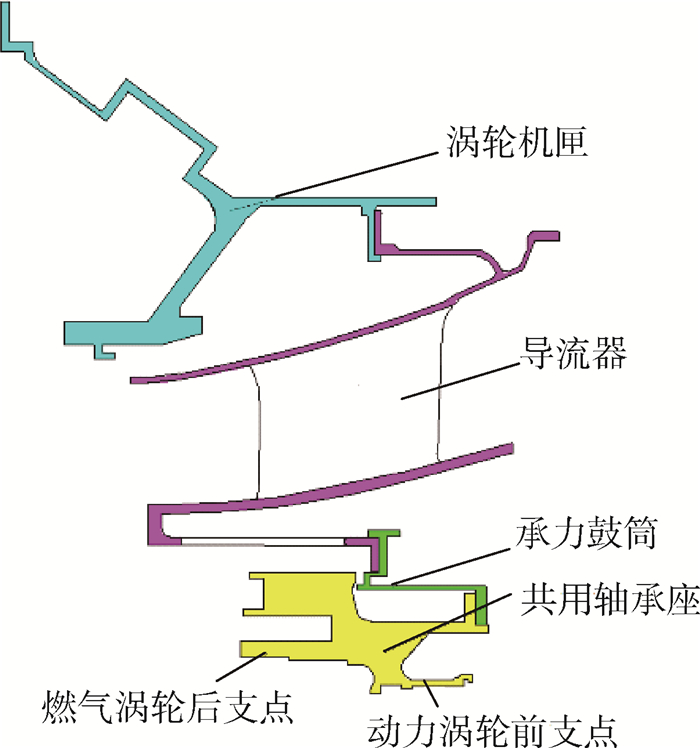 |
| 图 1 先进涡轮级间共用承力框架结构 Fig. 1 Advanced shared mid-turbine supporting frame structure |
| 图选项 |
导流器外安装边与涡轮机匣通过螺栓连接,外安装边的柔性锥壳结构设计能够减小导流器内外温度梯度下结构内的附加热应力。导流器内环向内延伸出折返式鼠笼,与其他串联的承力部件相比,其具有较弱的径向刚度,决定了承力框架的刚度水平,其位于低温环境下,能够降低承力结构支承刚度对于温度的敏感度;同时柔性折返式鼠笼与承力鼓筒通过法兰-螺栓相连,保证了法兰边位置的变形协调,提高了连接结构的稳健性。承力鼓筒与共用轴承座后伸安装边通过螺栓相连,二者同样构成折返式结构,与共用轴承座相比具有较弱的径向刚度。前2处螺栓连接轴向上处于同一平面,且位于共用轴承座重心位置,避免了附加弯矩产生的同时,减弱了共用轴承座各支点振动的相互影响。
综上所述,典型先进涡轮承力框架结构可看作是由不同几何构形及刚度、质量特征各不相同的结构单元通过多处折返式设计串联而成,具有明显的几何非连续及离散化的结构特征。
1.2 刚度/质量分布特征 针对图 1所示承力框架结构,建立三维有限元模型(见图 2),分析其刚度/质量分布的力学特征。有限元模型中,承力框架材料设为高温合金GH3652,具体部件材料属性如表 1所示。
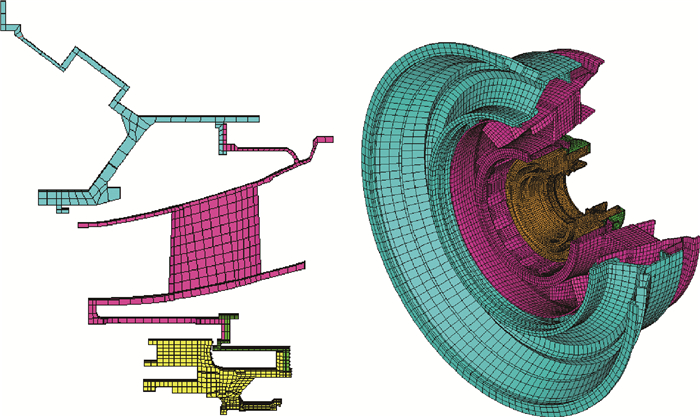 |
| 图 2 承力框架有限元模型 Fig. 2 Supporting frame finite element model |
| 图选项 |
表 1 承力框架材料参数 Table 1 Supporting frame material parameters
| 部件 | 密度/(kg·m-3) | 弹性模量/GPa | 泊松比 |
| 导流器叶片 | 8.44×103 | 164 | 0.308 |
| 其余部件 | 8.44×103 | 205 | 0.308 |
表选项
基于有限元模型,对承力框架各部件的质量、等效径向刚度以及刚度/质量特征进行计算,结果如表 2所示。
表 2 承力框架各部件非连续性刚度/质量分布特征 Table 2 Supporting frame parts' discrete stiffness/mass distribution characteristics
| 编号 | 部件 | 质量/kg | 刚度/ (N·m-1) | 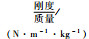 |
| 1 | 涡轮机匣 | 21.1 | 6.22×108 | 2.95×107 |
| 2 | 导流器 | 13.0 | 1.28×108 | 9.85×106 |
| 3 | 折返式鼠笼 | 2.0 | 8.13×107 | 4.07×107 |
| 4 | 承力鼓筒 | 0.9 | 2.32×108 | 2.58×108 |
| 5 | 共用轴承座 | 8.0 | 7.76×108 | 9.70×107 |
表选项
由表 2计算结果可知,承力框架结构各相邻部件间的刚度/质量分布特征均具有较大差异和突变,整体刚度/质量分布特征表现为非连续及离散化分布。
2 刚度/质量分布对隔振性的影响 2.1 理论分析 基于承力框架结构特征,分别建立等刚度/质量分布和变刚度/质量分布承力结构动力学模型,引用机械阻抗表征结构的隔振特性,分析不同刚度/质量分布特征对其产生的影响。模型中暂忽略系统阻尼,如图 3所示。
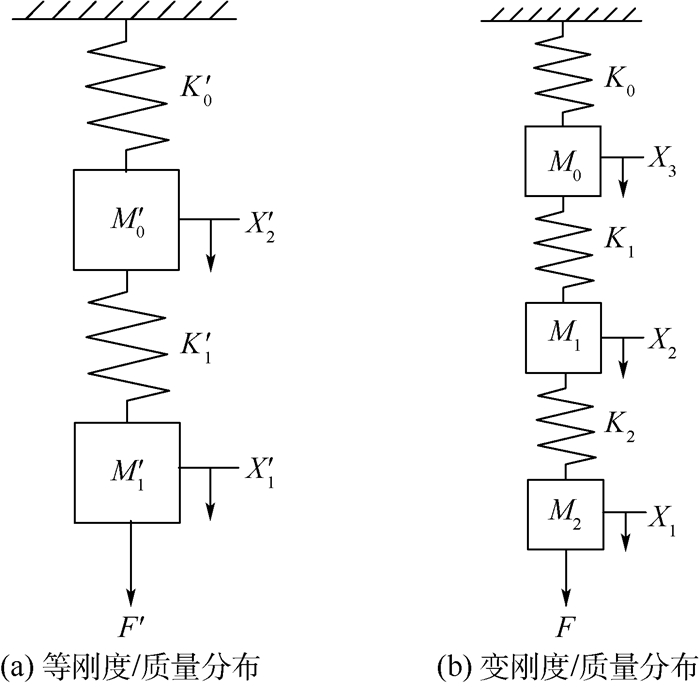 |
| 图 3 承力结构动力学模型 Fig. 3 Supporting structure dynamical model |
| 图选项 |
图 3(a)为等刚度/质量分布承力框架力学模型。其中,M0′、K0′分别为外机匣响应位置的质量、刚度,M1′、K1′分别为等刚度/质量分布承力结构的质量、刚度。假设M0′=m,K0′=100k,M1′=2m,K1′=k。图 3(b)为变刚度/质量分布承力框架力学模型。其中,M0、K0分别为外机匣响应位置的质量、刚度,M1、K1分别为大刚度/质量分布特征承力结构的质量、刚度,M2、K2分别为小刚度/质量分布特征承力结构的质量、刚度。假设M0=M1=M2=m,K0=K1=100k,K2=k。2个模型承力结构部分总质量相等、等效刚度近似相等。假设激振力F、F′的频率为ω。应用节点响应法[16]分别对2个模型计算激振点与响应位置间的传递阻抗(位移阻抗),并进行对比分析。
类比电网络图,用回路表示系统及振源组成的封闭系统,建立相应机械网络图,如图 4所示。
 |
| 图 4 承力结构机械网络 Fig. 4 Mechanical network of supporting structure |
| 图选项 |
在图 4(a)中:
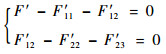 | (1) |
式中:F11′=Z1′X1′,F12′=Z2′(X1′-X2′),F22′=Z3′X2′,F23′=Z4′X2′,Z1′=-2mω2,Z2′=k,Z3′=-mω2,Z4′=100k,X1′、X2′分别为图 4(a)中1、2点的响应值。
代入式(1)求得等刚度/质量分布模型的传递阻抗为
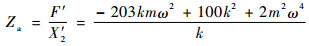 | (2) |
在图 4(b)中:
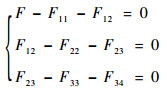 | (3) |
式中:F11=Z1X1,F12=Z2(X1-X2),F22=Z3X2,F23=Z4(X2-X3),F33=Z5X3,F34=Z6X3, Z1=Z3=Z5=-mω2,Z2=k,Z4=Z6=100k, X1、X2、X3分别为图 4(b)中1、2、3点的响应值。
代入式(3)整理可得
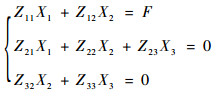 | (4) |
式中:
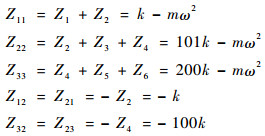 |
代入式(4)求得变刚度/质量分布模型的传递阻抗为
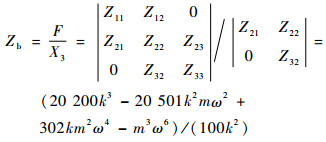 | (5) |
比较Za和Zb的大小,令Zb-Za得
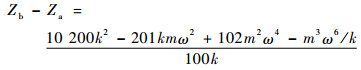 | (6) |
化简得
 | (7) |
式中:λ=ω2/ωn2,
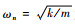
根据航空发动机中承力框架固有模态频率与转子不平衡激励频率的关系,可假设激振力频率范围为:0 < ω < 10ωn,即0 < λ < 100,可得Zb-Za>0,即
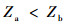 | (8) |
可见,在航空发动机转子工作转速范围内,承力结构刚度/质量分布非连续性设计相比于等刚度/质量分布具有更大的传递阻抗,表现出更好的隔振性能。
针对图 2所示的非连续承力框架实际结构,根据各部件刚度/质量分布特征,将其简化为五自由度的弹簧-质量系统,暂忽略系统阻尼,如图 5所示。由表 2中各部件的编号,图 5中的mi和ki(i=1, 2, …, 5)分别表示涡轮机匣至共用轴承座的质量和刚度。
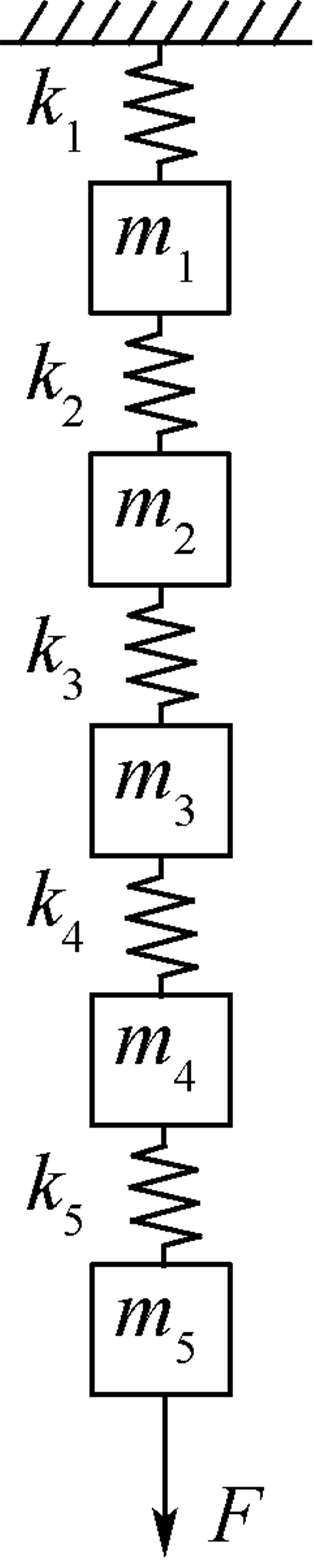 |
| 图 5 非连续承力结构动力学模型 Fig. 5 Discrete supporting structure dynamical model |
| 图选项 |
令激振力F的频率为ω,则图 5中质量单元阻抗为Ii=-miω2,弹簧单元阻抗为Ii′=ki,D1~D5分别表示部件1~5处的位移响应。得到简化阻抗如图 6所示。
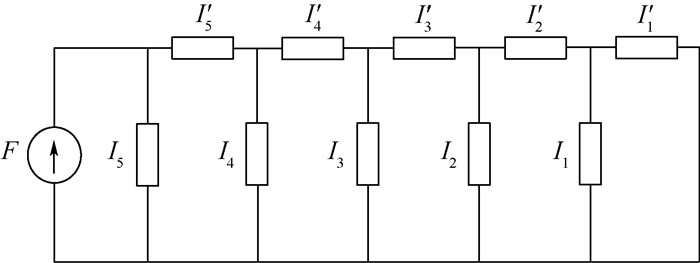 |
| 图 6 非连续承力结构简化阻抗示意图 Fig. 6 Schematic of simplified impedance of discrete supporting structure |
| 图选项 |
由图 6可知,令
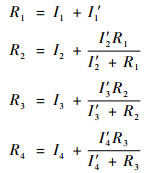 |
根据图 6中各元件间关系可得
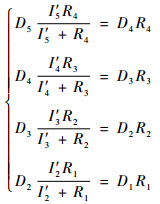 | (9) |
定义两测点位置的振动响应比值为测点间的振动传递系数,以此表征测点间结构的隔振特性。由式(9)可求得共用轴承座至涡轮机匣的振动传递系数为
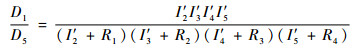 | (10) |
假设激振力F频率为1 000 Hz,根据表 2中各部件的刚度、质量值,计算得到涡轮机匣至共用轴承座的振动传递系数约为0.07,近90%的振动被衰减,说明承力板壳结构的非连续性设计具有良好的隔振效果。
2.2 仿真分析 基于图 2中非连续承力框架有限元模型,应用谐响应分析方法,通过有限元仿真分析其振动传递特性,并与刚性(连续性)承力框架结构(见图 7)进行对比,以验证承力结构非连续性设计良好的隔振效果。
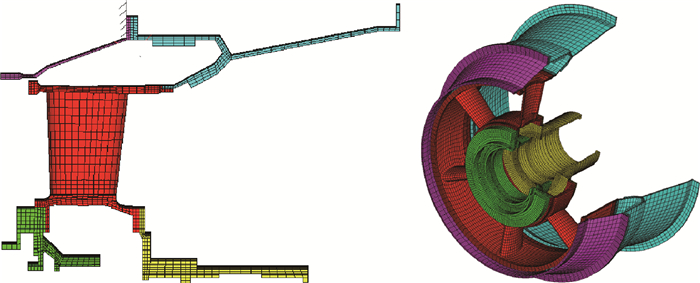 |
| 图 7 刚性(连续性)承力框架有限元模型 Fig. 7 Rigid (continuous) supporting frame finite element model |
| 图选项 |
为模拟承力框架实际工作状态,对涡轮机匣外安装边施加全约束,其余结构为自由状态;在燃气涡轮后支点处施加径向1 000 N作用力,计算频率范围为0~1 200 Hz。
分别提取支点与涡轮机匣内安装边位置处的位移响应,计算得到不同激振力频率下不同特征承力框架支点至涡轮机匣的振动传递系数(机匣响应/支点响应),如图 8所示。
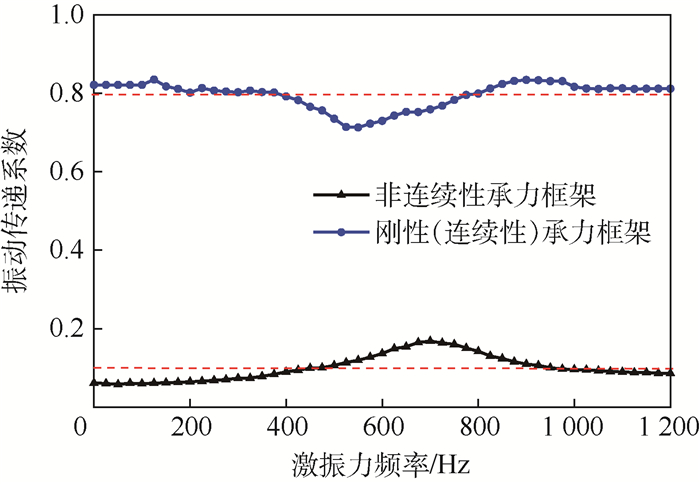 |
| 图 8 支点至涡轮机匣的振动传递系数 Fig. 8 Vibration transfer coefficient from bearing point to turbine motor case |
| 图选项 |
由数值仿真结果可知:①对于非连续性承力框架,相比于支点位置,涡轮机匣内安装边处响应幅值大幅减小,振动传递系数在0.1左右;②对于刚性(连续性)承力框架,支点至涡轮机匣的振动传递系数较大,在0.8左右,即振动衰减较弱;③在不同激振力频率下,受结构自身振动特性影响,振动传递系数有所不同。
通过上述2个模型仿真计算结果的对比,进一步验证了理论分析。结构构形突变及各构件间刚度/质量分布的非连续性设计,可显著降低振动传递系数,具有优异的隔振性能。
3 转子-承力框架试验 3.1 总体设计方案 在转子-承力框架试验系统设计中,转子采用柔性悬臂结构,总长为580 mm,质量为3.23 kg(包括轮盘)。利用电机经输出传动轴带动转子系统。采用双支点支承方案,在靠近电机处设置1#支点,采用滚珠轴承、刚性支承。在靠近轮盘处(远离电机一端)设置2#支点,采用滚棒轴承、弹性支承,用作承力框架试验支点,此处可采用单一轴承或双轴承并用支承状态。为了模拟试验支点处承力结构的几何构形及刚度/质量分布非连续特征,分别采用了刚度/质量分布特征各不相同的承力支架、承力鼓筒及折返式鼠笼以折返结构形式相连。轮盘安放在轴的一端,采用伸臂悬置方式。试验系统结构设计方案如图 9所示。图 10为装配后的试验系统实物图。
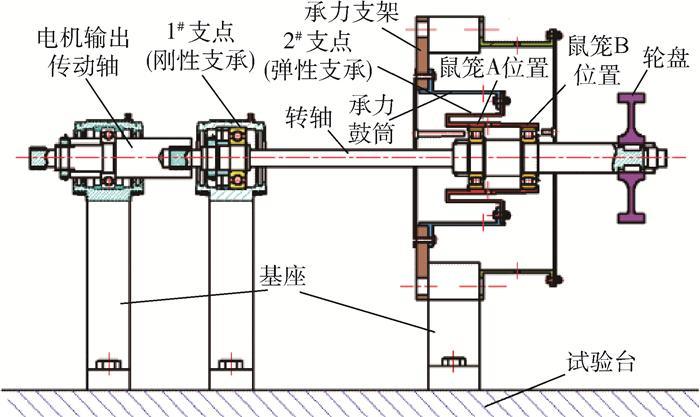 |
| 图 9 转子-承力框架试验系统设计方案 Fig. 9 Rotor-supporting frame experimental apparatus design scheme |
| 图选项 |
 |
| 图 10 转子-承力框架试验系统实物图 Fig. 10 Picture of rotor-supporting frame experimental apparatus |
| 图选项 |
3.2 测点布置 本试验主要针对承力框架各关键位置进行振动测量,具体测试项目为承力框架各位置的加速度信号。图 11为试验系统测点位置分布示意图,分别在承力框架的支点、承力鼓筒以及承力支架外端布置接触式加速度传感器(图中①、②、⑤位置)。由传感器获取的振动信号,通过前置放大器与电荷放大器转换为电压信号,统一输入到DASP采集卡中,通过DASP-V10智能数据采集和信号处理系统进行分析。
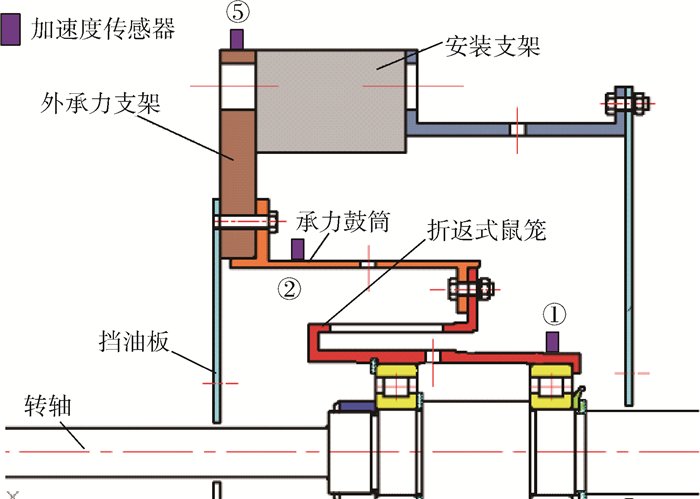 |
| 图 11 转子-承力框架试验系统测点位置分布 Fig. 11 Rotor-supporting frame experimental apparatus measuring point layout |
| 图选项 |
3.3 试验状态 根据各支承状态下临界转速测试结果,选取振动响应测试转速。双轴承并用时,最高试验转速选为5 500 r/min,单一轴承时最高试验转速选为5 000 r/min,采用阶梯转速控制方式。试验过程中转子不平衡量选为43.5 g·mm。
3.4 试验结果与分析 对试验支点处采用单一轴承支于鼠笼B位置状态进行试验测试,得到承力框架各测点位置径向振动响应信号(加速度信号)的幅频特性曲线,如图 12所示。
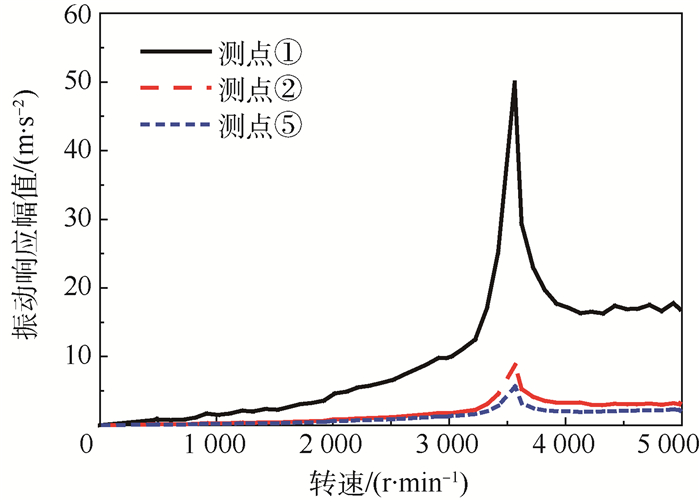 |
| 图 12 单一轴承支于鼠笼B位置的振动响应幅频曲线 Fig. 12 Vibration response amplitude frequency curves of single bearing on squirrel cage B position |
| 图选项 |
由图 12可知,承力框架不同位置振动响应不同,其变化规律为:距转子系统最近的支点位置(测点①)振动响应幅值最大;振动经折返式鼠笼传递至承力鼓筒位置(测点②)后,振动响应幅值大幅减小;距转子系统最远的承力支架位置(测点⑤)振动响应幅值最小。
分别将测点①、测点②、测点⑤位置振动响应幅值记为A1、A2、A5,可得各转速下不同结构间振动传递系数A5/A1、A5/A2与A2/A1,如图 13所示。
 |
| 图 13 单一轴承支于鼠笼B位置的振动传递系数 Fig. 13 Vibration transfer coefficient of single bearing on squirrel cage B position |
| 图选项 |
由图 13可知,本承力框架试验件由支点至承力支架外端的振动传递系数约为0.13,振动传递系数较小,可见所设计的刚度/质量分布非连续承力框架试验件具有较为优异的振动隔离特性。
通过对承力框架试验件各部分的力学特征分析可知:测点①、测点②间的承力鼓筒-折返式鼠笼结构与测点⑤、测点②间的承力支架相比,具有较大的刚度/质量分布特征差异,试验中测得振动由支点经折返式鼠笼至承力鼓筒的振动传递系数(A2/A1)在0.2左右,远小于承力鼓筒至承力支架外端的振动传递系数(A5/A2)(约0.65以上),可见结构较大的刚度/质量分布特征差异能够对振动起到更有效的衰减作用。
改用单一轴承支于鼠笼A位置以及双轴承并用不同支承状态,进一步探究承力框架试验件不同轴承支承位置与数量对隔振特性的影响。改用另外2种支承状态后承力框架试验件的振动传递系数如图 14所示。
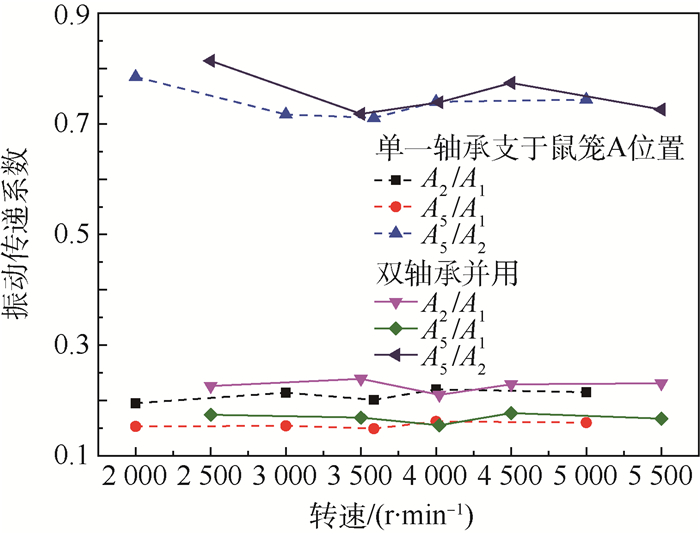 |
| 图 14 双轴承并用与单一轴承状态振动传递系数对比 Fig. 14 Comparison of vibration transfer coefficient between double bearings and single bearing |
| 图选项 |
由图 13和图 14可知,双轴承并用情况下,承力框架试验件各测点间的振动传递系数与单一轴承支承不同位置时相近,波动变化区间基本一致,说明双轴承并用不会改变承力结构内阻抗特性,对承力结构内振动传递与衰减特征无明显影响,此承力框架试验件在宽频域内对不同位置支点处的激励均具有良好的隔振性。
4 结论 本文通过对先进航空发动机涡轮承力框架结构、力学特征的分析,结合理论模型、仿真计算和试验验证,提出高隔振性承力结构设计理论,为航空发动机承力结构的设计与高隔振性改进提供指导。
1) 典型高隔振性航空发动机承力框架的板壳结构具有几何构形突变与离散化特点,以及刚度/质量分布非连续的力学特征。理论分析与仿真计算表明,非连续承力结构支点至涡轮机匣的振动传递系数约0.1左右。而在刚性(连续性)承力结构中振动传递系数可达0.8以上,远高于非连续结构。板壳支承结构的非连续性设计可实现结构内较大的机械阻抗及良好的隔振性能。
2) 转子-承力框架试验系统的试验结果表明,承力框架整体振动传递系数约为0.13,在刚度/质量分布具有阶跃变化特征的折返式鼠笼及承力鼓筒位置振动传递系数约为0.2,而刚度/质量分布均匀处振动传递系数较高,验证了结构非连续性和离散性特征可产生优异的隔振效果。
参考文献
| [1] | 温登哲.航空发动机机匣模型的若干动力学特性研究[D].哈尔滨: 哈尔滨工业大学, 2015. WEN D Z.Several dynamic characteristics of aero-engine case model[D].Harbin: Harbin Institute of Technology, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957253.htm |
| [2] | 陆泽琦, 陈立群. 非线性被动隔振的若干进展[J]. 力学学报, 2017, 49(3): 550-564. LU Z Q, CHEN L Q. Some recent progresses in nonlinear pa-ssive isolations of vibration[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 550-564. (in Chinese) |
| [3] | 方同, 薛璞. 振动理论及应用[M]. 西安: 西北工业大学出版社, 1998. FANG T, XUE P. Theory of vibration with applications[M]. Xi'an: Northwestern Polytechnic University Press, 1998. (in Chinese) |
| [4] | CREDE C E. Vibration and shock isolation[M]. New York: John Wiley and Sons, 1951. |
| [5] | 王祖华, 周海波, 计方. 典型舰船舱壁结构隔振优化设计[J]. 船舶, 2011, 22(1): 26-33. WANG Z H, ZHOU H B, JI F. Vibration isolation design of ty-pical hull bulkhead structures[J]. Ship and Boat, 2011, 22(1): 26-33. (in Chinese) |
| [6] | 况成玉.周期结构浮笩设计及隔振性能研究[D].上海: 上海交通大学, 2011. KUANG C Y.Design and vibration isolation characteristics research of a floating raft constructed with periodic structures[D].Shanghai: Shanghai Jiao Tong University, 2011(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10248-1011268070.htm |
| [7] | 姜洪源, 董春芳, 敖宏瑞, 等. 航空发动机用金属橡胶隔振器动静态性能的研究[J]. 航空学报, 2004, 25(2): 140-142. JIANG H Y, DONG C F, AO H R, et al. Research on dynamic and static characteristics of metal rubber isolator used in aero-engine[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(2): 140-142. DOI:10.3321/j.issn:1000-6893.2004.02.011 (in Chinese) |
| [8] | 徐鉴. 振动控制研究进展综述[J]. 力学季刊, 2015, 36(4): 547-565. XU J. Advances of research on vibration control[J]. Chinese Quarterly of Mechanics, 2015, 36(4): 547-565. (in Chinese) |
| [9] | 张春红, 汤炳新. 主动隔振技术的回顾与展望[J]. 河海大学常州分校学报, 2002, 16(2): 1-5. ZHANG C H, TANG B X. The retrospection and prospection of active vibration isolaion technique[J]. Journal of Hohai University Changzhou, 2002, 16(2): 1-5. (in Chinese) |
| [10] | 张磊, 付永领, 刘永光, 等. 主动隔振技术及其应用与发展[J]. 机床与液压, 2005(2): 5-8. ZHANG L, FU Y L, LIU Y G, et al. Active vibration isolation and its application and development[J]. Machine Tool and Hydraulics, 2005(2): 5-8. DOI:10.3969/j.issn.1001-3881.2005.02.002 (in Chinese) |
| [11] | NAGAI M, MORAN A, TAMURA Y, et al. Identification and control of nonlinear active pneumatic suspension for railway vehicles using neural networks[J]. Control Engineering Prac-tice, 1997, 5(8): 870-877. |
| [12] | 梅德庆, 陈子辰. 微制造平台的精密隔振系统研究[J]. 光学精密工程, 2001, 9(6): 506-510. MEI D Q, CHEN Z C. Research on precision isolation system of micro manufacturing platform[J]. Optics and Precision Engineering, 2001, 9(6): 506-510. DOI:10.3321/j.issn:1004-924X.2001.06.003 (in Chinese) |
| [13] | FULLER C C, ELLIOTT S, NELSON P A. Active control of vibration[M]. New York: Academic Press, 1996. |
| [14] | GAWRONSKI W K. Advanced structural dyanmaics and active control of structures[M]. New York: Springer, 2004. |
| [15] | 马艳红, 曹冲, 李鑫, 等. 涡轴发动机涡轮级间支承结构设计关键技术[J]. 航空发动机, 2014, 40(4): 34-40. MA Y H, CAO C, LI X, et al. Key design technology of mid turbine frame for turboshaft engine[J]. Aeroengine, 2014, 40(4): 34-40. (in Chinese) |
| [16] | 顾家柳, 丁奎元, 刘启洲, 等. 转子动力学[M]. 北京: 国防工业出版社, 1985. GU J L, DING K Y, LIU Q Z, et al. Rotordynamics[M]. Beijing: National Defense Industry Press, 1985. (in Chinese) |
