目前,在预测微细成形材料变形行为时仍采用宏观下广泛使用的Mises、Hill系列等屈服准则[9-10],没有考虑屈服准则在微尺度下的适用性。十字形试件双向拉伸实验可以方便地通过控制两轴的载荷或位移比例,使试样中心区得到不同的应力、应变状态[11],进而得到不同加载路径下双向拉伸区的任意屈服点,成为研究板料屈服行为有效的实验方法[12]。
然而,目前用于研究薄板微尺度屈服、强化行为的实验系统鲜有报道,使得宏观下的屈服准则在微观尺度下的有效性一直缺乏实验验证。针对微尺度下材料屈服、强化行为实验研究的不足,本文建立了超薄板微尺度双向加载的实验方法,结合数字散斑测量(DIC)技术和同步控制技术,实现了微尺度下应变测量和双向加载同步控制,为金属超薄板的屈服行为研究提供实验基础。
1 双向加载实验原理 薄板常用的单向拉伸实验、平面应变拉伸实验和圆板胀形实验,其平面内主应力比例分别为1:0、2:1和1:1。采用不同的实验方法仅能得到屈服轨迹上单拉点、平面应变点和等双拉点等特征点的变形情况,难以拟合出整个屈服轨迹,如图 1所示, σ1为面内第一主应力,σ2为面内第二主应力。为研究具有各向异性的金属超薄板屈服、强化行为,获得更多复杂应力状态来准确拟合其屈服轨迹,本文建立了微尺度双向加载实验方法,在一种实验系统上通过改变位移/载荷的比例或非比例加载路径获取复杂加载路径下的屈服点,用于微尺度下屈服强化行为的研究。
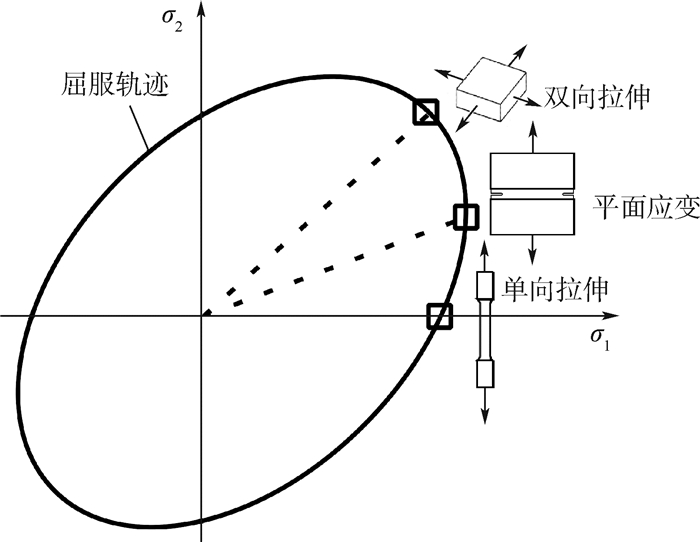 |
| 图 1 屈服轨迹的传统实验获取方法 Fig. 1 Traditional test acquisition method of yield principle |
| 图选项 |
与常规尺寸的十字形试样相比,适用于超薄板/箔材双向加载实验的试样厚度一般在0.02~0.5 mm之间,中心区变形难以通过接触测量获得,同时因承受载荷小,试样中心点易发生偏移。因此,试样中心区应变准确测量和四轴精确同步运动是实现双向加载实验的关键。
实验过程采用DIC技术实现二维变形场的实时测量,相比接触式测量方法,受外界影响小,隔震要求低。为实现四轴同步运动, 本文设计的微尺度双向加载实验原理如图 2所示。根据同步模式,实验分为位移控制和载荷控制2类。位移控制是在加载过程中十字形试样的x与y方向的位移保持比例或非比例同步,载荷控制是两方向的力传感器载荷值保持比例或非比例同步。
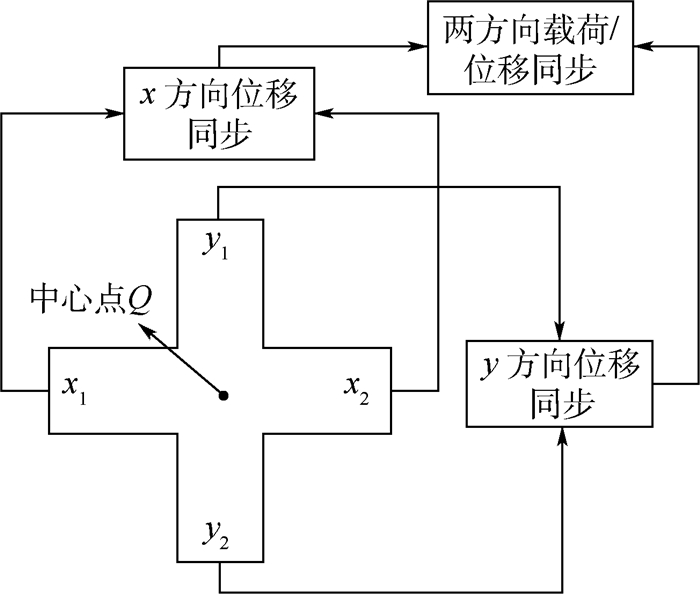 |
| 图 2 双向加载实验原理 Fig. 2 Principle of biaxial loading test |
| 图选项 |
考虑微尺度下实验结果的可靠性,实验过程中,图 2中试样中心点Q在x与y方向的偏移位置保持在±0.02 mm范围之内,同时双向加载实验同步精度需满足表 1中的指标要求。为满足不同厚度薄板测量需求,系统采用了1.25、5和25 kN三种不同量程的力传感器,根据不同厚度的板材可快速更换。
表 1 双向加载实验系统技术指标 Table 1 Technical indicators of biaxial loading test system
| 指标 | 位移分辨率/μm | 力传感器准确度等级 | 位移同步精度/mm | 载荷同步精度/kN |
| 数值 | 5 | 0.02~0.03 | 0.02 | 0.05 |
表选项
2 双向加载实验系统 双向加载实验系统由硬件平台和控制系统2部分组成。根据实验原理,选用合适的硬件以满足四轴运动同步控制和中心区应变测量的需要。在硬件平台基础上开发配套的具备可视化、检测、监控等功能的软件系统。
2.1 硬件系统 按照实验原理设计的双向加载实验系统硬件平台如图 3所示,主体部分是4个可独立运动的加载轴。硬件平台主要包括机架、防震平台、伺服电机、直线导轨、力传感器、光栅尺、机械夹具和CCD相机等。
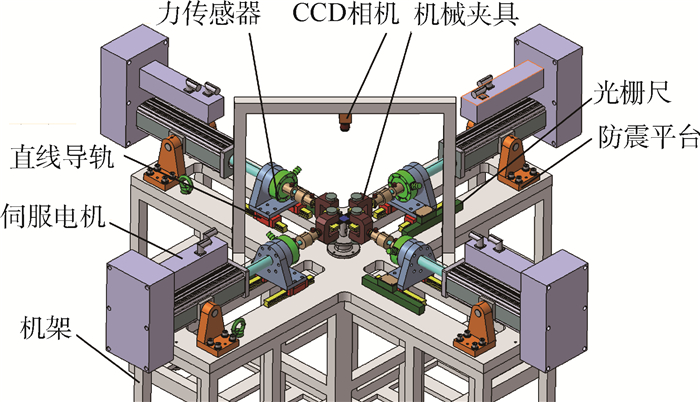 |
| 图 3 双向加载试验机硬件组成 Fig. 3 Hardware structure of biaxial loading test machine |
| 图选项 |
为满足四轴同步的控制需求,在硬件平台基础上搭建全闭环控制系统,具体实施方式如图 4所示。针对加载轴运动位置的高精度要求,采用以光栅尺为反馈的全闭环控制方式。控制系统硬件部分主要包括西门子SIMOTION D425运动控制器、SINAMICS S120组件、交流永磁同步电机(PMSM)、通信电缆以及带以太网通信的上位机等。其中上、下位机之间采用工业以太网Profinet通信,实现远程监控和数据传输等功能。
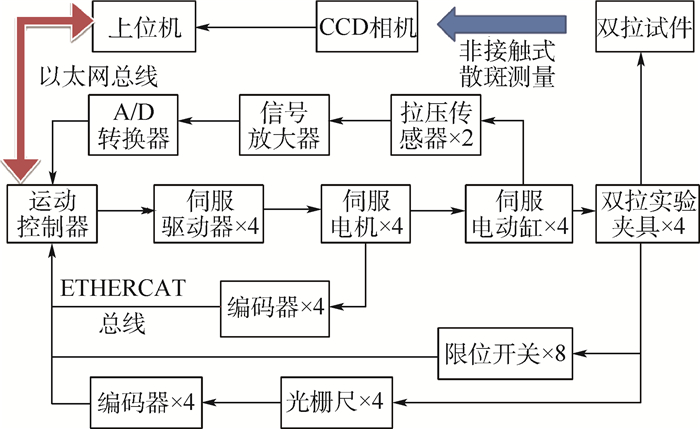 |
| 图 4 微尺度双向加载实验系统控制原理 Fig. 4 Control principle of micro-scaled biaxial loading test system |
| 图选项 |
2.2 软件系统 软件系统决定了双向加载实验系统的实验精度、功能、实用性。为实现同步控制、测量和监控等实验功能,控制系统软件采用了“上位机+运动控制器”分布式的控制形式,充分利用了下位机在运算控制逻辑方面与上位机数据在处理显示方面的优势,其具体组成模块如图 5所示。
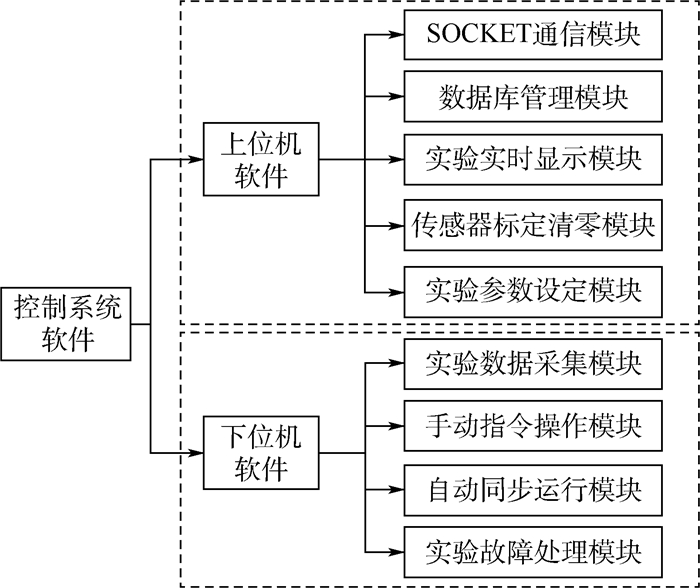 |
| 图 5 控制软件结构 Fig. 5 Structure of control software |
| 图选项 |
图 5中,上位机主要用来完成与下位机之间的通信,在显示和存储实验过程中位移、载荷等测量数据的同时保存该时刻采集的DIC照片。下位机软件主要是将上位机发送的控制指令转化成运动控制器的运动指令,并具备实时监控、故障处理等功能。下位机与上位机建立通信连接后,循环采集传感器数据发送到上位机界面,还可通过选择手动或自动程序,分别进行夹具位置的调整和自动控制的双向加载实验。双向加载实验控制流程如图 6所示。设图 2中的x方向为主动方向,x1和x2为主动轴,与x方向正交的y方向是从动方向,y1和y2为从动轴。四轴在虚主轴耦合下同步运动,当出现中心区偏移、同步误差过大、外界中止、试样拉断等情况时,结束实验。
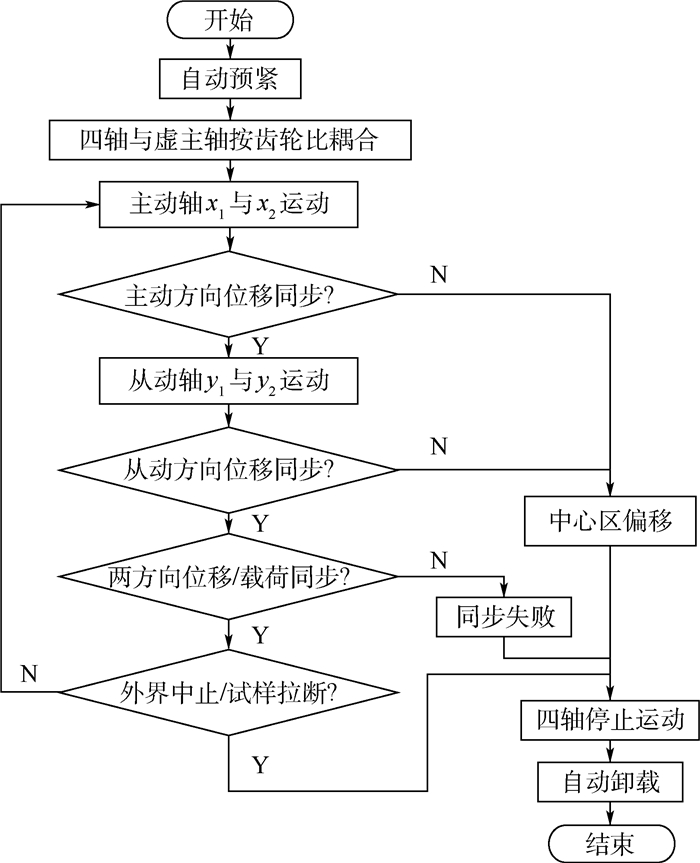 |
| 图 6 双向加载实验控制流程 Fig. 6 Control process of biaxial loading test |
| 图选项 |
2.3 微尺度应变测量方法 数字图像相关法测量全场应变技术具有非接触性、全场实时测量、精度高、便于自动化集成等优点[13],广泛用于材料力学、塑性力学等变形测量和力学性能测试。因此,适用于微成形的双向加载实验系统采用了二维数字散斑方法测量全场应变,实验前调整CCD相机位姿使采集到的照片2条中心线分别平行于十字形试样的x和y方向,便于后续的应力、应变计算。实验结束后,对比分析实验前与实验过程某时刻的散斑图像,通过数字散斑相关方法计算出该时刻的位移和变形。
定义相关系数[14]:
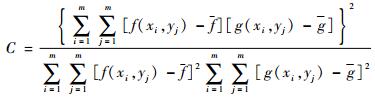 | (1) |
式中:f、g分别为变形前、后子区的平均灰度值;f(xi, yi)为变形前子区域内灰度值;g(xi, yi)为变形后子区域内灰度值。式(1)选择子区域像素范围是m×m。通过算法搜索[15]得到变形前、后子区相关系数最大的位移值:
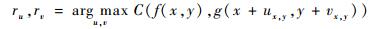 | (2) |
以此作为变形前后的位移(u, v),依据变形位移计算Cauchy应变分量:
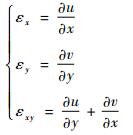 | (3) |
为验证数字图像相关法的应变测量精度,对0.2 mm、1 000℃热处理的SUS304不锈钢板进行单向拉伸实验,同时采用DIC和引伸计测量应变。2种方式测量的应力-应变曲线如图 7所示。可见,DIC计算结果与引伸计测量结果误差在2%以内,满足微尺度应变测量的要求。
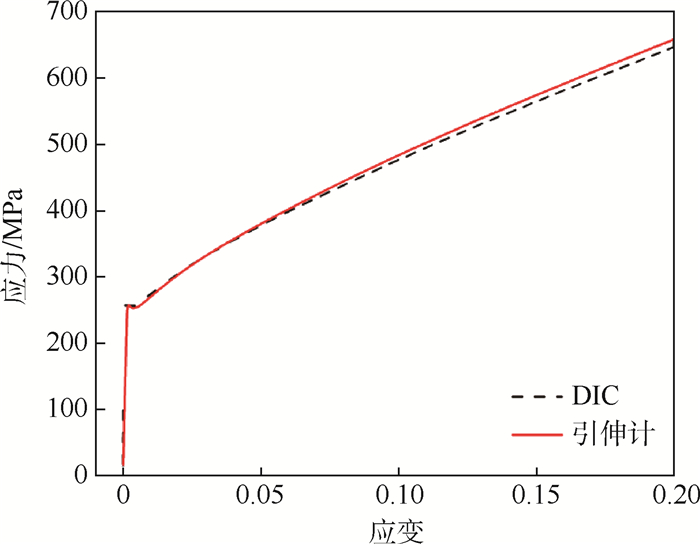 |
| 图 7 DIC与引伸计测量结果对比 Fig. 7 Comparison between DIC and extensometer measurement results |
| 图选项 |
3 控制系统设计 在双向加载实验的硬件系统与软件系统分析的基础上,设计相应的控制策略,以实现4个独立加载轴的平稳加载与同步运动。本文采用三相交流PMSM作为驱动单元,结合西门子运动控制器实现多轴控制。PMSM具备优异的动态性能,在航空航天、工业自动化、数控机床和机器人等领域都有广泛应用[16]。
3.1 单轴闭环控制模型 本文选用的西门子1FK7033高动态型PMSM,可采用空间矢量控制方法转化成等效的直流旋转电机。双向加载实验系统单轴的全闭环控制方式如图 8所示,其中速度反馈使用图 3中伺服电机内部自带的22位增量式编码器,角度分辨率为1.5×10-6 rad,位置反馈使用图 3中光栅尺,位置分辨率为0.005 mm。
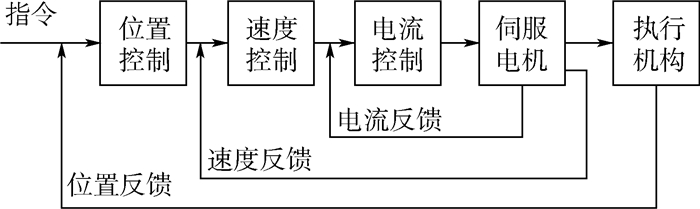 |
| 图 8 单轴闭环控制模型 Fig. 8 Single-axis closed-loop control model |
| 图选项 |
对于图 8中电流控制环节,本文采用id=0的控制策略,使定子电流只有交轴分量,将PMSM等价为他励直流电机,PMSM矢量控制的电流环可等效为一阶惯性环节[17],其时间常数为Tc。以电流闭环为基础,引入速度闭环的PI控制器。根据等效的直流电机运动控制方程,得到速度闭环控制的模型如图 9所示。
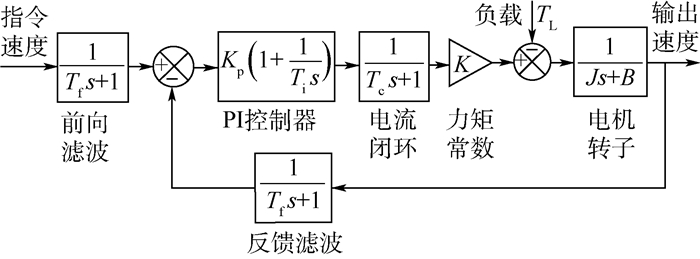 |
| 图 9 速度闭环控制模型 Fig. 9 Speed closed-loop control model |
| 图选项 |
图 9中:Tf为速度滤波器时间常数;Kp和Ti为速度PI控制器的常数;J为系统转动惯量;B为系统转子黏滞系数。速度闭环控制参数是伺服系统抑制波动、减少超调与振荡的关键。根据三阶最佳校正原则将速度闭环整定成一阶惯性环节[17]:
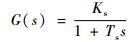 | (4) |
式中:Ks为速度环比例增益; Ts为速度环积分时间常数。
3.2 速度闭环控制参数辨识 对于速度闭环被控对象,输入10 Hz的正弦波指令速度,预测式(4)的输出与电机在该指令下实际电机内部编码器测量的速度进行对比。调节未知参数Ks和Ts,使得预测误差的方差达到最小,得到模型参数Ks=0.999 01,Ts=0.000 111 62 s。
为进一步验证辨识的速度闭环控制模型的有效性,输入频率在1 000 Hz以内的随机信号,对比电机内部编码器测得的速度与式(4)预测结果,如图 10所示。由于实验过程中四轴处在准静态加载状态,其速度变化较慢,速度闭环控制满足要求,因此选择速度控制模式来进行位置闭环控制。
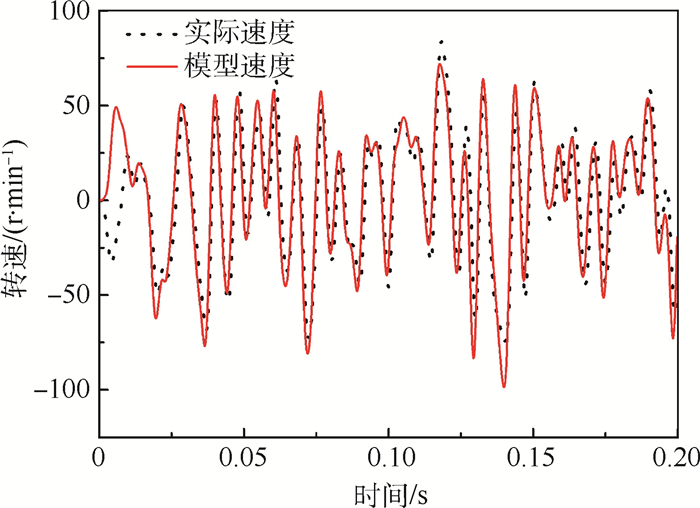 |
| 图 10 速度闭环控制模型输出结果与实际速度对比 Fig. 10 Comparison between speed closed-loop control model output results and actual speed |
| 图选项 |
3.3 位置闭环控制 在速度闭环基础上,空载下的位置开环为一阶惯性环节,结果如式(5)所示。采用同样的方法对被控对象的位置开环进行辨识,得到位置环比例增益Kpos=0.995 25,位置环积分时间常数Tpos=0.038 839 s。
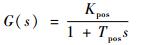 | (5) |
辨识的位置开环的时间常数Tpos远大于速度闭环的Ts,表明系统机械间隙等对位置闭环控制影响较大。由于PMSM转矩依次经过减速器、同步带、电动缸等环节作用于机械夹具上,此外变形过程中材料由弹性转换到塑性,电机的负载转矩与外界载荷之间存在非线性关系,如图 11所示。
 |
| 图 11 PMSM转矩与外界载荷的非线性关系 Fig. 11 Non-linear relationship between PMSM torque and external load |
| 图选项 |
为改善位置闭环的动态响应,设计位置闭环为前馈复合控制结构,如图 12所示。结合光栅尺的位置测量值与电机内部编码器的速度测量值,设计卡尔曼观测器获得每一时刻的最佳位置估计,作为位置闭环的反馈。
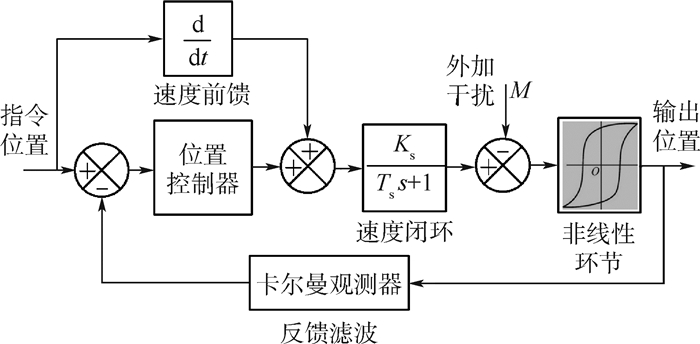 |
| 图 12 位置闭环控制模型 Fig. 12 Positional closed-loop control model |
| 图选项 |
随着位置控制的复杂程度提高和非线性要素增多,传统的PID难于满足控制精度要求。对于位置控制器设计3种控制方式:传统PID、模糊PID和非线性PID。其中传统PID是全量型数字PID,其输入是位置误差e,经整定后位置闭环控制的PID参数为Kp=4.1,Ti=1 000 ms,Td=40 ms。
在传统PID控制方式基础上,模糊PID的输入是位置误差e和位置误差率δe,采用对称三角型隶属度函数和相应的模糊控制规则[18]。非线性PID是在传统PID控制方式基础上串联非线性增益k(e),满足:
 | (6) |
式中:F为相关参数;Δ为允许的误差的阈值,用以实现带死区的非线性控制。
设置位置指令为速度1.5 mm/min的斜坡信号,检测3种控制方式下负载侧经滤波后的速度,结果如图 13所示。
 |
| 图 13 传统PID、模糊PID与非线性PID控制结果 Fig. 13 Traditional PID, fuzzy PID and nonlinear PID control results |
| 图选项 |
对比传统PID,模糊PID能加快调节时间,抑制超调,但在材料变形由弹性切换到塑性后容易引起调节振荡。非线性PID在传统PID基础上引入非线性增益,在误差较大时加快调节速度;在误差较小时,式中的k(e)= 0,避免因调节过度引起振荡。因此,本文选用非线性PID控制器用于单轴位置闭环控制,控制精度小于等于0.008 mm。
3.4 四轴同步控制策略 在实现单轴闭环控制基础上构建四轴同步控制策略,为提高同步控制精度,引入虚拟轴作为系统控制主轴,速度为v,实验过程中的载荷/位移比例同步系数为k。四轴位置测量值分别为Lx1、Lx2、Ly1、Ly2,两方向上传感器载荷测量值分别为Fx和Fy。对于位置同步模式,选择四轴独立驱动的并行控制,4个加载轴x1、x2、y1和y2的输入误差e1(t)、e3(t)、e2(t)和e4(t)分别为
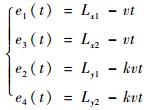 | (7) |
保证位移同步的四轴运动控制满足e1(t)=e2(t)=e3(t)=e4(t)=0,其控制模型如图 14所示。虚主轴的速度通过分布式电子齿轮分配给4个加载轴,用于图 12中位置闭环控制的速度前馈。四轴位移同步控制可简化成4个加载轴位置闭环的并行控制,通过改变齿轮同步配比可方便实现x与y方向位移以任意比例同步。
 |
| 图 14 位移比例同步控制模型 Fig. 14 Displacement proportional synchronous control model |
| 图选项 |
在薄板双向拉伸过程中,两方向上拉伸载荷相互耦合影响,使得双向加载位移载荷关系复杂。对于载荷同步控制模式,为保证控制过程载荷与位移的控制不互相干扰,在图 14基础上将y1、y2的位置闭环分别改成载荷、位移的主从闭环控制,实现载荷控制与位移控制解耦。类比位移同步控制,载荷同步的4个加载轴x1、x2、y1和y2的输入误差e1(t)、e3(t)、e2(t)和e4(t)分别为
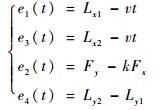 | (8) |
4 双向加载实验系统性能测试 本文所研发的微尺度双向加载实验系统如图 15所示。为验证该系统的有效性,需进一步检验系统的控制和同步精度。
 |
| 图 15 微尺度双向加载实验系统 Fig. 15 Micro-scaled biaxial loading test system |
| 图选项 |
4.1 同步精度 为评估双向加载实验的同步精度,可利用试样中心点的轨迹进行定量分析。中心区不发生偏移满足:
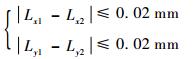 | (9) |
分析图 2试样中心点Q在4:4载荷比例实验条件下的位置变化轨迹,如图 16所示。
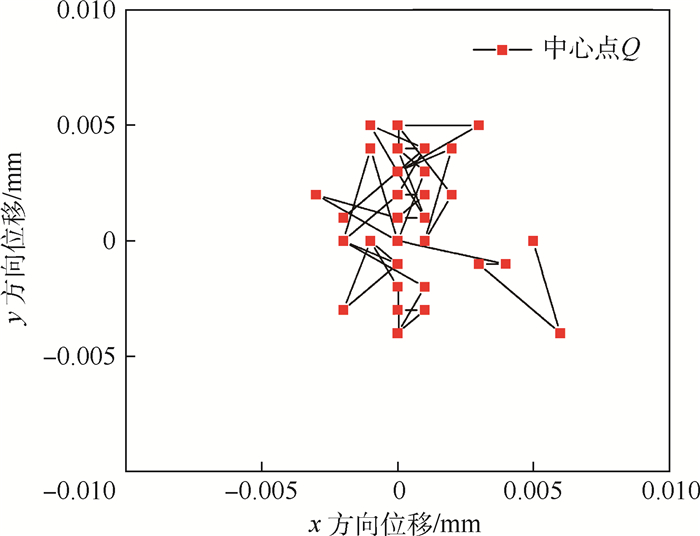 |
| 图 16 试样中心点轨迹 Fig. 16 Center point locus of sample |
| 图选项 |
位移同步是在式(9)的基础上同时满足同步精度eL:
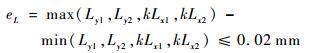 | (10) |
载荷同步是在式(9)基础上同时满足同步精度eF:
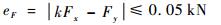 | (11) |
实验获得试验机的位移比例同步精度eL、载荷比例同步精度eF如图 17所示。
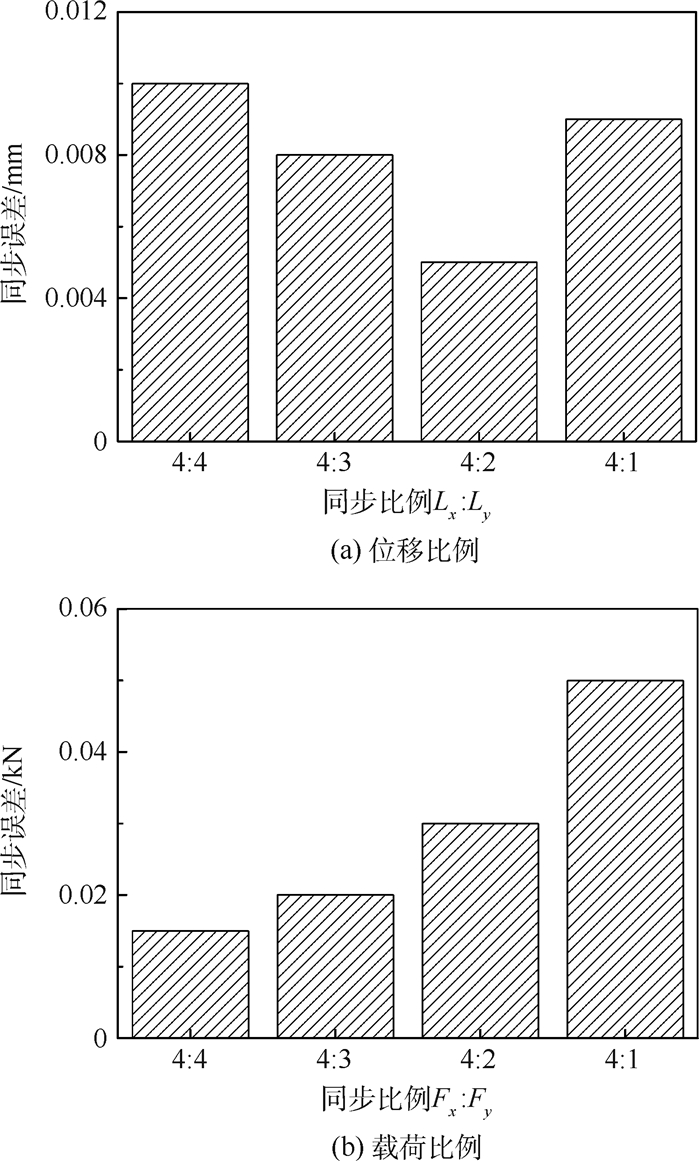 |
| 图 17 位移比例和载荷比例同步精度 Fig. 17 Displacement and load ratio synchronization accuracy |
| 图选项 |
实验结果表明,实验过程中心点Q位置的x、y两方向坐标处在±0.01 mm的范围内,且位移/载荷同步精度满足实验要求。
4.2 系统应用 验证双向加载实验系统的同步精度后,对厚度0.1 mm的SUS304不锈钢超薄板试样分别做0:4、1:4、2:4、3:4、4:4、4:3、4:2、4:1、4:0的载荷比例实验,获得不同加载路径下两方向的应力-应变曲线。利用0°方向单向拉伸实验的应力-应变曲线计算的屈服点处塑性功,根据等塑性功原理求得不同加载路径下屈服点处的两方向应力σ1和σ2。拟合屈服点得到第一象限的屈服轨迹曲线如图 18所示,表明开发的微尺度双轴加载试验机可用于超薄板屈服行为研究。
 |
| 图 18 不同加载路径下屈服点拟合的屈服轨迹 Fig. 18 Yield curves of yield point fitting under different loading paths |
| 图选项 |
5 结论 本文建立了适用于超薄板的微尺度双向加载实验方法,开发了微尺度双向加载实验系统。系统硬件平台是四轴独立驱动类型,软件结构采用上、下位机分离形式,采用非接触式散斑测量应变。
1) 针对材料变形非线性过程和电机转矩-拉伸载荷之间的非线性关系,提出非线性PID控制方法,有效提高了控制稳定性,位置闭环控制精度小于等于0.008 mm。
2) 基于虚拟主轴实现了四轴同步控制,实验过程中心点的偏移在±0.01 mm范围内,位移同步精度小于等于0.02 mm,载荷同步精度小于等于0.05 kN,满足微尺度屈服、强化行为实验研究的要求。
参考文献
| [1] | SCHROERS J, PHAM Q, DESAI A. Thermoplastic forming of bulk metallic glass-A technology for MEMS and microstructure fabrication[J]. Journal of Microelectromechanical Systems, 2007, 16(2): 240-247. DOI:10.1109/JMEMS.0007.892889 |
| [2] | MENG B, FU M W, FU C M, et al. Ductile fracture and deformation behavior in progressive microforming[J]. Materials & Design, 2015, 83: 14-25. |
| [3] | RAZALI A R, QIN Y. A review on micro-manufacturing, micro-forming and their key issues[J]. Procedia Engineering, 2013, 53(7): 665-672. |
| [4] | MANABE K, SHIMIZU K, KOYAMA T, et al. Validation of FE simulation based on surface roughness model in micro-deep drawing[J]. Journal of Materials Processing Technology, 2008, 204(1-3): 89-93. DOI:10.1016/j.jmatprotec.2007.10.081 |
| [5] | YEH F H, LI C L, LU Y H. Study of thickness and grain size effects on material behavior in micro-forming[J]. Journal of Materials Processing Technology, 2008, 201(1-3): 237-241. DOI:10.1016/j.jmatprotec.2007.11.138 |
| [6] | FU M W, WANG J L, KORSUNSKY A M. A review of geometrical and microstructural size effects in micro-scale deformation processing of metallic alloy components[J]. International Journal of Machine Tools & Manufacture, 2016(109): 94-125. |
| [7] | MENG B, FU M W. Size effect on deformation behavior and ductile fracture in microforming of pure copper sheets considering free surface roughening[J]. Materials & Design, 2015, 83: 400-412. |
| [8] | FU M W, CHAN W L. A review on the state-of-the-art microforming technologies[J]. International Journal of Advanced Manufacturing Technology, 2013, 67(9-12): 2411-2437. DOI:10.1007/s00170-012-4661-7 |
| [9] | DUBOS P A, FLEURIER G, HUG E.An experimental investigation of the size effects in forming processes of high-purity thin metallic sheets[C]//Materials Science Forum, 2017: 459-464. |
| [10] | PENG L F, XU Z T, FU M W, et al. Forming limit of sheet metals in meso-scale plastic forming by using different failure criteria[J]. International Journal of Mechanical Sciences, 2017, 120: 190-203. DOI:10.1016/j.ijmecsci.2016.11.021 |
| [11] | HANNON A, TIERNAN P. A review of planar biaxial tensile test systems for sheet metal[J]. Journal of Materials Processing Technology, 2008, 198(1): 1-13. |
| [12] | BANABIC D, BARLAT F, CAZACU O, et al. Advances in anisotropy and formability[J]. International Journal of Material Forming, 2010, 3(3): 165-189. DOI:10.1007/s12289-010-0992-9 |
| [13] | CHEN H, YE D, CHE R.High speed deformation measurement using digital speckle correlation method[C]//27th International Congress on High-Speed Photography and Photonics.Bellingham: SPIE, 2007: 62791O. |
| [14] | 陈华.基于数字散斑相关方法的视觉变形测量技术研究[D].哈尔滨: 哈尔滨工业大学, 2008: 15-22. CHEN H.Study of vision deformation measurement technologies based on digital speckle correlation method[D].Harbin: Harbin Institute of Technology, 2008: 15-22(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-2009224157.htm |
| [15] | MA S P, JI G C. Digital speckle correlation method improved by genetic algorithm[J]. Acta Mechanica Solida Sinica, 2003, 16(4): 366-373. |
| [16] | 汪海波, 周波, 方斯琛. 永磁同步电机调速系统的滑模控制[J]. 电工技术学报, 2009, 24(9): 71-77. WANG H B, ZHOU B, FANG S C. PMSM sliding mode control system based on exponential reaching law[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 71-77. DOI:10.3321/j.issn:1000-6753.2009.09.011 (in Chinese) |
| [17] | 陈鹏展.交流伺服系统控制参数自整定策略研究[D].武汉: 华中科技大学, 2010: 19-27. CHEN P Z.Study on the self-tuning strategy of control parameters for AC servo system[D].Wuhan: Huazhong University of Science and Technology, 2010: 19-27(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10487-2010184585.htm |
| [18] | 王述彦, 师宇, 冯忠绪. 基于模糊PID控制器的控制方法研究[J]. 机械科学与技术, 2011, 30(1): 166-172. WANG S Y, SHI Y, FENG Z X. A method for controlling a loading system based on a fuzzy PID controller[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(1): 166-172. (in Chinese) |
