航天器在空间中运行时会受到来自微流星体或空间碎片的撞击，若不能成功抵御则会导致严重事故的发生。因此，为了提高航天器在轨运行时的防护能力，Whipple^[1]在20世纪40年代提出了在航天器舱壁外层增设一层防护屏的结构，称为Whipple防护结构。在随后几十年中，Whipple防护结构逐渐发展为填充式防护结构，即在Whipple防护结构的前墙与舱壁之间加入先进填充材料作为中间层，来对空间碎片进行破碎和缓冲，以降低碎片云撞击舱壁的速度，达到对航天器更好的防护效果。
在空间碎片对航天器进行超高速碰撞的过程中，撞击是否能击穿航天器的防护结构，从而损伤航天器，是航天器超高速撞击防护研究的关键。
在此问题的研究上，国外主要依靠建立航天器防护结构的弹道极限方程来对碎片的撞击效果进行预测。其主要思想是：通过理论分析建立出极限方程的一般形式，再通过实验数据拟合的方法确定方程中的待定参数。经过几十年的发展，Cour-Palais^[2]、Robinson^[3]、Christiansen^[4]等针对不同防护结构建立了多种弹道极限模型，为航天器超高速撞击损伤的研究打下了良好的基础。此外，Ryan和Thaler^[5]在2013年采用人工神经网络直接利用大量实验数据进行学习，建立了Whipple防护结构的弹道极限方程，相比于显式弹道极限方程具有更好的预测效果。
随着中国载人航天工程的推进，多家机构也纷纷展开了对航天器防护结构的研究。柳森等^[6]首次利用实验研究了Whipple防护结构的防护性能随弹丸直径、速度、防护屏厚度的关系。管公顺^[7]系统地研究了铝双层板防护结构的防护性能，并得到了弹速小于5.5km/s时铝双层板防护结构的弹道极限曲线。张晓天等^[8]利用支持向量机(SVM)建立了单层板结构的航天器弹道极限方程。
近年来，随着对单、双层板防护结构研究的成熟，国内逐渐将研究重点转向填充式防护结构的超高速撞击损伤研究。贾光辉等^[9]利用穷举法对三指标^[10]耦合下的NASA填充式防护结构的弹道极限方程进行了双参数修正，使其更适合国内的填充式防护结构；同时其利用差异演化算法直接对文献[11]中建立的弹道极限方程进行多目标优化，在得到较优预测效果的同时，相比于穷举法节省了大量的时间^[12]。此外，哈尔滨工业大学的哈跃^[13]、张宝玺^[14]、祖士明^[15]通过大量超高速撞击实验研究了不同填充式防护结构在超高速撞击条件下的防护效果。
填充式防护结构由于填充方式不同，限制了通用型弹道极限方程的预测准确率，同时由于实验数据量过少而难以像文献[5]一样采用人工神经网络方式进行建模。鉴于此，本文采用集成学习方法，通过建立Adaboost预测模型，实现小数据情况下对填充式防护结构的超高速撞击损伤预测。相比于显式弹道极限方程，该方法具有更强的通用性。
1 NASA填充式防护结构弹道极限方程 在进行超高速撞击实验时，由于弹丸在低、中、高不同撞击速度区内会产生不同的物理和化学特性，因此在建立弹道极限方程时需要根据弹丸的撞击速度将方程分为3段。针对填充式防护结构(见图 1)，NASA工程师Christiansen等^[4]在1995年通过将防护结构参数与弹丸撞击参数作为弹丸临界直径的自变量，提出了一种适用性较强的通用弹道极限方程；并在2001年通过对弹丸撞击速度区间拐点以及低速区内的系数参数等进行修正，提出了适用性更强的通用型弹道极限方程^[16]。方程结构如下：

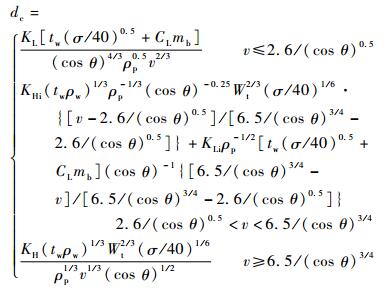(1)

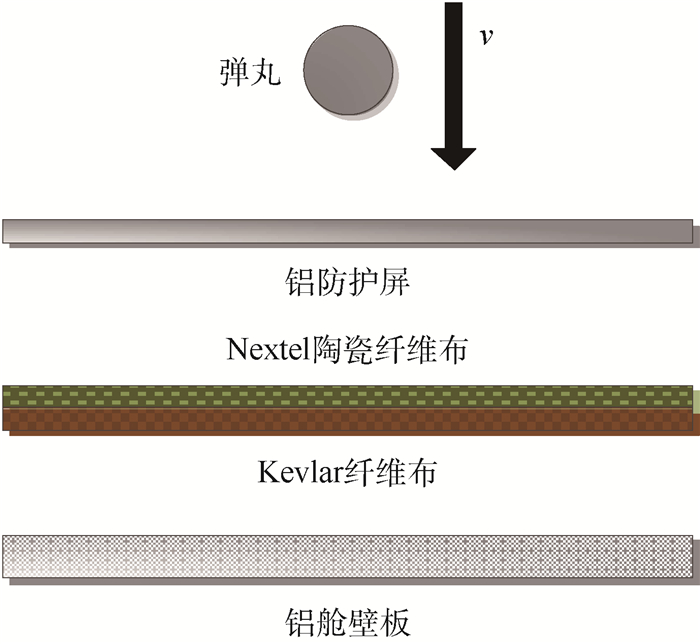图 1 Nextel/Kevlar填充式防护结构 Fig. 1 Stuffed Whipple shield of Nextel/Kevlar

图选项

式中：d_c、θ、v、ρ_p为弹丸撞击参数；d_c为临界弹丸直径，cm；θ为弹丸撞击角，(°)；v为弹丸撞击速度，km/s；ρ_p为弹丸密度，g/cm³；t_w、σ、ρ_w、m_b、W_t为防护结构参数；t_w为航天器舱壁厚度，cm；σ为航天器舱壁的屈服应力，ksi(1ksi=6.895MPa)；ρ_w为航天器舱壁密度，g/cm³；m_b为防护层前屏与填充织物的总面密度，g/cm²；W_t为防护层前屏与航天器舱壁间的距离，cm；K_L、K_H、C_L、K_Hi、K_Li为拟合系数，分别取K_L=2.35g^0.5·km^2/3·cm^-3/2·s^-2/3，K_H=0.6km^1/3/s^1/3，C_L=0.37cm³/g，K_Hi=0.321，K_Li=1.243g^0.5/cm^3/2。
2 NASA弹道极限方程的预测效果分析 对于填充式防护结构来说，当选用不同的填充材料作为防护结构的中间层时，由于填充材料的不同物理、化学特性会导致弹丸在超高速撞击时产生差异性破碎、熔化、气化现象，因此采用不同种填充材料需要对NASA弹道极限方程的适用效果进行分析。
不同于国外在进行填充式防护结构设计时所选用Nextel陶瓷纤维布与Kevlar纤维布的混合材料作为填充层，国内的相关研究主要是利用玄武岩纤维布作为Nextel陶瓷纤维布的替代材料进行研究。下面以文献[14]中的35组实验数据为例，对NASA弹道极限方程的损伤预测效果进行分析。
表 1给出了实验后的撞击结果以及通过NASA填充式防护结构弹道极限方程(见式(1))计算出的击穿临界弹丸直径。其中后墙出现穿孔、裂纹、剥落时，认为此次实验为防护失效。图 2更加直观地给出了实验数据的分布情况。其中纵坐标表示实验中实际弹丸直径与通过NASA弹道极限方程预测的临界弹丸直径之比，实心点表示该次实验后墙失效，空心点表示该次实验成功防护。当实心点位于1线上方，空心点位于1线下方时，认为该次预测结果准确，否则预测失效。
表 1 超高速撞击实验预测结果 Table 1 Prediction results of hypervelocity impact experiment

编号	实际弹丸直径/cm	弹丸撞击速度/(km·s-1)	穿透结果	临界弹丸直径/cm	预测结果
1	0.635	3.42	yes	0.5291	√
2	0.635	3.99	no	0.6231	×
3	0.635	4.153	no	0.65	√
4	0.635	4.21	no	0.6593	√
5	0.635	3.87	yes	0.6033	√
6	0.635	3.75	yes	0.5855	√
7	0.635	3.82	no	0.597	×
8	0.635	1.24	yes	0.65	×
9	0.635	1.04	no	0.7308	√
10	0.794	4.54	yes	0.7151	√
11	0.794	2.1	yes	0.4575	√
12	0.794	1.53	yes	0.565	√
13	0.794	0.7645	no	0.8972	√
14	0.794	1.3085	yes	0.6271	√
15	0.794	1.81	yes	0.5047	√
16	0.794	0.801	no	0.8692	√
17	0.794	0.595	no	1.0597	√
18	0.635	4.06	yes	0.6362	×
19	0.635	4.237	yes	0.6653	×
20	0.635	4.425	no	0.6961	√
21	0.635	4.345	yes	0.683	×
22	0.635	1.404	yes	0.5979	√
23	0.635	1.16	yes	0.679	×
24	0.635	1.12	no	0.6951	√
25	0.635	2.97	yes	0.4572	√
26	0.635	0.871	no	0.822	√
27	0.635	0.801	no	0.8692	√
28	0.635	1.062	no	0.7202	√
29	0.635	1.31	yes	0.6262	√
30	0.635	3.97	yes	0.6214	√
31	0.635	2.2	yes	0.4432	√
32	0.635	3.87	no	0.605	×
33	0.635	3.92	yes	0.6132	√
34	0.635	4.3941	yes	0.691	×
35	0.635	4.46	yes	0.7019	×

表选项

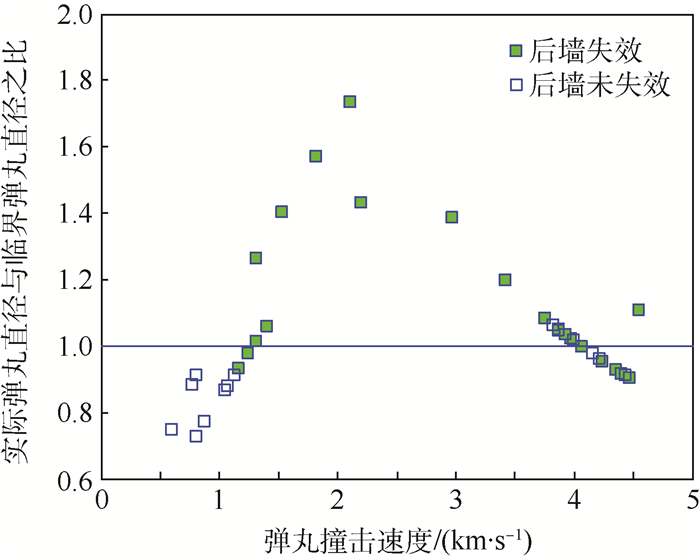图 2 NASA弹道极限方程的预测效果 Fig. 2 Prediction effect of NASA's ballistic limit equation

图选项

从表 1中可以看出，在35组超高速撞击实验中，通过NASA填充式防护结构弹道极限方程成功预测了25组，方程的总体预测率P_total=71.4%。其中方程对21组失效数据成功预测了14组，对14组未失效数据成功预测了11组，因此方程的安全预测率P_safe=80.0%。同时将这35组实验按式(1)中的区间分为低速段撞击实验及中速段撞击实验，其中方程对17组低速段撞击实验成功预测了15组，方程的总体预测率P_total=88.2%，安全预测率P_safe=88.2%。对18组中速段撞击实验成功预测了10组，方程的总体预测率P_total=55.6%，安全预测率P_safe=72.2%。由此可见，NASA的填充式防护结构弹道极限方程对采用不同填充物的填充式防护结构具有一定的预测效果，其中对于超高速撞击的低速段具有较好的预测效果，而对于超高速撞击的中速段预测效果较差。
3 基于Adaboost的超高速撞击损伤预测模型 通过对NASA填充式弹道极限方程预测效果的检验可以发现，方程对于中速段撞击实验的预测效果只能达到55.6%，可知式(1)中单纯通过低速段与高速段弹道极限方程插值得到的中速段方程并不能满足填充式防护结构在选择不同填充材料时对于中速段撞击的预测需求，因此本节利用Adaboost预测模型对填充式防护结构超高速撞击的损伤效果进行了预测研究。
3.1 Adaboost预测模型的适用性分析 空间碎片或微流星体对于航天器防护结构的超高速撞击结果可以分为2类，即撞击后舱壁是否失效。因此，填充式防护结构对于超高速撞击损伤的预测问题实际上是一个二分类问题，解决该问题只需要找出超高速撞击过程中所涉及到的分类特征，再采用恰当的分类方法即可实现对撞击结果的预测。
从第2节的分析中可以发现，NASA填充式弹道极限方程对于低速段撞击实验的预测成功率达到了88.2%，说明方程在低速段对于不同填充物结构的Whipple防护结构具有较强的预测效果，因此在接下来的建模过程中以式(1)中的弹丸撞击参数、防护结构参数作为模型的特征属性。
对于分类问题来说，常用的方法有k近邻(KNN)、SVM、集成学习Adaboost等。每种分类方法都有各自的优势与弊端，其中Adaboost相较其他方法具有以下特点：
1) Adaboost提供了一种计算框架，可以结合不同方法构建弱分类器，当所选择的弱分类器模型复杂程度不高时，不易发生过拟合现象。
2) Adaboost特别适合解决分类问题，尤其是当数据特征不多的情况下，也可以很好地对数据集进行分类，并且过程中不需要手动调整参数。
3) Adaboost在训练时可以重复使用训练样本，因此在数据集中数据量较少的情况下，也可以实现较好的分类效果。
4) Adaboost的弱分类器构造比较简单，相比于SVM，在解决类似此类非线性问题时，不需要花很大精力寻找合适的核函数。
综合以上分析，本文采用Adaboost对填充式防护结构超高速撞击的损伤情况进行预测。
3.2 Adaboost预测模型的搭建与测试 Adaboost是boosting算法的改进，其通过弱分类器进行样本分类时，会将分错的样本进行加权从而提升错误样本所占的权重，再将被加权后的新样本重新投入训练，直到达到预设的错误率或最大迭代次数，因而Adaboost具有自适应性。总体上，Adaboost分为3步：①初始化样本集所具有的权重。②通过自适应性训练弱分类器。③将训练得到的弱分类器集合为强分类器。整个建模过程如图 3所示。图中，最左侧框内代表训练样本，框中直方图不同的长度代表样本所占的权重大小，每经过一次迭代样本所占的权重都会相应变化，经过T次迭代后将经过训练的T个弱分类器加权叠加成一个强分类器，从而对数据进行分类预测。

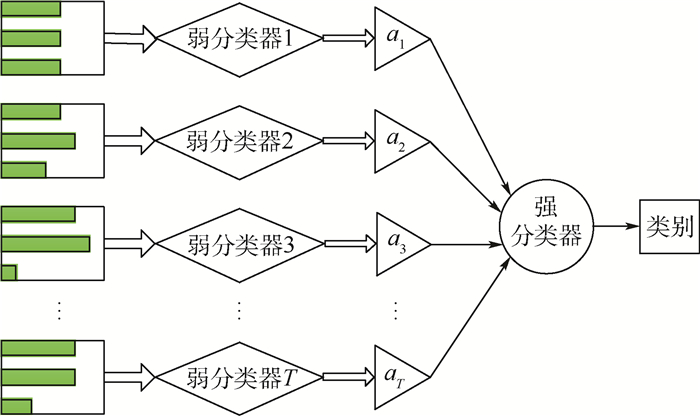图 3 Adaboost示意图 Fig. 3 Schematic of Adaboost

图选项

Real Adaboost是Adaboost框架中的一般形式，相较于最基本的Discrete Adaboost来说，其弱分类器的输出不仅仅局限于{-1, 1}，而是扩大到实数域，这个实数则作为Adaboost判别的置信度，使模型具有更小的训练误差。下面建立具有连续置信度输出的Real Adaboost预测模型。
1) 定义
① 输入样本空间：S={(x₁, y₁), (x₂, y₂), …, (x_n, y_n)}，x_i代表第i次超高速撞击实验中弹丸撞击及防护结构参数；y_i∈{-1, 1}代表第i次超高速撞击实验中后墙是否失效；i=1, 2, …, n。
② 初始化样本权重：ω_i¹=1/n，i=1, 2, …, n。
③ 弱分类器空间：H。
2) 迭代训练
循环迭代T次，For t=1 to T。
① 利用附有权值分布ω_i^t的训练样本S对弱分类器进行训练(其中弱分类器可以选用不同模型，如分类树、SVM、KNN等)。
a) 划分S：S=S₁∪S₂∪…∪S_m，当i≠j时，S_i∩S_j=?，m为分段数。
b) 统计S_j中后墙失效与未失效的累计样本权值：。
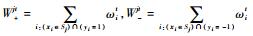
c) 设置弱分类器输出：对 为平滑因子。
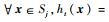
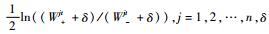
d) 计算归一化因子，并选取h_t(x)使Z_t最小，即。
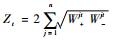
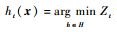
② 更新训练样本权重：

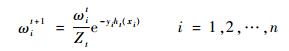(2)

3) 强分类器
集成训练后的弱分类器，得到最终的强分类器：

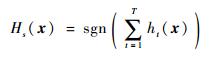(3)

4) 模型的训练错误率估计

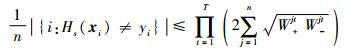(4)

除Real Adaboost外，本文还采用了Gentle Adaboost、Modest Adaboost(Adaboost variants)共同对填充式防护结构的超高速撞击损伤进行预测，以更全面地分析Adaboost预测模型对该问题的处理效果。其中，Gentle Adaboost与Real Adaboost类似，只是概率输出与Real Adaboost有所差别；Modest Adaboost则增加了弱分类器输出时训练样本的反向或倒数加权项。
1) Gentle Adaboost
输入：样本空间S={(x₁, y₁), (x₂, y₂), …, (x_n, y_n)}，循环迭代次数T。
输出：强分类器H_s：H_s(x)→{－1, 1}。
1.??初始化样本权重：ω_i^t=1/n，i=1, 2, …, n。
2. ??for t = 1 to T do
3.??将ω_i^t作为样本权值，利用x_i、y_i作加权最小二乘回归训练弱分类器h_t(x)。
4.??更新强分类器H_s(x)←H_s(x)+h_t(x)。
5. ??更新权值，归一化权重使。
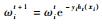
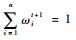
end
2) Modest Adaboost
输入：样本空间S={(x₁, y₁), (x₂, y₁), …, (x_n, y_n)}，循环迭代次数T。
输出：强分类器H_s：H_s(x)→{－1, 1}。
1.??初始化样本权重：ω_i¹=1/n，i=1, 2, …, n。
2.??for t=1 to T and while h_t(x)≠0 do
3.??将ω_i^t作为样本权值，利用x_i、y_i作加权最小二乘回归训练弱分类器h_t(x)。
4.??计算反向权重，归一化权重。
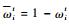
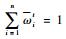
5.??计算：

6.??建立弱分类器：

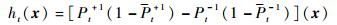7.??更新强分类器：H_s(x)←H_s(x)+h_t(x)。
8.??更新权值，归一化权重使。
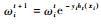
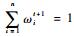
??end
为检验算法正确性，以UCI数据库中的Ionosphere数据集^[17]为例进行测试，其是一个典型的二分类数据集，包含34维特征351组数据。
测试过程中，以分类回归树(CART)^[18]作为弱分类器，测试方式为5折交叉检验(即数据集与训练集比为4:1，取5次测试错误率的均值来反映算法效果)，测试结果如图 4所示。

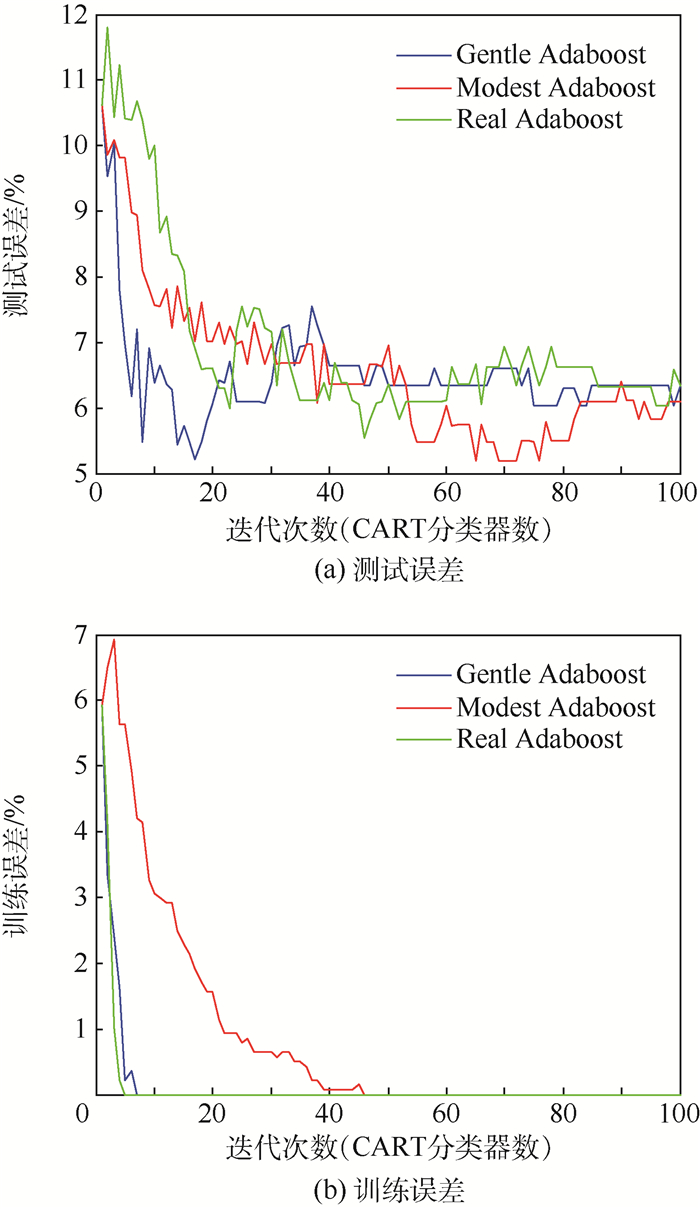图 4 Adaboost测试误差和训练误差 Fig. 4 Test error and training error of Adaboost

图选项

由图 4可知，当使用100个CART分类器时，Real Adaboost、Gentle Adaboost、Modest Adaboost在Ionosphere数据集上的平均测试误差分别为6.35%、6.34%、6.10%，低于文献[19]中6种分类算法错误率均值的11.58%，且训练误差均为0, 证明了本文算法的正确性。
4 基于Adaboost的超高速撞击损伤预测效果分析 如3.1节所述，预测填充式防护结构的超高速撞击损伤实际上是一个二分类问题。本节以临界弹丸直径、弹丸撞击角、弹丸撞击速度、弹丸密度作为弹丸撞击参数，航天器舱壁厚度、航天器舱壁屈服应力、航天器舱壁密度、防护层前屏与填充织物总面密度、防护层前屏与航天器舱壁间距离作为防护结构参数。以样本数据中的这2类特征和样本数据的超高速撞击损伤结果作为Adaboost预测模型的输入，通过训练从而建立基于Adaboost的隐式超高速撞击损伤预测模型，从而对测试样本进行预测，并通过与测试样本的实际撞击结果进行对比，分析本文预测模型的预测效果。流程如图 5所示。

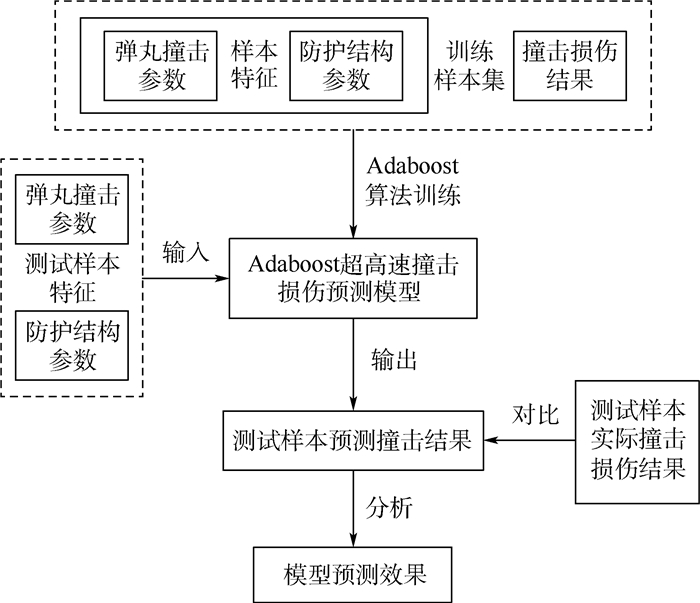图 5 基于Adaboost的超高速撞击损伤的预测流程 Fig. 5 Hypervelocity impact damage prediction process based on Adaboost

图选项

为进行验证实验，除文献[14]中的35组数据外，另外收集了72组填充式防护结构的超高速撞击实验数据，如表 2所示。
表 2 填充式防护结构的超高速撞击实验数据源 Table 2 Hypervelocity impact experimental data source of stuffed Whipple shield

数据来源	总实验次数	低速段次数	中速段次数	后墙失效次数	防护成功次数
文献[20]	5	2	3	0	5
文献[13]	17	1	16	9	8
文献[21]	27	19	8	16	11
文献[15]	23	12	11	16	7

表选项






4.1 预测效果检验 为检验基于Adaboost的填充式防护结构超高速撞击损伤预测效果，将表 2中的72组超高速撞击实验数据作为训练样本，将表 1中的35组超高速撞击实验数据作为测试样本进行预测效果的检验。测试过程中，采用CART作为弱分类器，结果如图 6所示。

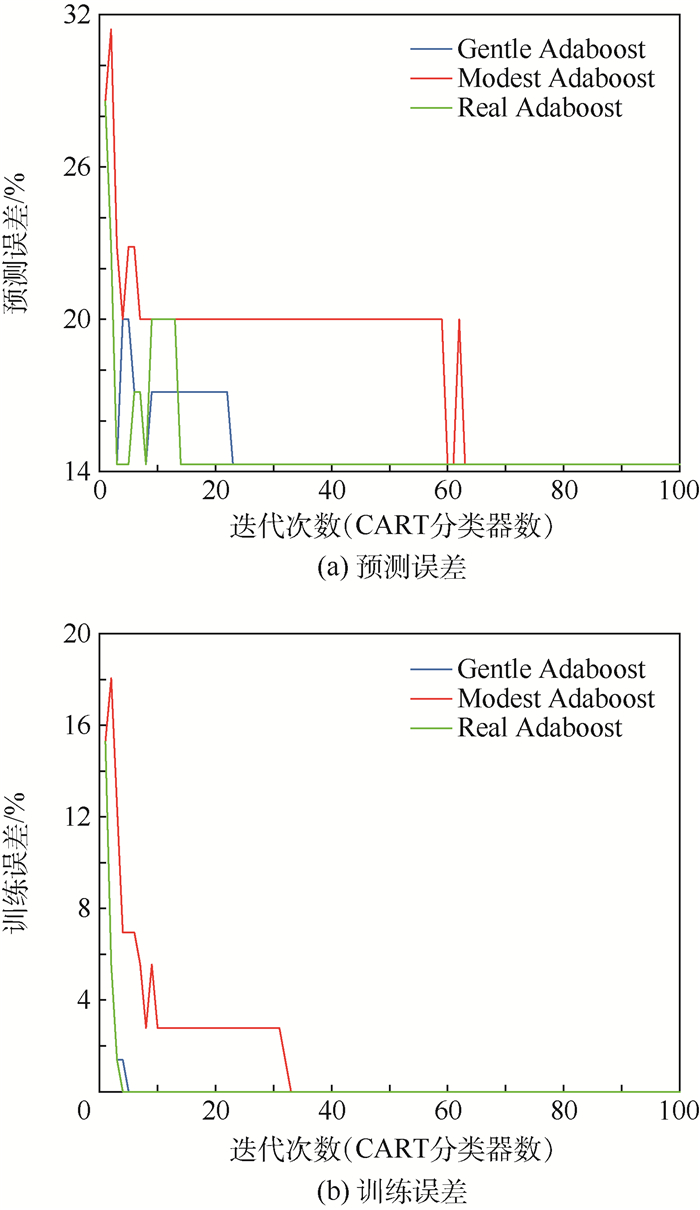图 6 Adaboost预测模型预测误差和训练误差 Fig. 6 Prediction error and training error of Adaboost prediction model

图选项

从图 6(a)中的预测结果来看，利用Adaboost预测模型对填充式防护结构进行超高速撞击损伤的预测准确率可以达到85.71%(等同于预测误差为14.29%)。其中，Real Adaboost模型的收敛速度最快，在14次迭代后(即利用14个CART分类器)预测准确率即可达到稳定；Gentle Adaboost较Real Adaboost预测稳定性稍差，在23次迭代后达到稳定；而Modest Adaboost则在第63次迭代时才能达到85.71%的预测准确率，预测效果稍差。同时从图 6(b)中可以看出，3种Adaboost预测模型在进行CART分类器的训练时，均可以使样本的训练误差快速降为0，表明本文模型具有较强的分类效果和学习能力，其中，Real Adaboost和Gentle Adaboost的训练效果尤为明显，分别在第4、第5次迭代时训练误差就已经收敛为0。
选取第100次迭代时的预测数据(已收敛)与NASA弹道极限方程的预测效果进行比较，比较结果如表 3所示。
表 3 填充式防护结构的超高速撞击实验预测对比 Table 3 Predictive comparison of hypervelocity impact experiment of stuffed Whipple shield

%
模型	总体(35组)			低速段(17组)			中速段(18组)
	Ptotal	Psafe		Ptotal	Psafe		Ptotal	Psafe
NASA弹道极限方程	71.4	80.0		88.2	88.2		55.6	72.2
Real Adaboost	85.7	94.3		100	100		72.2	88.9
Modest Adaboost	85.7	94.3		100	100		72.2	88.9
Gentle Adaboost	85.7	94.3		100	100		72.2	88.9

表选项






从表 3中可以看出，当迭代次数(CART分类器数量)达到100时，3种Adaboost预测模型对该35组数据的预测效果基本相同，总体预测率P_total与安全预测率P_safe相比于NASA的弹道极限方程均提高了14.3%。在低速段，Adaboost预测模型可以对填充式防护结构的超高速撞击实现100%预测；在中速段，模型的总体预测率P_total相比于NASA的弹道极限方程提高了16.6%，安全预测率P_safe提高了16.7%。因此，可以看出Adaboost预测模型对于填充式防护结构的超高速撞击具有较好的预测效果。
4.2 鲁棒性检验 为了对Adaboost预测模型的鲁棒性进行检验，采用K折交叉验证的方式对模型的预测效果进行检验。
首先以10折交叉检验为例对模型的预测效果进行说明。将表 1、表 2中的107组数据随机分成10份，轮流将其中9份作为训练集、1份作为预测集对模型进行效果检验，以10次预测结果的均值作为模型预测效果的估值，检验结果如图 7所示。

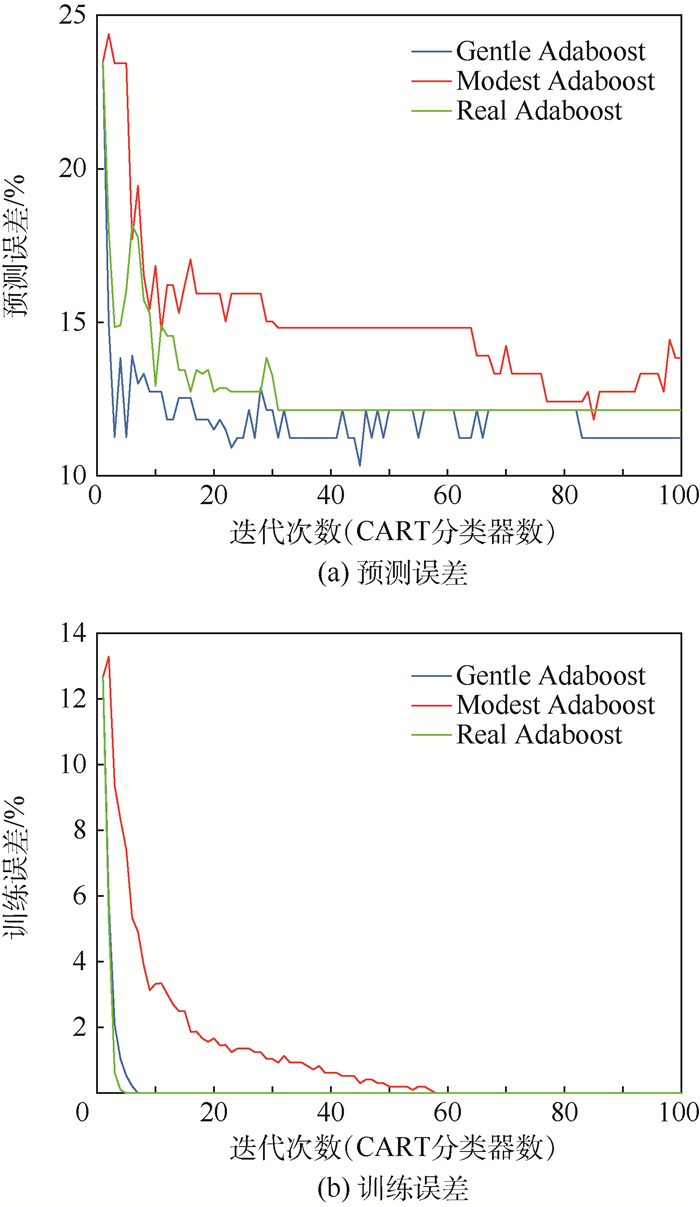图 7 10折交叉检验预测误差和训练误差 Fig. 7 Prediction error and training error of 10-fold cross check

图选项

从图 7(a)中的预测效果来看，Gentle Adaboost的预测效果最好，在83次迭代后预测准确率稳定为88.76%；Real Adaboost收敛性更强，在31次迭代后预测准确率稳定在87.85%；而Mod- est Adaboost收敛性较差，在第85次迭代时达到最优准确率88.17%。同时从图 7(b)可以看出，3种Adaboost预测模型均可以使样本的训练误差快速降为0，其中Real Adaboost和Gentle Adaboost的训练效果尤为明显，分别在第5、第7次迭代时训练误差就已经收敛为0。
为了避免在交叉检验过程中数据样本的随机选取会对模型的预测效果产生影响，进行10次10折交叉检验，迭代次数选为100，结果如表 4所示。
表 4 十次10折交叉检验结果 Table 4 Ten 10-fold cross check results

检验标准	Real Adaboost	Gentle Adaboost	Modest Adaboost
预测误差/%	12.15	11.83	13.85
	9.53	8.53	11.32
	13.32	14.09	14.61
	9.35	10.26	9.43
	12.30	12.49	11.49
	11.72	10.29	11.12
	13.22	13.22	13.22
	11.27	8.73	11.27
	12.40	12.08	13.51
	12.61	11.38	13.61
平均预测准确率/%	88.21	88.71	87.66

表选项






表 4中给出了Adaboost预测模型的10次10折交叉检验结果，其中3种框架的训练误差均收敛为0，因此该项未在表中给出。从预测结果来看，3种框架的Adaboost预测模型在10次10折交叉检验中的平均预测准确率均保持在88%左右。其中Gentle Adaboost预测效果最好，预测准确率达到88.71%；Real Adaboost次之，预测准确率为88.21%；Modest Adaboost最弱，预测准确率为87.66%。由此可以看出，当使用相同规模的不同训练样本时，Adaboost预测模型的平均预测准确率保持在88%左右，模型的预测效果良好。
对模型分别进行5次5折交叉检验和5次3折交叉检验，以检验不同规模的训练样本对Adaboost预测模型预测准确率的影响，结果如表 5所示。
表 5 不同规模训练样本的预测准确率 Table 5 Prediction accuracy of training samples with different scales

检验标准	Real Adaboost			Gentle Adaboost			Modest Adaboost
	5折	3折		5折	3折		5折	3折
预测误差/%	12.61	15.81		13.17	15.78		12.61	14.88
	13.14	10.68		12.09	9.57		12.09	12.01
	12.98	15.44		12.98	15.44		10.96	15.44
	14.40	13.07		13.84	12.00		16.15	12.00
	12.39	13.12		11.44	12.17		11.56	10.32
平均预测准确率/%	86.90	86.38		87.30	87.01		87.33	87.07

表选项






表 5给出了使用不同规模训练样本的交叉检验结果，结合表 4、表 5中的平均预测准确率可以看出，随着训练样本比例的减少，3种框架下的Adaboost预测模型对于填充式防护结构的超高速撞击损伤预测准确率虽有下降，但基本保持不变。其中Real Adaboost与Gentle Adaboost的预测准确率下降较多，最大降幅分别为1.83%和1.7%；Modest Adaboost的预测准确率下降最少为0.59%。可以看出，在小训练集的情况下，Modest Adaboost的预测效果更好。同时从表 5中可以看出，在降低训练样本比例后，Adaboost预测模型的平均预测准确率仍能保持在87%左右，表明训练样本的规模对模型的预测效果影响较小。
将表 1、表 2中的107组数据代入NASA填充式防护结构的弹道极限方程(见式(1))进行计算，得到实验数据的预测结果如图 8所示。

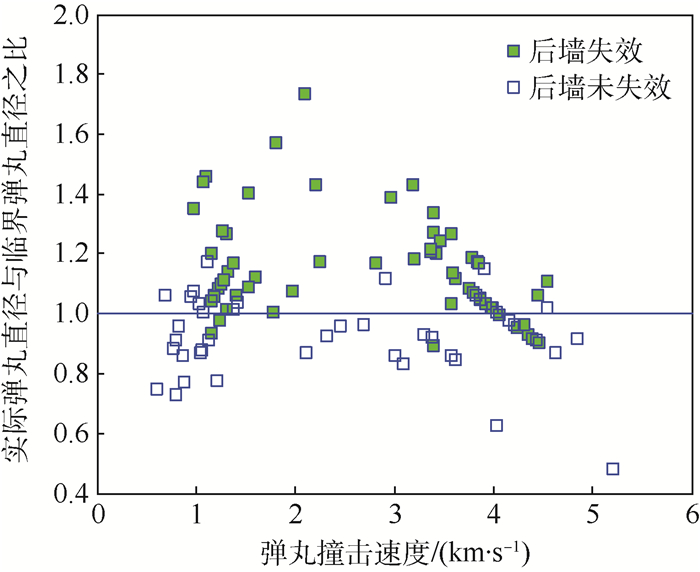图 8 NASA弹道极限方程在总体数据中的预测效果 Fig. 8 Prediction effect of NASA ballistic limit equation on all data

图选项

从图 8中可以看出，方程对于107组实验数据成功预测了82组，总体预测为76.64%，较Adaboost预测模型的预测准确率低了约11%。
综合以上检验结果可以看出，在选用不同规模的随机样本时，Adaboost预测模型仍可以对填充式防护结构的超高速撞击损伤保持稳定的预测效果，且平均预测准确率保持在87%左右，高于NASA的填充式防护结构弹道极限方程，证明了Adaboost预测模型具有良好的鲁棒性与准确性。
5 结论 采用恰当的防护结构以抵御空间中微流星体或空间碎片对航天器的撞击，是国内外航天工程的一项重要研究内容。继单层板、Whipple防护结构之后，填充式防护结构已成为近年来研究的重点。对此，本文建立了基于Adaboost的填充式防护结构超高速撞击损伤预测模型，得到如下结论：
1) 在Adaboost框架下以分类回归树CART作为弱分类器，通过多次迭代可以实现对填充式防护结构的超高速撞击损伤预测。且实验算例表明，在对不同填充物、不同填充方式下的填充式防护进行超高速撞击损伤预测时，Adaboost预测模型较NASA的填充式弹道极限方程具有更强的通用性，总体预测率与安全预测率均提高了14.3%。
2) 在小数据集的情况下，采用不同规模的训练样本进行学习后，Adaboost预测模型对填充式防护结构的超高速撞击损伤的预测效果仍保持稳定，证明了Adaboost预测模型具有良好的鲁棒性。且交叉检验结果表明，Adaboost预测模型的平均预测准确率较NASA的填充式弹道极限方程高11%。
3) 实验算例表明，Adaboost预测模型在低速段内可以对不同种填充式防护结构的超高速撞击损伤进行准确预测。而在中速段内，其预测准确率虽较NASA填充式弹道极限方程有较大提升，但效果仍不理想。因此，下一步应将不同填充物的面密度、填充组数、填充组间距等特征加入防护结构参数，以得到更准确的预测效果。
致谢 感谢哈尔滨工业大学哈跃、张宝玺、祖士明、傅翔、贾古寨等为本文撰写提供的实验数据。

参考文献

[1]	WHIPPLE F L. Meteorites and space travel[J]. The Astronomical Journal, 1947, 52: 131.
[2]	COUR-PALAIS B G, PIEKUTOWSKI A J.The multi-shock hypervelocity impact shield[M]//SCHMIDT S C, DICK R D, FORBES J W, et al.Shock compression of condensed matter-1991.Amsterdam: Elsevier, 1992: 979-982.
[3]	ROBINSON J H, HAYASHIDA K B.Double-plate penetration equations: NASA TM-2000-209907[R]. Washington, D.C.: NASA, 2000.
[4]	CHRISTIANSEN E L, CREWS J L, WILLIAMSEN J E, et al. Enhanced meteoroid and orbital debris shielding[J]. International Journal of Impact Engineering, 1995, 17(1): 217-228.
[5]	RYAN S, THALER S. Artificial neural networks for characterizing Whipple shield performance[J]. Procedia Engineering, 2013, 58(56): 31-38.
[6]	柳森, 李毅, 黄洁, 等. 用于验证数值仿真的Whipple屏超高速撞击试验结果[J]. 宇航学报, 2005, 26(4): 505-508. LIU S, LI Y, HUANG J, et al. Hypervelocity impact test results of Whipple shield for the validation of numerical simulation[J]. Journal of Astronautics, 2005, 26(4): 505-508. DOI:10.3321/j.issn:1000-1328.2005.04.024 (in Chinese)
[7]	管公顺.航天器空间碎片防护结构超高速撞击特性研究[D].哈尔滨: 哈尔滨工业大学, 2006. GUAN G S.Hypervelocity impact characteristics investigation on the spacecraft space debris shield configuration[D]. Harbin: Harbin Institute of Technology, 2006(in Chinese).
[8]	张晓天, 谌颖, 贾光辉. 航天器单层板结构弹道极限的支持向量机预测模型[J]. 宇航学报, 2014, 35(3): 298-305. ZHANG X T, SHEN Y, JIA G H. Support vector machine model for spacecraft single wall ballistic limit prediction[J]. Journal of Astronautics, 2014, 35(3): 298-305. DOI:10.3873/j.issn.1000-1328.2014.03.008 (in Chinese)
[9]	贾光辉, 欧阳智江, 蒋辉, 等. 填充式防护结构弹道极限方程的多指标寻优[J]. 北京航空航天大学学报, 2013, 39(12): 1573-1583. JIA G H, OUYANG Z J, JIANG H, et al. Multiple indicators optimization for stuffed Whipple shield ballistic limit equation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1573-1583. (in Chinese)
[10]	贾光辉, 欧阳智江, 蒋辉. 撞击极限方程预测指标剖析与实例[J]. 航空学报, 2013, 34(10): 2364-2371. JIA G H, OUYANG Z J, JIANG H. Analysis and instances of ballistic limit equations' predictive indicators[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2364-2371. (in Chinese)
[11]	姚光乐, 贾光辉. 填充式防护结构弹道极限方程形式建模[J]. 空间碎片研究, 2017, 17(1): 29-33. YAO G L, JIA G H. Formal modeling of ballistic limit equations for stuffed Whipple shield[J]. Space Debris Research, 2017, 17(1): 29-33. (in Chinese)
[12]	贾光辉, 姚光乐, 张帅. 填充式防护结构弹道极限方程的差异演化优化[J]. 北京航空航天大学学报, 2018, 44(7): 1489-1495. JIA G H, YAO G L, ZHANG S. Differential evolution optimization for stuffed Whipple shield ballistic limit equations[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(7): 1489-1495. (in Chinese)
[13]	哈跃.玄武岩纤维材料及其填充防护结构超高速撞击特性研究[D].哈尔滨: 哈尔滨工业大学, 2009. HA Y.Research on hypervelocity impact properties of woven of basalt fiber material and its stuffed shielding structure[D]. Harbin: Harbin Institute of Technology, 2009(in Chinese). http://kns.cnki.net/kns/detail/detail.aspx?QueryID=3&CurRec=10&recid=&FileName=2011015844.nh&DbName=CDFD0911&DbCode=CDFD&yx=&pr=&URLID=
[14]	张宝玺.超高速撞击玄武岩及Kevlar纤维布填充防护结构优化设计[D].哈尔滨: 哈尔滨工业大学, 2011. ZHANG B X.Optimum design of the protection structure of basalt and Kevlar fiber cloth filled with hypervelocity impact[D]. Harbin: Harbin Institute of Technology, 2011(in Chinese). http://kns.cnki.net/kns/detail/detail.aspx?QueryID=6&CurRec=6&recid=&FileName=1012002274.nh&DbName=CMFD2012&DbCode=CMFD&yx=&pr=&URLID=
[15]	祖士明.玄武岩及Kevlar纤维填充式防护结构超高速撞击性能研究[D].哈尔滨: 哈尔滨工业大学, 2013. ZU S M.The optimal structural design of stuffed shields whit basalt and Kevlar fiber clothes on hypervelocity impact[D]. Harbin: Harbin Institute of Technology, 2013(in Chinese). http://kns.cnki.net/kns/detail/detail.aspx?QueryID=9&CurRec=3&recid=&FileName=1014002506.nh&DbName=CMFD201401&DbCode=CMFD&yx=&pr=&URLID=
[16]	CHRISTIANSEN E L, KERR J H. Ballistic limit equations for spacecraft shielding[J]. International Journal of Impact Engineering, 2001, 26(1-10): 93-104. DOI:10.1016/S0734-743X(01)00070-7
[17]	http://archive.ics.uci.edu/ml/datasets/Ionosphere/[DB]. 1989-01-01.
[18]	苏锑, 杨明, 王春香, 等. 一种基于分类回归树的无人车汇流决策方法[J]. 自动化学报, 2018, 44(1): 35-43. SU T, YANG M, WANG C X, et al. Classification and regression tree based traffic merging for method self-driving vehicles[J]. Acta Automatica Sinica, 2018, 44(1): 35-43. (in Chinese)
[19]	李海生.基于证据理论的分类方法研究[D].广州: 华南理工大学, 2013. LI H S.Research of classification method based on evidence theory[D]. Guangzhou: South China University of Technology, 2013(in Chinese).
[20]	傅翔.玄武岩纤维布/铝丝网组合材料的空间碎片防护结构研究[D].哈尔滨: 哈尔滨工业大学, 2011. FU X.Hypervelocity impact characteristics investigation on the spacecraft space debris shield configuration of the basalt fiber woven/Al-mesh combination protective structure[D]. Harbin: Harbin Institute of Technology, 2011(in Chinese). http://kns.cnki.net/kns/detail/detail.aspx?QueryID=16&CurRec=2&recid=&FileName=1012002329.nh&DbName=CMFD2012&DbCode=CMFD&yx=&pr=&URLID=
[21]	贾古寨.玄武岩布防护机理及其填充防护结构撞击极限分析[D].哈尔滨: 哈尔滨工业大学, 2014. JIA G Z.Analysis on protection mechanism of basalt fabric and the limit of its stuffed shielding structure[D]. Harbin: Harbin Institute of Technology, 2014(in Chinese). http://kns.cnki.net/kns/detail/detail.aspx?QueryID=18&CurRec=2&recid=&FileName=1014082964.nh&DbName=CMFD201501&DbCode=CMFD&yx=&pr=&URLID=