根据姿态解算中目标函数的类型,视觉里程计可被分为直接法和特征法[10-11]。直接法将光度误差作为目标函数,避免了特征法中由人工设计因素带来的特征提取误差。但是,该类方法往往需要利用图像的全部灰度信息进行解算,因此,此类方法的时间复杂度较高。尽管一些改进的直接法[2, 12]可使用图像的部分纹理区域灰度信息参与解算,尽可能减少时间复杂度,但相对特征法,该方法的时间消耗依然较大。特征法利用匹配稀疏特征点构造重投影误差作为目标函数,进行姿态解算。由于仅利用到图像中提取的稀疏特征,位姿解算时间复杂度较低,但特征提取的精确度与特征匹配的准确度是影响该类算法性能的主要因素。为了提高特征提取与匹配的准确度,基于特征法中的一部分算法使用鲁棒性较强的复杂描述符提取图像特征,例如利用尺度不变特征变换(Scale-Invariant Feature Transform,SIFT)[13]和加速稳健特征(Speeded Up Robust Features,SURF)[4]等描述符,但这类特征提取与匹配计算的时间复杂度较高,影响实时性。另一类基于特征法的算法在图像中提取和匹配简单特征,如加速分割测试特征(Features from Accelerated Segment Test,FAST)[14]、方向FAST与旋转BRIEF特征(Oriented FAST and Rotated BRIEF,ORB)[15]、哈里斯特征(HARRIS)[16-17]等,以降低算法时间复杂度,但这些简单特征往往对图像噪声敏感,鲁棒性不足。考虑到实时性是衡量视觉里程计算法实用价值的重要指标,本文提出的视觉里程计采用特征法框架,并选用简单、快速的HARRIS特征提取算法获取图像的稀疏特征。针对视觉里程计中特征匹配使用单向闭环策略内点率不足的问题[5],第1类算法[6, 18]使用了强约束准则进行特征点筛选,导致特征点过少使解算误差过大。第2类算法使用鲁棒性较强的特征[4, 13],可以得到高内点率,但增加了匹配时间。本文针对单向闭环匹配策略中存在的内点率不足问题,从帧间特征点一致性出发,配合归一化图像特征描述符及特征位置预测,提出了有效的交叉检验闭环匹配策略,在特征匹配中通过交叉检验筛选特征点一致性高的匹配特征点,得到匹配特征点集合,相对于第1类算法提高了解算精度,相对于第2类算法缩短了解算时间。
除此以外,传统的视觉里程计在进行单帧图像间的姿态解算时,每帧解算的姿态都存在误差,误差必然随着图像帧数的增加而逐渐累积,形成姿态解算的累计误差。目前,解决累积误差问题的主要思想是联合使用多帧的运动信息进行姿态解算与优化,主要算法包括同时定位与建图(Simultaneous Localization and Mapping,SLAM)[3, 19]、集束调整(Bundle Adjustment,BA)[20]等,这2种算法时间复杂度高,无法满足实时性要求。本文考虑到算法的实时性要求,采用联合相邻若干帧的运动信息的方法克服累积误差。在定义目标函数时采用联合多帧运动信息的思想,通过构造基于特征生存周期的权值考察特征点的置信度,该方法可有效减少累积误差,降低时间复杂度,满足解算的实时性要求。
本文的主要工作可概括为以下3个方面:
1) 提出了一个高精度的视觉里程计框架,可实现自动驾驶或机器人导航系统的实时位姿解算。
2) 提出了一种基于特征交叉检验的闭环匹配策略,有效提高解算姿态的内点比例。
3) 提出了一种基于特征点生存周期的目标函数权值构造方法,有效降低解算累积误差。
1 特征提取与交叉检验闭环匹配策略 图像对之间的特征提取与匹配的准确程度,决定了视觉里程计的姿态解算精度,因此本节将详细介绍特征提取和交叉检验下的闭环匹配策略。
1.1 特征描述符的构造与提取 视觉里程计工作时,系统输入的图像序列是在连续运动状态下拍摄的,相邻图像帧间运动幅度较小,因此,相机的移动轨迹可以被假设为平滑的。在小幅度运动、平滑轨迹的假设下,帧间同一特征具有较高的相似性。强鲁棒性特征描述符(如SIFT和SURF特征)具有旋转和尺度不变特性,匹配精度高,但是其较高的计算复杂度不能满足视觉里程计的实时性要求。另一种策略为直接使用图像块灰度的绝对误差和(Sum of Absolute Differences,SAD)来快速计算特征之间的相似性,但是该方法对于图像的光照和噪声等因素十分敏感,匹配精度较差。为了保证视觉里程计系统的实时性,本文在图像中快速提取简单的HARRIS角点[16],并通过局部归一化描述符减少图像光照不均、噪声对特征鲁棒性的影响。
假设{Itl, Itr}和{It-1l, It-1r}为时间连续的左右立体图像对,下标t表示时间,上标l表示左视图,r表示右视图。在图像对中分别提取HARRIS角点,则每个像素点的角点响应值H定义为
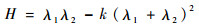 | (1) |
式中:k为人为设定的经验参数;λ1和λ1为矩阵Q的特征值,矩阵Q的定义为
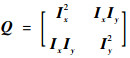 | (2) |
其中:矩阵Q中的Ix和Iy分别为图像I在X坐标轴方向和Y坐标轴方向的局部梯度。为了保证最终可以通过H筛选角点,参数k通常被设置在0.04~0.06。在计算图像中所有像素点的角点响应值H之后,假设Hmax为整幅图像中的角点响应最大值,传统的HARRIS角点检测方法将选取响应值H(P)大于阈值T=rHmax的像素点P作为候选特征点,其中参数r为经验值。
由于所拍摄的图像场景纹理分布差异大,且图像的纹理、灰度分布具有一定的区域性。仅使用单阈值对整幅图像进行HARRIS角点提取会导致角点分布不均匀,即部分低纹理区域可能无法检测出角点特征,而高纹理区域角点分布过于密集,这样分布的特征点并不利于姿态参数的求解。因此,为了解决上述问题,本文采用分块策略进行特征提取。首先,将每一幅图像分为若干20像素×20像素的图像块,由每个图像块i各自的最大角点响应值Hmaxi确定其阈值Tbini=rHmaxi。然后,通过图像块i中角点响应值大于Tbini的像素确定候选特征点位置,并且在3×3窗口中对候选特征点进行非极大值抑制,通过非极大值抑制的像素点最终被选为HARRIS角点。通常情况下,对于KITTI数据集中分辨率为376像素×1 241像素的室外的街景图像,采用上述过程的特征提取,每幅图像均可提取到2×103~4×103个特征点,为后续交叉检验闭环匹配环节提供足够数量且分布较为均匀的特征点作为系统的输入。
此外,视觉里程计系统输入的室外场景图像在拍摄中常受光照变化的影响而表现出图像对间的光照不均,影响HARRIS特征提取与匹配的鲁棒性。为了抑制光照以及噪声对特征提取的影响,本文采取了归一化图像块策略。
将图像中各个特征点周围N×N区域的灰度值作为其原始特征描述符,记为D,其中(i, j)位置的灰度值为Dij。对于D中每个位置使用式(3)进行去均值化,得到去均值化的描述符,记为D′,D′ij为描述符D′中(i, j)位置的去均值化后的灰度值。
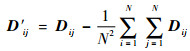 | (3) |
对于去均值化的描述符D′,使用式(4)进行归一化,将归一化后的描述符记为Dnorm,其中(i, j)位置的归一化灰度值为Dijnorm。
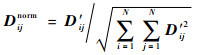 | (4) |
特征描述符归一化策略在建立特征匹配关系时有助于准确反映特征的相似性,有效提高特征匹配的内点比例。经实验验证,归一化图像特征描述策略可有效提高特征匹配内点比例。
1.2 交叉检验闭环的匹配策略 在时间连续的左右立体图像对中,利用归一化HARRIS特征描述符提取特征点后,本文将通过交叉检验下的闭环匹配策略建立前后立体图像对之间的特征点匹配关系。
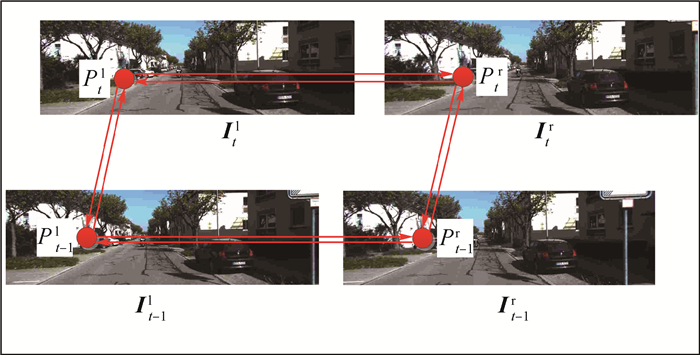
假设前一帧的立体图像对为{It-1l, It-1r},当前帧的立体图像对为{Itl, Itr},对于空间同一物点P在4幅图像{It-1l, It-1r, Itl, Itr}中的投影为{Pt-1l, Pt-1r, Ptl, Ptr},称{Pt-1l, Pt-1r, Ptl, Ptr}为一组匹配点集。为了解算姿态,必须在前后帧的立体图像对中建立鲁棒的匹配点集,通常采用闭环匹配策略增强特征匹配的准确度[5]。传统的单向闭环匹配策略如图 1所示。首先,从前一帧图像的左视图It-1l中选取特征点Pt-1l,在前一帧的右视图It-1r中搜索其匹配点对,计算特征描述符之间的SAD值,其中最小的SAD值对应的像素点即为Pt-1l在右视图It-1r的匹配点,记为Pt-1r,并将上述的匹配过程定义为:Pt-1l→Pt-1r。然后,类似的在图像对It-1r与Itr之间存在匹配过程:Pt-1r→Ptr;在图像对Itr与Itl之间存在匹配过程:Ptr→Ptl。最后,选取当前帧左视图Itl中的特征点Ptl,在前一帧左视图It-1l中搜索其匹配点,记为
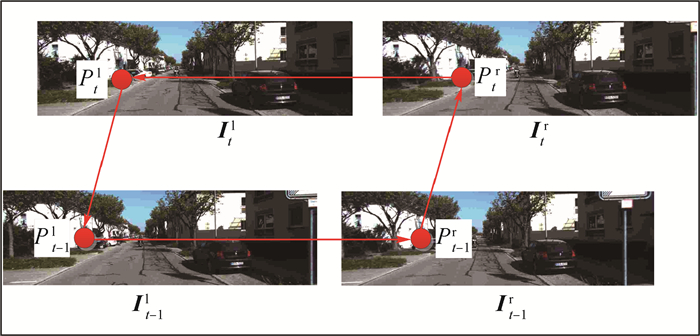 |
| 图 1 单向闭环匹配策略 Fig. 1 Single-track 'circle' matching strategy |
| 图选项 |
本文提出了交叉检验下的闭环匹配策略以提高匹配点集的准确度,如图 2所示。首先,在同一时刻的左、右立体图像对间进行交叉检验下的稀疏特征点匹配。具体的,对于前一时刻t-1的立体图像对,选取左视图It-1l中的特征点Pt-1l,在右视图It-1r中搜索其匹配点,假设得到其匹配点为Pt-1r,记匹配过程为:Pt-1l→Pt-1r。同时,由右视图It-1r中的像素点Pt-1r出发,在左视图It-1l中搜索其匹配点,假设得到的匹配点为
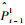
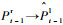
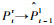
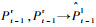
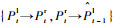
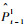
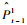
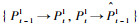
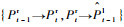
 |
| 图 2 特征交叉检验下的闭环匹配策略 Fig. 2 Crosscheck of feature 'circle' matching strategy |
| 图选项 |
在建立匹配点对的搜索过程中,对于同一时刻的左、右图像对,由于双目相机外部参数已知,可方便地建立极线约束关系,因此,采用极线约束沿极线方向搜索。实验表明,竖直极线方向的搜索误差容忍度为1个像素,可以满足解算精度要求。若能利用先验信息估计视差范围,在一维搜索空间中,稀疏特征点的匹配搜索时间复杂度较低,可快速建立匹配关系。而对于时间前后的帧间的特征点匹配搜索问题,不能事先建立准确的极线约束,因此,只能使用二维搜索窗口进行匹配点对的搜索。
交叉检验利用匹配特征点之间的一致性,解决了目前闭环检测中存在的不足,使得在闭环检测之前,每组图像对之间特征匹配是鲁棒的。满足左右一致性检验的匹配特征点的内点率较高,有利于下一步闭环检测。
利用交叉检验闭环匹配策略获得的匹配特征点集合中仍然存在少量不可靠的点。因此,本文采用RANSAC算法提炼匹配特征点集中的内点,即鲁棒匹配的特征点对,为视觉里程计位姿信息的估计提供了信噪比高的输入。通过实验验证,本文的交叉检验闭环的匹配策略可以有效获得鲁棒匹配点对,且采用RANSAC算法后,匹配内点率非常高。
1.3 匹配搜索窗口的预测 对于时间顺序上的前、后帧图像,无论左视图图像对,还是右视图图像对,由于当前时刻运动信息未知,在前后帧图像对间不能建立准确的极线约束,以帮助搜索匹配点。因此,在没有先验信息的情况下,为了保证匹配点能够被涵盖在候选区域内,特征匹配时所采用的二维搜索窗口往往尺寸较大,窗内候选点数量多,大大增加匹配计算量。考虑到搭载视觉里程计的无人驾驶汽车或移动机器人的运动姿态改变幅度一般较小,其前后运动具有一定的相关性,本文可利用前一帧已解算的姿态信息预测下一帧特征点出现的位置,可减少搜索范围,提高特征匹配效率。下文将详述如何通过前一帧图像解算的姿态信息,并结合其特征点的位置来预测当前帧中特征匹配搜索窗口。
基于运动的平滑性假设,本文认为前一帧运动的姿态信息与后一帧相差较小。假设前一帧运动姿态的旋转矩阵与平移向量分别被记为Rt-1和Tt-1,其中,旋转矩阵可由俯仰角α、偏航角β和滚转角γ 3个欧拉角计算得到;平移向量由X坐标轴方向偏移trx,Y坐标轴方向偏移try和Z坐标轴方向偏移trz 3个分量组成。通过分析多个视觉里程计所采集的姿态数据真值,本文为运动平滑性假设限定了以下3个约束:
1) 假设俯仰角α、偏航角β和滚转角γ均小于5°。
2) 假设前、后帧运动姿态的欧拉角变化很小,即Rt≈Rt-1。
3) 假设前、后帧运动姿态的平移向量的变化E小于0.1,其数学表达为
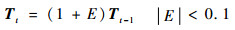 | (5) |
在相机模型中,假设(cu, cv)为相机的主点位置,f为相机的焦距,(x′, y′, z′)为当前帧中特征点对应的空间三维坐标。若已解算的前一帧平移矩阵Tt-1=[trx, try, trz]满足trz?try,trz?trx时,则在当前帧中预测的匹配特征点位置(u, v)为
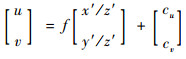 | (6) |
可以从前一帧计算出的特征点三维坐标(x, y, z)预测当前帧该特征点的三维坐标(x′, y′, z′),计算式为
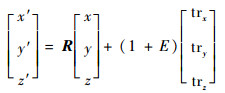 | (7) |
因此,本文根据平移向量变化E预测匹配搜索窗的位置与大小。相比于使用大尺寸、固定的传统匹配搜索窗口方法,预测得到的搜索窗口大部分尺寸较小,可大大降低匹配搜索时间。同时引入的预测机制可更加准确地进行初始匹配定位,也间接提高了匹配点集的内点比例。
2 视觉里程计姿态参数的解算 获得高比例内点的匹配点对集合后,本文将利用匹配点对集合解算帧间运动的姿态信息,其中包括旋转矩阵Rt和平移向量Tt。假设双目摄像系统的内部参数矩阵可经相机标定获得,左摄像机内参矩阵为Kl,右摄像机内参矩阵为Kr,两摄像机之间的基线长度为s,并以左摄像机坐标系为世界坐标系描述系统的姿态信息。将前一帧t-1时刻解算的位姿参数(Rt-1,Tt-1)作为当前帧t时刻的运动预测值,记为
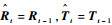
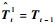
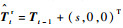
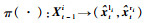
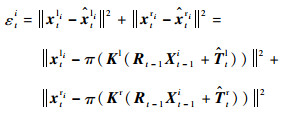 | (8) |
然后,由重投影误差构造目标函数。摄像机系统前后帧的姿态变化,即t时刻的姿态信息(Rt, Tt),可通过最小化重投影误差目标函数得以求解。上述重投影误差目标函数表达式为
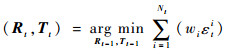 | (9) |
式中:Nt为特征点数目;wi为重投影误差权值。
求解目标函数式(9)的关键问题是如何设置重投影误差权值wi。第1类算法是根据重投影误差的大小设置该权值[11],该类算法认为重投影误差较大的特征点是外点的几率较大,应赋予较低的权值;而重投影误差较小的特征点是内点的几率较大,应赋予较高的权值。然而,此类算法仅考虑相邻两帧图像信息,随着时间推移,相邻帧的匹配误差在图像序列中不断扩散,得不到修正,降低最终位姿解算精度。第2类算法需要利用之前解算的运动轨迹[6-7]确定重投影误差权值,运动轨迹则包含了当前帧之前所有图像序列信息,计算量过大。第2类算法相比于第1类算法精度更高,如何降低其计算复杂度是其研究难点。本文在第2类算法的基础上,统计特征点连续存在的图像序列帧数,将特征点的生存周期作为重投影误差权值设置的考虑因素。特征点生存周期获取方便,额外增加的时间成本低,同时能够较好地衡量特征点的鲁棒性。基于特征点生存周期的目标函数可以考虑多帧的图像信息以防止匹配误差不断在图像序列中扩散,同时满足算法的实时性要求。根据经验,权重被设置为特征点的生存时间,使用age表示变量的生存时间,则有wn=agen,可以获得较高的姿态解算精度。最终,目标函数式(9)可重新记为
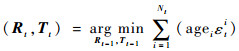 | (10) |
本文使用高斯牛顿优化算法对式(10)进行求解,即通过内点所构造雅可比矩阵对目标函数式(10)连续迭代优化。考虑到相邻帧间的运动较小,在初始化时,可令R=I,T=[0, 0, 0]T。一般情况下,目标函数式(10)迭代收敛速度较快,实验表明一般迭代次数少于10次即可收敛。
目标函数式(10)中,生存周期长的特征点将获得更大的重投影误差权值;而生存周期短的特征点也将被赋予较小的重投影误差权值参与解算位姿参数,并随着帧数增加有机会转变为生存时间较长的特征点参与解算。相对于直接舍弃生存时间较短的特征点这类算法[6],本文提出的权重赋值策略更符合视觉里程计输入图像序列的特点,可更为合理地利用有效信息。
在姿态参数解算过程中,本文利用了运动轨迹平滑性假设。虽然大部分时间内系统姿态变化缓慢,但在实际情况下,也不可避免地会发生姿态的跳变。当系统姿态发生跳变,在帧间图像对建立匹配关系时,沿用上述的预测搜索窗策略可能发生预测窗口定位偏差,导致特征点匹配错误,影响姿态解算精度。因此,当发现当前帧解算的姿态参数和前一帧解算结果差异过大时,将放弃预测匹配搜索窗口策略,直接使用无预测搜索窗的方法进行特征点匹配,并重新估计系统姿态,避免误差扩散。
3 实验验证 为了验证本文算法的有效性,采用公开发布的KITTI数据集[8]进行实验验证和精度评价,本文将解算得到的结果与真值比较并计算解算精度。
3.1 实验环境 在实验中,使用C++编程语言实现本文提出的视觉里程计解算方法,并利用了OpenCV库函数。为了加速程序的运行速度,还使用了基于OpenMP库的并行运算技术,有效地利用多核CPU(Core i7-4790, 4 core used@3.6 GHz),后续实验均在该环境下进行。
3.2 匹配点集中内点比例的检验 首先,验证经过交叉检验后,在左、右立体图像对中得到的匹配点集的内点比例。本文使用KITTI双目立体匹配数据集进行实验,该数据集包含200幅用于训练的立体图像对,及每组立体图像对视差真值,可用于验证交叉检验方法在左右立体图像对之间匹配的有效性。立体匹配研究中通常认为估计视差与真值相差1个像素以内的匹配点对是成功的匹配[8]。本文在数据集中200幅立体图像对上进行实验,统计成功匹配的特征点(即内点)的比例,图 3展示了200幅中第155幅立体图像对经过交叉检验后特征点对的匹配结果,红色为错误匹配结果,绿色为正确匹配结果,匹配准确率95.8%。实验结果显示200幅立体图像对匹配中内点的平均比例为91.11%,验证了经过交叉检验后,在左、右立体图像对得到的匹配点集中,大部分的匹配点对都为内点。
 |
| 图 3 经过特征交叉检验后,在左、右立体图像对中得到的匹配点集的内点情况 Fig. 3 An example of inlier in matching point set after crosscheck of feature between left image and right image |
| 图选项 |
然后,本文进一步验证经过交叉检验后,时间上的前、后图像对获得的内点比例。为了验证整个闭环策略中所采取各个步骤的有效性,本文进行了多组对比实验,即每次添加一个步骤,直到最后完成闭环匹配策略,并使用RANSAC算法统计添加各步骤后的内点比例。本文在KITTI数据集的第0组~第4组图像序列中各抽取前100帧图像进行实验验证。图 4为第0组~第4组图像序列计算得到的平均内点比例。其中步骤0表示利用传统的单向闭环匹配策略获得的内点比例,步骤1表示利用特征交叉检验的闭环匹配策略获得的内点比例,步骤2表示添加搜索窗口预测后获得的内点比例,步骤3表示添加归一化的特征点描述符后内点比例。
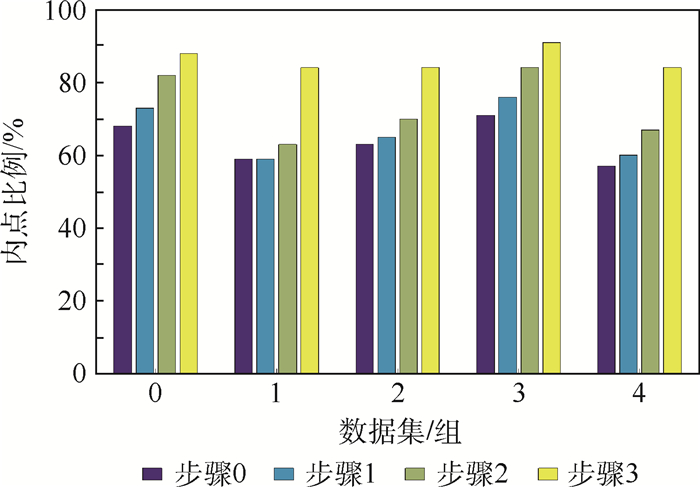 |
| 图 4 特征交叉检验中每个步骤提高内点比例的效果 Fig. 4 Improvements in inlier ratio of every crosscheck of feature step |
| 图选项 |
由图 4可以看出,从步骤0~步骤3,添加每个步骤后,内点比例都有提高,最终经过3个步骤后其比例均提高了20%~30%,验证了本文提出的特征匹配策略的每个步骤都是有效的。此外,从实验结果中可以看出,通过交叉检验的闭环匹配策略后,所有数据集的内点比例都在80%以上,有效提高视觉里程计位姿解算的精度。
同时,为了进一步验证前、后帧交叉检验的有效性,在利用RANSAC算法提取内点之后,本文利用数据集真值对内点进行重投影误差计算,图 5展示了KITTI数据集第0组数据序列中的第1帧与第2帧左视图经过前、后帧一致性检验后得到的匹配特征点对位置及真值投影结果。其中图 5(a)中的蓝色空心点表示前一帧的匹配特征点位置,5(b)中的青色实心点表示根据真值投影得到的真实匹配特征点位置。由图 5可以看出,匹配特征点位置与真实匹配特征点位置非常接近,直观地表明了利用特征交叉检验下的闭环匹配策略,可得到高精度的匹配特征点。统计KITTI数据集中第0组~第4组数据前200幅图像中重投影误差的均值,如表 1所示。从表 1可以看出,大部分重投影误差小于1个像素。同样证明了特征交叉检验下的闭环匹配策略可以有效获取内点。
 |
| 图 5 经过特征交叉检验后前、后帧图像匹配特征点及真值示例 Fig. 5 An example of consecutive frame image matching point and truth value after crosscheck of feature |
| 图选项 |
表 1 KITTI数据集第0组~第4组图像序列重投影误差统计结果 Table 1 Statistic results of reprojection error of KITTI dataset from 0 to 4th group of image sequence
| 数据集/组 | 0 | 1 | 2 | 3 | 4 |
| 平均重投影误差/像素 | 1.29 | 0.99 | 1.06 | 0.93 | 0.89 |
表选项
3.3 特征交叉检验闭环匹配策略有效性验证 为了验证本文交叉检验闭环匹配策略的有效性,本文选择不同的特征提取方法验证该框架对于提高内点比例的效果。
基于ORB-SLAM(Oriented FAST and Rotated BRIEF-Simultaneous Localization and Mapping)算法[14]中使用了计算速度较快,同时具有一定鲁棒性的ORB算子作为特征。为了验证本文提出框架的有效性,分别在有、无交叉检验的情况下,使用HARRIS与ORB算子选取图像特征,并统计内点比例,计算姿态解算精度。
图 6展示了采用ORB算子与采用本文提出的归一化HARRIS描述符在数据集第0组~第4组中特征匹配内点比例方面的情况。从图 6可以看出,采用本文提出的归一化HARRIS描述符获得的特征匹配精度略高于ORB算子,说明了本文提出的描述符具有较强的鲁棒性。同时,交叉检验的闭环匹配策略对于采用ORB算子提取的特征点,和本文所提出描述符提取的特征点,均可提高匹配点集的内点比例。证明交叉检验闭环匹配策略对于其他特征描述符的有效性。
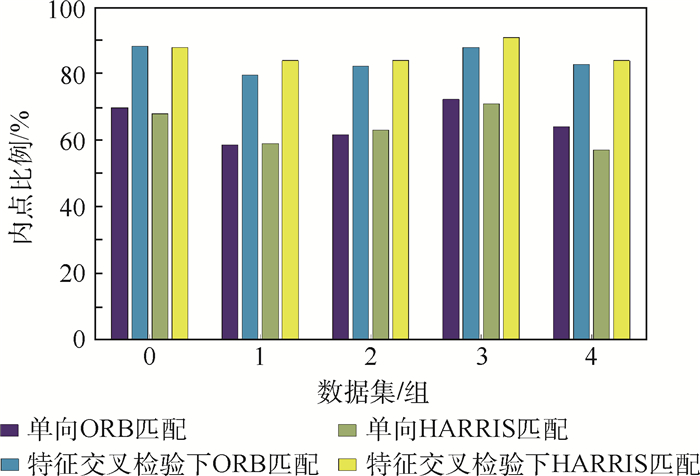 |
| 图 6 采用ORB算子与采用本文归一化HARRIS描述符在内点比例 Fig. 6 Inlier ratio by ORB operator and proposed normalized HARRIS descriptor |
| 图选项 |
表 2统计了在有、无特征交叉检验匹配策略的情况系下,归一化HARRIS描述符和ORB算子对KITTI数据集中第0组~第10组图像序列的姿态解误差。由表 2可以看出,通过利用本文的交叉检验闭环匹配策略,采用归一化HARRIS描述符提取图像特征可得到最佳的实验结果。考虑到运算的实时性是保证视觉里程计实用价值的重要指标,本文统计了采用不同特征描述符的系统运行时间,如表 3所示。归一化HARRIS描述符在平均运行时间上略少于ORB算子,可以达到实时处理。
表 2 ORB特征与归一化HARRIS特征KITTI数据集上解算的误差 Table 2 Estimation error for KITTI dataset using ORB feature and normalized HARRIS feature
| 选用特征 | 是否使用特征交叉检验 | 平移误差/% | 旋转误差/((°)·m-1) |
| 归一化HARRIS | 是 | 1.59 | 0.0065 |
| 否 | 2.44 | 0.0134 | |
| ORB | 是 | 1.89 | 0.0086 |
| 否 | 2.67 | 0.0156 |
表选项
表 3 KITTI数据集中第0组~第10组图像序列的姿态解算平均运行时间 Table 3 Average pose estimation processing time of KITTI dataset from 0 to 10th group of image sequence
| ms | ||||
| 选用特征 | 特征检测 | 特征匹配 | 姿态估计 | 总运行时间 |
| 归一化HARRIS | 25 | 62 | 11 | 98 |
| ORB | 15 | 117 | 11 | 143 |
表选项
3.4 姿态估计效果评价 为了验证本文提出的视觉里程计姿态解算框架的有效性,本文选择了经典的VISO2-S算法[5]与效果较好的RotRocc算法[18]作为对比算法,采用KITTI数据集提供的精度评价方法,通过解算运动轨迹与数据集真值的误差,计算在100, 200, 300, 400, …, 800 m各子序列中的平移误差和旋转误差的平均值,并以此评价姿态解算精度。表 4展示了3种算法在整个KITTI训练数据集上11组测试得到的平均平移误差、旋转误差以及每一帧的平均处理时间。通过比较可以看出,经典的VISO2-S算法计算速度较快,但解算精度不足;而目前精度比较高的RotRocc算法精度略高,但是平均计算速度较本文算法慢。
表 4 不同算法在KITTI数据集上第0组~第10组数据姿态解算平均误差及平均速度统计 Table 4 Average pose estimation errors and processing time of different algorithms on KITTI dataset from 0 to 10
| 算法 | 平移误差/% | 旋转误差/((°)·m-1) | 平均速度/s |
| RotRocc[18] | 1.25 | 0.0041 | 0.200 |
| VISO2-S[5] | 2.44 | 0.0114 | 0.050 |
| 本文算法 | 1.59 | 0.0065 | 0.098 |
表选项
为了展示各算法的实际处理效果,本文选择了KITTI数据集中的第0组与第5组的姿态解算结果绘制运动轨迹,并与上述经典算法做对比,结果如图 7所示。由实验结果可以看出,应用本文算法得到的运动轨迹与RotRocc算法得到的结果相近,都接近真值;而经典的VISO2-S算法获得的轨迹效果较差。
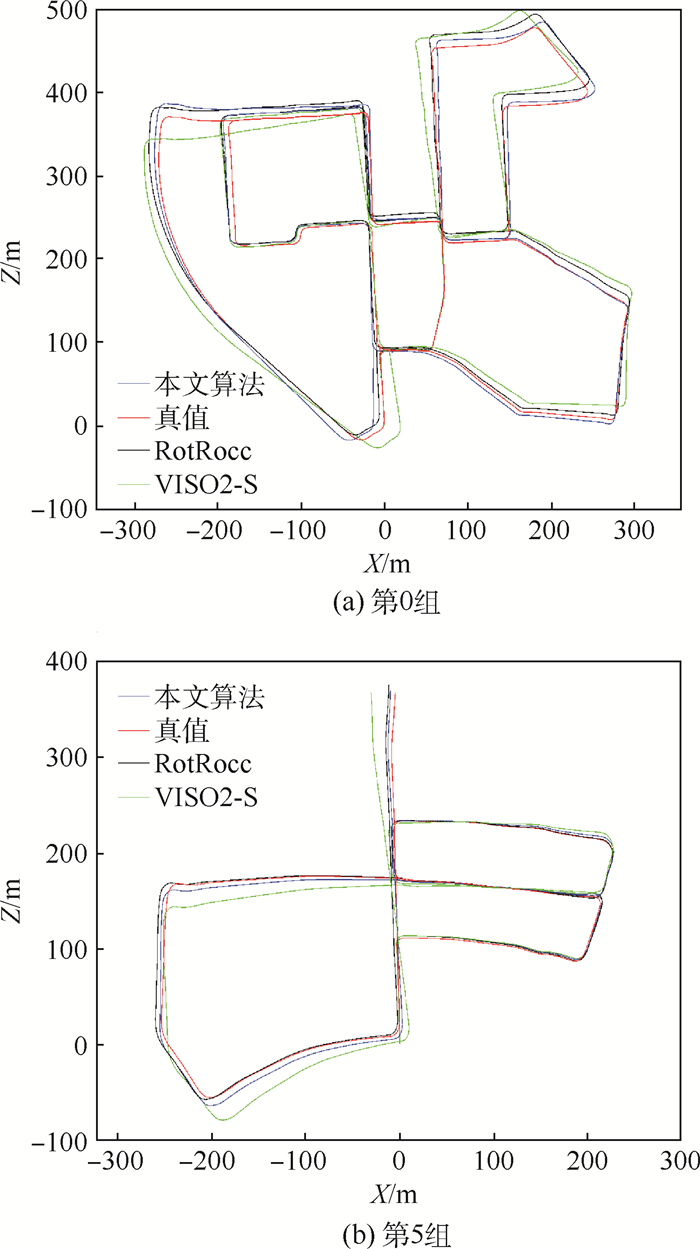 |
| 图 7 各算法对KITTI数据集中第0组和第5组数据的运动轨迹测试结果 Fig. 7 Test results of motion trajectory on KITTI dataset 0 and dataset 5 for each algorithms |
| 图选项 |
4 结论 本文提出了一种高精度、实时的视觉里程计方法。通过在KITTI数据集上的进行的实验,得到以下结论:
1) 交叉检验下的闭环特征匹配策略和基于特征点生存周期的权值设置方法均有利于算法的实时实现。
2) 该方法可以满足在低性能设备上实时处理的需求,同时获得满意的姿态解算精度。
下一步工作将着手于如何构造简单、但鲁棒性更强的特征提取方法,进一步提高特征提取与匹配精度,使算法具有更强的场景适应能力。
参考文献
| [1] | NISTER D, NARODITSKY O, BERGEN J.Visual odometry[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2004: 652-659. |
| [2] | FORSTER C, PIZZOLI M, SCARAMUZZA D.SVO: Fast semi-direct monocular visual odometry[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2014: 15-22. |
| [3] | DAVISON A J.Real-time simultaneous localisation and mapping with a single camera[C]//Proceedings 9th IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2008: 1403. |
| [4] | KITT B, GEIGER A, LATEGAHN H.Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme[C]//Intelligent Vehicles Symposium.Piscataway, NJ: IEEE Press, 2010: 486-492. https://ieeexplore.ieee.org/abstract/document/5548123 |
| [5] | GEIGER A, ZIEGLER J, STILLER C.StereoScan: Dense 3d reconstruction in real-time[C]//Intelligent Vehicles Symposium(Ⅳ).Piscataway, NJ: IEEE Press, 2011: 963-968. https://ieeexplore.ieee.org/document/5940405 |
| [6] | CVI?I?I, PETROVI? I.Stereo odometry based on careful feature selection and tracking[C]//2015 European Conference on Mobile Robots (ECMR).Piscataway, NJ: IEEE Press, 2015: 1-6. https://ieeexplore.ieee.org/abstract/document/7324219 |
| [7] | BADINO H, YAMAMOTO A, KANADE T.Visual odometry by multi-frame feature integration[C]//2013 IEEE International Conference on Computer Vision Workshops.Piscataway, NJ: IEEE Press, 2013: 222-229. https://www.ri.cmu.edu/pub_files/2013/12/badino_cvad13.pdf |
| [8] | GEIGER A, LENZ P, URTASUN R.Are we ready for autonomous driving? The KITTI vision benchmark suite[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2012: 3354-3361. |
| [9] | PERIS M, MAKI A, MARTULL S, et al.Towards a simulation driven stereo vision system[C]//International Conference on Pattern Recognition.Piscataway, NJ: IEEE Press, 2012: 1038-1042. https://ieeexplore.ieee.org/document/6460313 |
| [10] | SCARAMUZZA D, FRAUNDORFER F. Visual odometry[Tutorial][J]. IEEE Robotics & Automation Magazine, 2011, 18(4): 80-92. |
| [11] | FRAUNDORFER F, SCARAMUZZA D. Visual odometry:Part Ⅱ:Matching, robustness, optimization, and applications[J]. IEEE Robotics & Automation Magazine, 2012, 19(2): 78-90. |
| [12] | ENGEL J, STURM J, CREMERS D.Semi-dense visual odometry for a monocular camera[C]//IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2014: 1449-1456. |
| [13] | BEALL C, LAWRENCE B J, ILA V, et al.3D reconstruction of underwater structures[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2010: 4418-4423. https://www.cc.gatech.edu/~dellaert/pub/Beall10iros.pdf |
| [14] | HOWARD A.Real-time stereo visual odometry for autonomous ground vehicles[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2008: 3946-3952. https://ieeexplore.ieee.org/abstract/document/4651147 |
| [15] | MUR-ARTAL R, MONTIEL J M M, TARDóS J D. ORB-SLAM:A versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163. DOI:10.1109/TRO.2015.2463671 |
| [16] | KAESS M, NI K, DELLAERT F.Flow separation for fast and robust stereo odometry[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2009: 973-978. http://people.csail.mit.edu/kaess/pub/Kaess09icra.pdf |
| [17] | DEIGMOELLER J, EGGERT J.Stereo visual odometry without temporal filtering[C]//Pattern recognition.Berlin: Springer, 2016: 166-175. https://link.springer.com/chapter/10.1007%2F978-3-319-45886-1_14 |
| [18] | BUCZKO M, WILLERT V.Flow-decoupled normalized reprojection error for visual odometry[C]//IEEE International Conference on Intelligent Transportation Systems.Piscataway, NJ: IEEE Press, 2016: 1161-1167. https://www.researchgate.net/publication/309731985_Flow-Decoupled_Normalized_Reprojection_Error_for_Visual_Odometry |
| [19] | KLEIN G, MURRAY D.Parallel tracking and mapping for small AR workspaces[C]//IEEE and ACM International Symposium on Mixed and Augmented Reality.Piscataway, NJ: IEEE Press, 2008: 1-10. https://ieeexplore.ieee.org/document/4538852 |
| [20] | TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al.Bundle adjustment-A modern synthesis[C]//International Workshop on Vision Algorithms.Berlin: Springer, 1999: 298-372. https://lear.inrialpes.fr/pubs/2000/TMHF00/Triggs-va99.pdf |
