近年来,视觉跟踪技术取得了显著的进步,涌现出了大量的跟踪算法,主要分为2类[3]:生成式(generative)跟踪算法和判别式(discriminative)跟踪算法。生成式跟踪算法利用目标数据建立目标模型,通过在下一帧搜索与目标模型最相似的候选样本作为跟踪结果,是一种“模型驱动”的过程,典型的算法有:IVT(Incremental Visual Tracking)[4]、MTT(Multi-Task Tracking)[5]、ASLA(Adaptive Structural Local Appearance model)[6]等;判别式跟踪算法则将目标跟踪认为是前景(即目标)与背景的二值分类问题,通过划分前景与背景以实现跟踪的目的,是一种“数据驱动”的过程,典型的算法有:CT(Compressive Tracking)[7]、TLD(Tracking-Learning-Detection)[8]、MIL(Multiple Instance Learning)[9]等。在简单可控的跟踪环境下,这些算法都取得了不错的效果,但在背景遮挡、光照变化、目标形变、相似背景等复杂条件下,视觉跟踪技术仍然面临着巨大的挑战。
深度学习[10]的出现与快速发展,为解决上述复杂环境下的鲁棒跟踪问题提供了新的解决方案。Wang和Yeung[11]利用离线预训练与在线微调相结合,把深度模型运用在视觉跟踪任务上;文献[12]将堆栈式消噪自编码器与粒子滤波相结合,提出了一种“通用—专用”的跟踪策略,取得了与文献[11]相似的跟踪效果;Zhang等[13]将卷积神经网络(Convolutional Neural Network,CNN)应用到视觉跟踪中,利用图像的卷积特征提高了跟踪的成功率。诸如此类的深度学习跟踪算法,利用深层架构从样本中自动学习更加抽象、本质的高层特征,在性能上较传统方法有明显提升,成为了视觉跟踪领域的新趋势。
然而,基于深度学习的跟踪方法还存在一些难点问题[14]。首先,因为实际问题中的标签样本十分有限,尤其是正样本往往都是单一样本,因此要得到稳定的深层网络通常需要进行非监督预训练,而预训练需要大量的非标签数据,训练过程不仅费时复杂,极易出现“过拟合”现象;其次,利用梯度下降法训练深层网络时,传统的误差反向传播(Back Propagation,BP)算法容易出现“梯度消失”问题,导致深层网络的训练难以完成;再次,基于粒子滤波[15]框架的深度学习跟踪算法会出现“坏粒子”,从而造成跟踪漂移。
针对以上问题,本文提出了一种基于深度稀疏学习的鲁棒视觉跟踪算法。该算法针对单一正样本问题,对其进行数据扩充,以解决正负样本不平衡问题;同时将ReLU(Rectifier Linear Unit)[16]激活函数与稀疏自编码器(Sparse Autoencoders, SAE)相结合,构建一种深度稀疏神经网络结构,避免了传统深层网络复杂耗时的预训练过程,并且有效解决了传统神经网络训练过程中的梯度消失问题;针对“坏粒子”造成的跟踪漂移,采用密集采样搜索(dense sampling search)策略,生成目标候选区域的局部置信图,最后得到跟踪结果。利用大量的视频序列测试本文算法,实验结果表明:在相似背景、光照变化、目标形变等复杂环境下,本文算法不仅能够鲁棒地跟踪目标,而且具有较快的跟踪速率。
1 深度稀疏神经网络 神经网络的稀疏性[16]是用最少(最稀疏)的隐藏单元对输入层特征进行表征,其实际上是寻找一组“超完备”基向量来更高效地表示样本数据,能够更有效地找出隐含在输入数据内部的结构与模式。深度稀疏神经网络就是具有这种稀疏性的深层神经网络。与传统神经网络相比,其具有更好的稀疏性和表现性。本节首先介绍了稀疏自编码器的基本原理,然后将ReLU激活函数与稀疏自编码器相结合,通过堆叠多层稀疏自编码器,从而构造了与跟踪任务相适应的深度稀疏神经网络。
1.1 稀疏自编码器 自编码器(AE)[17]是一种无监督学习训练算法,是深度学习中常用的算法之一。图 1为自编码器的基本结构。
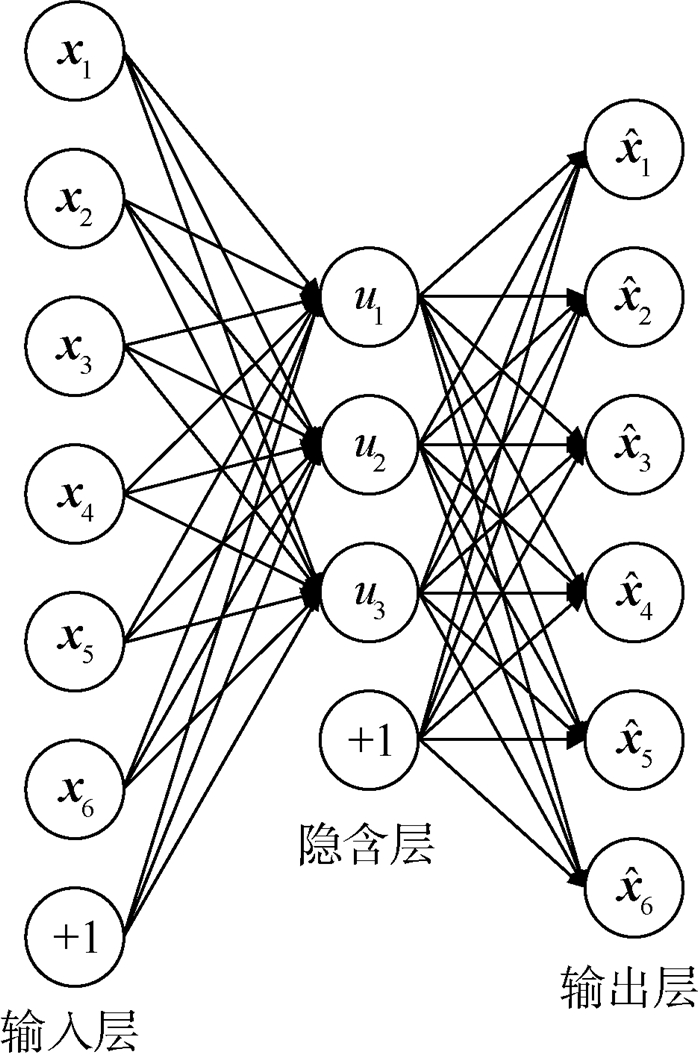 |
| 图 1 自编码器基本结构 Fig. 1 Basic structure of AE |
| 图选项 |
对于一组无标签的训练样本x=(x1, x2, …, xm),xi∈Rl,Rl表示l维实数集,m为训练样本数量。自编码器通过学习输入数据x,使其重构输出
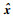
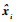
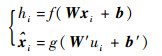 | (1) |
式中:ui为隐含节点激活值;f(·)和g(·)分别为编码器和解码器的非线性激活函数。
自编码器的训练过程就是在通过寻找参数集θ={W, W′, b, b′},使样本集x的重构代价函数最小的过程。代价函数定义为
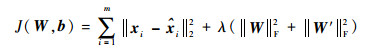 | (2) |
式中:λ为权重惩罚因子,用来平衡权重和重构损失之间的关系;||·||F为F范数,||A||F=
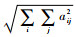
为了能够更加有效地学习到隐含在输入数据内部的结构与模式,通常会对自编码器加入稀疏性限制,得到稀疏自编码器[18]。稀疏性限制使得自编码器隐含层的神经元大部分时间都被抑制,从而更容易发现输入数据更有效的特征表达。
在式(2)中添加稀疏目标ρ与平均激活度
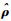
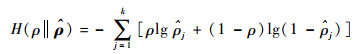 | (3) |
 | (4) |
式中:H(ρ||
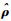
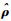

从而得到新的代价函数
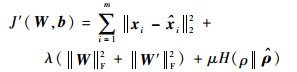 | (5) |
式中:μ为稀疏惩罚因子。
采用梯度下降法求解J′(W, b)的最优解,每次迭代时需要对参数W和b进行更新:
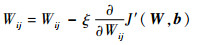 | (6) |
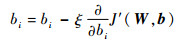 | (7) |
式中:ξ为学习率;Wij∈W;bi∈b。
1.2 构建深度稀疏跟踪网络 堆叠多层稀疏自编码器,并利用逐层贪婪算法进行训练,可以得到一个深层的神经网络结构,其通过对输入数据进行多层重构,可以得到鲁棒稳定的多层特征表达。但是,要得到稳定可靠的深层网络,往往需要大量的样本数据来进行预训练,训练样本过少或过多,分别会造成网络的欠拟合或者过拟合现象,导致提取的特征并不能有效反映输入数据的本质特征,而且即使利用了GPU加速技术,其预训练也是一个相当费时的过程。
为解决预训练难题,缓解训练深层网络的过拟合问题,Glorot等[16]对传统的非线性激活函数进行了修正,提出了一种新的激活函数——ReLU函数。如图 2所示,与Sigmoid函数和tanh函数相比,ReLU函数与脑神经元模型更加相似,是一种单侧抑制函数,其函数表达式为
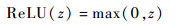 | (8) |
 |
| 图 2 激活函数曲线 Fig. 2 Activation function curves |
| 图选项 |
式中:z为激活函数的输入值。
ReLU的单侧抑制性使其具有稀疏表达性,使得神经网络在构建之初就有约50%的隐含层神经元被抑制,提高了深层网络的稀疏性。Glorot等[16]通过实验证明,这种稀疏性可以有效地缓解深层网络训练中的过拟合现象,具有与传统的预训练过程相似的效果,从而可以缩小有无进行预训练对深层网络性能的影响。
同时,ReLU的单侧响应端为非饱和的线性函数,有效地解决了传统神经网络训练过程中的梯度消失问题;另外由于梯度恒为1,其在训练过程中不用进行复杂的梯度计算,从而减小了计算复杂度,提高了网络的训练速度。
因此,为了实现鲁棒快速的跟踪,避免深层网络的过拟合问题,本文采用ReLU函数作为稀疏自编码器的激活函数,利用逐层贪婪算法堆叠多层稀疏自编码器,构建一个深度稀疏的神经网络模型,用于目标在线跟踪中的特征提取,并在最后一层添加Sigmoid分类层,计算输入样本的置信度,选择置信度最大的样本以实现目标的跟踪。其网络结构如图 3所示,Sigmoid函数为
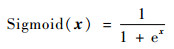 | (9) |
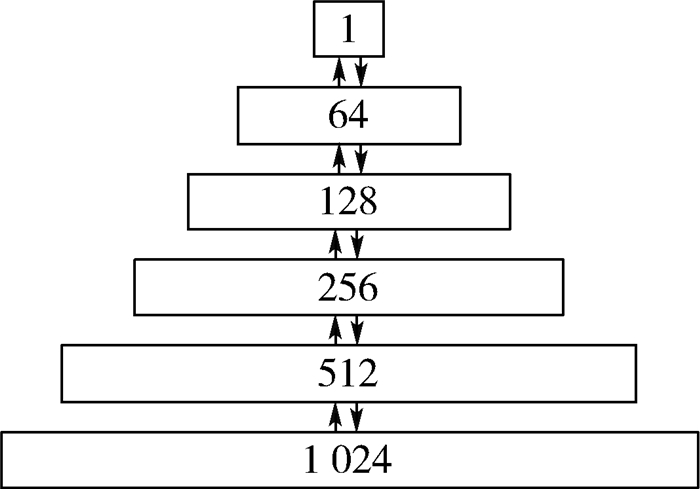 |
| 图 3 跟踪网络模型 Fig. 3 Model of tracking network |
| 图选项 |
2 基于深度稀疏学习的鲁棒视觉跟踪算法 针对算法在复杂环境中易出现跟踪漂移的问题,本文提出了一种基于深度稀疏学习的鲁棒视觉跟踪算法。算法通过构造深度稀疏跟踪网络模型,得到目标可能区域的局部置信图,从而选取置信度最大的样本点作为跟踪结果。算法解决了单一正样本跟踪问题,省去了复杂费时的网络预训练过程,同时有效地抑制了跟踪漂移问题。
2.1 跟踪网络初始化 利用初始帧给定的目标状态s0={x0, y0, w0, h0},其中x0、y0为目标初始位置,w0、h0为目标初始的宽和高,在初始帧进行采样,可以得到单个正样本。同时在(x0, y0)周围随机采样可以得到100个负样本,对其进行归一化处理,可以得到大小为32×32像素的标准灰度图像作为网络输入。
但考虑到正负样本数量差异太大时,往往会对跟踪网络的鲁棒性产生影响,所以要对正样本进行数据扩充,以增加正样本的数量。文献[11]通过在正样本区域附近±2个像素点内进行采样扩充,但这种方法易造成正样本的累积偏移,影响跟踪结果。文献[19]中通过对图像进行缩放、平移、旋转、加噪、镜像、裁剪、亮度变化等变换造出新的数据,来增加其数据量。本文通过对采集到的单个正样本进行亮度、对比度、加噪、滤波、镜像旋转等方面的变换来进行扩充,将其扩充为10个正样本,结果如图 4所示。
 |
| 图 4 对于单个正样本进行数据扩充 Fig. 4 Data augmentation for single positive sample |
| 图选项 |
利用扩充后的10个正样本与随机采样的100个负样本作为标签数据,对图 3的跟踪网络进行初始化训练,就可得到与特定任务相适应的跟踪网络参数。
2.2 局部置信图 以图像中的任意一个像素点(xi, yi)为采样中心,(wi, hi)为样本尺寸进行采样,将采样样本送入图 3的跟踪网络中进行检测,通过Sigmoid分类层,每个采样样本都可以得到一个[0, 1]区间内的值,即样本的置信度ζi,置信度的大小反映了采样样本为正样本(跟踪目标)的可能性的大小。
在跟踪过程中,对于第t帧图像,以t-1帧图像跟踪结果的中心位置为中心点,向其上、下、左、右各扩展N个像素点得到一个搜索区域A,区域A包含了(2N+1)2个像素点。将A内的所有像素点作为采样中心分别进行密集采样搜索,送入跟踪网络进行检测即可得到所有样本的置信度,从而得到了区域A的置信图,将其进行可视化,能够更直观地反映目标在此区域内可能的位置。通常选取置信度最大的采样样本为本帧目标跟踪结果,即
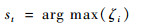 | (10) |
式中:st为t帧时的目标状态,st={xt, yt, wt, ht}。
图 5为N=50时部分视频的局部置信图示例,红色越深,表示置信度越高。
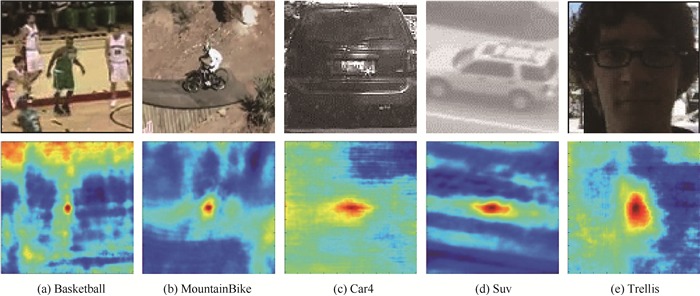 |
| 图 5 部分视频局部置信图示例 Fig. 5 Examples of local confidence maps of some videos |
| 图选项 |
同时,考虑到跟踪过程中目标的尺度变化,可以在采样时对样本尺寸(wi, hi)加一个随机扰动r=(wr, hr),以得到更加适合跟踪目标尺度的采样样本,此时样本尺寸变为(wi+wr, hi+hr)。在本文中,wr和hr均为均值为0、方差为0.1的正态分布的随机数。
2.3 跟踪网络更新策略 跟踪过程受到光照变化、目标形变、背景变化等因素影响或者长时间跟踪时,容易出现跟踪网络与当前任务不匹配的情况,造成跟踪漂移,此时需对跟踪网络参数进行更新,更新条件为
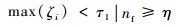 | (11) |
式中:τ1为网络更新阈值;nf为自上一次更新到当前跟踪帧的累计跟踪帧数;η为最大累计帧数。
更新策略为:建立正样本的时间滑动窗[20],将当前帧及其前9帧的跟踪结果作为正样本放入滑动窗,且实时更新,如图 6所示。同时,重新进行负样本采样。将100个负样本、10个初始帧正样本、10个时间滑动窗正样本送入跟踪网络进行训练,从而更新网络参数。
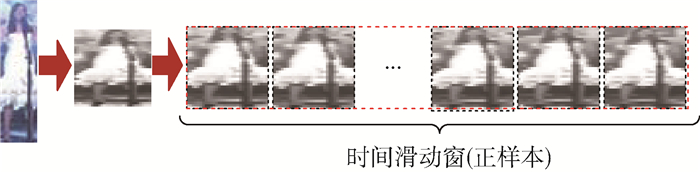 |
| 图 6 正样本时间滑动窗 Fig. 6 Sliding time window of positive samples |
| 图选项 |
2.4 局部搜索区域更新策略 当物体受到遮挡时,原来的局部搜索范围可能会找不到正确的跟踪目标,此时,需在一定范围内扩大搜索区域,以确保能正确定位跟踪目标。更新条件为
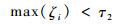 | (12) |
式中:τ2为搜索更新阈值。更新策略为
 | (13) |
式中:δ为搜索范围N的增加值。
2.5 算法流程 综合上述对基于深度稀疏学习的鲁棒视觉跟踪算法的关键部分的描述,本文跟踪算法的具体步骤如算法1所示,算法流程如图 7所示。
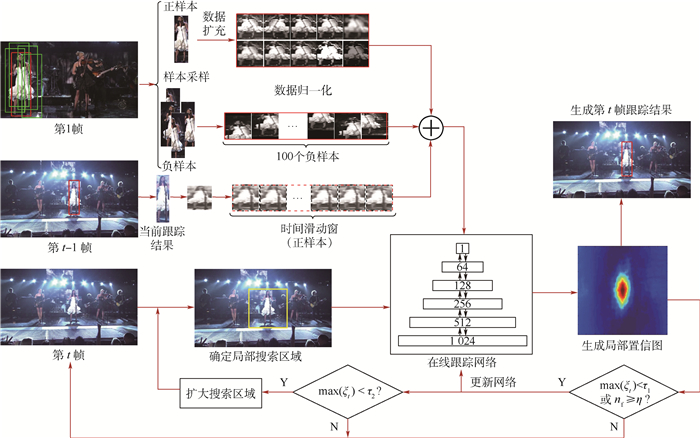 |
| 图 7 基于深度稀疏学习的鲁棒视觉跟踪算法流程图 Fig. 7 Flowchart of robust visual tracking based on deep sparse learning |
| 图选项 |
算法1??基于深度稀疏学习的鲁棒视觉跟踪算法
输入:图像序列I1,I2,…,In,目标初始状态s0,初始搜索区域大小N。
输出:每帧图像中目标的估计状态

步骤1??首帧采集正负样本,进行归一化处理,并对正样本进行数据扩充。
步骤2??初始化跟踪网络。
步骤3??对于i=1, 2, …, n,do:
1) 根据si-1和N,确定Ii局部搜索区域;
2) 在搜索区域内进行密集采样搜索,得到局部置信图mapi;
3) 利用式(10)确定Ii跟踪结果

4) 将跟踪结果

5) 根据式(11)和式(12)分别对跟踪网络和搜索区域大小进行更新。
结束。
3 仿真实验 采用MATLAB编程方式实现本文算法,并在Intel Xeon 2.4 GHz处理器的计算机配置平台上测试算法性能,同时利用TITAN-X型号的GPU对算法进行加速。测试参数设置如下:学习率ξ=0.01,权重惩罚因子λ=0.005,稀疏目标ρ=0.05,稀疏惩罚因子μ=0.2,最大累计帧数η=50,网络更新阈值τ1=0.9,搜索更新阈值τ2=0.5,初始搜索范围N=10,搜索更新增加值δ=5。这些参数的设置在所有测试序列上都是一致的。
文献[21]给出了一个测试数据集,称之为Benchmark,其中包括50组不同环境下的测试视频和51组目标的准确结果(测试视频“Jogging”包含2个不同的目标)。为充分验证算法的有效性,选取7种当前主流的跟踪算法与本文算法在Benchmark测试数据集中进行对比测试。选取的对比算法有:TLD[8]、MIL[9]、ASLA[6]、CT[7]、MTT[5]、DFT(Distribution Fields Tracker)[22]、DLT[11]。其中,DFT是一种最近提出的基于像素分布域(distribution fields)描述子的跟踪算法,MTT、ASLA为生成式跟踪算法的代表,TLD、MIL、CT为判别式跟踪算法的代表,DLT为深度学习跟踪算法的代表。这些算法在测试中均使用默认参数。
3.1 定性分析 图 8为8种对比算法在Benchmark上的部分实验结果。其中,不同颜色的矩形框表示不同的算法的跟踪结果,红色代表本文所提算法,图片左上角数字为图像帧数。从以下6个方面对算法进行定性分析:
 |
| 图 8 8种跟踪算法的定性比较 Fig. 8 Qualitative comparison of 8 tracking algorithms |
| 图选项 |
1) 复杂背景:以视频“Singer2”、“Freeman4”为例,背景与目标具有很大的相似性,对算法的跟踪准确性具有很大的挑战性。在“Singer2”中,从第184帧开始,除本文算法外的其余7种对比算法都不同程度地出现了漂移现象,而本文算法却始终能够准确地跟踪目标;“Freeman4”中,除本文算法外,对比算法都被相似背景所干扰,从第82帧开始就出现了目标丢失现象。
2) 背景遮挡:以视频“Suv”、“Tiger2”为例,目标在跟踪过程中出现了不同程度的遮挡。在“Suv”中,第523帧目标被树木部分遮挡,只有本文算法和DLT能够正确跟踪目标,第788帧目标被全部遮挡又重新出现时,只有本文算法能有效跟踪目标。
3) 非刚体形变:以视频“Basketball”为例,跟踪过程中非刚体目标发生快速、连续、剧烈的外形和姿态变化。第302帧时,TLD、MIL、CT、MTT算法失效,丢失了目标;第592帧时,只有本文算法、DFT、DLT算法能够正确跟踪目标,但DFT与DLT算法不同程度地偏离了跟踪目标的准确位置。
4) 光照变化:以视频“Trellis”、“Car4”为例,跟踪过程中光照条件出现了剧烈的变化,造成了目标表观的变化,这要求算法对光照影响具有较好的鲁棒性。视频“Trellis”中,当光照出现剧烈变化时,对比算法陆续失效,第425帧后,只有本文算法能够准确跟踪目标。
5) 目标旋转:以视频“MountainBike”、“FleetFace”为例。视频“MountainBike”中,跟踪过程中出现了平面内的目标旋转,使得TLD、DFT和CT算法失效,而本文算法始终能够准确地跟踪目标;视频“FleetFace”中,目标在第631帧出现了平面外的旋转,使得当前目标状态与初始状态产生了较大的差异,但本文算法仍能较好地对目标进行跟踪。
6) 运动模糊:以视频“Boy”为例,第268帧时,目标运动速度较快,出现了模糊现象,MIL、ASLA、DFT和MTT算法都出现了跟踪漂移;第599帧后,只有本文算法和DLT算法能够准确地跟踪目标。
3.2 定量分析 对算法的定量分析从算法对于单个视频的单一性能和对于Benchmark上的全部50组视频的综合性能2个方面进行。
3.2.1 对单个测试视频的定量分析 针对单个测试视频,采用平均中心位置误差和成功率2个通用的评价指标对算法进行定量分析。中心位置误差是指单帧视频中算法跟踪结果与目标真实位置之间的中心点的欧氏距离,整个序列的平均欧式距离即为其平均中心位置误差。成功率的大小与跟踪结果的覆盖率α有关,覆盖率计算公式为
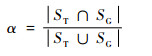 | (14) |
式中:ST和SG分别表示算法的跟踪结果区域和目标准确区域;∩和∪分别表示交集和并集操作;|·|表示计算图像区域内所包含像素点的个数。
每帧图像中,给定覆盖率阈值t0,当满足α>t0时则认为目标跟踪成功。在整个视频序列中,算法跟踪成功的帧数与总帧数的比值即为跟踪算法在此视频序列的跟踪成功率。
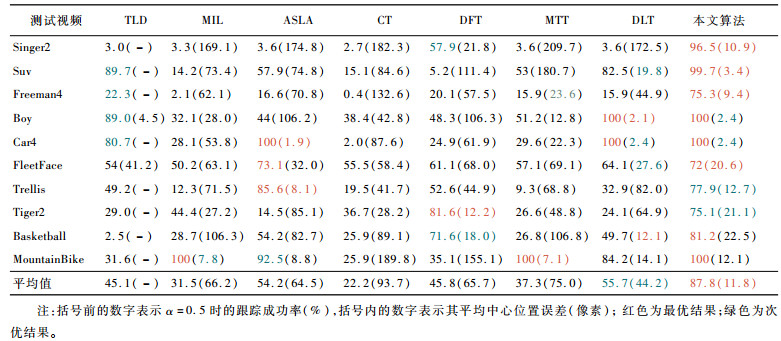
对于定性分析中10组测试视频,表 1展示了8种跟踪算法在单个视频上的跟踪成功率和平均中心位置误差。由表 1可以看出,在10组测试视频中,本文算法的跟踪成功率和平均中心位置误差都取得了8个对比算法中最优或次优的结果,展现出了本文算法在单个视频序列中的良好的跟踪性能。
表 1 8种跟踪算法在10组视频中的跟踪结果对比 Table 1 Comparison of tracking results among 8 tracking algorithms on 10 videos
 |
表选项
3.2.2 算法综合性能的定量分析 将本文算法在Benchmark的全部50组视频中进行了测试,并画出其在50组视频下的精度曲线和成功率曲线以分析算法的综合性能。
实验过程中,对50组测试视频采用一次评价(One-Pass Evaluation,OPE)[21]的评估方法,得到的精度曲线和成功率曲线如图 9所示,其中,图 9(a)、图 9(b)的图例分别按照平均中心位置误差为20像素时的精度值、成功率曲线的AUC(Area Under Curve)值对算法进行排序。表 2给出了8种对比算法在50组测试视频下的平均跟踪速率。
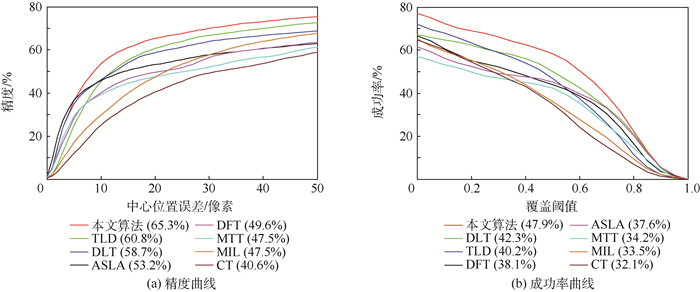 |
| 图 9 测试结果的精度曲线和成功率曲线 Fig. 9 Precision curves and success rate curves of test results |
| 图选项 |
表 2 8种跟踪算法平均跟踪速率对比 Table 2 Comparison of average tracking speed rate among 8 tracking algorithms
| 跟踪算法 | TLD | MIL | ASLA | CT | DFT | MTT | DLT | 本文算法 |
| 平均跟踪速率/(帧·s-1) | 21.74 | 28.06 | 7.48 | 38.76 | 11.04 | 0.99 | 16.51 | 16.51 |
表选项
对于50组测试视频,由图 9的跟踪精度曲线与成功率曲线可以看出,本文算法相对其他7种对比算法中均为最优。与同样基于深度学习的DLT算法相比,本文算法的跟踪精度和成功率分别提高了11.24%和19.15%。在跟踪速率上,由表 2可以看出,本文算法的平均跟踪速率约为16.51帧/s,与同样基于深度学习的DLT算法速率相近,但低于CT、MIL和TLD算法。分析原因,本文算法虽然省去了复杂费时的预训练过程,但网络的更新频率增加;同时,算法采用穷搜索方法生成局部置信图,也在一定程度上增加了算法的跟踪用时。
4 结论 本文提出了一种基于深度稀疏学习的鲁棒视觉跟踪算法。
1) 本文算法将ReLU激活函数与稀疏自编码器相结合,构建了一种深度稀疏神经网络结构,其避免了传统深层网络复杂耗时的预训练过程,使其仅利用有限的标签样本进行在线学习,就能够得到稀疏鲁棒的跟踪网络来完成特定的跟踪任务。
2) 本文算法通过对单一正样本进行数据扩充,解决了正负样本不平衡问题,使得训练的跟踪网络更加稳定。
3) 本文算法利用构建的跟踪网络在目标可能出现的区域内进行密集采样搜索,得到局部置信图,最后得到跟踪结果。
4) 实验结果表明,在相似背景、光照变化、目标形变、背景遮挡等复杂条件下,本文算法都表现出了良好的鲁棒性,能够有效解决复杂环境下的跟踪漂移问题,且具有较快的跟踪速率。
同时在实验中发现,由于本文算法对于跟踪中尺度的处理较简单,当目标尺度变化较大时,该算法的跟踪适应性不是很好。因此,如何提高该算法的尺度适应性,将是以后研究的重点方向。
参考文献
| [1] | SMEULDERS A W M, CHU D M, CUCCHIARA R, et al. Visual tracking:An experimental survey[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1442–1468.DOI:10.1109/TPAMI.2013.230 |
| [2] | 侯志强, 韩崇昭. 视觉跟踪技术综述[J].自动化学报, 2006, 32(4): 603–617. HOU Z Q, HAN C Z. A survey of visual tracking[J].Acta Automatica Sinica, 2006, 32(4): 603–617.(in Chinese) |
| [3] | LI X, HU W M, SHEN C H, et al. A survey of appearance models in visual object tracking[J].ACM Transactions on Intelligent Systems and Technology, 2013, 4(4): Article 58. |
| [4] | ROSS D A, LIM J, LIN R S. Incremental learning for robust visual tracking[J].International Journal of Computer Vision, 2008, 77(1-3): 125–141.DOI:10.1007/s11263-007-0075-7 |
| [5] | ZHANG T Z, GHANEM B, LIU S, et al.Robust visual tracking via multi-task sparse learning[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:2042-2049. |
| [6] | JIA X, LU H, YANG M H.Visual tracking via adaptive structural local sparse appearance model[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:1822-1829. |
| [7] | ZHANG K H, ZHANG L, YANG M H.Real-time compressive tracking[C]//Proceedings of European Conference on Computer Vision.Heidelberg:Springer Verlag, 2012, 7574:864-877. |
| [8] | KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-learning-detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409–1422.DOI:10.1109/TPAMI.2011.239 |
| [9] | BABENKO B, YANG M H, BELONGIE S. Robust object tracking with online multiple instance learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619–1632.DOI:10.1109/TPAMI.2010.226 |
| [10] | SCHMIDHUBER J. Deep learning in neural networks:An overview[J].Neural Network, 2014, 61: 85–117. |
| [11] | WANG N Y, YEUNG D.Learning a deep compact image representation for visual tracking[C]//Proceedings of Advances in Neural Information Processing Systems.Lake Tahoe:NIPS Press, 2013:809-817. |
| [12] | XU T Y, WU X J.Visual object tracking via deep neural network[C]//2015 IEEE 1st International Smart Cities Conference.Piscataway, NJ:IEEE Press, 2015:1-6. |
| [13] | ZHANG K H, LIU Q S, WU Y, et al. Robust visual tracking via convolutional networks[J].IEEE Transactions on Image Processing, 2015, 25(4): 1779–1792. |
| [14] | GLOROT X, BENGIO Y.Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of International Conference on Artificial Intelligence and Statistics.Brookline, MA:Microtome Publishing, 2010, 9:249-256. |
| [15] | WANG F S.Particle filters for visual tracking[C]//Proceedings of International Conference on Advanced Research on Computer Science and Information Engineering. Heidelberg:Springer Verlag, 2011, 152:107-112. |
| [16] | GLOROT X, BORDES A, BENGIO Y.Deep sparse rectifier neural networks[C]//Proceedings of International Conference on Artificial Intelligence and Statistics.Brookline, MA:Microtome Publishing, 2011, 15:315-323. |
| [17] | HINTON G E, SALAKHUTDINOV R. Reducing the dimensionality of data with neural networks[J].Science, 2006, 313(5786): 504–507.DOI:10.1126/science.1127647 |
| [18] | ZHANG Y, ZHANG E H, CHEN W J. Deep neural network for halftone image classification based on sparse auto-encoder[J].Engineering Applications of Artificial Intelligence, 2016, 50(1): 245–255. |
| [19] | EIGEN D, PUHRSCH C, FERGUS R.Depth map prediction from a single image using multi-scale deep network[C]//Proceedings of Advances in Neural Information Processing Systems.Montreal:Springer, 2014:2366-2374. |
| [20] | GAO C, CHEN F, YU J G, et al. Robust visual tracking using exemplar-based detectors[J].IEEE Transactions on Circuits & Systems for Video Technology, 2017, 27(2): 300–312. |
| [21] | WU Y, LIM J, YANG M H.Online object tracking:A benchmark[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2013, 9:2411-2418. |
| [22] | SEVILLA-LARA L, LEARNED-MILLER E.Distribution fields for tracking[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:1910-1917. |
