因此,本文提出了一种融合视觉传感器和惯性传感器的组合导航方法,采用基于ORB(Oriented FAST and Rotated BRIEF)特征的光流法估计无人机速度信息,采用图标法里程计估计位置信息,并应用扩展卡尔曼滤波(Extended Kalman Filter,EKF)将惯导的角速度和加速度信息与视觉光流和里程计进行融合,利用单目/双目视觉系统和惯性传感器搭建导航平台,应用于小型无人机的室内导航。
1 基于ORB特征的光流法的速度估计 1.1 ORB特征提取与描述 ORB[11]是一种实时性较高的特征提取与描述方法,它融合了FAST[12]和BRIEF(Binary Robust Independent Elementary Features)[13]2种描述子。FAST具有很强的实时性,但其不具备尺度不变性,且不包含方向因子。BRIEF用简单的二进制形式描述特征,实时性比较高,但其无法保证旋转和尺度不变性,对噪声比较敏感。ORB基于FAST和BRIEF方法,具体实现如下。
1) 建立图像高斯金字塔,对每一层图像提取FAST特征点。
2) 为特征点添加方向因子。以特征点为中心建立一个图像块,定义图像块各像素点的矩为
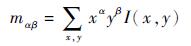 | (1) |
式中:α、β为矩的阶次;I(x, y)为图像灰度表达式。利用零阶矩和一阶矩来计算质心的坐标,即
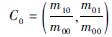
3) 引入旋转因子。利用BRIEF方法描述特征点,并在此基础上采用方向因子驱动法实现二进制字符串向量的旋转。
在BRIEF方法中,对于一个N×N大小的图像块P,有如下定义:
 |
选取n个特征点得到的n维向量如下:
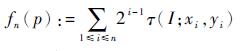 | (2) |
定义一个2×n的矩阵:S=
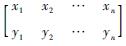
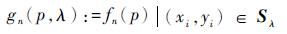 | (3) |
本文对ORB、SIFT[14]和SURF[15]的特征提取时间开销进行了试验分析,如表 1所示。
表 1 SIFT、SURF和ORB特征提取时间开销对比 Table 1 Comparison of time consumption of feature extraction among SIFT, SURF and ORB
| 方法 | 特征点数 | 时间/ms |
| SIFT[14] | 171 | 18.89 |
| 253 | 18.99 | |
| 234 | 19.66 | |
| SURF[15] | 86 | 12.44 |
| 254 | 16.21 | |
| 187 | 13.86 | |
| ORB | 168 | 2.82 |
| 299 | 4.11 | |
| 251 | 4.7 |
表选项
在对不同场景进行特征点提取时,ORB比SIFT和SURF的耗时小,相差一个数量级。这是因为:①FAST角点提取时间复杂度低。②SIFT特征为128维描述子,占据512Bytes空间;SURF特征为64维描述子,占据256Bytes空间。而用BRIEF描述每个特征点仅需一个长度为256的向量(二进制形式向量),存储空间为32Bytes,降低了后续特征匹配的时间复杂度。因此将ORB特征提取方法用于稀疏光流场特征提取,可以减小时间开销。
1.2 改进的Lucas-Kanade光流提取 基于特征点的Lucas-Kanade算法(简称LK算法)是经典的光流提取算法,该算法基于以下3种假设:目标图像亮度一致、图像空间连续和图像变化在时间上连续。I(u, v, t)表示t时刻像素点处图像灰度值,基于以上假设可以得到像素点的亮度守恒方程为
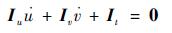 | (4) |
式中:
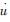

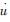

LK算法的3个假设在实际场景中很难满足,传统的解决办法包括:①保证足够大的图像帧速率;②引入图像金子塔,通过对不同尺度的图像的光流提取保证连续性。为了提高前后帧特征点追踪准确性,本文在传统方法的基础上采用前后双向追踪策略和随机采样一致滤波(Random Sampling Consensus, RANSAC)提高光流场的提取精度。
1) 前后双向追踪策略
如图 1所示,针对前后2帧图像,首先提取第1帧图像的特征点,得到特征点集A,然后通过金字塔LK算法在第2帧图像中得到对应特征点集A的特征点集B,此为前向追踪。之后,针对特征点集B,返回在第1帧追踪得到对应的特征点集,记为C,此为后向追踪。
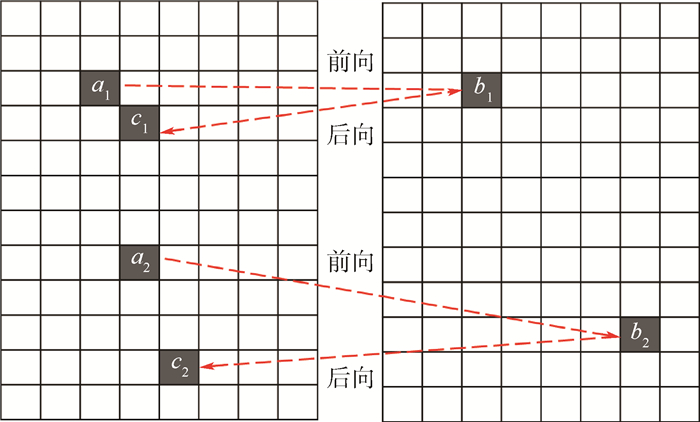 |
| 图 1 前后双向追踪示意图 Fig. 1 Schematic of forward-backward tracking |
| 图选项 |
由于噪声影响,前后追踪的特征点并非完全一致。对此,选取误差和相似度2个标准对匹配点对进行滤波。其中,误差指A、C中对应点的距离,距离越小,误差越小。相似度指对A、C中对应的每一对点,分别选取10×10大小的邻域,对2个邻域进行模板匹配,选择归一化相关系数匹配法,将匹配的结果作为相似度。匹配值越大,表示越相似。最后选取相似度大且误差小的点对。
2) 随机采样一致滤波
本文借助随机采样一致的思想,在前后双向追踪得到的特征点对中随机选取8对点对,算出基础矩阵,然后利用该基础矩阵对应的极性约束,对剩余的匹配进行测试。RANSAC算法认为,支持集合越大,得到的矩阵正确的可能性越大。最终选取较大的支持集合的特征点对应的光流值来估计速度。
RANSAC[16]算法的实现如下:
步骤1??初始:假设D是N个特征对应的集合。
步骤2??开启循环:
1) 随机选取集合D中的S个采样点;
2) 为该S个采样点拟合一个模型;
3) 计算D集合中的其他点与该模型的距离;
4) 所有距离小于阈值的点构成一个内联集;
5) 存储内联集;
6) 返回1)继续,直到迭代到最大迭代次数。
步骤3??选择拥有最大内联集合的采样点S*,并用所有的内联集估计该模型。
图 2显示了RANSAC算法前后的匹配效果。经过RANSAC算法,错误的匹配被有效滤除。
 |
| 图 2 采用RANSAC算法对特征点对滤波 Fig. 2 Filtering features by RANSAC algorithm |
| 图选项 |
1.3 融合惯导角速度的速度解算 当相机没有水平移动而仅存在姿态变化时,依然会产生光流场,因此在实际由光流场解算速度时,需要考虑姿态变化的影响。
以下视安装的单目相机为例,如图 3所示。t-1到t时刻,相机从A1点(坐标为Pwt-1)运动到A2点(坐标为Pwt)。假设相机安装在飞机重心,像平面与机体xy平面平行,则相机到机体的旋转矩阵Cck可以求出,相机之间的移动可用单应矩阵H表示。令t时刻在图像中提取到n个特征点pkt,k = 1,2,…,n,特征点在相机坐标系下的投影为Pc, kt,对应于地面的点为Pw, kt。已知相机内参矩阵为M,相机焦距为f,f和M可由标定相机得到,特征点在相机坐标系Oc轴上尺度为Zc。
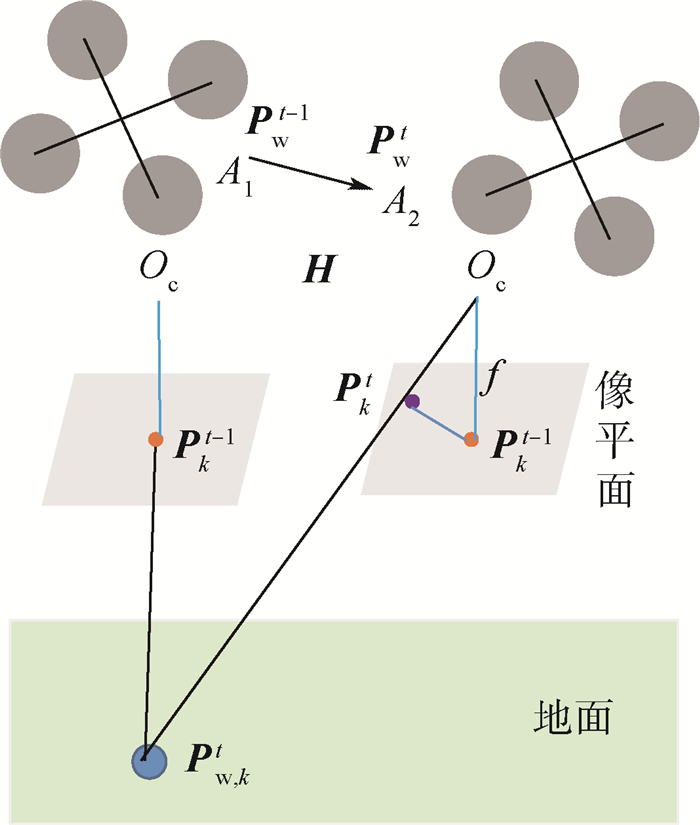 |
| 图 3 相机运动时空间点成像变化 Fig. 3 Point-mapping changing caused by moving camera |
| 图选项 |
鉴于图像更新频率很快(大于80 Hz),认为连续两帧之间相机与地面的距离h未有明显的变化。则在t时刻有
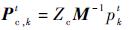 | (5) |
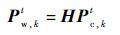 | (6) |
t-1到t时刻n个特征点的稀疏光流为
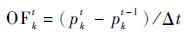 | (7) |
单位时间相机在空间的移动(vbx, vby)远远大于投影到像平面的像素的移动(Δu, Δv),相机距地面的高度h远远大于镜头的焦距f。则光流与无人机线运动、角运动的关系可以描述为
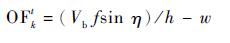 | (8) |
则有
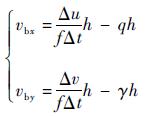 | (9) |
式中:Vb为无人机线速度;η为无人机x轴与无人机-目标之间连线的夹角;w为无人机角速率;vbx、vby分别为x、y方向的线速度;γ、q分别为滚转和俯仰角速率,可通过精度较高的IMU测量得到。高度数据h可用超声传感器测量,对于前视双目相机的光流解算则需要获取每一对特征的深度d,用d代替h。如式(10)所示,(u1, v1)和(u2, v2)分别为左相机和右相机中的一对匹配点的图像层的坐标,以像素为单位。MiL和MiR分别为左右相机的内参数,通过相机标定获得。(X, Y, Z)为该对匹配点对应的外部空间(即世界坐标系)点的实际坐标。在此,令世界坐标系与左相机的相机坐标系重合(见式(11)),求解出图像点对应的场景中的点的坐标(X, Y, Z),即场景特征到相机的相对位置。工程应用中采用最小二乘法求解,以降低因数据噪声带来的解算误差。最后,采用卡尔曼滤波处理速度信息。
 | (10) |
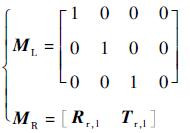 | (11) |
手持相机做平稳往复运动,图 4显示了本文方法与Guidance和PX4Flow[17]等的测速性能对比。大的姿态角变化会引起较大的速度测量误差,使速度曲线产生大的“尖峰”,从图中可以看出(箭头指示),因为引入了惯导角速率,本文方法能较好地降低姿态角变化带来的干扰。
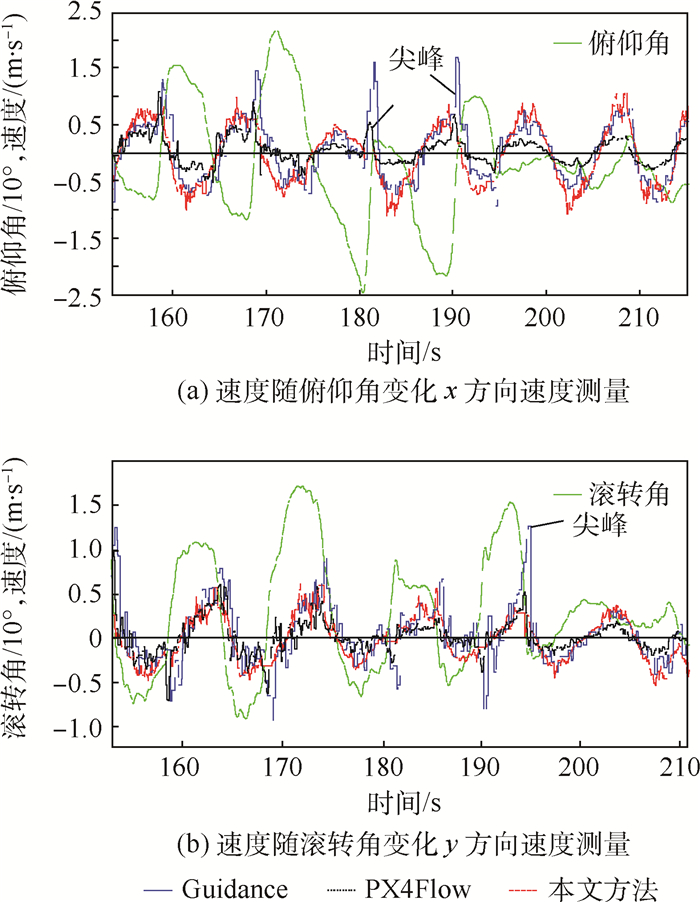 |
| 图 4 姿态变化时测速对比 Fig. 4 Velocity comparison with changing attitude |
| 图选项 |
2 图标法里程计 针对室内地板格环境,本文采用图标法里程计,以地板格直线的交点为图标,通过追踪图标进行定位。算法基本流程如图 5所示。
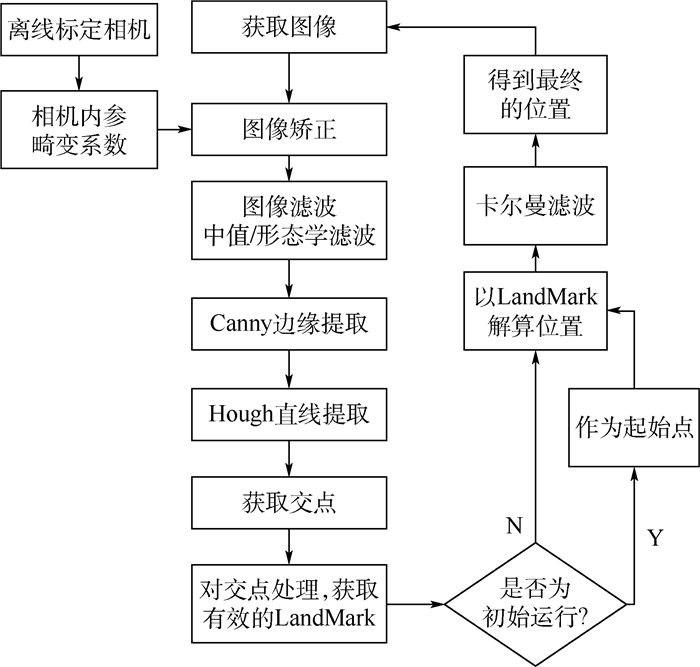 |
| 图 5 图标法里程计算法基本流程 Fig. 5 Algorithm flowchart of icon odometry |
| 图选项 |
首先对摄像头获取的地板灰度图像进行滤波,利用Canny算子进行边缘提取(见图 6)。然后对获取的边缘图像利用Hough变换提取线段。根据以下原则对线段滤波:①合并“同线”的线段;②保留“水平”和“垂直”的线段;③滤除“较短”的线段。最后,求取线段所在直线的交点。
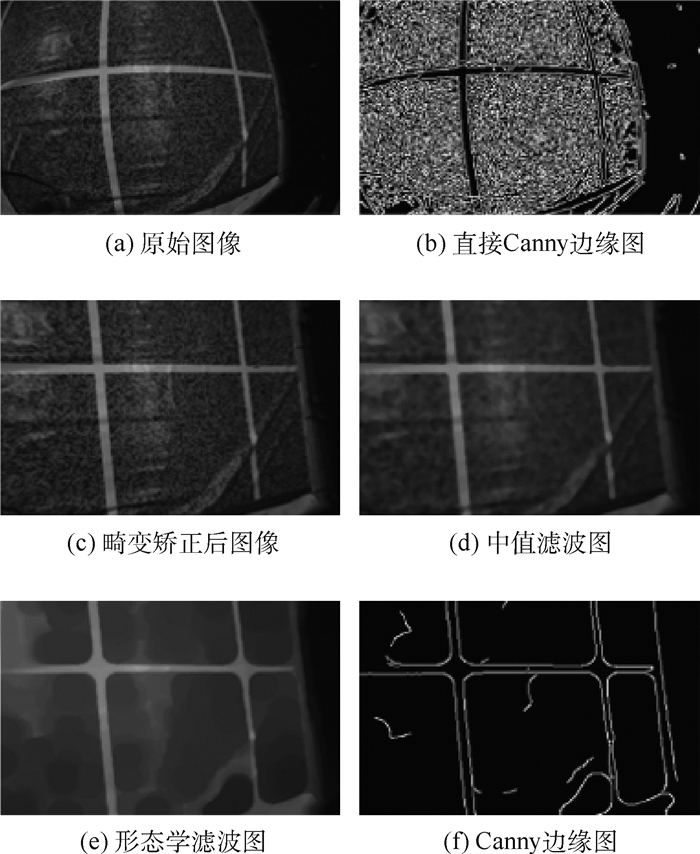 |
| 图 6 图像滤波与边缘提取 Fig. 6 Image filtering and edge extraction |
| 图选项 |
地板直线的交点表现在图像中是一个图像块,取图像块的几何中心的像素值(u*, v*)用于二维图像平面到三维空间的映射[18]。
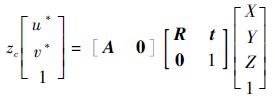 | (12) |
式中:A为相机的内参矩阵; R和t分别为相机坐标系与导航坐标系的旋转矩阵和平移向量。鉴于飞行器飞行高度远远大于相机的焦距H?f,因此可以令Z≈H,这样Z可以通过超声传感器获得。
相机与飞机固连且垂直向下安装。如图 7所示,假设飞机在1个直线交点的附近起飞,其相机定位到的第1个交点作为原点。则定义交点0为原点,即导航坐标系的(0, 0, 0),飞机此时的位置为(0, 0, H)。假设飞机沿着红色箭头的方向直线飞行到交点3的上空。在这个过程中,椭圆曲线范围内的点在不断变化,利用椭圆内点的定位平均值作为当前飞机的位置估计。之所以定义一个椭圆的范围,主要是因为考虑图像边缘畸变大,定位误差大,该椭圆的中心与图像的中心重合。而利用椭圆包围的点进行定位,误差小,只有当椭圆内搜索不到点时,才考虑椭圆外的点。已知地板格为边长为1m的正方形,因此在飞机从0点到3点运动过程中,y方向的值从0变为1。
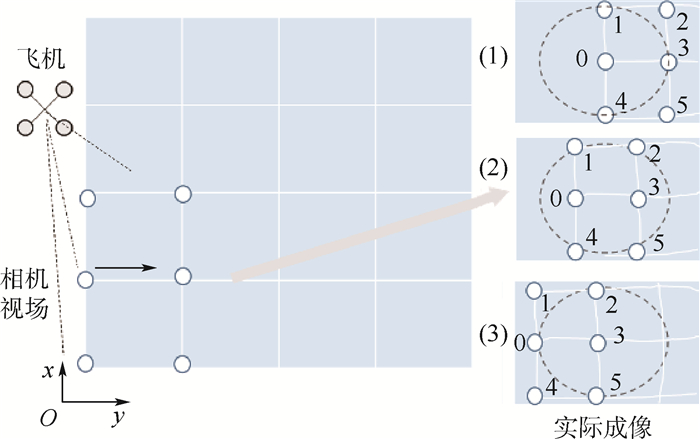 |
| 图 7 图标法里程计定位 Fig. 7 Positioning based on icon odometry |
| 图选项 |
利用图标法里程计,只要保证视野里始终有交点,便可以实现对飞机的有效定位。
3 基于EKF的数据融合 第1节和第2节所述的光流法和图标法里程计都依赖于视觉传感器和外界特征(特征点和交点)。但在实际飞行中,由于种种原因,会出现视觉传感器失效的状况。为此,考虑视觉和惯导融合进行速度和位置的估计。
3.1 全状态下的视觉/惯导融合 假设图标法里程计和图像光流场比较稳定,将里程计、光流和惯导做数据融合,本文将这种情况定为全状态。
假设在极小的Δt时间内系统为非线性的匀变速过程。定义系统的状态量为导航坐标系下的飞机的三维全局位置,三维速度和三维加速度和飞机的俯仰角、滚转角、偏航角:
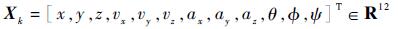 |
系统的观测量为视觉里程计测量的x, y, z方向的位置,光流法获得的速度,以及MTI的三轴线性加速度信息和姿态角:
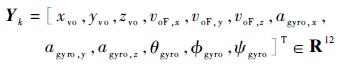 |
定义过程模型为
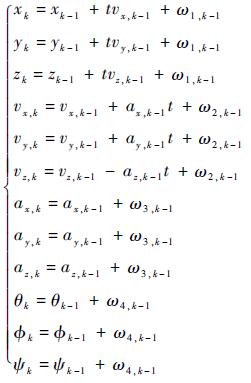 | (13) |
系统的观测模型为
 | (14) |
式中:ω为观测噪声; δ为量测噪声; Cnb为导航-机体坐标系转换矩阵; g为重力加速度;e为单位向量。观测方程为非线性模型,根据EKF公式将fk在最优估计点处展开,将观测方程线性化。
3.2 非全状态下的视觉/惯导融合 1) 图标法里程计失效的情况
当地面没有可用的边线用于图标法里程计时,里程计的定位将失效。具体表现为视野内没有可用的交点。此时,置VO_KEY为False,仅利用光流和惯导组合,估计定位信息。此时观测量为
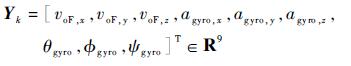 |
状态方程参考式(11),观测模型为
 | (15) |
2) 视觉传感器失效的情况
如果视觉传感器失效,则利用惯导积分做短时的导航,直到光流速度或者里程计的测量恢复。这里判断光流速度失效的原则为连续图像光流点数量小于4个,或连续出现野值。
3.3 视觉、惯导的多速率问题 惯性传感器数据更新速率快,视觉传感器的数据更新速率慢,因此其中涉及了多速率融合的问题。对此的解决方法为:保证状态和噪声的定义与之前的定义相同,修改传感器的观测。系统的基本采样周期为T0,惯导和视觉传感器的采样周期分别为T1和T2。这里保证T1和T2为T0的整数倍,即T1=n1T0, T2=n2T0。令κT0为各个观测数据的采样周期的最小公倍数,则定义观测矩阵和观测噪声协方差如下:
 | (16) |
 | (17) |
式中:mod(·)为求余函数。
已知试验所用的视觉传感器的数据更新速率约为50Hz,惯导的更新速率为100Hz,令T0=10ms, 则T1=20ms, T2=10ms,n1=2, n2=1。在ROS操作系统中,多线程采集到的数据可以通过时间戳进行数据对准,并可以根据时间戳来判断是否采样得新数据,这样根据式(16)和式(17)便可以方便地编程实现多速率数据的融合。
图 8显示了“地板格”从有(视觉里程计可用、下视光流可用)到无(纯白色地面、视觉里程计失效、下视相机失效)时的位置估计,包括三维轨迹及高度、速度和位置随时间的变化。手持相机运动到约2m的位置时,开始移动出地板(朝着位置增加的方向)。在3次往返后,终点和起点近似重合,依然可以实现有效定位。
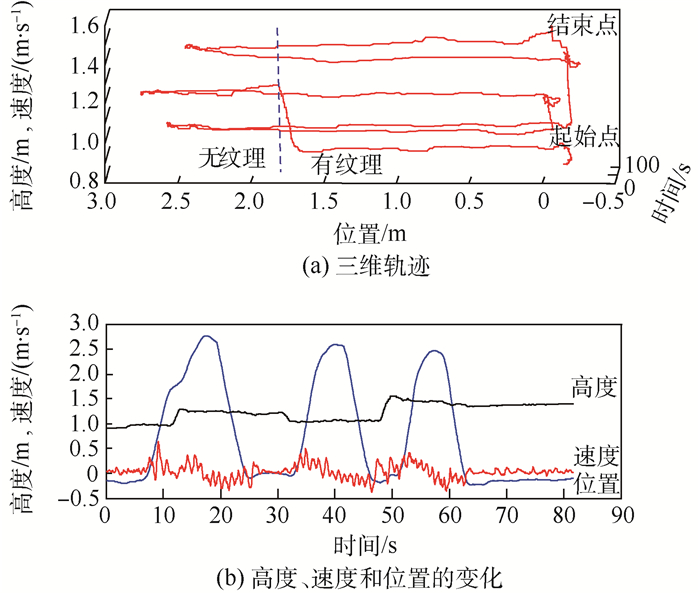 |
| 图 8 定位测试 Fig. 8 Localization test |
| 图选项 |
4 试验与分析 鉴于运动捕捉系统OptiTrack的数据延迟小(低于5ms),定位误差小(约0.1mm),可以OptiTrack的定位数据作为基准,衡量本文方法的精度和延迟。本文采用美国OptiTrack Prime 41相机搭建运动捕捉系统进行试验。
图 9~图 11分别为将本文方法与运动捕捉系统获得的位置和速度信息进行对比结果,可得本文方法延迟约50ms,位置误差约0.15m,速度误差约0.05m/s,基本满足室内环境下小型无人机的飞行需求。
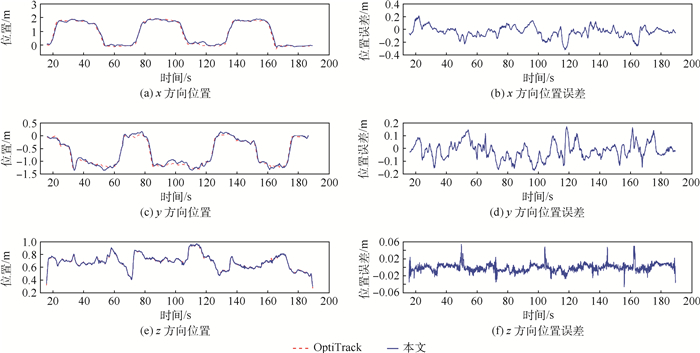 |
| 图 9 三维位置估计与位置误差 Fig. 9 Localization estimation and positioning error in 3D-directions |
| 图选项 |
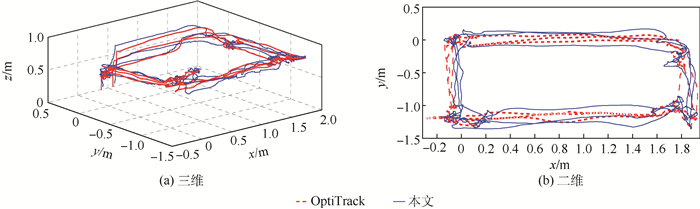 |
| 图 10 三维/二维运动轨迹 Fig. 10 Three/two-dimensional motion trajectory |
| 图选项 |
 |
| 图 11 三维速度估计与速度误差 Fig. 11 Velocity estimation and velocity error in 3D-directions |
| 图选项 |
本文搭建四轴八桨多旋翼无人机平台(见图 12),以手控的方式操纵飞机飞行(见图 13),实时记录导航数据,并将本文方法的测速数据与Guidance和PX4Flow导航模块的测速数据进行了对比。
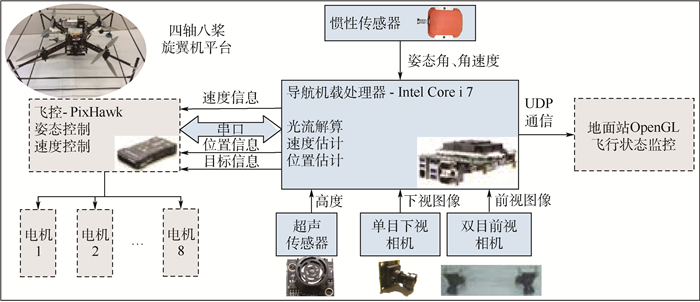 |
| 图 12 无人机平台及系统结构 Fig. 12 UAV platform and system structure |
| 图选项 |
 |
| 图 13 飞行视频截图 Fig. 13 Screenshots of flight video |
| 图选项 |
图 14显示了不同速度下本文方法与Guidance导航模块测速情况对比。无人机的飞行速度基本在0~2.5m/s的范围。在此速度范围内本文方法可以有效实现对无人机的导航。当速度大于2m/s时,有效特征点数下降,提到的光流场数量降低,当速度大于2.5m/s时,有效光流场数量频繁出现小于8的状态,单纯的视觉信息将不再可靠。
 |
| 图 14 手控飞行速度测试 Fig. 14 Flight velocity test via manual control |
| 图选项 |
图 15和图 16显示了某次飞行测试的导航数据。其中导航速度信息与PX4Flow的测速信息进行了对比。从图中的数据可以看出,本文方法在实际的无人机平台上比较稳定,可以尝试用于自动(闭环)飞行。
 |
| 图 15 位置估计 Fig. 15 Position estimation |
| 图选项 |
 |
| 图 16 速度估计与飞机姿态 Fig. 16 Velocity estimation and aircraft attitude |
| 图选项 |
5 结论 本文提出了一种视觉和惯导融合用于估计小型无人机速度和位置的方法,可得到以下结论:
1) 基于ORB特征点的前后向追踪的光流提取算法,提高了光流场的提取精度,降低了算法的时间开销。
2) 基于图标法里程计的快速定位算法,可以有效应对带地板格的室内环境定位。该算法简单,实时性好。
3) 利用EKF将图标法里程计、光流速度和惯导信息进行融合,降低了方法对环境的依赖。
4) 以延迟小于5ms,精度小于0.01mm的运动捕捉系统为参考基准,与本文提出的运动估计方法进行对比验证,得到本文方法延迟约50ms,定位误差约0.15m,速度误差约0.05m/s。同时搭建了多旋翼平台进行飞行验证。
参考文献
| [1] | SHEN S J.Autonomous navigation in complex indoor and outdoor environments with micro aerial vehicles[D].Philadelphia:University of Pennsylvania, 2014. |
| [2] | 吴琦, 蔡志浩, 王英勋. 用于无人机室内导航的光流与地标融合方法[J].控制理论与应用, 2015, 32(11): 1511–1517. WU Q, CAI Z H, WANG Y X. Optical flow and landmark fusion method for UAV indoor navization[J].Control Theory & Applications, 2015, 32(11): 1511–1517.(in Chinese) |
| [3] | LI P, LAMBERT A.A monocular odometer for a quadrotor using a homogra-phy model and inertial cues[C]//IEEE Conference on Robotics and Biomimetics.Piscataway, NJ:IEEE Press, 2015:570-575. |
| [4] | 叶长春. IARC第7代任务中定位与目标跟踪方法研究[D]. 杭州: 浙江大学, 2016. YE C C.Research on localization and object tracking for the IARC mission7[D].Hangzhou:Zhejiang University, 2016(in Chinese). |
| [5] | MUR-ARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM:A versatile and accurate monocular SLAM system[J].IEEE Transactions on Robotics, 2015, 31(5): 1147–1163.DOI:10.1109/TRO.2015.2463671 |
| [6] | LEUTENEGGER S, FURGALE P, RABAUD V, et al.Keyframe-based visual-inertial SLAM using nonlinear optimization[C]//Robotics:Science and Systems, 2013:789-795. |
| [7] | CHAO H, GU Y, GROSS J, et al.A comparative study of optical flow and traditional sensors in UAV navigation[C]//American Control Conference(ACC).Piscataway, NJ:IEEE Press, 2013:3858-3863. |
| [8] | MAMMARELLA M, CAMPA G, FRAVOLINI M L, et al. Comparing optical flow algorithms using 6-dof motion of real-world rigid objects[J].IEEE Transactions on, Systems, Man, and Cybernetics, Part C:Applications and Reviews, 2012, 42(6): 1752–1762.DOI:10.1109/TSMCC.2012.2218806 |
| [9] | DJI Innovations.PHANTOM 4 user's manual V1.2[EB/OL].(2016-12-23)https://dl.djicdn.com/downloads/phantom_4/cn/Phantom_4_User_Manual_cn_v1.2_160328.pdf. |
| [10] | Hover Camera 2016[EB/OL].(2016-12-23)http://gethover.com. |
| [11] | RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB:An efficient alternative to SIFT or SURF[J].Proceedings, 2011, 58(11): 2564–2571. |
| [12] | ROSTEN E, DRUMMOND T.Machine learning for high-speed corner detection[C]//European Conference on Computer Vision.Berlin:Springer-Verlag, 2006:430-443. |
| [13] | CALONDER M, LEPETIT V, STRECHA C, et al.BRIEF:Binary robust independent elementary features[C]//European Conference on Computer Vision.Berlin:Springer-Verlag, 2010:778-792. |
| [14] | LOWE D G. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision, 2004, 60(2): 91–110.DOI:10.1023/B:VISI.0000029664.99615.94 |
| [15] | BAY H, TUYTELAARS T, GOOL L V. SURF:Speeded up robust features[J].Computer Vision & Image Understanding, 2006, 110(3): 404–417. |
| [16] | CHUM O, MATAS J, KITTLER J. Locally optimized RANSAC[J].Lecture Notes in Computer Science, 2003, 2781: 236–243.DOI:10.1007/b12010 |
| [17] | HONEGGER D, MEIER L, TANSKANEN P, et al.An open source and open hardware embedded metric optical flow cmos camera for indoor and outdoor applications[C]//International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2013:1736-1741. |
| [18] | HARTLEY R I, ZISSERMAN A. Multi-view geometry in computer vision[M].Cambrige: Cambridge University Press, 2004: 239-247. |
