近年来,国内外研究人员逐渐认识到通过增大方位角[7-8],并利用先进的信号处理技术能够显著提升SAR图像质量,因此,多方位角观测代表未来星载SAR技术发展的趋势之一。单方位角观测一次过境仅能获取单幅图像,得到目标信息相对有限,不利于目标的精细判读解译;多方位角观测可获取多幅序贯图像,利用序贯图像信息的冗余性和互补性,不仅能降低图像斑点噪声,还可显著增强目标特征,减少判图工作中目标的误判或遗漏。
1979年,Daily等[9]首先将雷达图像与Landsat-MSS卫星图像的复合图像用于地质解释,开创了遥感图像融合的先河。自此之后,图像融合技术快速发展,被广泛应用于可见光、红外、多光谱、SAR图像处理中。图像融合技术充分利用待融合图像中所包含的冗余信息和互补信息,对处理序贯图像非常有效。针对多方位角SAR图像融合,文献[10-11]提出基于小波分解和贝叶斯分类的决策级融合方法,通过主成分分析提取特征向量并分类,以实现类别决策。文献[12]首先提取目标特征,然后假设目标模型,通过评估假设模型与目标特征的匹配程度衡量融合效果。上述决策级融合需要一定的先验知识,相比更加精细的像素级融合方法,对场景原始信息保留较少。文献[13]介绍了均值融合和加权融合方法,这2种融合方法的优点是简单易行,但融合效果有限,得到的图像较为模糊,难以体现多方位角观测融合图像的优势。文献[14]综合利用小波变换和方向模板加强方向信息,但使用的方向模板不能覆盖所有边缘种类,难以解决多方位角观测目标散射特性的差异性问题。
针对目标散射特性随方位角变化对图像融合效果的影响,本文提出了一种基于小波变换和边缘检测的图像融合方法。小波变换具有良好的时频特性[15],可以有效分离图像的低频近似部分和高频细节部分,通过对低频和高频部分分别进行融合处理,建立新的多分辨表征,整合多方位角序贯图像中目标的多方位信息;同时利用边缘检测针对性地加强高频能量,增强目标与背景的对比度,并采用一定的融合方法提取和完善目标轮廓[16-17]。文献[18]介绍了常用的6种边缘检测算子及优缺点,其中Prewitt算子及Robinson算子均考虑了8个方向的边缘种类,且能够有效地抑制噪声,边缘定位精度较高,而Robinson算子计算效率更高,因而本文提出的融合方法中采用Robinson算子进行边缘检测。之后为了兼顾融合效果和抑制噪声,使用改进的Robinson算子进行边缘增强。
本文首先分析多方位角观测图像的特性,并对多方位角图像进行预处理。在此基础上,提出了基于小波变换和边缘检测的多方位角SAR图像融合方法,利用小波变换完成低频信息和高频信息的分离,实现图像的多分辨表征及序贯图像多方位角信息的融合,并利用改进的Robinson算子增强图像的轮廓特征。最后利用TerraSAR-X真实图像展开实验,定量化的评估结果验证了本文方法可有效地完成图像的融合,有利于图像判读解译。
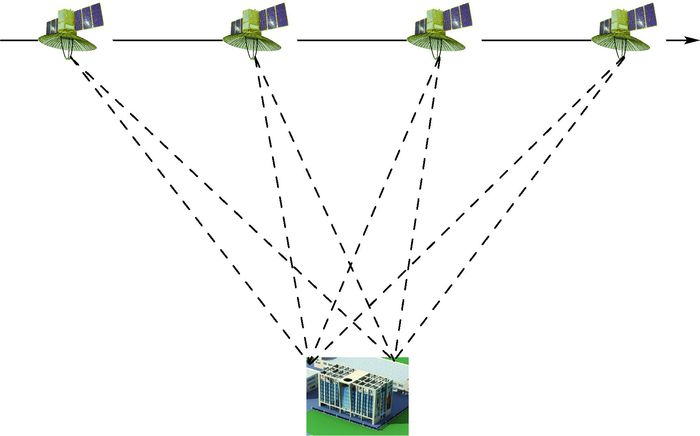
1 多方位角序贯图像特性分析及预处理 星载SAR系统的发射信号具有一定的带宽,且合成孔径时间内载荷具有一定的位移,在观测时间内,目标的散射特性随信号频率与空间角度变化。图 1为多方位角观测系统示意图。
 |
| 图 1 多方位角观测示意图 Fig. 1 Schematic of multi-aspect observation |
| 图选项 |
通过调整雷达的波束指向,可以获得目标在不同方位角的散射特性,即对目标进行多方位角观测得到序贯图像。与传统单方位角一次过境观测图像相比,多方位角观测SAR系统的主要优势在于:在观测各向同性目标时,可以获得比条带模式更大的多普勒带宽,从而具有更好的分辨率和信噪比;当目标在方位向存在多个散射中心时,多方位角观测可以获取目标非各向同性散射信息,反映目标的散射特征变化。
本文方法的核心是融合序贯图像中随方位角变化的信息。因此,为提高处理效率,需首先确认图像中随方位角散射特性变化显著的区域。多方位角星载SAR系统中,在不同观测条件下获取的关于同一目标的SAR图像可认为是相互独立的,则SAR图像间的几何距离定义为[19]
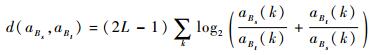 | (1) |
式中:Bs和Bt分别为2幅不同方位角观测得到的图像;L为等效视数;aBs(k)和aBt(k)为k处的像素值。
多方位角图像由于量化、作用距离等原因导致灰度分布特性存在差异,使图像融合失去意义。因此,在确认散射特性变化区域之前,先对配准后的多方位角序贯图像进行标准差和均值均衡,使均衡后的图像灰度值具有一致的标准值和方差,保证图像的亮度在同一等级。
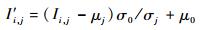 | (2) |
调整后所有N幅图像的均值和标准差分别为
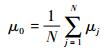 | (3) |
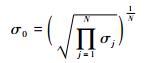 | (4) |
式中:Ii, j和I′i, j分别为第j幅图像第i个像素调整前和调整后的灰度值;μj和σj分别为第j幅图像的像素均值和标准差。
为验证处理效果,以TerraSAR图像数据为例,图 2给出了校正和配准后的一景图像及经过差异提取得到的差异程度,图 2(b)中图例表示差异程度值的大小。
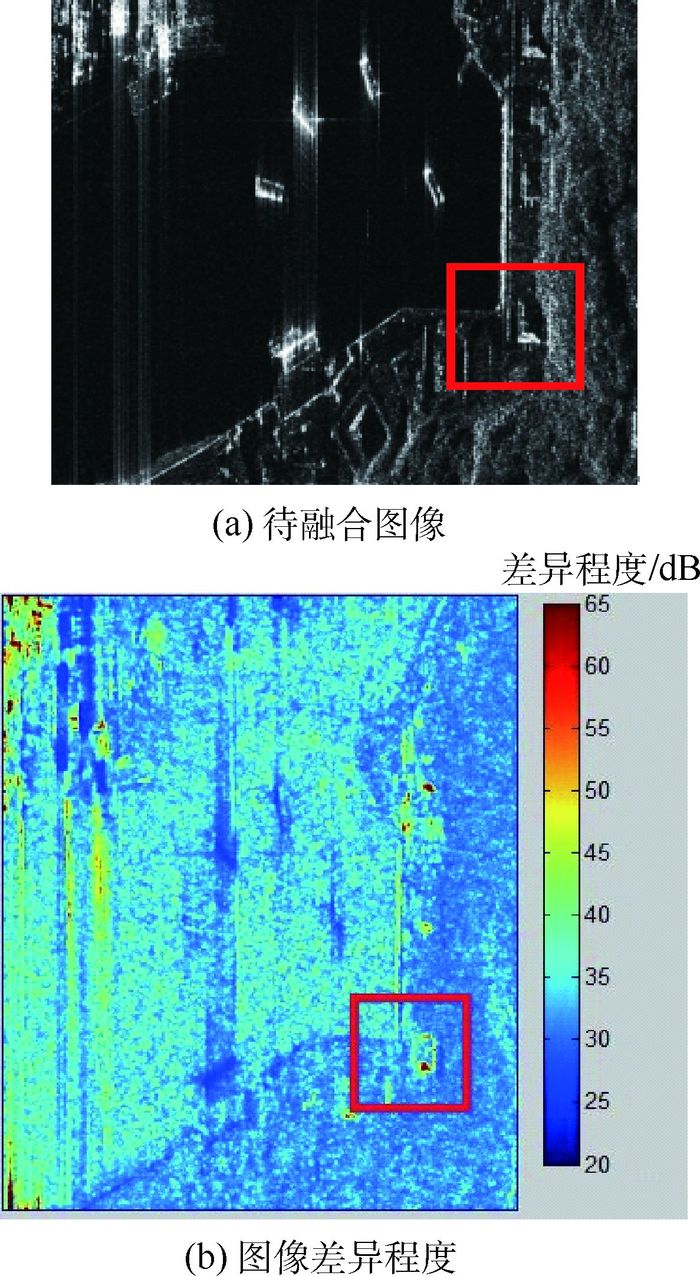 |
| 图 2 待融合图像及图像差异程度 Fig. 2 Image to be fused and degree of image discrepancy |
| 图选项 |
从图 2(b)可知,红框选中区域为目标散射特性变化显著的区域。图 3展示了6幅序贯图像中该区域对应的图像。可以看出,目标在多方位角序贯图像中的非各向同性特征表现较为明显。例如,第3景图像目标下部散射单元呈现较强的散射特性,而第5景的同一目标左侧散射单元呈现较强的散射特性,完成这种差异性的融合可显著提高目标的轮廓特征。
 |
| 图 3 提取出的差异区域 Fig. 3 Extracted zone of difference |
| 图选项 |
为验证图像均衡的效果,图 4给出了图像均衡后角度3和角度5图像的直方图,横坐标表示图像像素点的灰度值,范围为0~255,纵坐标表示每个灰度值对应像素点个数。从结果可看出,均衡后的图像直方图分布基本相同,保证了后续图像融合的效果。
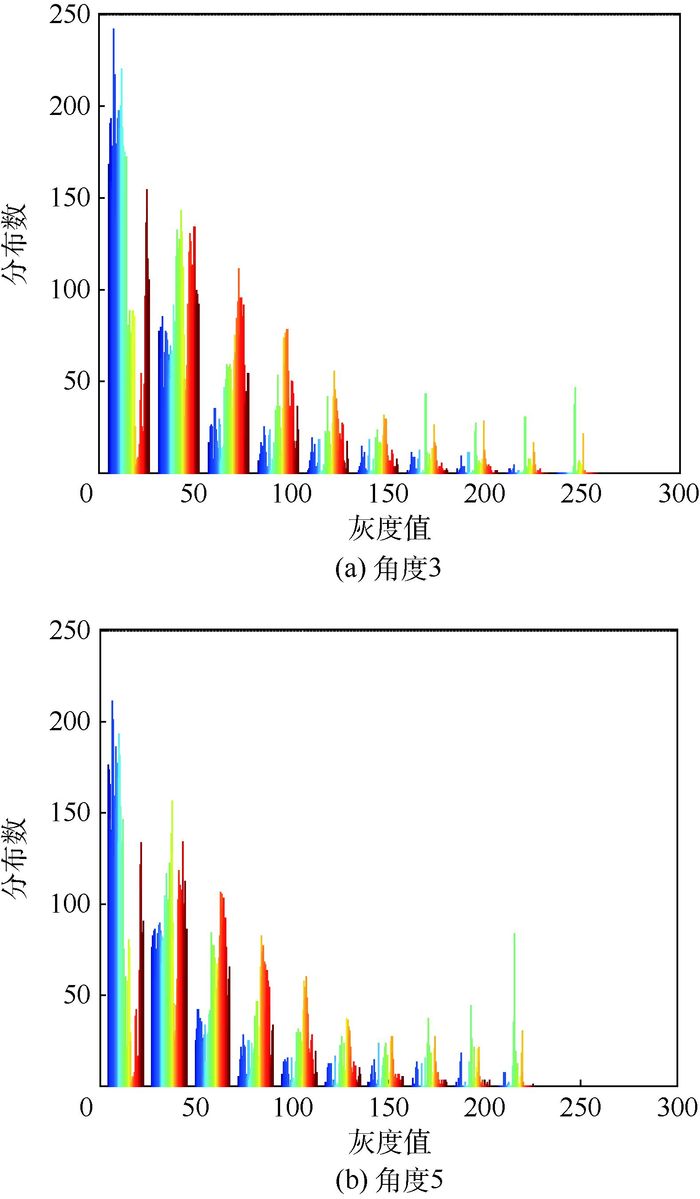 |
| 图 4 灰度分布直方图 Fig. 4 Gray level distribution histogram |
| 图选项 |
2 多方位角SAR图像融合 目标的边缘及散射特征是目标识别的重要依据,小波变换的高低频分离、多尺度变换特点既能保留图像的低频近似部分,又能对图像高频部分进行边缘增强处理。因此,本文所提方法的基本思想是:对多方位角图像进行小波变换,按照特定的融合规则,建立新的多分辨表征,即融合后图像的小波域表示。同时,依据边缘融合规则判断出的边缘种类增强边缘信息,对复合的多分辨表征反变换,即可得到融合图像。图 5给出了本文方法的流程示意图。
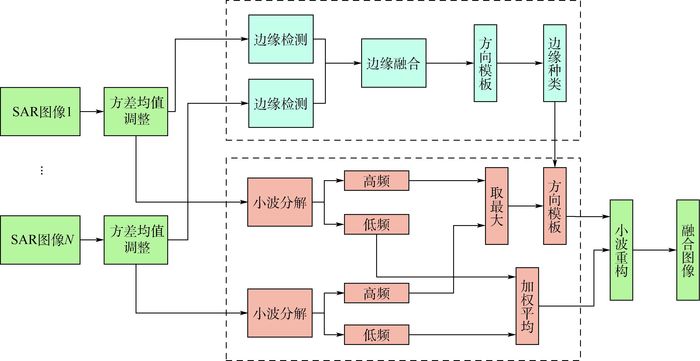 |
| 图 5 融合流程示意图 Fig. 5 Flowchart of fusion method |
| 图选项 |
2.1 图像的小波变换 小波变换基(小波函数)主要有Haar小波[20]、Daubechies小波系[21]、Biorthogonal(biorNr.Nd)小波系[22]、SymletsA(symN)小波系[23]等,其中Daubechies小波系应用较多。Daubechies小波系是由著名的小波分析****Daubechies构造的小波函数,记作dbN,N为小波阶数。Daubechies小波系支撑区为2N-1,小波函数Ψ(t)的消失矩阶数为N,其特点是消失矩阶数随着阶数N的增大而增大,此外dbN小波具有较好的正则性,使得信号重构过程比较光滑[21]。使用Daubechies小波系对同等分辨率SAR图像进行紧支集正交小波变换,具体公式为
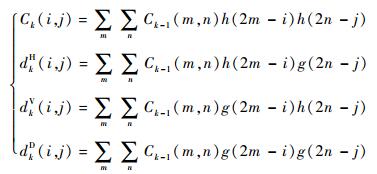 | (5) |
式中:Ck、dkH、dkV和dkD分别对应源图像在该分辨率下的低频近似分量、水平高频分量、垂直高频分量和对角高频分量,3个高频分量体现了源图像的边缘或区域边界,为后续进行边界锐化提供有利条件;k为分解级数;h和g分别为尺度方程和小波方程的系数序列,分别为低通滤波器和高通滤波器。
基于上述小波变换对信号分解的分析可知,小波变换的高频部分对应图像中变化剧烈的边缘等特征,人眼对于这些特征较为敏感,而低频部分反映图像整体灰度值分布概况。融合规则需要遵循既保留目标尽可能多的方向边缘信息和细节信息,又保留图像整体轮廓的原则,基于上述融合处理原则,制定在小波域的融合规则如下[13-14]:
1) 针对水平、垂直、对角3个方向高频部分,为了保留目标尽可能多的方向边缘信息,取对应方向的6个高频部分最大绝对值作为融合后图像的相应方向高频部分值,即
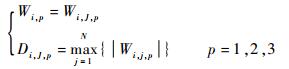 | (6) |
式中:j为源图像序号;p为方向序号;Wi, p为p方向矩阵中第i个值;J为高频矩阵最大值对应的图像序号。
2) 针对低频部分,既要保留整体特征,又要体现融合处理的原则,按照均值加权处理,即
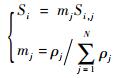 | (7) |
式中:Si为低频矩阵第i个像素值;ρj为低频矩阵均值;mj为加权系数。
2.2 边缘检测加强方向信息 小波变换得到的3个高频矩阵具有方向性,即dkH、dkV和dkD分别对应图像的水平高频分量、垂直高频分量以及对角高频分量,这就为边缘检测和锐化处理提供了有利条件[24]。经过上述对高频和低频部分进行融合处理后得到的矩阵视为融合图像的高频和低频矩阵,为了增强图像中感兴趣的目标的高频信息,本文对融合得到的高频矩阵进行边缘增强,提升图像可读性。图 6给出了图像边缘检测的流程。本文使用Robinson算子进行边缘检测,Robinson算子使用如图 7及表 1所示的8个方向模板顺次检测图像[25],输出最大值由与被检测区域最为相似的模板决定。Robinson算子不仅可以得到图像的边缘信息,同时给出了边缘的方向,有利于后续图像边缘增强操作及噪声的平滑。
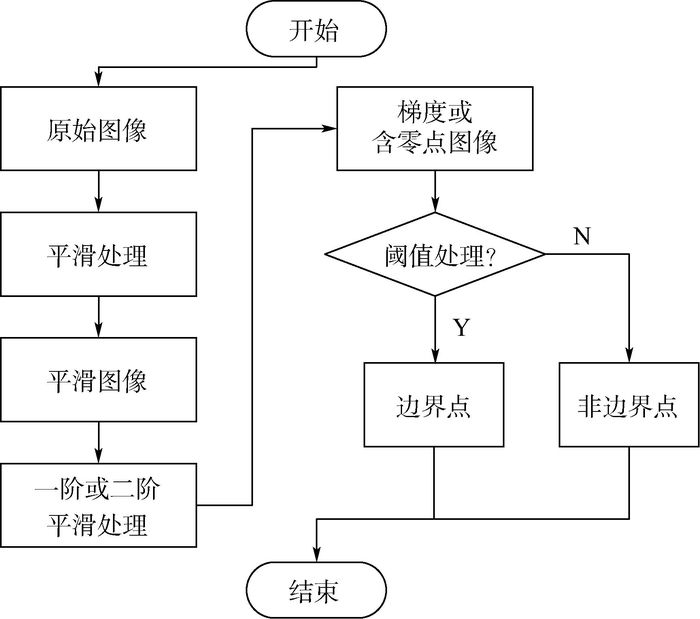 |
| 图 6 图像边缘检测流程图 Fig. 6 Flowchart of image edge detection |
| 图选项 |
 |
| 图 7 8个方向模板 Fig. 7 Direction of 8 templates |
| 图选项 |
表 1 8个方向模板对应的矩阵 Table 1 Corresponding matrixes of direction of 8 templates
| 方向模板 | 0° | 45° | 90° | 135° | 180° | 225° | 270° | 315° |
| 对应矩阵 |  | 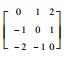 |  | 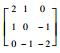 | 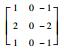 | 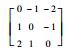 | 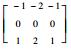 | 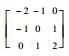 |
表选项
利用Robinson算子对图 3调整灰度值后的6幅待融合图像分别进行边缘检测。为了保留较多的边缘信息,按照某一像素处有2个或以上边界时,认定此像素为融合图像边界的原则。图 8给出了角度3和角度5的边界提取结果及6幅图像的边界融合结果。可以看出,边界融合后图像的轮廓特征显著提升,有利于图像的判读及典型目标的判定。
 |
| 图 8 边缘检测及融合结果 Fig. 8 Edge detection and fusion result |
| 图选项 |
进一步对Robinson算子判断出的边界方向对应的高频矩阵进行锐化处理。锐化处理通过增强图像的高频分量增加图像锐度和边缘信息实现,其核心是锐化倍数的设置,太小效果不明显,太大则引入的噪声也随之增大。锐化处理时,既要突出目标的边界,又不能破坏图像整体的灰度分布规律,因此表 2给出了改进的Robinson算子锐化矩阵及相应的锐化目标。实验表明,使用此锐化算子进行图像锐化,能兼顾增强高频信息和抑制低频区域的噪声。
表 2 锐化处理规则 Table 2 Sharpening processing rule
| 方向模板 | 锐化矩阵 | 锐化目标 |
| 0° |  | 垂直方向 |
| 45° |  | 对角方向 |
| 90° |  | 水平方向 |
| 135° | 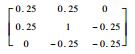 | 对角方向 |
| 180° |  | 垂直方向 |
| 225° | 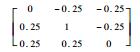 | 对角方向 |
| 270° | 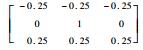 | 水平方向 |
| 315° | 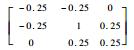 | 对角方向 |
表选项
上述融合规则使用小波变换在小波域进行融合处理,并使用改进的Robinson算子进行边缘增强,以提高目标的可辨识率。此后,将融合及增强处理后的高频部分和加权处理后的低频部分进行小波重构,经过基于最小均方误差准则的维纳线性降噪处理后即得到融合后的图像,与式(5) 对应的重构公式为
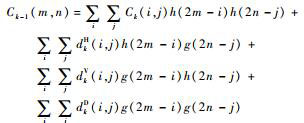 | (8) |
3 融合实验及图像评估 为了验证第2节分析的正确性,在图像预处理并制定融合规则的基础上,本节给出了融合实验结果及对比实验,并对本文方法和对比实验结果进行了定量化评估。
3.1 融合实验 基于本文所提的小波变换和边缘检测的多方位角SAR图像融合方法,表 3给出了实验的相关参数。
表 3 实验参数 Table 3 Experiment parameters
| 参数 | 数值 |
| 分辨率/(m×m) | 1×1 |
| 距离向入射角/(°) | 40.69 |
| 方位向角度范围/(°) | ±2.2 |
| 波段 | X波段 |
| 成像模式 | 聚束模式 |
| 小波函数 | Daubechies |
| 小波阶数 | 1 |
| 融合图像数 | 6 |
表选项
使用6幅多方位角观测TerraSAR图像进行融合实验,并使用文献[13]中提出的均值融合、加权均值融合及传统的小波融合方法作为对比实验以验证本文所提方法的有效性。
图 9给出了4种融合方法得到的融合结果。可以看出,均值融合和加权均值融合均使图像产生了明显的模糊,这对于目标识别十分不利;相比于传统的小波融合方法,本文方法得到的图像边界更加清晰,细节部分保留更为完整。
 |
| 图 9 融合结果 Fig. 9 Fusion results |
| 图选项 |
3.2 图像评估 融合图像的评估方法主要分为两大类:主观评估方法和客观评估方法。主观评估方法由判图人员通过目测图像进行评价,其结果与判图人员的相关知识水平、判读经验、心态等主观因素有较大关系,重复性差且带有片面性;客观评估方法使用图像统计特征、信息量特征等量化指标评估图像质量,独立性好且有较强的说服力[26]。文献[27]指出,融合图像的评估包含对融合图像的评估和融合图像对源图像的信息反映的评估;文献[13]给出了基于统计特性的评价、基于清晰度的评价、基于信息量的评价等指标的定义式。
本文采用基于信息量的评价指标[13]:信息熵、平均交叉熵及均方根交叉熵,这3种图像质量量化指标理论性强,物理意义明确,评价效果易于判断,同时使用信噪比评估融合图像的噪声。表 4给出了4种融合方法得到的融合图像的评估结果。
表 4 评估结果 Table 4 Evaluation results
| 融合方法 | 信息熵 | 平均 交叉熵 | 均方根 交叉熵 | 信噪比/ dB |
| 均值融合[13] | 6.672 3 | 0.126 5 | 0.141 9 | 9.264 2 |
| 加权均值融合[13] | 6.684 0 | 0.119 4 | 0.134 9 | 9.206 2 |
| 传统小波融合[14] | 6.604 2 | 0.391 0 | 0.428 7 | 8.544 0 |
| 本文方法 | 6.734 1 | 0.083 7 | 0.093 8 | 8.930 5 |
表选项
从表 4可以得出,本文方法得到的融合图像具有较高的信息熵,说明此图像包含的信息更为丰富;另外,本文方法得到的融合图像的平均交叉熵和均方根交叉熵均较小,说明此融合图像更接近待融合图像,即更好地保留了待融合图像的信息。本文方法的融合图像信噪比优于传统小波融合方法;均值融合和加权均值融合方法信噪比较高,但其造成的图像模糊不利于目标判别。
4 结论 1) 本文针对多方位角观测的SAR图像中目标散射信息提取问题,提出了一种基于小波变换和边缘检测的多方位角SAR图像融合处理的新方法。
2) 利用小波变换将多幅图像的细节部分进行优势互补,既保留了图像的整体轮廓信息,又融合了多方位角图像提供的目标多方位信息。在此基础上,基于目标边缘判断和多方位信息获取的需求,进行边缘提取及融合处理。
3) 融合实验表明,融合处理后的图像与融合前的源图像相比,目标边缘轮廓信息更加清晰,信息熵、平均交叉熵、均方根交叉熵等量化评估结果也证明了本文方法的有效性。
参考文献
| [1] | KIM J H, HEER C, SCHAEFER C.Astrium technology development for next generation SAR[C]//2013 IEEE International Asia-Pacific Conference on Synthetic Aperture Radar(APSAR), 2013:24-26. |
| [2] | GANTERT S, KERN A, DVRING R, et al.The future of X-band SAR:Terra-SAR-X next generation and WorldSAR constellation[C]//2013 IEEE International Asia-Pacific Conference on Synthetic Aperture Radar(APSAR), 2013:20-23. |
| [3] | PAPSON S.The exploitation of multi-look synthetic aperture radar and inverse synthetic aperture radar images for non-cooperative target recognition[D].State College:The Pennsylvania State University, 2007:1-20. |
| [4] | RUNKLE P, NGUYEN L H, MCCLELLAN J H, et al. Multi-aspect target detection for SAR imagery using hidden Markov models[J].IEEE Transactions on Geoscience & Remote Sensing, 2001, 39(1): 46–55. |
| [5] | 张豪杰, 陈杰, 杨威, 等. 基于FDTD的高保真SAR回波信号仿真方法[J].系统工程与电子技术, 2016, 38(1): 45–52. ZHANG H J, CHEN J, YANG W, et al. High-precision simulation of SAR echo using FDTD method[J].Systems Engineering and Electronics, 2016, 38(1): 45–52.DOI:10.3969/j.issn.1001-506X.2016.01.08(in Chinese) |
| [6] | WANG K, CHEN J, YANG W, et al.High accuracy SAR echo generation approach using space-time-variant backscattering characteristics[C]//IEEE International Geoscience and Remote Sensing Symposim.Piscataway, NJ:IEEE Press, 2014, 30:656-659. |
| [7] | DAVIDSON G W, CUMMING I G, ITO M R. A chirp scaling approach for processing squint mode SAR data[J].IEEE Transactions on Aerospace & Electronics Systems, 1996, 32(1): 121–133. |
| [8] | 李悦丽, 梁甸农, 黎向阳. 一种改进方位向非线性CS大斜视角SAR成像算法[J].国防科技大学学报, 2008, 30(5): 62–67. LI Y L, LIANG D N, LI X Y. A refined azimuth nonlinear chirp scaling algorithm for high squint SAR imaging[J].Journal of National University of Defense Techology, 2008, 30(5): 62–67.(in Chinese) |
| [9] | DAILY M, FARR T, ELACHI C. Geologic interpretation from composited radar and Landsat imagery[J].Photogrammetric Engineering and Remote Sensing, 1979, 45(8): 1109–1116. |
| [10] | 宦若虹, 杨汝良. 多方位角图像决策融合的SAR目标识别[J].遥感学报, 2010, 14(2): 252–261. HUAN R H, YANG R L. SAR target recognition using multiple views decision fusion[J].Journal of Remote Sensing, 2010, 14(2): 252–261.(in Chinese) |
| [11] | BROWN M Z. Analysis of multiple-view Bayesian classification for S-SAR ATR[J].Proceedings of SPIE-The International Society for Optical Engineering, 2003, 5095: 265–274. |
| [12] | SNYDER W C. Model-based fusion of multilook SAR for ATR[J].Proceedings of SPIE-The International Society for Optical Engineering, 2002, 4727: 277–289. |
| [13] | 郭雷, 李晖晖, 鲍永生. 图像融合[M].北京: 电子工业出版社, 2008. GUO L, LI H H, BAO Y S. Image fusion[M].Beijing: Publishing House of Electronics Industry, 2008.(in Chinese) |
| [14] | 李卫斌, 张顺利, 解争龙, 等. 基于小波分析与方向模板的SAR图像融合技术研究[J].计算机应用研究, 2007, 24(3): 280–282. LI W B, ZHANG S L, XIE Z L, et al. Application of SAR image fusion based on wavelet and directional template[J].Application Research of Computers, 2007, 24(3): 280–282.(in Chinese) |
| [15] | MALLAT S G. Multiresolution approximations and wavelet orthonormal bases of L2(R)[J].Transactions of the American Mathematical Society, 1989, 315(1): 69–87. |
| [16] | 韦春桃, 吕健刚, 杨先武, 等. 一种利用方向模板的遥感影像道路提取方法[J].桂林理工大学学报, 2010, 30(3): 378–383. WEI C T, LV J G, YANG X W, et al. Road extraction method in remote sensing image based on direction template[J].Journal of Guilin University of Technology, 2010, 30(3): 378–383.(in Chinese) |
| [17] | 秦宣云, 卜英勇. 多方向模板的构造及匹配的快速算法[J].计算机工程与设计, 2003, 24(6): 91–92. QIN X Y, BU Y Y. Construction of multi-direction template and fast algorithm for template matching[J].Computer Engineering and Design, 2003, 24(6): 91–92.(in Chinese) |
| [18] | 张洁. 数字图像边缘检测技术的研究[D]. 合肥: 合肥工业大学, 2009. ZHANG J.Research on the techniques of digital image edge detection[D].Hefei:Hefei University of Technology, 2009(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10359-2009155288.htm |
| [19] | DELEDALLE C A, DENIS L, TUPIN F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights[J].IEEE Transactions on Image Processing, 2009, 18(12): 2661–2672.DOI:10.1109/TIP.2009.2029593 |
| [20] | 杨静, 田金文. 整数Haar小波变换及其在无失真图像压缩中的应用[J].贵州大学学报(自然科学版), 1999, 16(3): 161–167. YANG J, TIAN J W. Integer Haar wavelet transforms and lossless image compression[J].Journal of Guizhou University (National Science), 1999, 16(3): 161–167.(in Chinese) |
| [21] | GOUD P A, BINULAL G S. Simplified method of designing daubechies wavelets in class room[J].International Journal of Recent Trends in Engineering, 2009, 1(4): 52–54. |
| [22] | COHEN A, DAUBECHIES I, FEAUVEAU J. Biorthogonal bases of compactly supported wavelets[J].Communications on Pure & Applied Mathematics, 1988, 41(7): 909–996. |
| [23] | DAUBECHIES I, HEIL C. Ten lectures on wavelets[J].Computers in Physics, 1992, 6(6): 697. |
| [24] | HERIC D, ZAZULA D. Combined edge detection using wavelet transform and signal registration[J].Image & Vision Computing, 2007, 25(5): 652–662. |
| [25] | 贺国旗, 凌凤彩, 林晓. 基于Canny思想的Robinson边缘检测算法[J].计算机工程与科学, 2016, 38(4): 755–760. HE G Q, LING F C, LIN X. A Robinson edge detection algorithm based on Canny idea[J].Computer Engineering and Science, 2016, 38(4): 755–760.(in Chinese) |
| [26] | 韩瑜, 蔡云泽, 曾清. 图像融合的客观质量评估[J].指挥控制与仿真, 2013, 35(4): 1–7. HAN Y, CAI Y Z, ZENG Q. Objective image fusion performance assessment[J].Command Control & Simulation, 2013, 35(4): 1–7.(in Chinese) |
| [27] | 周芳, 王鹏波, 李春升. 遥感图像融合效果评估方法[J].现代雷达, 2013, 35(3): 19–23. ZHOU F, WANG P B, LI C S. Evaluation method of remote sensing image fusion effect[J].Modern Radar, 2013, 35(3): 19–23.(in Chinese) |
