目前的高光谱遥感图像与全色遥感图像融合算法大致分为四大类:成分替换方法、多分辨分析方法、矩阵分解方法和贝叶斯方法。成分替换方法是使用全色遥感图像替换高光谱遥感图像的空间分量,如强度色彩饱和度(Intensity-Hue-Saturation, HIS)[3]、主成分分析(Principal Component Analysis, PCA)[4]和施密特正交变化(Gram-Schmidt, GS)[5],该类算法简单易于实现,能够取得较好的空间性能,但是可能会产生光谱失真[6]。多分辨分析方法通过对全色遥感图像进行多分度分解,得到空间细节注入到高光谱遥感图像中,常见的多分辨分析方法有小波变换[7]、拉普拉斯金字塔(Laplacian Pyramid, LP)[8]、亮度调节的平滑滤波法(Smoothing Filter based Intensity Modulation, SFIM)[9]等,该类算法能够较好地保持光谱信息,同时呈现较好的空间细节,但是融合的高光谱图像可能会出现细节过度注入的情况。基于矩阵分解的方法和基于贝叶斯的方法是近年提出的方法,均是基于模型的方法,典型方法有约束非负矩阵分解(Coupled Nonnegative Matrix Factorization, CNMF)[10]、贝叶斯HySure[11]和贝叶斯稀疏表示(Bayesian Sparse Representation, BSR)[12]等,这2类算法融合得到的高光谱图像在空间和光谱方面可以得到较好的融合结果,但是计算量很大,不利于实现实时性。
为了解决现有算法的问题,本文提出了一种使用边缘保持滤波和结构张量的融合算法,能够更好地保持高光谱遥感图像的光谱信息,且有效地提高其空间分辨率,计算量小于矩阵分解和贝叶斯方法。该算法通过边缘保持滤波提取高光谱遥感图像的空间信息,可以避免低频混叠。对全色遥感图像采用空间域滤波法进行图像锐化,降低噪声且锐化细节信息。不同于仅从全色遥感图像中提取空间信息的现有融合算法,本文算法使用基于结构张量的自适应加权策略,同时从高光谱遥感图像和全色遥感图像二者中得到总空间信息,取得的总空间信息更全面完整。通过构建合适的增益矩阵,将取得的总空间信息与插值的高光谱遥感图像结合起来得到最终的融合图像。主观和客观的实验结果表明,本文算法比其他融合算法更好地保持了光谱信息,且更有效地提升了空间信息。
1 边缘保持滤波和结构张量 1.1 边缘保持滤波 边缘保持滤波指在滤波时可以保持图像的边缘信息,根据工作原理主要分为2种:①全局优化滤波器,即同时优化处理整幅图像,滤波后边缘保持的效果较好,但是计算时间较长;②基于局部优化的滤波器,即将图像分为局部块进行优化处理,这种滤波器比全局滤波器的算法简单,计算时间短,且也能够取得较好的边缘保持效果。引导滤波器[13]是一种较新颖的边缘保持滤波器,属于局部优化处理滤波器,可以有效保持边缘结构信息,同时不会产生梯度反转效应。
引导滤波器假设在一个局部窗口w内,引导图像X与滤波输出的图像Y是线性变换模型:
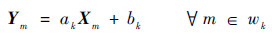 | (1) |
式中:窗口wk大小为(2r+1)×(2r+1),是以像素k为中心,r为窗口半径;ak和bk为常系数。为了确定常系数ak和bk,在保持式(1)的同时,需要约束输入X和输出图像Y尽量保持相似,因此可构建如下代价函数:
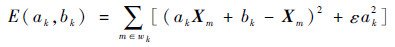 | (2) |
式中:ε为正则化参数。通过最小化代价函数式(2),可以解得ak和bk的最优解。由于像素k被多个覆盖k的窗口包含,且不同窗口内的ak和bk取值不同,所以需要对窗口内所有可能的取值取平均值:
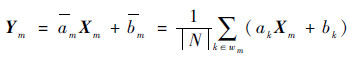 | (3) |
式中:|N|为窗口wk中像素的数量。
1.2 结构张量 结构张量是可以用来描述图像空间信息的有用工具[14]。对一副灰度图像Z,当2个相邻的像素点无限接近时,微分dZ可以表示为
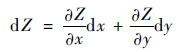 | (4) |
其平方范数可以表示为
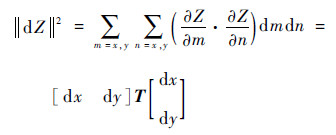 | (5) |
式中:矩阵T为结构张量,表达形式为
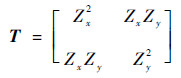 | (6) |
其中:Zx=?Z/?x和Zy=?Z/?y分别为沿x轴和y轴的一阶偏导数。
由式(6)可知,结构张量T为半正定矩阵,具有2个非负特征值μ1和μ2,其中较大的特征值表明图像在该像素点的边缘强度,对应的特征向量为该像素点的梯度方向,是灰度变化最快的方向。
2 高光谱和全色遥感图像融合算法 图 1为本文提出的高光谱图像融合算法的总框图。与现有融合算法的不同之处主要为:①提出了使用边缘保持滤波提取高光谱遥感图像的空间信息的方法,可以避免低频混叠;②传统的融合算法一般只考虑全色遥感图像的空间信息,会引起光谱扭曲或者加入的空间信息不足,本文算法不仅考虑了全色遥感图像的空间信息,还考虑了高光谱遥感图像的空间信息,提出了基于结构张量的自适应加权策略得到足够的总空间信息,该策略与全局加权方法相比,可以减少光谱和空间失真;③构建相匹配的增益矩阵,在进一步减少空间和光谱失真的条件下得到融合的高光谱图像。
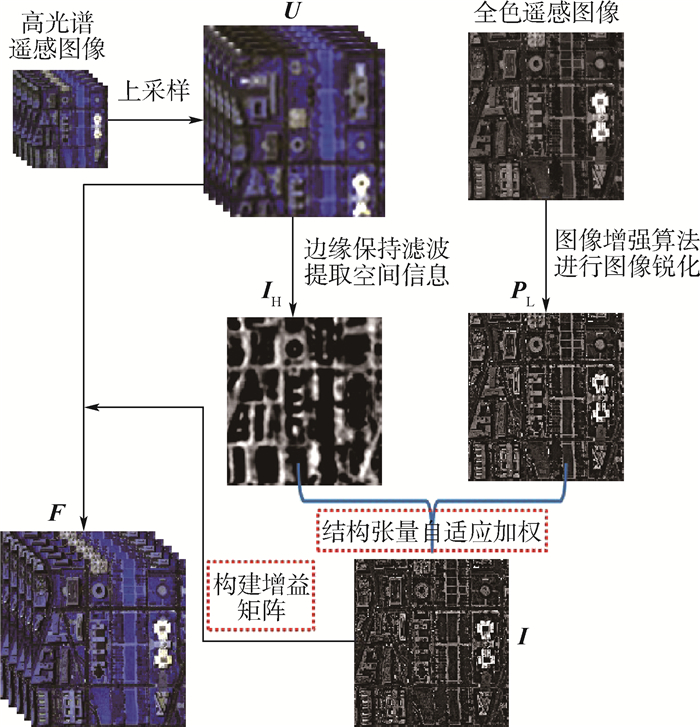 |
| 图 1 高光谱图像融合算法框图 Fig. 1 Block diagram of proposed hyperspectral image fusion algorithm |
| 图选项 |
2.1 使用边缘保持滤波提取高光谱遥感图像的空间信息 输入低空间分辨率的高光谱遥感图像和高空间分辨率的全色遥感图像后,对高光谱遥感图像进行上采样至与全色遥感图像相同大小。将上采样得到的高光谱遥感图像命名为U。对插值的高光谱遥感图像的每个波段使用高斯低通滤波器滤波。
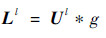 | (7) |
式中:l=1, 2, …, n,n为高光谱遥感图像的波段数;L为高斯滤波后得到的图像;Ul和Ll分别为插值的高光谱遥感图像和高斯滤波后图像的第l个波段;g为高斯滤波器。高斯滤波后得到的图像的每个波段是高光谱遥感图像的每个波段的低频图像,去除了高频细节信息。
将边缘保持滤波器作用在L图像的每个波段上。边缘保持滤波器采用引导滤波器,依次使用插值的高光谱遥感图像的每个波段作为引导图像,将L图像的每个波段作为输入图像,该引导滤波过程可以表示为
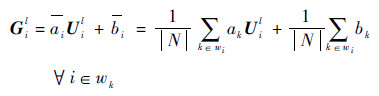 | (8) |
式中:G为引导滤波后得到的图像;Gl为G图像的第l个波段;wk为以像素k为中心的局部窗口,窗口大小设置为58。ak和bk可通过计算求解如式(2)所示的代价函数,得到以下结果:
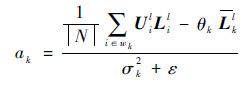 | (9) |
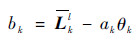 | (10) |
式中:θk和σk2分别为引导图像Ul的均值和方差;Lkl为在窗口wk内输入图像Ll的均值;ε为正则化参数,设置为10-6。
根据边缘保持滤波器的原理可知,对于第l个波段(l=1, 2, …, n),引导图像Ul的空间细节信息可以传递给输出图像Gl。引导图像Ul是插值的高光谱遥感图像第l个波段,包含其第l个波段的空间细节信息。因此,边缘保持滤波后得到的图像Gl含有引导图像Ul的空间细节信息,即含有高光谱遥感图像第l个波段的空间信息。而输入图像Ll是高光谱遥感图像的第l个波段的低频图像,不包含高频空间细节信息。对Gl图像与Ll图像做差,可得到高光谱遥感图像第l个波段的空间细节信息。
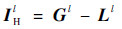 | (11) |
式中:IHl为高光谱遥感图像的第l个波段的空间信息。将每个波段的空间信息相加可以得到高光谱遥感图像的总空间信息。
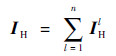 | (12) |
式中:IH为高光谱遥感图像的总空间信息。相比于直接使用高光谱遥感图像减去低频高光谱遥感图像,得到高频图像作为高光谱遥感图像的空间信息,经过边缘保持滤波提取高光谱遥感图像的空间信息,可以保证提取的信息均为空间结构信息,而直接使用高频图像作为高光谱遥感图像的空间信息,可能会含有部分低频信息。因此,使用边缘保持滤波提取高光谱遥感图像的空间信息,提取的信息全部为空间信息,分离更明确,可以避免低频混叠。
2.2 使用图像增强算法锐化全色遥感图像 全色遥感图像含有丰富的空间信息,为了进一步突出其空间细节,且减少噪声,对全色遥感图像使用图像增强算法进行空间细节锐化。本文采用空间域滤波法锐化全色遥感图像,选择高斯-拉普拉斯(Laplacian of Gaussian,LOG)图像增强算法。LOG算法先使用高斯卷积滤波器去噪,再使用拉普拉斯算子进行图像增强。
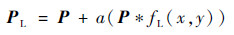 | (13) |
式中:P为全色遥感图像;PL为增强的全色遥感图像;fL(x, y)为LOG算子的核函数;a为常数,若核fL(x, y)的中心系数为正数,a=1,若为负数,a=-1,本文中心系数为负数,a=-1。
LOG算子核函数fL(x, y)为
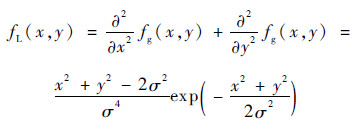 | (14) |
式中:
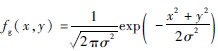
2.3 使用基于结构张量的自适应加权策略得到总空间信息 传统的高光谱图像融合算法通常只考虑了全色遥感图像包含的空间信息,将全色遥感图像的空间信息注入到高光谱遥感图像中,这些传统算法可能会引起光谱失真或者空间增强程度不足。为了克服这些问题,本文使用基于结构张量的自适应加权策略,得到总的空间信息,同时包含了高光谱遥感图像和全色遥感图像包含的空间信息。
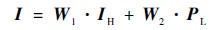 | (15) |
式中:I为总的空间信息;W1和W2为自适应加权矩阵,可以根据输入的高光谱遥感图像和全色遥感图像自适应地得到相应的加权矩阵。自适应矩阵加权方法相较全局常数加权方法,可以自动选取合适的加权数据,进一步减少光谱和空间失真。
自适应加权矩阵W1和W2可根据如下基于结构张量的方法求得。根据式(6),高光谱遥感图像的空间信息IH和增强的全色遥感图像PL的第i个像素点的结构张量矩阵
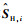
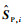
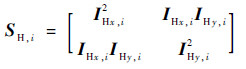 | (16) |
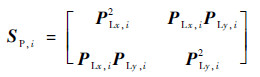 | (17) |
式中:IHx和IHy分别为IH沿x轴和y轴的偏导数;PLx和PLy分别为PL沿x轴和y轴的偏导数。式(16)和式(17)为一个像素点的结构张量矩阵,为了包含局部空间信息,使用高斯核函数与上述2个结构张量矩阵(式(16)、式(17))进行卷积。
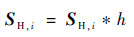 | (18) |
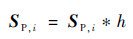 | (19) |
式中:SH, i和SP, i为得到的第i个像素点包含局部空间信息的结构张量;h为高斯核函数。SH, i和SP, i为半正定矩阵,可以分解为
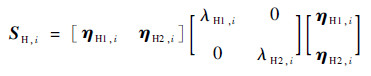 | (20) |
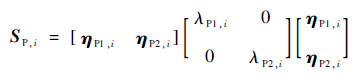 | (21) |
式中:λH1, i、λH2, i和λP1, i、λP2, i分别为2个在第i个像素点结构张量的非负特征值;ηH1, i、ηH2, i和ηP1, i、ηP2, i为在第i个像素点相对于特征值的特征向量。
对IH和PL图像的第i个像素点,假设λH1, i和λP1, i为较大的特征值,较大的特征值λH1, i和λP1, i分别表明IH和PL图像在第i个像素点的边缘强度,对应的特征向量ηH1, i和ηP1, i为该像素点的梯度方向,是灰度变化最快的方向。因此,由于较大的特征值λH1, i和λP1, i表明了IH和PL图像在第i个像素点的强度变化程度,则若λH1, i>λP1, i,认为IH在该像素点处边缘强度大,即含有的空间信息更多,因此IH在该像素点处应该占更大一些的加权比例;反之,若λH1, i < λP1, i,则PL在该像素点处占更大一些的加权比例;若λH1, i和λP1, i相等,则IH和PL在该像素点处占比例相等,均为0.5。由上述分析可以得到,自适应加权矩阵W1和W2的第i个像素点可以计算得到
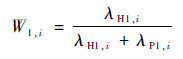 | (22) |
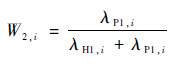 | (23) |
式中:W1, i和W2, i分别为矩阵W1和W2第i个像素点的值。
2.4 构建增益矩阵得到融合的高光谱图像 得到总空间信息后,通过构建每个波段对应的增益矩阵,合成空间信息与插值的高光谱遥感图像,得到融合的高光谱图像。
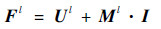 | (24) |
式中:F为融合的高光谱图像;M为增益矩阵;Fl和Ml分别为融合的高光谱图像和增益矩阵的第l个波段。构建增益矩阵M的原则是控制空间和光谱失真。为了减少光谱失真,任意每对高光谱图像的波段之间的比例应该保持不变。定义一个调节参数β控制注入的空间信息的量,达到减少空间失真的目的。因此,增益矩阵M为
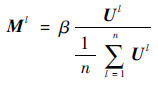 | (25) |
式中:β为调节参数,可以根据高光谱图像融合的空间客观指标选取得到,在本文中,分析选取不同β值的空间指标相关系数CC。根据结果分析可以得到,由于β=0.1时,空间指标相关系数CC的取值最优,空间失真最少,β应选取0.1。
3 实验结果及分析 为了验证本文算法的有效性,使用Pavia University、Moffett field和Washington DC数据集进行实验测试。Pavia University数据集由反射光学系统成像光谱仪(ROSIS)拍摄,高光谱遥感图像包含115个波段,波长范围为0.43~0.86 μm,去除水波段和噪声波段,剩余103个波段用做实验;实验使用的全色遥感图像大小为260×260,空间分辨率为1.3 m;用于测试的高光谱遥感图像大小为52×52,空间分辨率为6.5 m。Moffett field数据集由机载可见光-红外成像光谱仪(AVIRIS)拍摄,该数据集的高光谱遥感图像光谱覆盖范围为0.4~2.5 μm,包含224个波段,在去除水波段和噪声波段后,剩余176个波段用于实验测试;实验使用的全色遥感图像大小为260×150,空间分辨率为20 m;用于测试的高光谱遥感图像大小为52×30,空间分辨率为100 m。Washington DC数据集是一个机载高光谱数据,包含210个波段,191个波段用于实验测试,波长范围为0.4~2.4 μm;用于实验测试的高光谱遥感图像大小和全色遥感图像大小分别为50×50和250×250。这3套数据集是合成数据集,模拟的高光谱遥感图像和全色遥感图像可以根据Wald协议[15]得到。
针对融合得到的结果,分别从主观和客观2方面进行评价。客观评价指标包括相关系数CC、光谱角映射SAM、均方根误差RMSE[16]和相对整体维数综合误差ERGAS[17]。CC为空间指标,反映融合图像与参考图像的对应波段的相似程度,最优值为1。SAM为光谱指标,表示光谱失真程度,理想值为0。RMSE和ERGAS为对融合结果进行总体评价的指标,理想值均为0。
将本文算法与以下几种先进的高光谱图像融合算法进行比较:PCA、自适应施密特正交变化方法(Adaptive Gram-Schmidt, GSA)[18]、BSR、基于高通调制的广义调制传递函数拉普拉斯金字塔方法(Modulation transfer function Generalized Laplacian pyramid with High pass modulation, MGH)[8]和引导滤波PCA杂交方法(Guided Filter PCA, GFPCA)[19]。
为了验证本文提出的使用边缘保持滤波提取高光谱遥感图像的空间信息的方法的有效性,将本文算法与直接使用高光谱遥感图像减去低频高光谱遥感图像得到高频图像作为高光谱遥感图像的空间信息的方法(该方法命名为GSI)进行了比较。表 1中列出了2种融合算法的客观评价指标值,最优值用粗体表示。可以看到,本文算法在大多数的评价指标上取得了最优值。这是由于提出的使用边缘保持滤波提取高光谱遥感图像的空间信息的方法可以保证得到的信息均为空间结构信息,使分离更明确。实验结果说明,提出的使用边缘保持滤波提取高光谱遥感图像的空间信息的方法是有效的,且可以取得较好的性能。
表 1 边缘保持滤波方法对各数据集的客观评价指标 Table 1 Objective evaluation indices of edge-preserving filtering method for each dataset
| 数据集 | 算法 | CC | SAM | RMSE | ERGAS |
| Pavia University | GSI | 0.930 4 | 6.774 0 | 0.044 9 | 4.439 9 |
| 本文 | 0.930 4 | 6.568 6 | 0.038 5 | 4.148 6 | |
| Moffett field | GSI | 0.954 3 | 6.355 0 | 0.030 2 | 4.052 2 |
| 本文 | 0.965 0 | 6.347 0 | 0.030 1 | 4.030 9 | |
| Washington DC | GSI | 0.866 2 | 7.233 0 | 0.013 1 | 74.957 2 |
| 本文 | 0.879 4 | 7.232 0 | 0.013 3 | 73.674 9 |
表选项
许多传统的图像融合算法通常只考虑了全色遥感图像包含的空间信息。本文中提出了基于结构张量的自适应加权策略得到总的空间信息,同时包含了高光谱遥感图像和全色遥感图像包含的空间信息。在提出的基于结构张量的自适应加权策略中,自适应加权矩阵W1和W2是自适应地基于结构张量的方法求得。为了验证提出的基于结构张量的自适应加权策略得到的加权矩阵的有效性,将本文算法与多种全局常数加权方法进行了对比,如表 2所示。在对比实验中,只从全色遥感图像中提取空间信息的方法(即在式(15)中,2个加权系数分别为全局常系数0和1)命名为GFP;平均加权方法(即在式(15)中,2个加权系数分别为全局常系数0.5和0.5)命名为GFGW;由于全色遥感图像的空间信息多于高光谱遥感图像的空间信息,认为全色遥感图像的空间信息PL所占比例应该较大一些,因此,在式(15)中,2个加权系数可以分别选取为全局常系数0.2和0.8,该方法命名为GFPL。表 2中列出了本文算法与上述融合算法的客观评价指标值,最优值用粗体表示。可以看到,提出的基于结构张量的自适应加权策略与其他几种加权方法相比,取得了更好的性能。说明提出的基于结构张量的自适应加权策略是有效的,且取得了较好的实验结果。
表 2 基于结构张量的自适应加权策略对各数据集的客观评价指标 Table 2 Objective evaluation indices of structure tensor based adaptive weighting strategy for each dataset
| 数据集 | 算法 | CC | SAM | RMSE | ERGAS |
| Pavia University | GFP | 0.932 6 | 6.593 2 | 0.042 5 | 4.235 8 |
| GFGW | 0.906 6 | 6.766 4 | 0.041 2 | 4.783 2 | |
| GFPL | 0.925 6 | 6.586 4 | 0.039 4 | 4.257 1 | |
| 本文 | 0.930 4 | 6.568 6 | 0.038 5 | 4.148 6 | |
| Moffett field | GFP | 0.957 5 | 6.347 0 | 0.031 4 | 4.351 8 |
| GFGW | 0.956 6 | 6.358 0 | 0.031 0 | 4.337 2 | |
| GFPL | 0.962 3 | 6.348 0 | 0.030 5 | 4.031 5 | |
| 本文 | 0.965 0 | 6.347 0 | 0.030 1 | 4.030 9 | |
| Washington DC | GFP | 0.873 8 | 7.232 1 | 0.013 6 | 73.695 0 |
| GFGW | 0.865 9 | 7.232 5 | 0.014 0 | 76.223 0 | |
| GFPL | 0.874 5 | 7.232 4 | 0.013 4 | 74.326 6 | |
| 本文 | 0.879 4 | 7.232 0 | 0.013 3 | 73.674 9 |
表选项
图 2为Pavia University数据集使用多种融合算法得到的融合视觉结果。可以看出,PCA融合得到的图像空间性能较好,但是该算法融合的图像较暗,具有一定的光谱失真。GFPCA融合的图像在一些细节区域较为模糊,如放大区域。BSR和MGH融合得到的图像整体也稍微偏暗,且在某些细节信息不够清晰。GSA和本文算法的融合结果清晰明亮,在空间方面效果都较好,在光谱保持性能方面,本文算法保持得较好,GSA有轻微的光谱失真。因此,与其他融合算法相比,本文算法有效提升了空间信息,且更好地保持了光谱信息。表 3中列出了多种融合算法的客观评价指标值,最优值用粗体表示。可以看到,本文算法的CC值最大,SAM、RMSE和ERGAS值均最小。说明本文算法在客观指标上较其他算法有更好的性能表现,且进一步证明了本文算法在光谱和空间方面均能够取得优秀的融合效果。
 |
| 图 2 不同融合算法得到的Pavia University数据集的融合结果 Fig. 2 Fusion results of different fusion algorithms for Pavia University dataset |
| 图选项 |
表 3 Pavia University数据集的融合结果客观评价指标 Table 3 Objective evaluation indices of fusion results for Pavia University dataset
| 算法 | CC | SAM | RMSE | ERGAS |
| PCA | 0.923 4 | 7.656 6 | 0.040 8 | 4.783 0 |
| GFPCA | 0.795 2 | 9.449 5 | 0.061 6 | 7.135 8 |
| GSA | 0.921 9 | 8.799 2 | 0.038 9 | 4.532 1 |
| BSR | 0.900 3 | 8.676 6 | 0.044 1 | 5.301 6 |
| MGH | 0.930 2 | 6.909 0 | 0.038 9 | 4.235 5 |
| 本文 | 0.930 4 | 6.568 6 | 0.038 5 | 4.148 6 |
表选项
图 3为不同融合算法得到的Moffett field数据集的融合结果。可以看出,PCA和GSA的融合结果取得了较好的空间性能,但是光谱失真较严重。GFPCA融合得到的图像在一些细节信息上不清晰,有严重的空间失真。BSR融合得到的图像在某些细节信息也有轻微的模糊。MGH融合的结果具有较好的光谱保持性能,但是一些细节区域的空间信息过于锐利。相较于这些算法,本文算法在光谱信息保持和空间信息提升方面均有较好的效果。表 4为多种融合算法的客观评价指标。可以看出,本文算法的CC、RMSE和ERGAS指标均优于其他融合算法的相应指标值。对于SAM指标,本文算法仅次于MGH。这些主观和客观方面的比较结果说明,本文算法比其他算法更有效地提升了空间信息,保持了光谱信息。
 |
| 图 3 不同融合算法得到的Moffett field数据集的融合结果 Fig. 3 Fusion results of different fusion algorithms for Moffett field dataset |
| 图选项 |
表 4 Moffett field数据集的融合结果客观评价指标 Table 4 Objective evaluation indices of fusion results for Moffett field dataset
| 算法 | CC | SAM | RMSE | ERGAS |
| PCA | 0.905 0 | 12.425 5 | 0.047 5 | 6.698 0 |
| GFPCA | 0.915 7 | 10.319 8 | 0.044 1 | 6.287 6 |
| GSA | 0.949 7 | 8.660 5 | 0.036 1 | 5.044 4 |
| BSR | 0.954 0 | 8.037 2 | 0.032 3 | 4.713 1 |
| MGH | 0.964 4 | 6.007 8 | 0.032 5 | 4.356 8 |
| 本文 | 0.965 0 | 6.347 0 | 0.030 1 | 4.030 9 |
表选项
图 4为不同融合算法得到的Washington DC数据集的融合结果。可以看出,PCA取得了较好的空间质量,但是光谱失真较严重。由于加入的空间信息不足,GFPCA取得的结果有严重的空间失真。GSA和BSR取得的结果在某些空间细节方面也有轻微的模糊,BSR还有一定的光谱失真。与其他算法对比,本文算法和MGH更有效地增强了空间信息,且保持了光谱信息。表 5为多种融合算法的客观评价指标。可以看出,本文算法的CC、SAM和RMSE指标优于其他融合算法的相应指标值。另外,本文算法的ERGAS指标仅次于GFPCA。这些实验结果说明,本文算法与其他融合算法相比,取得了更好的空间和光谱性能。
 |
| 图 4 不同融合算法得到的Washington DC数据集的融合结果 Fig. 4 Fusion results of different fusion algorithms for Washington DC dataset |
| 图选项 |
表 5 Washington DC数据集的融合结果客观评价指标 Table 5 Objective evaluation indices of fusion results for Washington DC dataset
| 算法 | CC | SAM | RMSE | ERGAS |
| PCA | 0.853 2 | 7.361 9 | 0.013 6 | 83.414 5 |
| GFPCA | 0.768 9 | 9.932 2 | 0.013 9 | 67.944 1 |
| GSA | 0.870 1 | 7.258 0 | 0.018 4 | 83.997 9 |
| BSR | 0.826 9 | 10.012 5 | 0.013 8 | 77.749 1 |
| MGH | 0.877 7 | 7.261 8 | 0.015 6 | 79.859 8 |
| 本文 | 0.879 4 | 7.232 0 | 0.013 3 | 73.674 9 |
表选项
4 结论 本文提出了一种基于边缘保持滤波和结构张量的高光谱和全色遥感图像融合算法。
1) 使用边缘保持滤波提取高光谱遥感图像的空间信息,保证提取的信息全部为空间细节信息,避免低频混叠。
2) 不同于传统的只提取全色遥感图像空间信息的融合算法,本文算法利用基于结构张量的自适应加权策略得到高光谱遥感和全色遥感图像的总空间信息,不仅包含全色遥感图像的空间信息,还包含高光谱遥感图像的空间信息,可以有效地保持光谱信息,且加入足够的空间信息。
3) 可以根据输入的高光谱遥感图像和全色遥感图像自适应地得到相应的加权矩阵,相对于全局常数加权,可以自动地选取更加合适的加权数据。
4) 在Pavia University、Moffett field和Washington DC数据集上进行实验测试,对比分析了本文算法与几种先进的常见算法的融合性能。实验结果的主观视觉效果和客观定量分析表明,本文算法与其他算法相比,能够在有效保持高光谱图像丰富光谱信息的同时,更有效地提升空间性能,从而得到高质量的融合图像。
参考文献
| [1] | LI Y S, HU J, ZHAO X, et al. Hyperspectral image super-resolution using deep convolutional neural network[J]. Neurocomputing, 2017, 266: 29-41. DOI:10.1016/j.neucom.2017.05.024 |
| [2] | MOOKAMBIGA A, GOMATHI V. Comprehensive review on fusion techniques for spatial information enhancement in hyperspectral imagery[J]. Multidimensional Systems and Signal Processing, 2016, 27(4): 863-889. DOI:10.1007/s11045-016-0415-2 |
| [3] | TU T M, SU S C, SHYU H C, et al. A new look at IHS-like image fusion methods[J]. Information Fusion, 2001, 2(3): 177-186. DOI:10.1016/S1566-2535(01)00036-7 |
| [4] | CHAVEZ P S, KWARTENG A Y. Extracting spectral contrast in Landsat thematic mapper image data using selective principal component analysis[J]. Photogrammetric Engineering and Remote Sensing, 1989, 55(3): 339-348. |
| [5] | LABEN C, BROWER B.Process for enhancing the spatial resolution of multispectral imagery using pan-sharpening: United States Patent 6011875[P].2000-01-04. |
| [6] | QU J H, LI Y S, DONG W Q. Hyperspectral pansharpening with guided filter[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 2152-2156. DOI:10.1109/LGRS.2017.2755679 |
| [7] | MALLAT S. A theory for multiresolution signal decomposition:The wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [8] | VIVONE G, RESTAINO R, MAURO D M, et al. Contrast and error-based fusion schemes for multispectral image pansharpening[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(5): 930-934. DOI:10.1109/LGRS.2013.2281996 |
| [9] | LIU J G. Smoothing filter based intensity modulation:A spectral preserve image fusion technique for improving spatial details[J]. International Journal of Remote Sensing, 2000, 21(18): 3461-3472. DOI:10.1080/014311600750037499 |
| [10] | YOKOYA N, YAIRI T, IWASAKI A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 528-537. DOI:10.1109/TGRS.2011.2161320 |
| [11] | SIMOES M, DIAS J B, ALMEIDA L B, et al. A convex formulation for hyperspectral image superresolution via subspace-based regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3373-3388. DOI:10.1109/TGRS.2014.2375320 |
| [12] | WEI Q, DIAS J M, DOBIGEON N, et al. Hyperspectral and multispectral image fusion based on a sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3658-3668. DOI:10.1109/TGRS.2014.2381272 |
| [13] | HE K, SUN J, TANG X. Guided image filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397-1409. DOI:10.1109/TPAMI.2012.213 |
| [14] | HARRIS C.A combined corner and edge detector[C]//Proceedings of the Alvey Vision Conference, 1988: 147-151. |
| [15] | WALD L, RANCHIN T, MANGOLINI M. Fusion of satellite images of different spatial resolutions:Assessing the quality of resulting images[J]. Photogrammetric Engineering and Remote Sensing, 1997, 63(6): 691-699. |
| [16] | LONCAN L, ALMEIDA L B, DIAS J M, et al. Hyperspectral pansharpening:A review[J]. IEEE Geoscience Remote Sensing Magazine, 2015, 3(3): 27-46. DOI:10.1109/MGRS.2015.2440094 |
| [17] | ZHANG L, ZHANG L, TAO D, et al. On combining multiple features for hyperspectral remote sensing image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 879-893. DOI:10.1109/TGRS.2011.2162339 |
| [18] | AIAZZI B, BARONTI S, SELVA M. Improving component substitution pansharpening through multivariate regression of MS+pan data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3230-3239. DOI:10.1109/TGRS.2007.901007 |
| [19] | LIAO W, HUANG X, COILLIE F, et al. Processing of multiresolution thermal hyperspectral and digital color data:Outcome of the 2014 IEEE GRSS data fusion contest[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2984-2996. DOI:10.1109/JSTARS.2015.2420582 |
