自20世纪80年代以来，电子节气门(Electronic Throttle Body，ETB)在汽车上的应用越来越广泛，与传统的机械式节气门相比，ETB能够快速精准控制节气门的开度，发挥发动机最佳性能，提高车辆动力性和经济性^[1]。
ETB系统由直流电机、减速齿轮箱、节流板、复位弹簧、位置传感器等组成，表现出强非线性特性^[2-3]。其非线性主要来源于：①复位弹簧扭矩不连续；②部件间存在的黏滞摩擦和库仑摩擦；③齿轮间存在的间隙。与压电陶瓷执行器的迟滞特性成因不同，该系统主要是由于分布的不同元件(齿轮箱、复位弹簧、阀片)之间各自所带有的非线性特性以及惯性特性最终组合在一起导致的一个集总的动态迟滞非线性特性。
对于这样一个强非线性的机电系统，已发表的一些ETB建模研究只能辨识少数易测量的参数，无法获得所有参数的精确值^[4-5]。文献[6-9]采用简化模型来近似描述系统中出现的由摩擦和弹簧所引起的非线性行为，但是这种方法很难用来描述不同工况下的ETB响应，更不用说发动机状态转换过程中的瞬态行为^[10-11]。文献[12]对参数进行了辨识，由于辨识过程中采用过多近似，仿真结果和实际曲线误差较大。文献[13]采用Wiener结构建立ETB系统模型，模型很好地描述ETB系统的静态特性(0.005 Hz激励信号)和动态特性(0.01~0.05 Hz激励信号)，但是利用该模型不利于基于模型的线性控制器设计。以上可见，由于ETB系统中多种非线性环节与动力学响应之间存在着复杂的相互作用，基于物理机理建立精确的动态非线性的模型有很大困难，所建立的模型往往只能近似描述系统的动态线性特性。因此研究能够同时描述ETB系统静态非线性特性和动态特性的模型，且模型结构有利于基于模型的控制器设计，对于ETB系统的应用具有重要的意义，这也是本研究所关注的。
本文基于模块化的Hammerstein结构，建立了ETB系统的动态非线性模型。尽管实际的物理系统是一个Wiener模型，但是为了后续对该系统进行控制，将该系统当作黑箱处理，采用Hammerstein模型对其进行建模。模型由一个静态非线性子系统与一个线性子系统串联构成。目前包含静态迟滞算子的Hammerstein模型辨识工作包括含有relay算子、backlash型算子、stop型算子的Hammerstein模型辨识，针对不同类型的静态迟滞算子****们提出了保证参数收敛的辨识算法^[14-17]。但由于ETB系统表现出的特殊静态迟滞非线性特性，其无法由现有的任一种静态迟滞算子所描述，因此也无法使用已有的这些辨识算法。
本文针对ETB的特殊迟滞特性建立了新的静态迟滞算子，并提出了相应的辨识算法。首先，通过分析ETB实验迟滞曲线的特性构造了一种全新的静态迟滞算子用以描述ETB系统的非线性记忆特性并作为静态非线性子系统。然后, 推导了静态迟滞算子的解析逆模型并设计了逆补偿器，估计得到Hammerstein模型的中间变量。最后，采用最小二乘估计辨识得到线性子系统，并证明了辨识系统的等效性。本文采用模块化Hammerstein结构的优势在于：子系统与实际的物理系统或部件之间不需要有物理对应关系^[16]；模型包含静态非线性子系统和动态线性子系统，能够描述ETB系统的静态非线性特性和系统的动力学响应；此外采用了Hammerstein模型结构以及静态迟滞算子解析逆的存在，为基于非线性逆补偿策略设计控制器提供了方便。
1 ETB系统及建模 1.1 ETB系统 ETB系统包括以下几个部分：直流电机、减速齿轮箱、节流板、复位弹簧以及用来提供阀门开度信息的位置传感器等，如图 1所示^[18]。

图 1 ETB系统[18] Fig. 1 ETB system[18]

图选项

系统的输入信号u(t)是PWM脉冲信号的占空比。直流电机施加在阀门上的推力与PWM脉冲信号占空比u(t)成比例。在一定输入信号作用下，由于受到复位弹簧和摩擦力的约束，阀门会维持在某个确定的位置。系统的输出是阀门位置信号y(t)，其输出范围在(0.5, 4.8) V，0.5 V表示阀门完全关闭，4.8 V表示阀门完全打开。当没有PWM脉冲信号作用于系统时，系统的阀门会维持在“跛行回家”的位置，这时位置传感器的读数为0.85 V。
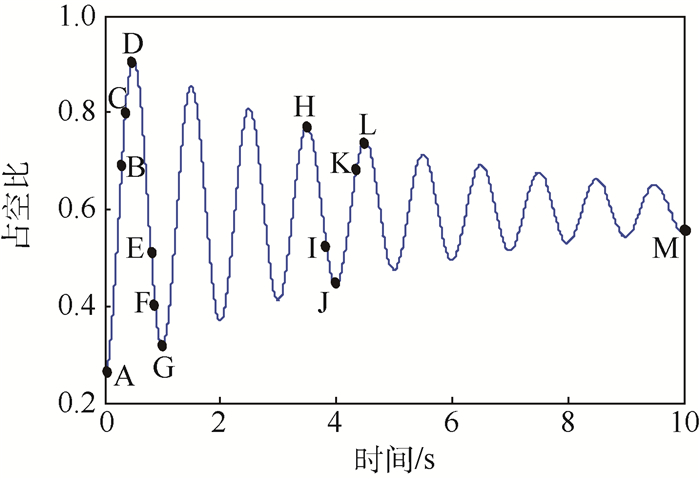
图 2给出了ETB系统输出阀门位置与输入占空比之间的关系，由图中可见系统输入输出之间存在着显著的滞环特性，随着输入信号频率变化系统的迟滞特性也会变化，即系统迟滞特性是率相关的。此外，系统的输出表现出明显的饱和特性。ETB系统存在着多个非线性环节：阀在转动中受到黏性摩擦和库仑摩擦的作用，其中，库仑摩擦为静摩擦，而黏性摩擦则与阀门转速有关；节气门复位弹簧采用非线性弹簧，并且弹簧在越过平衡位置后扭矩发生突变；减速齿轮箱中存在着间隙。如图 2所示的ETB系统的非线性特性是上述多个非线性环节与惯性特性共同作用的结果。完整地描述这样复杂的非线性动力学特性和精确的参数辨识有很大困难。

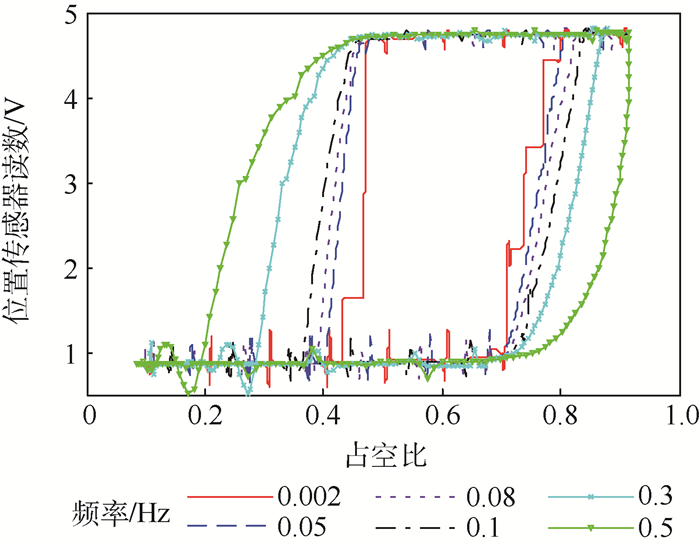图 2 不同频率正弦信号下的ETB系统响应 Fig. 2 ETB system response to sinusoidal signal with different frequencies

图选项

1.2 建模问题重述 鉴于基于物理机理的精确建模和参数辨识很困难，本文采用模块化Hammerstein模型结构来描述ETB非线性系统^[19]。
假设1??ETB系统的动态迟滞非线性特性可由图 3所示的Hammerstein模型描述，该模型由一个静态迟滞非线性子系统H[·]和一个动态线性子系统G[·]串联而成，中间变量w(t)无法测量，其中t为时间。

图 3 Hammerstein模型结构 Fig. 3 Structure of Hammerstein model

图选项

基于假设1，ETB系统的建模问题就变成图 3所示Hammerstein系统的辨识问题，描述如下：

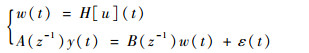(1)

式中：ε(t)∈ R为有界零均值平稳各态遍历的随机独立噪声；A(z^-1)和B(z^-1)为待辨识的关于单位后移算子z^-1的多项式，其定义如(2)所示，假设系统阶次n为已知，a₁~a_na及b₁~b_nb分别表示A(z^-1)和B(z^-1)各项系数，且有n_a=n_b=n。

(2)

2 ETB系统辨识 为了辨识图 3系统中的Hammerstein模型，本文采用分步法分别辨识其中的静态迟滞非线性子系统H[·]和动态线性子系统G[·]。
2.1 非线性子系统辨识
2.1.1 ETB滞环特性 从图 2中可以看出，系统在达到最大/最小开度后会出现高频抖动，为了获得更好的辨识精度，辨识前对原始数据进行滤波。图 4绘制了不同输入幅值的滤波前后准静态信号(指相对于系统动态特性足够低的频率信号，本文中采用0.002 Hz正弦信号)作用下，ETB系统的滞环曲线。

图 4 同一频率不同占空比下的迟滞环 Fig. 4 Hysteresis loops with different duty cycles at the same frequency

图选项

由图 4可知，ETB系统的迟滞非线性具有以下特性：
1) 准静态信号作用下，系统具有局部记忆性，系统当前的输出只和当前的输入和过往状态有关，即在输入输出关系图中通过某一点的曲线只有一条或两条。
2) 准静态信号作用下，滞环具有显著的不对称特性和饱和特性。
3) 周期信号作用下，滞环轨迹为逆时针方向。
4) 与图 5所示的经典的具有局部记忆性的迟滞算子相比，包括relay算子(阈值为a)、stop算子(阈值为m)和play算子(阈值为r)^[20-21]，图 4中的ETB的迟滞特性与它们均不同。

图 5 具有局部记忆的迟滞算子 Fig. 5 Hysteresis operator with local memories

图选项

2.1.2 S-stop算子 由于没有现成的迟滞算子可以描述ETB系统的非线性特性，本文构造了新的迟滞非线性算子——类stop算子(以下简称S-stop算子)来描述ETB系统的特殊迟滞特性。值得注意的是，S-stop算子仅其饱和特性与stop算子的滞环形状相似，但具体的滞环特性与stop算子的滞环特性是不同的。
所构造的S-stop算子如图 6所示，具体表达式为

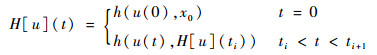(3)

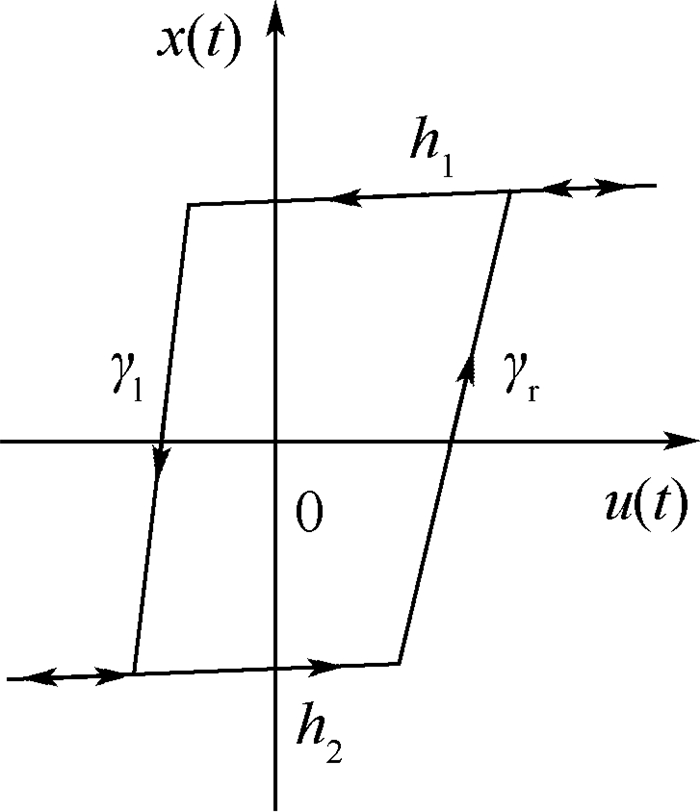图 6 S-stop算子 Fig. 6 S-stop operator

图选项

式中：

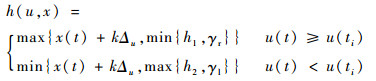其中：
γ_l=k₂u(t)-r₂, γ_r=k₁u(t)-r₁, h₁=ku(t)-r_h1和h₂=ku(t)-r_h2为S-stop算子的各包络线函数，γ_l>γ_r; k₁、k₂、k、r₁、r₂、r_h1和r_h2为S-stop算子需要辨识的参数; Δ_u=u(t)-u(t_i), t_i为第i次采样的时间。

2.1.3 参数辨识 在一个准静态激励信号作用下，Hammerstein系统的线性环节被视为一个静态增益K，由系统的输入输出可以辨识得到H^*=KH[·]作为非线性子系统。选取0.002 Hz的正弦信号作为激励信号对非线性子系统进行辨识，依据式(3)得到等效非线性子系统H^*的参数：r₁=26.328，r₂=35.973，r_h1=-4.65，r_h2=-0.861，k=0.1，k₁=39.94，k₂=84.905。
辨识结果如图 7所示，与实验结果比较，非线性子系统的相对误差RE=5.71%，均方根误差RMSE=0.177 3 V。该结果表明，在低频信号下，该模型可以较好地描述系统的静态迟滞非线性特性。

图 7 非线性子系统建模结果 Fig. 7 Modeling result of nonlinear subsystem

图选项

2.1.4 S-stop算子迟滞特性 为了更好地显示所提出的S-stop算子的迟滞特性，施加如图 8所示的按指数衰减的正弦激励信号：x_data=0.4sin(0.002πt)e^{-0.000 2t}+0.6，图 9给出在相同的输入信号作用下S-stop算子、stop算子、play算子的输入输出关系图，对比可发现，S-stop算子的迟滞特性与其他算子显著不同。

图 8 按指数衰减的正弦信号 Fig. 8 Exponentially damped sinusoidal signals

图选项

图 9 静态迟滞算子输出 Fig. 9 Output of static hysteresis operator

图选项

根据2.1.3节辨识得到的S-stop算子的参数，仿真结果如图 9所示。
2.2 非线性子系统逆补偿器设计 令

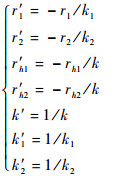(4)

可以求得式(3)所示的非线性算子的逆模型(见图 10)为

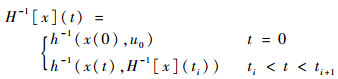(5)

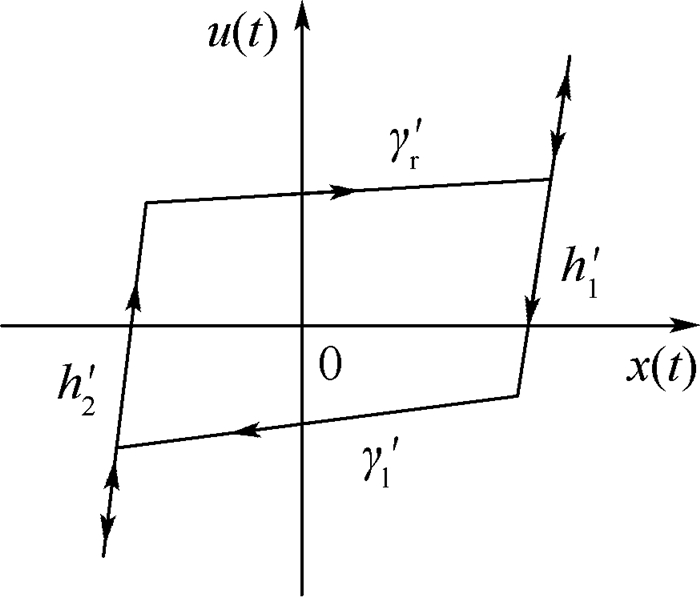图 10 S-stop算子逆模型 Fig. 10 Inverse model of S-stop operator

图选项

式中：

其中：
γ′_r=k′₁x(t)-r′₁, γ′_l=k′₂x(t)-r′₂, h′₁=k′x(t)- r′_h1和h′₂=k′x(t)-r′_h1为S-stop算子逆模型的各包络线函数，γ′_r>γ′_l；Δ_x=x(t)-x(t_i)。在逆算子中，k′₁、k′₂、k′、r′₁、r′₂、r′_h1和r′_h2根据算子参数由式(4)计算得到。将2.1.3节的参数代入式(4)，可得到等效的非线性逆模型H^*-1的参数：r′₁=-0.659，r′₂=-0.424，r′_h1=46.5，r′_h2=8.61，k′=10，k′₁=0.025，k′₂=0.012。
为验证所提逆模型的有效性，进行如下仿真：给定输入信号v(t)，使其分别经过非线性逆模型H^*-1[·]和非线性模型H^*[·]，得到输出信号y(t)，如图 11所示。

图 11 迟滞逆补偿 Fig. 11 Hysteresis inverse compensation

图选项

仿真得到输入输出响应曲线如图 12所示，可见，输入输出曲线的斜率为1，说明基于逆算子的补偿器很好地消除了迟滞特性。

图 12 逆模型验证结果示意图 Fig. 12 Schematic diagram of inverse model verification result

图选项

2.3 线性子系统辨识 基于2.1节中辨识得到的等效非线性子模型H^*，经过如图 11示的迟滞逆补偿后，中间信号可表示为w^*=u′/K，所以输出y′=G/Ku′。采用含有丰富频率信息的正弦衰减扫描信号u′作为激励信号，收集输入输出序列，即可由输入输出数据(u′, y′)辨识得到线性子模型G^*=G/K。
待辨识的线性子系统模型表达式为

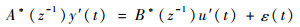(6)

式中：A^*(z^-1)和B^*(z^-1)为单位后移算子z^-1的多项式，z^-1y(t)=y(t-1)，其形式如(2)所示。线性系统各项系数为待辨识参数。根据输入输出数据，利用最小二乘算法^[22]得到的线性子系统的离散传递函数为

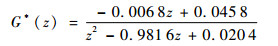(7)

该线性子系统的-3 dB带宽约为0.642 5 Hz。
2.4 辨识算法 给出ETB系统Hammerstein模型辨识步骤如下：
1) 首先给ETB系统一个准静态正弦激励信号u(t)，并测量系统的输出y(t)。
2) 由输入输出数据(u, y)，采用所建立的非线性模型式(3)辨识出等效非线性迟滞子系统H^*的参数。
3) 根据所辨识得到的H^*，基于式(5)设计逆补偿器H^*-1。
4) 将H^*-1与原系统串联，如图 13所示，使得静态迟滞非线性环节H获得补偿，即可由输入输出数据(u′, y′)辨识出等效线性系统G^*。

图 13 经过迟滞逆补偿的ETB系统 Fig. 13 ETB system with hysteresis inverse compensation

图选项

模型等效性证明如下：
易证明所辨识得到的Hammerstein系统(H^*, G^*)与原系统(H, G)是等效的。若(A(z^-1), B(z^-1), H[·])是如图 3所示系统的解，则(A(z^-1), μB(z^-1), H_μ[·])也是图 3系统的解，其中实数μ≠0且有H_μ[·]=H[·]/μ^[15]。令1/μ=K，其中K为图 3中线性动态子系统G的增益，可证明基于本文提出的辨识算法得到的辨识结果(A^*(z^-1), B^*(z^-1), H^*[·])有H^*[·]=KH[·]，A^*(z^-1)=A(z^-1)，B^*(z^-1)=B(z^-1)/K，即所辨识的结果与原系统是等效的^[23]。
3 实验验证 分别采用0.05、0.08、0.1和0.3 Hz的单频信号作为输入来检验该模型的建模效果。图 14给出了单频信号激励下的模型检验曲线。表 1是各频率下的模型检验均方根误差和相对误差。从图 14中可以看出，在控制带宽范围内，尤其是0.002~0.1 Hz范围内，相对误差均小于6%，随着频率的增大，辨识误差逐渐增大，主要是因为Hammerstein系统作为一种模块化模型难以准确描述系统的高频动态特性。

图 14 基于Hammerstein模型的ETB系统建模效果 Fig. 14 Modeling effect of ETB system based on Hammerstein model

图选项

表 1 基于S-stop算子的Hammerstein模型建模效果 Table 1 Modeling effect of Hammerstein model based on S-stop operator

频率/Hz	RMSE/V	RE/%
0.05	0.101 7	3.20
0.08	0.144 2	4.67
0.1	0.162 8	5.14
0.3	0.458 9	14.80

表选项






节气阀在实际应用时跟踪阶跃信号，本文给出了所建立的动态非线性模型的开环阶跃响应与实验结果的比较，如图 15所示，由图中可见开环系统调节时间分布在1 s左右。表 2给出了不同占空比下开环系统的阶跃响应相对误差。从模型结果与实验结果的对比中可以看出，不同幅值阶跃信号下相对误差为1.23%~6.55%，所提出的非线性模型可以较好的描述ETB系统的阶跃响应。

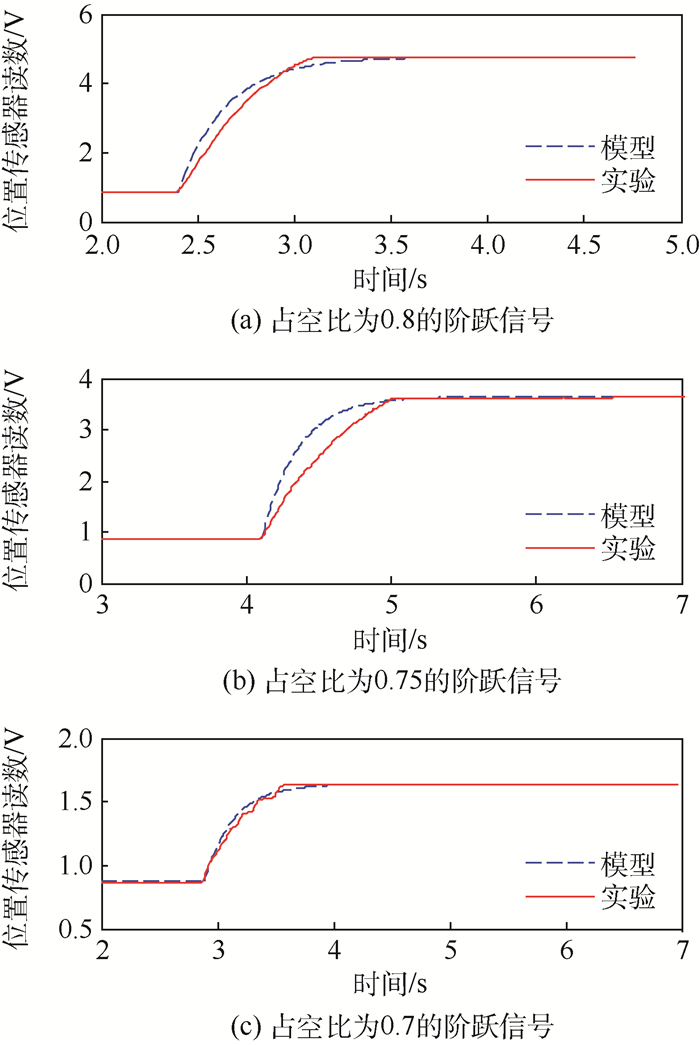图 15 开环系统的阶跃响应 Fig. 15 Step response of open-loop system

图选项

表 2 开环系统的阶跃响应相对误差 Table 2 Step response relative error of open-loop system

占空比	0.8	0.75	0.7
RE/%	4.40	6.55	1.23

表选项






4 结论 本文提出一种基于Hammerstein模型(非线性环节串联线性环节)的ETB系统建模方法：
1) 首次提出一种用以描述ETB系统特殊的迟滞特性S-stop算子，对非线性子系统进行辨识，并求得其解析逆模型。
2) 基于算子逆模型设计迟滞逆补偿器对中间状态进行估计。采用最小二乘方法对线性动态子系统进行辨识。
通过实验验证证明, 所建立的Hammerstein模型可以有效地描述ETB系统的动态迟滞特性。

参考文献

[1]	葛晓成, 彭忆强. 电子节气门辨识建模方法研究[J]. 车用发动机, 2009(3): 5-9. GE X C, PENG Y Q. Research on modeling method of electronic throttle identification[J]. Vehicle Engine, 2009(3): 5-9. DOI:10.3969/j.issn.1001-2222.2009.03.002 (in Chinese)
[2]	GREPL R, LEE B. Modeling, parameter estimation and nonlinear control of automotive electronic throttle using a rapid-control prototyping technique[J]. International Journal of Automotive Technology, 2010, 11(4): 601-610. DOI:10.1007/s12239-010-0072-7
[3]	DEUR J, PAVKOVIC D, PERIC N, et al. An electronic throttle control strategy including compensation of friction and limp-home effects[J]. IEEE Transactions on Industry Applications, 2004, 40(3): 821-834. DOI:10.1109/TIA.2004.827441
[4]	YUAN X F, WANG Y N, WU L H. SVM-based approximate model control for electronic throttle valve[J]. IEEE Transactions on Vehicular Technology, 2008, 57(5): 2747-2756. DOI:10.1109/TVT.2008.917222
[5]	RAJAEI N, CHEN X, ZHENG M.Estimation of spring torque in an electronic throttle valve[C]//Proceeding of IEEE Vehicle Power and Propulsion Conference.Piscataway, NJ: IEEE Press, 2010: 1-6.
[6]	THOMASSON A, ERIKSSON L. Model-based throttle control using static compensators and pole placement[J]. Oil & Gas Science and Technology, 2011, 66(4): 717-727.
[7]	SALEM A, JENS B, MICHAEL T.Electronic throttle simulation using nonlinear Hammerstein model[C]//SAE 2006 World Congress & Exhibition.Warrendale: SAE International, 2007: 12-21.
[8]	ANSON L, WITT T, JAN S P, et al. Electronic throttle control system:Modeling, identification and model-based control designs[J]. Engineering, 2013, 5(7): 587-600. DOI:10.4236/eng.2013.57071
[9]	SCATTOLINI R, SIVIERO C, MAZZUCCO M, et al. Modeling and identification of an electromechanical internal combustion engine throttle body[J]. Control Engineering Practive, 1997, 5(9): 1253-1259. DOI:10.1016/S0967-0661(97)84364-X
[10]	肖寿高.电子节气门控制系统的研究与仿真[D].西安: 长安大学, 2011: 1-6. XIAO S G.The research and simulation of electronic throttle control system[D].Xi'an: Chang'an University, 2011: 1-6(in Chinese). http://d.wanfangdata.com.cn/Thesis/Y1948205
[11]	陈凤祥, 刘玲, 章桐. 基于自抗扰控制技术的电子节气门控制[J]. 中国科技论文, 2014, 9(10): 1188-1191. CHEN F X, LIU L, ZHANG T. Control of electronic throttle based on active disturbance rejection control of technique[J]. China Science Paper, 2014, 9(10): 1188-1191. DOI:10.3969/j.issn.2095-2783.2014.10.020 (in Chinese)
[12]	宋同好.基于Backstepping的电子节气门控制[D].长春: 吉林大学, 2009: 2-5. SONG T H.Electronic throttle control based on Backstepping[D].Changchun: Jilin University, 2009: 2-5(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201104009.htm
[13]	TAN Q Y, GAO H L, CHEN X, et al.Wiener structure based model identification for an electronic throttle body[C]//Proceeding of the 13th IEEE International Conference on Control and Automation.Piscataway, NJ: IEEE Press, 2017: 18-22.
[14]	BAI E. Identification of linear systems with hard input nonlinearities of known structure[J]. Automatica, 2002, 38(5): 853-860. DOI:10.1016/S0005-1098(01)00281-3
[15]	GIRI F, ROCHDI Y, BROURI A, et al. Identification of Hammerstein systems in presence of hysteresis-backlash and hysteresis-relay nonlinearities[J]. Automatica, 2008, 44(3): 767-775. DOI:10.1016/j.automatica.2007.07.005
[16]	GIRI F, BAI E. Block oriented nonlinear system identification[M]. Berlin: Springer Verlag, 2010: 2-3.
[17]	GIRI F, ROCHDI Y, BROURI A, et al. Parameter identification of Hammerstein systems containing backlash operators with arbitrary-shape parametric borders[J]. Automatica, 2011, 47(8): 1827-1833. DOI:10.1016/j.automatica.2011.05.008
[18]	TAN Q Y, CHEN X, ZHENG M.Control of electronic throttle body through extremum seeking approach[C]//Proceeding of 36th Chinese Control Conference.Piscataway, NJ: IEEE Press, 2017: 1232-1238.
[19]	郭咏新, 毛剑琴. 超磁致伸缩作动器的率相关建模与跟踪控制[J]. 北京航空航天大学学报, 2013, 39(10): 1360-1365. GUO Y X, MAO J Q. Rate-dependent modeling and tracking control of giant magnetostrictive actuators[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1360-1365. (in Chinese)
[20]	AI JANAIDEH M, RAKHEJA S, SU C Y.A generalized Prandtl-ishlinskii model for characterizing rate dependent hysteresis[C]//Proceeding of IEEE International Conference on Control Applications.Piscataway, NJ: IEEE Press, 2007: 343-348.
[21]	KRASNOSEL'SKⅡ M A, PIKROVSKⅡ A V. Systems with hysteresis[M]. Berlin: Springer Verlag, 1983: 22-24.
[22]	BARONE P, LARI I. On a class of parameters estimators in linear models dominating the least squaresone[J]. Digital Signal Processing, 2016, 54: 27-34. DOI:10.1016/j.dsp.2016.04.001
[23]	ZHANG Z, DU C L, GAO T T, et al.Hysteresis modeling and compensation of PZT milliactuator in hard disk drives[C]//Proceeding of 13th International Conference on Control Automation Robotics & Vision.Piscataway, NJ: IEEE Press, 2014: 980-985.