数值模拟具有效率高、成本低的特点,因此国内外研究人员采用数值仿真技术在滑动轴承润滑性能研究中开展了大量工作。国内外研究人员主要采用数值仿真技术分析滑动轴承润滑性能。如使用差分法、有限元法和有限体积法对Reynolds方程进行数值求解[2-3],为了仿真得到更准确的润滑性能,数值求解中边界条件的处理上也逐步由未考虑油膜破裂情况的经典的Sommerfeld边界条件,发展至考虑实际情况的Reynolds边界条件以及考虑介质的汽化相变的质量守恒边界条件等[4-5]。此外,在轴承润滑分析中也关注了油膜的温度影响因素,并由二维绝热流动的能量方程,发展至考虑三维黏度变化的广义Reynolds方程,这已经成为当前研究热流体润滑的基本理论方程[6-10]。由于轴承内部油膜压力的不均匀分布,必然会引起结构发生弹性甚至是塑性形变,温度的变化也会使轴承的结构发生热变形。因此,国内外研究人员开展了滑动轴承的多场耦合仿真研究[11-18],分析了压力、载荷、温度、结构变形等因素对油膜间的耦合作用机理及滑动轴承润滑特性的分布规律,也形成了弹性流体动压润滑理论[19]。此外,当膜厚比低于4时,固体壁面的微元凸峰相互接触使得润滑问题变为混合润滑状态,在分析的过程中需要考虑计入表面形貌的作用[20]。在目前阶段,对于计入表面形貌的润滑计算理论发展得还不够充分,没能建立准确的计算模型和计算方法,在理论分析和实验领域依然存在许多问题有待于研究人员去探索解决的方法。
由于航空燃油泵所采用的滑动轴承与一般滑动轴承结构存在较大差异,出于缩减体积和质量的考虑,燃油泵的滑动轴承与卸荷槽及间隙补偿装置为一体式结构设计,且燃油泵滑动轴承没有独立配置润滑系统,而是通过开孔和开槽等手段,将燃油泵出口的高压燃油作为润滑介质引入滑动轴承内部进行自冷却。由于燃油泵采用的润滑介质为低黏度的航空3号煤油,在0~100℃条件下,燃油介质黏度为滑油介质黏度的1/100~1/10。黏度对轴承润滑性能影响非常大,流体的黏性剪切效应是产生动压支撑效果的主要原因。因此,燃油介质的黏度低就意味着动压支撑效果不及滑油介质,当燃油泵径向载荷超出动压油膜的承载能力时,会使固体壁面直接接触,根据微凸体接触理论,微元粗糙峰会发生接触产生大量的热使油膜的温度升高。若滑动轴承设计不合理则温度的升高会导致燃油介质发生剪切稀化现象,使黏度进一步降低,最终导致轴承发生灼伤、胶合等故障。为此本文通过对航空燃油泵滑动轴承的润滑性能进行数值仿真研究,探索低介质黏度和自冷却工作条件下的航空发动机燃油泵的滑动轴承的润滑特性分布规律,为滑动轴承的设计分析提供理论指导。
1 燃油泵滑动轴承润滑模型 图 1为典型的自冷却结构的航空燃油泵滑动轴承。
 |
| 图 1 航空燃油泵滑动轴承 Fig. 1 Sliding bearing of aviation fuel pump |
| 图选项 |
图 1中,滑动轴承对应燃油泵的进口及出口部位,开有与困油区相通的卸荷槽,在燃油泵高压侧卸荷槽开孔,将出口处高压燃油引入轴承进行自冷却润滑,同时在旋转轴的带动下产生动压起到支撑作用。该型滑动轴承是包角为360°的典型圆柱型结构,为了保证轴与轴孔能够安装和拆卸,同时也为了加工的方便,轴承存在一个轴向的退刀槽,部分结构参数见表 1。
表 1 滑动轴承基本参数 Table 1 Basic parameters of sliding bearing
| 参数 | 数值 |
| 轴承宽度B/mm | 24 |
| 轴孔直径D/mm | 20.021 |
| 介质黏度μ/(Pa·s) | 9.66×10-4 |
| 介质密度ρ/(kg·m-3) | 779 |
| 轴颈直径d/mm | 19.92 |
| 转速n/(r·min-1) | 8000 |
| 偏心率e | 0.8 |
| 介质比热Cp/(J·(kg·℃)-1) | 2000 |
表选项
1.1 Reynolds润滑方程及压力边界条件 流体动压润滑是滑动轴承内部油膜产生油膜压力的基本原理,其Reynolds润滑方程为
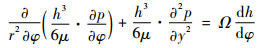 | (1) |
式中:p为油膜压力;φ为柱坐标下的角度;r为轴承半径;h为油膜厚度;Ω为轴颈旋转速度。
对于Reynolds方程的求解,需要给定其压力的边界条件。对于圆柱型滑动轴承,Sommerfeld边界条件认为,扩散区及收缩区都存在完整的油膜,周向的油膜压力呈现周期性变化,即
 | (2) |
但目前的实验已经验证,间隙扩散段油膜并不完整,而是呈现出许多细条状。Gümbel条件或半Sommerfeld条件认为,完整的油膜只存在于间隙的收缩段,即Φ=θ及Φ=θ+π时,p=pa,Φ=θ~θ+π时,p≥pa,θ为周向角度,pa为当地测量压力。
间隙的扩散区内油膜完全破裂,即
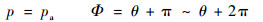 | (3) |
式(3)的半Sommerfeld条件得到的结果会比较保守。而航空燃油泵滑动轴承通常认为介质不产生汽化相变,因此采用Reynolds边界条件可比较合理地认为油膜的破裂取决于下列情况:
 | (4) |
而在轴向方向也就是y方向,轴承两端的压力和外界压力相等,如果把原点取在轴承长度的中点,就可以得到
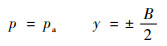 | (5) |
在求解Reynolds方程时,对于刚性动压润滑模型,认为油膜的厚度分布是已知的,油膜厚度方程为
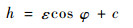 |
式中:c为半径间隙;ε为偏心距。
1.2 滑动轴承绝热流动 燃油黏度随温度变化且分布呈现出不均匀性,因此在计算的过程中,需要考虑温度及黏度分布的不均匀性。实际轴承安装在泵壳体内部,通过壳体的热传导量和热辐射量非常少,内部热量的传递主要依靠燃油介质的端泄漏量,因此假设油膜流动为绝热流动。通过建立微元控制体的能量守恒方程,具体中间推导过程略去,得到滑动轴承内部油膜流动的能量方程为
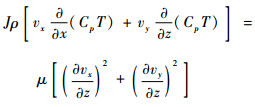 | (6) |
式中:J为热功当量;T为油膜温度。
因滑动轴承的油膜厚度非常薄,可以认为沿油膜厚度方向速度、温度不存在梯度,具体中间推导过程略去,得到绝热流动过程沿油膜厚度的能量方程的积分形式为
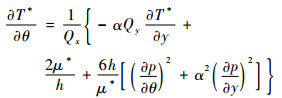 | (7) |
式中:*代表该参数进行了无量纲化; α为无量纲系数;Qx和Qy分别为油膜在x和y方向上的泄漏量。
为确定温度对黏度的影响,本文中对比了Reynolds方程、斯洛特(K.F.Slotte)方程和伏格尔(H.Vogel)方程的计算精度。根据航空3号煤油的温度黏度试验数据(-40~120℃),分别对以上3种温度-黏度关系进行拟合分析,对比结果如图 2所示。可以看出,Reynolds方程、斯洛特方程和伏格尔方程中,伏格尔方程可以更好地拟合燃油黏度和温度之间的关系,精度是最高的。因此,在本文中后续的计算及仿真中,将使用伏格尔方程作为燃油温度和黏度之间的关系式。
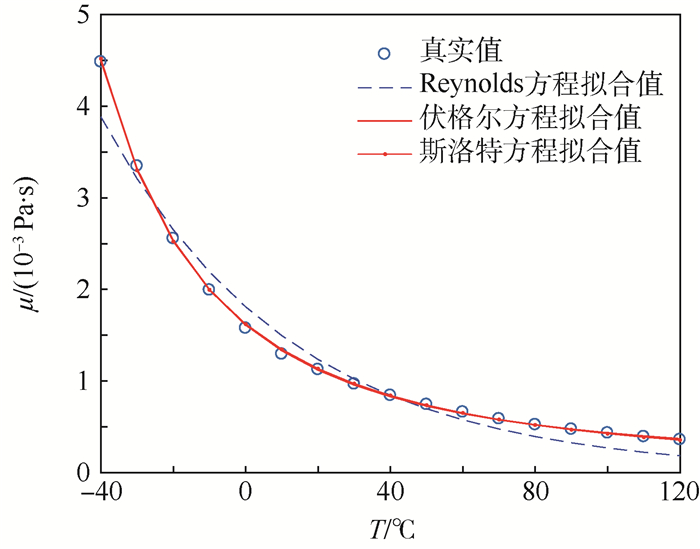 |
| 图 2 不同方程拟合值与真实值对比 Fig. 2 Comparison between fitting values of different equations and actual values |
| 图选项 |
1.3 滑动轴承油膜润滑特性计算 1) 油膜承载力
将轴颈表面受到的压力进行积分即可得到油膜的承载力F,用Fξ表示水平方向的受力,用Fη表示垂直方向的受力,则有
 | (8) |
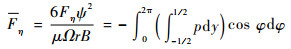 | (9) |
式中:ω为角速度; Fξ和Fη分别为水平和垂直方向的无量纲承载力;ψ为滑动轴承间隙比。
2) 摩擦阻力
油膜流动与轴颈之间的摩擦作用是导致滑动轴承内部温度升高的主要原因,要计算油膜的温升,需要准确计算轴颈受到的摩擦阻力。摩擦阻力f可以看成是由剪切流阻力Ft1和压力流阻力Ft2叠加作用,剪切流阻力可分别由油膜承载区和非承载区的计算叠加得到
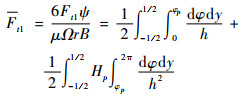 | (10) |
式中:φp为油膜破裂的角度;Hp为破裂边上的油膜厚度。由于燃油泵中滑动轴承的包角为360°,所以积分的起始角度和终止角度分别为0和2π。
压力流阻力Ft2可由力偶平衡得到
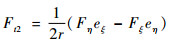 | (11) |
式中:eξ为单位面积水平方向的受力;eη为单位面积垂直方向的受力。
3) 端泄漏量
油膜内部压力迫使润滑介质不断向轴瓦两侧泄漏流出,使泄漏量带走摩擦产生热量。航空燃油泵滑动轴承的压力分布是左右对称的,因此其轴瓦两端的无量纲泄漏量为
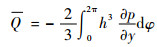 | (12) |
4) 油膜温升
轴颈与油液的摩擦作用是滑动轴承内部温度升高的主要原因。认为各点处油膜的温度保持一致,且全部由端泄漏量通过对流换热作用带走,根据热平衡方程得出油膜的温升为
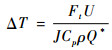 | (13) |
式中:Ft为轴颈表面处的摩擦阻力;U为轴颈滑动速度;Q*为滑动轴承的端泄漏量;ΔT为润滑介质的温升。
2 基于CFD的径向载荷计算 燃油泵的径向载荷是准确分析润滑性能的重要因素。为了更为精确地计算齿轮齿面上的油压力的作用力产生的径向载荷,本文通过采用CFD数值模拟的方法计算齿轮工作面油压引起的径向力,通过对压力分别积分得到其径向载荷。本文中利用PumpLinx流体仿真软件对转速为6 400和8 000 r/min条件下,不同出口压力工况下的燃油泵模型进行仿真(网格划分、边界条件设定等步骤略过),并将仿真结果与该燃油泵的试验数据进行对比,验证CFD仿真方法的准确性。
图 3为转速分别为6 400、8 000 r/min时不同出口压力工况下的压力分布云图。可以看出,该燃油泵的压力分布趋势符合一般燃油泵的变化规律,从进口处至出口处,随着转速的变化越来越大,且随着转速升高,其压力越大。
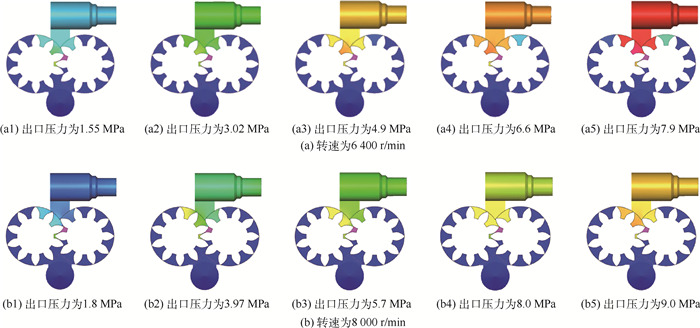 |
| 图 3 不同条件下的燃油泵压力分布云图 Fig. 3 Pressure distribution contours under different conditions of fuel pump |
| 图选项 |
图 4给出了转速为6 400、8 000 r/min时燃油泵的出口压力Pout、流量的仿真数据与试验数据对比结果,P为进口压力。可以看出,不同工作工况下的仿真数据与试验数据吻合较好,仿真精度在0.1%~4.0%以内,数值模拟具有高的仿真精度。因此,可基于PumpLinx环境下的仿真方法所得出燃油泵进出口的压力分布,对其进行积分得到燃油泵径向载荷。该型燃油泵滑动轴承的径向载荷计算结果如表 2所示。
 |
| 图 4 不同条件下的燃油泵仿真数据与试验数据对比 Fig. 4 Comparison between simulation data and experimental data under differernt conditions of fuel pump |
| 图选项 |
表 2 滑动轴承径向力计算结果 Table 2 Radial force calculation results of sliding bearing
| 径向力 | 扭矩径向力 | 液压径向力 | 主动轮合力 | 从动轮合力 |
| 数值/N | 1 135.5 | 4 232.5 | 3 149.9 | 5 284.0 |
表选项
3 滑动轴承润滑特性仿真分析 本文在计算滑动轴承的润滑特性中,首先对Reynolds方程进行无量纲化,凸显各变量的作用,使方程形式更加紧凑,同时为了避免病态问题的出现,采用有限差分法进行求解。在实现Reynolds边界条件和计算过程中采用迭代方法,当计算出的无量纲油膜压力p < 0时,将此处的压力值强制设置为0,当周向方向首次出现压力为0的节点时,就认为是油膜的破裂点,此后的节点压力同样也设置为0。为了保证收敛性和收敛速度,在迭代计算的过程中设置了松弛因子β,将得到的新旧值的差乘以β,并与旧值求和作为该节点处新的迭代值,直到满足近似解及预先给定的收敛精度。
3.1 不同结构参数对滑动轴承润滑特性仿真分析 本节研究分析不同间隙比、宽径比条件下,滑动轴承油膜压力、端泄漏量、摩擦阻力等润滑特性的变化规律。滑动轴承润滑介质的工作温度定为30℃,此时燃油介质的黏度为9.666×10-4 Pa·s。
1) 不同间隙比及偏心率下润滑特性分析
图 5为相同轴颈及宽径比下,不同间隙比和偏心率对滑动轴承油膜承载力的影响。
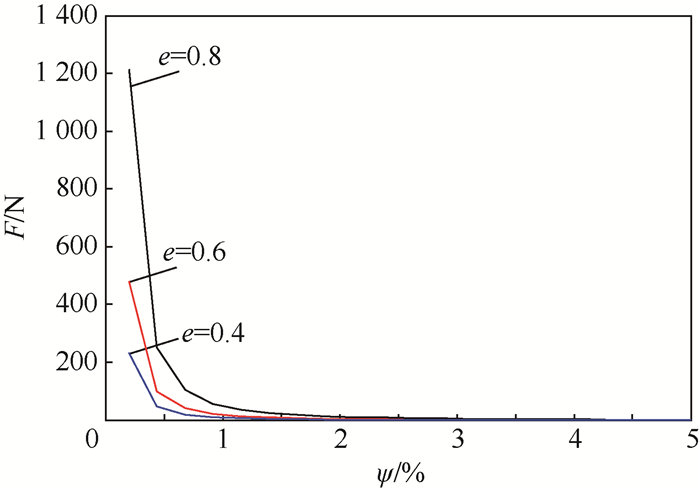 |
| 图 5 油膜承载力随间隙比和偏心率的变化 Fig. 5 Variation of oil film bearing capacity with clearance ratio and eccentricity ratio |
| 图选项 |
由图 5可以看出,当偏心率一定时,滑动轴承的油膜承载力随着间隙比的增加而单调下降。以偏心率为0.8为例,在间隙比小于0.5%时,油膜的承载力随间隙比的增加迅速下降,当间隙比增加到1%以后,油膜的承载力则呈现出较平缓的变化趋势。在其他偏心状态下,油膜承载力与间隙比的变化趋势与此类似。随着轴颈工作偏心率的降低,图中曲线逐步下移,说明当间隙比相同时,随着偏心率的减小,油膜的承载力也在逐渐减小。
图 6给出了间隙比分别为0.2%、0.3%和0.5%时,轴颈处于不同偏心状态下的油膜压力分布。
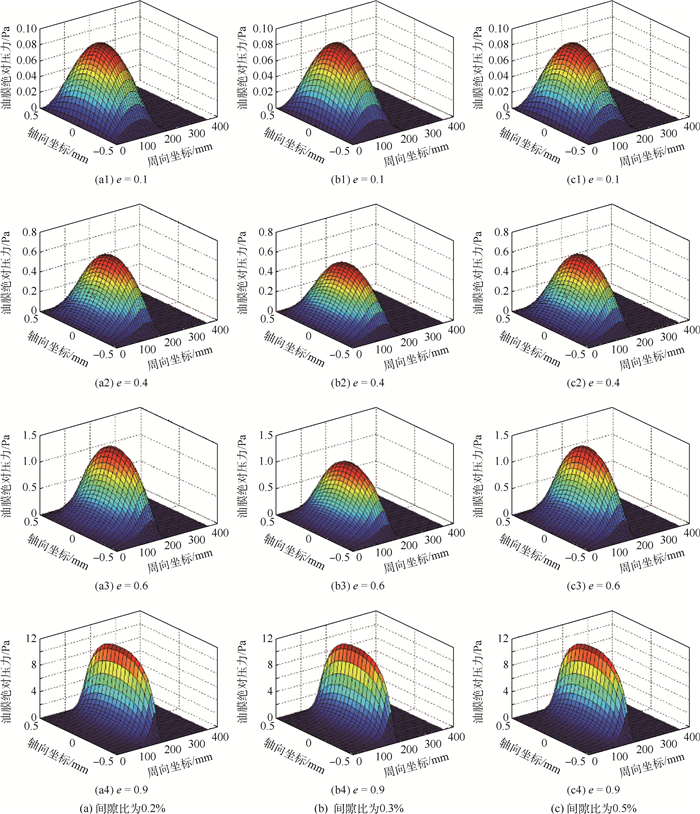 |
| 图 6 不同间隙比和偏心率下的油膜压力分布 Fig. 6 Oil film pressure distribution at different clearance ratios and eccentricity ratios |
| 图选项 |
当间隙比为0.2%时,滑动轴承在不同偏心状态下的一组压力分布情况如图 6(a)所示。在收敛间隙内,油膜的压力逐渐增加,而在扩散间隙内,油膜的压力保持为零,这与Reynolds边界条件保持一致。说明收敛间隙区域为滑动轴承的主要承载区,而在扩散间隙处,油膜发生破裂,不能再承担外载荷。此外,随着偏心率的提高可以看出,油膜压力的峰值在不断增加,所以油膜承载力也相应增大。此外,高偏心(偏心率为0.9)状态下,承载区内部的压力梯度增大,油膜的破裂位置向上游移动,因而偏位角也逐渐减小。当间隙比为0.3%时(见图 6(b)),在偏心率为0.1较低的情况下,油膜压力分布并没有太大的变化,而在大偏心率0.9的状态下,油膜压力分布的峰值有了明显的下降。当间隙比为0.5%时(见图 6(c)),油膜压力分布的规律与间隙比为0.2%和0.3%时相一致。但需注意的是,偏心率的提高使油膜压力分布变得更加陡峭,将不利于滑动轴承内部的燃油流出,即不利于滑动轴承的散热。
对比图 6可以看出,随着间隙比从0.2%到0.3%、0.5%的逐步增加,油膜的绝对压力分布逐渐下降,因而承载力也在减小。假如油膜中的动压承载力无法承受外部载荷时,固体壁面就会相互接触而导致液体润滑条件失效,润滑状态转变为边界润滑甚至是干摩擦状态,从而引发磨损、胶合等故障的发生,因此润滑性能分析中必须考虑油膜的温升效应,防止滑动轴承内部温升过高。
图 7给出了不同偏心率和间隙比下油膜厚度的变化情况。从图 7(a)中可以分析得到,在同一间隙比条件下,油膜厚度随着偏心率的增高而下降。而在同一偏心率下,随着间隙比的增高油膜厚度在增加。图 7(b)则给出了偏心率为0.4、0.6、0.8时,油膜厚度随间隙比的变化情况。可以看到,当偏心率一定时,油膜厚度与间隙比呈线性正比关系。
 |
| 图 7 油膜厚度随偏心率和间隙比的变化 Fig. 7 Variation of oil film thickness with eccentricity ratio and clearance ratio |
| 图选项 |
2) 不同偏心率及宽径比下润滑特性分析
图 8给出了滑动轴承宽径比B/D与油膜承载力F之间的关系。
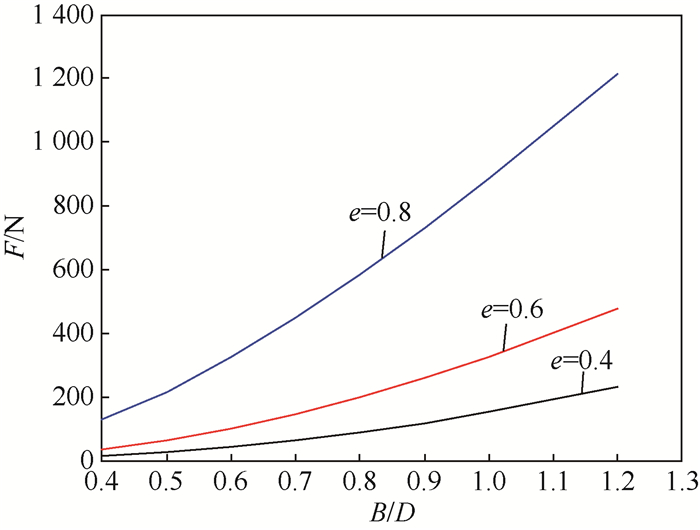 |
| 图 8 油膜承载力随宽径比和偏心率的变化 Fig. 8 Variation of oil film bearing capacity with width diameter ratio and eccentricity ratio |
| 图选项 |
从图 8中可以看出,当偏心率一定时,滑动轴承的油膜承载力随着宽径比的增加而增加,这主要是因为滑动轴承的宽度增加,轴承的承载范围增大使得承载能力提高。
不同偏心率和宽径比条件下,对滑动轴承内部油膜压力分布沿轴向方向上的变化规律进行仿真,仿真结果如图 9所示。
 |
| 图 9 不同宽径比和偏心率下油膜压力的轴向分布 Fig. 9 Axial pressure distribution of oil film at different width diameter ratios and eccentricity ratios |
| 图选项 |
由图 9可以看出,滑动轴承的轴向油膜压力呈现出对称的抛物线性分布,在中间区域压力的梯度最小。随着宽径比的增加,中间区域的压力变得更加平缓。而轴承中心燃油的流动依靠的是压力的梯度差而建立的,即在较大的宽径比条件下,滑动轴承的燃油流量会减少。而滑动轴承内部油膜的流动近似可认为是绝热流动,因此摩擦产生的热量大部分都由燃油的端部泄漏带走,因此流量的下降必然导致油膜内温度的升高,必须考虑温度对润滑性能的影响。
3.2 滑动轴承热流动特性分析 根据图 9中的分析可知,分析燃油泵滑动轴承润滑特性时必须考虑温度影响,为此本文进行滑动轴承热流体润滑仿真计算。图 10为热流体润滑下滑动轴承无量纲油膜承载力F、摩擦阻力f与偏心率的关系。
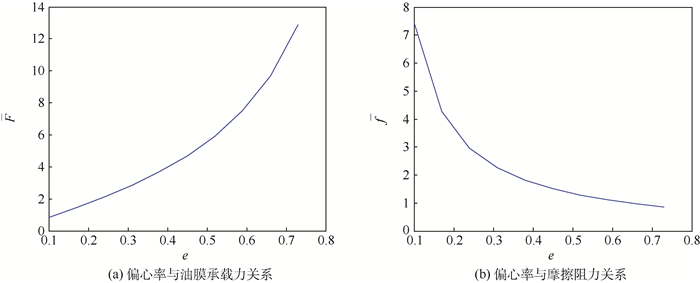 |
| 图 10 滑动轴承无量纲油膜承载力、摩擦阻力与偏心率的关系 Fig. 10 Relationship among non-dimensional oil film bearing capacity, friction force and eccentricity ratio of sliding bearing |
| 图选项 |
图 10(a)中,与等温油膜滑动轴承油膜承载力与偏心率的关系类似,热流体润滑的计算结果同样表明,随着偏心率的增大,油膜的承载力会逐渐增大。与等温油膜不同的是,随着偏心率的增加,承载力增加的速度明显加快。
图 10(b)给出了滑动轴承摩擦阻力与偏心率之间的关系。随着轴颈工作位置的偏心率提高,滑动轴承油膜内的摩擦阻力也逐渐降低。这主要是因为随着偏心率的增高,油膜破裂的位置提前,因此剪切流阻力下降。于此同时,偏心率的提高使偏位角减小,根据力偶平衡原则,压力流阻力也因此而减少。摩擦阻力的减小,会使油膜产生的热量下降。但是需要指出的是,如果不能够保证一定的油膜厚度,偏心率的提高有可能使固体壁面的凹凸体互相摩擦,从而生成大量的热。此外,偏心率的提高还会使燃油的端泄漏量减小,因而会影响轴承的散热。因此,不能单纯依靠滑动轴承的摩擦阻力判断油膜的温度是否满足要求。
图 11(a)给出了滑动轴承在不同偏心率下油膜厚度的变化关系。油膜厚度在轴向方向上没有变化,这主要是假设轴颈与轴孔的同心率比较高,不存在轴心偏离的情况。而在周向方向上,油膜厚度从最初0°时的最大值逐渐降低,至180°时油膜厚度达到最小值,这一段也就是间隙的收敛段,即轴承的主要的承载区。而在180°~360°的区间范围内,油膜间隙不断增加,实际上此时已经进入间隙的扩张段,油膜已经发生了破裂。此处的压力较低,没有承载能力。对比不同偏心状态下的最大油膜厚度和最小油膜厚度可以看出,随着偏心率的提高,最小油膜厚度不断下降,而最大油膜厚度不断提高,因而收敛间隙的梯度相应增高,动压效果会更加明显,承载能力也可得到提升。
 |
| 图 11 不同偏心率下的滑动轴承润滑特性 Fig. 11 Lubrication characteristics of sliding bearing under different eccentricity ratios |
| 图选项 |
图 11(b)为根据热流体润滑计算结果得到的偏心率与油膜压力分布之间的关系。在油膜的承载区,油膜压力在中心位置最高,呈现出尖峰形状。在低偏心率情况下,压力分布比较平缓,而在高偏心率情况下,压力分布变得越来越陡峭。这主要是因为油膜在高偏心率条件下会提前破裂,使非承载区的范围扩大,同时压力的尖峰值却在升高,导致压力分布变得陡峭。
图 11(c)给出了油膜温度分布与偏心率间的关系。可以看出,温度峰值主要有4个,分别位于轴承中心位置、最小油膜厚度的端部以及承载部位的前部。这主要是因为油膜温度分布与油膜厚度及压力梯度相关。从能量方程的关系来看,油膜温度与油膜厚度成反比,所以在最大油膜厚度处油膜温度最低,而在最小油膜厚度处油膜温度最高。此外,油膜温度与压力在周向方向的梯度的平方成正比,即在±(?p/?φ)2处油膜温度最高。油膜温度还与压力在轴向方向的梯度平方±(?p/?y)2成正比,因此油膜温度会在宽度方向上呈现出中间低、两边高的分布。可以看出,随着偏心率的升高,油膜温度的峰值越来越明显,而温升也不断提高。当油膜温度升高时,润滑介质的黏度是逐渐降低的。当偏心率较低时,由于油膜的温度变化不大,因而黏度场区域均匀。而随着偏心率的升高,油膜温度分布的不均匀性开始表现出来,对应的油膜中的黏度也随之降低。
4 结论 本文针对低介质黏度的航空燃油泵滑动轴承,开展了滑动轴承的润滑特性分析研究。
1) 为了得到更为准确的温度和载荷边界,对比了几类温-黏关系可知,伏格尔方程获得的航空3号煤油温-黏关系的精度最高,计算中可选取该温-黏关系保证润滑性能分析精度。此外,采用CFD数值模拟与试验相结合的方法计算轴承径向载荷,其计算精度在0.1%~4.0%以内,能够为分析润滑特性提供准确的载荷边界。
2) 同一偏心率下,滑动轴承的油膜承载力随着间隙比的增加而单调下降,油膜厚度随着间隙比的增高而增加。同一间隙比下,油膜的承载力随着偏心率的减小也逐渐减小,油膜厚度随着偏心率的增高而下降。提高偏心率可提高滑动轴承的油膜承载力,但偏心率的提高会使压力分布变得更加陡峭,不利于滑动轴承的散热和冷却控制,仿真中必须考虑油膜的温升效应。当偏心率一定时,可通过增加宽径比提高滑动轴承的油膜承载力,但在较大的宽径比条件下,滑动轴承的燃油流量会减少,流量的下降必然导致油膜内温度的升高。
3) 热流体润滑计算中,偏心率的增大会使得油膜承载力提高,端泄漏量减小,油膜厚度下降,摩擦阻力逐渐减小。端泄漏量减小会影响轴承的散热;油膜厚度下降使得其收敛间隙的梯度相应增高而增强动压效果,从而提升轴承的承载能力。摩擦阻力的减小会使油膜产生的热量下降。而油膜温度与油膜厚度成反比,油膜温度在轴承宽度方向上呈现出中间低、两边高的分布,且随着偏心率的升高,油膜温度的峰值越来越明显,温升也不断提高,油膜温度分布的不均匀性加剧,因此对应的油膜中的黏度也随之降低。在滑动轴承的设计中,应综合考虑油膜承载力、端泄漏量、油膜厚度和温升间的相互制约因素,合理地优化间隙比、宽径比和偏心率以提高滑动轴承润滑性能。
参考文献
| [1] | 张绍基. 航空发动机控制系统的研发与展望[J]. 航空动力学报, 2004, 19(3): 375-382. ZHANG S J. A review of aeroengine control system[J]. Journal of Aerospace Power, 2004, 19(3): 375-382. DOI:10.3969/j.issn.1000-8055.2004.03.018 (in Chinese) |
| [2] | 岑少起, 张少林, 郭红. 超重载滑动轴承EHL数值解快速收敛及黏压指数的影响[J]. 机械传动, 2007, 31(1): 3-6. CEN S Q, ZHANG S L, GUO H. The speediness convergence of EHL solution of sliding bearing and influence of the viscosity-pressure relation under super heavy load[J]. Journal of Mechanical Transmission, 2007, 31(1): 3-6. DOI:10.3969/j.issn.1004-2539.2007.01.002 (in Chinese) |
| [3] | 张准, 朱克勤. 电流变液滑动轴承的数值研究[J]. 力学学报, 2003, 35(2): 135-139. ZHANG Z, ZHU K Q. Numerical study of journal bearings with electrorheological lubricants[J]. Acta Mechanica Sinica, 2003, 35(2): 135-139. DOI:10.3321/j.issn:0459-1879.2003.02.002 (in Chinese) |
| [4] | HUANG P. Numerical calculation of lubrication[M]. Beijing: Tsinghua University Press, 2013. |
| [5] | 李强, 郑水英, 刘淑莲. 计入JFO边界条件的滑动轴承性能分析[J]. 机械强度, 2010, 32(2): 102-106. LI Q, ZHENG S Y, LIU S L. Analysis of the performance of journal bearing with JFO boundary condition[J]. Journal of Mechanical Strength, 2010, 32(2): 102-106. (in Chinese) |
| [6] | ST?HL J. Narrow journal bearings[J]. Proceedings of the Institution of Mechanical Engineers.Part J:Journal of Engineering Tribology, 2002, 216(5): 343-346. DOI:10.1243/135065002760364877 |
| [7] | GITA T, MARC C. Performance of a plain journal bearing with flooded ends[J]. Tribology Transactions, 2002, 45(3): 310-317. DOI:10.1080/10402000208982554 |
| [8] | JOHANSSON L, WETTERGREN H. Computation of the pre-ssure distribution in hydrodynamic bearings using Newton's method[J]. Journal of Tribology, 2004, 126(2): 404-407. DOI:10.1115/1.1631009 |
| [9] | DOWSON D, HUDSON J D, HUNTER B, et al. An experimental investigation of the thermal equilibrium of steadily loaded journal bearings[M]. Boca Raton: CRC Press, 1994: 251-269. |
| [10] | 苏红, 毛军, 薛琳. 一种复合式滑动轴承的实验研究[J]. 北京交通大学学报, 2003, 27(4): 11-13. SU H, MAO J, XUE L. Research and experiment on a compound sliding bearing[J]. Journal of Northern Jiaotong University, 2003, 27(4): 11-13. DOI:10.3969/j.issn.1673-0291.2003.04.003 (in Chinese) |
| [11] | DWORK C, NAOR M, PITASSI T, et al.Differential privacy under continual observation[C]//Proceedings of the 2010 ACM International Symposium on Theory of Computing.New York: ACM, 2010: 715-724. |
| [12] | SHAO J, YANG X, WANG Y, et al.Research on thermal deformation field of heavy hydrostatic thrust bearing rotation-workbench at different auxiliary-hole position[C]//Proceedings of 2011 International Conference on Electronic & Mechanical Engineering and Information Technology.Piscataway, NJ: IEEE Press, 2011: 912-915. |
| [13] | VERMA R S, RAHMAN L, VERMA R K, et al. Post harvest storage method for rose-scented geranium (L'Herit.ex Ait.)[J]. Journal of Essential Oil-Bearing Plants, 2013, 16(5): 693-698. DOI:10.1080/0972060X.2013.862930 |
| [14] | JIN C, WU B, HU Y.Theoretical calculation of thermal contact resistance of ball bearing under different loads[C]//6th International Conference on Informatics in Control, Automation and Robotics, 2009: 181-188. |
| [15] | TAKABI J, KHONSARI M M. On the dynamic performance of roller bearings operating under low rotational speeds with consideration of surface roughness[J]. Tribology International, 2015, 86: 62-71. DOI:10.1016/j.triboint.2015.01.011 |
| [16] | DHANDE D Y, PANDE D W.Multiphase flow analysis of hydrodynamic journal bearing using CFD coupled fluid structure interaction considering cavitation[C]//International Conference on Automatic Control and Dynamic Optimization Techniques, 2016: 964-971. |
| [17] | 蔡林.流体动压滑动轴承静特性研究[D].哈尔滨: 哈尔滨工程大学, 2012. CAI L.Investigation on static performance of hydrodynamics bearing[D].Harbin: Harbin Engineering University, 2012(in Chinese). |
| [18] | 王迎佳, 刘敏珊, 岑少起, 等. 混合流态下径向滑动轴承的静态特性研究[J]. 润滑与密封, 2014, 39(5): 41-46. WANG Y J, LIU M S, CEN S Q, et al. Static lubrication characteristics of radial sliding bearings under coexistence fluid state of laminar flow and turbulence[J]. Lubrication Engineering, 2014, 39(5): 41-46. DOI:10.3969/j.issn.0254-0150.2014.05.008 (in Chinese) |
| [19] | ZHANG X J, HUANG Y, GUO Y B, et al. A dynamic rheological model for thin-film lubrication[J]. Chinese Physics B, 2013, 22(1): 426-433. |
| [20] | 张振山, 戴旭东, 张执南, 等. 轴颈倾斜的径向轴承热弹性流体动力润滑分析[J]. 上海交通大学学报, 2013, 47(9): 1347-1352. ZHANG Z S, DAI X D, ZHANG Z N, et al. Thermoelastohydrodynamic lubrication analysis of misaligned plain journal bearings[J]. Journal of Shanghai Jiaotong University, 2013, 47(9): 1347-1352. (in Chinese) |
