当前,基于核的学习算法,例如支持向量机(Support Vector Machine, SVM)、核超限学习机(Kernel Extreme Learning Machine, KELM)等,已经被广泛应用到故障诊断领域中,并且展示出优越的性能[8-9]。多核学习(Multi-Kernel Learning, MKL)作为一种灵活性更强、解释能力更好的核学习算法[10],近些年来受到了广泛的关注。文献[11-12]已经将MKL引入到了包括模拟电路、变压器等系统的故障诊断中,并通过大量实例证明基于MKL的诊断算法在面对单故障、多故障以及并发故障时均能取得更高的诊断精度。
目前,大多数的文献主要面向基于SVM的MKL算法研究,而对于MKL的具体形式则主要采用有限个给定基核的线性凸组合。半定规划,二次约束二次规划,半无限线性规划等算法相继被提出去解MKL问题。文献[13]在2008年提出了一种更有效的算法,称作SimpleMKL,其使得MKL对于大样本问题更加实用。但在这些算法中,每个基核的权重在整个输入空间保持不变,显然忽视了输入空间的局部多样性。不同的核函数针对不同的样本具有不同的可用性,为了体现这种可用性上的差异性,有必要为每一个样本点调节核系数[14-15]。基于这种思想,局部算法被引入MKL中,即采用一种依赖样本的方式为基核分配权重。为此,科研人员已经开展了相关研究。
G?nen和Alpaydin提出了最初的局部多核学习(Localized Multi-kernel Learning, LMKL)算法[16]。取代直接优化局部权重,文献[16]采用一系列选通函数去近似局部权重,以解决局部权重的优化形式二次非凸的问题。文献[17-18]基于文献[16]的思想,提出2种改进算法。前者依据半径-间距界将最小超球的半径融入到LMKL中;后者构造了一种概率置信核以此充当选通函数。文献[19]提出了一个p范数约束的LMKL模型。通过使用二阶Taylor展开来近似p范数,将局部权重的优化问题转化为一个非凸的单约束二次规划问题,最终采用半定规划进行求解。LMKL算法将局部权重拟合到每一个确定样本上,虽然可以充分描述样本的类内多样性,但也可能会导致过拟合问题的出现。同时,需要优化的变量个数等于样本数乘以基核数,当数据规模较大时算法的复杂性将变得无法控制。
为此,考虑到来自于同一聚类的数据具有相似的局部特征,趋向于具有相似的性质。本文结合航空电子设备及其子系统故障诊断的实际,提出一种基于近邻传播(Affinity Propagation, AP)局部聚类MK-ELM(LCMKELM)诊断模型。该模型通过为具有相似分布特性的故障样本分配相同的局部权重,在继承一般LMKL算法局部特征自适应表示能力的同时,避免了过学习风险的出现,有效约减了局部算法的计算复杂性。同时,通过分别构造面向输入空间和特征空间的选通函数,并以选通函数近似局部权重,提出一种2步交替优化的策略,有效解决了局部权重二次非凸的优化形式难以求解的问题。
1 问题描述 对于一个具有c(c≥2)种故障模式的诊断问题,设训练和测试数据集分别为DTr和DTe。令DTr={(x1, y1), (x2, y2), …, (xi, yi), …, (xn, yn)}。其中:xi∈Rd为训练数据实例,d∈R为xi的维数;yi∈{1, 2, …, c}为xi对应的故障模式。令DTe={(x′1, y′1), (x′2, y′2), …, (x′j, y′j), …, (x′n′, y′n′)}。其中,x′j∈Rd为测试数据实例;y′j未知。故障诊断模型设计的目的就是要基于DTr寻找一个映射函数f(·):Rd→R,以使得DTe中的任一个数据实例x′j都可以通过映射得到相应的故障模式y′j∈{1, 2, …, c}。
LMKL中局部权重定义为γ={γq(xi)}q=1, 2, …, ri=1, 2, …, n,每一个局部权重既与基核相关,又与对应的样本相关。设{k1(·, ·), k2(·, ·), …, kq(·, ·), …, kr(·, ·)}为预定义的r个基核;{?1(·), ?2(·), …, ?q(·), …, ?r(·)}为对应于基核的特征映射;{K1, K2, …, Kq, …, Kr}为数据集通过基核得到的核矩阵。则根据ELM理论,LMK-ELM的初始优化问题定义为
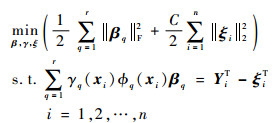 | (1) |
式中:β=[β1T,β2T,…, βrT]为ELM的输出总权重;βq∈R|?q(·)|×m为基于第q个基核的ELM输出权重,|?q(·)|为第q个特征空间的维数,m为ELM输出节点个数;ξi=[ξi1, ξi2, …, ξim]T为模型对应于训练样本xi的训练误差向量,且有ξ=[ξ1, ξ2, …, ξn]T;Yi=[Yi1, Yi2, …, Yim]T为对应于训练样本xi的理想输出向量,且有Y=[Y1, Y2, …, Yn]T;C为正则化因子。
基于初始优化问题的Lagrange函数,可以进一步得到LMK-ELM的对偶优化问题:
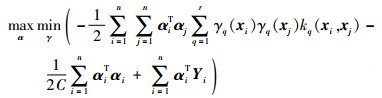 | (2) |
式中:αi为Lagrange乘子,对应于ELM的模型参数,且α=[α1, α2, …, αn]T,αi=[αi1, αi2, …, αim]T。
为了解上述的对偶优化问题,通常采用一种交替优化的策略交替更新ELM模型参数和局部核权重,最终得到决策函数:
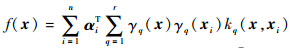 | (3) |
无论怎样,在优化过程中:①局部权重的数量等于基核数乘以样本数,算法复杂性较高,且存在过学习风险;②在式(2)中关于局部权重的优化是一个困难的二次非凸问题。
针对上述问题,本文取代一般LMKL算法中将局部权重拟合到每一个确定样本上,而是将局部权重拟合到空间中具有相似局部结构的一类群组上,进而提出一种新的面向聚类的LMK-ELM模型。该模型的基本框架如图 1所示。
 |
| 图 1 本文模型的基本框架 Fig. 1 General framework of proposed model |
| 图选项 |
2 LCMKELM诊断模型 2.1 基于AP算法的样本空间划分 为挖掘故障样本中隐含的局部分布特征,本节引入AP算法[20-21]。相比于经典的K-均值聚类,AP算法不需要指定聚类的数目,对初始值的选取不敏感,并且文献[20]证明其具有更低的误差平方和。这使得在AP算法中先验经验成为应用的非必要条件,因而更适合本文的应用背景。
首先,定义样本间的相似性度量准则为
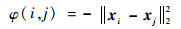 | (4) |
显然,φ(i, j)越大,则2个数据点之间的相似性越高。进一步得到n个样本点组成的相似度矩阵S,即
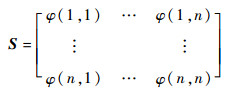 |
AP算法中传递2种类型的消息,分别称作吸引信息和归属信息,并存储在2个矩阵V和W中。V中的v(i, j)描述了数据对象j适合作为数据对象i的聚类中心的程度,表示的是从i到j的消息。而W中的w(i, j)描述了数据对象i选择数据对象j作为其聚类中心的适合程度,表示的是从j到i的消息。v(i, j)与w(i, j)越强,则j点作为聚类中心的可能性就越大,并且i点隶属于以j点为聚类中心的聚类的可能性也越大。吸引信息和归属信息的更新方程分别定义为
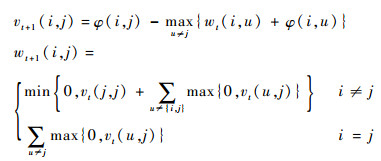 |
式中:下标t为当前迭代次数。
为了避免振荡,AP算法更新信息时引入了衰减系数λ∈(0, 1)。通常,λ越接近于0,振荡越大,收敛越慢,生成的聚类个数较多;而λ越接近于1,振荡越小,收敛越快,生成的聚类个数也相对较少。为此,进一步令
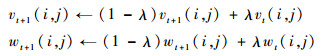 |
V和W初始均为全0矩阵,AP算法通过迭代过程不断更新每一个点的吸引度和归属度,如果决策信息经过若干次迭代之后保持不变或者算法执行超过设定的最大迭代次数,则算法终止。此时,决策矩阵定义为V+W,决策矩阵主对角线元素{v(i, i)+w(i, i)}中所有大于0的G个点被选择作为聚类中心,其余的点根据式(5)定义的规则被分配到相应的聚类中:
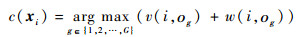 | (5) |
式中:οg为第g个聚类中心在原始训练数据集中对应的样本序号;c(xi)为xi所对应的聚类标签。
这样,数据实例集合X={x1, x2, …, xn}将被划分为G个子集,即X1, X2, …, XG,并且每个子集满足:①Xs≠ ?,s=1, 2,…, G;②
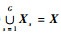
2.2 LCMKELM诊断模型优化 根据2.1节的聚类结果,当将局部权重拟合到每一个聚类上时,新的局部权重可以表示为γ={γqg}q=1, 2, …, rg=1, 2, …, G。这样,式(2)所示的对偶优化问题可以改写为
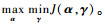
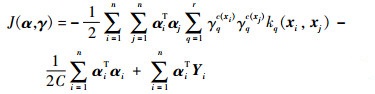 | (6) |
式中:c(xi)和c(xj)分别为样本xi和xj通过式(5)得到的聚类标签。
由式(6)可知,J是一个关于α和γ的多目标函数。当γ固定时,关于α最大化J,意味着最小化全局分类误差;当α固定时,关于γ最小化J,意味着在最大化类内相似性的同时,最小化类间相似性。下面采用一种两步交替优化的策略,交替更新ELM模型参数α和局部核权重γ。
2.2.1 在已知γ的条件下更新α 当γ固定时,为了表示方便,本节采取一种矩阵向量化的操作。对于Lagrange乘子矩阵α∈Rn×m,所谓的矩阵向量化记作α′=ψ(α),即α′∈Rmn×1,且有α′=[α1T, α2T, …, αnT]T。同理,理想输出矩阵Y经过矩阵向量化操作得到的新向量记作Y′∈Rmn×1,且有Y′=[Y1T, Y2T, …, YnT]T。
组合核矩阵记作
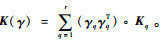
 |
式中:K(γ)ij为K(γ)中第i行的第j个元素,且有
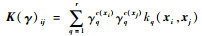
因此,式(6)所示的优化问题进一步被改写为
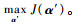
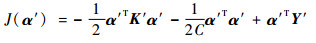 | (7) |
式(7)对α′求偏导,并令结果等于0,得到
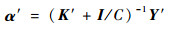 | (8) |
式中:I为一个m×n阶单位矩阵。
最终,ELM的模型参数可以通过一个矩阵向量化的反操作得到,记作α=ψ-1(α′)。
2.2.2 在已知α的条件下更新γ 结合聚类信息,式(6)所示的优化问题的目标函数等效于下面的形式:
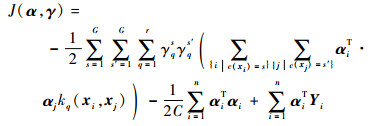 |
为了表示方便,不妨令
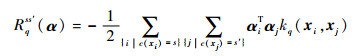 | (9) |
Rqss′(α)体现了聚类s和聚类s′关于第q个基核的相关性。当s和s′相等时,Rqss′(α)表示类内相似性;当s和s′不相等时,Rqss′(α)表示类间相似性。相应地,优化问题式(6)被简写为
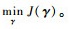
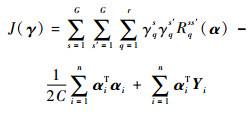 | (10) |
式(10)中局部权重的优化是一个困难的二次非凸问题。受文献[16]的启发,本节从训练数据在输入空间和特征空间的统计特性出发,提出2种不同的选通函数。
1) 函数M1:面向输入空间的选通函数
在输入空间中,第g个聚类在第q个基核上的选通函数定义为
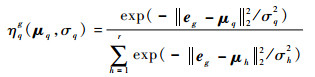 | (11) |
式中:{μh, σh}h=1r为选通模型参数;eg为通过2.1节计算得到的第g个聚类的聚类中心。令γqg≈ηqg(μq, σq),在γqg中分别对模型参数μp,σp求偏导,可以得到
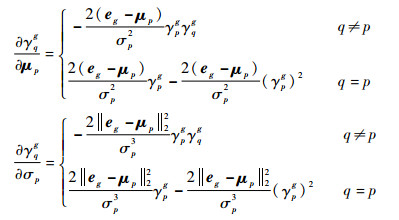 |
基于上述结果,式(10)中的J(γ)对μp,σp分别求偏导,进一步得到
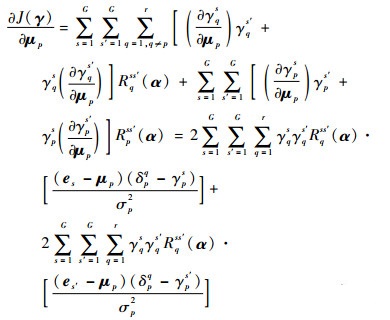 | (12) |
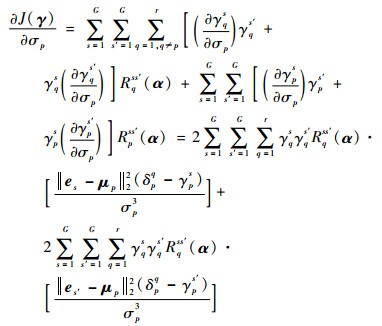 | (13) |
式中:δpq为一个单位冲激函数,当q=p时, δpq=1,否则δpq=0。
得到目标函数J(γ)关于模型参数的梯度之后,采用梯度下降法依次更新各模型参数,即
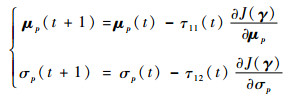 | (14) |
式中:τ11(t)和τ12(t)为迭代步长,在迭代过程中采用线性搜索算法得到。
2) 函数M2:面向特征空间的选通函数
在特征空间中,第g个聚类在第q个基核上的选通函数定义为
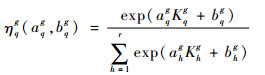 | (15) |
式中:{ahg, bhg}h=1, 2, …, rg=1, 2, …, G为选通函数的模型参数;Kqg为特征空间中第g个聚类与第q个核函数相关的统计特性。用ng为第g个聚类包含的样本数量,则Kqg定义为
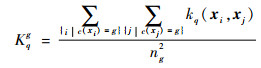 | (16) |
令γqg≈ηqg(aqg, bqg),在γqg中分别对模型参数apg,bpg求偏导,可以得到
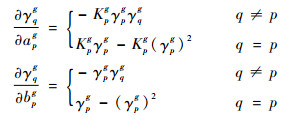 |
基于以上结果,式(10)中的J(γ)对apg,bpg分别求偏导,进一步得到
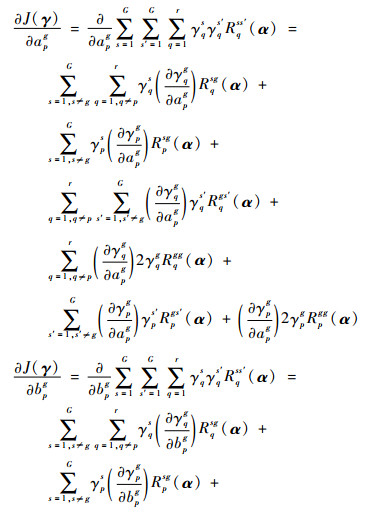 |
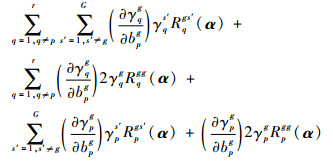 |
由式(9)可知,Rqss′(α)关于s和s′是对称的。所以,基于上述结果可得
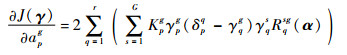 | (17) |
同理得到
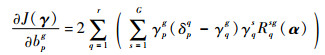 | (18) |
得到目标函数J(γ)关于模型参数的梯度之后,同样采用梯度下降法更新各模型参数,即
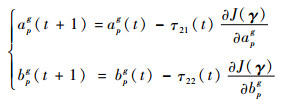 | (19) |
式中:τ21(t)和τ22(t)为迭代步长,在迭代过程中采用线性搜索算法得到。
2.3 诊断决策 在诊断过程中,给定一个测试数据实例x′j,本文模型首先根据AP聚类找出它所属的群组Xs(s=1, 2,…, G);然后将群组Xs的局部核权重{γqs}q=1r分配给样本x′j。假设通过2步交替优化过程,得到的最优的诊断模型参数为α*和γ*,则根据式(3),本文模型的决策函数定义为
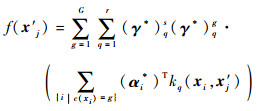 | (20) |
决策过程如图 2所示。
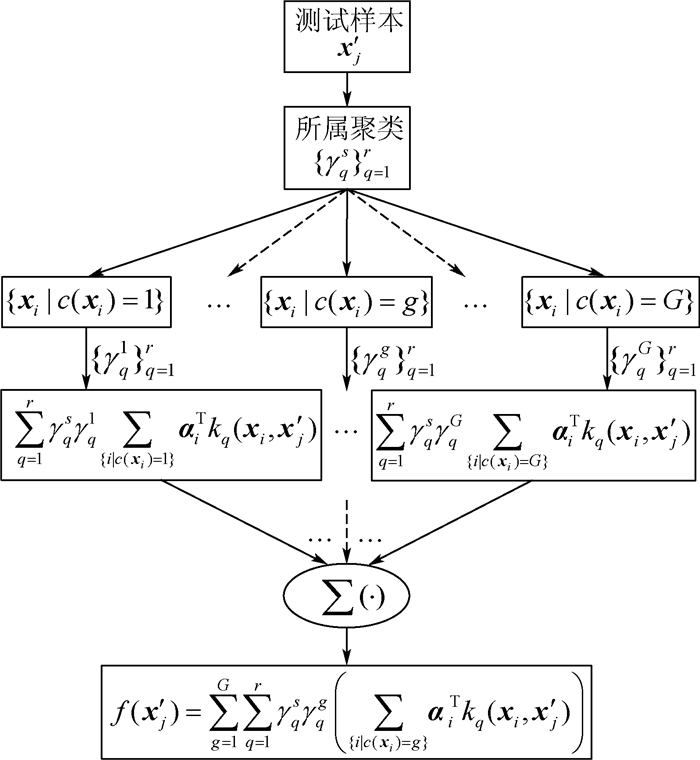 |
| 图 2 本文模型的决策过程 Fig. 2 Decision-making process of proposed model |
| 图选项 |
对于LCMKELM诊断模型而言,其输出节点个数m等于故障模式的个数c。如果第i个样本对应的故障模式是l,那么分类器的理想输出应该为Yi=[0, …, 0,
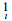
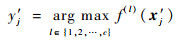 | (21) |
本文故障诊断模型流程图如图 3所示。
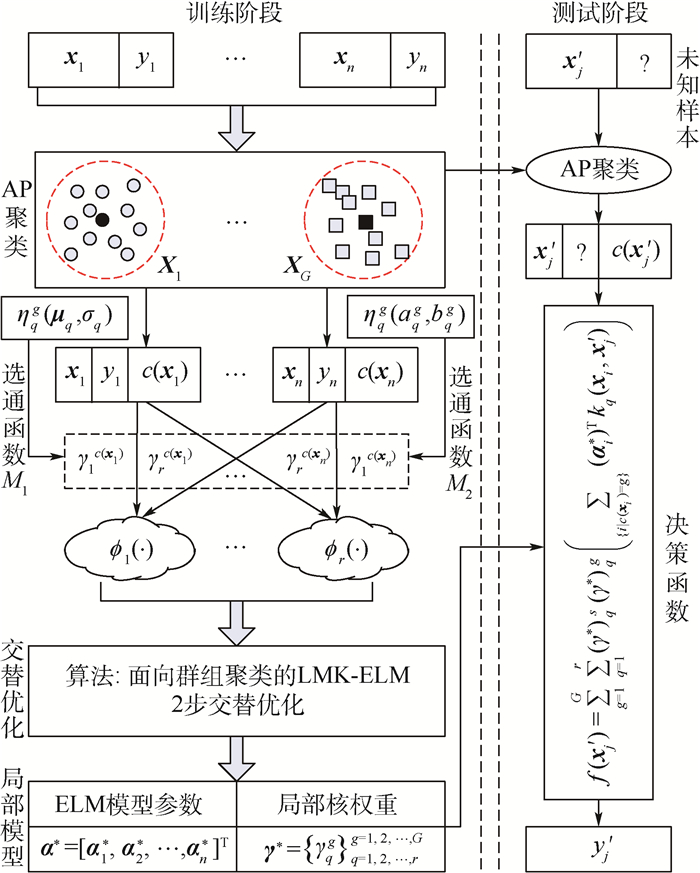 |
| 图 3 本文故障诊断模型流程图 Fig. 3 Flowchart of proposed fault diagnosis model |
| 图选项 |
3 算法流程 为表示方便,将本文诊断模型记作LCMKELM。当采用不同选通函数时,分别记作M1-LCMKELM和M2-LCMKELM。根据图 3将诊断模型的详细流程总结如下:
步骤1??输入训练数据集DTr={(x1, y1), (x2, y2), …, (xi, yi), …, (xn, yn)};设置基核{kq(·, ·)}q=1r;AP算法衰减系数λ,最大迭代次数以及ELM正则化因子C。
步骤2??通过式(4)构建训练样本相似度矩阵S,并基于AP算法对训练样本进行聚类划分{Xg}g=1G;若采用选通函数M1,初始化模型参数{μq, σq}q=1r,基于聚类划分提取聚类中心{eg}g=1G;若采用选通函数M2,初始化模型参数{aqg, bqg}q=1, 2, …, rg=1, 2, …, G;基于式(16)计算统计量{Kqg}q=1, 2, …, rg=1, 2, …, G。
步骤3??若采用选通函数M1,令γqg≈ηqg(μq, σq),并计算{γqg}q=1, 2, …, rg=1, 2, …, G;若采用选通函数M2,令γqg≈ηqg(aqg, bqg),并计算{γqg}q=1, 2, …, rg=1, 2, …, G。
步骤4??基于{γqg}q=1, 2, …, rg=1, 2, …, G计算组合核矩阵K(γ),并计算K(γ)的增广矩阵K′;同时,计算矩阵向量化后的理想输出向量Y′。
步骤5??通过式(8)计算α′,并进一步得到ELM模型参数α;同时,通过式(9)计算Rqss′(α)。
步骤6??令t=1,通过式(10)计算Jt(γ)。
步骤7??若采用选通函数M1,通过式(12)和式(13)分别计算
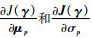
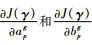
步骤8??执行步骤3~步骤5;通过式(10)计算Jt+1(γ);如果|Jt+1(γ)-Jt(γ)|>10-3,t=t+1,返回步骤7;否则,执行步骤9。
步骤9??输入测试样本实例x′j,j=1, 2, …, n′;通过式(4)计算x′j与每个聚类中心的相似度,进而确定x′j所属的群组s∈{1, 2, …, G};根据s为x′j分配局部核权重{γqs}q=1r。
步骤10??通过式(20)计算决策模型输出值f(x′j);通过式(21)得到测试数据实例x′j对应的故障模式y′j。
4 实验分析 本节通过2个实验来验证本文模型的性能。SimpleMKL[13]、GMKL-SVM[12]和LMKL[16]被采用作为比较算法,对于多分类问题,其均采用“一对一”的原则。在实验中所有的数据首先进行Z-score标准化处理,而所有的核矩阵则被正规化到具有单位迹,即tr(Kq)=1。正则化参数C采用5倍交叉验证从集合{10-2, 0.1, 1, 10, 102, 103, 104}中选择。AP算法中令λ=0.8,最大迭代次数设置为1 000。算法复杂性通过训练时间(不包括交叉验证时间)和测试时间共同评价。所有实验结果通过MATLAB 2015a得到,实验电脑配置为:2.27 GHz Intel Core i3 CPU,2 GB RAM。
4.1 算法有效性验证 本节采用文献[16]中使用的人工数据集Gauss 4来验证本文模型的有效性。该数据集由服从4种不同高斯分布的1 200个样本组成,包括2个类别,每个类别包括2种分布。每种分布的先验概率、均值向量和协方差矩阵分别为
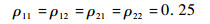 | (22) |
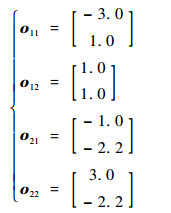 | (23) |
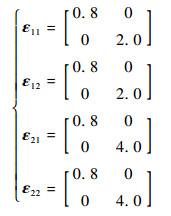 | (24) |
实验中,随机选择2/3数据作为训练样本,剩余1/3作为测试样本。首先采用AP算法对训练样本进行聚类,800组训练样本被划分为26个群组,聚类结果如图 4所示。
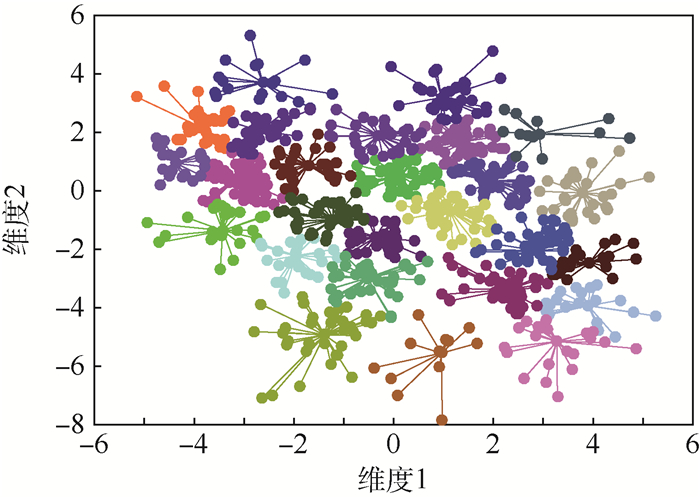 |
| 图 4 Gauss 4训练样本AP算法聚类结果 Fig. 4 Clustering results of Gauss 4 training samples based on AP algorithm |
| 图选项 |
SimpleMKL被用来与本文模型进行比较。多核设置为线性核,多项式核(参数为2),高斯核(参数为1)。评价指标采用文献[22]中定义的分类精度、F1值和G-mean。实验共进行5次,将所得结果的均值和标准差记录于表 1中。
表 1 Gauss 4数据集分类结果比较 Table 1 Comparison of classification results on Gauss 4 dataset
| 评价指标 | M1-LCMKELM | M2-LCMKELM | SimpleMKL |
| 分类精度/% | 90.500 0±0.684 7 | 90.850 0±0.602 1 | 89.350 0±1.206 8 |
| F1值 | 0.904 9±0.006 8 | 0.908 5±0.006 1 | 0.895 8±0.012 4 |
| G-mean | 0.904 6±0.006 9 | 0.908 2±0.006 2 | 0.893 2±0.011 9 |
表选项
由表 1的结果看到,基于选通函数M1、M2的LCMKELM均可以实现比SimpleMKL更优的分类性能。其克服了局部算法将基核权重拟合到每一个确定样本上时可能出现的过学习问题。对于分类精度,相比于SimpleMKL,M1-LCMKELM和M2-LCMKELM分别提升了1.65%和1.85%。
为了更加直观地比较本文模型的性能,将其与SimpleMKL的接受者操作特性曲线(Receiver Operating characteristic Curve, ROC)绘制在图 5中。由图 5可见,2种算法的曲线下方区域(Area Under the Curve, AUC)明显大于SimpleMKL的AUC值,这从另一个角度进一步证明了本文模型的有效性。
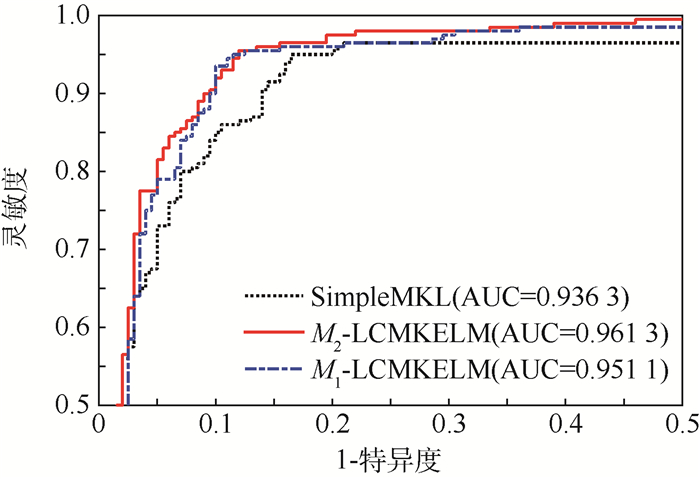 |
| 图 5 Gauss 4数据集ROC曲线比较 Fig. 5 Comparison of ROC curves on Gauss 4 dataset |
| 图选项 |
为验证训练样本数量对模型精度的影响。设置训练样本数量分别等于16, 32, 48, 64, 144, 400, 600, 800。每次随机选择100组测试样本,将其注入到训练得到的不同模型中。实验共进行5次,将所得结果的均值与标准差记录于表 2中。
表 2 不同训练样本数量下分类精度比较 Table 2 Comparison of classification accuracy with different sizes of training sample
| 训练样本数量 | 分类精度/% | |
| M1-LCMKELM | M2-LCMKELM | |
| 16 | 81.8±1.923 5 | 82.6±1.673 3 |
| 32 | 85.2±1.483 2 | 86.2±1.483 2 |
| 48 | 86.4±2.073 6 | 86.6±1.516 5 |
| 64 | 86.4±1.516 5 | 86.6±1.673 3 |
| 144 | 87.2±1.095 4 | 87.4±1.140 2 |
| 400 | 87.0±1.870 8 | 87.2±1.303 8 |
| 600 | 87.8±1.095 4 | 88.2±0.836 7 |
| 800 | 88.0±0.707 1 | 88.6±0.894 4 |
表选项
由表 2看到,训练样本的增加确实提升了诊断模型的分类性能。但是2种算法通过挖掘样本中蕴含的局部特征信息,在小样本条件下可以得到与较大样本条件下相近的分类精度。该结果证明了将本文模型应用于小样本条件下故障诊断任务的可行性。
4.2 旋转变压器激励发生电路诊断实例 旋转变压器激励发生电路如图 6所示。它用于产生旋转变压器磁绕组所需的正弦信号,为旋转变压器运行提供激励。以满足无刷直流电机、航空永磁同步电机等系统检测需求。该电路主要由电源模块、频率控制模块、正弦信号产生模块和幅值调理及驱动能力调节模块组成。
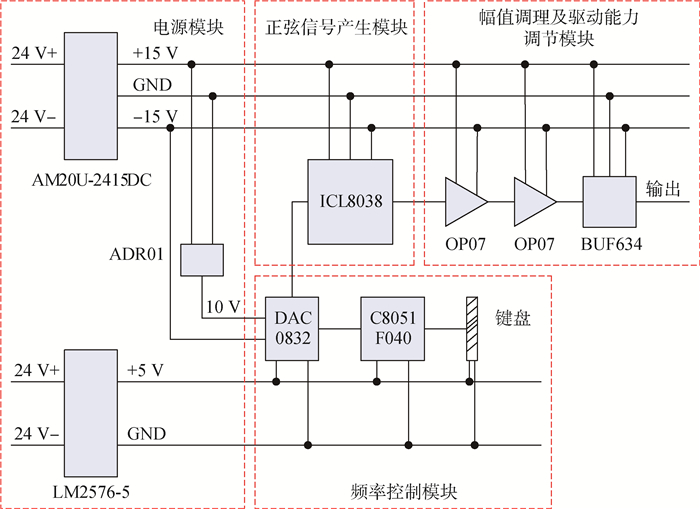 |
| 图 6 旋转变压器激励发生电路原理图 Fig. 6 Schematic diagram of rotary transformer excitation generating circuit |
| 图选项 |
在基于自动测试系统(Automatic Test System, ATS)的测试流程中共包含9个测试项目:信号频率(Q1),信号幅值(Q2),正弦模块输入电压值(Q3),信号频率稳定度(Q4),+15 V电压值(Q5),-15 V电压值(Q6),电路板工作温度(Q7),+5 V电压值(Q8),+10 V电压值(Q9)。用F0,F1,F2,F3及F4分别表示正常模式、频率控制模块故障、幅值调理及驱动能力调节模块故障、电源模块故障和正弦信号产生模块故障。各模式下ATS共采集原始数据量分别为22,18,16,14及22。
将采集到的数据随机选择1/2作为训练样本,其余作为测试样本。多核设置为:线性核,多项式核(参数2),高斯核(参数2,10,20,30,40,50)。首先采用AP算法对训练样本进行聚类,46组训练样本被划分为8个群组,如表 3所示。
表 3 诊断数据聚类结果 Table 3 Clustering results of diagnosis data
| 聚类 | 聚类中心 | 类内元素 |
| 1 | 5 | {2, 4, 5, 6, 9, 11, 15, 18, 34, 35} |
| 2 | 12 | {8, 10, 12, 13, 20, 25} |
| 3 | 17 | {1, 3, 7, 17} |
| 4 | 23 | {16, 23, 33} |
| 5 | 26 | {14, 19, 26, 29, 32} |
| 6 | 30 | {24, 30, 31, 41} |
| 7 | 40 | {21, 22, 28, 37, 38, 40, 42, 45} |
| 8 | 43 | {27, 36, 39, 43, 44, 46} |
表选项
用本文模型与SimpleMKL、GMKL-SVM、LMKL-softmax和LMKL-sigmoid分别基于上述数据进行诊断测试,所得结果如图 7和表 4所示。
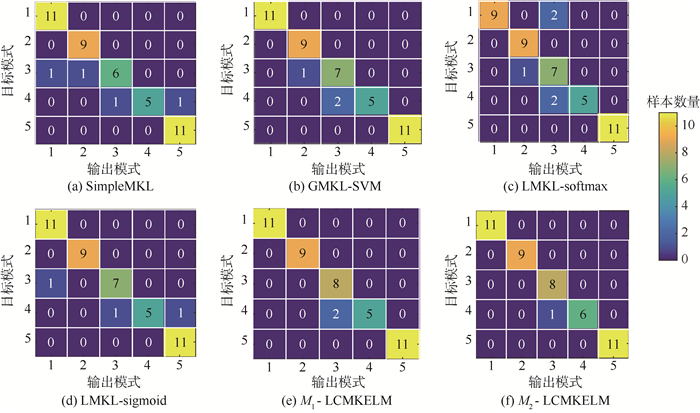 |
| 图 7 不同算法的混淆矩阵 Fig. 7 Confusion matrices of different algorithms |
| 图选项 |
表 4 不同算法诊断结果比较 Table 4 Comparison of diagnosis results based on different algorithms
| 算法 | 漏警率/ % | 虚警率/ % | 训练诊断精度/% | 测试诊断精度/% |
| SimpleMKL | 2.857 1 | 0 | 100 | 91.304 3 |
| GMKL-SVM | 0 | 0 | 100 | 93.478 3 |
| LMKL-softmax | 0 | 5.405 4 | 100 | 89.130 4 |
| LMKL-sigmoid | 2.857 1 | 0 | 100 | 93.478 3 |
| M1-LCMKELM | 0 | 0 | 100 | 95.652 2 |
| M2-LCMKELM | 0 | 0 | 100 | 97.826 1 |
表选项
由图 7和表 4可以得到:①本文算法在漏警率与虚警率上表现出色,实现了0漏警,0虚警。②2种LMKL算法尽管具有100%的训练诊断精度,但其测试诊断精度不高,尤其是当采用softmax选通函数时。究其原因在于将局部权重拟合到确定样本上时导致算法泛化性能下降。而本文算法通过聚类将局部权重拟合到一组具有相似局部特征的群组上,在挖掘局部特征的同时避免了算法过学习。相比于其他4种算法(SimpleMKL、GMKL-SVM、LMKL-softmax和LMKL-sigmoid),M1-LCMKELM将测试诊断精度分别提升了4.35%、2.17%、6.52%和2.17%;M2-LCMKELM将测试诊断精度分别提升了6.52%、4.35%、8.70%和4.35%。③比较发现M2-LCMKELM在诊断精度上要优于M1-LCMKELM,原因在于当使用选通函数M1时产生局部权重的稀疏解,当使用选通函数M2时产生局部权重的非稀疏解,如图 8所示。稀疏解虽然易于解释,但可能会丢失有用的信息。
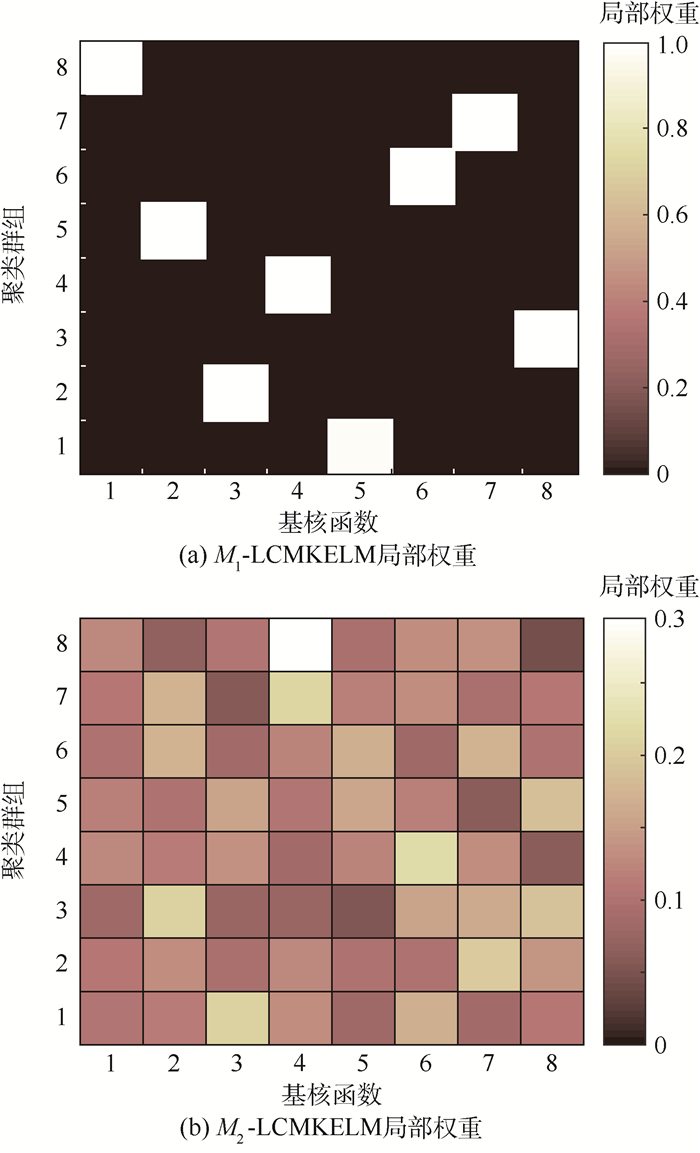 |
| 图 8 本文算法局部权重分布 Fig. 8 Localized weight distribution of proposed algorithms |
| 图选项 |
不妨用TP表示某种故障模式被正确识别的数量,FN表示该故障模式被错误识别的数量,FP表示误诊断为该故障模式的样本数量。则将召回率定义为TP/(TP+FN),而准确率定义为TP/(TP+FP)。因此,根据图 7得到4种故障模式的召回率、准确率直方图,如图 9所示。
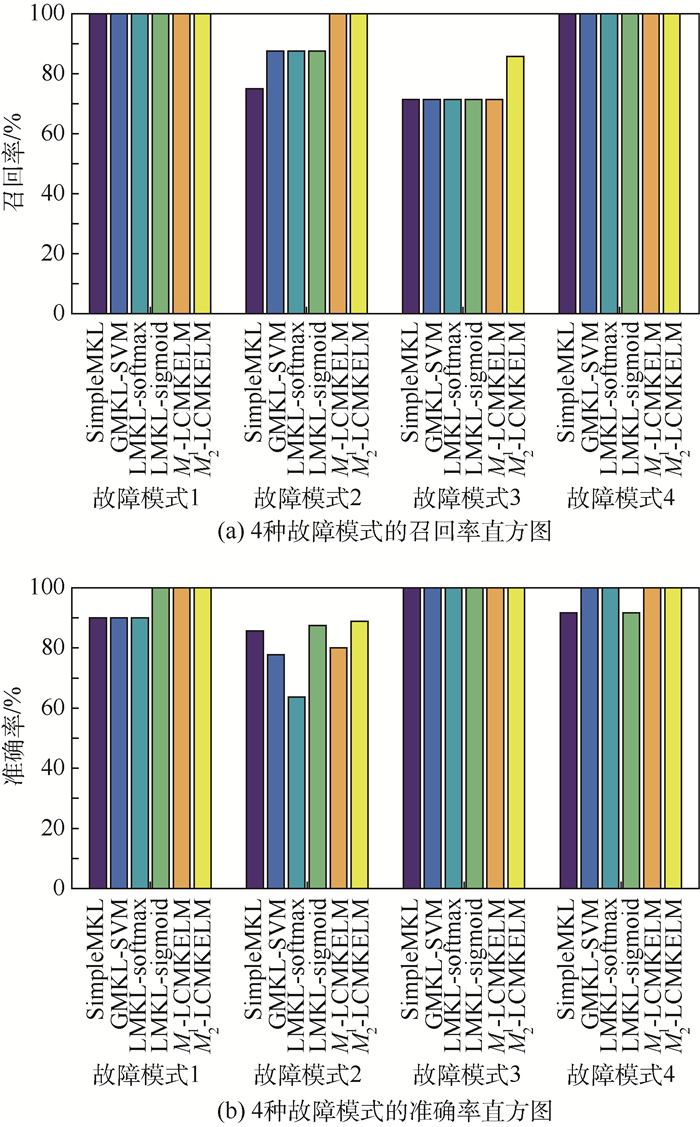 |
| 图 9 不同算法的召回率、准确率比较 Fig. 9 Comparison of recall and precision based on different algorithms |
| 图选项 |
根据文献[23]中关于多分类问题F1值及G-mean的定义,结合图 9得到表 5所示的诊断结果统计特性。表 5从诊断精度之外的另一个角度展示了各种诊断算法的性能。可以看到本文算法依旧展示出更好的诊断性能。
表 5 不同算法F1值和G-mean比较 Table 5 Comparison of F1 score and G-mean based on different algorithms
| 算法 | F1值 | G-mean |
| SimpleMKL | 0.898 7 | 0.882 6 |
| GMKL-SVM | 0.920 8 | 0.910 3 |
| LMKL-softamx | 0.885 5 | 0.874 5 |
| LMKL-sigmoid | 0.924 3 | 0.910 3 |
| M1-LCMKELM | 0.944 4 | 0.934 9 |
| M2-LCMKELM | 0.972 9 | 0.969 6 |
表选项
此外,为了比较各种算法的时间花费,重复运行实验5次,将各种算法训练时间与测试时间的均值与标准差记录在表 6中。
表 6 不同算法诊断时间花费比较 Table 6 Comparison of diagnosis time cost based on different algorithms
| 算法 | 训练时间/s | 测试时间/s |
| SimpleMKL | 0.991 7±0.082 9 | 0.201 8±0.045 1 |
| GMKL-SVM | 0.832 5±0.036 0 | 0.167 9±0.008 2 |
| LMKL-softamx | 1.493 4±0.062 5 | 0.173 5±0.011 1 |
| LMKL-sigmoid | 2.715 9±0.129 2 | 0.176 9±0.015 7 |
| M1-LCMKELM | 2.497 9±0.213 7 | 0.129 9±0.005 9 |
| M2-LCMKELM | 1.789 7±0.201 4 | 0.152 1±0.016 7 |
表选项
由表 6可知,①在训练时间上,采用LMKC明显要比一般的MKL花费更多的时间,而所提的2种局部MKL算法与2种流行的局部MKL算法相比较,拥有相似、甚至更短的训练时间。②在测试时间上,本文算法花费时间最少,尤其是M1-LCMKELM。这是因为ELM相比于SVM本身就是一种计算更加高效的分类器,同时当采用输入空间选通函数M1时,能够产生局部权重的稀疏解。③本文提出的是一种线下故障诊断算法,通过牺牲一定的时间花费获得诊断精度上的提升是可以接受的;况且,本文主要面向于小样本条件下的诊断问题,因此时间花费也是可控的。
5 结论 针对小样本条件下,基于ATS测试数据的航空电子部件功能故障诊断问题,本文提出一种LCMKELM诊断模型。通过实验验证了所提模型的有效性和适用性,结果表明:
1) 在诊断精度上,相比于4种常用的MKL算法,本文模型在实现低漏警率、低虚警率的同时能显著提升诊断的正确率。对于旋转变压器激励发生电路,M1-LCMKELM将诊断精度平均提升了3.80%,而M2-LCMKELM将诊断精度平均提升了5.98%。
2) 在诊断时间上,相比于2种流行的LMKL算法,本文模型具有相似、甚至更短的训练时间;同时得益于ELM快速的计算效率,可以实现更短的测试时间。
3) M1-LCMKELM产生局部权重的稀疏解,M2-LCMKELM产生局部权重的非稀疏解。这使得M2-LCMKELM的诊断精度要优于M1-LCMKELM,但是M1-LCMKELM的测试时间要优于M2-LCMKELM。
参考文献
| [1] | LUO H, WANG Y R, LIN H, et al. Module level fault diagnosis for analog circuits based on system identification and genetic algorithm[J].Measurement, 2012, 45(4): 769–777.DOI:10.1016/j.measurement.2011.12.010 |
| [2] | 孙伟超, 李文海, 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J].北京航空航天大学学报, 2015, 41(10): 1902–1909. SUN W C, LI W H, LI W F. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902–1909.(in Chinese) |
| [3] | KNVPPEL T, BLANKE M, ?STERGAARD J. Fault diagnosis for electrical distribution systems using structural analysis[J].International Journal of Robust and Nonlinear Control, 2014, 24(8-9): 1446–1465.DOI:10.1002/rnc.v24.8-9 |
| [4] | JAMIL T, MOHAMMED I. Simulation of VICTOR algorithm for fault diagnosis of digital circuits[J].International Journal of Computer Theory and Engineering, 2015, 7(2): 103–107.DOI:10.7763/IJCTE.2015.V7.939 |
| [5] | DAI X W, GAO Z W. From model, signal to knowledge:A data-driven perspective of fault detection and diagnosis[J].IEEE Transactions on Industrial Informatics, 2013, 9(4): 2226–2238.DOI:10.1109/TII.2013.2243743 |
| [6] | 蒋栋年, 李炜. 基于自适应阈值的粒子滤波非线性系统故障诊断[J].北京航空航天大学学报, 2016, 42(10): 2099–2106. JIANG D N, LI W. Fault diagnosis of particle filter nonlinear systems based on adaptive threshold[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2099–2106.(in Chinese) |
| [7] | GAO Z W, CECATI C, DING S X. A survey of fault diagnosis and fault tolerant techniques-Part Ⅰ:Fault diagnosis with model-based and signal-based approaches[J].IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757–3767.DOI:10.1109/TIE.2015.2417501 |
| [8] | SAHRI Z B, YUSOF R B. Support vector machine-based fault diagnosis of power transformer using k nearest-neighbor imputed DGA dataset[J].Journal of Computer and Communications, 2014, 2(9): 22–31.DOI:10.4236/jcc.2014.29004 |
| [9] | YIN G, ZHANG Y T, LI Z N, et al. Online fault diagnosis method based on incremental support vector data description and extreme learning machine with incremental output structure[J].Neurocomputing, 2014, 128: 224–231.DOI:10.1016/j.neucom.2013.01.061 |
| [10] | G?NEN M, ALPAYDIN E. Multiple kernel learning algorithms[J].Journal of Machine Learning Research, 2011, 12: 2211–2268. |
| [11] | YE F M, ZHANG Z B, CHAKRABARTY K, et al. Board-level functional fault diagnosis using multikernel support vector machines and incremental learning[J].IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2014, 33(2): 279–290.DOI:10.1109/TCAD.2013.2287184 |
| [12] | LI Y X, REN C Q, BO J Y, et al. The application of GMKL algorithm to fault diagnosis of local area network[J].Journal of Networks, 2014, 9(3): 747–753. |
| [13] | RAKOTOMAMONJY A, BACH F R, CANU S, et al. SimpleMKL[J].Journal of Machine Learning Research, 2008, 9: 2491–2521. |
| [14] | HAN Y N, YANG K, MA Y L, et al. Localized multiple kernel learning via sample-wise alternating optimization[J].IEEE Transactions on Cybernetics, 2014, 44(1): 137–147.DOI:10.1109/TCYB.2013.2248710 |
| [15] | SONG Y, ZHENG Y T, TANG S, et al. Localized multiple kernel learning for realistic human action recognition in videos[J].IEEE Transactions on Circuits and Systems for Video Technology, 2011, 21(9): 1193–1202.DOI:10.1109/TCSVT.2011.2130230 |
| [16] | G?NEN M, ALPAYDIN E. Localized algorithms for multiple kernel learning[J].Pattern Recognition, 2013, 46(3): 795–807.DOI:10.1016/j.patcog.2012.09.002 |
| [17] | WANG X M, HUANG Z X, DU Y J. Improving localized multiple kernel learning via radius-margin bound[J].Mathematical Problems in Engineering, 2017, 2017: 4579214. |
| [18] | HAN Y N, LIU G Z. Probability-confidence-kernel-based localized multiple kernel learning with Lp norm[J].IEEE Transactions on Systems, Man and Cybernetics-Part B:Cybernetics, 2012, 42(3): 827–837.DOI:10.1109/TSMCB.2011.2179291 |
| [19] | HAN Y N, YANG K D, LIU G Z. Lp norm localized multiple kernel learning via semi-definite programming[J].IEEE Signal Processing Letters, 2012, 19(10): 688–691.DOI:10.1109/LSP.2012.2212431 |
| [20] | FREY B J, DUECK D. Clustering by passing messages between data points[J].Science, 2007, 315(5814): 972–976.DOI:10.1126/science.1136800 |
| [21] | NAPOLEON D, BASKAR G, PAVALAKODI S. An efficient clustering technique for message passing between data points using affinity propagation[J].International Journal on Computer Science and Engineering, 2011, 3(1): 8–13. |
| [22] | SOKOLOVA M, LAPALME G. A systematic analysis of performance measures for classification tasks[J].Information Processing and Management, 2009, 45(4): 427–437.DOI:10.1016/j.ipm.2009.03.002 |
| [23] | PHOUNGPHOL P, ZHANG Y Q, ZHAO Y C. Robust multiclass classification for learning from imbalanced biomedical data[J].Tsinghua Science and Technology, 2012, 17(6): 619–628.DOI:10.1109/TST.2012.6374363 |
