Boosting算法是分类器的一种组合策略,拥有坚实的理论基础,能将只比随机猜测好一些的弱分类器提升为分类精度高的强分类器,在实际中也得到了深入研究和广泛的应用。作为一种算法框架, Boosting算法几乎可以应用于所有目前流行的机器学习算法,以进一步加强原算法的预测精度, 应用十分广泛。AdaBoost算法是其中最成功的代表, 被评为数据挖掘十大算法之一[1]。在算法的应用领域,手写字体识别是AdaBoost算法最早也是最为成功的实际应用之一[2],在文本分类和检索、图像识别和检索、语音识别和检索、写字字符识别和机械故障诊断等领域都得到了广泛应用。
在航空发动机故障诊断研究领域中,徐启华和杨瑞[3]用AdaBoost算法对神经网络的故障分类器进行提升,验证了故障分类器泛化能力的提高和噪声鲁棒性的改善。夏利民和戴汝为[4]用模糊分类的规则与Boosting算法结合,在滚动轴承故障问题中也取得了较好的诊断效果。孙超英等[5]将支持向量机(SVM)作为弱分类器,通过Boosting算法的加权融合,运用实测数据验证了诊断的准确率由SVM的79.4%提高到Boosting-SVM算法的85.7%。胡金海等[6-7]也对AdaBoost算法用于航空发动机故障诊断作了大量理论与应用研究。因此,本文通过AdaBoost相关算法的结合,以SVM作为基础分类器,建立一种多分类AdaBoost的发动机故障诊断模型。
1 多分类AdaBoost算法 1.1 AdaBoost算法 Kearns和Vliant[8]在研究PAC学习模型时提出了一个有趣的问题:弱学习是否等价于强可学习,即Boosting问题。这一问题,经Schapire证明给出了肯定的回答,并在Schapire和Freund[9-10]的深入研究后,提出了AdaBoost算法。该算法的核心思想是:加大分类错误的样本分布权重,降低分类正确的样本分布权重,从而得到新的样本分布,在新的样本分布下再次训练得到新的弱分类器。以此类推,得到若干弱分类器,经一定权重的叠加(boost),从而形成强分类器,如图 1所示。
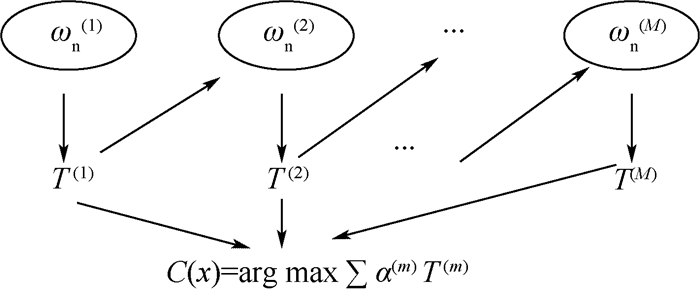 |
| 图 1 AdaBoost算法结构 Fig. 1 Structure of AdaBoost algorithm |
| 图选项 |
1.1.1 二分类问题的AdaBoost.M1算法 二分类问题一般由AdaBoost.M1算法来解决,如图 1中,T(1), T(2), …, T(M)是算法在M轮循环中产生的M个弱基础分类器。在每次循环中,本轮弱分类T(m)产生的加权样本分类错误率err(m)将决定这一轮的弱分类器在最后分类决策所占权重α(m), err(m)也决定了下一轮分类样本的分布权重ωi+1。在进行M轮循环后,对M个分类器的分类结果进行加权组合,综合判断结果C(x)来进行选择。
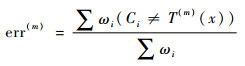 | (1) |
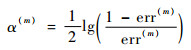 | (2) |
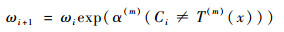 | (3) |
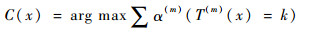 | (4) |
由式(1)和式(2)知,err(m)带有样本加权,因此在计算过程中会使分类器越来越考虑错分样本的重要性;而参数α(m)可以直观反映分类器重要程度,由α(m)计算式可知,错误率err(m)越小,α(m)将会越大。更新样本权重ωi+1并归一化后,在新的样本权重分布下,进入下一轮循环。由此,可得到M个加权的弱分类器。
AdaBoost.M1算法只需要调节训练轮数M,要求α(m)为正数,即1-err(m) > 1/2,表明对二分类弱分类器要求精度只需大于50%,比随机猜想好就可以,而正确率会随着训练数M的增加而增加,理论上可以趋近于1。实际中,由于过分专注分类错误的样本,可能会导致数据不平衡的退化问题[11],对此可以通过AdaBoost一些改进算法来避免退化。
对AdaBoost算法的改进主要集中在以下3个方面:①调整权值更新方法,以提升分类器性能、减缓退化等;②改进AdaBoost的训练方法,使AdaBoost能更高效地进行拓展;③结合其他算法和一些额外信息而产生的新算法,达到提高精确度的目的[12]。
1.1.2 多分类问题的AdaBoost.SAMME算法 发动机故障诊断问题是一个多分类问题,AdaBoost用于多分类问题时,可采用AdaBoost.SAMME算法,该算法是对AdaBoost.M1算法进行的改进。Zhu等[13]通过改变权重分配α(m)的规则,提出了符合第1种情况的改进。令α(m)=

1.2 AdaBoost算法基础分类器的选择 由于AdaBoost算法只是一种用来提升分类精度的组合策略,算法本身并不能对样本进行分类,因此解决分类诊断问题时,还需要选择适合所要解决问题的基础分类器。
SVM基于统计学习理论,采用结构风险最小化,以提高学习机器泛化能力。在小样本、非线性、高维模式的情况下,能获得良好的统计规律,适用于航空发动机故障样本数目少的情况。在模式识别的问题中,SVM的基本思想是:寻找最大分类间隔的最优分类面。
线性分类时,设n个样本训练集D={(xi, yi)|i=1, 2, …, n}, x∈R, y∈{-1, 1}。
当样本线性可分时,对于二分类问题的最优分类超平面为:ω·x+b=0。此时的分类间隔为2/||ω||,当||ω||最小时,分类间隔最大。问题转化为求约束条件下的优化问题:
 | (5) |
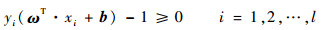 | (6) |
当训练样本线性不可分且存在噪声问题时,需要引入非负松弛变量ξi, i=1, 2, …, n。求解最优分类面问题转化为
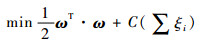 | (7) |
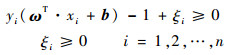 | (8) |
式中:C为规则化常数(惩罚参数),用来权衡经验风险∑ξi最小化与复杂性(VC维),数值越大,表示对分类错误惩罚越大。
通过构造拉格朗日函数:
 | (9) |
将问题转化为对偶泛函数,求解得到决策函数:
 | (10) |
非线性分类时,需要通过核函数K(xi, xj)将样本x映射到新的高维空间,在高维空间中对样本进行线性划分。由于高维计算具有复杂性,因此可在Hilbert-Schmidt理论和Mercer条件下,选用特定核函数来减小计算复杂性。常用的核函数为多项式核函数、sigmoid感知核函数、高斯核函数、多二次曲面核函数等。本文采用以高斯核函数
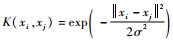
AdaBoost算法与SVM算法结合,产生了AdaBoost-SVM算法。该算法属于AdaBoost算法改进措施中第3种改进算法,即采用与其他算法结合的方法来产生改进的算法。以SVMRBF (高斯径向基核函数SVM)作为AdaBoost算法的弱分类器,由于在AdaBoost算法中要求弱分类器不能太强也不能太弱,太强容易导致数据退化问题,太弱也要满足比随机猜测要好。用SVM做基础分类器时,为避免弱分类器错误高度相关,需通过核参数σ和规则化常数C的调整,来改变SVMRBF的分类性能复合要求。采用AdaBoost-SVM算法解决分类问题时,首先应调整参数C和σ初值对应较弱学习能力的SVM,保持合适的C值不变,在多轮循环中使用这一σ值,直至分类正确率低于阈值。此时,只需调节σ的数值来提高后续循环中所使用分类器的分类精度,依次继续循环,实现对SVM使用AdaBoost算法进行准确度的提高。
1.3 发动机多分类故障诊断的流程设计 结合AdaBoost.SAMME算法和AdaBoost-SVM算法,以SVM作为基础弱分类器,本文设计了一种多分类的AdaBoost算法用于航空发动机的故障诊断。
算法具体流程如图 2所示。
 |
| 图 2 发动机故障诊断的多分类AdaBoost算法流程图 Fig. 2 Flowchart of multi-classification AdaBoost algorithm for engine fault diagnosis |
| 图选项 |
在输入训练样本后,根据交叉验证法,选定SVM参数范围。设定适当训练循环数M、规则化常数C值、σ初始值σini、σ下限值σmin以及σ减小步长σstep。采用AdaBoost.SAMME算法对分类器权重α(m)进行调整,使分类情况适用于发动机故障类型的多分类情况;并且以SVM为基础分类器,以适应航空发动机故障诊断中故障样本数量少、不对称、高维度的特点。以此利用AdaBoost算法来提升单独使用SVM进行发动机故障诊断的能力。
2 发动机故障诊断模型 2.1 数据预处理
2.1.1 数据来源 发动机故障诊断指印图(见图 3)是实际诊断中的重要工具,标识了不同故障对应的发动机主要性能参数的小偏差量。根据小偏差故障数据的线性关系,不同程度的同类故障数据之间存在比值关系。实际偏差数据与指印图偏差数据比值为1时,表示该故障与指印图中对应故障的类型和程度完全一致;当比值为N时,表示该故障与指印图中对应故障的类型一致,但程度不同。所以在运用指印图进行故障诊断时,还应考虑如何正确识别故障发展阶段程度不同的同一故障。
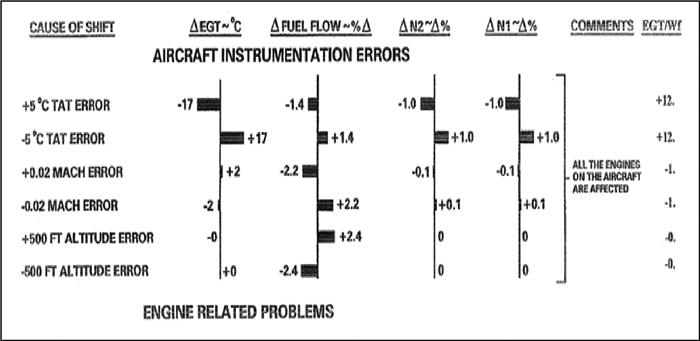 |
| 图 3 发动机故障诊断指印图 Fig. 3 Fingerprint map for engine fault diagnosis |
| 图选项 |
为了使通过指印图所得数据能够用于实际诊断,应将指印图中故障标识数据进行处理,以便得到适应范围更广的训练数据。本文参考文献[16]中的相关系数法和比值系数法,在此基础上提出了单位向量法,由指印图故障小偏差数据作为基础训练数据。
选取PW4000发动机指印图作为基础数据,提取性能参数小偏差数据,如表 1所示。
表 1 PW4000指印图故障偏差数据 Table 1 Fault deviation data of PW4000 fingerprint map
| 故障序号 | 故障类别 | ΔEGT/℃ | ΔFF/% | ΔN2/% | ΔN1/% |
| 1 | +5℃ TAT | -17.0 | -1.4 | -1.0 | -1.0 |
| 2 | -5℃ TAT | 17.0 | 1.4 | 1.0 | 1.0 |
| 3 | +0.02MACH | 2.0 | -2.2 | -0.1 | -0.1 |
| 4 | -0.02MACH | -2.0 | 2.2 | 0.1 | 0.1 |
| 5 | +500 ALT | 0 | 2.4 | 0 | 0 |
| 6 | -500 ALT | 0 | -2.4 | 0 | 0 |
| 7 | -2% HPC | 12.0 | 1.6 | 0 | 0 |
| | |||||
| 24 | -2% LPT | -2.0 | -2.1 | 0.7 | -1.7 |
表选项
为囊括不同程度的所有故障并得到模型所需训练数据,需对基础数据进行扩充。比值系数法是将指印图各故障偏差数据ΔEGT(排气温度偏差)、ΔFF(燃油流量偏差)、ΔN2(高压转子转速偏差)、ΔN1(低压转子转速偏差)转换为ΔEGT/ΔFF、ΔN2/ΔFF、ΔN1/ΔFF,用故障数据的相对比值来表征故障类别。相关系数法是用原始故障偏差数据之间,某一故障与各故障之间的线性相关系数,将4维表征数据变为24维。
单位向量法是将指印图中各偏差数据进行单位向量化,使各故障向量落于单位向量组成的“球”空间中,从而规避同一故障程度差异的影响,如表 2所示。在图 3所示指印图中,还存在一项数据ΔEGT/ΔFF作为诊断的指标,在单位向量法下,加入ΔEGT/ΔFF指标来扩充数据识别维度,作为该方法的补充。
表 2 单位向量法故障标识 Table 2 Fault identification of unit vector method
| 故障序号 | ΔEGT/℃ | ΔFF/% | ΔN2/% | ΔN1/% | ΔEGT/ΔFF |
| 1 | -0.993 | -0.082 | -0.058 | -0.058 | 12 |
| 2 | 0.993 | 0.082 | 0.058 | 0.058 | 12 |
| 3 | 0.672 | -0.739 | -0.034 | -0.034 | -1 |
| 4 | -0.672 | 0.739 | 0.034 | 0.034 | -1 |
| 5 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | -1 | 0 | 0 | 0 |
| 7 | 0.991 | 0.132 | 0 | 0 | 8 |
| | |||||
| 24 | -0.583 | -0.612 | 0.204 | -0.495 | 1 |
表选项
2.1.2 数据噪声的添加方法 噪声的添加可以使诊断模型适应随机偏差的影响,增加模型的鲁棒性。利用指印图故障偏差数据添加噪声进行训练时,存在2种噪声添加思路:
1) 在表 1所示原始偏差数据加入一定程度的随机噪声,然后用比值系数法等方法处理后所得数据,作为训练和测试样本。诊断时,需要将实际参数的偏差数据进行比值方法等处理得到类似表 2中的转化数据,再进行诊断。
2) 在表 2的数据中,直接根据已经转化后的数据进行噪声添加。此时如果直接引入同一程度的随机误差,显然对各标识数据影响程度不同。因此应添加自身数值一定程度(比例)的偏差,来保证噪声数据一定程度也呈故障的线性比例。
在第1种思路下,由于采用比值系数法相除后会将偏差放大,单位向量各故障标识数据之间差值较小。因此,原始数据不宜加入过大噪声,而相关系数由于维数增多和故障类型增多会使问题复杂化,故障问题增多时不适合这一情况。在第2种思路下,可以加入较大的噪声,但应根据具体故障标识数据采用不同程度的噪声添加。
2.2 多分类AdaBoost算法故障诊断模型的分析和检验 训练数据准备方法的不同对训练结果会产生较大的影响。为了能够加入较大噪声来体现AdaBoost算法的提升效果,采用第2种噪声添加思路来进行诊断模型的分析。构造相应方法下的训练集24×200组、测试集24×100组数据进行训练和测试。在多分类AdaBoost诊断模型建立之前,要先用交叉验证法,分别寻找3种方法的基础分类器——SVM参数C与σ合适的取值范围。这样在多分类AdaBoost诊断模型训练时,预设置训练轮数M为50次来观察训练情况,由文献[14]知,σ的减小步长σstep的设置对最终的性能影响不大,通常设置为1~3,实验中设置其为1。
图 4显示了在交叉验证情况下,单个SVM采用不同的数据准备方法获得的训练数据,所建4类诊断模型的诊断正确率。图中:C=2c, σ=2g。可以看出,由于添加了较大噪声,各单一诊断模型正确率并不高。在训练中,弱分类器选取最优的C值和核参数σ情况下,单个弱分类器(高斯径向基核函数C-支持向量分类机)的最高正确率如表 3所示。通过图 4中单个SVM正确率随核参数的变化范围,可以对多分类AdaBoost算法中的相关参数进行设置。经多分类AdaBoost算法训练后,得到M个加权弱分类器进行诊断。以比值系数法中的训练过程为例,在M=50时,第50次的迭代中产生的50个弱分类器的训练误差情况如图 5所示。可以看到,采用的各个弱分类器的正确率均低于单个弱分类器的最高正确率。
 |
| 图 4 不同训练数据下单个SVM模型的正确率 Fig. 4 Accuracy of single SVM under different training data |
| 图选项 |
表 3 交叉验证法中最优参数下的正确率和经AdaBoost算法提升后的正确率 Table 3 Comparison between accuracy of cross-validation method with the best parameters and that improved by AdaBoost algorithm
| % | ||
| 故障诊断模型 | 弱分类器最高正确率 | 应用AdaBoost算法后正确率 |
| ?比值系数法 | 77.00 | 97.3 |
| ?相关系数法 | 70.10 | 87.50 |
| ?单位向量法 | 64.38 | 86.52 |
| ?单位向量法 (加入ΔEGT/ΔFF) | 83.04 | 87.45 |
表选项
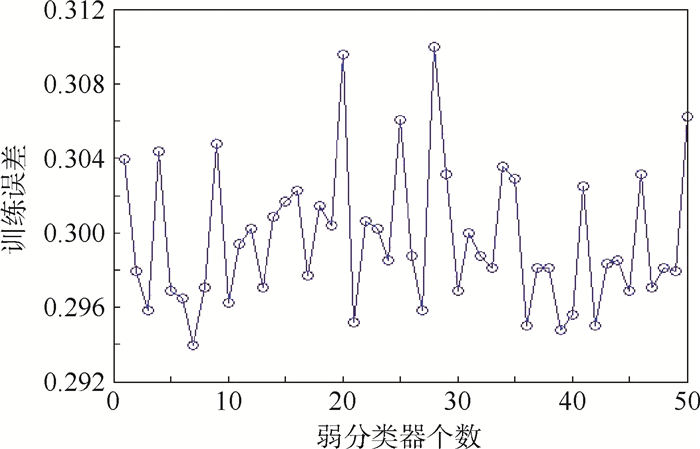 |
| 图 5 M=50时各弱分类器的训练误差 Fig. 5 Training errors of each weak classifier when M=50 |
| 图选项 |
在选定训练数据和训练方法后,弱分类器的个数选择会直接影响到训练时间和精度。图 6显示了运用AdaBoost算法,不同诊断模型的错误率随弱分类器个数增加的变化情况。可以看出,初始时单个弱分类器的精度并不高,在弱分类器数量不多(小于5个)的情况下,弱分类器错误率明显上升,当弱分类器个数增多时,错误率明显下降,最后趋于相对稳定的波动。AdaBoost算法之所以能提升正确率,在于训练多个模型来诊断,模型增多增加了训练时间,这一算法实质是以牺牲时间效率来提高正确率,因此可根据计算时间和诊断准确率综合确定弱分类器的数量,如上例弱分类器个数为20即可。
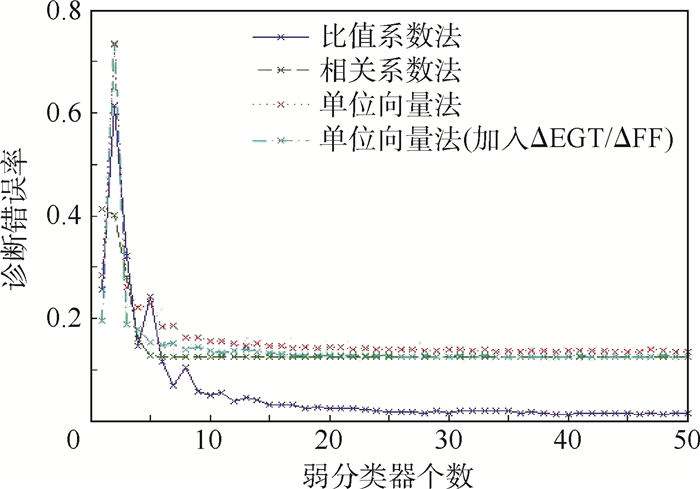 |
| 图 6 不同模型诊断错误率随弱分类器个数的变化 Fig. 6 Variation of diagnosis error rate of different models with number of weak classifier |
| 图选项 |
注意到在图 6中,相关系数法和单位向量法的相关诊断模型错误率没能随着弱分类器个数的提升而进一步减小。对此进行分析发现,与比值系数法相比,采用相关系数法和单位向量法准备的一些故障数据标识过于接近(如表 4中第7、8、9类3种故障),导致某些故障与另一种故障容易混淆。而AdaBoost.SAMME算法虽然放宽弱分类器错误率限制,但其没有关注到弱分类器的质量,不能保证每次被弱分类器正确分类的训练样本权值一定大于其错分到其他任一类别的训练样本权重,从而不能确保最终强分类器正确率的提升[17],即算法中多个弱分类器将某一故障固定地诊断为另一种故障引起诊断错误。
表 4 相关系数法中数值相似的故障标识 Table 4 Numerical approximation fault identification of correlation coefficient method
| 故障序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … | 24 |
| 1 | 1 | -1 | -0.803 | 0.803 | 0.311 | -0.311 | -0.994 | -0.995 | -0.993 | … | 0.377 |
| | |||||||||||
| 7 | -0.994 | 0.994 | 0.734 | -0.734 | -0.208 | 0.208 | 1 | 0.999 | 0.999 | … | -0.435 |
| 8 | -0.995 | 0.995 | 0.740 | -0.740 | -0.217 | 0.217 | 1 | 1 | 1 | … | -0.422 |
| 9 | -0.994 | 0.994 | 0.734 | -0.734 | -0.208 | 0.208 | 0.999 | 1 | 1 | … | -0.405 |
| | |||||||||||
| 24 | 0.377 | -0.377 | 0.031 | -0.031 | -0.414 | 0.414 | -0.435 | -0.422 | -0.405 | … | 1 |
表选项
通过第2种思路的噪声添加处理后,各数据准备方法下用多分类AdaBoost算法在进行20次迭代训练后,模型诊断正确率如表 3所示。
通过表 3能够看出,不同训练数据加入相同程度的噪声后,单个SVM分类正确率并不高,由于单位向量法的训练数据数值比较接近,因此其弱分类器的最高正确率比另外2种方法低,但在增加了一项维度后,正确率明显有所提高。但在弱分类器最高正确率较低的情况下,多分类AdaBoost算法组合M个正确率较低的弱分类器的诊断结果后,却能显著地提升诊断的正确率。
由上述分析可知,采用多分类AdaBoost算法后模型诊断正确率均有显著提升,同时发现,初始训练数据对诊断结果也会产生较大影响,这也反映了各种数据准备方法所构建的数据在反映不同故障特征时的差异。
综上可知,在实际诊断中,只通过某种训练数据所得模型进行诊断,可能诊断某些故障中出现错误。因此,为了全面反映故障的特征,在满足指印图数据所代表故障含义的基础上,通过多种训练数据进行建模,再将多种建模结果同时用于分析诊断,可以获得比较可靠的诊断结果。
2.3 案例诊断 选取某航空公司3起未造成严重后果,只引起特征参数不正常的故障案例进行诊断分析。通过监控软件观察到发动机参数短时间有较大变化,表明发动机状态不正常,由各参数与基线值的偏差分析,得到相应参数偏差值[18]。已知3起案例的性能参数小偏差值如下。案例1:ΔEGT=22℃, ΔFF=2.8%, ΔN2=1%,ΔN1=0.2%;案例2:ΔEGT=8℃,ΔFF=1%,ΔN2=0%,ΔN1=-0.2%;案例3:ΔEGT=-50.3℃,ΔFF=-1.13%,ΔN2=-2.7%,ΔN1=-22.57%。根据上述4个模型进行诊断,结果如表 5所示(表 5中(1)、(2)分别表示在第1种、第2种噪声添加方法下所得诊断模型的诊断结果,诊断结果的编号值表示指印图中标识的第几种故障)。
表 5 案例诊断结果 Table 5 Cases' diagnosis results
| 故障诊断模型 | 故障序号 | ||
| 案例1 | 案例2 | 案例3 | |
| 比值系数法(1) | 7 | 7 | 20 |
| 比值系数法(2) | 7 | 7 | 1 |
| 相关系数法(2) | 8 | 7 | 1 |
| 单位向量法(1) | 7 | 7 | 1 |
| 单位向量法(2) | 7 | 12 | 1 |
| 单位向量法(加入ΔEGT/ΔFF)(2) | 7 | 7 | 2 |
表选项
由于一些故障标识数据间存在高度相似性(见表 3)和一些故障类型存在相关性,各模型诊断正确率并不相同,因此模型诊断可能存在一定偏差。但通过表 5中各分类模型诊断结果综合分析,最有可能的故障为7、7、1,根据指印图可知第7类故障为高压压气机组件性能损失,第1种为总温指示偏差。实际故障情况,案例1为高压压气机叶片出现损坏(见图 7),案例2为某2.5级放气活门连接曲柄与连接环出现脱落,案例3为Tt2探头出现问题。案例1和案例3诊断结果完全正确。案例1中,当发动机高压压气机叶片出现损伤时,发动机压气效率会降低,推力也会降低,为保持推力稳定,需要增加燃油量使压气机转速增加,来提高增压比,因此各参数均出现增加;案例2中,2.5级放气活门全开,会使引气量减少,压气机效率表现出下降,因此会影响高压压气机组件效率;案例3中,Tt2探头出现问题时,由于测量参数需要利用总温进行修正,在发动机EPR测量参数不改变时,这4个气路参数会有同正负方向的偏差,且ΔEGT偏差过分异常表明了指示系统故障的可能性较高。
 |
| 图 7 案例1的实际排故检测结果 Fig. 7 Actual detection and troubleshooting results of Instance 1 |
| 图选项 |
由上可见,根据上述方法所建立的模型,在实际诊断中诊断准确性很高,对于故障诊断具有较大的指导意义。由于指印图中标识的一些故障只是相关单元体的性能问题,如案例2中并未指明导致故障具体原因,因此在实际故障诊断中仍需采用孔探等其他手段进一步的分析和探查。
3 结论 运用多分类AdaBoost算法的综合改进算法,以SVM为基础分类器,显著提高了诊断的准确率。在实际案例诊断中,采用不同训练数据建立了多个AdaBoost诊断模型,将其用于实际故障的诊断,通过综合分析诊断结果,可以更加准确地判断故障种类。
需指出的是,本文采用的AdaBoost算法及其改进算法仍有改善空间[17],如对难以区分的样本进行再处理等方法,可以在后续研究中加以完善,从而能够进一步提高训练模型的正确率。
参考文献
| [1] | WU X, KUMAR V. The top ten algorithms in data mining[M].Boca Raton: CRC Press, 2009: 127-149. |
| [2] | 曹莹, 苗启广, 刘家辰, 等. AdaBoost算法研究进展与展望[J].自动化学报, 2013, 39(6): 745–758. CAO Y, MIAO Q G, LIU J C, et al. Advance and prospects of AdaBoost algorithm[J].Acta Automatica Sinica, 2013, 39(6): 745–758.(in Chinese) |
| [3] | 徐启华, 杨瑞. 基于AdaBoost算法的故障诊断仿真研究[J].计算机工程与设计, 2005, 26(12): 3210–3212. XU Q H, YANG R. Simulation research on fault diagnosis using AdaBoost algorithm[J].Computer Engineering and Design, 2005, 26(12): 3210–3212.DOI:10.3969/j.issn.1000-7024.2005.12.016(in Chinese) |
| [4] | 夏利民, 戴汝为. 基于Boosting模糊分类的滚动轴承故障诊断[J].模式识别与人工智能, 2003, 16(3): 323–327. XIA L M, DAI R W. Fault testing on rolling bearing based on Boosting fuzzy classification[J].Pattern Recognition and Artificial Intelligence, 2003, 16(3): 323–327.DOI:10.3969/j.issn.1003-6059.2003.03.011(in Chinese) |
| [5] | 孙超英, 刘鲁, 刘传武. 基于Boosting-SVM算法的航空发动机故障诊断[J].航空动力学报, 2010, 25(11): 2584–2588. SUN C Y, LIU L, LIU C W. Aero-engine fault diagnosis based on Boosting-SVM[J].Journal of Aerospace Power, 2010, 25(11): 2584–2588.(in Chinese) |
| [6] | 胡金海, 谢寿生, 蔡开龙, 等. Diverse AdaBoost-SVM分类方法及其在航空发动机故障诊断中的应用[J].航空学报, 2007, 28(5): 1085–1090. HU J H, XIE S S, CAI K L, et al. Classification method of diverse AdaBoost-SVM and its application to fault diagnosis of aero-engine[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1085–1090.DOI:10.3321/j.issn:1000-6893.2007.05.010(in Chinese) |
| [7] | 胡金海, 骆广琦, 李应红, 等. 一种基于指数损失函数的多类分类AdaBoost算法及其应用[J].航空学报, 2008, 29(4): 811–816. HU J H, LUO G Q, LI Y H, et al. An AdaBoost algorithm for multi-class classification based on exponential loss function and its application[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 811–816.DOI:10.3321/j.issn:1000-6893.2008.04.007(in Chinese) |
| [8] | KEARNS M, VALIANT L. Cryptographic limitations on learning Boolean formulae and finite automata[J].Journal of the ACM, 1994, 41(1): 67–95.DOI:10.1145/174644.174647 |
| [9] | FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to Boosting[J].Journal of Computer and System Sciences, 1997, 55(1): 119–139.DOI:10.1006/jcss.1997.1504 |
| [10] | FREUND Y, SCHAPIRE R E.Experiments with a new Boosting algorithm[C]//Proceedings of the 13th Conference on Machine Learning, 1996: 148-156. |
| [11] | 李斌, 王紫石, 汪卫, 等. AdaBoost算法的一种改进方法[J].小型微型计算机系统, 2004, 25(5): 869–871. LI B, WANG Z S, WANG W, et al. Enhancing method for AdaBoost[J].Mini-Micro Systems, 2004, 25(5): 869–871.DOI:10.3969/j.issn.1000-1220.2004.05.020(in Chinese) |
| [12] | 廖红文, 周德龙. AdaBoost及其改进算法综述[J].计算机系统应用, 2012, 21(5): 240–244. LIAO H W, ZHOU D L. Review of AdaBoost and its improvement[J].Computer Systems & Applications, 2012, 21(5): 240–244.(in Chinese) |
| [13] | ZHU J, ZOU H, ROSSET S, et al. Multi-class AdaBoost[J].Statistics and Its Interface, 2009, 2(3): 349–360.DOI:10.4310/SII.2009.v2.n3.a8 |
| [14] | 李应红, 尉询楷. 航空发动机的智能诊断、建模与预测方法[M].北京: 科学出版社, 2013: 82-85. LI Y H, WEI X K. The methods of aero-engine's modeling, intelligent fault diagnosis and prognosis[M].Beijing: Science Press, 2013: 82-85.(in Chinese) |
| [15] | FRIEDMAN J, HASTIE T, TIBSHIRANI R. Additive logistic regression:A statistical view of boosting[J].Annals of Statistics, 2000, 28(2): 337–407. |
| [16] | 张卓.基于SVM多分类的PW4000故障诊断研究[D].天津: 中国民航大学, 2015: 42-49. ZHANG Z.Research on fault diagnosis of PW4000 based on SVM multi-classification[D].Tianjin: Civil Aviation University of China, 2015: 42-49(in Chinese). |
| [17] | 杨新武, 马壮, 袁顺. 基于弱分类器调整的多分类AdaBoost算法[J].电子与信息学报, 2016, 38(2): 373–380. YANG X W, MA Z, YUAN S. Multi-class AdaBoost algorithm based on the adjusted weak classifier[J].Journal of Electronics & Information Technology, 2016, 38(2): 373–380.(in Chinese) |
| [18] | 曹惠玲, 庞思凯, 薛鹏, 等. 基于双发差异的航空发动机故障诊断方法研究[J].中国民航大学学报, 2014, 32(3): 41–44. CAO H L, PANG S K, XUE P, et al. Research of aero-engine fault diagnosis method based on monitoring of twin differences[J].Journal of Civil Aviation University of China, 2014, 32(3): 41–44.DOI:10.3969/j.issn.1674-5590.2014.03.010(in Chinese) |
