目前, 机动目标转弯角速度辨识的问题已经得到了许多****的关注。文献[3-5]将转弯角速度作为目标状态变量, 通过重新构造状态方程, 分别使用扩展卡尔曼滤波(EKF)/无迹卡尔曼滤波(UKF)、基于5阶球径容积规则的高阶容积卡尔曼滤波(HCKF)等非线性滤波算法估计角速度和其他状态变量, 其缺点是角速度估计的精度依赖于目标初始状态及协方差、过程噪声等因素。文献[6]根据角速度与目标速度方向角之间的物理关系, 通过采用滤波算法对目标速度方向角进行估计, 间接求出了角速度的估计值, 该方法的缺点是采用方向角等中间变量间接地估计角速度, 将引入新的估计误差。文献[7]将角速度当作系统的未知参数, 采用期望最大化(EM)算法将角速度与目标状态进行联合估计与辨识, 该方法的缺点是使用的是全量测数据, 算法运行时间长, 不能满足空战中实时识别的要求。
在实际空战中, 目标的角速度是未知且时变的, 并且与目标状态相互耦合, 因此在进行联合状态估计与角速度辨识时, 为了获得角速度辨识的解析解, 需要解除这种耦合关系。对在传统意义上的状态估计与参数辨识中, 通常认为量测噪声之间是相互独立的, 但是在实际跟踪过程中, 雷达的采样频率过高[8], 使得相邻量测噪声之间的相关性往往不能够被忽略, 因此, 在对角速度辨识和目标状态估计的过程中必须考虑这种相关性。针对上述问题, 本文基于EM算法框架提出一种带有色量测噪声的联合估计与辨识算法, 并引入滑窗思想, 以提高辨识的实时性:E-step利用当前估计的角速度以及经过带有色量测噪声的高阶容积卡尔曼平滑(HCKS)获得的后验平滑概率密度和联合概率密度, 计算完备数据似然函数的条件期望; M-step通过使期望最大化进而更新获得下一次迭代的角速度估计量。
1 问题描述 蛇形机动可以分解成若干个具有不同转弯角速度的圆弧转弯机动, 因此蛇形机动目标转弯角速度的辨识问题转化成圆弧转弯机动的角速度辨识问题。在有色量测噪声背景下, 假设目标在二维平面中运动, 转弯机动模型状态方程及量测方程为
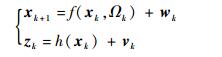 | (1) |
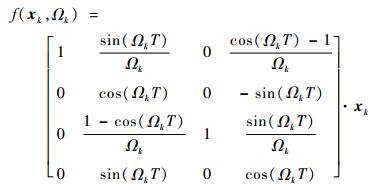 |
式中:T为采样间隔; Ωk为待辨识的转弯角速度;
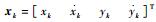
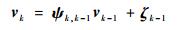 | (2) |
其中:ψk, k-1为已知的常数矩阵; ζk∈Rm为零均值高斯白噪声, 协方差为R。wk和ζk互不相关。初始状态x0与wk和ζk无关, 并且满足x0~N(x0;
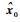
由式(1)可知, 蛇形机动目标的转弯角速度Ωk这一未知参数耦合在状态转移矩阵之中, 为了获取转弯角速度的解析解, 需要解除转弯角速度与状态转移矩阵之间的非线性耦合关系, 从而将状态方程等价转换成如式(3)形式:
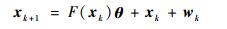 | (3) |
式中:
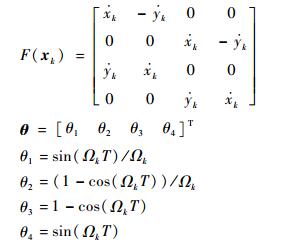 |
则通过辨识出参数θ, 进而根据
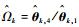
由于在有色噪声条件下, 传统的高斯近似滤波器和平滑器估计性能不佳, 进而影响EM算法的辨识效果, 所以为了实现目标状态的精确估计和转弯角速度的准确辨识, 需要解除相邻量测之间相互耦合的关系, 实现有色量测噪声的白化[10]。本文采取量测差分的方法实现有色量测噪声的白化, 重新构造量测方程如下:
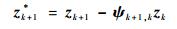 | (4) |
式中:zk+1*为重新构造的白色量测。
依据式(1)和式(2)可以得到具有一步状态延迟的量测方程:
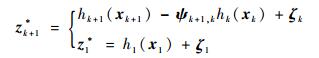 | (5) |
定理1[11]??如果pθ(xs|Z1*k)服从高斯分布, pθ(xs|Z1k)也服从高斯分布, 则在最小均方差意义下满足:
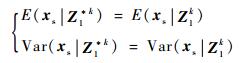 |
也就是说在最小均方差误差意义下, 基于白化后的量测Z1*k的状态估计与基于有色量测Z1k的状态估计是等价的。
2 基于HCKS-EM的联合估计与辨识算法 基于极大似然估计准则, 本文提出了一种带有色量测噪声的联合估计与辨识算法对未知角速度进行辨识, 具体的算法框架如图 1所示。在第t次迭代时, 通过将带有色噪声的量测序列经过HCKS, 获得目标状态的平滑估计量, 并采用EM算法进行参数θ的辨识, 辨识后的参数θ用于第t+1次的状态估计, 不断迭代直到满足设定的要求为止[12-13]。
 |
| 图 1 联合估计与辨识算法 Fig. 1 Joint estimation and identification algorithm |
| 图选项 |
在系统状态X1k={x1, x2, …, xk}缺失, 量测序列Z1*k={z1*, z2*, …, zk*}已知的前提下, k为当前时刻量测数据样本数, 则可知完备数据似然函数为[14-15]
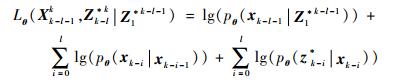 | (6) |
给定第t次迭代后得到的参数θ的估计值

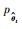
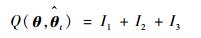 | (7) |
式中:
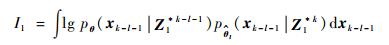 | (8) |
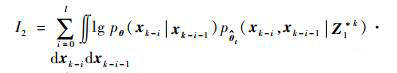 | (9) |
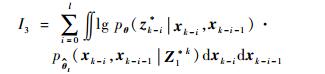 | (10) |
其中:l为滑动窗口的长度, 其长度大小可依据实际需求自行设定。当l=k-1时, I1是一个常数, 与待辨识量θ无关; 当0≤l < k-1时, I1与θ相关性较弱, 而且为了满足实时性的要求, 辨识算法应尽量关注当前时刻的数据或者邻近时刻的数据, 所以本文仅仅考虑I2和I3对条件期望函数的影响。
假设先验概率密度函数pθ(xk-i|xk-i-1)和pθ(zk-i*|xk-i, xk-i-1)均服从高斯分布, 并且满足
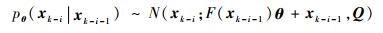 | (11) |
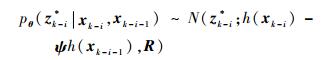 | (12) |
则将式(11)和式(12)分别代入I2和I3当中, 可知I3与未知参数θ无关, 所以, 在辨识参数θ时, 仅仅考虑I2对条件期望函数的影响, 即条件期望函数
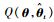
EM算法通过不断迭代求得
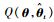
2.1 E-step E-step的主要任务是根据先验概率密度、后验平滑概率密度以及xk-i和xk-i-1的联合概率密度进行确定性采样计算条件期望函数
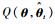
通过上述的分析可知, 条件期望函数
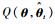
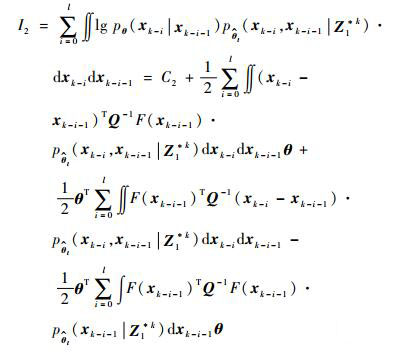 | (13) |
式中:后验平滑概率密度和基于滑窗内数据的xk-i和xk-i-1的联合概率密度满足如下分布:
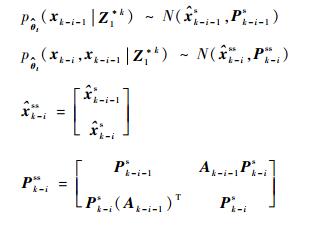 |
其中:平滑量

为了求解I2, 首先定义如下2种积分函数:
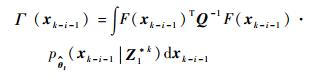 | (14) |
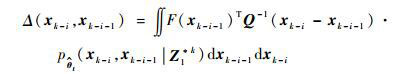 | (15) |
然后分别将F(xi)和xi按xi的分量进行分解, 可得
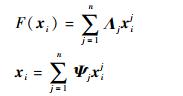 |
式中:Λj为常数矩阵; xij表示xi的第j个分量; Ψj表示n×n单位矩阵的第j列; n为xi的维数。
Γ(xk-i-1)和Δ(xk-i, xk-i-1)可分别表示为
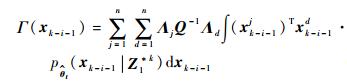 | (16) |
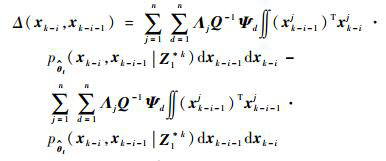 | (17) |
根据状态平滑

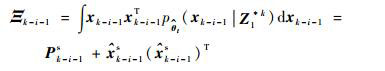 | (18) |
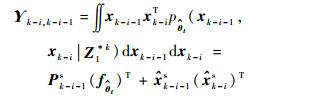 | (19) |
则
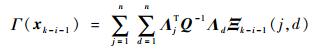 | (20) |
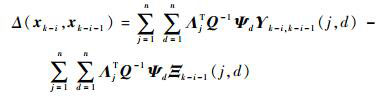 | (21) |
2.2 M-step M-step的主要任务是解决I2的极大化问题, 即求解使I2满足极大值时所对应的
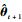
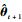
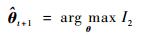 | (22) |
当I2取得极大值时满足
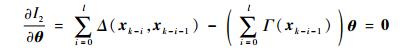 | (23) |
则可求得参数θ的迭代表达式为
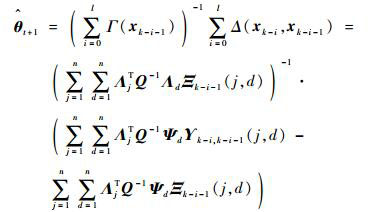 | (24) |
通过不断迭代最终求得k时刻参数θ的估计值
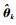
2.3 带有色量测噪声的HCKS算法的设计 由于vk为高斯有色噪声, 通过白化有色噪声vk而获得的量测zk+1*与xk+1和xk相关, 为方便后续的计算, 在此将目标状态进行扩维, 表示为
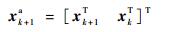 |
在最小均方误差意义下, 扩维状态的一步预测
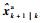
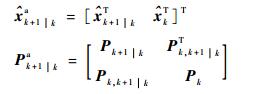 |
众所周知, 平滑是在滤波的基础之上进行的, 因此首先设计一种带有色量测噪声的HCKF算法, 算法如下:
算法1??带有色量测噪声的高斯滤波算法框架。
步骤1??状态预测。
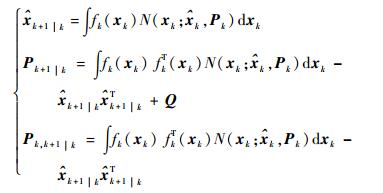 | (25) |
步骤2??状态修正。
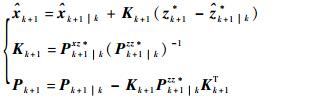 | (26) |
 | (27) |
式中:hk+1*(xk+1|ka)=hk+1(xk+1)-ψk+1, khk(xk)。
带有色量测噪声的HCKS算法是一类前向后向平滑器, 其主要包括2个部分:前向一步平滑和后向固定区间平滑, 具体算法如下:
算法2??带有色量测噪声的高斯平滑算法框架。
步骤1??前向一步平滑。
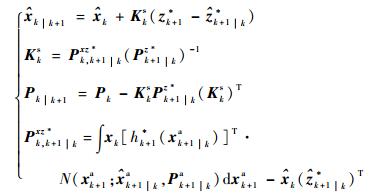 | (28) |
步骤2??后向固定区间平滑。
 | (29) |
2.4 带有色量测噪声的HCKS算法的实现 本文中采用了Jia等[5]提出的5阶球径容积规则计算式(25)、式(27)和式(28)中的非线性高斯积分:
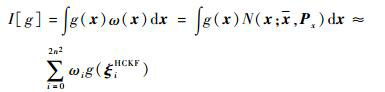 | (30) |
式中:Px=SxSxT; ξiHCKF=ξiSx+x。
 | (31) |
式中:ei为n维单位向量, 且其第i个元素为1。
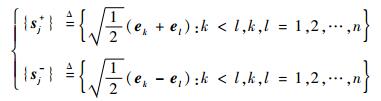 | (32) |
容积点所对应的权重ωi为
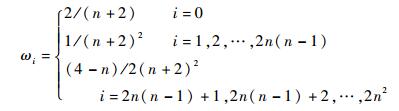 | (33) |
可将本文算法总结如下:
算法3??基于HCKS-EM的联合估计与辨识算法
初始化:给定量测集合Z1*k, 目标初始状态x0和协方差P0, 角速度初始值为Ω0, 最大迭代次数为5。
步骤1??E-step。已知第t次迭代后参数θ的估计值为θt, 由式(28)和式(29)可以求得后验平滑概率密度和基于滑窗内数据的xk-i和xk-i-1的联合概率密度, 进而可以求解得到I2的值。
步骤2??M-step。通过式(23)和式(24)可求解得到参数θ的估计值
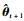
步骤3??迭代终止。给定一个阈值ε, 如果
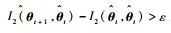
递归:t=0, k←k+1, 并将参数θ的初值设为上次迭代结束时的辨识值, 进入下一轮迭代。
3 仿真分析 本文利用水平方向上的转弯机动非线性动态模型, 仿真出一条蛇形机动轨迹。假设机动目标在1~80 s以Ω1=-2(°)/s作转弯运动, 在k=81 s时转弯角速度突变为Ω2=2(°)/s并持续到300 s。设置转弯角速度初始值为Ω0=-1(°)/s, 采样周期T=1 s, q1=0.1 m2/s3, 过程噪声wk的协方差为Q。
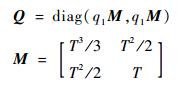 |
通过载机雷达可以获得目标与载机之间的相对距离r、方向角φ的信息, 则可获得系统的非线性量测方程为
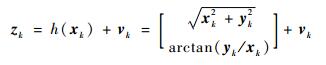 |
式中:vk为高斯有色噪声, 与其对应的ζk是零均值高斯白噪声, 协方差为Rk=[σr2 σφ2], σr=10 m,
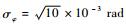
基于HCKS-EM联合估计与辨识算法和扩维法的初始状态以及协方差分别为
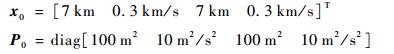 |
扩维法初始状态和协方差的分别设置为
 |
为了评估分析本文联合估计和辨识算法的性能, 设置了如下3组仿真:
仿真1??窗口长度l分别设置为5、10、15、20, 最大迭代次数均为5次, 各执行100次蒙特卡罗仿真。图 2为不同窗口长度下角速度辨识结果, 图 3为不同窗口长度下角速度辨识均方根误差(RMSE)。从图 2和图 3可以看出, 随着窗口长度的增大, 该算法在第一阶段收敛于真实值的时刻就越早, 精度越高, 并且越稳定, 但是当角速度发生突变时, 对于突变的角速度反应的就越慢。并且从图 4和表 1可以看出, 窗口长度越大, 该算法估计的目标状态整体精度就越高, 但是消耗的时间越长, 这显然是时间与精度之间的“博弈”问题, 当窗口大于10时, 由窗口长度即量测数据带来的精度收益优势不太明显, 相反运算时间的增加确实比较可观的, 也就是说算法的执行效率降低了。并且在角速度发生突变时刻及其附近, 窗口长度为10时的估计效果明显好于其他3个窗口。
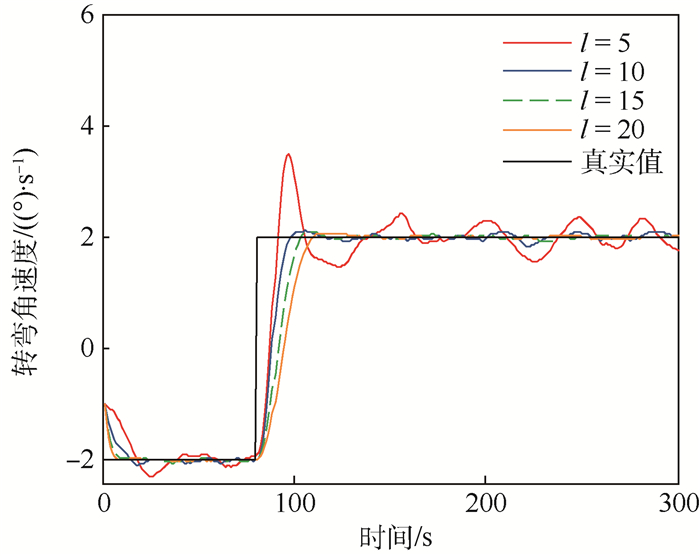 |
| 图 2 不同窗口长度下转弯角速度辨识结果 Fig. 2 Turn rate identification results with different window lengths |
| 图选项 |
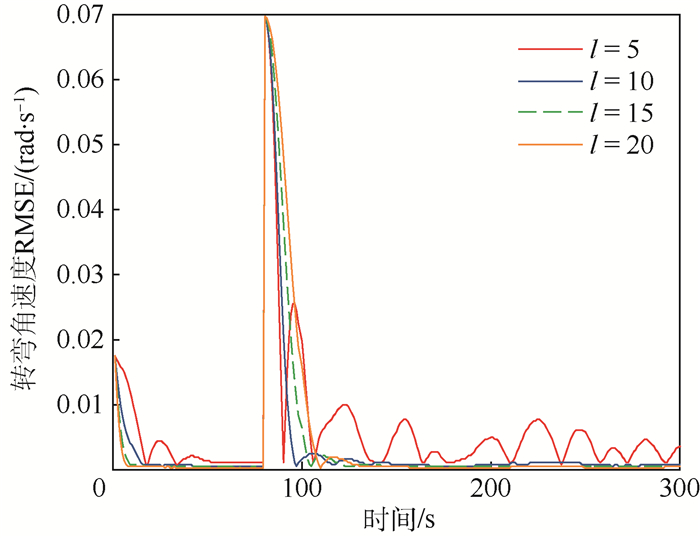 |
| 图 3 不同窗口长度下转弯角速度辨识的均方根误差 Fig. 3 RMSE of turn rate identification with different window lengths |
| 图选项 |
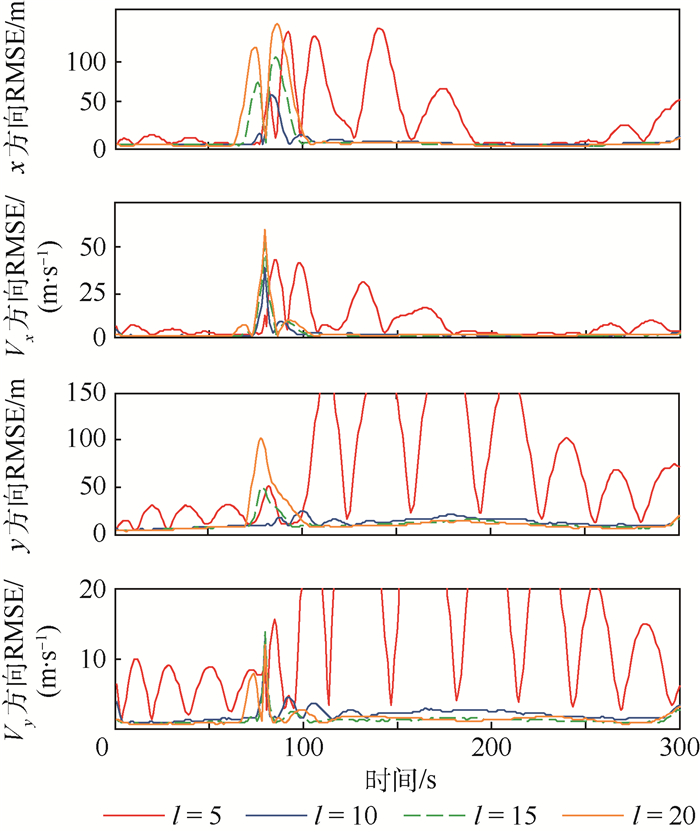 |
| 图 4 不同窗口长度下位置和速度估计均方根误差 Fig. 4 RMSE of position and velocity estimation with different window lengths |
| 图选项 |
表 1 k=50 s时的角速度和状态所耗费的时间 Table 1 Turn rate and state calculation time when k=50 s
| 滑动窗口长度 | 时间/s |
| 5 | 0.046 5 |
| 10 | 0.104 8 |
| 15 | 0.122 2 |
| 20 | 0.164 9 |
表选项
仿真2??窗口长度设置为10, 最大迭代次数r分别设置为3、5、10、15, 各执行100次蒙特卡罗仿真。从图 5和图 6可以看出, 随着迭代次数的增加, 该算法在初始时刻收敛于真实值的时刻就越早, 并且对于角速度突变反应的也比较灵敏。从图 7目标状态4个分量的RMSE可以看出, 迭代次数越大, 该算法估计的目标状态整体精度就越高, 但是根据表 2中的运算时间可知花费的时间也会相应地增大。尤其是当最大迭代次数大于5时, 最大迭代次数增加所带来的精度收益越发的不明显。
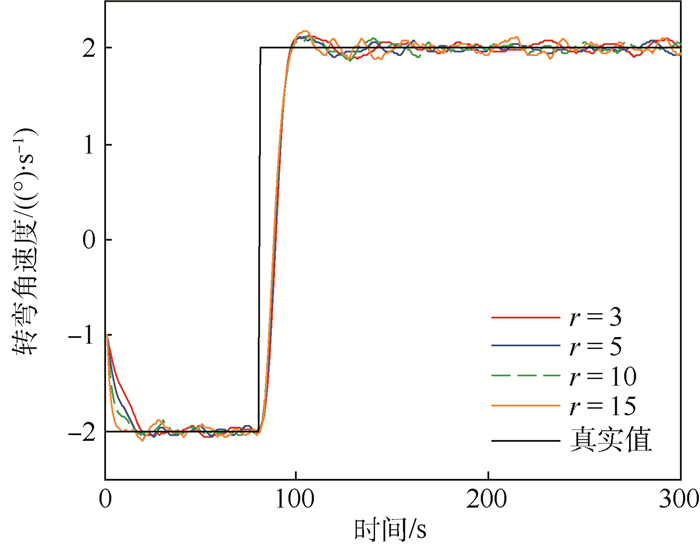 |
| 图 5 不同最大迭代次数下转弯角速度辨识结果 Fig. 5 Turn rate identification result with different numbers of maximum iterations |
| 图选项 |
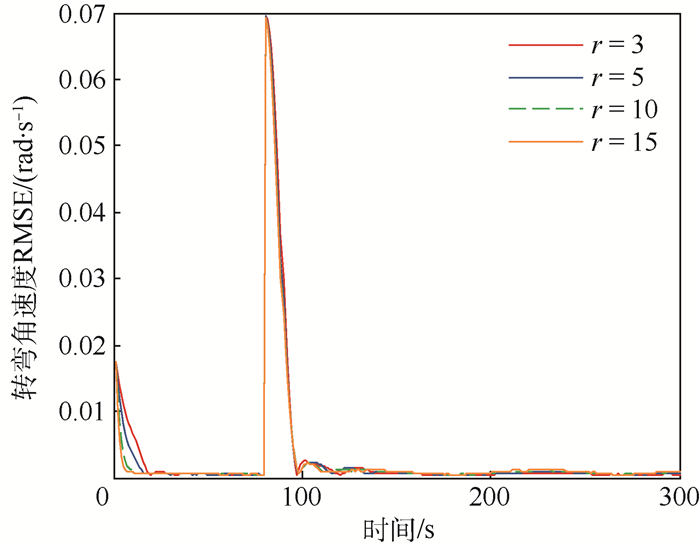 |
| 图 6 不同迭代次数下转弯角速度辨识的均方根误差 Fig. 6 RMSE of turn rate identification with different numbers of iterations |
| 图选项 |
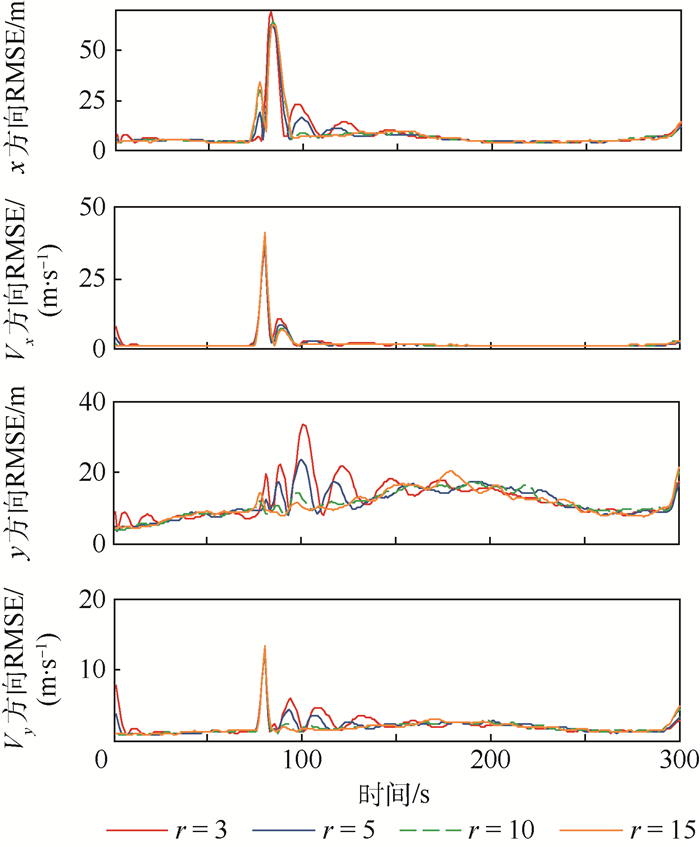 |
| 图 7 不同迭代次数下位置和速度估计均方根误差 Fig. 7 RMSE of position and velocity estimation with different numbers of iterations |
| 图选项 |
表 2 k=120 s时的角速度和状态所耗费的时间 Table 2 Turn rate and state calculation time when k=120 s
| 最大迭代次数 | 时间/s |
| 3 | 0.049 5 |
| 5 | 0.082 7 |
| 10 | 0.159 9 |
| 15 | 0.257 7 |
表选项
仿真3??将本文联合估计与辨识算法窗口长度设置为10, 最大迭代次数设置为5, 将该算法与带有色的UKF算法和带有色的HCKF算法各执行100次蒙特卡罗仿真。从图 8和图 9可以看出, 本文EM算法收敛于角速度真实值的时刻比带有色的UKF算法和带有色的HCKF算法都要早, 并且稳定、精度高, 但是当角速度发生突变时, 对于突变的角速度反应的速度比较慢。从图 10目标状态4个分量的RMSE可以看出, 除了在角速度突变时刻及其邻近时刻之外, 本文EM算法估计的精度都要明显高于带有色的UKF算法和带有色的HCKF算法估计的精度, 带有色的HCKF算法比带有色的UKF算法估计的精度要高。
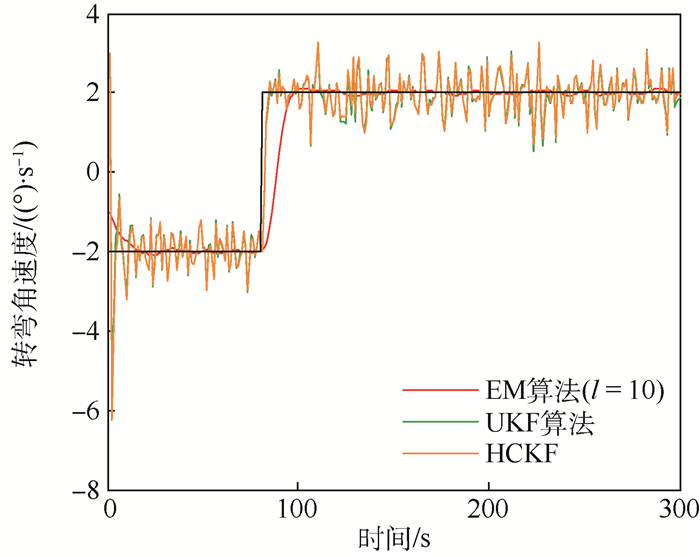 |
| 图 8 EM算法与扩维法之间的对比 Fig. 8 Comparison between EM algorithm and augmentation method |
| 图选项 |
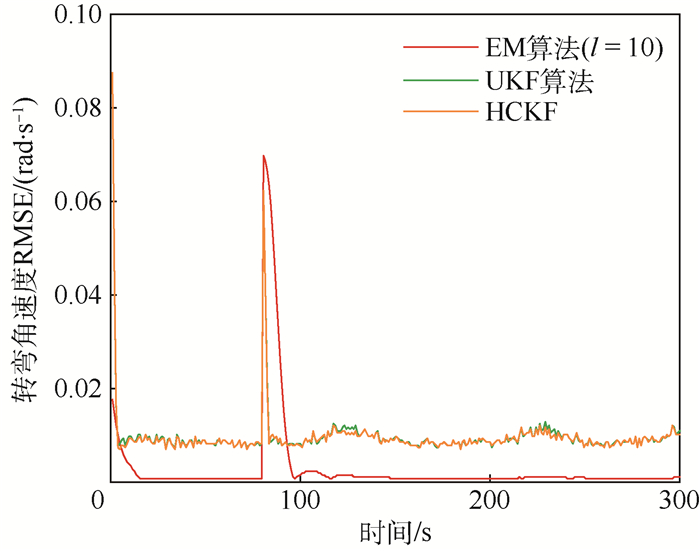 |
| 图 9 转弯角速度辨识均方根误差 Fig. 9 RMSE of turn rate identification |
| 图选项 |
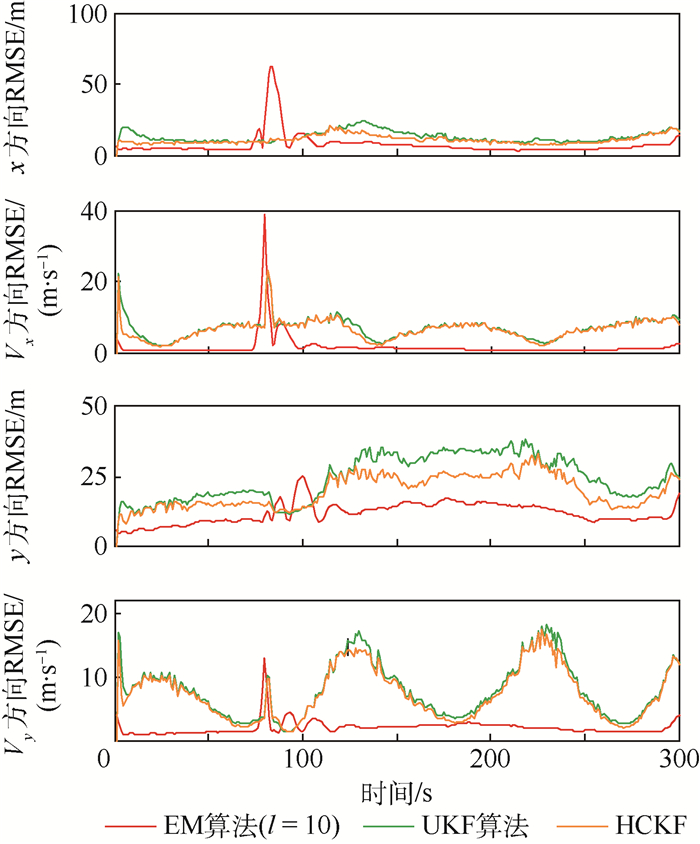 |
| 图 10 位置和速度估计均方根误差 Fig. 10 RMSE of position and velocity estimation |
| 图选项 |
4 结论 针对蛇形机动目标角速度辨识与目标状态联合估计的问题, 基于EM算法框架提出一种带有色量测噪声的联合估计与辨识算法。主要结论有:
1) EM算法设计:在E-Step, 通过将完备似然函数进行分解, 从而将其转换成带参数θ的解析表达式, 提高了辨识与估计的精度, 降低了由状态扩维法扩维所带来的复杂性; 在M-Step, 通过极大化完备似然函数求得高精度的解析解。
2) 带有色量测噪声的HCKS算法的设计:考虑到在实际空战中, 相邻噪声序列之间的相关性对于目标状态估计与转弯角速度辨识的影响, 设计了带有色量测噪声的HCKS算法用于消除这种影响, 提高了联合辨识与估计的精度。
参考文献
| [1] | 宋华, 章新华, 许林周. 基于离散隐马尔科夫模型的空中目标战术机动识别[J].仪器仪表学报, 2007, 28(4): 588–592. SONG H, ZHANG X H, XU L Z. Aerial combat maneuver identification based on discrete hidden Markov model[J].Chinese Journal of Scientific Instrument, 2007, 28(4): 588–592.(in Chinese) |
| [2] | 钟友武, 柳嘉润, 申功璋. 自主近距空战中敌机的战术动作识别方法[J].北京航空航天大学学报, 2007, 33(9): 1056–1059. ZHONG Y W, LIU J R, SHEN G Z. Recognition method for tactica maneuver of target in autonomous close-in air combat[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(9): 1056–1059.DOI:10.3969/j.issn.1001-5965.2007.09.013(in Chinese) |
| [3] | ROTH M, HENDEBY G, GUSTAFSSON F.EKF/UKF maneuvering target tracking using coordinatd turn models with polar/Cartesian velocity[C]//17th International Conference on Information Fusion (FUSION).Piscataway, NJ: IEEE Press, 2014: 1-8. |
| [4] | ARASARATNAM I, HAYKIN S. Cubature Kalman smoother[J].Automatica, 2011, 47(10): 2245–2250.DOI:10.1016/j.automatica.2011.08.005 |
| [5] | JIA B, XIN M, CHENG Y. High-degree cubature Kalman filter[J].Automatica, 2013, 49(2): 510–518.DOI:10.1016/j.automatica.2012.11.014 |
| [6] | 黄伟平, 徐毓, 王杰. 基于改进"当前"统计模型的转弯机动跟踪算法[J].控制与决策, 2011, 26(9): 1412–1416. HUANG W P, XU Y, WANG J. Algorithm based on modified current statistic mode fo turn maneuver[J].Control and Decision, 2011, 26(9): 1412–1416.(in Chinese) |
| [7] | SONG B, WANG X X, LIANG Y, et al.Analytical identification of system parameter nonlinearly coupled in dynamic transition matrix[C]//American Control Conference(ACC).2016: 1832-1837. |
| [8] | 王小旭, 梁彦, 潘泉, 等. 带有色量测噪声的非线性系统Unscented卡尔曼滤波器[J].自动化学报, 2012, 38(6): 986–998. WANG X X, LIANG Y, PAN Q, et al. Unscented Kalman filter for nonlinear systems with colored measurement noise[J].Acta Automatica Sinica, 2012, 38(6): 986–998.(in Chinese) |
| [9] | WANG X X, LIANG Y, PAN Q, et al. Nonlinear Gaussian smoothers with colored measurement noise[J].IEEE Trasactions on Automatic Control, 2015, 60(3): 870–876.DOI:10.1109/TAC.2014.2337991 |
| [10] | 黄玉龙, 张勇刚, 李宁, 等. 一种带有色量测噪声的非线性系统辨识方法[J].自动化学报, 2015, 41(11): 1877–1892. HUANG Y L, ZHANG Y G, LI N, et al. An identification method for nonlinear systems with colored measurement noise[J].Acta Automatica Sinica, 2015, 41(11): 1877–1892.(in Chinese) |
| [11] | WANG X X, LIANG Y, PAN Q, et al. Nonlinear Gaussian smoothers with colored measurements noise[J].IEEE Transactions on Automatic Control, 2015, 60(3): 870–876.DOI:10.1109/TAC.2014.2337991 |
| [12] | NOBUHIRO Y. Parameter estimation of aircraft dynamics via unscented smoother with expectation-maximization algorithm[J].Journal of Guidance, Control, and Dynamics, 2011, 34(2): 426–436.DOI:10.2514/1.51696 |
| [13] | LAN H, LIANG Y, YANG F, et al. Joint estimation and identification for stochastic systems with unknown inputs[J].IET Control Theory & Appications, 2013, 7(10): 1377–1386. |
| [14] | SCHON T, WILLS A, NINNESS B. System identification of nonlinear state-space models[J].Automatica, 2011, 47(1): 39–49.DOI:10.1016/j.automatica.2010.10.013 |
| [15] | HUANG Y, ZHANG Y G, LI N, et al. Latency probability estimation of non-linear systems with one-step randomly delayed measurements[J].IET Control Theory & Appications, 2016, 10(7): 843–852. |
