随着作战环境的复杂化、作战过程的动态化、作战任务的多样化，多无人作战飞机(Unmanned Combat Aerial Vehicles，UCAVs)协同攻击多目标将是一种未来的重要作战模式。UCAVs协同任务分配是UCAV协同作战的关键技术之一，其目的是在一定战场环境和任务要求下，考虑执行任务的约束条件和技术指标，将目标合理地分配给不同的UCAV，使得整个编队作战效能达到最大。
目前，对UCAVs协同任务分配技术的研究已经成为UCAV作战研究中的热点。针对任务分配问题，文献[1]采用多种协商机制建立分布式UCAVs控制系统；文献[2]提出了基于多层树的协同攻击多目标模型；也可以采用智能优化算法对UCAVs任务分配问题求解，比如萤火虫优化算法^[3]、粒子群算法^[4]等。在实际的UCAV协同任务执行过程中，可能会出现任务获取信息不完整，或者在任务执行过程中存在战场环境和任务需求以及任务信息的变化，导致现有的任务分配方案对实时环境的不适应^[5-6]。同时，相关文献中的任务分配算法模型同时或部分存在以下问题，如：①未考虑目标之间的支援关系；②未考虑电子干扰下的任务分配；③动态的任务分配没有用时间指标体现出来。
针对动态任务分配的特点，同时考虑到以上存在的问题，本文采用了时间片下基于改进灰狼优化(Grey Wolf Optimization, GWO)算法^[7]的任务分配方法。通过对UCAV编队信息和任务目标信息的分析，提出了基于时间片的多约束动态任务分配模型；针对动态任务分配数学模型，采用了自适应灰狼优化(Self-Adaptive GWO, SAGWO)算法进行求解；最后进行了仿真验证。
1 UCAVs动态任务分配模型 本文以UCAV执行空对地打击任务为背景，假设我方有M架无人作战飞机V={V_i, i=1, 2, …, M}，敌方地面有N个确定目标T={T_j, j=1, 2, …, N}，其中V_i表示我方的第i个UCAV，T_j表示地面第j个任务目标。设目标的分配矩阵为X_M×N，当X_ij为1时，表示第i个UCAV对第j个任务目标进行攻击；X_ij为0时，表示V_i未分配到T_j。假设我方第i个UCAV可携带L_i枚导弹，则编队可携带的导弹数量为。
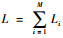
假设攻击目标的L枚导弹构成集合K={k, k=1, 2, …, L}，则UCAV编队的第k枚导弹与无人机V_i的第l枚导弹对应的关系为

(1)

式中：i={1, 2, …, M}；l={1, 2, …, L_i}。
1.1 UCAV优势概率 UCAV对目标的优势概率与UCAV距离威胁因子、速度威胁因子和角度威胁因子有关。UCAV编队中V_i对目标T_j的优势概率可以表示为

(2)

式中：c₁和c₂分别为无人机V_i相对任务目标T_j的距离-角度威胁和速度威胁的权重；T_{ij, D}、T_{ij, θ}和T_{ij, v}分别为距离威胁概率、角度威胁概率和速度威胁概率^[8]。
距离威胁概率为

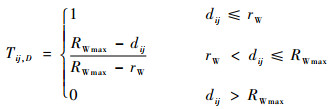(3)

式中：d_ij为V_i相对于T_j的距离；r_W为我方UCAV导弹的有效作用距离；R_Wmax为UCAV的最大跟踪距离。
角度威胁概率为

(4)

式中：θ_ij为UCAV速度方向与视线之间的夹角；λ₁和λ₂为正常数。
速度威胁概率为

(5)

式中：v_i和v_Tj分别为第i个UCAV和任务目标T_j的速度矢量。
1.2 任务威胁分析 战场目标威胁信息分析对UCAV执行任务成功率是非常重要的。对于目标威胁特性，将目标威胁分为探测类目标威胁和杀伤类武器威胁^[9]。探测类目标威胁一般指雷达威胁，杀伤类武器威胁包括地空导弹和高炮，其威胁概率采用文献[7]的模型。
当UCAV在多目标威胁空间中执行任务时，面临的威胁程度增加。这种威胁程度增加的原因不仅仅是由于多个威胁源独立探测和杀伤的叠加效果，而且是由于整个目标网络化信息管理与共享。因此，提出了目标依赖矩阵来反映目标之间的关系^[10]。
定义1??A_N×N为目标内部之间依赖矩阵。矩阵元素a_ij为第i个目标对第j个目标的依赖程度，也可以说第j个目标对第i目标的信息共享或者火力支援能力。
对于多个目标的威胁，考虑到目标之间相互支援的情况，则目标对UCAV的威胁概率为

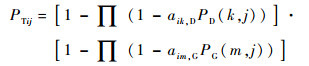(6)

式中：P_Tij为目标i对无人作战飞机j的威胁概率；a_{ik, D}为任务目标中探测类武器对其他武器的依赖程度；a_{im, G}为任务目标中攻击类武器对其他武器的依赖程度；P_D(k, j)为单个探测类武器的威胁概率；P_G(m, j)为单个攻击类武器的威胁概率(包括地空导弹威胁概率与高炮威胁概率)。
对于攻击类目标，考虑到信息资源相互共享与火力支援，同时其威胁过程是即发现就攻击，探测概率为1，因此，只计算攻击类目标对UCAV的威胁概率：

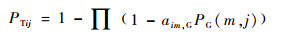(7)

1.3 任务时间分析 UCAV完成任务的时间主要是根据任务类型、可执行该任务的UCAV特性及载荷类型等先验经验得到完成各项任务的统计时间。观测某一时刻的分配情况、任务目标对UCAV的威胁、UCAV对任务目标的杀伤情况以及完成任务的效果需要引入时间片这个概念。
定义2??任务时间片^[11]是指对事件变量集的某一次观察。在协同攻击多目标的任务分配问题中，时间片就是每隔一定的时间去观测UCAV的任务情况。时间片的间隔越小，意味着系统观测分配结果、目标威胁程度、UCAV的杀伤情况以及对各方兵力信息的统计分析频率越高，那么决策越精细，其实时性提高；但是间隔小的时间片会引起信息量的增大，系统处理数据的时间增长，不利于战场快速决策，因此，要选取一定任务时间片是分配决策的关键问题。
定义3??UCAV飞行矩阵T_fly是(M+N)×N矩阵，行包含UCAV和目标，列包含目标，t_ij表示节点i到节点j的时间消耗。T_fly取决于UCAV的速度和位置、任务目标的位置以及其机动性，T_fly可表示为

对于T_fly元素t_ij的计算主要与在时间片结束时刻UCAV的速度和位置、任务目标的位置有关，如下：

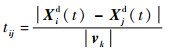(8)

式中：X_i^d(t)和X_js^d(t)分别为t时间片第i个节点和第j个节点的位置。
定义4??任务累计完成时间t_i^[12]是指第i个UCAV在执行任务集S_i={T_{i, 1}, T_{i, 2}, …, T_{i, j}}的累计完成时间。t_i可表示为

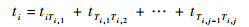(9)

式中：t_{iTi, 1}、t_{Ti, 1Ti, 2}和t_{Ti, j-1Ti, j}分别为第i个UCAV从所在位置节点到目标T_{i, 1}节点的时间、T_{i, 1}到T_{i, 2}的时间和T_{i, j-1}到T_{i, j}的时间。
假设给某一架UCAV分配有j个目标，则分配方案有A_j^j个。通过计算这A_j^j个方案的执行任务累计时间，然后根据优先判断原则，选择最小的t_i，这个t_i就是任务优先判断后的执行任务累计时间，对应的分配方案也就是这架UCAV的执行任务次序^[13]。
1.4 协同任务分配评价指标 UCAVs协同对地攻击任务目标是以整个编队的作战效能作为最优目标，而评价整个编队的作战效能指标有目标价值毁伤(Target Value Damage，TVD)、UCAV编队损耗代价(UCAV attrition)和执行任务预计消耗时间(Task Expending Time，TET)。
1) 目标价值毁伤最大化
无人机V_i完成任务T_j的目标毁伤收益值的大小体现了任务的重要程度和UCAV的执行能力，也可以量化目标价值毁伤值。编队对多目标的协同打击中，产生总的价值毁伤为

(10)

式中：f₁为编队完成任务目标的价值毁伤；V_Tj表示摧毁目标T_j获得的价值量，其由指挥人员预先设定，在作战过程中随着态势的变化和作战意图的变化可以进行调整。
2) UCAV编队损耗代价最小化
如果在UCAV编队中无人机携带软杀伤武器，那么无人机会因为欺骗和干扰设备而增大无人机的生存概率。假设第i架无人机V_i携带n_i个欺骗和干扰设备，则该机的损耗代价为

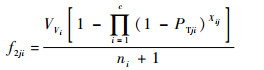(11)

式中：V_Vi为无人机V_i的价值量。
在整个UCAV编队攻击过程中所遭受的损耗代价为

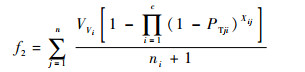(12)

3) 任务时间消耗最短
执行任务的时间可以用UCAV与任务目标间的距离来衡量，距离目标越短，则执行任务消耗的时间越短。任务消耗时间最短模型如下：

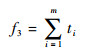(13)

式中：f₃为任务时间消耗指标。
4) 总评价指标
在多机协同过程中，设计总评价指标函数时，考虑到任务目标价值毁伤最大化、UCAV编队损耗代价最小化以及任务时间消耗最短，因此，分配模型的总体评价指标函数为

(14)

式中：J(Π)为UCAV编队协同攻击多目标的总体评价指标函数，Π为分配方案；ω₁和ω₂分别为衡量减少UCAV代价损耗和时间损耗的权重，其来源于决策者的偏好。协同攻击多目标分配问题实质就是寻找一个方案Π使评价指标函数最小，使问题转化为寻优问题。
约束条件：
1) ，UCAV任务目标的总数量不能超过编队的导弹数量。
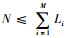
2) X_1j+X_2j+…+X_Lj=1，不允许多个UCAV导弹攻击同一个任务目标。
3) c_i≤L_i，单架UCAV执行任务数量c_i不超过UCAV可携带最大导弹数量L_i。
4) 由于UCAV性能和挂架的限制，UCAV和其挂载的武器或者导弹之间存在约束，UCAV影响武器效能的发挥可以用UCAV-武器适应度表进行描述，该适应度表中的元素用[0, 1]之间的数表示，数值的大小表示武器攻击效能发挥程度，数值越小表明UCAV越不利于武器的发挥。
2 自适应灰狼优化算法 2.1 基本GWO算法及改进策略 受灰狼的社会等级制度和猎食行为的启发，Seyedali等提出了GWO算法^[14]。同其他启发式优化算法相比，GWO算法具有实现简单、全局优化能力强、收敛速度快等特点，一经提出便受到了众多****的关注与研究^[15-17]。
在寻找最优解过程中，根据灰狼猎食的3个重要步骤，即接近、包围、攻击猎物，GWO算法建立了一个数学模型：狼群中每一个个体都是一个潜在解，其中α狼的位置是最好的解，β和δ的位置分别为优解和次优解，其他的候选解是ω的位置。猎食过程如图 1所示, C₁、C₂和C₃分别为α、β和δ狼的位置系数；a₁、a₂、a₃分别为α、β和δ狼的控制参数；D_α、D_β和D_δ分别为α、β和δ狼到ω狼的距离。在文献[14]中，通过大量的仿真实验表明，GWO在函数优化问题时具有较快的收敛速度，但是控制参数a线性变化忽略了要解决的优化问题多样性，尤其在解决多峰值函数问题时容易陷入局部最优，很难达到全局最优。

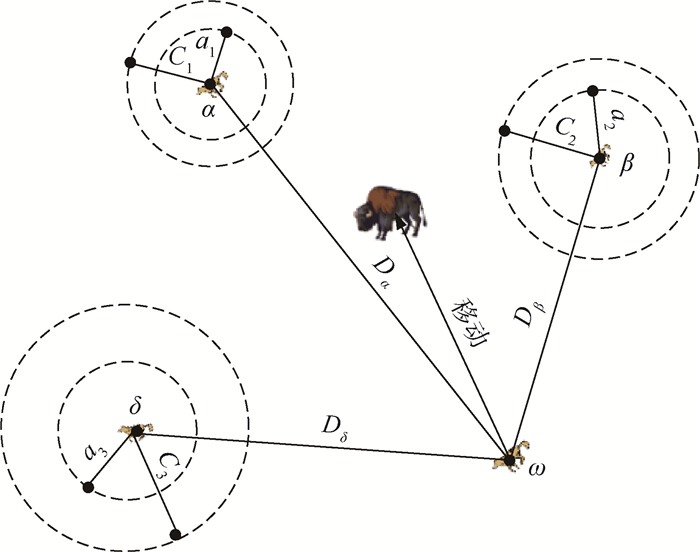图 1 GWO算法猎食过程 Fig. 1 Hunting process of GWO algorithm

图选项

针对以上缺点与不足，本文提出了自适应调整策略，通过学习种群最优位置信息去控制种群的搜索方向；另一方面，改进算法利用最优个体与当前个体之间的位置矢量差，跳出局部最优区域来保持种群多样性。对于控制参数a(包括a₁、a₂和a₃)来说，根据文献[18-20]的分析，为了确保算法在多种条件下具有好的优化结果，a采用二次曲线策略。
1) 自适应调整策略
为了进一步提高算法的收敛速度，采用自适应调整策略，将当前个体的适应度值J_i与灰狼群的平均适应度值J_avg进行比较，如果J_i优于J_avg，继续使用原策略更新灰狼位置；如果J_i次于J_avg，利用式(15)变异灰狼位置^[7]。

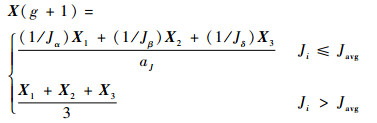(15)

式中：X(g+1)为第g代位置更新后的灰狼位置，即第g+1代灰狼位置, g为当前迭代次数；X₁、X₂和X₃分别为当前灰狼到α、β和δ灰狼的距离；a_J为1/J_α、1/J_β与1/J_δ之和，J_α、J_β和J_δ分别为α、β和δ的适应度值。
2) 跳出局部最优策略
针对原种群多样性较差，该策略对更新后的位置进行重置，通过最优个体与当前个体之间的位置矢量差随机控制当前个体不在当前局部最优解的区域内^[21]：

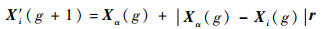(16)

式中：X′_i(g+1)和X_i(g)分别为跳出局部最优的智能个体位置；X_α(g)为当代最优解；r为[-2, -1]和[1, 2]的随机向量。
3) 控制参数非线性调整策略
对于基本的GWO算法，选择二次曲线来设计控制参数a的调整策略。利用二次曲线在区间[0, 1]上非线性递增，将GWO算法的迭代次数映射到[0, 1]上，控制参数调整策略为

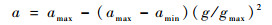(17)

式中：a_max和a_min分别为控制参数的最大值和最小值，一般分别取2和0；g_max为最大迭代次数。
2.2 SAGWO算法流程 由于GWO存在收敛速度慢，容易陷入局部最优的缺点，结合上面策略，提出了SAGWO算法。下面给出了SAGWO算法的流程：
步骤1??初始化灰狼种群，即随机产生n个智能个体的位置；初始化a、距离系数A和位置系数C^[14]；初始化X_α、X_β和X_δ的值。
步骤2??处理越界智能个体，计算每个智能体的适应度值，计算灰狼群的平均适应度值J_avg。
步骤3??更新当前迭代期间的X_α、X_β和X_δ。
步骤4??根据式(17)，计算各个优解的a、A和C。
步骤5??采用式(15)的策略更新当前智能个体的位置。
步骤6??通过式(16)，使智能个体跳出局部最优解的区域。
步骤7??输出最优解X_α和最优值J_α。
步骤8??如果达到结束条件(最大迭代次数或连续5次结果相差小于一定的精度)，则结束；否则转到步骤2。
2.3 SAGWO算法的收敛性分析 SAGWO算法也是一种随机算法，可以通过随机算法的收敛准则来判断该算法是否收敛。文献[22]给出了随机优化算法求解最小问题的收敛准则。假设对于优化问题＜S, f＞，S和f分别为解空间和优化问题目标函数。算法F_al满足条件1和条件2，则算法F_al产生的序列{x_k}_k=0^∞有：，也就是算法F_al收敛，其中，P(x_k∈R_{ε, M})是算法F_al第k次的搜索结果x_k在R_{ε, M}上的概率测度，x_k为第k次迭代的结果，条件1与条件2分别为：
条件1??若f(F_al(x, ξ))≤f(x)，且ξ∈S，则有f(F_al(x, ξ))≤f(ξ)。
条件2???B∈S，s.t.v(B)＞0，(1-u_k(B))=0。
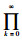
其中：x_k+1=F_al(x_k, ξ)为下一次迭代结果；S为解空间；f为优化函数；ξ为迭代过程中得到的解；v(B)为集合B的Lebesgue测度；u_k(B)为算法F_al第k次迭代解在集合B上的概率测度。
定理1??SAGWO算法收敛于全局最优。
证明??首先，SAGWO算法每次迭代都保存了灰狼群体的最优位置，保证了目标函数的适应度值的非增性，所以算法的收敛满足条件1。
其次，再需要证明SAGWO算法满足条件2，便可根据文献[23]的随机优化算法收敛定理，得到SAGWO算法收敛于全局最优。根据文献[14]的灰狼群体位置更新公式转换，可得

(18)

式中：X₁(g)为更新X(g)而产生与最优解有关的中间变量；r₁与r₂为随机变量。
由式(18)对每一代左右累乘，可得

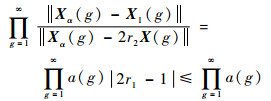(19)

对于式(19)等号后的部分，根据式(17)可知，，则有

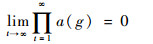(20)

根据式(19)与式(20)，可得

(21)

因此必有

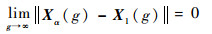(22)

同理可得，优解、次优解、X₂与X₃收敛于最优解X_α。由式(15)可知，当g→∞时，X(g+1)收敛于最优解X_α。
SAGWO算法的单个灰狼智能体搜素空间是有限的，则由n个灰狼组成的群体的状态也是有限的。当前的群体状态仅与上一时刻的群体状态有关，所以，狼群状态具有Markov性。狼群的转移状态与时间g无关，则狼群位置的状态序列是齐次的。综上述分析，狼群位置的状态序列是有限齐次Markov链。
设优化问题＜S, f＞的全局最优解为X_α，定义狼群位置的最优状态集为

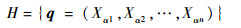(23)

对于狼群状态序列{X_α(t); g≥0}，最优状态集H是群体状态空间S上的一个闭集。由式(22)和狼群状态序列是有限齐次Markov链可知，S中不存在H之外的非闭空间，即群体状态序列必将进入最优状态集H，连续无穷次搜索不到全局最优解的可能性是0，则满足2.3节条件2，故SAGWO算法收敛于全局最优。???????????????????????????????????????????????????????????证毕
2.4 SAGWO算法的复杂度分析 根据SAGWO算法的特点与执行步骤，在这里讨论算法每一步时间复杂度。在2.2节的步骤1中，对D维空间下的n个灰狼进行初始化，需要nD次运算；在步骤2中，计算狼群的适应度值需要n次运算，一般的适应度函数的复杂度为O(D)，还要计算种群适应度值平均值，需要n次运算；在步骤3中，通过比较得到3个优解，最多需要3n-3次运算；在步骤4中，计算更新各个优解的a、A和C需要3nD；在步骤5中，计算各个狼到X_α、X_β和X_δ的距离需要3nD次运算，根据式(15)需要D+n，包括计算更新位置与比较；在步骤6中，跳出局部最优策略需要nD；在步骤7和8中，输出最优解与判断算法是否满足终止条件，其复杂度均为常数。由于算法最多执行g次，则SAGWO算法的时间复杂度为O(((3n+1)·D+n)g)≈O(3nDg)。
3 UCAVs动态任务分配方法 3.1 目标任务序列编码 在GWO算法中，每个智能个体就是一个备选解，多个智能个体通过种群搜索和其位置更新来寻优。协同攻击多目标的任务决策关键在于确定：哪架UCAV来执行哪些任务和UCAV执行任务的时序^[23]。
对于UCAV导弹与执行目标之间的关系，第1个L维向量的数值代表该UCAV用空地导弹攻击的目标的序号；第2个L维向量的数值表示UCAV执行该任务在该UCAV任务集中的次序，可以通过任务累计时间去判别任务的优先执行次序。例如，如图 2所示，第2架UCAV要执行的任务是目标1和目标5，其中导弹3执行任务目标1，导弹4执行任务目标5，而根据任务累计时间的分析，UCAV首先执行目标5，然后执行目标1。

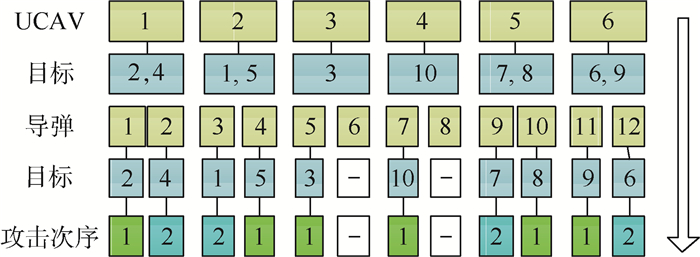图 2 目标任务序列编码 Fig. 2 Target task sequence coding

图选项

3.2 多目标动态任务分配流程 UCAV在执行任务过程中，所有的元素都可能随着时间发生变化。设定动态的任务分配的适应度函数为

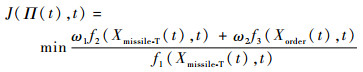(24)

其中：X_missile-T(t)为UCAV携带的导弹对任务目标的分配方案；X_order(t)为UCAV执行任务的顺序方案；t表示执行任务中的时刻。
具体基于SAGWO算法的UCAV协同攻击多目标动态任务分配流程如下：
步骤1??定义任务时间片长度t_slice。根据估算最小的任务飞行时间min(t_ij)，将其划分为n_t个时间片，因此，可以计算得到

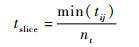(25)

步骤2??初始化UCAV与目标的信息。在分配开始之前，获取初始UCAV的位置、数量、速度以及其武器信息，探测得到目标的位置、数量和机动性。计算目标的威胁概率和UCAV对目标的毁伤概率。
步骤3??初始化参数。设置GWO的基本参数，控制参数最大值a_max和最小值a_min，GWO参数A、C，搜索方程的惯性权重ω，最大迭代次数g_max，搜索空间智能个体数为n_agent。
步骤4??随机生成一组实数然后基于编码生成初始分配方案。
步骤5??当t=0时，根据2.2节的步骤2~步骤8，计算初始最优分配方案。
步骤6??UCAV根据初始分配方案，对将要执行的任务目标进行动态追踪。
步骤7??在第一个时间片开始时，获取UCAV失效信息与目标是否发生变化。
步骤8??在时间片内，根据变化的信息，随机生成一组分配方案，重复步骤5，寻求信息变化后的最优分配方案。
步骤9??在时间片末，根据步骤8的最优方案，利用追踪法更新UCAV的位置信息，并且输出最优分配结果。
步骤10??在下一个时间片或者在t+t_slice时刻，重复步骤7~步骤9，直到t≥min(t_ij)或者开始执行航路规划层的时候，输出最终结果。
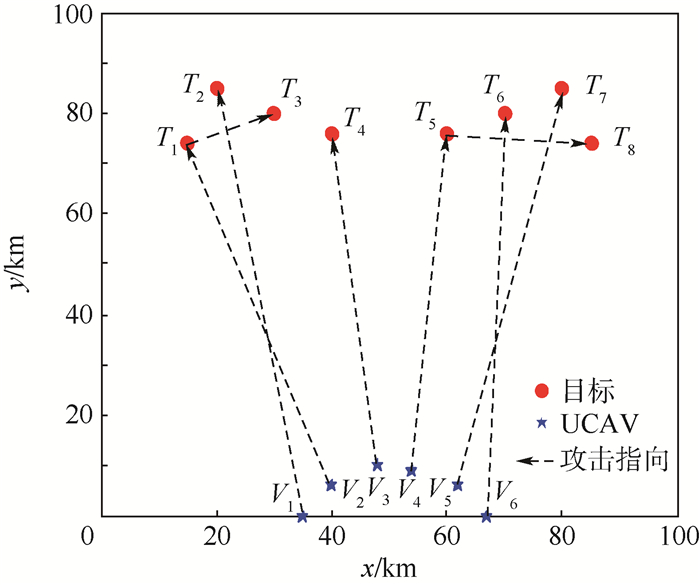
4 仿真实验及分析 4.1 任务想定 为验证算法的有效性，针对6架UCAV对8个具有威胁的敌方目标的任务分配进行仿真实验，如图 3所示，x和y分别为横向和纵向坐标。其中，UCAV编队拥有6架无人机，每架无人机携带2枚空地导弹，其攻击目标的任务是毁伤目标，相关属性见表 1和表 2；敌方由雷达(Radar)、SAM(Surface-to-Air Missile)防空导弹和AAGun(Anti-Aircraft Gun)防空炮3种类型目标组成，每个目标最多只能被我方1个UCAV攻击，其相关属性见表 3和表 4。A型空对地导弹的性能参数：有效作用距离r_W-A=10 km、最大跟踪距离R_Wmax-A=60 km；B型空对地导弹的性能参数：r_W-B=10 km、R_Wmax-B=80 km。表 2表示UCAV与机载导弹之间约束。

图 3 仿真环境初始设置 Fig. 3 Initial setting of simulation environment

图选项

表 1 UCAV编队信息设置 Table 1 Information setting of UCAV formation

UCAV	位置/ km	导弹数量×型号	软杀伤武器数量	速度/ (m·s-1)	价值量
V1	(35, 0)	2×A-AGM	2	238	0.8
V2	(40, 6)	2×B-AGM	1	238	0.9
V3	(48, 10)	2×A-AGM	2	238	0.95
V4	(54, 9)	2×B-AGM	1	238	0.95
V5	(62, 6)	2×A-AGM	2	238	0.85
V6	(67, 0)	2×B-AGM	0	238	0.8

表选项






表 2 UCAV的武器适应度 Table 2 Weapon fitness of UCAV

导弹编号	V1	V2	V3	V4	V5	V6
1	0.98	0.95	0.99	0.99	0.99	0.95
2	1	1	0.96	0.97	1	1

表选项






表 3 目标信息设置 Table 3 Information setting of targets

目标	类型	位置/km	价值量
T1	SAM	(15, 74)	0.75
T2	Radar	(20, 85)	0.7
T3	SAM	(30, 80)	0.75
T4	AAGun	(40, 76)	0.5
T5	AAGun	(60, 76)	0.5
T6	AAGun	(70, 80)	0.5
T7	SAM	(80, 85)	0.75
T8	Radar	(85, 74)	0.7

表选项






表 4 目标间依赖矩阵 Table 4 Dependence matrix of targets

目标	T1	T2	T3	T4	T5	T6	T7	T8
T1	1	0.2	0.9	0.95	0.95	0.95	0.9	0.1
T2	0.2	1	0.2	0.1	0.1	0.1	0.1	0.5
T3	0.9	0.8	1	0.95	0.95	0.95	0.9	0.8
T4	0.1	0.1	0.3	1	0.1	0.1	0.1	0.1
T5	0.1	0.1	0.3	0.1	1	0.1	0.1	0.1
T6	0.1	0.1	0.3	0.1	0.1	1	0.1	0.1
T7	0.9	0.8	0.95	0.95	0.95	0.9	1	0.8
T8	0.2	1	0.2	0.1	0.1	0.1	0.1	1

表选项






表 3表示敌方目标的编号、类型、位置信息以及价值量，由文献[7, 9]可知，雷达目标性能参数：雷达参数K_R=1.0×10¹² m⁴，最大作用距离R_max=100 km；防空导弹SAM性能参数：杀伤区近界水平距离d_sj=30 km，杀伤区远界水平距离d_sy=100 km；高炮AAGun性能参数：有效火力半径R_g=10 km，圆锥死界半径r_g=0.9 km。表 4表示目标间相互支援能力。
SAGWO算法和GWO算法种群数大小设置为30，迭代次数为100次，控制参数值的最大值a_max、最小值a_min分别取值为2和0。对于IPSO、ACA、GA、GWO算法，其算法参数设置与文献[7]相同，便于比较参考。
任务分配模型中的威胁优势权重c₁和c₂分别为0.6和0.4，总体评价指标函数中的衡量减少UCAV代价损耗和时间损耗的权重ω₁和ω₂分别为0.6和0.4。
本文采用MATLAB 2014a进行仿真，运行环境为Inter(R)Core(TM)i5-3470处理器，操作系统为Windows7。
4.2 静态任务分配仿真 为了验证SAGWO算法的求解有效性，对该实验运行30次，得到最优分配方案、算法耗时和平均最优函数值。根据优势概率模型，计算得到我方无人机编队各个UCAV对敌方目标的优势概率，如表 5所示；根据目标对UCAV的威胁模型，求出各目标对UCAV的威胁概率，如表 6所示。
表 5 UCAV对目标的优势概率 Table 5 Advantage probability of UCAV to target

UCAV	导弹编号	T1	T2	T3	T4	T5	T6	T7	T8
V1	1	0.398	0.380	0.399	0.398	0.387	0.398	0.390	0.388
	2	0.400	0.406	0.421	0.400	0.408	0.400	0.391	0.403
V2	3	0.459	0.395	0.441	0.487	0.457	0.396	0.395	0.389
	4	0.465	0.420	0.446	0.485	0.461	0.401	0.400	0.400
V3	5	0.399	0.396	0.411	0.399	0.401	0.386	0.395	0.399
	6	0.396	0.394	0.396	0.369	0.396	0.390	0.396	0.396
V4	7	0.435	0.398	0.442	0.498	0.508	0.461	0.399	0.467
	8	0.434	0.397	0.440	0.496	0.506	0.458	0.397	0.465
V5	9	0.399	0.400	0.394	0.399	0.407	0.399	0.402	0.399
	10	0.403	0.400	0.404	0.405	0.400	0.411	0.400	0.400
V6	11	0.395	0.395	0.387	0.395	0.426	0.396	0.395	0.430
	12	0.410	0.405	0.400	0.399	0.431	0.404	0.424	0.432

表选项






表 6 目标对UCAV的威胁概率 Table 6 Threat probability of target to UCAV

目标	V1	V2	V3	V4	V5	V6
T1	0.528	0.651	0.705	0.668	0.573	0.400
T2	0.124	0.159	0.175	0.160	0.126	0.079
T3	0.523	0.649	0.706	0.669	0.575	0.421
T4	0.121	0.158	0.176	0.163	0.130	0.083
T5	0.120	0.157	0.201	0.162	0.130	0.082
T6	0.122	0.157	0.217	0.154	0.130	0.101
T7	0.514	0.638	0.695	0.660	0.567	0.397
T8	0.124	0.159	0.175	0.161	0.127	0.080

表选项






仿真结果：SAGWO算法耗时为0.281 06 s，最优函数值为0.733 8，最优任务分配结果如表 7所示，具体分配如图 4所示。
表 7 UCAVs最优任务分配 Table 7 Best task allocation of UCAVs

目标	T1	T2	T3	T4	T5	T6	T7	T8
UCAV	V2	V1	V2	V3	V4	V6	V5	V4

表选项

图 4 UCAV编队攻击目标的任务分配 Fig. 4 Attack target task allocation of UCAV formation

图选项

由图 5可知，最优适应度值随着迭代次数的增加，渐趋于稳定，在第42代以后最优适应度值基本不再变化，其值为0.733 8；平均函数值也随着迭代次数增加而趋于稳定，虽然有微小波动，但是总体趋势不再变化。由图 6可知，任务分配的各个指标值在最开始有波动，但是随着迭代次数增加，各指标值区趋于稳定，编队损耗代价值随着迭代增加而减小，目标价值毁伤值相对原来变化不大，任务时间消耗值比迭代初期减少，基本符合任务分配的目标毁伤最大化、编队损耗最小化、任务时间消耗最小化的原则。综合以上分析，SAGWO算法对任务分配问题是有效的。

图 5 SAGWO算法的适应度值变化曲线 Fig. 5 Fitness variation curves of SAGWO algorithm

图选项

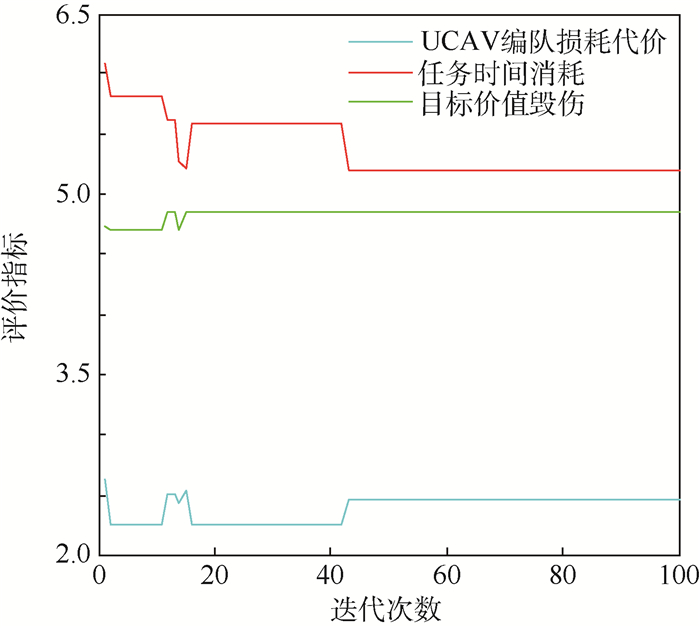图 6 SAGWO算法各评价指标曲线 Fig. 6 Evaluation index curves of SAGWO algorithm

图选项

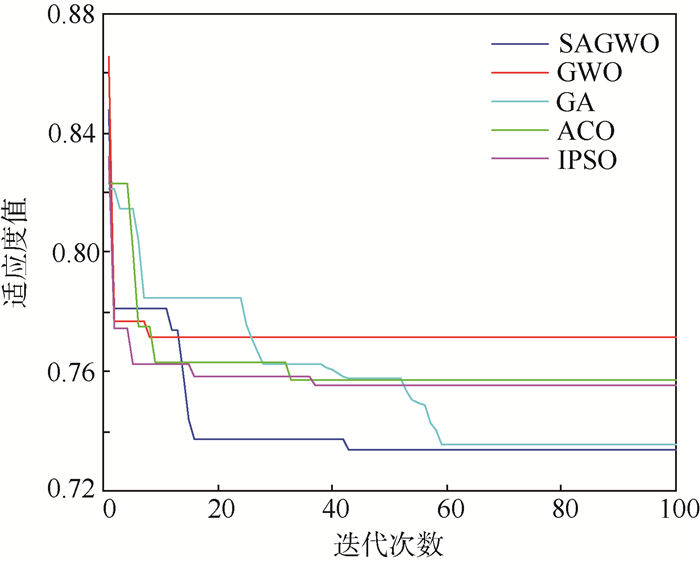
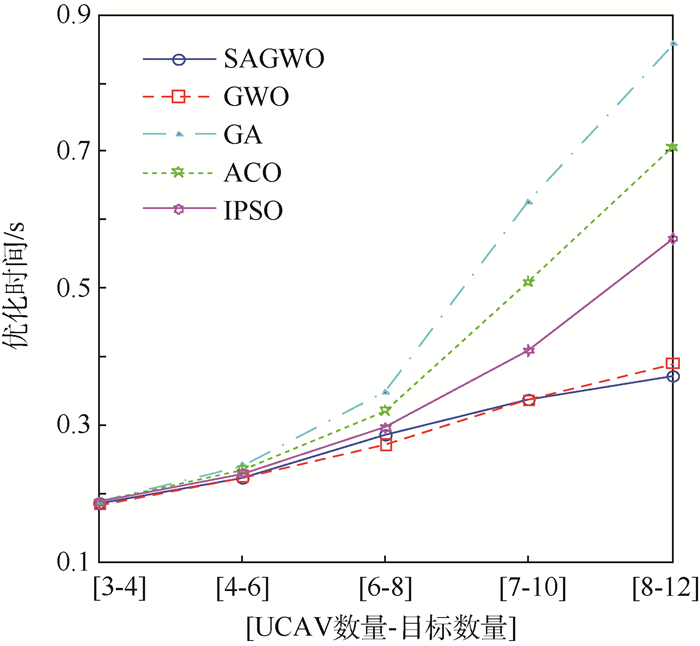
为了验证改进算法的求解质量与求解稳定性，将SAGWO算法与IPSO、ACO、GA、GWO算法相比较^[7]，并且应用于不同规模。从图 7可以分析出，在分配方案变化不大的基础上，5种算法的最优函数值随着迭代次数的增加渐渐趋于稳定，只是求解精度与求解速度不一样，GWO、ACO和IPSO算法相对于其他2种算法过早的收敛，陷入局部最优；GA算法在58代时达到最优解，但是收敛速度较慢，SAGWO算法在43代达到最优解，相较于GA算法收敛速度较快。图 8是针对不同规模的任务分配问题，采用不同算法的优化时间对比结果，从其可以看出，基于各个算法的任务分配优化时间随着任务分配规模增加而增加，其中GA、ACO、IPSO算法对问题规模增加更加敏感，优化时间增加得更快，而SAGWO算法与GWO算法的优化时间增加程度基本上一样。通过以上基于不同算法的任务分配实验，进一步验证了SAGWO算法的求解稳定性和有效性，也验证了SAGWO算法的求解精度好于其他4种算法，而且优化时间也好于GA、ACO、IPSO算法。

图 7 基于不同算法的6架UCAV编队攻击8目标适应度值变化曲线 Fig. 7 Fitness variation curves of 6-UCAV formation attacking 8 targets based on different algorithms

图选项

图 8 不同规模任务分配优化时间对比 Fig. 8 Comparison of optimization time for different scales of task allocation

图选项

4.3 动态任务分配仿真 1) 基于目标移动的动态任务分配仿真
为了验证基于目标移动的动态任务分配有效性，对6架UCAV编队攻击8目标的动态任务分配实验运行30次，得到一定时间片末的最优分配方案、算法耗时和平均最优函数值。首先通过UCAV飞行时间矩阵定义得到表 8，根据时间片定义与分析，确定最小飞行时间min(t_ij)和时间片数n_t分别为279.3和270，得到时间片长度为1 s(取整数，方便计算)，满足大于每次任务分配优化时间。其次设置机动目标参数，如表 9所示，合速度为x、y方向速度平方和的开方。在实验中，取定前240个时间片进行仿真与分析，首先对整个过程的动态任务分配进行分析，选取240个时间片其中的4个时间片与0时刻进行对比分析，然后对240个时间片的函数值曲线进行分析，最后对第240个时间片优化函数值曲线和指标值变化曲线进行分析。
表 8 UCAV飞行时间矩阵 Table 8 Fly time matrix of UCAV

UCAV	T1	T2	T3	T4	T5	T6	T7	T8
V1	322.1	362.7	336.8	320.0	336.2	366.9	404.1	375.3
V2	304.4	342.4	313.7	294.1	305.9	335.5	372.1	342.6
V3	302.5	336.4	303.7	279.3	281.8	308.3	342.6	310.6
V4	318.5	349.8	314.9	287.6	282.6	305.8	337.5	302.6
V5	347.3	375.9	338.8	308.3	294.2	312.7	340.4	301.6
V6	380.1	408.1	370.3	338.9	320.7	336.4	361.3	320.0

表选项






表 9 机动目标速度 Table 9 Speed of maneuvering targets

目标	合速度/ (m·s-1)	x方向速度/ (m·s-1)	y方向速度/ (m·s-1)
T1	25	25sin(πt/180)	25cos(πt/180)
T2	10	10sin(π/4)	-10cos(π/4)
T3	25	-25sin(πt/180)	-25cos(πt/180)
T4	7	-7	0
T5	7	7sin(π/3)	7cos(π/3)
T6	7	7	0
T7	25	-25sin(π/6)	-25cos(π/6)
T8	10	-10	0

表选项






图 9和表 10是针对基于目标移动的动态任务分配问题的任务分配图和其中5个时间片的任务分配方案。从图 9可以看出，经过240个时间片，UCAV根据自己的优势去攻击相应的目标，分配结果比较均匀。表 10中的5个时间片任务分配方案随着时间片的变化，其有一定的变动，这是因为目标位置发生变化，UCAV也发生变化，导致分配方案也发生变化。

图 9 基于目标移动的动态任务分配 Fig. 9 Dynamic task allocation based on target movement

图选项

表 10 5个时间片的任务分配方案比较 Table 10 Comparison of task allocation scheme for 5 time slices

时间/s	V1	V2	V3	V4	V5	V6
0	T1	T3, T2	T4	T5, T8	T7	T6
60	T2	T1, T3	T4	T5	T6, T7	T8
120	T3	T1, T2	T4	T5	T6, T7	T8
180	T3, T2	T1	T5	T4	T6	T8, T7
240	T3	T1, T2	T5	T4	T6	T8, T7

表选项






表 11是针对基于目标移动的动态任务分配问题选取其中5个时间片的优化时间和适应度值进行比较分析，图 10表示240个时间片的平均函数值与最优函数值随时间片变化的曲线。通过以上结果分析，随着时间变化，基于移动目标的任务分配方法是有效的，而且任务分配方案也是变化的。图 11为第240个时间片的最优适应度值、平均值以及各评价指标值随迭代次数增加的变化趋势。通过图 11的结果分析，时间片内基于SAGWO算法的任务分配是有效的，而且趋于稳定，得到最优值。
表 11 5个时间片的任务分配优化时间消耗与适应度值 Table 11 Task allocation optimization time and fitness for 5 time slices

时间/s	优化时间/s	最优适应度值	平均适应度值
0	0.286 8	0.771 5	0.868 2
60	0.269 3	0.817 6	0.971 2
120	0.263 8	0.702 6	0.907 6
180	0.263 5	0.546 4	0.732 2
240	0.262 5	0.323 5	0.498 0

表选项

图 10 240个时间片的适应度值变化曲线 Fig. 10 Fitness curve for 240 time slices

图选项

图 11 第240个时间片的优化结果 Fig. 11 Optimized results fitness in the 240th time slice

图选项

2) 基于UCAV失效的动态任务分配仿真
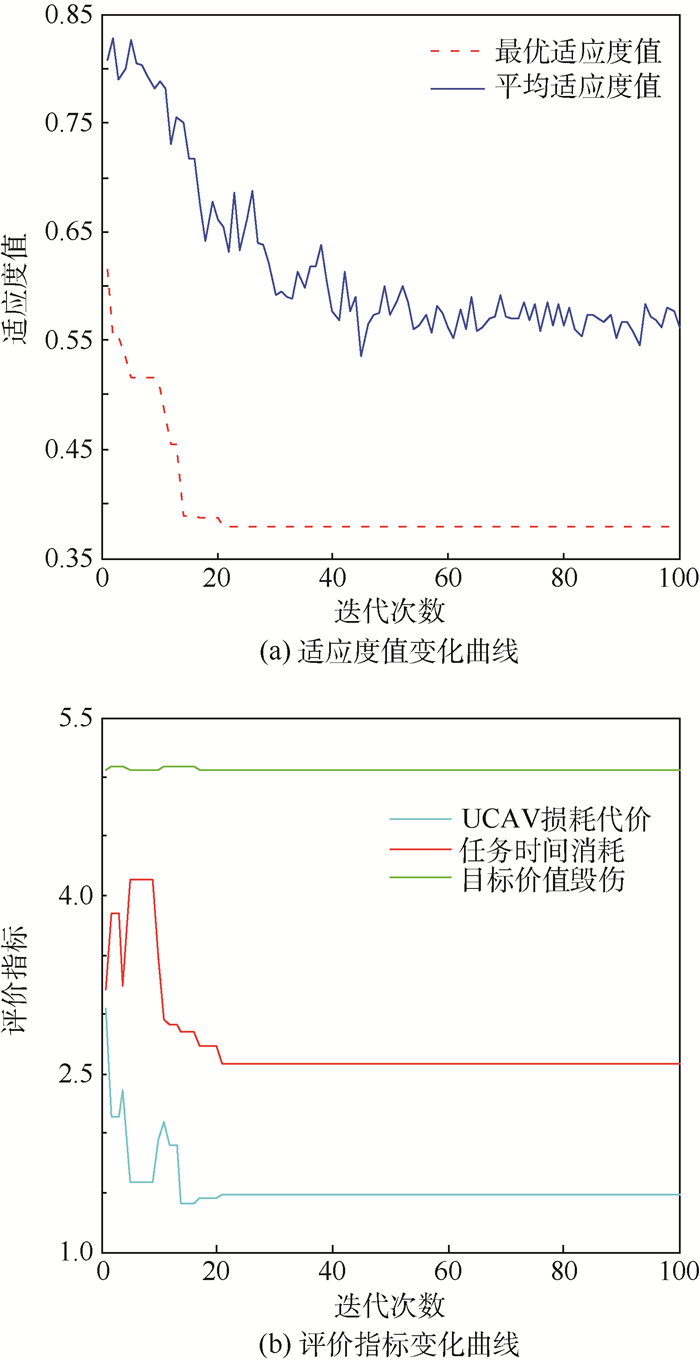
在第240个时间片，V₄被击伤，退出战场，通过仿真实验，得到表 12、表 13和图 12。表 12中“0”表示无目标可执行。从表 13的仿真结果可以知道，随着UCAV减少一架，优化时间消耗也减少。从图 12中可以看出，随着迭代次数的增加，最优函数值和平均函数值趋于稳定，任务分配的各个指标值也渐趋于稳定，而且其值走向符合编队损耗代价值最小化、任务时间消耗最小化和目标价值毁伤最小化的原则。
表 12 一架UCAV失效前后的任务分配方案比较 Table 12 Comparison of task allocation scheme before and after invalidation of an UCAV

UCAV	V1			V2			V3			V4			V5			V6
	失效前	失效后		失效前	失效后		失效前	失效后		失效前	失效后		失效前	失效后		失效前	失效后
目标	T3	T4, T3		T1, T2	T1, T2		T5	T5		T4	0		T6	T6		T8, T7	T8, T7

表选项






表 13 一架UCAV失效前后的任务分配优化结果对比 Table 13 Comparison of task allocation optimized result before and after invalidation of an UCAV

优化指标	优化时间/s			最优适应度值			平均适应度值
	失效前	失效后		失效前	失效后		失效前	失效后
数值	0.262 5	0.249 3		0.323 5	0.376 4		0.498 0	0.542 0

表选项

图 12 一架UCAV失效后一个时间片内的优化结果 Fig. 12 Optimized result in a time slice after invalidation of an UCAV

图选项

3) 基于新增2个目标的动态任务分配仿真
对新增2个目标的性能参数如表 14和表 15所示。在第240个时间片之后，发现2个新目标——T₉和T₁₀，通过仿真实验，得到图 13、表 16和表 17。从表 17可以看出，随着在240时间片之后增加2目标，最优函数值和种群平均函数值都增加，并且优化时间消耗也增加。从图 13可知，任务分配的最优函数值和平均函数值随着迭代次数的增加趋于稳定，任务分配的各个指标值随迭代次数增加而渐趋于稳定，而且其值走向符合任务分配各指标优化原则，提高打击敌方目标效费比。
表 14 新增目标的信息设置 Table 14 Information setting of increased targets

目标	类型	位置/km	价值量	速度/(m·s-1)
T9	SAM	(47, 53)	0.75	(-25, 0)
T10	SAM	(69, 68)	0.75	(25, 0)

表选项






表 15 新增目标依赖矩阵 Table 15 Dependence matrix of increased targets

目标	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10
T9	0.5	0.2	0.6	0.3	0.1	0.1	0.6	0.1	1	0.9
T10	0.4	0.1	0.55	0.2	0.3	0.2	0.7	0.1	0.9	1

表选项

图 13 增加目标后一个时间片内的优化结果 Fig. 13 Optimized result in a time slice after increased targets

图选项

表 16 增加目标前后的任务分配方案比较 Table 16 Comparison of task allocation scheme before and after increased targets

UCAV	V1			V2			V3			V4			V5			V6
	增加目标前	增加目标后		增加目标前	增加目标后		增加目标前	增加目标后		增加目标前	增加目标后		增加目标前	增加目标后		增加目标前	增加目标后
目标	T3	T3		T1, T2	T1, T2		T5	T9，T4		T4	T10，T5		T6	T6		T8, T7	T8, T7

表选项






表 17 增加目标前后的任务分配优化结果对比 Table 17 Comparison of task allocation optimized result before and after increased targets

优化指标	优化时间/s			最优适应度值			平均适应度值
	增加目标前	增加目标后		增加目标前	增加目标后		增加目标前	增加目标后
数值	0.262 5	0.287 1		0.323 5	0.441 6		0.498 0	0.883 0

表选项






5 结论 1) 针对UCAVs协同对地打击多目标任务分配问题的实时性、高效性以及复杂性，对UCAV编队信息以及对任务目标信息进行分析，设计了基于时间片的多约束动态任务分配模型。
2) 传统算法对动态任务分配问题求解速度慢、求解精度不高的缺点，提出了一种基于SAGWO算法的动态任务分配方法，同时证明了改进算法全局收敛，并分析了时间复杂度。
3) 本文对所设计的基于SAGWO的任务分配从静态与动态2种情况进行仿真验证。仿真结果表明，SAGWO算法可快速精确地求解出动态任务分配，且分配结果符合作战要求。由于篇幅有限，对于UCAVs武器分配尚且研究有限，需要进一步深入研究。

参考文献

[1]	龙涛, 朱华勇, 沈林成. 多UCAV协同中基于协商的分布式任务分配研究[J].宇航学报, 2006, 27(3): 457–462. LONG T, ZHU H Y, SHEN L C. Negotiation-based distributed task allocation for cooperative multiple unmanned combat aerial vehicles[J].Journal of Astronautics, 2006, 27(3): 457–462.DOI:10.3321/j.issn:1000-1328.2006.03.026(in Chinese)
[2]	杨啸天, 刘小军, 冯金富, 等. 不确定环境下空地多目标攻击优先权决策[J].南京理工大学学报, 2012, 36(4): 567–571. YANG X T, LIU X J, FENG J F, et al. Priority decision of air to surface multi-target attack under uncertainty[J].Journal of Nanjing University of Science and Technology, 2012, 36(4): 567–571.DOI:10.3969/j.issn.1005-9830.2012.04.003(in Chinese)
[3]	王永泉, 罗建军. 基于多群体改进萤火虫算法的UCAV协同多目标分配[J].西北工业大学学报, 2014, 32(3): 451–455. WANG Y Q, LUO J J. Target assignment in cooperative attacking of UCAVs based on multi-intelligence improved glowworm swarm optimization algorithm[J].Journal of Northwestern Polytechnical University, 2014, 32(3): 451–455.DOI:10.3969/j.issn.1000-2758.2014.03.023(in Chinese)
[4]	颜骥, 李相民, 刘波. 基于离散粒子群-郭涛算法分配多无人机协同任务[J].国防科技大学学报, 2015, 37(4): 165–171. YAN J, LI X M, LIU B. Cooperative task allocation of multi-UAVs with mixed DPSO-GT algorithm[J].Journal of National University of Defense Technology, 2015, 37(4): 165–171.(in Chinese)
[5]	RABBATH C A, GOGNON E, LAUZON M. On the cooperative control of multiple unmanned aerial vehicles[J].IEEE Canadian Review, 2004(46): 15–19.
[6]	AMATO P, FARINA M. An alift-inspired evoluntionary algorithm for dynamic multiobjective optimization problems[J].Soft Computing:Methodologies and Applications, 2005, 32: 113–125.
[7]	魏政磊, 赵辉, 韩邦杰, 等. 基于自适应GWO的多UCAV协同攻击目标决策[J].计算机工程与应用, 2016, 52(18): 257–261. WEI Z L, ZHAO H, HAN B J, et al. Research on cooperative attack decision of unmanned combat aerial vehicles using self-adaptive grey wolf optimization[J].Computer Engineering and Application, 2016, 52(18): 257–261.DOI:10.3778/j.issn.1002-8331.1601-0316(in Chinese)
[8]	罗德林, 段海滨, 吴顺祥, 等. 基于启发式蚁群算法的协同多目标攻击空战决策研究[J].航空学报, 2006, 27(6): 1166–1170. LUO D L, DUAN H B, WU S X, et al. Research on air combat decision-making for cooperative multiple target attack using heuristic ant colony algorithm[J].Acta Aeronautica et Astronautica Sinica, 2006, 27(6): 1166–1170.DOI:10.3321/j.issn:1000-6893.2006.06.034(in Chinese)
[9]	郑昌文, 严平, 丁明跃. 飞行器航迹规划研究现状与趋势[J].宇航学报, 2007, 28(6): 1441–1446. ZHENG C W, YAN P, DING M Y. Research status and trend of route planning for flying vehicles[J].Journal of Astronautics, 2007, 28(6): 1441–1446.DOI:10.3321/j.issn:1000-1328.2007.06.001(in Chinese)
[10]	王宝龙, 黄考利, 马立元, 等. 基于依赖矩阵的测试性分析[J].计算机测量与控制, 2011, 19(6): 1260–1265. WANG B L, HUANG K L, MA L Y, et al. Dependency matrix based testability analysis[J].Computer Measurement & Control, 2011, 19(6): 1260–1265.(in Chinese)
[11]	王庆江, 彭军, 曾儒伟, 等. 无人机对地多目标攻击决策研究[J].电光与控制, 2014, 21(11): 57–61. WANG Q J, PENG J, ZENG R W, et al. Decision-making of UAVs for air-to-ground multi-target attacking[J].Electronics Optics & Control, 2014, 21(11): 57–61.DOI:10.3969/j.issn.1671-637X.2014.11.011(in Chinese)
[12]	潘峰, 陈杰, 任智平, 等. 基于计算智能方法的无人机任务指派约束优化模型研究[J].兵工学报, 2009, 30(12): 1706–1713. PAN F, CHEN J, REN Z P, et al. Research on vehicle assignment model for constraints handing based on computational intelligence algorithms[J].Acta Armamentarii, 2009, 30(12): 1706–1713.DOI:10.3321/j.issn:1000-1093.2009.12.026(in Chinese)
[13]	CHANDLER P R, PACHTER M, SWAROOP D, et al. Complexity in UAV cooperative control[C]//The Proceedings of American Control Conference. Piscataway, NJ: IEEE Press, 2012: 1831-1836.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1023833
[14]	SEYEDALI M, SEYED M M, ANDREW L. Grey wolf optimizer[J].Advances in Engineering Software, 2014, 69: 46–61.DOI:10.1016/j.advengsoft.2013.12.007
[15]	SEYEDALI M, SHAHRZAD S, SEYED M M, et al. Multi-objective grey wolf optimizer:A novel algorithm for multi-criterion optimization[J].Expert Systems With Application, 2016, 47: 106–119.DOI:10.1016/j.eswa.2015.10.039
[16]	ZHU A J, XU C P. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J].Journal of Systems Engineering and Electronics, 2015, 26(2): 317–328.DOI:10.1109/JSEE.2015.00037
[17]	龙文, 赵东泉, 徐松金. 求解约束优化问题的改进灰狼优化算法[J].计算机应用, 2015, 35(9): 2590–2595. LONG W, ZHAO D Q, XU S J. Improved grey wolf optimization algorithm for constrained optimization problem[J].Journal of Computer Application, 2015, 35(9): 2590–2595.DOI:10.3969/j.issn.1001-3695.2015.09.007(in Chinese)
[18]	魏政磊, 赵辉, 李牧东, 等. 控制参数值非线性调整策略的灰狼优化算法[J].空军工程大学学报(自然科学版), 2016, 17(3): 104–110. WEI Z L, ZHAO H, LI M D, et al. A grey wolf optimization algorithm based on nonlinear adjustment strategy of control parameter[J].Journal of Air Force Engineering University(Natural Science Edition), 2016, 17(3): 104–110.(in Chinese)
[19]	周敏, 李太勇. 粒子群优化算法中的惯性权重值非线性调整[J].计算机工程, 2011, 37(5): 68–72. ZHOU M, LI T Y. Nonlinear adjustment strategy of inertia weight in particle swarm optimization algorithm[J].Computer Engineering, 2011, 37(5): 68–72.DOI:10.3969/j.issn.1000-3428.2011.05.023(in Chinese)
[20]	CHATTERJEE A, SIARRY P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J].Computers & Operations Research, 2006, 33(3): 859–871.
[21]	李牧东, 赵辉, 翁兴伟. 具有广泛学习策略的回溯搜索优化算法[J].系统工程与电子技术, 2015, 37(4): 958–963. LI M D, ZHAO H, WENG X W. Backtracking search optimization algorithm with comprehensive learning strategy[J].Systems Engineering and Electronics, 2015, 37(4): 958–963.(in Chinese)
[22]	SOLIS F, WETS R. Minimization by random search techniques[J].Mathematics of Operations Research, 1981, 6(1): 19–30.DOI:10.1287/moor.6.1.19
[23]	TAL S, STEVEN J R, ANDREW G S, et al. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms[J].Computers & Operations Research, 2006, 33(11): 3252–3269.