由于材料及加工、装配的限制,转子中存在各种连接结构,如止口、端齿等。转子弯曲变形会造成连接结构连接界面间产生应力分布急剧变化或相对位移,导致转子弯曲刚度降低,这是造成转子振动过大的隐患[2]。因此,对于高转速的准刚性转子系统,必须考虑弯曲变形时连接界面对振动特性的影响。
早期转子动力学分析中通常忽略连接结构的动力学效果[3-4],但带连接界面的非连续转子系统的振动特性具有一些不同的特点,近年来国内外****在连接结构对转子系统振动特性的影响方面已开展了大量的研究工作。目前,转子动力学分析中考虑连接结构刚度特性的方法主要包括等效弹簧法[5-9]、虚拟材料法[10-12]和修正刚度矩阵法[13-14]等。等效弹簧法是采用弹簧元件等效表征界面刚度特性。Hartwigsen[5]和Song[6]等通过瞬态激励试验得到螺栓连接梁响应,从中识别界面力学参数,并与整体构件的矩阵进行组集构成系统的动力学方程;Link等[7]为考虑界面的非线性特性,引入非线性弹簧,非线性弹簧刚度由基础激励试验获得,采用类似方法植入系统的动力学方程中;Luan等[8]采用双线性弹簧描述连接界面轴向拉压刚度特性,分析了拉压刚度不对称对结构轴向响应的影响;Gao等[9]将界面等效为铰链和角向弹簧的组合,建立了应变能与角向弹簧刚度之间的关系。虚拟材料法借助薄层单元在有限元模型中模化连接特性。Iranzad和Ahmadian[10]基于弹塑性薄层单元有效模拟了螺栓连接界面由完全接触到产生微滑移以及宏滑移的变化过程;姚星宇等[11-12]基于分布式薄层单元法研究了结构参数与载荷对连接刚度的影响。修正刚度矩阵法将界面作为一个特殊截面,通过修正连接界面处的抗弯刚度考虑界面对结构刚度的影响。Caddemi等[13]采用奇异点描述连接结构弯曲刚度的阶跃特征;卢明剑等[14]基于Riccati传递矩阵,引入接触修正系数、预紧修正系数和拉杆修正系数,对拉杆转子接触轴段的刚度矩阵进行修正,研究了非连续拉杆组合转子的动力学特征。
根据上述已有研究可知,目前研究中多借助轴向拉压刚度及角向刚度描述连接界面刚度特性,而界面作为一个特殊截面,对其等效抗弯刚度与载荷环境及转子力学特性间的交互影响缺乏研究。本文基于连接界面的力学特性,建立了连接界面刚度损失模型,分析了刚度损失产生机理。针对非连续转子系统动力学设计,提出了基于应变能分布优化的刚度损失抑制方法,为高转速准刚性转子系统的动力学优化设计提供参考。
1 带连接界面的转子结构力学特征 1.1 转子结构非连续性 图 1为先进涡轴发动机结构。燃气发生器转子采用1-0-1支承方案,转子长径比约为13,整体弯曲刚性较弱,导致转子工作转速靠近弯曲临界,在工作过程中会产生弯曲变形。由于结构功能和质量的限制,转子结构由不同材料通过连接结构形成组合体,转子结构特征参数(几何尺寸、材料性质)在连接界面处产生突变,进而造成力学特征参数(刚度、阻尼)及其分布产生阶跃,具有非连续特征。
 |
| 图 1 先进涡轴发动机 Fig. 1 Advanced turboshaft engine |
| 图选项 |
1.2 连接界面刚度特性 航空发动机转子中的连接结构(如止口、螺栓等),均为多个构件在预紧力F作用下通过连接界面连接形成的非连续结构,在工作过程中需承受弯曲载荷。如图 2所示,以带有连接界面的非连续鼓筒结构为例,研究弯曲变形下连接界面的刚度特性。
 |
| 图 2 带连接界面的非连续结构 Fig. 2 Discontinuous structure with joint interfaces |
| 图选项 |
上述问题为空间轴对称问题,可采用位移函数法进行求解。基于弯曲载荷M作用下,端面切应力沿鼓筒厚度方向按抛物线形式分布,提出如下位移假设:
 | (1) |
式中:u(x, z)和w(x, z)分别为对应x、z坐标下的轴向位移和径向位移;α、β为与鼓筒结构参数有关的函数;A为鼓筒的横截面积;B为与鼓筒结构参数有关的常数;E为材料弹性模量。
进一步根据几何关系得到
 | (2) |
式中:γyz为连接界面处切应变;εx为连接界面处正应变。故连接界面处应力分布为
 | (3) |
式中:τyz为连接界面处切应力;σx为连接界面处正应力;G为材料剪切模量。
由式(3)可知,在弯曲载荷作用下,弯曲拉应力大于预紧压应力的区域上,界面间将失去力的相互作用,因此连接界面上的应力分布与外载荷密切相关且呈现非连续特征。连接界面刚度特性不仅与结构特征参数有关,同时也受到配合参数和载荷参数的影响。
2 转子连接结构刚度损失模型 由于连接界面只能承受压力而不能承受拉力,在外载荷作用下其力学特征表现为:界面有效接触面积不连续,界面应力分布非线性,界面间转角不连续,使得连接界面处产生抗弯刚度损失。通过建立考虑这三方面的力学模型,采用刚度综合修正系数η定量描述刚度损失,综合修正系数由3个修正系数相乘得到
 | (4) |
2.1 界面接触面积修正系数 以2个具有不同刚度特性的弹性构件间存在连接界面为例,通过施加预紧力F确定构件间的相对位置,并使连接界面间产生接触作用,如图 3所示。预紧力作用下,若有效接触面积mn小于界面总面积,会导致界面等效抗弯刚度减小,产生刚度损失。
 |
| 图 3 连接界面有效接触面积示意图 Fig. 3 Schematic of effective contact area of joint interface |
| 图选项 |
可根据连接界面有效接触面积的抗弯刚度对界面刚度进行修正。界面抗弯刚度可通过EI的乘积来表示(I为惯性矩)。定义界面接触面积修正系数η1为有效接触面积的抗弯刚度EI′与界面总面积的抗弯刚度EI之比,即
 | (5) |
2.2 界面应力修正系数 由于连接界面仅传递压力,界面压应力的大小反映了连接界面提供约束的能力,进而反映了连接界面的刚度特性。
对于连接界面,由于应力与外载荷和界面接触状态等多种因素间存在交互的力学关系,弯曲载荷作用下连续界面上的应力多呈非线性分布,如图 4(a)所示。假设初始状态下轴向预紧力F在有效接触面积Ω上产生均匀的正应力,且弯矩作用下连接界面有效接触面积保持不变。
 |
| 图 4 连接界面应力等效模型 Fig. 4 Stress equivalent model of joint interface |
| 图选项 |
假设在弯曲载荷作用下界面正应力与到中性轴的距离y呈二次曲线关系,即
 | (6) |
根据连接界面弯矩平衡方程:
 | (7) |
式中:ds为连接界面上的面积微元。
求得系数a:
 | (8) |
式中:f(m, n)为通过有效接触面积几何参数表示的函数。
为定量描述弯曲载荷作用下连接界面的抗弯刚度,可将连接界面非线性应力分布按照应变能相等的原则等效为线性应力分布,如图 4(b)所示。
用正应力表示的连接界面总应变能为
 | (9) |
式中:vε为每个面积微元上的应变能。
假设等效的线性分布σx′的表达式为
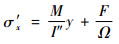 | (10) |
根据应变能相等的等效原则:
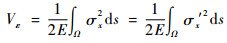 | (11) |
可求得连接界面在弯曲载荷作用下的等效惯性矩I″。定义在弯曲载荷作用下等效抗弯刚度EI″与在初始状态下连接界面的抗弯刚度EI′之比为界面应力修正系数,表达式为
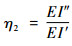 | (12) |
由上述分析可知,连接界面在弯曲载荷作用下应力呈非线性分布,界面的等效抗弯刚度降低,是产生刚度损失的原因之一。
2.3 界面弯曲变形修正系数 在弯曲载荷作用下,连接界面上应力呈非线性分布,当界面只产生弹性形变时,由胡克定律可知,界面上的应变也呈非线性分布,即非连续结构在弯曲变形时连接界面变为曲面,如图 5(a)所示。
 |
| 图 5 非连续结构转角不连续示意图 Fig. 5 Schematic of discontinuous rotation of discontinuous structure |
| 图选项 |
根据界面应力修正系数,将连接界面的应力分布等效为线性分布,即将弯曲变形后变为曲面的连接界面等效为平面,如图 5(b)所示。当连接界面间部分区域在弯曲载荷作用下发生分离时,等效后连接界面间将会产生相对转角θ。
非连续结构在受弯曲载荷时连接界面部分区域分离导致的界面间产生相对转角是造成非连续结构弯曲刚度损失的原因之一。在工程实际中,可通过有效接触面积(黏滞区域和滑移区域面积总和)对界面间相对转角进行定量分析,即定义界面弯曲变形修正系数为在弯曲载荷作用下界面有效接触面积与无弯曲载荷作用下界面有效接触面积之比。界面弯曲变形修正系数反映了连接界面间相对转角对非连续结构弯曲角变形的影响。
综上,连接界面在弯曲载荷作用下,有效接触面积及受力状态产生变化,约束失效,造成连接结构弯曲刚度损失,可通过有效接触面积、应力分布和界面弯曲变形这3方面的力学特征参数对其进行定量描述。
3 止口连接转子系统振动特性 对于高转速准刚性转子系统,若连接结构在工作循环中存在较大的弯曲变形,则应考虑连接结构刚度损失对转子系统振动特性的影响。应变能的大小可准确定量地反映结构的弯曲变形程度,因此可通过优化应变能分布,降低连接结构处的应变能,抑制连接结构处刚度损失及其对转子系统振动特性的影响。
图 6为三级轴流压气机试验器转子结构。转子采用大跨度支承,并带有多个止口连接结构,转子最大工作转速为40 000 r/min。在ANSYS中,采用实体单元SOLID185模拟转子结构,弹簧单元COMBIN14模拟前后支点,假定各连接界面为刚性连接,建立转子整体模型,共计206 437个单元。在不考虑转子结构非连续性所产生的弯曲刚度损失时,其弯曲临界转速为55 020 r/min,共振安全裕度约为37%。
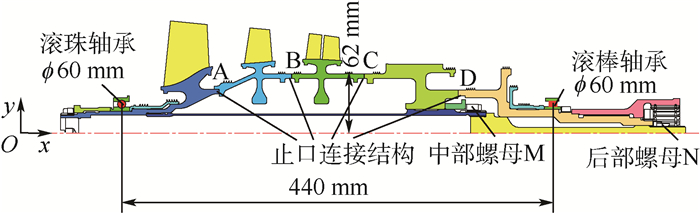 |
| 图 6 三级轴流压气机试验器转子结构 Fig. 6 Rotor structure of three-stage axial compressor tester |
| 图选项 |
由图 7中转子弯曲振型及应变能分布可知,转子弯曲变形下,止口连接结构附近应变能较大,刚度损失的影响不可忽视。
 |
| 图 7 弯曲振型及其应变能分布 Fig. 7 Bending mode of vibration and its strain energy distribution |
| 图选项 |
弯曲振型下各连接结构应变能占比如表 1所示。各连接结构处均具有一定的弯曲变形,其中转接盘与后轴颈间止口D应变能占比最高,弯曲变形程度较大,该止口处的刚度损失最为显著。
表 1 弯曲振型下连接结构应变能占比 Table 1 Ratio of strain energy of joint structure under bending mode of vibration
| % | ||||
| 连接结构 | 止口A | 止口B | 止口C | 止口D |
| 应变能占比 | 0.7 | 1.1 | 1.8 | 2.9 |
表选项
进一步建立带连接界面的转子模型,分析弯曲载荷对界面刚度特性的影响。中心拉杆的轴向变形对转子产生预紧作用,因预紧力的大小与转子载荷环境有关,本文采用设置接触面初始偏移位移的方式施加预紧力。经计算,图 6中部螺母M处接触面初始偏移量为1.5 mm时,预紧力近似为120 000 N;在压气机转子压紧的基础上,后部螺母N处接触面初始偏移量为1.2 mm时,预紧力近似为80 000 N。仿真得到装配状态下止口D连接界面接触状态如图 8(a)所示,采用上述刚度损失计算方法,得到界面接触面积修正系数(见表 2);对转子施加最大工作转速,并将转子质心所在截面的y方向位移进行耦合,并施加1 000 N的y方向载荷,作为模拟高负荷转子弯曲变形状态的等效横向载荷。连接界面接触应力和接触状态如图 8(b)、(c)所示,界面应力修正系数和弯曲变形修正系数如表 3和表 4所示。
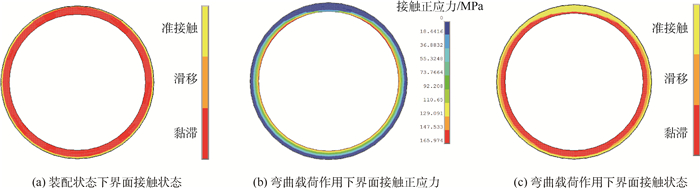 |
| 图 8 连接界面接触状态及接触正应力 Fig. 8 Joint interface contact state and contact normal stress |
| 图选项 |
表 2 界面接触面积修正系数 Table 2 Interfacial contact area correction coefficient
| 界面总面积的抗弯刚度EI/(Pa·mm4) | 有效接触面积抗弯刚度EI′/(Pa·mm4) | 界面接触面积修正系数η1 |
| 1.5×104 | 0.82×104 | 0.55 |
表选项
表 3 界面应力修正系数 Table 3 Interfacial stress correction coefficient
| 等效线性应力分布 | 等效抗弯刚度EI″/(Pa·mm4) | 界面应力修正系数η2 |
| σx′=1.19×104y+5.16 | 0.72×104 | 0.88 |
表选项
表 4 界面弯曲变形修正系数 Table 4 Interfacial bending deformation correction coefficient
| 受力状态 | 有效接触面积/mm2 | 界面弯曲变形修正系数η3 |
| 装配状态 | 1 170.7 | |
| 弯曲变形 | 956.2 | 0.82 |
表选项
根据式(4)可求得界面刚度综合修正系数为0.40。结果表明:在弯曲变形下,连接结构处刚度显著降低。根据应变能占比对转子不同位置连接结构刚度综合修正系数进行估算,结果如表 5所示。
表 5 各连接结构刚度综合修正系数 Table 5 Comprehensive correction coefficient of stiffness for different joint structures
| 连接结构 | 止口A | 止口B | 止口C | 止口D |
| 刚度综合修正系数 | 0.86 | 0.77 | 0.63 | 0.40 |
表选项
结构弯曲刚度由其各截面抗弯刚度EI所决定,为了便于将连接结构的弯曲刚度损失组集到转子系统的动力学模型中,本文采用修正弹性模量的方法,即不改变结构几何特征(I不变),同时连接界面处设为固接,与转子整体模型共同进行网格划分,并根据刚度综合修正系数降低连接结构局部材料弹性模量E。该方法可较好地模化连接结构刚度损失的局部特征。
选择修正区域的方法为:在弯曲载荷作用下,采用刚度修正模型计算得到的结构变形特征与采用接触模型的计算结果基本一致,具有相似变形弹性线,即可认为修正区域选择合理。若出现变形特征不一致情况,则应适当增大或减小修正区域,直至修正前后变形特性相近,如图 9所示。
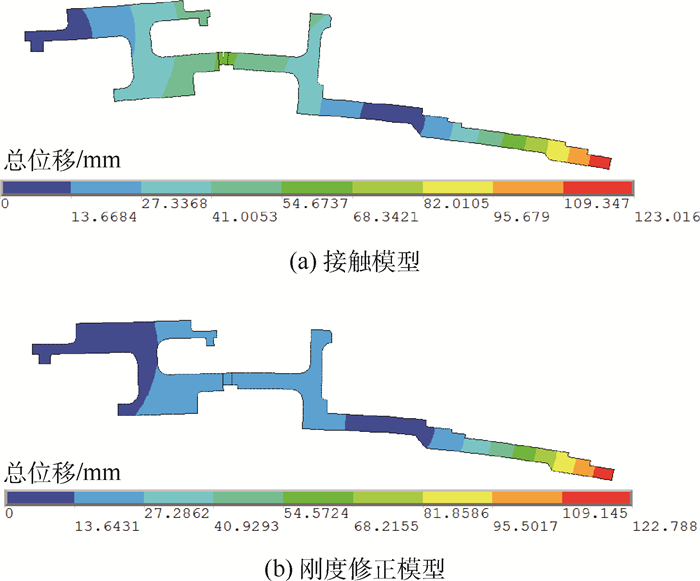 |
| 图 9 接触模型与刚度修正模型变形总位移云图 Fig. 9 Contour of total displacement deformation of contact model and stiffness correction model |
| 图选项 |
表 6给出了连接结构刚度损失对转子系统振动特性影响的计算结果。结果表明,连接结构刚度损失对平动和俯仰临界转速影响较小,对弯曲临界转速影响较大。考虑连接结构刚度损失后,转子弯曲临界转速下降约22%,共振安全裕度降低至7%。
表 6 刚度损失对转子系统临界转速的影响 Table 6 Effect of stiffness loss on critical speed of rotor system
| 振型 | 临界转速/(r·min-1) | 考虑刚度损失后临界转速下降比例/% | |
| 不考虑刚度损失 | 考虑刚度损失 | ||
| 平动 | 8 640 | 8 460 | 2 |
| 俯仰 | 16 140 | 15 720 | 3 |
| 弯曲 | 55 020 | 42 915 | 22 |
表选项
为抑制连接结构刚度损失及其对转子弯曲振型临界转速的影响,应降低弯曲振型下连接结构处应变能。根据转子系统振动特性与支承刚度的相关性[15-16],可调整支承刚度以优化应变能分布及弯曲临界转速。图 10给出了前支点支承刚度的变化对连接结构应变能的影响。由于前支点远离转子弯曲振型的节点,连接结构应变能对该支承刚度的变化较为敏感。
 |
| 图 10 弯曲振型下连接结构应变能随前支点支承刚度的变化 Fig. 10 Variation of strain energy of joint structure with support stiffness of front bearing under bending mode of vibration |
| 图选项 |
由图 10可知,将前支点支承刚度由1×107 N/m(设计值)调整为3×107 N/m后,连接结构处的应变能总和降低20%。对于工程中常用的鼠笼式弹性支承,通过增加筋条数目或增大筋条厚度可使支承刚度提高。将前支点刚度调整为3×107 N/m,按相同方法得到优化后连接结构刚度损失对转子系统振动特性的影响,如表 7所示。
表 7 优化后刚度损失对转子系统临界转速的影响 Table 7 Effect of stiffness loss on critical speed of rotor system after optimization
| 振型 | 临界转速/(r·min-1) | 考虑刚度损失后临界转速下降比例/% | |
| 不考虑刚度损失 | 考虑刚度损失 | ||
| 平动 | 9 745 | 9 581 | 2 |
| 俯仰 | 18 086 | 17 728 | 2 |
| 弯曲 | 62 564 | 54 436 | 13 |
表选项
结果表明,通过将转子连接结构应变能占比降低20%,降低了刚度损失对转子系统弯曲临界转速的影响,共振安全裕度提高至36%。为保证具有多个连接界面的高转速准刚性转子振动特性较优,通过调整支承刚度对转子弯曲振型下应变能分布进行优化设计,降低连接结构处应变能,可有效抑制弯曲变形下连接结构处的刚度损失,降低转子弯曲临界转速对刚度损失的敏感度,保证转子系统振动特性的稳健性。
4 结论 通过理论与仿真分析,本文得到主要结论如下:
1) 对于高转速准刚性转子系统,由于转子结构弯曲刚度较低,在工作中容易产生弯曲变形,在弯曲变形下,转子连接结构处会产生弯曲刚度损失,进而对转子系统振动特性产生影响。
2) 分析了连接结构刚度损失的产生机理。转子产生弯曲变形时,连接界面间由于有效接触面积和受力状态的变化,会产生约束失效,造成连接结构刚度损失。可通过连接界面的有效接触面积、应力分布和界面弯曲变形这3方面的力学特征参数对其进行定量描述。
3) 为带连接界面的高转速转子系统振动特性优化设计提供了参考。连接结构刚度损失会导致转子弯曲临界转速大幅降低。为有效抑制连接结构处刚度损失,可通过调整支承刚度,对转子应变能分布进行优化设计,降低连接结构处应变能,使转子弯曲临界转速对刚度损失不敏感,保证转子系统振动特性的稳健性。
后续将开展高速转子连接结构刚度损失对转子振动特性影响的试验研究。
参考文献
| [1] | 李松柏. 小型挠性转子(准刚性转子)动平衡的工艺分析[J]. 南方航空科技, 1994(1): 22-25. LI S B. Process study of dynamic balance of small flexible rotor(quasi-rigid rotor)[J]. Southern Aeronautics Technology, 1994(1): 22-25. (in Chinese) |
| [2] | IBRAHIM R A, PETTIT C L. Uncertainties and dynamic problems of bolted joints and other fasteners[J]. Journal of Sound and Vibration, 2005, 279(3): 857-936. |
| [3] | 陈萌, 马艳红, 刘书国, 等. 航空发动机整机有限元模型转子动力学分析[J]. 北京航空航天大学学报, 2007, 33(9): 1013-1016. CHEN M, MA Y H, LIU S G, et al. Rotordynamic analysis of whole aero-engine models based on finite element method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(9): 1013-1016. DOI:10.3969/j.issn.1001-5965.2007.09.003 (in Chinese) |
| [4] | 谢强.转子活塞发动机动力学特性研究与分析[D].长沙: 国防科学技术大学, 2013: 36-38. XIE Q.The dynamic characteristics research and analysis of the rotor engine[D].Changsha: National University of Defense Technology, 2013: 36-38(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1015958790.htm |
| [5] | HARTWIGSEN C J, SONG Y, MCFARLAND D M, et al. Experimental study of non-linear effects in a typical shear lap joint configuration[J]. Journal of Sound and Vibration, 2004, 277(1-2): 327-351. DOI:10.1016/j.jsv.2003.09.018 |
| [6] | SONG Y, HARTWIGSEN C J, MCFARLAND D M, et al. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements[J]. Journal of Sound and Vibration, 2004, 273(1-2): 249-276. DOI:10.1016/S0022-460X(03)00499-1 |
| [7] | LINK M, BOESWALD M, LABORDE S, et al.An approach to non-linear experimental modal analysis[C]//Proceedings of the IMAC-XXVⅡ, 2011: 119-128. |
| [8] | LUAN Y, GUAN Z Q, CHENG G D, et al. A simplified nonlinear dynamic model for the analysis of pipe structures with bolted flange joints[J]. Journal of Sound and Vibration, 2013, 331(2): 325-344. |
| [9] | GAO J, YUAN Q, LI P, et al. Effects of bending moments and pretightening forces on the flexural stiffness of contact interfaces in rod-fastened rotors[J]. Proceedings of the ASME Turbo Expo, 2012, 134(10): 1492-1494. |
| [10] | IRANZAD M, AHMADIAN H. Identification of nonlinear bolted lap joint models[J]. Computers & Structures, 2012, 96-97(4): 1-8. |
| [11] | 姚星宇, 王建军, 翟学. 航空发动机螺栓连接薄层单元建模方法[J]. 北京航空航天大学学报, 2015, 41(12): 2269-2279. YAO X Y, WANG J J, ZHAI X. Modeling method of bolted joints of aero engine based on thin-layer element[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2269-2279. (in Chinese) |
| [12] | 姚星宇, 王建军. 航空发动机螺栓连接载荷与结构参数对连接刚度影响规律[J]. 推进技术, 2017, 38(2): 424-433. YAO X Y, WANG J J. Effects of load and structure parameters of aero engine bolted joints on joint stiffness[J]. Journal of Propulsion Technology, 2017, 38(2): 424-433. (in Chinese) |
| [13] | CADDEMI S, CALIO I, CANNIZZARO F. Closed-form solutions for stepped Timoshenko beams with internal singularities and along-axis external supports[J]. Archive of Applied Mechanics, 2013, 83(4): 559-577. DOI:10.1007/s00419-012-0704-7 |
| [14] | 卢明剑, 孙岩桦, 周健, 等. 拉杆组合转子的刚度修正及动力学建模[J]. 航空动力学报, 2016, 31(9): 2203-2209. LU M J, SUN Y H, ZHOU J, et al. Stiffness modification and dynamic modeling of a rod fastening rotor[J]. Journal of Aerospace Power, 2016, 31(9): 2203-2209. (in Chinese) |
| [15] | 凤朝军.新式支承布局反向旋转双转子系统动力特性研究[D].南京: 南京航空航天大学, 2016: 15-20. FENG C J.The research of the dynamic characteristics of the new bearing layout counter-rotating dual-rotor system[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2016: 15-20(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1016925574.htm |
| [16] | 史亚杰, 王孝利, 洪杰, 等. 柔性转子动力特性研究[J]. 航空发动机, 2005, 31(1): 14-17. SHI Y J, WANG X L, HONG J, et al. Investigation of dynamic characteristics of flexible rotor system[J]. Aeroengine, 2005, 31(1): 14-17. DOI:10.3969/j.issn.1672-3147.2005.01.004 (in Chinese) |
