航路网络结构优化指通过调整航路点及航段的数量和位置以改变原有网络的性质和布局,从而实现优化目标[2]。根据规模大小,航路网络结构优化分为全局性优化和区域性优化[3]。全局性优化针对主干航路进行,其优化过程复杂,改造成本较大;区域性优化则是在已有航路网的基础上,针对一定范围内的支线航路进行,改造成本较小,应用更为广泛。
目前,国内外****针对区域航路网络的优化模型和算法进行了大量研究。王世锦和公言会[4]根据中国空域实际情况,建立了多目标优化模型,并利用蚁群算法[5]和元胞自动机[6]完成了模型求解。Dunn和Wilkinson[7]针对自然灾害造成的部分航段失效,提出了基于节点重分布的自适应重构策略和永久改航策略。康金霞[8]利用复杂网络建模方法对航路网络抗毁性进行分析,提出了单航路点失效时的改航方法。严伟等[9]以网络经济性与安全性为基础建立多目标优化模型,并采用烟花算法进行求解。然而,传统规划方法采用的目标函数及约束条件较少,规划策略单一,且未能将网络拓扑设计与飞行流量大小相结合,难以满足实际需要。
本文在对两航路、多航路交叉点容量进行细致讨论的基础上,以网络的最小运行费用、最小飞行冲突系数、最小非直线系数和最小航路角度改变量为优化目标,以“三区”约束、容量约束和优化范围约束为限制条件,建立了区域航路网络优化模型。进而提出移动、融合、分解等航路点优化策略和优化步骤,并使用更为精确的NSGA-Ⅲ算法完成模型求解。实现了网络细节与整体性能的统筹规划,有效提升了区域航路网络的安全性、精确性和综合性,弥补了传统规划方法的不足。
1 区域航路网络建立 1.1 组成要素 区域航路网络由航路点和航路构成,且包含了节点连接关系、飞行流量和飞行容量等要素。其中,航路分为境内航路、过境航路和出境航路,它们由多条依次相连的航段组成;航路点分为固定航路点和移动航路点,前者指机场及区域边境点,能够产生和吸收飞行流量,后者指航路交叉点及转向点,能够传递飞行流量[10]。
1.2 表达形式 为了反映区域航路网络特性,对各组成要素进行数学描述,可表示为N(P, D, f, C),具体含义如下:
1) P(N)={P1, P2,…, Pn, Pn+1, …, Pn+m}为航路点集,前n项为固定航路点,后m项为移动航路点。
2) D(N)为航路连接距离矩阵,可表示为
 | (1) |
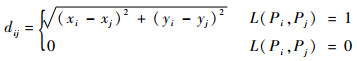 | (2) |
式中:(xi, yi)为Pi坐标;L(Pi, Pj)用来判断航路点Pi与Pj是否相连,若是,值为1,若否,值为0。
3) f(N)为网络流量参数,指单位时间内通过某航段或某航路点的航空器数目,包括航段PiPj的流量fij和航路点Pi的流量fi。
4) C(N)为网络容量参数,包括航段PiPj的容量Cij和航路点Pi的容量Ci。
1.3 容量分析 区域航路网络容量是衡量网络容纳性的参数,分为航段容量和航路点容量。
航段容量指单位时间内航段上某点允许通过的最大飞行架次[11]。令航空器巡航速度为v,最小管制距离为Lmin,可得
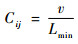 | (3) |
航路点容量指在特定航路结构中的交叉点单位时间内允许通过的最大飞行架次[6],如图 1所示。PA′PO、PB′PO为汇聚航段,POPD′、POPH′为离散航段,α、β、?、φ为航段夹角。
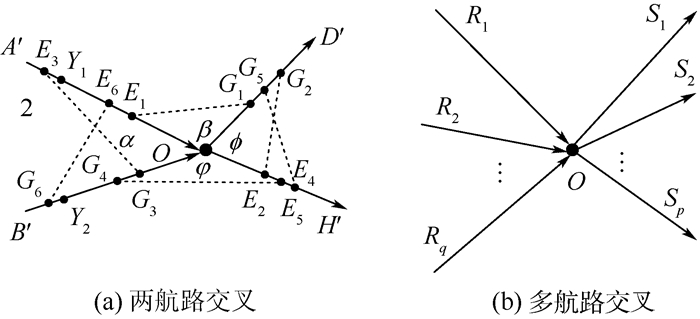 |
| 图 1 航路点容量示意图 Fig. 1 Schematic of waypoint capacity |
| 图选项 |
若t=0时,前继航班位于PB′PO上的O点,后续航班位于PA′PO上的Y1点,L=|Y1O|,相邻航班间距为F,则存在以下3种情况:
1) 当t∈(0, L/v)时,前继航班运行至G1点,后续航班运行至E1点,有
 | (4) |
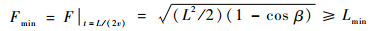 | (5) |
进一步推导可得,当
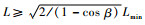

2) 当t∈[L/v, +∞)时,前继航班运行至G2点,后续航班运行至E2点,有
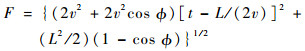 | (6) |
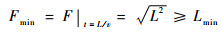 | (7) |
则航路点O能正常运行时,其容量为v/Lmin。
3) 当t∈(-∞, 0]时,前继航班运行至G3点,后续航班运行至E3点,有
 | (8) |
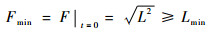 | (9) |
则航路点O能正常运行时,其容量为v/Lmin。
若t=0时,前继航班位于PA′PO上的O点,后续航班位于PB′PO上的Y2点,L=|Y2O|,相邻航班的间隔为F。类比上述推导过程,可得当前继航班位于G4点、G5点和G6点,后继航班位于E4点、E5点和E6点时,航路点O对应的容量为
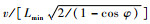
综上所述,当两航路交叉且来流方向固定时,O点的容量取值有6种情况。在实际运行过程中,为保证O点的安全运行,应使其容量取最小值,则有
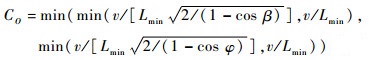 | (10) |
由于
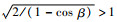
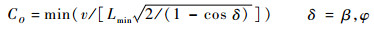 | (11) |
根据上述思路,当多条航路发生交叉时(见图 1(b)),可将其划分为若干个两航路交叉的情况进行处理,则交叉点O的容量为
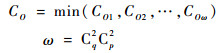 | (12) |
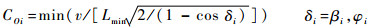 | (13) |
式中:COi(i=1, 2, …, ω)和δi(i=1, 2, …, ω)分别为第i种两航路交叉情况下对应的点容量和相应航段夹角。
2 区域航路网络结构优化模型 2.1 模型假设 区域航路网络结构复杂,为了模拟实际运行环境,构建网络优化模型,做出以下假设:
1) 网络中的航空器均位于同一高度层,其真航线角为[0, π]或[π, 2π]。
2) 航路点之间的连接关系和飞行流量保持不变,“三区”空域不可穿越。
3) 航空器巡航速度为800 km/h,规定的最小雷达管制间隔为20 km,航路点的优化范围为±50 km。
4) 不考虑进近管制区的飞行冲突。
5) 不考虑网络优化过程中的成本。
2.2 特性指标及约束 在区域航路网络优化过程中,需要设定若干特性指标以提升网络经济性、安全性和可行性,促进网络结构优化合理。
1) 运行费用
 | (14) |
式中:T(N)为运行费用;dij为航段PiPj的长度。
2) 飞行冲突系数
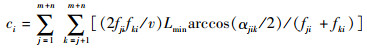 | (15) |
式中:ci(i=1, 2, …, m+n)为交叉航路点Pi的飞行冲突系数;αjik为航段PjPi和航段PkPi的夹角。
3) 非直线系数
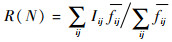 | (16) |
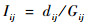 | (17) |
式中:R(N)为网络非直线系数;Gij为航路点Pi至航路点Pj的实际距离;Iij为航路Pi-Pj的非直线系数
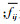
4) 航路角度改变量
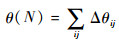 | (18) |
式中:Δθij为航路Pi-Pj中相邻航段之间的角度改变量。
为了保证网络优化后满足实际需求,必须制定相应约束对航路走向、航路点分布做出限制。
1) “三区”约束
 | (19) |
式中:line(Pi, Pj)为航段PiPj穿越的空域范围;U(N)为网络中的“三区”空域。
2) 容量约束
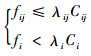 | (20) |
式中:λi、λij为裕度因子,表示由于管制员、流量增长等因素带来的影响。可避免航段或航路点陷入失效状态,保持网络的运行能力。
3) 优化范围约束
 | (21) |
式中:ximin、ximax为Pi横坐标的优化范围;yimin、yimax为Pi纵坐标的优化范围。
2.3 模型建立 区域航路网络的高效运转不仅取决于其结构的安全合理,还取决于飞行流量与网络容量的匹配关系,结合区域航路网络的特性指标及约束条件,建立以下多目标网络优化模型:
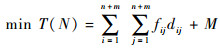 | (22) |
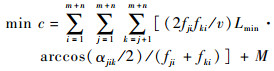 | (23) |
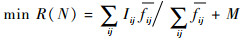 | (24) |
 | (25) |
 | (26) |
式(22)~式(25)分别表示区域航路网络的最小运行费用、最小飞行冲突系数、最小非直线系数和最小航路角度改变量。式(26)表示“三区”约束、容量约束和优化范围约束。式中:c为总飞行冲突系数,表征网络风险水平;M为罚函数,可将部分约束条件转化为目标函数的一部分,表示如下:
 | (27) |
 | (28) |
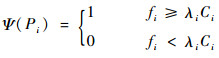 | (29) |
其中:σ为罚因子,可取σ=1 000[12];m′为航路交叉点个数;Ω(PiPj)用来判断航段PiPj是否经过“三区”;Ψ(Pi)用来判断航路点Pi的容量是否符合条件。
3 区域航路网络结构优化模型求解 3.1 优化策略 区域航路网络的具体结构取决于移动航路点的布局[10]。在优化过程中,为满足实际情况,提高区域航路网络的性能,需制定以下优化策略。
1) 构建空域环境
利用栅格法将空域划分为若干个单位长度为l′的栅格以表示初始区域航路网络的基本结构。
2) 增加改航转向点
由于经济发展、历史遗留等客观原因,现有航路布局可能存在缺陷。当航路穿越“三区”时,可采用几何法确定新增改航转向点的初步位置,使飞行器沿“三区”边缘通过[13]。
3) 移动航路点
当交叉点或改航点位置不合理,造成局部节点失效或影响网络整体性能时,可利用NSGA-Ⅲ算法对其布局进行改进,保证区域航路网络正常运转。
4) 融合航路点
当航路交叉点分布密集且飞行流量较小时,空域安全度高,可将一定范围内的多个交叉点融合成单个交叉点,如图 2所示,融合后有
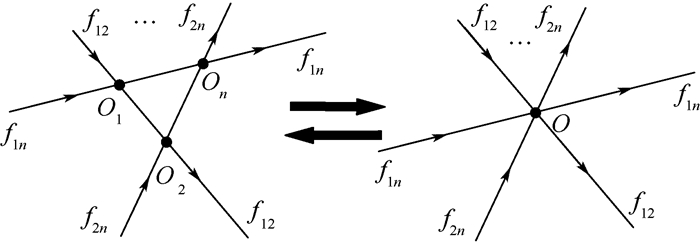 |
| 图 2 航路点融合、分解示意图 Fig. 2 Schematic diagram of waypoint integration and separation |
| 图选项 |
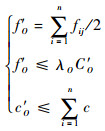 | (30) |
式中:fO′和CO′分别为融合后O点流量和容量;cO′为融合后O点飞行冲突系数;λO为裕度因子。
5) 分解航路点
当航路交叉点流量较大,出现容流冲突,影响空域安全时,可将单个交叉点分解为多个交叉点,如图 2所示,其关系如下:
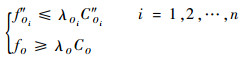 | (31) |
式中:fOi″和COi″(i=1, 2, …, n)分别为分解后航路点的流量和容量;fO和CO分别为分解前航路点的流量和容量;λOi为裕度因子。
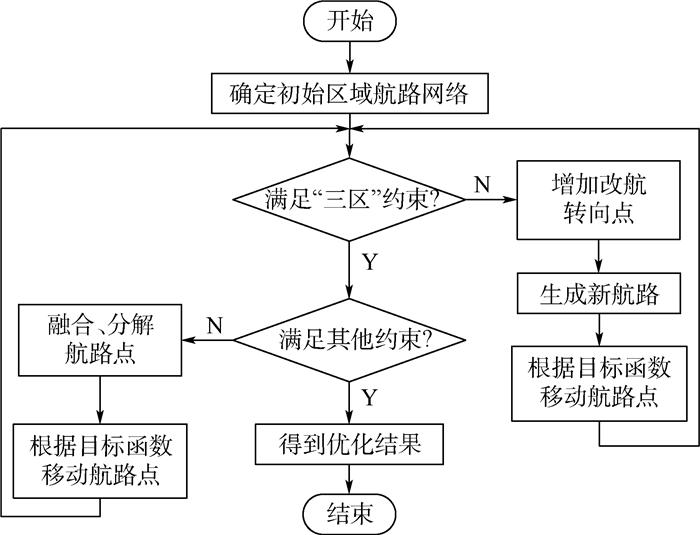
3.2 优化步骤 区域航路网络优化需综合考虑网络外在结构的合理性和内在运行的稳定性。因此,必须全面系统地统筹优化策略,设计优化方法。根据区域航路网络的结构特征及运行规律,制定以下优化步骤(见图 3):
 |
| 图 3 区域航路网络优化步骤 Fig. 3 Optimization steps of regional air route network |
| 图选项 |
步骤1??确定初始区域航路网络。
步骤2??判断是否满足“三区”约束。
步骤3??若不满足,则根据几何法增加改航转向点,连接转向点生成新航路并利用多目标网络优化模型求解航路点最优布局,执行步骤2。
步骤4??若满足,则判断是否符合其他约束。
步骤5??若不符合,则采取融合、分解航路点策略,进而利用多目标网络优化模型求解航路点最优布局,执行步骤2。
步骤6??若符合,取其中最优解集,网络优化完毕。
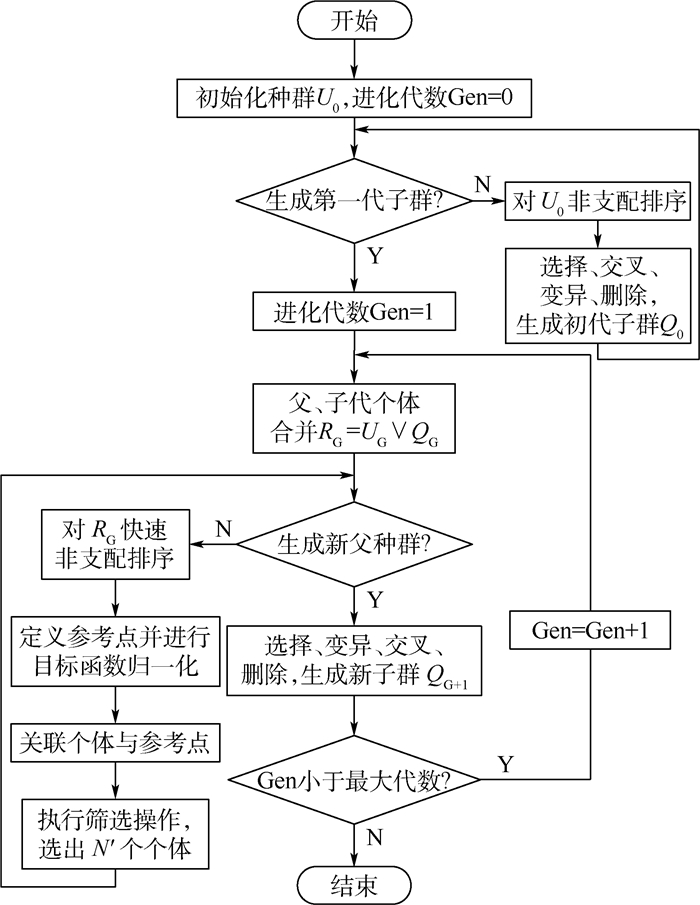
3.3 NSGA-Ⅲ算法 基于参考点的非支配排序遗传算法,即NSGA-Ⅲ是Kalyanmoy和Himanshu[14]提出的第三代多目标规划算法。该算法在继承NSGA-Ⅱ非支配排序的基础上,利用关联操作求解参考距离的方法代替了原来的拥挤度算子,提高了种群多样性。当目标函数较多时,其规划效果明显优于传统多目标规划方法。
1) 染色体构建
区域航路网络结构取决于移动航路点的分布情况,因此可采用实数编码方式构建染色体,如x11x12…xα1xα2…xk1xk2,k为移动航路点个数,2k为染色体长度,xα1、xα2分别为航路点Pα的横、纵坐标。
2) 操作算子
为了改进算法性能,提高运算效率,NSGA-Ⅲ算法在采取选择、变异、交叉3种传统操作算子的同时,引入删除算子,其表述如下:
① 选择算子。计算复合种群所有个体的目标函数值并根据结果进行快速非支配排序,当序号为N′的个体位于第l层时,采取关联操作计算第l层个体到其对应参考线的垂直距离,根据距离筛选符合条件的个体进入子代种群。
② 变异算子。采用基本变异方式,先确定变异个体及位置,进而由变异概率确定是否变异及变异后个体值。
③ 交叉算子。采取模拟二进制交叉算子,先确定交叉个体及位置,进而由交叉概率判断是否发生交叉。
④ 删除算子。对航路点坐标超出规划范围的染色体执行删除操作,重新生成染色体。
3) 算法步骤
NSGA-Ⅲ算法的基本步骤与传统遗传算法相似[15],但在选择机制上有所创新,如图 4所示。
 |
| 图 4 NSGA-Ⅲ算法流程 Fig. 4 Flowchart of NSGA-Ⅲ algorithm |
| 图选项 |
其中,选择操作的具体步骤可描述如下:
步骤1??非支配排序。将种群个体按照非支配规则分为m层,其中前l层个体记为Πl,数目为|Πl|,且|Πl|>N′。前l-1层个体记为Πl-1,数目为|Πl-1|,且|Πl-1| < N′。令H=N′-|Πl-1|,则需在第l层中选出H个个体。
步骤2??定义参考点。若目标函数个数为M′,染色体长度为2k,则参考点j个数为CM′+2k-12k,j可自行设置在M′-1维的归一化超平面上。
步骤3??归一化目标函数。计算理想点和极值点,转换目标函数,最终完成归一化操作。
步骤4??关联操作。连接参考点和原点构成参考线,计算所有个体到与之最近的参考线的距离,将个体与对应参考点进行关联。
步骤5??筛选操作。确定每个参考点j关联的前l-1层个体数目ρj,令关联数目较少的参考点组成集合
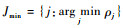
4 实例分析 以北京飞行情报区二连浩特P11、土木尔台P12和锡林浩特P19组成的区域航路网络为例进行结构优化仿真,令航空器的真航线角范围为[0, π],栅格边长l′为23.58 km,其示意图如图 5所示。其中,空心圆代表边境点和机场,实心圆代表航路交叉点,ZTi为“三区”,箭头指向表示流量运行方向。航段容量为40架次/h,令λi=λij=0.75,图 5所示的区域航路网络的相关数据见表 1和表 2[16-17]。
 |
| 图 5 初始区域航路网络 Fig. 5 Initial regional air route network |
| 图选项 |
表 1 移动航路点信息 Table 1 Information of mobile waypoint
| 航路点 | 汇聚航段交叉角 | 航路点流量/ (架次·h-1) | 航路点容量/ (架次·h-1) |
| P13 | ∠P11P13P12 | 11.4 | 20.96 |
| P14 | ∠P13P14P12 | 12.5 | 32.31 |
| P15 | ∠P12P15P14 | 12.9 | 38.03 |
| P16 | ∠P15P16P18 | 16.6 | 34.77 |
| P17 | ∠P16P17P6 | 14.9 | 27.04 |
| P18 | ∠P9P18P14 | 14.9 | 26.92 |
表选项
表 2 航段信息 Table 2 Information of air leg
| 航路 | 航段 | 长度/km | 流量/(架次·h-1) |
| B548 | P11P12 | 216.9 | 8.8 |
| A575 | P11P13 | 124.9 | 5.7 |
| A575 | P15P4 | 59.0 | 6.9 |
| H13 | P2P12 | 49.5 | 10.6 |
| H13 | P18P19 | 120.0 | 6.5 |
| H6 | P15P16 | 58.9 | 8.2 |
| B339 | P9P18 | 179.2 | 8.4 |
| J201 | P6P17 | 18.9 | 6.1 |
| B548 | P12P3 | 113.17 | 7.2 |
| A575 | P13P14 | 96.7 | 5.8 |
| G218 | P12P13 | 129.7 | 5.7 |
| H13 | P12P14 | 122.6 | 6.7 |
| H13 | P19P8 | 96.7 | 5.9 |
| H6 | P16P17 | 37.7 | 8.8 |
| B339 | P18P16 | 148.5 | 8.4 |
| J201 | P17P19 | 195.7 | 6.4 |
| A575 | P1P11 | 35.47 | 10.5 |
| A575 | P14P15 | 122.6 | 6 |
| G218 | P13P10 | 141.5 | 5.7 |
| H13 | P14P18 | 99.0 | 6.5 |
| H6 | P12P15 | 198.0 | 6.9 |
| H6 | P17P7 | 51.9 | 8.7 |
| B339 | P16P5 | 30.7 | 7.8 |
表选项
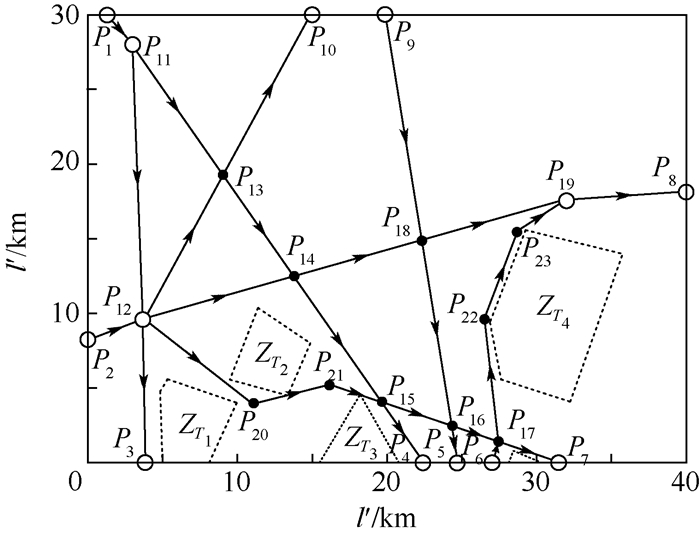
由表 1和表 2可知,航路交叉点均符合容量约束,但航段P12P15和航段P17P19穿越“三区”,需要增加部分改航点,则经过初步规划后的区域航路网络如图 6所示。
 |
| 图 6 初步规划结果 Fig. 6 Preliminary planning result |
| 图选项 |
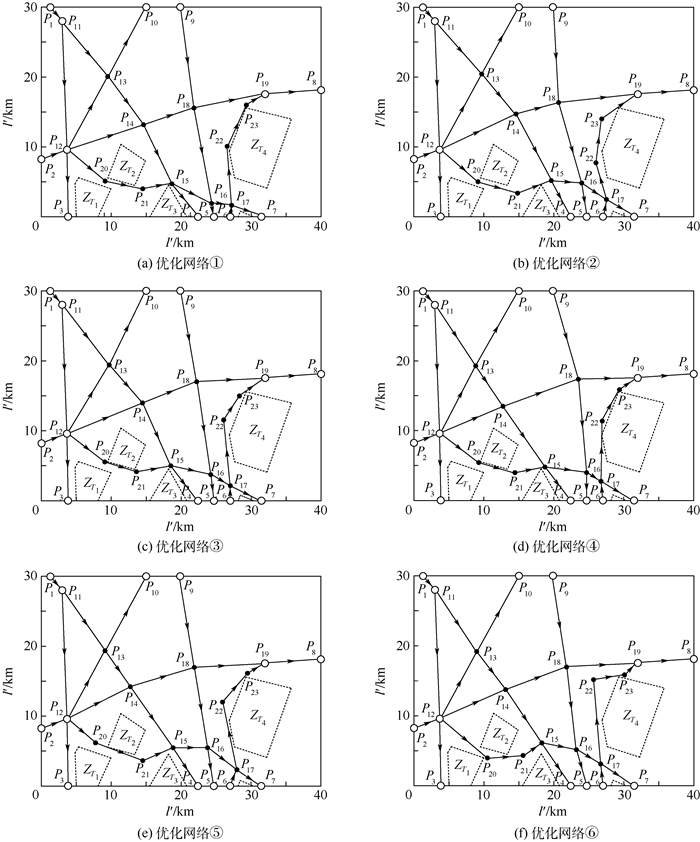
图 6中,区域航路网络的总运行费用为5.424×103,飞行冲突系数为1.151,非直线系数为1.248,角度改变量为215.9°。根据区域航路网络优化步骤,分别采用NSGA-Ⅲ算法、NSGA-Ⅱ算法和粒子群算法对图 6中移动航路点的布局进行优化。设置种群大小为100,进化代数为800,变异率为0.1,杂交率为0.15,可得如图 7所示的优化结果。
 |
| 图 7 区域航路网络优化结果示意图 Fig. 7 Schematic of regional air route network optimization results |
| 图选项 |
图 7中,(a)~(d)为利用NSGA-Ⅲ算法得到的区域航路网络;(e)、(f)为利用NSGA-Ⅱ算法和粒子群算法得到的区域航路网络,各网络具体特征值如表 3所示。
表 3 区域航路网络特性指标 Table 3 Property indexes of regional air route network
| 网络序号 | 运行费用 | 飞行冲突系数 | 非直线系数 | 角度改变量/(°) |
| ① | 5.409×103 | 1.092 | 1.244 | 266.5 |
| ② | 5.425×103 | 0.954 | 1.251 | 268.1 |
| ③ | 5.413×103 | 0.972 | 1.245 | 238.7 |
| ④ | 5.418×103 | 0.971 | 1.246 | 216.5 |
| ⑤ | 5.437×103 | 0.969 | 1.257 | 282.3 |
| ⑥ | 5.495×103 | 0.879 | 1.276 | 330.2 |
| ⑦ | 5.424×103 | 1.151 | 1.248 | 215.9 |
| ⑧ | 5.405×103 | 1.089 | 1.227 | 63.34 |
表选项
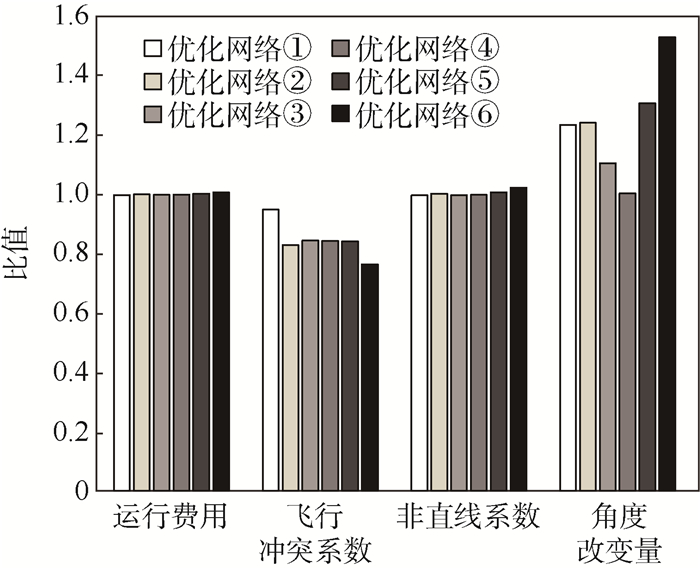
表 3中,⑦为初步规划后的网络,⑧为初始区域航路网络。通过对比可知,各优化网络的运行费用、非直线系数和角度改变量相比于初始网络均有所增加,但是这些网络的飞行冲突系数下降显著,同时实现了对障碍区域的规避,从而使得空域安全性得以提高。其中,网络③、④的运行费用、非直线系数和角度改变量较优,其改进效果较佳;网络①、②的各项指标较为均衡,改进效果良好;网络⑤、⑥的飞行冲突系数较小,但是其多项指标排名靠后,整体性能一般。为突出差异,对各优化网络指标与网络⑦指标的比值进行分析,如图 8所示。
 |
| 图 8 优化网络对比 Fig. 8 Contrast diagram of optimization network |
| 图选项 |
不难看出,优化网络②~④的综合性能优于优化网络⑤、⑥,其中优化网络④的改进效果最佳。相比于初步规划后的网络,优化网络④的运行费用减少了0.11%,飞行冲突系数减少了15.6%,非直线系数减少了0.16%,仅角度改变量略有增加;相比于初始网络,优化网络④符合全部约束条件,同时其飞行冲突系数减少了10.8%,运行费用与非直线系数略有增加,仅角度改变量变化较大。
因此,NSGA-Ⅲ算法能够有效求解基于航路点布局的网络优化模型,且单次运算可提供多种属性各异的优化网络,方便规划人员在不同任务目标和约束条件下进行选择。
5 结论 本文建立了基于航路点布局的多目标网络结构优化模型,并利用NSGA-Ⅲ算法对模型进行求解,验证了区域航路网络结构优化方法在解决航路避障和网络节点失效时的可行性。从仿真分析中可以得出:
1) 优化后的网络符合相应约束条件,且飞行冲突系数改进明显,空域安全性显著提升。
2) 利用航路点的移动、融合、分解策略可有效解决容流匹配问题和“三区”避让问题。
3) 利用NSGA-Ⅲ算法求解多目标优化问题的效果较优,且能为规划者提供多种备选方案。
4) 优化后的网络契合中国空域“碎片化”特点和飞行流量日益增长的实际情况,可有效弥补现有网络缺陷。
区域航路网络与全局航路网络是局部与整体的关系,今后将考虑其关联作用对网络结构优化的影响。
参考文献
| [1] | 王世锦, 公言会, 郦晴云. 航路网络规划技术研究综述[J]. 交通信息与安全, 2014, 32(6): 8-14. WANG S J, GONG Y H, LI Q Y. A review of air transportation network planning methods[J]. Transportation Information and Safety, 2014, 32(6): 8-14. DOI:10.3963/j.issn.1674-4861.2014.06.002 (in Chinese) |
| [2] | 公言会.航路网络规划技术研究[D].南京: 南京航空航天大学, 2016. GONG Y H.Research on air route network planning technology[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2016(in Chinese). |
| [3] | CHEN D, HU M H, ZHANG H H, et al. A network based dynamic air traffic flow model for en route airspace system traffic flow optimization[J]. Transportation Research Part E:Logistics and Transportation Review, 2017, 106: 1-19. DOI:10.1016/j.tre.2017.07.009 |
| [4] | WANG S J, GONG Y H. Research on air route network nodes optimization with avoiding the three areas[J]. Safety Science, 2014, 66: 9-18. DOI:10.1016/j.ssci.2014.01.008 |
| [5] | WANG S J, LI Q Y, CAO X, et al. Optimization of air route network nodes to avoid "three areas" based on an adaptive ant colony algorithm[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(4): 469-478. |
| [6] | WANG S J, CAO X, LI H Y, et al. Air route network optimization in fragmented airspace based on cellular automata[J]. Chinese Journal of Aeronautics, 2017, 30(3): 1184-1195. DOI:10.1016/j.cja.2017.04.002 |
| [7] | DUNN S, WILKINSON S M. Increasing the resilience of air traffic networks using a network graph theory approach[J]. Transportation Research Part E:Logistics and Transportation Review, 2016, 90: 39-50. DOI:10.1016/j.tre.2015.09.011 |
| [8] | 康金霞.航路网络特征及其抗毁性研究[D].南京: 南京航空航天大学, 2016. KANG J X.Research on the structure and its invulnerability of China air route network[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1016791245.htm |
| [9] | 严伟, 王瑛, 孟祥飞, 等. 航空网络航路点布局的多目标优化设计[J]. 空军工程大学学报, 2017, 18(6): 20-26. YAN W, WANG Y, MENG X F, et al. A multi-objective optimization design for crossing waypoint location in air route network[J]. Journal of Air Force Engineering University, 2017, 18(6): 20-26. DOI:10.3969/j.issn.1009-3516.2017.06.004 (in Chinese) |
| [10] | 郦晴云.基于交通流特征的航路网络节点布局优化[D].南京: 南京航空航天大学, 2016. LI Q Y.Air route network node optimization based on traffic flow feature[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1016791258.htm |
| [11] | DU W B, LIANG B Y, YAN G, et al. Identifying vital edges in Chinese air route network via memetic algorithm[J]. Chinese Journal of Aeronautics, 2017, 30(1): 330-336. DOI:10.1016/j.cja.2016.12.001 |
| [12] | SAVURAN H, KARAKAYA M. Efficient route planning for an unmanned air vehicle deployed on a moving carrier[J]. Soft Computing, 2016, 20(7): 2905-2920. DOI:10.1007/s00500-015-1970-4 |
| [13] | ZHANG X G, MAHADEVAN S. Aircraft re-routing optimization and performance assessment under uncertainty[J]. Decision Support Systems, 2017, 96: 67-82. DOI:10.1016/j.dss.2017.02.005 |
| [14] | KALYANMOY D, HIMANSHU J. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach.Part Ⅰ:Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [15] | BI X J, WANG C. An improved NSGA-Ⅲ algorithm based on elimination operator for many-objective optimization[J]. Meme-tic Computing, 2017, 9(4): 361-383. DOI:10.1007/s12293-017-0240-7 |
| [16] | 中国民用航空局. 从统计看民航2017[M]. 北京: 中国民航出版社, 2018. CAAC. From the statistical view of civil aviation 2017[M]. Beijing: China Civil Aviation Press, 2018. (in Chinese) |
| [17] | 李明娟. 杰普逊航图及应用[M]. 北京: 北京航空航天大学出版社, 2016. LI M J. Jeppesen charts and applications[M]. Beijing: Beihang University Press, 2016. (in Chinese) |
