据美国大西洋导弹测试基地的统计,美国军方90%的武器系统的鉴定、评估数据来自于半实物仿真的结果,中国的航天、航空部门也规定“未经过半实物仿真的产品不能参与发射或飞行测试”[8]。可见,地磁导航半实物仿真平台建设的好坏直接影响地磁导航的工程化进程。目前,中国对地磁导航半实物仿真的研究很少。文献[9]将地磁导航的原理与半实物仿真的特点相结合,设计了一套地磁导航半实物仿真系统总体方案,指出地磁场数据库源数据获取、载体干扰磁场补偿、地磁场环境仿真和地磁匹配导航算法是需要重点解决的4项关键技术。从目前国内外研究成果来看,地磁场数据库源数据获取[10-11]、载体干扰磁场补偿[12-13]以及地磁匹配导航算法[14-15]这3方面都取得了较为丰硕的理论成果,而针对地磁场环境仿真的研究相对较少。文献[16]指出在实验室等磁场较为复杂的环境下,地磁场环境仿真系统必须采用“磁屏蔽装置+磁场模拟器”组合的方式来实现。当前,单就磁屏蔽装置或者磁场模拟器而言,其研制成熟度相对已经很高[17-19],但是如果将二者组合在一起就会带来新的问题:磁场模拟器产生的磁场会对磁屏蔽装置及其屏蔽效果产生怎样的影响?磁屏蔽装置又会对磁场模拟器产生的磁场造成什么样的影响?二者之间的耦合问题需要进行深入的探究。
针对磁屏蔽装置与磁场模拟器的耦合问题,本文采用了仿真分析与实验验证相结合的方法,通过仿真实验对磁屏蔽装置与磁场模拟器的耦合关系进行了探索性研究,并搭建了小型的地磁场环境仿真系统,进而通过实测实验对仿真分析得到的结论进行了验证,揭示了二者之间的耦合关系,为地磁导航半实物仿真系统中地磁场环境仿真系统的设计提供了理论依据。
1 地磁场环境仿真技术理论 1.1 地磁导航半实物仿真原理 地磁导航原理就是把提前规划好的飞行航迹上某些点的地磁场特征量(一般为地磁总场值)绘制成地磁基准图,存储在导航计算机中,当载体飞越匹配区域时,由磁传感器实时测量出飞越点的地磁场特征量,并构成实时测量序列得到实时图,实时图与导航计算机中的地磁基准图通过匹配算法解算出飞行器的坐标位置,从而修正惯性导航的误差,最终实现精确导航的目的[20]。其原理如图 1所示[9]。
 |
| 图 1 地磁匹配导航原理示意图[9] Fig. 1 Schematic diagram of principle of geomagnetic matching navigation[9] |
| 图选项 |
进行地磁导航半实物仿真,重点是对载体飞行航迹上的磁场变化进行仿真。实验室内的用电设备较多,文献[16]表明,即使在周末晚上实验室内设备都处于关闭状态的情况下,仍有100 nT左右的干扰磁场,由此可以推测日常工作时实验室内的干扰磁场将更大,因此,在模拟载体飞行航迹上的地磁场之前,必须先将磁场模拟器与磁传感器置于磁屏蔽装置内部以降低干扰磁场对仿真的影响。由于在实验室环境下无法实现载体的真实运动,这就需要将载体在地磁场中的运动转换为地磁场相对于载体的运动,通过仿真计算机控制磁场模拟器以一定的时间步长产生载体飞行航迹上一系列的磁场值,使置于磁场模拟器内部的磁传感器敏感到该磁场,最后将磁传感器测得的“实时图”与存储在仿真计算机中的地磁基准图通过匹配算法进行匹配解算,输出定位结果,实现对惯性导航误差的修正。这就是地磁导航半实物仿真的工作原理[9]。典型的地磁导航半实物仿真系统结构组成如图 2所示[9]。
 |
| 图 2 地磁导航半实物仿真系统结构组成示意图[9] Fig. 2 Schematic diagram of hardware in the loop simulation system for geomagnetic navigation[9] |
| 图选项 |
从图 1和图 2可以看出,地磁场环境仿真技术是地磁导航由计算机仿真过渡到半实物仿真的“桥梁”,而“磁屏蔽装置+磁场模拟器”是地磁场环境仿真的实现形式,二者之间的耦合势必会对地磁场环境的仿真造成影响,进而影响整个半实物仿真系统的性能,因此,对于二者之间的耦合研究具有重要的理论价值和工程价值。
1.2 磁场模拟器的生磁原理 现阶段对地磁场环境进行仿真,主要还是依靠物理模拟的手段来实现。由电磁理论中的毕奥-萨伐尔定律[21]可知,通电导线会在其周围空间产生磁场,产生的磁场方向与通电电流方向满足右手定则。因此,目前磁场模拟器都是采用通电线圈的方法产生磁场,磁场的大小和方向由线圈中电流的大小和方向决定。实际情况中,地磁场在较小范围内是一个均匀场,而螺线管线圈或亥姆霍兹线圈可以在其中心点附近产生均匀磁场,故通常采用这2种线圈形式来模拟地磁场。
1.3 磁屏蔽装置的磁屏蔽原理 磁屏蔽装置的磁屏蔽原理可以采用磁路原理来解释。磁路原理与电路原理相似,即将一个由高导磁率材料(如硅钢片、坡莫合金等)构成的屏蔽装置置于干扰磁场中,这时屏蔽装置与其内部的空气介质构成一个并联磁路,由于空气的相对磁导率接近于1,而屏蔽材料的相对磁导率为几千甚至上万,故空气的磁阻R0要比磁屏蔽装置的磁阻Rm大得多,当外界存在干扰磁场时,绝大部分磁力线会沿着磁阻低的屏蔽壳通过,进入屏蔽体内腔的磁力线很少,从而达到屏蔽磁场的目的。其原理如图 3所示。
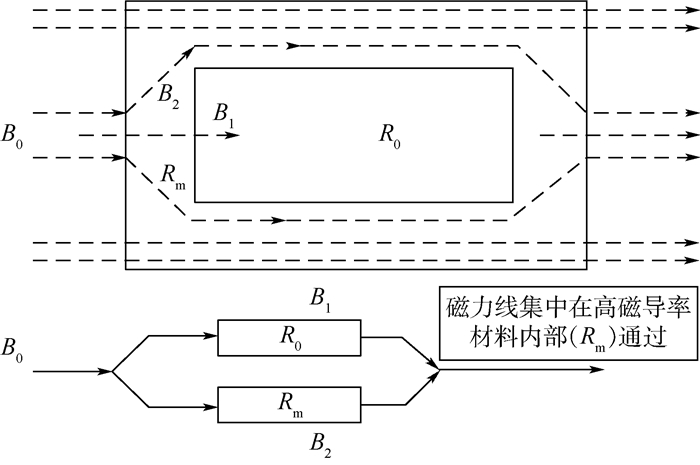 |
| 图 3 磁屏蔽原理 Fig. 3 Magnetic shielding principle |
| 图选项 |
从图 3所示的磁屏蔽原理可知,当磁屏蔽装置内部的磁场模拟器产生磁场时,由于附近存在高磁导率材料,该磁场的磁力线势必会改变原来的路线,大部分的磁力线会沿着高磁导率材料通过,磁场模拟器产生的磁场势必会与初始设计的结果出现偏差,因此,二者之间的耦合是必然存在的,对二者之间的耦合关系进行探究是十分必要的。
2 耦合关系仿真分析 仿真实验的目的就是探究磁屏蔽装置与磁场模拟器的耦合对各自性能的影响。对于磁屏蔽装置,磁屏蔽效果是其主要性能指标,目前对其研究主要集中在磁屏蔽性能的理论计算[22-23];对于磁场模拟器,磁场的线性度、均匀性以及实时性是其主要性能指标,大部分的工程应用均对磁场的均匀性有较高的要求,故目前对其研究主要集中在磁场分布的均匀性方面[24-25],由于大部分工程应用只需要模拟静态磁场,因此很少关注其动态实时性指标。鉴于目前对磁屏蔽装置和磁场模拟器的研究均是独立进行的,没有考虑耦合的影响,其结论是否会因为二者的耦合而发生改变还有待考证。因此,本文从以上4个方面设计相应的仿真实验进行探索研究。
为了探究磁屏蔽装置与磁场模拟器的耦合关系,本文利用Ansoft Maxwell这款商用电磁场有限元分析软件对其进行数值仿真分析,该软件不仅具备常规电磁场有限元分析软件的特点,还具有参数化建模的功能,可以连续计算不同参数所对应的计算结果,从而方便地找到参数变化对计算结果的影响规律[26]。仿真中,初始化设定磁屏蔽装置为80 mm×80 mm×40 mm的长方体,屏蔽材料厚度为t=1 mm,相对磁导率为μr=10 000;磁场模拟器为半径R=10 mm的圆形亥姆霍兹线圈,2个线圈之间的间距等于线圈的半径,即10 mm,线圈激励为电流,初始值设定为I=3 A,生成的磁场方向沿z轴,建立的三维仿真模型如图 4所示。
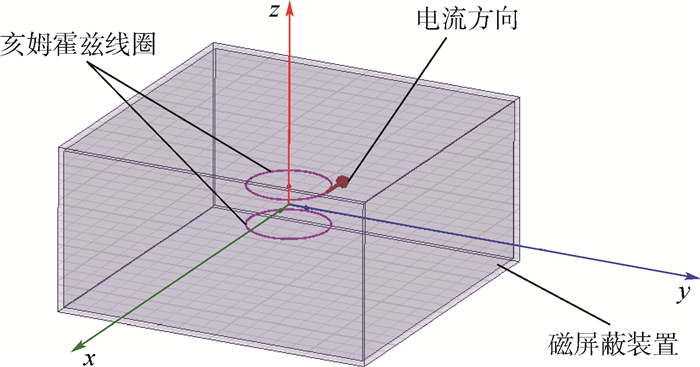 |
| 图 4 磁屏蔽装置与磁场模拟器耦合模型 Fig. 4 Coupling model of magnetic shielding device and magnetic field simulator |
| 图选项 |
2.1 磁场模拟器对磁屏蔽装置的影响 理论上,磁屏蔽材料磁化越严重,其屏蔽效果越差,因此,仿真中可以以磁屏蔽材料的磁化效果来反映磁屏蔽装置的屏蔽效果。当磁场模拟器放入磁屏蔽装置后,通入3 A的电流产生的磁场对磁屏蔽装置产生的磁化效果如图 5所示。
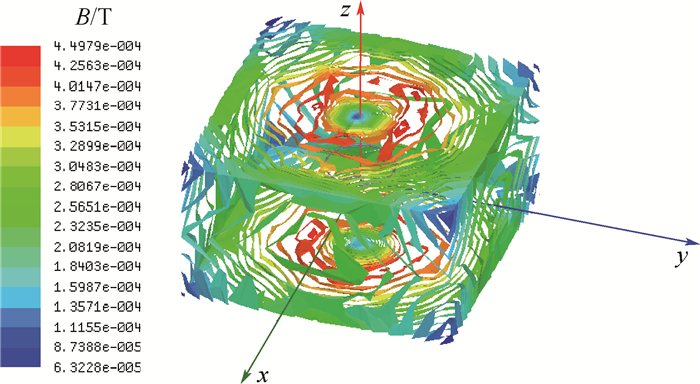 |
| 图 5 磁场模拟器对磁屏蔽装置的磁化效果(I=3 A) Fig. 5 Magnetization effect of magnetic field simulator on magnetic shielding device (I=3 A) |
| 图选项 |
从图 5可以看出,与磁场方向垂直的平面的磁化最为严重,最高达到了449.79 μT,其他方向的磁化相对比较小。改变电流的大小,分别通入6 A和9 A的电流,磁化效果如图 6所示。
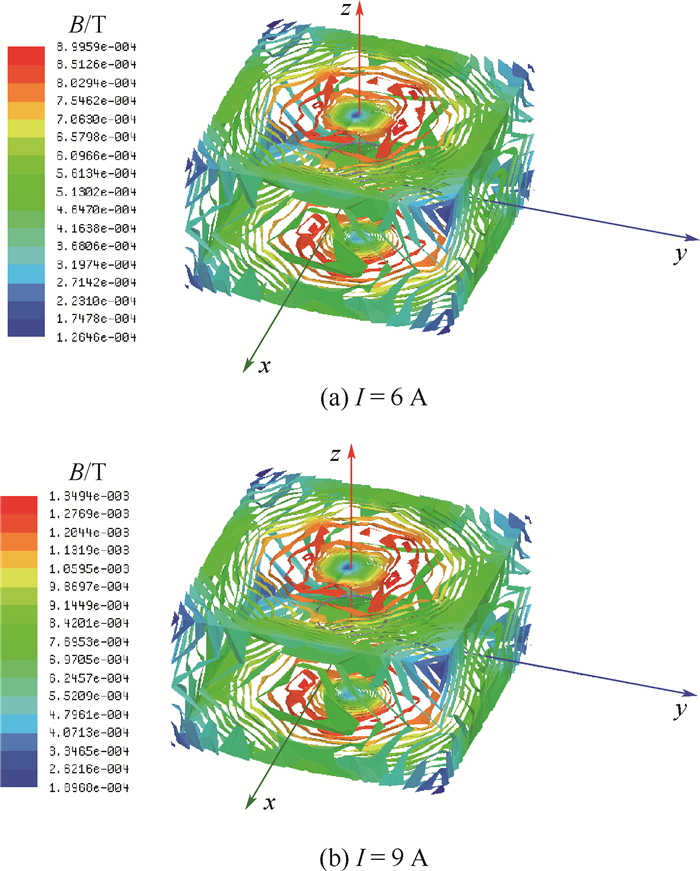 |
| 图 6 磁场模拟器对磁屏蔽装置的磁化效果(I=6 A, 9 A) Fig. 6 Magnetization effect of magnetic field simulator on magnetic shielding device (I=6 A, 9 A) |
| 图选项 |
从图 6可以看出,通入6 A和9 A电流时,与磁场方向垂直的平面的磁化更为严重,最高分别达到了899.59 μT和1 349.4 μT。可见,随着电流的增大,磁场模拟器产生的磁场对磁屏蔽装置的磁化也越来越严重,这势必会使磁屏蔽装置的屏蔽效果变差。
“磁场模拟器产生的磁场会对磁屏蔽装置造成严重的磁化”这一结论具有重要的理论和工程意义。如果磁场模拟器长时间在大电流的情况下工作,磁屏蔽材料极有可能会达到磁饱和,那么其屏蔽效果会大大折扣,因此,在工程实际中,必须对磁屏蔽装置内部进行定期消磁。
2.2 磁屏蔽装置对磁场模拟器线性度的影响 由电磁理论中的毕奥-萨伐尔定律可知,亥姆霍兹线圈在其轴线中心点产生的磁场大小与电流成正比,即磁场与电流具有良好的线性关系。为了探究磁屏蔽装置对磁场模拟器线性度的影响,采用Ansoft Maxwell软件中参数化建模的方法,将电流值设定为变化参数,使其从1 A变化到10 A,步长为1 A,以线圈轴线中心点处的磁场值为观测对象,在无磁屏蔽装置和有磁屏蔽装置的情况下进行仿真,结果如图 7所示。
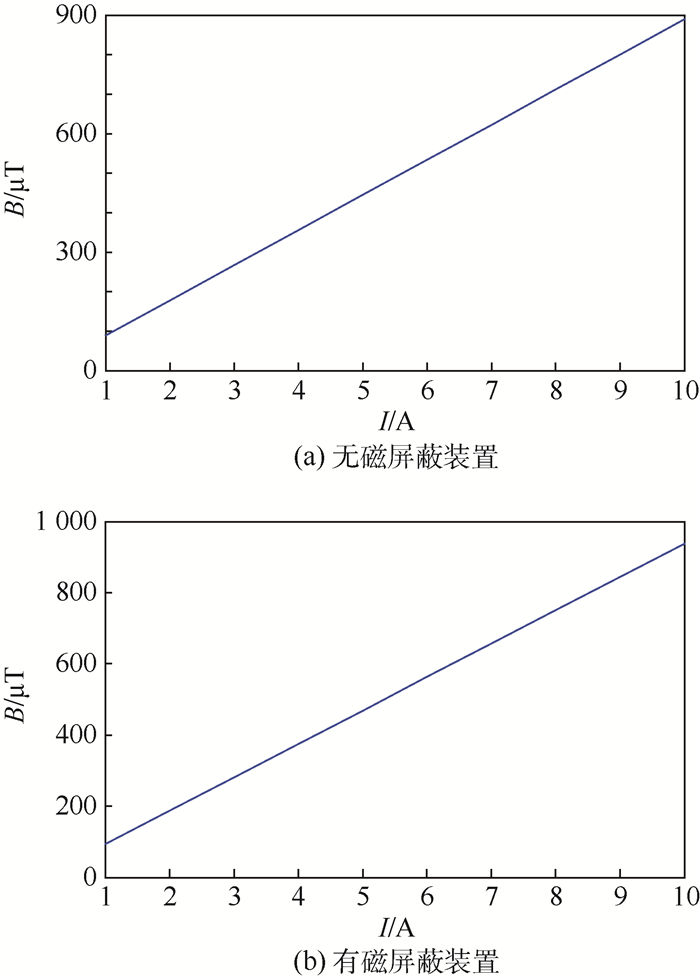 |
| 图 7 磁场模拟器的磁场线性度 Fig. 7 Magnetic field linearity of magnetic field simulator |
| 图选项 |
从图 7可以看出,在无磁屏蔽装置的情况下,线圈在中心点处产生的磁场与电流具有良好的线性度,加入磁屏蔽装置后,依然具有良好的线性度,说明磁屏蔽装置不会影响磁场模拟器的线性度。将2种情况下的计算数据导出,采用最小二乘拟合的方法进行拟合,得到磁场与电流的线性关系为
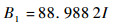 | (1) |
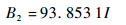 | (2) |
式(1)为无磁屏蔽装置时的线性关系,式(2)为有磁屏蔽装置时的线性关系,B为线圈轴线中心点处的磁场值,单位为μT,I为通入的电流值,单位为A。
对比式(1)和式(2)可以发现,式(2)的系数比式(1)的系数略大,也就是说,通入相同的电流,有磁屏蔽装置的情况下产生的磁场要比无磁屏蔽装置的情况下产生的磁场大。分析原因,由于亥姆霍兹线圈产生的磁力线是向外扩散的,当磁场模拟器放入磁屏蔽装置后,其产生的磁力线大部分被束缚在磁屏蔽材料内,其总体磁力线的回路缩短,这样就会增强中心区域的磁场。
“磁屏蔽装置不会影响磁场模拟器的线性度”这一结论具有重要的理论和工程意义。在实际系统输入输出关系标定过程中,如果由于耦合原因使得磁场模拟器的输入输出关系不满足线性关系,那么就需要进行遍历标定,这样会加大标定的复杂程度。满足线性关系的好处在于,只要采样少量的输入输出数据,根据最小二乘方法进行拟合就可以精确地确定系统的输入输出关系,同时,由于二者的耦合不影响线性度,在设计阶段不用过多考虑耦合对线性度的影响,只要设计的磁场模拟器线性度良好,那么将二者组合在一起后其依然具有良好的线性度,这样就可以大大降低系统的设计和操作难度。
2.3 磁屏蔽装置对磁场模拟器均匀性的影响 亥姆霍兹线圈在中心点附近能够产生均匀磁场,这是其重要特性。为了探究磁屏蔽装置对磁场模拟器均匀性的影响,在Ansoft Maxwell软件中设定z轴(即亥姆霍兹线圈中心轴线)方向-5~+5 mm线段上的磁场值为观测对象,在无磁屏蔽装置和有磁屏蔽装置的情况下进行仿真,结果如图 8所示。
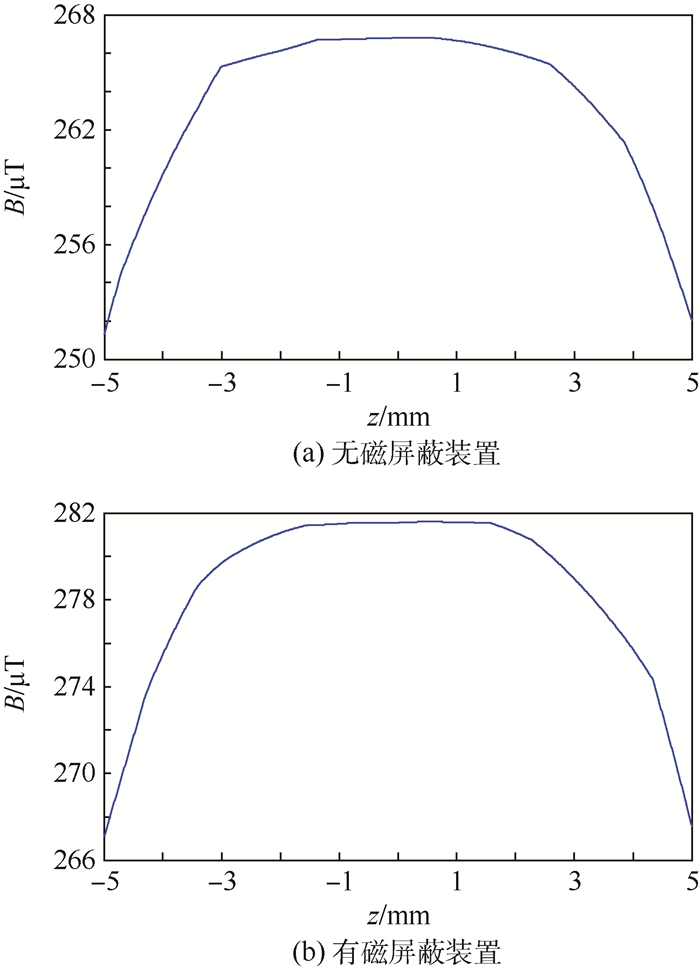 |
| 图 8 磁场模拟器的磁场均匀性 Fig. 8 Magnetic field uniformity of magnetic field simulator |
| 图选项 |
从图 8可以看出,在无磁屏蔽装置的情况下,线圈在中心点附近产生的磁场接近于直线段,说明具有良好的均匀性,加入磁屏蔽装置后,依然具有良好的均匀性,说明磁屏蔽装置不会影响磁场模拟器的均匀性。同时,对比图 8(a)、(b)还可以发现,在相同位置处,有磁屏蔽装置的情况下产生的磁场要比无磁屏蔽装置的情况下产生的磁场大,这与2.2节中得到的仿真结论一致。
将2种情况下的计算数据导出,以中心点为原点,在其上下各2 mm的范围内,对计算结果进行统计,结果如表 1所示。
表 1 磁场模拟器中心区域磁场均匀性仿真数据 Table 1 Simulated uniformity data of magnetic field of center area of magnetic field simulator
| 仿真条件 | 最大磁场值/μT | 最小磁场值/μT | 绝对误差/μT | 相对误差/% |
| 无磁屏蔽装置 | 266.82 | 266.03 | 0.79 | 0.296 |
| 有磁屏蔽装置 | 281.59 | 281.09 | 0.50 | 0.178 |
表选项
由表 1数据可以看出,加入磁屏蔽装置后,在-2~+2 mm的范围内,磁场模拟器产生的磁场最大相对误差为0.178%,可见其具有良好的均匀性。
“磁屏蔽装置不会影响磁场模拟器的均匀性”这一结论具有重要的理论和工程意义。在半实物仿真系统实际工作过程中,系统的输入输出关系是基于中心点处的测量值进行标定的,理论上采用不同位置的测量值进行标定得到的输入输出关系也不相同。在实际工作中,由于要模拟载体的姿态变化,势必会造成磁传感器位置的微动,而磁屏蔽装置不会影响磁场模拟器的均匀性,也就是说,中心点附近位置的输入输出关系都可以用中心点处的输入输出关系来表示,这样就大大降低了标定的复杂程度。同时,由于二者的耦合不影响均匀性,在设计阶段不用过多考虑耦合对均匀性的影响,只要设计的磁场模拟器均匀性良好,那么将二者组合在一起后其依然具有良好的均匀性,这样就可以大大降低系统的设计和操作难度。
2.4 磁屏蔽装置对磁场模拟器实时性的影响 半实物仿真的核心是实现模型与实物的直接相连,仿真时钟必须与自然时钟相一致,这就对实时性提出了较高的要求[27]。由于线圈中电感的存在,使得线圈通入电流后不可能迅速产生稳定的磁场,这是影响地磁导航半实物仿真系统实时性最主要的原因。理论上,线圈的电感越大,系统的实时性也就越差,因此可以通过测量电感的变化来反映实时性的变化。
为了探究磁屏蔽装置对磁场模拟器实时性的影响,在Ansoft Maxwell软件中计算线圈的电感值,通过仿真计算得到在无屏蔽装置和有屏蔽装置的情况下的电感值,结果如表 2所示。
表 2 磁场模拟器线圈电感值 Table 2 Coil inductance of magnetic field simulator
| 仿真条件 | 自感值/nH | 互感值/nH |
| 无磁屏蔽装置 | 52.17 | 5.24 |
| 有磁屏蔽装置 | 53.06 | 5.95 |
表选项
从表 2可以看出,加入磁屏蔽装置后,线圈的自感和互感均有所增加,其中自感增加了1.71%,互感增加了13.55%,这就说明磁屏蔽装置会使磁场模拟器的实时性变差。分析其原因,电感的定义是线圈的磁通量与生产此磁通量的电流之比,由于加入磁屏蔽装置后,线圈产生的磁力线大部分被束缚在磁屏蔽材料内,使得磁路变短磁通量加大,而电流是不变的,即分母不变分子变大,故电感增大,从而导致实时性变差。
“磁屏蔽装置会使磁场模拟器实时性变差”这一结论具有重要的理论和工程意义。在进行磁场模拟器的实时性设计时,要在线圈的响应速度上留出足够的冗余量,从而弥补耦合带来的滞后影响。
3 耦合关系实验验证 为了检验仿真结论的正确性,也为了体现“磁屏蔽装置+磁场模拟器”耦合结论的普遍适用性,采用螺线管线圈作为磁场模拟器以代替仿真中的圆形亥姆霍兹线圈,采用5层坡莫合金材料加工制成圆柱形磁屏蔽装置,构建了一个小型的地磁场环境仿真系统用于验证磁屏蔽装置与磁场模拟器的耦合关系,硬件设施如图 9所示。
 |
| 图 9 螺线管线圈和圆柱形多层磁屏蔽筒 Fig. 9 Solenoid coil and cylindrical multilayer geomagnetic shielding canister |
| 图选项 |
3.1 磁化效果验证实验 实际测量中,很难像仿真那样可以直接测量磁场模拟器对磁屏蔽装置的磁化。理论上,磁屏蔽材料的磁化越严重,其屏蔽效果就越差,内部的剩磁就会越大,因此,通过测量磁屏蔽装置内部的剩磁大小就可以反映出磁场模拟器对磁屏蔽装置屏蔽效果的影响。
实验中,将螺线管线圈放入磁屏蔽装置内部,从0 mA开始,每隔10 mA通入一次电流,每通入一次电流持续工作1 min后断开电源,测量并记录中心点的剩磁,直到90 mA结束,测量结果如图 10所示。
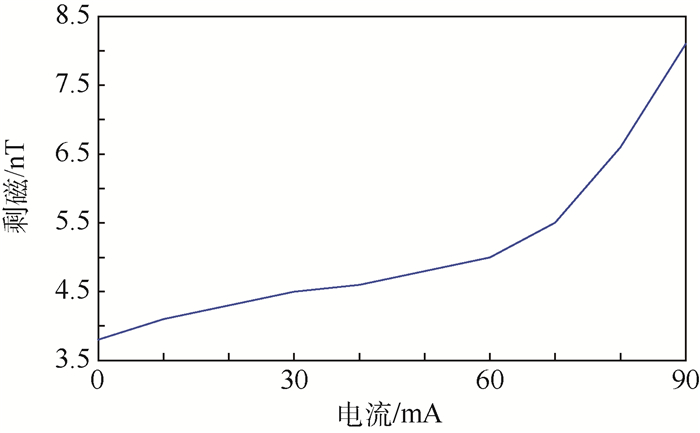 |
| 图 10 磁场模拟器通电情况下对磁屏蔽装置剩磁的影响 Fig. 10 Influence of magnetic field simulator on remanence of magnetic shielding device under the condition of electrifying |
| 图选项 |
从图 10可以看出,不通电的情况下,系统的初始剩磁为3.8 nT;在通入电流较小的情况下,磁屏蔽装置内部中心点处的剩磁增幅较小,说明磁场模拟器在小电流的情况下对磁屏蔽装置的屏蔽效果影响较小;在通入大电流的情况下,磁屏蔽装置内部中心点处的剩磁增幅较大,当通入90 mA电流时,其剩磁已经达到8.1 nT,是初始剩磁的2.13倍,说明磁场模拟器在大电流的情况下已经严重影响到磁屏蔽装置的屏蔽效果,这与仿真得到的结论具有一致性。如果磁场模拟器长时间在大电流的情况下工作,必须对磁屏蔽装置内部进行定期消磁,必要时还需要在磁屏蔽装置内部安装消磁线圈。
3.2 线性度验证实验 将螺线管线圈放入磁屏蔽装置内,分别通入5,10,15,20,25,30,35,40,45,50,55,60 mA的电流,待每一个电流生成的磁场值稳定后进行记录,实验数据如图 11所示。
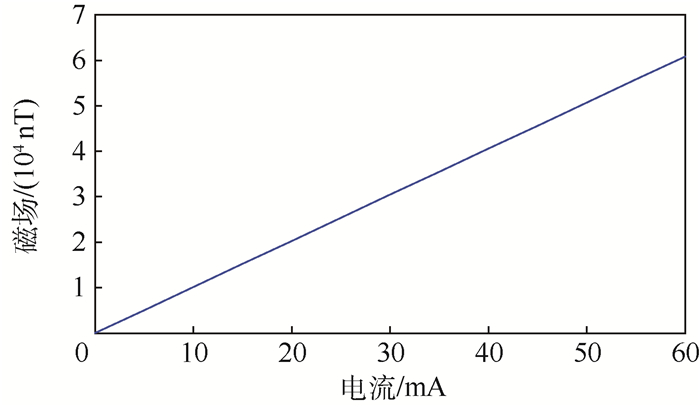 |
| 图 11 磁屏蔽装置内螺线管线圈产生的磁场与电流的关系 Fig. 11 Relationship between current and magnetic field generated by solenoid coil in magnetic shielding device |
| 图选项 |
从图 11可以明显看出,电流与磁场具有良好的线性关系,说明在磁屏蔽装置内,磁场模拟器产生的磁场依然具有良好的线性度,这与仿真得到的结论具有一致性。
3.3 均匀性验证实验 将螺线管线圈放入磁屏蔽装置内,通入I=50 mA的电流,以螺线管线圈轴线中心点为原点,沿着轴线方向,磁传感器向前移动距离为正,向后移动距离为负,每隔1 cm测量并记录磁场值,测量数据如表 3所示。
表 3 磁屏蔽装置内螺线管线圈轴向磁场均匀性实验数据 Table 3 Experimental uniformity data of axial magnetic field of solenoid coil in magnetic shielding device
| 距离/cm | 磁场/nT |
| -4 | 50 641 |
| -3 | 50 627 |
| -2 | 50 653 |
| -1 | 50 738 |
| 0 | 50 725 |
| 1 | 50 755 |
| 2 | 50 676 |
| 3 | 50 631 |
| 4 | 50 645 |
表选项
由表 3的数据可以看出,在电流I=50 mA的情况下,沿着轴线方向偏离中心点4 cm的范围内,磁场值变化最大为128 nT,以中心点的磁场值为基准,其相对误差最大为0.25%,说明在磁屏蔽装置内,磁场模拟器产生的磁场依然具有良好的均匀性,这与仿真得到的结论具有一致性。
3.4 实时性验证实验 由地磁学知识可知,中国地磁场的变化范围为41 000~60 000 nT[28],因此,对地磁场环境仿真系统实时性要求最高的情况就是磁场由41 000 nT变化至稳定的60 000 nT。这里,就以完成这一过程所需要的时间作为考察其实时性的指标。
在无磁屏蔽装置的情况下对螺线管线圈的输入输出关系进行标定,通过标定关系计算出其产生41 000 nT和60 000 nT需要的电流值分别为43.247 mA和63.259 mA。首先通入43.247 mA的电流,待产生的磁场值稳定后,将电流变为63.259 mA,直到产生的磁场值再次稳定,将这一过程的磁场值全部记录下来。测量过程中采用的磁传感器的采样频率为20 Hz,即每记录一个数据所用的时间为50 ms,因此可以根据磁场从稳定的41 000 nT变为稳定的60 000 nT这一过程中记录的过渡值的个数来确定系统的实时性。为避免单次实验的偶然性,重复实验20次,测得最小时间间隔为0.9 s,最大时间间隔为0.95 s,取其中的时间间隔最大值作为其响应时间,即0.95 s。
同理,将螺线管线圈放入磁屏蔽装置中,通过标定关系计算出其产生41 000 nT和60 000 nT需要的电流值分别为40.442 mA和59.189 mA。采用同样的方法,测得其响应时间为1.05 s。
对比2个实验结果可以看出,在有磁屏蔽装置的情况下,磁场模拟器的实时性有所下降,相比于无磁屏蔽装置的情况滞后了0.1 s,下降幅度为10.53%,这与仿真得到的结论具有一致性。
4 结论 针对地磁场环境仿真系统中磁屏蔽装置与其内部磁场模拟器的耦合问题,本文采用仿真分析与实验验证相结合的方法,利用Ansoft Maxwell仿真软件对二者的耦合关系进行了探索性研究,并基于小型地磁场环境仿真系统对仿真得到的结论进行了实验验证,得到如下重要结论:
1) 磁场模拟器产生的磁场会磁化磁屏蔽装置,尤其是在大电流强磁场的工作情况下,会使磁屏蔽装置的屏蔽性能下降,因此,在设计地磁场环境仿真系统时要配备必要的消磁设备,并在实际工作中对磁屏蔽装置进行定期消磁。
2) 磁屏蔽装置不会影响磁场模拟器的线性度和均匀性,但是会增大轴线中心点附近的磁场值。在设计地磁场环境仿真系统时,只需要单独考虑磁场模拟器的线性度和均匀性即可,从而减小系统的整体设计难度。
3) 磁屏蔽装置会使磁场模拟器的实时性变差,这是由于耦合使得电感增大所导致的。在进行磁场模拟器的实时性设计时,要在线圈的响应速度上留出足够的冗余量以弥补耦合带来的滞后影响。
地磁导航半实物仿真是地磁导航由理论走向工程应用的一个关键也是必经环节,而地磁场环境仿真技术是地磁导航由计算机仿真过渡到半实物仿真的“桥梁”,本文得出的研究结论可以为地磁场环境仿真系统的设计提供理论依据。
参考文献
| [1] | WEN Q Y, KOU Y M, XIA H W, et al. Advantages and drawbacks of applying vector decomposition to geomagnetic navigation systems[J].Control Engineering of China, 2011, 18(2): 223–227. |
| [2] | GOLDENBERG F. Geomagnetic navigation beyond the magnetic compass[C]//IEEE on Position, Location, and Navigation Symposium. Piscataway, NJ: IEEE Press, 2006: 684-694. |
| [3] | TYREN C. Magnetic anomalies as a reference for ground-speed and map-matching navigation[J].Journal of Navigation, 1982, 35(2): 242–254.DOI:10.1017/S0373463300022025 |
| [4] | 郭才发, 胡正东, 张士峰, 等. 地磁导航综述[J].宇航学报, 2009, 30(4): 1314–1319. GUO C F, HU Z D, ZHANG S F, et al. A survey of geomagnetic navigation[J].Journal of Astronautics, 2009, 30(4): 1314–1319.(in Chinese) |
| [5] | STORMS W F. Magnetic field aided indoor navigation[D]. Dayton: Air Force Institute of Technology, 2009: 67. |
| [6] | 周军, 葛致磊, 施桂国, 等. 地磁导航发展与关键技术[J].宇航学报, 2008, 29(5): 1467–1472. ZHOU J, GE Z L, SHI G G, et al. Key technique and development for geomagnetic navigation[J].Journal of Astronautics, 2008, 29(5): 1467–1472.(in Chinese) |
| [7] | 王仕成, 吕志峰, 张金生, 等. 基于半实物仿真的地磁导航等值线匹配算法评估[J].北京航空航天大学学报, 2015, 41(2): 187–192. WANG S C, Lü Z F, ZHANG J S, et al. Evaluation of ICCP algorithm for geomagnetic navigation based on hardware-in-the-loop simulation[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 187–192.(in Chinese) |
| [8] | 王恒霖, 曹建国. 仿真系统的设计与应用[M].北京: 科学出版社, 2003: 176-177. WANG H L, CAO J G. The design and application of the simulation system[M].Beijing: Science Press, 2003: 176-177.(in Chinese) |
| [9] | 吕志峰, 孙渊, 张金生, 等. 地磁匹配导航半实物仿真方案设计及关键技术分析[J].电光与控制, 2015, 22(2): 59–64. Lü Z F, SUN Y, ZHANG J S, et al. The design and key techno-logy analysis of hardware-in-the-loop simulation for geomagnetic matching navigation[J].Electronics Optics & Control, 2015, 22(2): 59–64.(in Chinese) |
| [10] | 孙渊, 王仕成, 张金生, 等. 地磁导航基准图三分量数学仿真方法研究[J].系统仿真学报, 2012, 24(5): 160–165. SUN Y, WANG S C, ZHANG J S, et al. Three-component mathematic simulation method for geomagnetic navigation reference map[J].Journal of System Simulation, 2012, 24(5): 160–165.(in Chinese) |
| [11] | 常宜峰, 种洋, 柴洪洲, 等. 世界地磁场模型精度评价[J].武汉大学学报(信息科学版), 2016, 41(10): 1398–1403. CHANG Y F, CHONG Y, CHAI H Z, et al. Evaluation of world magnetic model accuracy[J].Geomatics and Information Science of Wuhan University, 2016, 41(10): 1398–1403.(in Chinese) |
| [12] | PANG H F, ZHU X J, PAN M C, et al. The component compensation of geomagnetic field vector measurement system[J].Journal of Magnetism & Magnetic Materials, 2015, 381: 390–395. |
| [13] | PANG H F, ZHU X J, PAN M C, et al. Misalignment calibration of geomagnetic vector measurement system using parallelepiped frame rotation method[J].Journal of Magnetism & Magnetic Materials, 2016, 419: 309–316. |
| [14] | LI M M, LU H Q, YIN H, et al. Novel algorithm for geomagnetic navigation[J].Journal of Central South University, 2011, 18(3): 791–799.DOI:10.1007/s11771-011-0764-9 |
| [15] | 邓翠婷, 黄朝艳, 赵华, 等. 地磁匹配导航算法综述[J].科学技术与工程, 2012, 12(24): 6125–6131. DENG C T, HUANG C Y, ZHAO H, et al. Review of geomagnetic matching navigation algorithm[J].Science Technology and Engineering, 2012, 12(24): 6125–6131.DOI:10.3969/j.issn.1671-1815.2012.24.032(in Chinese) |
| [16] | 吕志峰, 张金生, 王仕成, 等. 高精度地磁场模拟系统的设计与研究[J].宇航学报, 2014, 35(11): 1284–1290. LV Z F, ZHANG J S, WANG S C, et al. Design and research of high-accuracy geomagnetic field intensity simulation system[J].Journal of Astronautics, 2014, 35(11): 1284–1290.DOI:10.3873/j.issn.1000-1328.2014.11.009(in Chinese) |
| [17] | BORK J, HAHLBOHM H D, KLEIN R, et al. The 8-layered magnetically shielded room of the PTB: Design and construction[C]//Proceedings of the 12th International Conference on Biomagnetism. Berlin: Springer-Verlag, 2000: 970-973. |
| [18] | 李立毅, 孙芝茵, 潘东华, 等. 近零磁环境装置现状综述[J].电工技术学报, 2015, 30(15): 136–140. LI L Y, SUN Z Y, PAN D H, et al. Status reviews for nearly zero magnetic field environment facility[J].Transactions of China Electrotechnical Society, 2015, 30(15): 136–140.DOI:10.3969/j.issn.1000-6753.2015.15.015(in Chinese) |
| [19] | 吕志峰, 贺浩, 张金生, 等. 仿真地磁的磁场模拟装置[J].电光与控制, 2014, 21(6): 76–80. Lü Z F, HE H, ZHANG J S, et al. The magnetic field generating device used for the simulation of magnetic field[J].Electronics Optics & Control, 2014, 21(6): 76–80.(in Chinese) |
| [20] | 李素敏, 张万清. 地磁场资源在匹配制导中的应用研究[J].制导与引信, 2004, 25(3): 19–21. LI S M, ZHANG W Q. Study on the application of geomagnetic field contour in matching guidance[J].Guidance and Fuze, 2004, 25(3): 19–21.(in Chinese) |
| [21] | 邓法金. 大学物理学[M].2版北京: 科学出版社, 2004: 525-529. DENG F J. College physics[M].2nd edBeijing: Science Press, 2004: 525-529.(in Chinese) |
| [22] | 赵万章, 吴琼, 刘江涛. 屏蔽效能的工程计算[J].长春工业大学学报(自然科学版), 2005, 26(4): 335–339. ZHAO W Z, WU Q, LIU J T. Engineering arithmetic of shielding efficiency[J].Journal of Changchun University of Technology(Natural Science Edition), 2005, 26(4): 335–339.(in Chinese) |
| [23] | 任士焱, 刘情新, 任琳. 径向干扰磁场下电流比较仪双层磁屏蔽效能[J].华中科技大学学报(自然科学版), 2014, 42(12): 6–9. REN S Y, LIU Q X, REN L. Double-layer magnetic shielding effectiveness of current comparator for radial direction magnetic interference[J].Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(12): 6–9.(in Chinese) |
| [24] | 刘坤, 张松勇, 顾伟. 方形亥姆霍兹线圈磁场系统均匀性分析[J].现代电子技术, 2012, 35(7): 190–194. LIU K, ZHANG S Y, GU W. Analysis on magnetic field homogeneity of magnetic system based on square Helmholtz coils[J].Modern Electronics Technique, 2012, 35(7): 190–194.(in Chinese) |
| [25] | 蔡欣华, 张金生, 樊宇韬, 等. 基于亥姆霍兹线圈理论的磁场模拟生成装置[J].计算机仿真, 2014, 31(7): 54–58. CAI X H, ZHANG J S, FAN Y T, et al. Magnetic field generating device based on Helmholtz coils'theory[J].Computer Simulation, 2014, 31(7): 54–58.(in Chinese) |
| [26] | 刘慧娟, 上官明珠, 张颖超, 等. Ansoft Maxwell 13电机电磁场实例分析[M].北京: 国防工业出版社, 2014: 158-163. LIU H J, SHANGGUAN M Z, ZHANG Y C, et al. Analysis of motor's electromagnetic field by Ansoft Maxwell 13[M].Beijing: National Defence Industry Press, 2014: 158-163.(in Chinese) |
| [27] | 单家元, 孟秀云, 丁艳. 半实物仿真[M].北京: 国防工业出版社, 2008: 236. SHAN J Y, MENG X Y, DING Y. Hardware in the loop simulation[M].Beijing: National Defence Industry Press, 2008: 236.(in Chinese) |
| [28] | 管志宁. 地磁场与磁力勘探[M].北京: 地质出版社, 2005: 7. GUAN Z N. Geomagnetic field and magntic exploration[M].Beijing: Geological Publishing House, 2005: 7.(in Chinese) |
