对于柔性机构，目前应用最广泛的为微定位平台^[1]，其结构形式有串联、并联、混联等，其中以并联微定位平台为主^[2-3]，广泛应用于原子力显微镜、扫描隧道显微镜以及超精机床微进给机构、航空航天等领域^[4-6]。
刚度影响机构的动态性能与精度，因此是评价并联微定位平台的重要指标。目前，并联微定位平台刚度的研究方法主要包括伪刚体模型法、柔度矩阵法、有限元法等。于靖军等^[7]利用柔度矩阵法建立了三自由度柔性微定位平台刚度，考虑了柔性铰链及长杆变形，将短杆视为刚体，利用坐标变换、位移协调以及力平衡进行求解。Liu等^[8]将宏动机构刚度分析理论应用于微动机构，分析了微动机构雅可比矩阵、刚度与机构参数关系以及运动空间等。孙立宁等^[9]通过刚度组集以及协调方程建立大行程柔性铰链的6-PSS并联机构的整体系统刚度，并分析得到刚度影响图谱。李育文等^[10]利用有限元软件分析微定位平台刚度，以此来检验理论分析的正确性。由以上研究可知，刚度建模过程中，求解繁琐，通用性不好，并且为方便计算，常将机构全部或部分视为刚体^[11-12]，因此影响精度。
本文以带折叠梁的大行程并联微定位平台为例，将各单元视为柔性体，建立各单元传递矩阵，根据各相邻单元公共结点的关系建立末端位移与输入力之间的刚度矩阵，将其计算结果与ANSYS分析结果进行对比，分析其误差产生的原因并考虑各子单元之间的界面关联特性，对本文方法进行了修正，误差在10%以内，证明了方法的精确性。
1 传递矩阵法 如图 1所示为任意梁单元受力图，由结点力及作用于p点的外载荷组成。定义状态向量如下：

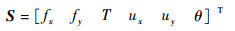(1)

图 1 梁单元结点力及外载作用 Fig. 1 Node force and external load of beam unit

图选项

式中：f_x、f_y和T分别为轴向力、剪力和弯矩；u_x、u_y和θ分别为其所对应的轴向位移、横向位移和转角。
左结点i与右结点j的传递关系为

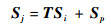(2)

式中：T_(6×6)为梁单元由左结点i到右结点j的传递矩阵；S_p(6×1)为外载荷的状态向量。T及S_p由力平衡及虚功原理求得，文献[13-14]给出了求解过程及表达式。当无外载荷F_p时，S_p为零。
为方便计算，将式(2)写为

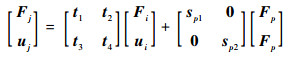(3)

式中：

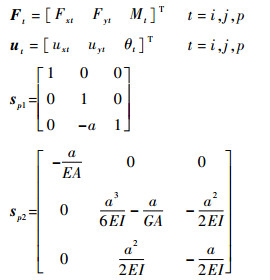其中:E为弹性模量; A为截面面积; G为剪切模量; I为惯性积。在局部坐标系下，传递矩阵传递方向为由左结点到右结点。当梁单元旋转角度α时，需要通过坐标变换得到参考坐标系下的传递矩阵。

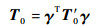(4)

式中：T₀为参考坐标系下的传递矩阵；T′₀为局部坐标系下的传递矩阵；，R为旋转矩阵，即

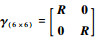
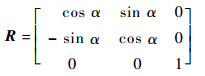为了求解机构的刚度，需根据机构结构将其划分单元，考虑各单元变形求解传递矩阵，根据相邻2个单元共享的同一结点可将各单元组合。对于并联机构各支链，还需利用变形协调方程求解末端位移。由于本文中公式较多，规定如t₁^hgf代表传递矩阵T_h、T_g、T_f相乘后所得到的分块矩阵的第1项，以及各子单元的旋转变换不再赘述。
2 大行程并联微定位平台刚度 2.1 机构描述 本文设计了一个大行程并联微定位平台，如图 2所示，该平台由2条支链构成，关于动平台对角线对称。由压电陶瓷分别驱动A点及C点。每条支链包括含折叠梁的杠杆放大机构及平行四杆机构，依据螺旋理论，每条支链中具有实际约束效果的部分只有折叠梁和平行四杆机构，其中杠杆放大机构的作用是增大折叠梁的实际驱动行程，因此基于其对应的伪刚体模型，动平台的主运动特征为沿x方向和y方向的平移。

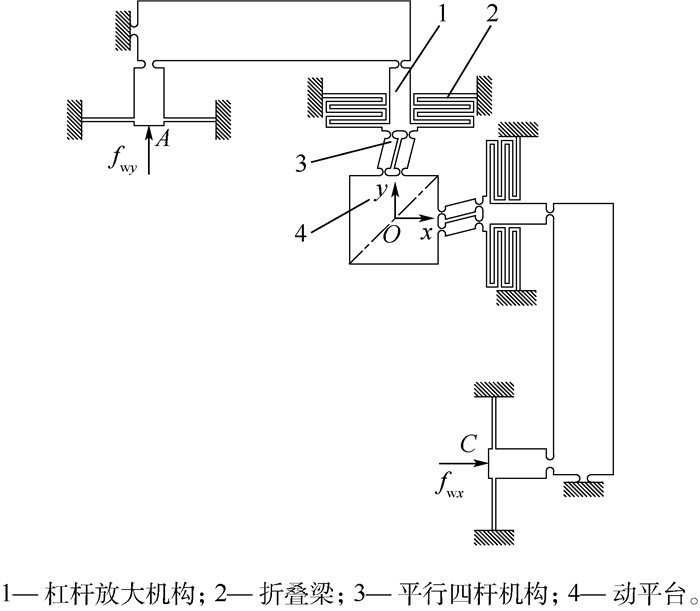图 2 大行程并联微定位平台 Fig. 2 Large stroke parallel micro-positioning platform

图选项

2.2 子单元刚度 根据结构将大行程并联微定位平台进行单元划分，其中包括直梁、柔性铰链、弹性移动副及弹性折叠梁，直梁及柔性铰链为基本的单元类型，其传递矩阵的表达式参见文献[14]。

2.2.1 弹性移动副 现有的弹性移动副刚度的求解将中间单元视为刚体，利用悬臂梁理论求解^[15]。本文将弹性移动副视为全柔性求解，将其根据结构划分如图 3所示的4个单元。

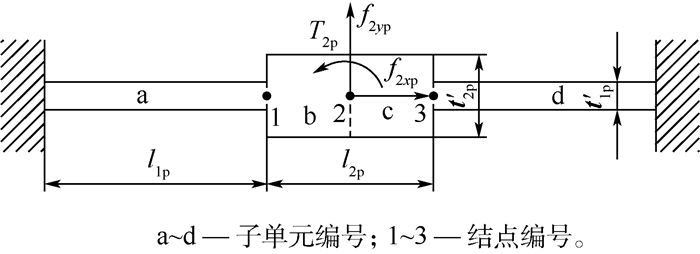图 3 弹性移动副单元划分 Fig. 3 Compliant prismatic pair unit division

图选项

单元a为悬臂梁，因此：

(5)

式中：k_lp为悬臂梁的刚度。
单元b的传递矩阵关系如下：

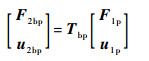(6)

由式(5)、式(6)可以得到

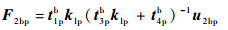(7)

单元c和d分别与单元a和b为对称关系，因此：

(8)

式中：

外力F_2p作用于点2，由力平衡和位移连续性可以得到各单元结点力与外力F_2p的关系：

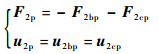(9)

由式(7)~式(9)可以计算出弹性移动副刚度为

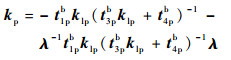(10)

2.2.2 弹性折叠梁 弹性折叠梁的结构如图 4所示，根据其结构形式将其划分为A~D共4个单元。

图 4 弹性折叠梁单元划分 Fig. 4 Compliant folded beam unit division

图选项

对于弹性折叠梁的单元A，根据结构划分为a~m共9个单元，如图 5所示。

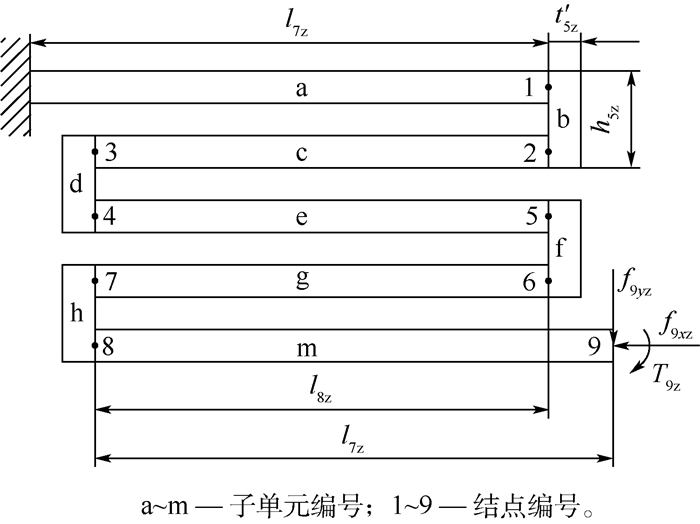图 5 弹性折叠梁单元A划分 Fig. 5 Compliant folded beam unit A division

图选项

单元a~m为串联结构，其各单元的传递矩阵如下：

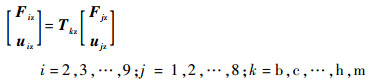(11)

相邻单元共用的结点力为作用力与反作用力，位移连续。因此：

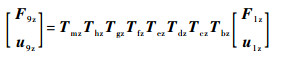(12)

单元a为悬臂梁，因此：

(13)

式中：k_lz为悬臂梁的刚度。
联立式(11)~式(13)，弹性折叠梁中单元A的刚度为

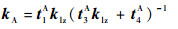(14)

式中：。
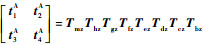
其余同弹性移动副刚度解法，因此弹性折叠梁的刚度为

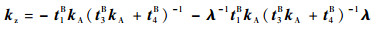(15)

2.3 大行程并联微定位平台刚度求解
2.3.1 杠杆放大机构 根据结构将杠杆放大机构划分为如图 6所示的a~h共8个单元。

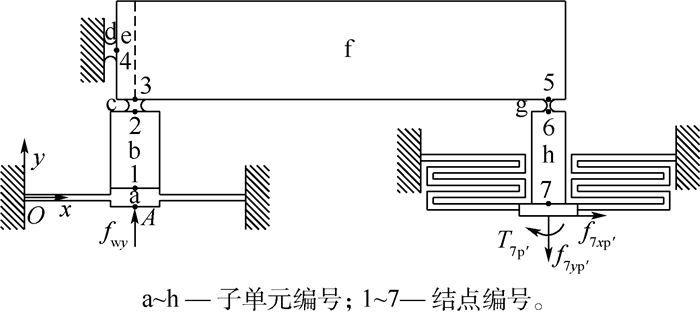图 6 柔性杠杆放大机构单元划分 Fig. 6 Flexible lever magnifying mechanism unit division

图选项

F_7p′为平行四杆机构对其产生的作用力。结点7为杠杆放大机构、平行四杆机构以及折叠梁的结合处，因此在下文的求解过程中，将结点7处的力与位移的命名与其单元相联系，如F_7h表示在单元h上结点7的力。
各子单元传递矩阵关系如下：

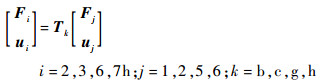(16)

根据传递矩阵传递性可得

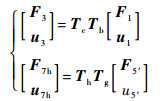(17)

单元f的受力分析如图 7所示, 结点3作用一外载荷F_3′。

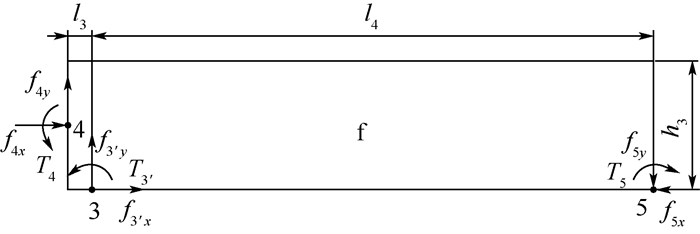图 7 单元f受力分析 Fig. 7 Force analysis of unit f

图选项

因此，单元f的传递矩阵关系为

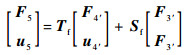(18)

单元f弯矩不可忽略。因此，单元f的传递矩阵中t₁^f由力平衡可得

(19)

式中：

单元d为一端固定的柔性铰链单元，因此：

(20)

式中：k_r4为该单元在结点4处的刚度。
由于结点位移的连续性，结点4的位移可以通过结点3与结点4之间的直梁单元e由式(3)求得

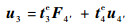(21)

对于单元a，由力平衡可以得到

(22)

式中：F_y为压电陶瓷作用于单元a的外力，可以写成矩阵形式[0 f_wy 0]^T；k_1p为弹性移动副单元a的刚度。
由式(17)~式(22)可以得到

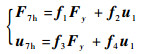(23)

式中：


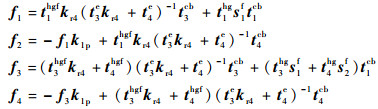2.3.2 平行四杆机构 平行四杆机构结构如图 8所示，根据其结构特点将其划分为p₁~p₈共8个单元。

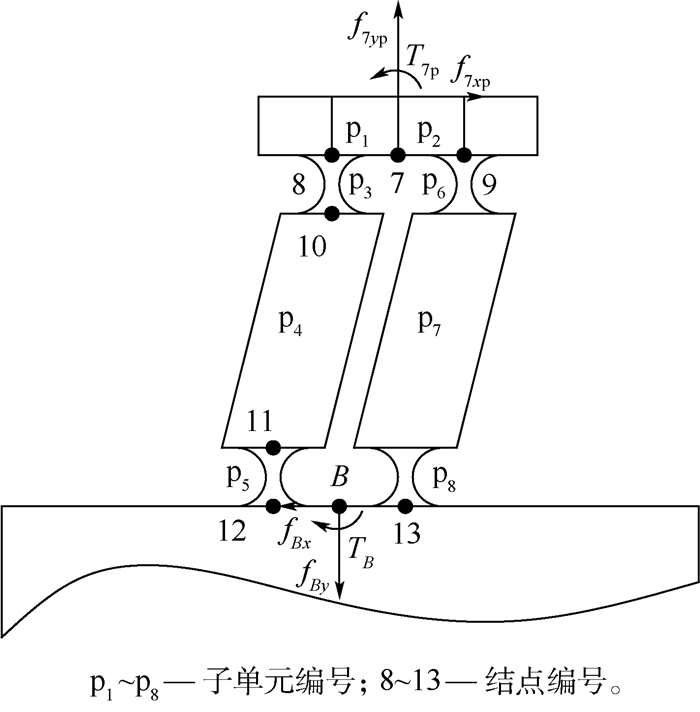图 8 柔性平行四杆机构单元划分 Fig. 8 Flexible parallel four-bar mechanism unit division

图选项

平行四杆机构中各子单元传递矩阵关系如下：

(24)

对于支链p₁/p₃/p₄/p₅，可以得到以下关系：

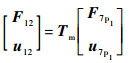(25)

式中：T_m=T_p5T_p4T_p3T_p1。
支链p₂/p₆/p₇/p₈与支链p₁/p₃/p₄/p₅相似，因此：

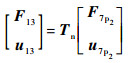(6)

式中：T_n=T_p8T_p7T_p6T_p2。
杠杆放大机构对平行四杆机构产生作用力F_7p，对于结点7，由力平衡可得

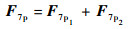(27)

由于动平台相比于其他单元结构尺寸大，可将其视为刚体，则B点力与位移平衡协调。

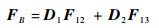(28)

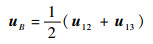(29)

式中：

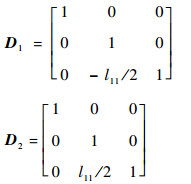当动平台为刚体时，与平台相连接的柔性铰链转动角度相等，即θ₁₂=θ₁₃。由于其旋转角度微小，因此：

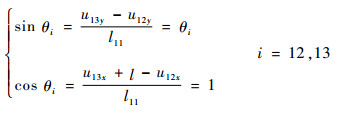(30)

由式(30)得到结点13与结点12位移之间的关系：

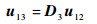(31)

式中：

由式(25)~式(29)、式(31)得

(32)

式中：t₁^p=f₅f₇^-1；t₂^p=f₅f₇^-1f₈-f₆；t₃^p=f₇^-1；t₄^p=f₇^-1f₈；f₅=2D₁t₁^m(t₃^m)^-1(D₃+E)^-1+2D₂t₁ⁿ(t₃ⁿ)^-1·(D₃^-1+E)^-1；f₆=D₁t₁^m(t₃^m)^-1t₄^m+D₂t₁ⁿ(t₃ⁿ)^-1t₄ⁿ；f₇=2(t₃^m)^-1(D₃+E)^-1+2(t₃ⁿ)^-1(D₃^-1+E)^-1；f₈=(t₃^m)^-1t₄^m+(t₃ⁿ)^-1t₄ⁿ。

2.3.3 计算整体刚度 结点7同时受到弹性折叠梁、杠杆放大机构、平行四杆机构的作用力，因此由力平衡可以得到

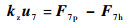(33)

由式(23)、式(32)、式(33)得

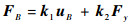(34)

式中：k₁=f₁₂f₁₀^-1; k₂=f₁₁-f₁₂f₁₀^-1f₉；f₉=(t₃^pk_z+t₄^p)·f₃+t₃^pf₁；f₁₀=(t₃^pk_z+t₄^p)f₄+t₃^pf₂；f₁₁=(t₁^pk_z+t₂^p)·f₃+t₁^pf₁；f₁₂=(t₁^pk_z+t₂^p)f₄+t₁^pf₂。
水平支链与竖直支链关于动平台对角线对称，因此进行坐标变换即可得到竖直支链末端力。

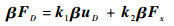(35)

式中：F_x为[f_wx 0 0]^T; β为坐标变换矩阵，即

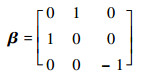2条支链对动平台作用力及运动示意图如图 9所示，由动平台力平衡得

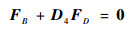(36)

图 9 动平台作用力及运动示意图 Fig. 9 Moving platform force and motion diagram

图选项

式中：

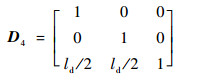由图 9可以计算出动平台旋转角度θ_d时：

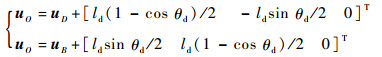(37)

θ_d值接近零，因此sin θ_d≈θ_d；cos θ_d≈1。式(37)可简化为

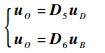(38)

式中：

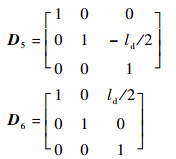为方便计算，将平台所受到的x方向与y方向输入力转换为外力矢F=[F_x F_y 0]^T。

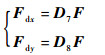(39)

式中：

联合式(34)~式(39)，即可得到输入力与输出位移之间的关系:

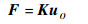(40)

式中：

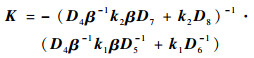3 算例分析 3.1 传递矩阵法与有限元法结果对比 分析比较本文方法与有限元分析之间的误差。运用ANSYS14.0建立大行程并联微定位平台模型进行刚度研究，单元类型选择三维20结点实体单元Solid95，设定柔性杠杆放大机构的材料为60Si2Mn，基本材料参数为：E=206 GPa；μ=0.27；G=79 GPa。
大行程并联微定位平台模型参数如图 10所示，取其结构参数为：厚度b=8 mm, l₁=14 mm, t′₁=1 mm, l₂=8 mm, h₁=15.5 mm, R₁=1 mm, h₂=13.5 mm, t′₂=2 mm, R₂=1 mm, t′₃=2 mm, l₃=3 mm, l₄=67.25 mm, l₅=73 mm, h₃=16 mm, R₃=1 mm, t′₄=0.5 mm, l₆=5.5 mm, h₄=15 mm, l₇=16 mm, l₈=14 mm, t′₅=1 mm, h₅=3 mm, l₉=9.5 mm, h₆=2 mm, t′₆=0.5 mm, l₁₀=8.25 mm, h₇=3.4 mm, R₄=1 mm, l₁₁=4.5 mm, θ=76°，l_d=23.75 mm。

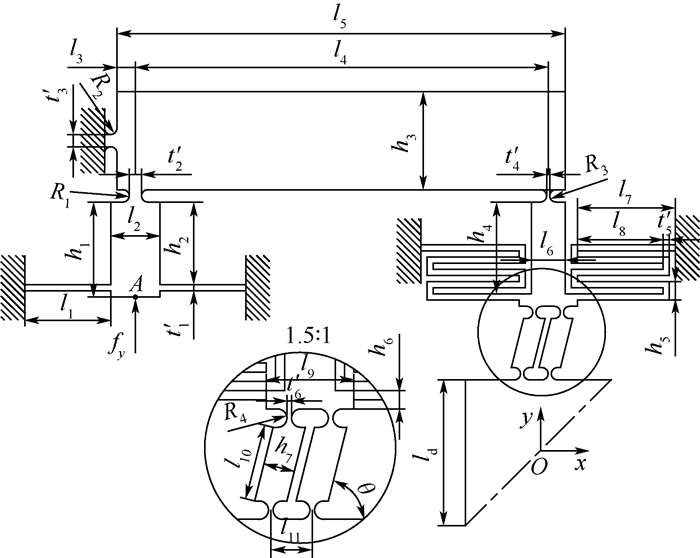图 10 大行程并联微定位平台参数模型 Fig. 10 Large stroke parallel micro-positioning platform parameter model

图选项

图 11为大行程并联微定位平台有限元模型变形云图。其分析过程为：分别约束2条支链的弹性移动副两端、弹性折叠梁两端，以及柔性铰链连接底座的一端。如图 2所示，在C点处施加f_wx，在A点处施加f_wy。在分析过程中，令f_wx=100 N，f_wy为变量。求解后提取动平台中心点的位移量将其与本文求解结果对比，如表 1所示。

图 11 大行程并联微定位平台有限元模型 Fig. 11 Finite element model of large stroke parallel micro-positioning platform

图选项

表 1 传递矩阵法与有限元分析值对比 Table 1 Comparison between transfer matrix method and finite element analysis

fwy/N	0	50	100	150	200
ux有限元法/μm	-2.030 63	1.556 45	5.143 53	8.730 61	12.317 70
ux修正前/μm	-2.094 30	1.308 69	4.711 68	8.114 66	9.816 16
ux修正后/μm	-2.013 07	1.410 88	4.834 82	8.258 77	11.682 70
ux修正前误差/%	3.135	15.918	8.396	7.055	20.309
ux修正后误差/%	0.865	9.353	6.002	5.404	5.155
uy有限元法/μm	7.184 39	6.170 25	5.156 11	4.141 96	3.127 82
uy修正前/μm	6.805 97	5.758 83	4.711 68	4.188 10	3.140 65
uy修正后/μm	6.847 90	5.841 36	4.834 82	3.828 29	2.821 75
uy修正前误差/%	5.267	6.668	8.619	1.114	0.410
uy修正后误差/%	4.684	5.330	6.231	7.573	9.785

表选项






由表 1中修正前误差数据可以看出，传递矩阵法与有限元分析值误差在20.5%以内，其误差产生的原因为：传递矩阵法基于梁理论，在计算过程中是建立在一定假设条件下，如忽略轴向变形等；将微定位平台划分子单元求解，忽略了单元之间的联系及单元之间的接触变形。
3.2 考虑界面关联特性的修正方法 根据传递矩阵法误差产生的原因提出考虑单元之间联系性的修正方法。以单元a与单元b求解过程为例。单元a、b结构图如图 12所示。

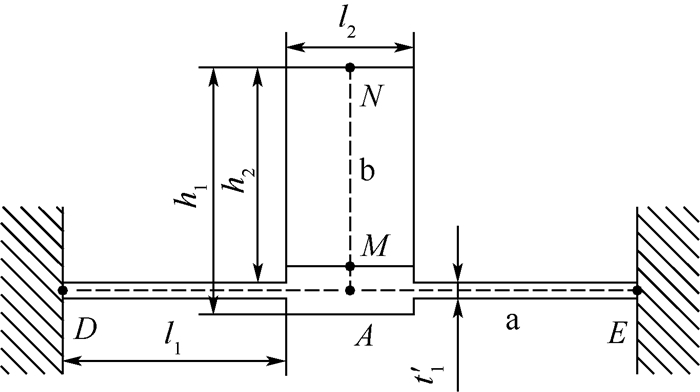图 12 单元a、b结构图 Fig. 12 Unit a, b structure chart

图选项

单元a、b在求解过程中将其简化为梁单元，单元a为变截面横向梁单元DE，最终求解的为结点A的刚度。单元b为竖向梁单元MN，其2个结点之间的传递矩阵关系如式(41)所示。在以上求解过程中，视结点M与结点A力为作用力与反作用力位移连续。而实际中结点M与结点A不重合，忽略了结点M与结点A之间的关系。而结点M与结点A之间的关系可由竖向梁单元MA求解(见式(42))。

(41)

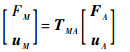(42)

因此，结点N与结点A之间的传递矩阵关系为

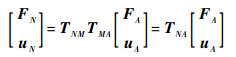(43)

所以为求解精确，在求解单元b传递矩阵时，单元b的长度由MN修正为NA。
利用此方法考虑各相邻单元之间的联系对大行程并联微定位平台弹性折叠梁及单元h的长度进行修正。其计算结果如表 1中修正后误差数据所示，传递矩阵法修正后的结果与有限元分析值误差在10%以内，精度得到提高，证明了此修正方法的有效性。
4 结论 1) 本文设计了一种压电陶瓷驱动的大行程并联微定位平台，采用含折叠梁的杠杆放大机构，提高其位移输出倍率，减少传动链的阻力，实现大行程位移输出。
2) 利用传递矩阵法求解并联微定位平台，将平台按结构划分单元，分别求解各单元传递矩阵，根据各相邻单元公共结点实现其传递性；再由变形协调方程、力平衡方程求解整体刚度；并求解了弹性移动副及弹性折叠梁考虑全柔性的刚度公式。
3) 将本文求解结果与有限元分析结果对比，误差在20.5%以内，分析其误差产生的原因并提出了考虑各子单元界面关联特性的修正方法，修正后误差降低到10%以内，证明了修正方法的有效性和传递矩阵的准确性。

参考文献

[1]	于靖军, 郝广波, 陈贵敏, 等. 柔性机构及其应用研究进[J].机械工程学报, 2015, 51(13): 53–68. YU J J, HAO G B, CHEN G M, et al. State-of-art of compliant mechanisms and their applications[J].Chinese Journal of Mechanical Engineering, 2015, 51(13): 53–68.(in Chinese)
[2]	杨启志, 郭宗和, 马履中, 等. 全柔性机构在并联微动机器人中的应用[J].机械设计与研究, 2005, 21(5): 45–48. YANG Q Z, GUO Z H, MA L Z, et al. Application of the fullly compliant mechanism in the parallel micro-motion robots[J].Machine Design and Research, 2005, 21(5): 45–48.(in Chinese)
[3]	HAO G B, KONG X W. A novel large-range XY compliant parallel manipulator with enhanced out-of-plane stiffness[J].Journal of Mechanical Design, 2012, 134(6): 061009.DOI:10.1115/1.4006653
[4]	艾青林, 黄伟锋, 张洪涛. 并联机器人刚度与静力学研究现状与进展[J].力学进展, 2012, 42(5): 583–592. AI Q L, HUANG W F, ZHANG H T. Review of stiffness and statics analysis of parallel robot[J].Advances in Mechanics, 2012, 42(5): 583–592.DOI:10.6052/1000-0992-11-073(in Chinese)
[5]	STANFORD B, BERAN P. Conceptual design of compliant mechanisms for flapping wing with topology optimization[J].AIAA Journal, 2011, 49(4): 855–867.DOI:10.2514/1.J050940
[6]	WISSA A, TUMMALA Y, HUBBARD J E, et al. Passively morphing ornithopter wings using a novel compliant spine:Design and testing[J].Smart Materials and Structures, 2012, 21(9): 094028.DOI:10.1088/0964-1726/21/9/094028
[7]	于靖军, 毕树生, 宗光华. 空间全柔性机构位置分析的刚度矩阵法[J].北京航空航天大学学报, 2002, 28(3): 323–326. YU J J, BI S S, ZONG G H. Stiffness matrix method for displacement analysis of fully spatial compliant mechanisms[J].Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(3): 323–326.(in Chinese)
[8]	LIU X J, WANG J, GAO F, et al. On the design of 6-DOF parallel micro-motion manipulators[C]//Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway: IEEE Press, 2001: 343-348.
[9]	孙立宁, 董为, 杜志江. 基于大行程柔性铰链的并联机器人刚度分析[J].机械工程学报, 2005, 41(8): 90–95. SUN L N, DONG W, DU Z J. Stiffness analysis on a wide-range flexure hinge-based parallel manipulator[J].Chinese Journal of Mechanical Engineering, 2005, 41(8): 90–95.(in Chinese)
[10]	李育文, 张华, 杨建新, 等. 6-UPS并联机床静刚度的有限元分析和实验研究[J].中国机械工程, 2004, 15(2): 112–115. LI Y W, ZHANG H, YANG J X, et al. Finite element analysis and experimental study for the stiffness of a 6-UPS parallel kinematics machine[J].China Mechanical Engineering, 2004, 15(2): 112–115.(in Chinese)
[11]	YU Y Q, FENG Z L, XU Q P. A pseudo-rigid-body 2R model of flexural beam in compliant mechanisms[J].Mechanism and Machine Theory, 2012, 55(9): 19–33.
[12]	邱丽芳, 霍明磊, 李威. 六杆柔顺机构的伪刚体模型[J].北京科技大学学报, 2013, 35(5): 682–686. QIU L F, HUO M L, LI W. Pseudo-rigid-body model of a six-bar full-compliant mechanism[J].Journal of University of Science and Technology Beijing, 2013, 35(5): 682–686.(in Chinese)
[13]	李青宁. 变截面杆元传递矩阵法[J].西安建筑科技大学学报, 2001, 33(1): 18–23. LI Q N. The transfer matrix method of bar elements with variable cross-section[J].Journal of Xi'an University of Architecture & Technology, 2001, 33(1): 18–23.(in Chinese)
[14]	郑洋洋, 宫金良, 张彦斐. 基于传递矩阵法的柔性杠杆放大机构刚度分析[J].北京航空航天大学学报, 2017, 43(4): 849–856. ZHENG Y Y, GONG J L, ZHANG Y F. Rigidity analysis of a flexible lever magnifying mechanism based on transfer matrix method[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 849–856.(in Chinese)
[15]	杨春辉. 平行板型柔性移动副的刚度计算及分析[J].现代制造工程, 2013(12): 30–33. YANG C H. The stiffness design calculation and analysis of parallel plate flexible prismatic pair[J].Modern Manufacturing Engineering, 2013(12): 30–33.(in Chinese)