目前,边界层抽吸在进气道内的实际应用较为广泛,而射流技术的运用研究也已有初步成果,如Gorton[7]、Allan[8]等利用主动射流对进气道边界层进行控制,但主要针对低马赫数来流;van Wie等[9]进行了通过主动射流实现进气道再起动的实验,但对起动机理并未深入,其后续工作也未见报道;冯喜平等[10]利用射流技术改善了高超声速进气道的前体波系结构,提高了进气道在起动状态的气动性能;方传波等[11]依靠主动射流技术提高了超声速进气道唇口前马赫数,实现了进气道在迟滞区的再起动,并研究了射流流量、速度、总温对起动性能的影响。
基于上述研究成果,本文总结经验,对所选的二元高超声速进气道在自不起动状态进行数值模拟,研究了进气道在引入射流前后的流场结构,分析了射流技术降低起动马赫数的机理,并对射流速度、压强及倾角对起动能力的影响规律进行讨论,得到了上述参数对进气道起动影响的系统性结论,为进气道设计及优化提供可供参考的经验。
1 数值模拟方法 采用三维雷诺时均Navier-Stokes方程作为流动控制方程。在一般曲线坐标系下,守恒形式的方程组可以表示为
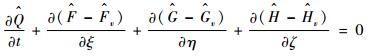 |
式中:
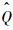
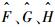

流动控制方程采用有限体积法进行计算,无黏通量的空间离散采用Roe格式,使用minmod限制器;黏性项采用二阶中心格式进行离散;时间推进采用LU-SGS隐式方法,湍流模型采用Menter SST两方程模型。
2 计算模型与网格 物理模型为文献[12]中的进气道试验模型,图 1为本文采用的简化模型,展向长为30 mm,射流出口距前端155 mm,射流截面宽度为0.809 mm,与壁面夹角为θj,如图 1中圆圈所示。计算网格采用结构网格,保证网格之间的过渡,除对法向网格进行加密外,并对重点关注区域进行适当加密,总网格量约为280万,对称面网格如图 2所示。
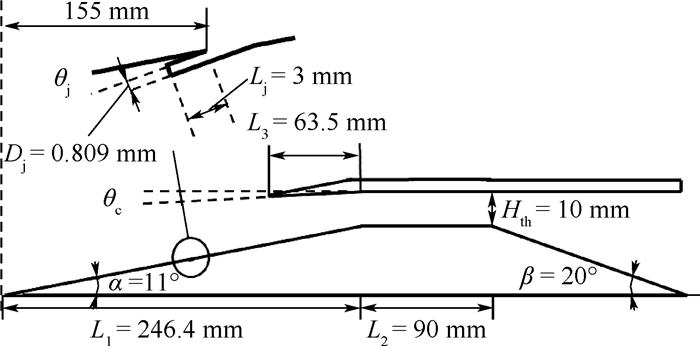 |
| Dj—射流截面宽度;Lj—射流缝深;L1—压缩段长度;L2—隔离段长度;L3—内缩段长度;α—压缩面倾角;β—扩张段倾角;Hth—隔离段高度; θc—唇口壁面倾角。 图 1 模型示意图 Fig. 1 Sketch map of model |
| 图选项 |
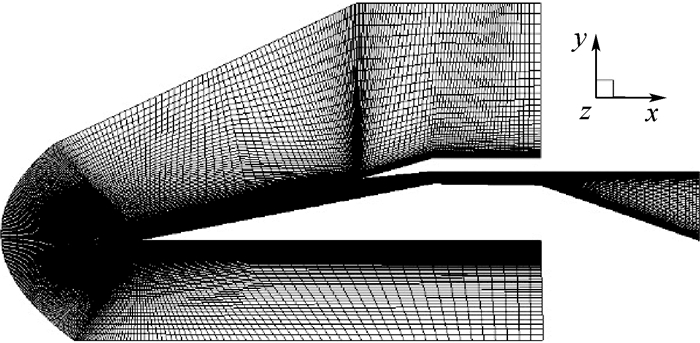 |
| 图 2 进气道计算网格 Fig. 2 Grids for calculation of inlet |
| 图选项 |
3 计算方法准确性验证 本文采用与文献[13]相同的MI-CFD计算平台,图 3为其对球头逆向喷流的计算结果(射流总压比K=0.8),流场结构与实验结果基本一致,验证了程序的可靠性。为评估程序对进气道计算结果的精确性,对θc=3°、6° 2个外型进行计算并同实验对比。计算条件选用文献[12]的试验条件:来流马赫数Ma∞=4.03,静温T∞=216.6 K,静压P∞=8 728.8 Pa。计算与实验的壁面压强分布如图 4所示,P为壁面压力,x为沿程长度。同实验值相比,计算结果的压强峰值偏小,但对激波与膨胀波之间相交和反射现象的捕捉较为准确,能够较好反映出进气道内流场的主要特征。
 |
| 图 3 实验纹影图与CFD等密度线图对比[13] Fig. 3 Experimental schlieren photographs versus CFD density contours[13] |
| 图选项 |
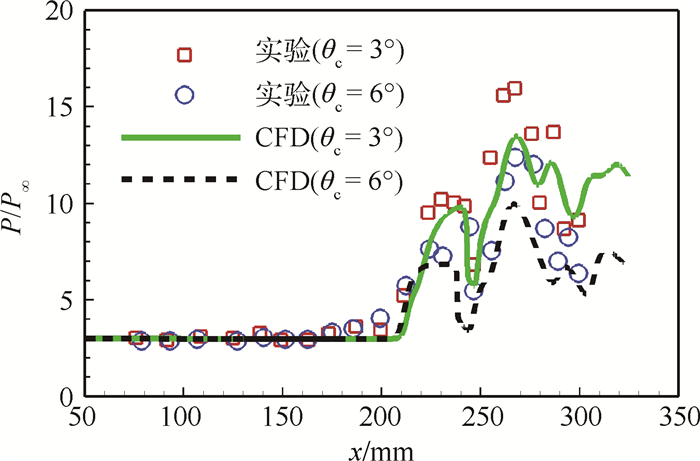 |
| 图 4 壁面压强分布 Fig. 4 Wall pressure distribution |
| 图选项 |
4 计算结果及分析 保持来流压强及温度不变,降低来流马赫数模拟进气道(θc=3°)“起动—不起动”过程,通过数值计算,本文确定的不起动区间为Ma∞=3.30~3.28,如图 5所示。表 1给出了进气道喉道位置的总压恢复系数和流量系数,在进气道起动前后,两者之间存在巨大差异。
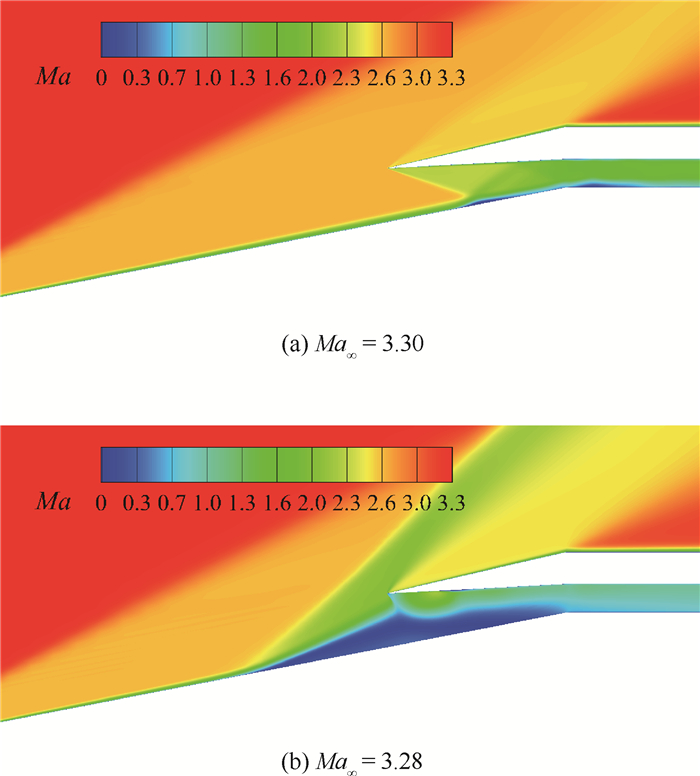 |
| 图 5 马赫数分布 Fig. 5 Mach number distribution |
| 图选项 |
表 1 不同马赫数下的总压恢复系数及流量系数 Table 1 Total pressure recovery coefficient and mass-captured coefficient under different Mach numbers
| 工况 | 总压恢复系数/% | 流量系数/% |
| Ma∞=3.30 | 69.00 | 53.69 |
| Ma∞=3.28 | 27.62 | 26.65 |
| Ma∞=3.20 | 28.28 | 24.80 |
表选项
研究者们对进气道不起动机理进行了长期探索,结果表明进气道不起动的原因可能有以下3个方面[14-15]:来流马赫数过低、隔离段反压过大、喉道壅塞。图 6(a)给出了Ma∞=3.30状态的等马赫线图,可以看到进气道内存在由激波/边界层干扰形成的低速区;随着马赫数下降,激波与边界层的干扰作用增强,过肩点膨胀后,喉道后侧的分离包增大,分离包与壁面形成的虚拟喉道使进气道的内缩比降低,气流在喉道处产生堵塞,致使当地压强升高,声速线向外扩张,分离区扩大,并向前移动,流场结构可对比图 6(b)(Ma∞=3.295)的等马赫线图。
 |
| 图 6 不同马赫数下的流场结构 Fig. 6 Flow field structure with different Mach numbers |
| 图选项 |
基于对上述流场结构的分析,本文认为喉道附近的分离包是影响进气道起动能力的重要因素,分离包的持续发展将导致不起动现象,抑制或改变干扰区的存在形式为提高进气道起动能力提供了途径。本文以主动射流作为流动控制手段,选取Ma∞=3.20的不起动状态为研究对象,对施加射流前后的进气道流场进行数值模拟,以验证所提方案的有效性,Ma∞=3.20的总压恢复系数及流量系数可参见表 1。
4.1 射流速度对于起动性能的影响 射流条件通过给定的出口速度、压强以及温度并结合气体方程确定,射流条件如下:θj=9°,Pj=40 kPa,Tj=580 K(与无射流工况相同位置的气体参数近似相同),射流速度分别取为Vjet=3.5ain,4.0ain,4.5ain,5.5ain ,6.5ain ,7.0ain (ain为来流声速),以验证方案的可行性并对比不同速度对进气道起动性能的影响。图 7给出了各工况的起动情况,随着射流速度增大,进气道由不起动转为起动状态,下壁面局部低速区逐渐变小,并且总压恢复系数明显上升,总压恢复系数参见图 8;当Vjet < 4.0ain时,进气道仍为不起动状态,但由于射流影响,前体分离泡明显变小,相比于无射流状态,总压恢复系数上升约50%,流量系数增大约25%。
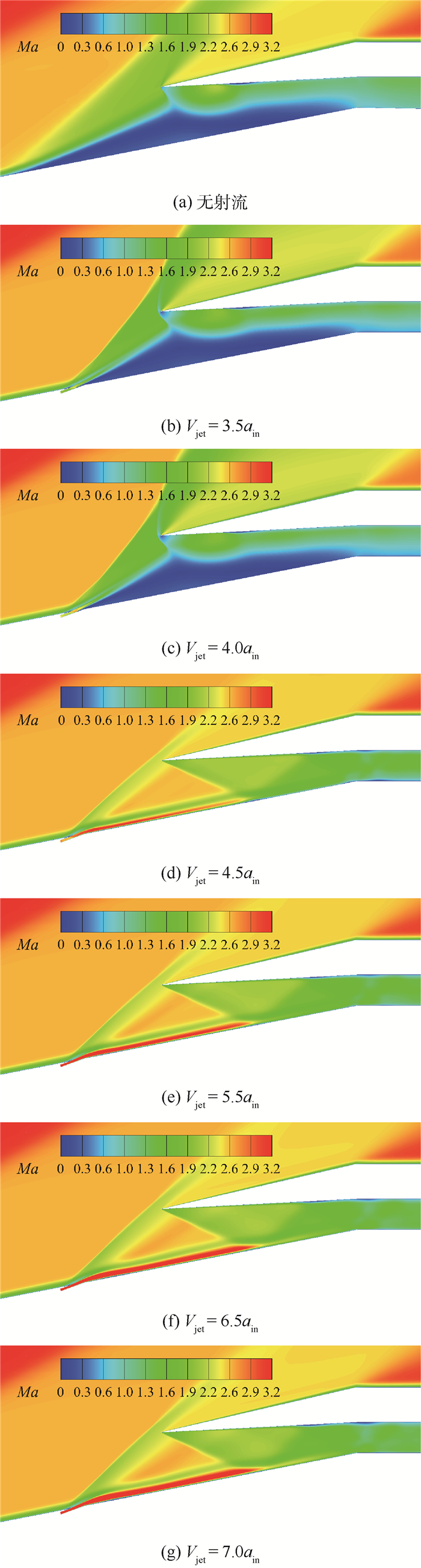 |
| 图 7 不同射流速度下的马赫数分布 Fig. 7 Mach number distribution at different jet velocities |
| 图选项 |
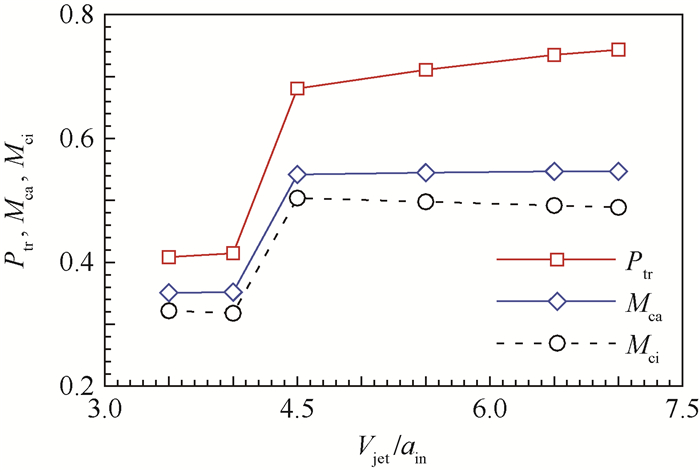 |
| 图 8 总压恢复系数及流量系数随射流速度变化 Fig. 8 Variation of total pressure recovery coefficient and mass-captured coefficient with jet velocity |
| 图选项 |
施加射流后,进气道内流动可分为3个部分:主流、射流及两者间的剪切层,由于马赫数不同,唇口入射激波在主流、射流层以及剪切层的倾角并不一致。少量的高速射流在小倾角下进入主流,流动方向很快改变,附着于进气道壁面,唇口入射激波与高马赫数的射流边界层干扰,作用点后移,同时抑制了局部低速区的形成,这是进气道起动的主要原因。增大射流速度,实际上增加了输入边界层的动量,利于进气道起动;但随着射流流量增大,进气道壁面内的边界层变厚,入口用以捕获来流的有效面积减少,进气道内实际捕获流量略有下降。流量系数随射流速度的变化规律可参见图 8,Ptr为总压恢复系数,Mca为全部流量系数,Mci为实际流量系数(不含射流)。
4.2 射流压强对于起动性能的影响 为研究射流压强对进气道起动性能的影响,共选择Pj1=0.92P∞、Pj2=1.83P∞、Pj3=2.29P∞、Pj4=3.44P∞、Pj5=4.58P∞、Pj6=5.73P∞、Pj7=6.87P∞、Pj8=9.17P∞、Pj9=11.46P∞ 9个压强,对各压强选取不同射流速度进行计算(θj=9°),得到进气道起动状况如表 2所示,st为起动,un为不起动。
表 2 不同射流压强及速度的起动特性 Table 2 Starting characteristics under different jet pressure and velocities
| 射流压强 | Vjet/ain | ||||||||||
| 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 8.0 | |
| Pj1 | un | st | |||||||||
| Pj2 | un | st | st | st | |||||||
| Pj3 | un | st | st | ||||||||
| Pj4 | un | st | st | st | |||||||
| Pj5 | un | un | st | st | st | st | |||||
| Pj6 | un | un | st | st | st | st | |||||
| Pj7 | un | st | st | st | st | st | un | ||||
| Pj8 | un | st | un | un | |||||||
| Pj9 | un | un | un | un | |||||||
表选项
从表 2中可以看出:①不同压强下,进气道起动情况随射流速度变化趋势具有一致性;②随射流压强下降,能使进气道起动的最小射流速度随之降低,控制效果提高,射流速度的有效区间增大;③压强一定时,随射流速度增大,进气道易于起动,与4.1节的结论一致,但持续增大射流速度,进气道会再次出现不起动现象。
图 9对比了壁面压强P在不同射流速度下的分布,其中射流压强为Pj7,内缩段的壁面压强在不同射流速度下分布一致,但随着射流速度增加,隔离段压强增大,激波前移,因此继续增加射流速度将使激波串被压出隔离段,形成不起动现象。不同射流压强下的壁面压强分布在图 10中给出,其中Vjet=4.5ain,可以看出增大射流压强同样会使隔离段的出口压强增加,为避免因隔离段反压过大而出现不起动现象,可用于调节边界层的最大射流速度降低,缩小了射流速度的有效区间。
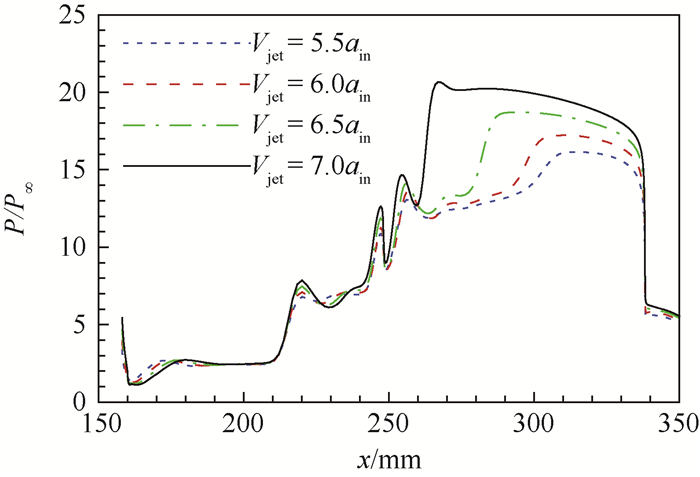 |
| 图 9 不同射流速度下的壁面压强分布 Fig. 9 Distribution of wall pressure at different jet velocities |
| 图选项 |
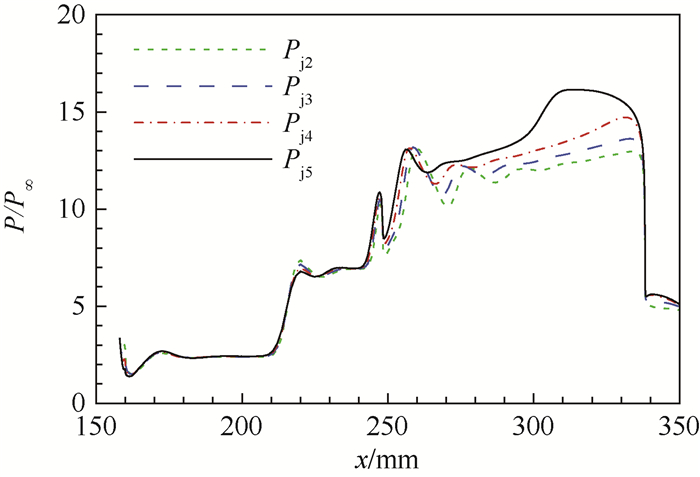 |
| 图 10 不同射流压强下的壁面压强分布 Fig. 10 Distribution of wall pressure under different jet pressure |
| 图选项 |
图 11及图 12分别给出了流量系数及总压恢复系数在不同射流压强下的变化规律,总压恢复系数及流量系数均随射流压强升高而下降;相对于射流速度,流量系数随射流压强变化更为明显;在压强Pj8及Pj9下,不起动状态的流量系数下降显著,与无射流状态相当。
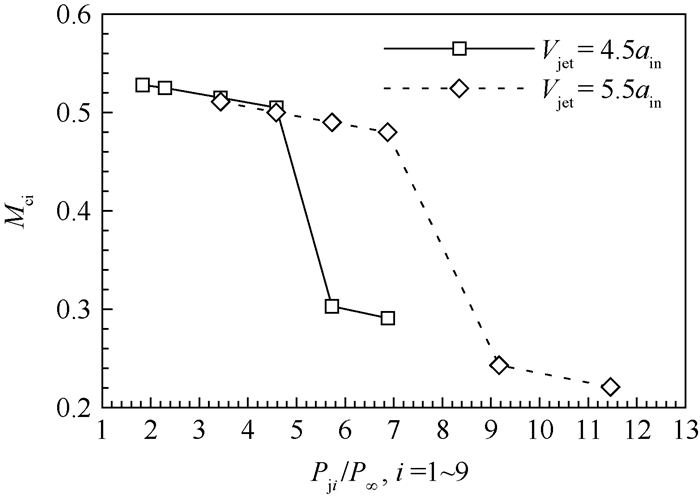 |
| 图 11 不同射流压强下的流量系数 Fig. 11 Mass-captured coefficient under different jet pressure |
| 图选项 |
 |
| 图 12 不同射流压强下的总压恢复系数 Fig. 12 Total pressure recovery coefficient under different jet pressure |
| 图选项 |
图 13给出了2种不起动状态的等马赫线图,施加射流后,进气道内的实际分离区由膨胀区与其前后的分离区共同组成,射流压强或射流速度增大,将使射流膨胀区及上游分离区面积增加,致使进气道虚拟喉道变窄(如图 13圆圈位置所示),导致捕获流量下降。
 |
| 图 13 不同射流压强下的流动结构(不起动) Fig. 13 Flow structure under different jet pressure(unstart) |
| 图选项 |
图 14对比了不同射流压强下的起动状态流场。压强增大,射流的膨胀作用增强,进气道主流的气动通道变窄,同时上游诱导激波变强,并脱离唇口,形成超声速溢流,使总压恢复系数及流量系数下降;另一方面,主流与射流之间的剪切层变厚,剪切层变厚使激波同边界层的作用点发生改变,在图 14(b)中第2道反射激波与边界层干扰的位置明显前移,这解释了能使进气道起动的最小射流速度随射流压强增大而上升的原因。
 |
| 图 14 不同射流压强下的流动结构(起动) Fig. 14 Flow structure under different jet pressure(start) |
| 图选项 |
4.3 射流倾角对于起动性能的影响 为考察射流倾角对进气道起动性能的影响,共选取了7个射流倾角,分别在射流静压PjA=2.29P∞及PjB=6.87P∞下开展相关计算,得到进气道起动情况如表 3及表 4所示,并在图 15及图 16给出了部分状态流量系数和总压恢复系数的变化规律。可以看出,不同射流倾角下,射流压强及速度对起动性能的影响具有一致性;射流倾角的有效性与射流速度和压强相关,增大射流速度或减小压强可以扩大射流倾角的有效区间;在测试的2个压强下,射流在θj=19°时,控制效果最好,而θj=79°时,施加射流后,进气道均出现不起动现象,且流量系数及总压恢复系数低于无射流状态。
表 3 不同射流倾角及速度下的起动特性(PjA) Table 3 Starting characteristics at different jet angles and velocities (PjA)
| θj/(°) | Vjet/ain | |||
| 3.65 | 4.0 | 4.5 | 5.0 | |
| 9 | un | st | st | st |
| 19 | st | st | st | st |
| 29 | un | st | st | st |
| 39 | un | st | st | st |
| 49 | un | un | st | st |
| 59 | un | un | un | st |
| 79 | un | un | un | |
表选项
表 4 不同射流倾角及速度下的起动特性(PjB) Table 4 Starting characteristics at different jet angles and velocities (PjB)
| θj/(°) | Vjet/ain | |||
| 4.5 | 5.0 | 6.0 | 7.0 | |
| 9 | un | st | st | st |
| 19 | un | st | st | st |
| 29 | un | st | st | |
| 39 | un | st | st | |
| 49 | un | un | un | |
| 59 | un | un | un | |
| 79 | un | un | un | |
表选项
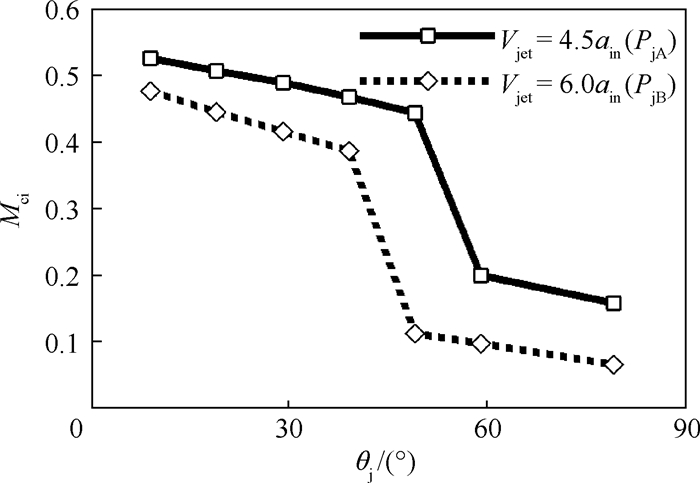 |
| 图 15 不同射流倾角下的流量系数 Fig. 15 Mass-captured coefficient under different jet angles |
| 图选项 |
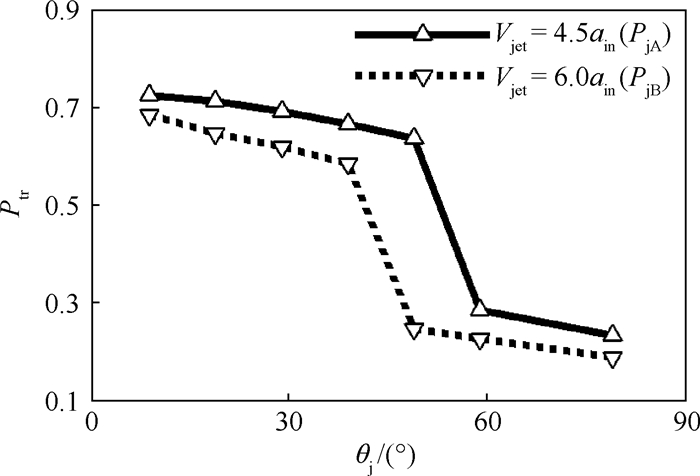 |
| 图 16 不同射流倾角下的总压恢复系数 Fig. 16 Total pressure recovery coefficient under different jet angles |
| 图选项 |
图 17给出了进气道在不同射流倾角的等压强线图(Vjet=4.0ain)。射流倾角从9°增加到49°,射流进入主流后膨胀效果变强,提高了进气道唇前马赫数,使唇口入射激波后移,同时上游分离激波增强并脱离唇口,形成超声速溢流,减小了进气道的实际流量,对进气道起动起积极作用;但随着射流倾角增大,射流在喷口附近膨胀到低压状态,并同周围高压气体作用,使再附激波增强,并影响超声速边界层,如图 18所示,过激波后,边界层内的马赫数降低,抵抗分离能力下降,对进气道起动起不利影响。总的来看,蕴含高动量的边界层和唇前高马赫数是维持进气道起动状态的主要原因,但再附激波会降低射流的控制效果,最佳射流倾角是三方面共同作用的结果。
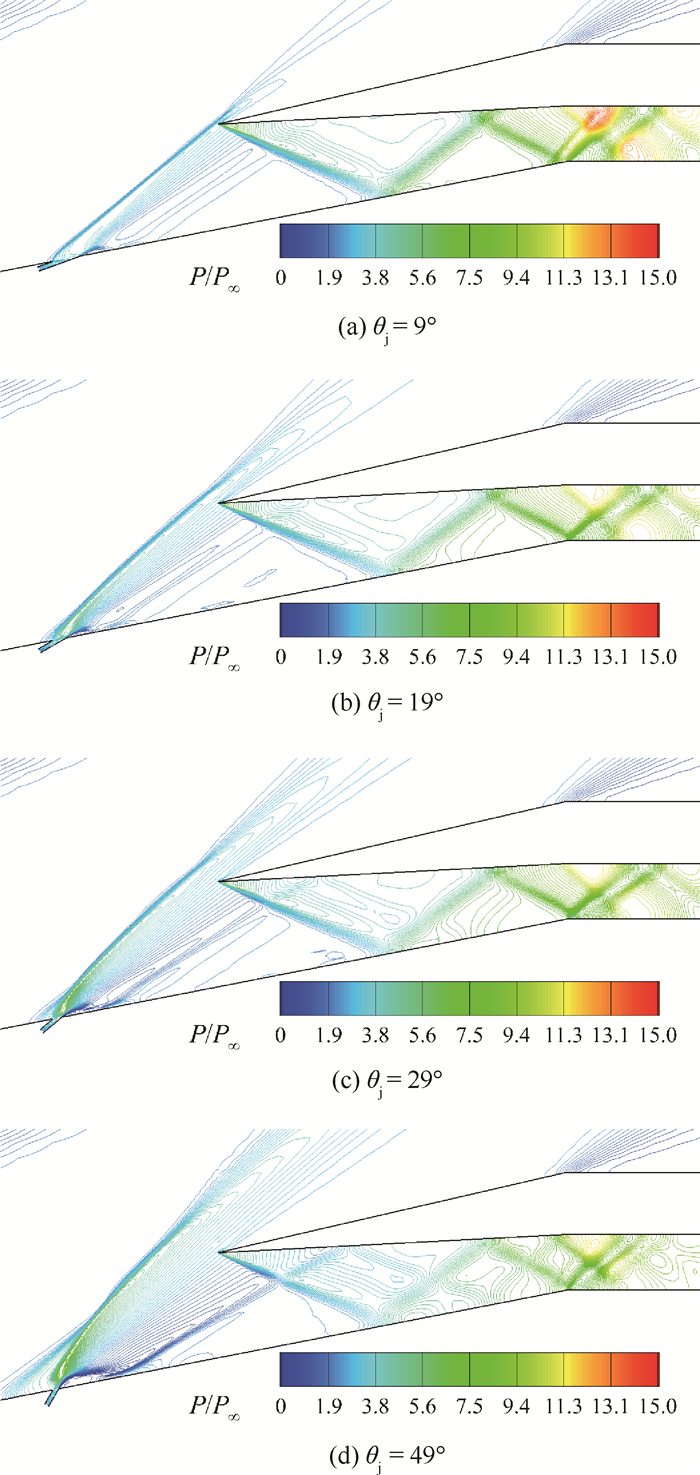 |
| 图 17 不同射流倾角下的流动结构(PjA) Fig. 17 Flow structure under different jet angles (PjA) |
| 图选项 |
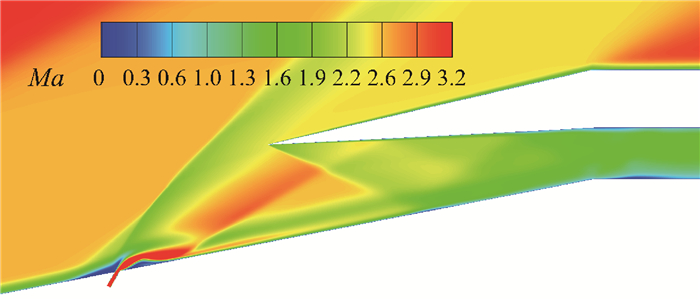 |
| 图 18 θj=49°下的马赫数分布(PjA) Fig. 18 Mach number distribution with θj=49° (PjA) |
| 图选项 |
图 19给出了某不起动状态的等马赫线图,射流倾角为79°,可以看出喷口上下游形成了大面积的分离区,将进气道入口基本堵塞,严重影响了进气道的气动性能;也有研究表明,在大倾角射流下,可建立充分的超声速主流流场,从而实现进气道起动,这种情况可能与入射位置和时间有关,关于这一方面的研究将在后续展开。
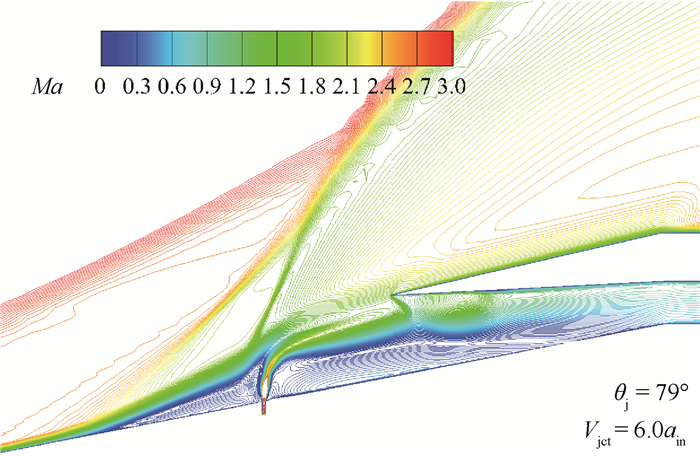 |
| 图 19 不起动状态的流动结构(PjB) Fig. 19 Flow structure under unstart state(PjB) |
| 图选项 |
5 结论 本文模拟了高超声速进气道在不起动状态有无射流的流场结构,分析了边界层控制的作用机理,研究了射流速度、压强及倾角对起动能力的影响规律,得到:
1) 在小射流倾角下,内缩段激波/边界层干扰形式改变,是降低起动马赫数的主要原因。
2) 增大射流速度,提高了输入边界层的动量,有助于实现进气道起动,但持续增大射流速度,会使隔离段反压升高,激波串被压出隔离段,再次出现不起动现象。
3) 射流压强较小时,可使进气道起动的最小射流速度变小,射流量降低,提高了控制效率;射流压强较大时,隔离段出口压强增大,限制了用以进气道起动的最大射流速度,缩小了射流速度的有效区间。
4) 在不同射流倾角下,上述2条规律表现一致,但随着射流倾角增大,唇前马赫数增大,同时再附激波增强,两者对进气道起动性能起相反作用,控制效果随射流倾角增大先提高后下降。
参考文献
| [1] | HABERLE J, GULHAN A.Investigation of the performance of a scramjet inlet at Mach 6 with boundary layer bleed:AIAA-2006-8139[R].Reston:AIAA, 2006.http://arc.aiaa.org/doi/abs/10.2514/6.2006-8139 |
| [2] | SMART M K, TREXLER C A. Mach 4 performance of hypersonic inlet with rectangular-to-elliptical shape transition[J].Journal of Propulsion and Powder, 2004, 20(2): 288–293.DOI:10.2514/1.1296 |
| [3] | WHITE M E, LEE R E, THOMPSON M W, et al. Tangential mass addition for shock/boundary-layer interaction control in scramjet inlets[J].Journal of Propulsion, 1991, 7(6): 1023–1029.DOI:10.2514/3.23422 |
| [4] | ROZARIO D, ZOUAOUI Z.Computational fluid dynamic analysis of scramjet inlet:AIAA-2007-0030[R].Reston:AIAA, 2007. |
| [5] | BITYURIN V A, BOCHAROV A N, LINEBERRY J T, et al.Experimental and theoretical study of MHD interaction in hypersonic ionized air flow over a wedge:AIAA-2004-1194[R].Reston:AIAA, 2004.http://arc.aiaa.org/doi/abs/10.2514/6.2004-1194 |
| [6] | SHEIKIN E G, KURANOW A L.MHD control in hypersonic aircraft:AIAA-2005-1335[R].Reston:AIAA, 2005. |
| [7] | GORTON S, OWENS L, JENKINS L, et al.Active flow control on a boundary-layer-ingesting inlet:AIAA-2004-1203[R].Reston:AIAA, 2004. |
| [8] | ALLAN B, OWEN L, BERRIER B.Numerical modeling of active flow control in a boundary layer ingesting offset inlet:AIAA-2004-2318[R].Reston:AIAA, 2004. |
| [9] | VAN WIE D M, KWOK F T, WALSH R T.Starting characteristics of supersonic inlets:AIAA-1996-2914[R].Reston:AIAA, 1996. |
| [10] | FENG X P, LIN Z Y, ZHENG Y, et al. Adjusting principle of gas jet controlling inlet and numerical verification[J].Science China Technological Sciences, 2011, 54(11): 2981–2986.DOI:10.1007/s11431-011-4553-3 |
| [11] | 方传波, 夏智勋, 胡建新, 等. 基于主动射流控制的二元混压式进气道起动特性研究[J].固体火箭技术, 2010, 33(3): 280–284. FANG C B, XIA Z X, HU J X, et al. Study on starting characteristics of a two-dimensional supersonic inlet based on actve injection control[J].Journal of Solid Rocket Technology, 2010, 33(3): 280–284.(in Chinese) |
| [12] | EMAMI S, TREXLER C A, AUSLENDER A H, et al.Experimental investigation of inlet-combustor isolators for a dual-mode scramjet at a Mach number of 4:NASA Technical Paper 3502[R].Washington, D.C.:NASA, 1995. |
| [13] | 林博希, 阎超, 李亚超. 喷流干扰气动热数值模拟的若干影响因素[J].北京航空航天大学学报, 2016, 42(6): 1210–1218. LIN B X, YAN C, LI Y C. Some influence factors in aerodynamic heat transfer numerical simulation of jet-interaction flow[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(6): 1210–1218.(in Chinese) |
| [14] | PATRICK E R, EMAMI S, CARL A T. Unsteady pressure behavior in a ramjet/scramjet inlet[J].Journal of Propulsion and Power, 1996, 12(3): 486–493.DOI:10.2514/3.24061 |
| [15] | COX C, LEWIS C, PAP R.Prediction of unstart phenomena in hypersonic aircraft:AIAA-1995-6018[R].Reston:AIAA, 1995. |
