大型民机发展以减阻减重为技术主线，以提高安全性、环保性，降低成本为目标，因此，减小气动阻力是民机设计的重要任务。对于民用客机，阻力降低1%可以减小0.2%直接使用成本^[1]，而直接使用成本直接关系着民机的市场竞争力。另一方面，减小巡航阻力可降低油耗，进而降低二氧化碳、氮氧化物等的排放量，是未来“绿色航空”的必然需求^[2]。
自第一代大型民用客机(如波音707) 运营以来，气动布局形式虽然没有发生大的变化，但在气动特性方面有了很大的改善。发展到今天，传统的气动设计技术已经比较成熟，想要在此基础上获得较大的收益十分困难^[3]。为此，各国研究****开始探索进一步提高民用客机气动性能的新技术，其中包括机翼后缘连续变弯度^[4]。
机翼后缘连续变弯度的设计思想最早由Kota教授^[5]于1994年提出。2003年，Kerr-Jia和Kota^[6]以变后缘机翼为例阐述了柔性机构的设计方法。Marques等^[7]设计了后缘连续变弯度襟翼并用来减小翼型和机翼的阻力。de Gaspari等^[8]采用CST(Class function/Shape function Transformation)方法实现机翼前缘和后缘变弯度，并以支线客机为研究对象，探索通过机翼连续变弯度提高飞机性能的方法。Yokozeki和Sugiura^[9]采用瓦楞结构实现了机翼后缘光滑无缝偏转，并通过风洞试验对比了后缘连续变弯度翼型和传统后缘襟翼偏转翼型的气动特性，试验结果表明后缘连续变弯度翼型具有更好的升力特性。Kaul和Nguyen^[10]研究了后缘连续变弯度对翼型气动特性的影响，并对比分析了不同后缘偏转角度时翼型的气动特性。Lyu和Martins^[11]以第四届阻力预测会议提供的NASA-CRM构型的单独机翼为研究对象，基于梯度优化算法研究了后缘变弯度对气动特性的影响。
从国外的公开文献来看，基于机翼后缘连续变弯度的研究主要集中在变弯度机构的实现机理、后缘变弯度对二维翼型或单独机翼的气动特性影响。针对宽体客机翼身组合体构型开展机翼后缘连续变弯度对气动特性影响的研究较少，尚未看到基于全局优化算法开展气动优化设计研究的文献。在国内，多以二维翼型为对象，开展变弯度的结构建模^[12-13]和气动特性^[14-16]研究。
现代大型民用客机的气动性能仅在设计点是最优的；而在整个巡航阶段，飞机有很大一部分飞行状态偏离设计点，其对应的气动性能不是最优的。为此，本文基于建立的考虑机翼后缘连续变弯度的全局优化设计系统，针对宽体客机翼身组合体构型开展了机翼后缘连续变弯度对非设计点气动特性的影响研究。
此外，在机翼后缘连续变弯度的影响研究中，大多仅考虑外翼段后缘连续变弯度^[4]。为了更加全面地研究后缘连续变弯度对宽体客机翼身组合体气动特性的影响，本文分别针对外翼段和内外翼后缘连续变弯度开展两轮优化设计研究。
1 基于FFD技术的机翼后缘连续变弯度的参数化方法 自由型面变形(Free Form Deformation, FFD)方法以弹性体受力后变形的思想来解决几何变形问题^[17]。该方法无需对初始外形进行拟合，能够光滑描述曲线、曲面和三维几何体的外形，并能方便地应用于整体和局部外形设计。
采用FFD方法对研究对象几何进行参数化时，首先，构建FFD控制体，将研究对象包络在控制体内(见图 1机翼后缘)。其次，基于控制体构建局部坐标系，并建立研究对象的局部坐标、全局坐标(笛卡儿坐标系)与控制体顶点(即FFD控制点)之间的映射关系，表达式为

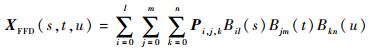(1)

图 1 机翼后缘偏转的FFD控制体 Fig. 1 FFD control framework for trailing-edge deflection of wing

图选项

式中：X_FFD为控制体内任一几何点在笛卡儿坐标系内的坐标值，s、t、u为该点的局部坐标值；P_{i, j, k}为FFD控制点的全局坐标；B_il(s)、B_jm (t)、B_kn(u)分别为l、m、n次Bernstein多项式基函数。在研究对象几何外形改变过程中，几何点的局部坐标是不改变的。当FFD控制点改变时，可通过式(1) 求得任意几何点变形后的全局坐标，得到研究对象变形后的几何。
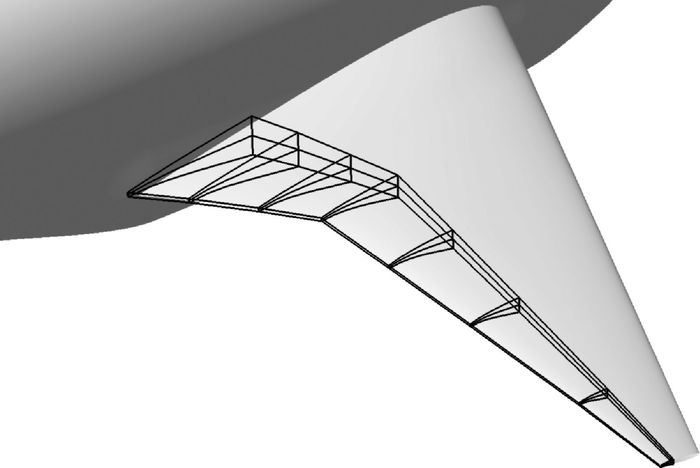
为了实现机翼后缘连续变弯度的参数化，并允许不同展向位置偏转不同的角度，沿机翼展向布置8个控制截面，以控制相应展向位置的后缘偏转角度；在每个展向截面沿弦线方向布置7个控制点，垂直弦线方向布置3个控制点(见图 2)。后缘偏转的转轴为过“四边形”控制点方向与机翼展向平行的直线。在变形过程中，原则上应将同一截面所有控制点偏转，但为了保证后缘偏转部分和机翼前面部分有较好的过渡，实际操作中“圆形”控制点不动；而其余控制点绕转轴转动同一角度，因此每个展向截面仅有一个自由度，即绕转轴的偏转角度，也是机翼后缘连续变弯度的设计变量。每个展向截面布置多个控制点是为了保证只偏转“三角形”控制点和偏转所有控制点的情况下，机翼的变形尽可能相同。

图 2 机翼控制截面处FFD控制体的放大图 Fig. 2 Amplification of FFD control framework at certain wing control section

图选项

2 流场数值求解方法 随着数值计算方法和计算机的不断发展，计算流体力学(CFD)逐渐成为现代民用客机设计的关键技术^[18]。
本文采用基于RANS(Reynolds-Averaged Navier-Stokes)方程的数值评估方法，采用全湍模式进行计算，其中湍流模型为Shear Stress Transport(SST)；空间离散格式为二阶Roe格式；并利用多重网格技术提高求解速度。
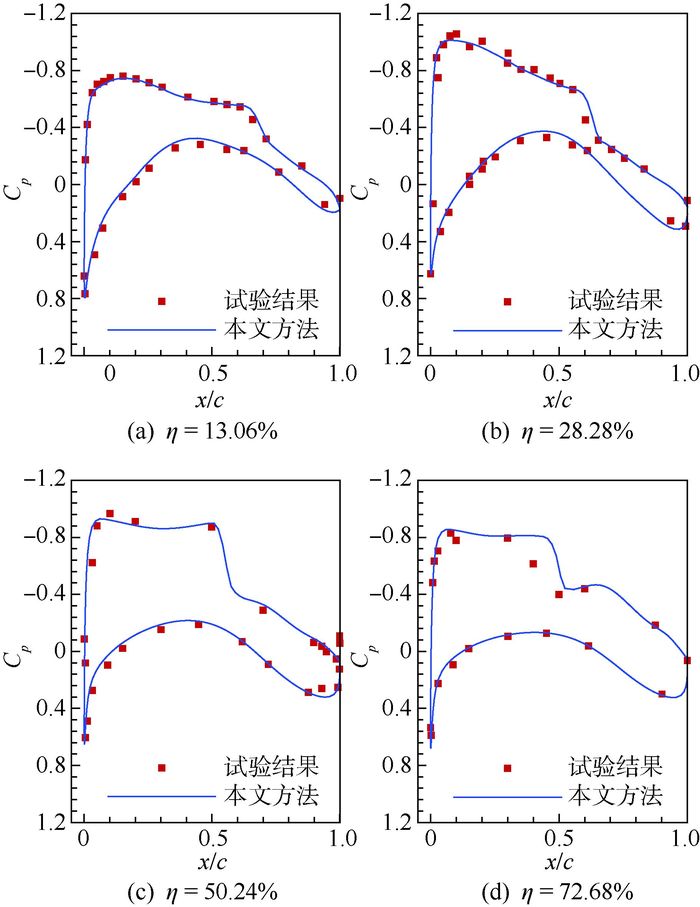
CRM是第四届和第五届阻力预测会议的标准模型，是典型的大展弦比宽体跨声速民用客机构型。本文以此模型为对象，采用流场求解器对典型试验状态^[19](马赫数Ma=0.85，升力系数C_L=0.52) 进行气动特性评估。计算与试验结果的压力系数C_p分布对比如图 3所示，x/c为弦长方向的相对位置，η为压力系数剖面在机翼展向的相对位置。可以看出，本文方法计算结果与试验结果吻合的较好，从而证明本文所采用的CFD求解器的精度能够满足优化设计要求。

图 3 本文方法计算的剖面压力系数分布与试验结果对比 Fig. 3 Comparison of section pressure coefficient distribution between calculation of proposed method and test results

图选项

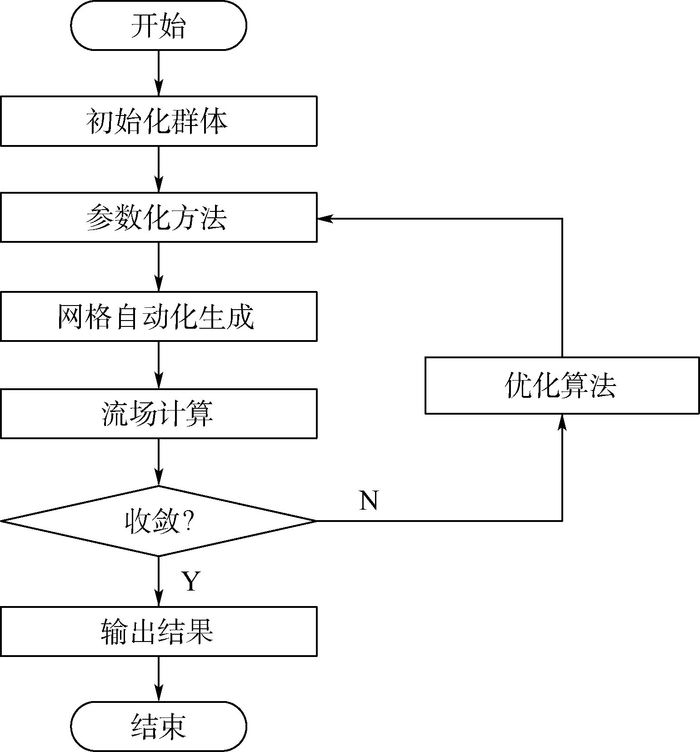
3 优化设计系统 本文搭建的优化设计系统的优化流程如图 4所示。该系统主要以下几个模块组成：基于FFD技术的气动外形参数化模块；基于动网格技术的网格自动生成模块；流场数值计算模块；优化搜索模块。其中，网格自动生成模块采用径向基函数(Radial Basis Function, RBF)插值动网格方法^[20]，该方法具有实现简单、结果准确和耗时少等优点。优化搜索模块采用遗传算法，该算法模仿生物进化过程中的遗传繁殖机制，具有较好的全局性。

图 4 优化设计系统的优化流程图 Fig. 4 Optimization flowchart of optimization design system

图选项

4 宽体客机翼身组合体优化设计 本文的研究对象为宽体客机翼身组合体构型(见图 5)。该构型通过综合设计优化得到，设计马赫数Ma=0.85，设计升力系数C_L=0.5，雷诺数Re=50.0×10⁶。

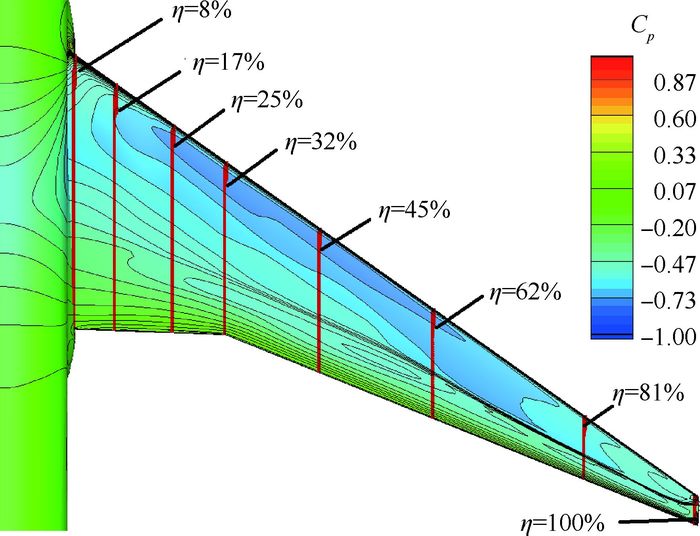图 5 初始翼身组合体构型巡航点的表面压力系数云图 Fig. 5 Surface pressure coefficient contours of original wing-body configuration under cruise condition

图选项

图 5为初始构型(Original)基于RANS方程计算得到的设计点上翼面压力系数云图，从图中可以看到，内翼段压力分布基本为无激波形态；从机翼拐折到翼梢，激波强度逐渐增加，并在翼梢附近形成较强的激波。沿机翼展向截取8个控制剖面翼型(如图 5中红线所示)，其展向位置与FFD控制体截面位置相同，从翼根到翼梢依次命名为Section 1~Section 8。
4.1 后缘连续变弯度机翼优化设计 本文采用基于RANS方程的数值评估方法求解翼身组合体的气动力，开展两轮气动优化设计。第1轮优化构型(Optimized_1) 仅考虑外翼段后缘偏转，设计变量为外翼段4个FFD控制截面的偏转角度；第2轮优化构型(Optimized_2) 考虑整个机翼后缘的偏转，设计变量为内外翼8个FFD控制截面的偏转角度。在优化设计中，以阻力系数C_D最小为目标，针对非设计点(Ma=0.85，Re=50.0×10⁶时, C_L=0.45，0.55) 进行优化。其中，变弯度的范围为机翼后缘30%弦长，各个控制截面的偏转角度范围为-2°~2°。
优化前后翼身组合体的气动力系数对比如表 1所示，α为迎角。从表中可知，C_L=0.45时，两轮优化阻力系数分别降低1.1%(2.1 counts，1 count=0.000 1) 和1.4%(2.7 counts)；C_L=0.55时，两轮优化阻力系数分别降低1.0%(2.2 counts)和1.1%(2.5 counts)。
表 1 优化前后气动特性对比 Table 1 Comparison of aerodynamic performance before and after optimization

构型	CL=0.45		CL=0.55
	α/(°)	CD	α/(°)	CD
Original	1.12	0.018 84	1.71	0.023 03
Optimized_1	1.25	0.018 63	1.57	0.022 81
Optimized_2	1.47	0.018 57	1.59	0.022 78

表选项






两轮优化各个控制剖面翼型(编号为n)的后缘偏转角度β如图 6所示，其中后缘下偏为正。从图中可以看出，在第1轮优化中，C_L=0.45时，外翼段后缘主要向上偏转；C_L=0.55时，外翼段后缘向下偏转。在第2轮优化中，C_L=0.45时，从翼根的大幅度上偏到翼梢的小幅度下偏；C_L=0.55时，从翼根的小幅度上偏到翼梢的大幅度下偏。

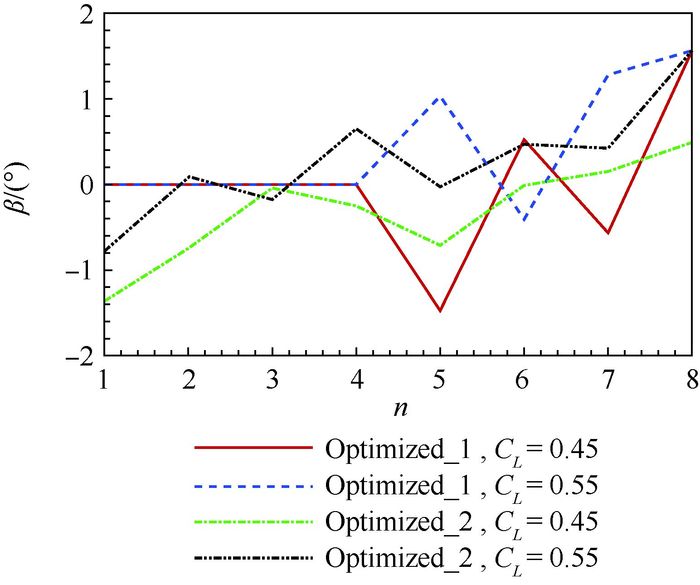图 6 优化后各控制剖面翼型后缘偏转角度 Fig. 6 Trailing-edge deflection degrees of each control section airfoils after optimization

图选项

4.2 优化结果对比 本节将初始构型与两轮优化设计的结果进行对比，研究后缘连续变弯度对翼身组合体气动特性的影响，并分析两轮优化设计结果的异同。
图 7为C_L=0.45时初始构型与两轮优化构型机翼控制剖面压力系数分布对比图。从图中可以看出，相比于Original，Optimized_1内翼段的激波强度基本不变，外翼段的激波强度明显减小，主要体现在第2个激波强度的降低，因此激波阻力也减小；Optimized_2外翼段的激波强度明显较小，但内翼段的激波强度有些许增加，因此激波阻力减小不明显。

图 7 优化前后控制剖面压力系数分布对比(CL=0.45) Fig. 7 Comparison of control section pressure coefficient distribution before and after optimization (CL=0.45)

图选项

图 8为C_L=0.45时初始构型与两轮优化构型的展向升力系数c_l分布对比图。其中，“Ellipse”为根据机翼的椭圆形环量分布得到的最佳升力系数分布。由图中可以看出，相比于初始构型，Optimized_1的载荷有些许内移，偏离最佳升力系数分布，因此诱导阻力相比初始构型增加；Optimized_2的载荷外移，趋近最佳升力系数分布，因此诱导阻力减小。

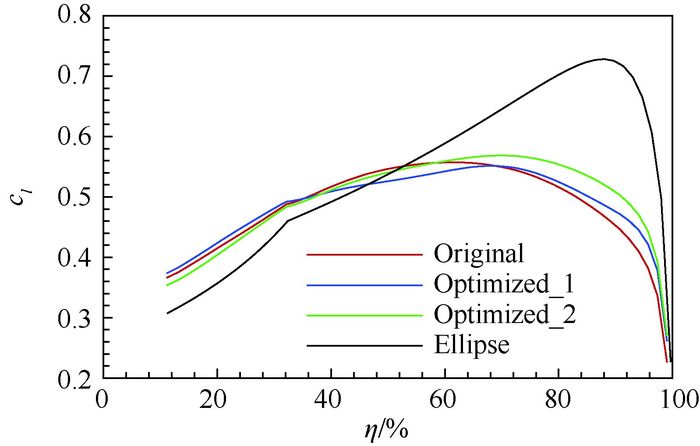图 8 优化前后机翼展向升力系数分布(CL=0.45) Fig. 8 Spanwise lift coefficient distribution of wing before and after optimization (CL=0.45)

图选项

图 9为C_L=0.55时初始构型与两轮优化构型的机翼控制剖面的压力系数分布对比图。从图中可以看出，Optimized_1和Optimized_2相比Original，激波强度都有所减弱，且Optimized_2减弱的更多一些，但均不明显。

图 9 优化前后控制剖面压力系数分布对比(CL=0.55) Fig. 9 Comparison of control section pressure coefficient distribution before and after optimization (CL=0.55)

图选项

图 10为C_L=0.55时初始构型与两轮优化构型的展向升力系数分布对比图。从图中可以看出，相比Original，Optimized_1和Optimized_2载荷明显外移，诱导阻力均减小。

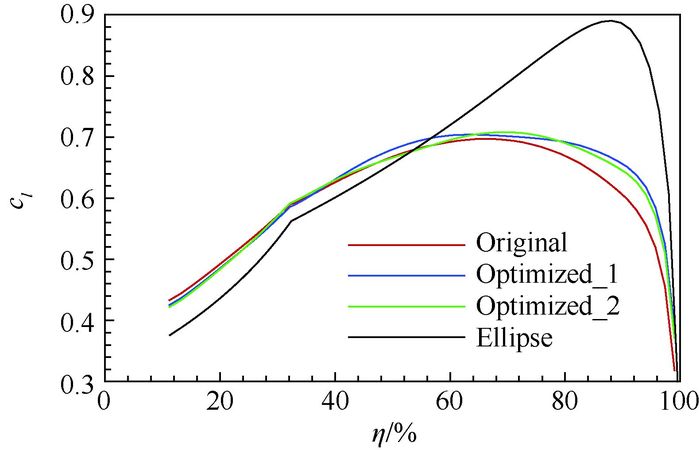图 10 优化前后机翼展向升力系数分布(CL=0.55) Fig. 10 Spanwise lift coefficient distribution of wing before and after optimization (CL=0.55)

图选项

4.3 减阻机理分析 对于C_L=0.45，当仅考虑外翼段后缘变弯时，后缘上偏有利于激波阻力减小，具体原因如下。当翼身组合体的升力系数小于设计点时，来流迎角也随之减小，上翼面头部附近的气流加速区变短，使得气流的动能较小，不足以维持超声速流动，在翼面靠前的位置产生激波；激波发生后，剖面翼型曲率的增加使得气流再次加速并达到超声速，进而产生了第2个激波，且由于加速区较长使得第2个激波的强度较大(见图 7初始构型压力分布)。在相同升力系数下，向上偏转后缘，机翼所需的来流迎角增加，从而增加上翼面头部附近气流的动能，使得第1个激波位置后移(见图 7)，进而减小激波后气流的加速区域；另一方面，向上偏转后缘使得剖面翼型上翼面在第1个激波后更加平坦(见图 11，y/c为剖面翼型法向的相对位置)，从而减缓了气流的二次加速(见图 12，z为剖面翼型法向的绝对位置)。因此对于小升力系数，仅考虑外翼段后缘连续变弯度时，向上偏转能够降低激波强度(见图 7 Optimized_1压力系数分布)。

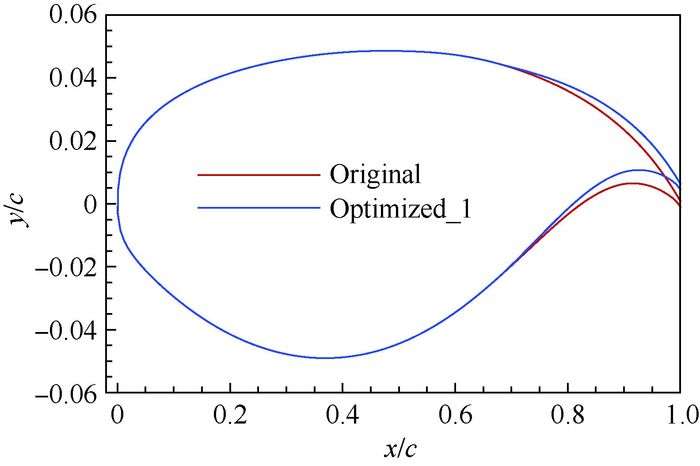图 11 初始和Optimized_1构型的Section 5剖面翼型对比(CL=0.45) Fig. 11 Comparison of Section 5 airfoil between Original and Optimized_1 configurations (CL=0.45)

图选项

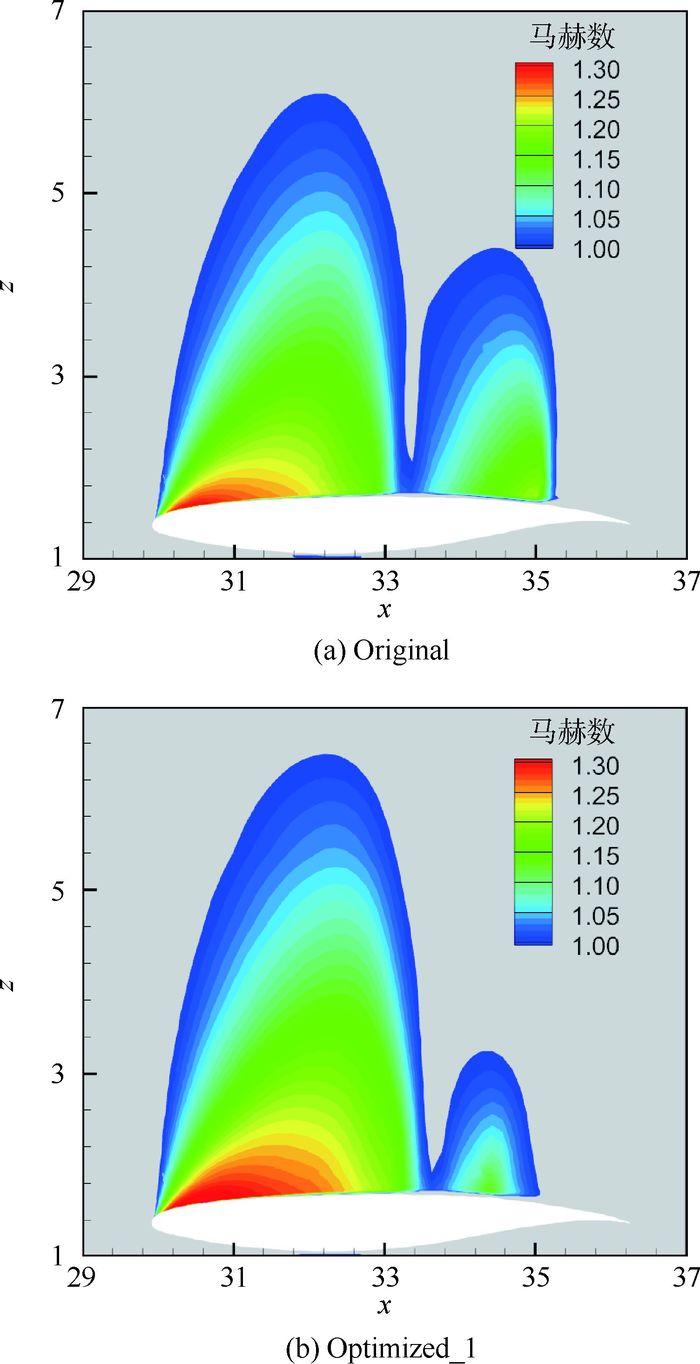图 12 初始和Optimized_1的Section 5展向位置处，马赫数大于1的空间分布云图对比(CL=0.45) Fig. 12 Comparison of Mach number (exceeding 1) spatial distribution contour of spanwise direction of Section 5 between Original and Optimized_1 configurations (CL=0.45)

图选项

与激波阻力不同的是，在C_L=0.45时外翼段后缘下偏使得机翼沿展向载荷外移，更加接近最佳载荷分布，有利于诱导阻力减小。因此，当只考虑外翼段后缘变弯时，对于小升力系数C_L=0.45，降低诱导阻力和降低激波阻力对后缘偏转方向的总体要求是相反的，很难实现激波阻力和诱导阻力同时降低。
对于C_L=0.45，当同时考虑内外翼后缘连续变弯度时，从翼根至翼梢后缘向上偏转的角度逐渐减小可以保证载荷外移，以减小诱导阻力(见图 6和图 8)；同时由于外翼段后缘向上偏转，有利于降低二次激波的强度，从而减小激波阻力(见图 6和图 7)。因此，同时考虑内外翼后缘连续变弯度时，诱导阻力和激波阻力同时减小，其减阻量较仅偏转外翼段后缘设计结果更为明显。可见，在小升力系数下，同时考虑内外翼后缘连续变弯度是必要的。
对于C_L=0.55，当仅考虑外翼段后缘连续变弯度时，后缘下偏有利于激波阻力减小(见图 6和图 9)。后缘下偏相当于增加机翼控制剖面翼型的后加载，在相同的升力系数下降低了翼身组合体的迎角，导致上翼面头部附近的气流加速区域减小，进而降低负压峰值且上翼面激波之前维持一个较高的压力系数，使得上翼面的激波强度减弱(见图 9)。而外翼段后缘使载荷外移，更加接近最佳载荷分布(见图 6和图 10)，进而使诱导阻力降低。由此可见，对于大升力系数，有利于降低诱导阻力的后缘偏转方向和有利于降低激波阻力的偏转方向是相同的。
对于C_L=0.55，当同时考虑内外翼后缘连续变弯度时，通过增加更多的自由度可以使阻力系数进一步降低，但减小的幅度较小，这主要有两方面原因：初始构型内翼段的激波强度较小，改善空间有限；在大升力系数下，仅外翼段后缘偏转就可以实现激波阻力和诱导阻力同时降低。
5 结论 1) 后缘连续变弯度能够显著提高宽体客机翼身组合体非设计点的气动特性。
2) 升力系数小于设计升力系数时，仅考虑外翼后缘连续变弯度时，后缘下偏有利于降低诱导阻力，后缘上偏有利于降低激波阻力，优化中很难实现激波阻力和诱导阻力同时降低；内外翼后缘均连续变弯度时，诱导阻力和激波阻力同时减小，减阻效果较前者更为明显。
3) 升力系数大于设计升力系数时，仅考虑外翼后缘连续变弯度时，后缘向下偏转，激波阻力和诱导阻力同时减小；内外翼后缘均连续变弯度时，阻力略小于前者，但不明显。

参考文献

[1]	RENEAUX J.Overview on drag reduction technologies for civil transport aircraft[C]//European Congress on Computational Methods in Applied Sciences and Engineering.Jyv?skyl?:University of Jyv?skyl?, 2004:7-24.
[2]	BRUNET M, LAFAGE R, AUBRY S, et al.The clean sky programme:Environmental benefits at aircraft level[C]//15th AIAA Aviation Technology, Integration, and Operations Conference.Reston:AIAA, 2015:6-22.
[3]	陈迎春. C919飞机空气动力设计[J].航空科学技术, 2012(5): 10–13. CHEN Y C. C919 aircraft aerodynamic design[J].Aeronautical Science & Technology, 2012(5): 10–13.(in Chinese)
[4]	URNES J, NGUYEN N, IPPOLITO C, et al.A mission adaptive variable camber flap control system to optimize high lift and cruise lift-to-drag ratios of future n+3 transport aircraft[C]//51th AIAA Aerospace Sciences Meeting.Reston:AIAA, 2013:1-7.
[5]	KOTA S.Shape control of adaptive structures using compliant mechanisms:AFRLSR-BL-TR-00-0125[R].Ann Arbor:Department of Mechanical Engineering and Applied Mechanics, 2000.
[6]	KERR-JIA L, KOTA S. Design of compliant mechanisms for morphing stricture shapes[J].Journal of Intelligent Material Systems and Structures, 2003, 14(6): 279–391.
[7]	MARQUES M, GAMBOA P, ANDRADE E.Design of a variable camber flap for minimum drag and improved energy efficiency[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston:AIAA, 2009:1-19.
[8]	DE GASPARI A, RICCI S, ANTUNES A, et al.Application of active camber morphing concept to a regional aircraft[C]//22nd AIAA/ASME/AHS Adaptive Structures Conference.Reston:AIAA, 2014:1-13.
[9]	YOKOZEKI T, SUGIURA A.Development and wind tunnel test of variable camber morphing wing:AIAA-2014-1261[R].Reston:AIAA, 2014.
[10]	KAUL U K, NGUYEN N T.Drag optimization study of variable camber continuous trailing edge flap using overflow:AIAA-2014-2444[R].Reston:AIAA, 2014.
[11]	LYU Z J, MARTINS J R R A. Aerodynamic shape optimization of an adaptive morphing trailing-edge wing[J].Journal of Aircraft, 2015, 52(6): 1951–1970.DOI:10.2514/1.C033116
[12]	王婷, 王帮峰, 芦吉云, 等. 一种拓扑优化方法在机翼可变后缘中的研究[J].机械科学与技术, 2011, 30(1): 1660–1663. WANG T, WANG B F, LU J Y, et al. The study of a topological optimization method on the adaptive wing's trailing edge[J].Mechanical Science and Technology for Aerospace Engineering, 2011, 30(1): 1660–1663.(in Chinese)
[13]	尹维龙, 石庆华, 田冬奎. 变体后缘的索网传动机构设计与分析[J].航空学报, 2013, 34(8): 1824–1831. YIN W L, SHI Q H, TIAN D K. Design and analysis of transmission mechanism with cable networks for morphing trailing edge[J].Acta Aeronoutica et Astronautica Sinica, 2013, 34(8): 1824–1831.(in Chinese)
[14]	陈钱, 白鹏, 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析[J].空气动力学报, 2010, 28(1): 46–53. CHEN Q, BAI P, YIN W L, et al. Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J].Acta Aerodynamica Sinica, 2010, 28(1): 46–53.(in Chinese)
[15]	郭同彪, 白俊强, 杨体浩. 后缘连续变弯对跨音速翼型气动特性影响研究[J].航空学报, 2016, 37(2): 513–521. GUO T B, BAI J Q, YANG T H. The influence investigation of continuous trailing-edge variable camber on the aerodynamic characteristics of transonic airfoils[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 513–521.(in Chinese)
[16]	梁煜, 单肖文. 大型民机翼型变弯度气动特性分析与优化设计[J].航空学报, 2016, 37(3): 790–798. LIANG Y, SHAN X W. Aerodynamic analysis and optimization design for variable camber airfoil of civil transport jet[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 790–798.(in Chinese)
[17]	SEDERBERG T W, PARRY S R. Free-form deformation of solid geometric models[J].Computer Graphics, 1986, 20(4): 151–160.DOI:10.1145/15886
[18]	JOHNSON F T, TINOCO E N, YU N J. Thirty years of development and application of CFD at Boeing commercial airplanes, seattle[J].Computers & Fluids, 2005, 34(10): 1115–1151.
[19]	LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the fifth computational fluid dynamics drag prediction workshop[J].Journal of Aircraft, 2014, 51(4): 1194–1213.DOI:10.2514/1.C032389
[20]	BOER A D, SCHOOT V D, BIJL H. Mesh deformation based on radial basis function interpolation[J].Computers & Structures, 2007, 85(11-14): 784–795.