为了实现超长时间续航(一周以上),典型氢动力无人机(如“鬼眼”和“全球观察者”[1-2])往往采用分布式推进的大展弦比上单翼布局,其机翼展弦比很大(大于20),翼载荷较低,约为15~30 kg/m2(介于大展弦比常规动力飞机与太阳能飞机之间),具有双梁结构形式。为减轻结构重量,这种大展弦比机翼往往采用轻质高性能碳纤维增强复合材料;其翼盒作为主要受力结构,来承担大部分弯矩和所有剪力;蒙皮除传递扭矩外还要承担部分弯矩;翼肋仅有传递载荷、支撑蒙皮的作用。
由于展弦比过大,在飞行受载时,这种机翼的结构可能发生严重变形,其静气动弹性特性变得突出。一方面,在气动载荷作用下,机翼容易产生严重的弯扭变形,变形后的结构平衡态相对于刚性结构差异明显,具有几何非线性特征;但是,机翼局部翼载并不大,结构内部的应变仍满足小变形假设,应力和应变维持线性本构关系。另一方面,结构平衡态下的几何非线性变形反作用于机翼,使其气动载荷发生显著变化,甚至可能使飞机气动性能恶化,严重影响飞行安全。因此,亟待以氢动力无人机为背景,对这种大展弦比机翼进行较深入的静气弹特性分析。
针对大展弦比机翼的静气弹问题,国内外已广泛开展了研究。Patil等[3]采用非线性梁理论和ONERA气动力模型,开展了大展弦比机翼的静气弹和动气弹研究。Wang等[4]采用非线性梁理论和改进的非定常涡格气动力模型,进行了大展弦比机翼的非线性气动弹性分析。近年来,随着计算技术的发展,流固耦合(CFD/CSD)求解逐渐成为气弹分析的主流方法之一[5-7]。Allen和Rendall[8]发展了一种基于径向基函数(RBF)的CFD/CSD耦合插值方法,对Brite-Euram MDO机翼进行了气动弹性分析。Garcia[9]采用一种松弛技术来提高CFD/CSD强耦合静气弹计算的效率。Carnie和Qin[10]应用FLUENT和ANSYS的接口程序,对大展弦比机翼进行了静气弹分析。Heinrich和Kroll[11]通过插值进行数据交换,完成静气弹和动气弹的计算。马铁林和张华[12-13]等应用FLUENT/NASTRAN弱耦合求解,开展了大展弦比机翼的静气弹分析。聂雪媛等[14]采用RBF方法来实现网格变形与耦合界面数据交换,对客机机翼进行了气动弹性分析。
这些研究大多应用CFD/CSD弱耦合方法针对常规无人机和太阳能无人机进行气弹分析,对氢动力无人机大展弦比机翼关注较少。为此,本文建立了CFD/CSD强耦合的分析方法,对氢动力超长航时无人机大展弦比机翼进行了静气弹分析,并基于分析结果,给出了一种考虑静气弹效应的刚性机翼气动特性修正方法。
1 静气动弹性计算分析方法 CFD/CSD强耦合进行静气动弹性研究,涉及CFD方法、CSD方法、耦合界面相容条件、数据交换方法、动网格技术和耦合计算方法。
本文CFD求解采用基于SA湍流模型的雷诺平均Navier-Stokes方程的有限体积法。空间离散使用Roe格式,时间推进采用LU-SGS双时间步隐式时间推进方式,SA模型采用二阶精度的中心差分求解。
CSD方面采用牛顿-拉普森迭代法求解非线性结构动力学方程,结构方程在一载荷步内迭代收敛后,再增加载荷求解下一个载荷步,直至加载到满载荷,求解出最终的结构变形。下面对研究中所涉及的耦合相关方法进行说明。
1.1 耦合界面相容条件 CFD/CSD强耦合求解时,耦合界面上网格通常不匹配,为保证流体-结构耦合的一致性,耦合界面的数据传递需要满足力学平衡条件和运动学相容条件,即
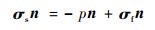 | (1) |
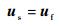 | (2) |
式(1) 为耦合界面力的平衡条件,σs和σf分别为结构应力张量和流体黏性应力张量,n为耦合界面单元的单位外法向量,p为流体压力;式(2) 为位移相容条件,us和uf分别为耦合界面上的结构位移矢量和流体位移矢量。
1.2 数据交换方法 本文采用守恒插值方法[15]实现耦合界面的数据交换。该方法在数据交互过程中满足能量守恒,耦合界面上流体载荷、固体力在界面位移上所做的虚功相等,即
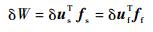 | (3) |
式中:δus和δuf分别为耦合界面上固体、流体虚位移;fs和ff分别为耦合界面上固体、流体表面力。
耦合界面上流体、固体的虚位移之间关系可以用下式表示:
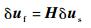 | (4) |
式中:H为界面位移映射矩阵。
则耦合界面上流体、固体的表面力之间关系可以表示为
 | (5) |
耦合界面的节点-单元搜索算法采用桶式搜索[16-17]和强力搜索相结合的方法。首先对每个单元建立一个仅包含该单元的桶区域,将区域适当放大以包含周围若干节点;然后在区域内应用强力搜索来确定单元-节点的匹配关系。
1.3 动网格技术 动网格可用来模拟流场随结构变形而改变的问题。本文网格运动采用基于壁面距离的扩散光顺方法,扩散方程为
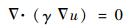 | (6) |
式中:▽为哈密顿算子;γ为扩散系数;u为网格位移速度。γ与正则壁面距离d及扩散参数C有关:
 | (7) |
C越大,远离壁面处可吸收更多网格变形,壁面附近网格变形越小,从而保证运动边界附近的网格质量。
1.4 CFD/CSD耦合计算方法 CFD/CSD耦合静气弹分析一般分为弱耦合方法和强耦合方法[7]。
弱耦合方法是在每个时间步内分别依次对流场和结构求解,交错时间推进获得系统的响应。这种方法在每个物理时间步内流场与结构的信息交换仅有一次,效率较高。但由于积分时间的不同步,耦合界面无法实现动态平衡,时间精度较低。
强耦合方法在每个物理时间步内进行预估-校正迭代计算(如图 1所示),使得流场与结构在时间积分上达到同步,提高了计算精度,取得了较好的结果。强耦合方法的计算过程更接近于弹性机翼变形的物理本质。本文采用强耦合方法,利用CFD和CSD模块进行气动结构耦合计算,应用插值接口模块进行耦合界面信息传递。
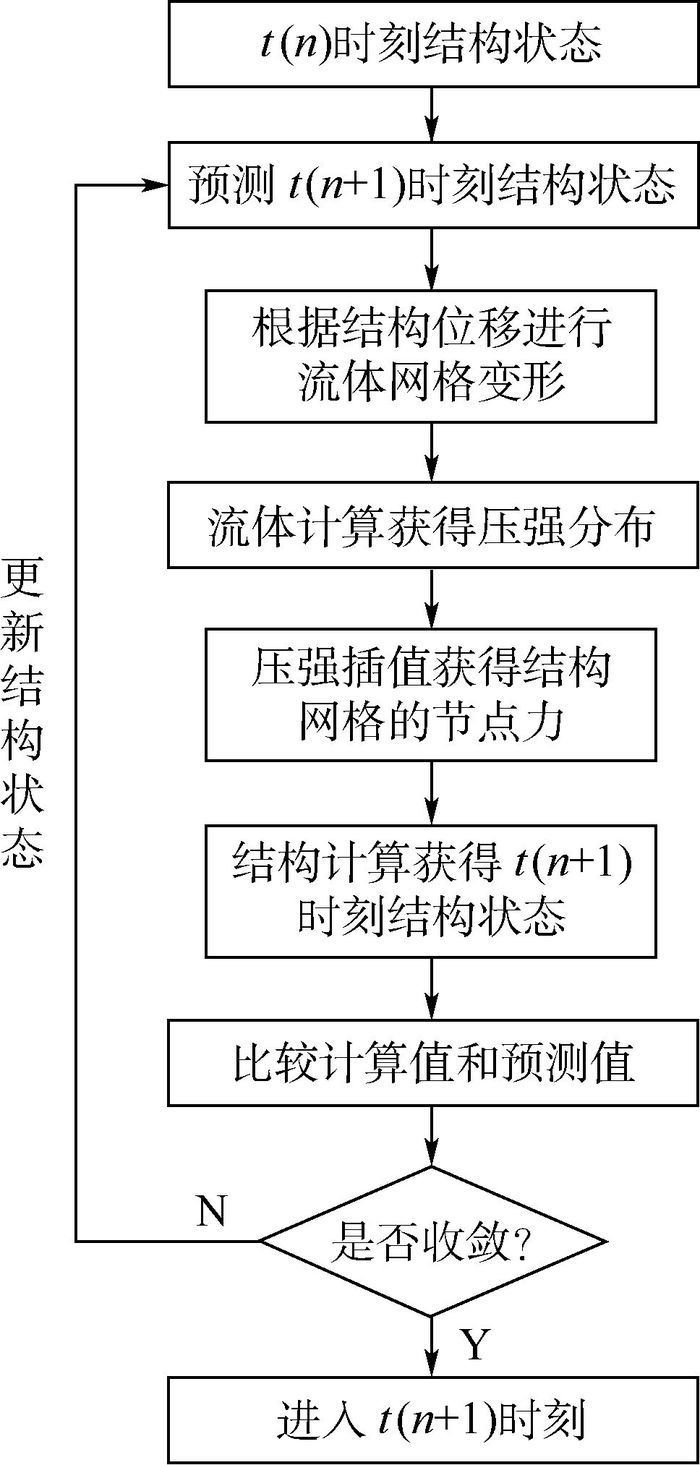 |
| 图 1 CFD/CSD预估-校正迭代方法流程 Fig. 1 Procedure of CFD/CSD prediction-correction iterative method |
| 图选项 |
2 机翼静气弹计算分析 2.1 基本静气弹计算分析 图 2为某氢动力超长航时无人机的几何模型,采用上单翼单垂尾常规布局。其机翼选用升阻特性较好的低雷诺数翼型,展弦比为30,采用两段机翼设计,内翼为矩形机翼,半展长为26 800 mm,弦长为3 500 mm;外翼为梯形机翼,上反角为3°,半展长为20 000 mm,翼梢弦长为1 750 mm。机翼结构形式为双梁式结构,材料为HT8/5288碳纤维复合材料。
 |
| 图 2 氢动力超长航时无人机模型 Fig. 2 Model of hydrogen-powered ultra-long endurance UAV |
| 图选项 |
计算状态为:压强为5 529.31 Pa,来流马赫数为0.237 2,巡航迎角为0°。本文耦合计算数据交换时间步长为0.001 s,收敛条件为翼尖后缘挠度及机翼升力系数的相邻2次结果之差小于1%。图 3为计算翼尖后缘挠度及机翼升力系数的收敛曲线,由图可知,迭代1 000次后,计算结果收敛。
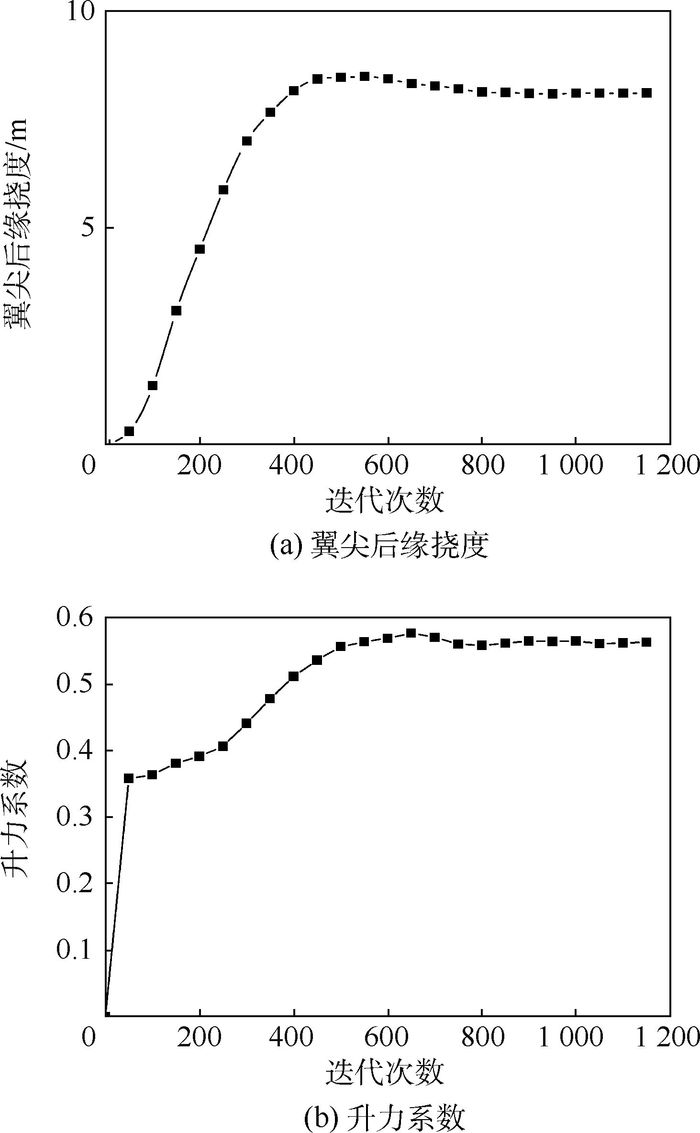 |
| 图 3 翼尖后缘挠度及机翼升力系数的收敛曲线 Fig. 3 Convergence curves of wingtip trailing edge deflection and lift coefficient |
| 图选项 |
图 4为机翼弹性状态的结构变形和流场,由图可知,机翼结构具有明显的几何非线性变形,机翼绕流和压强分布也发生了相应的变化;显然,CFD/CSD强耦合计算能够捕捉到精细化的气动和结构变化特征。图 5为机翼后缘挠度及剖面扭转角沿展向变化情况,翼尖后缘挠度最大为8.107 m,翼尖剖面扭转角为-1.1°,由图可知,机翼几何非线性变形特征突出。
 |
| 图 4 机翼结构变形和流场 Fig. 4 Structure deformation and flow field of wing |
| 图选项 |
 |
| 图 5 机翼后缘挠度及剖面扭转角沿展向变化曲线 Fig. 5 Change curves of wing trailing edge deflection and twist angle along spanwise direction |
| 图选项 |
2.2 静气弹变形下气动性能分析 为了进一步研究机翼静气动弹性变形对气动性能的影响,开展了小迎角(α)、小侧滑角(β)下的静气弹特性计算,计算状态为:0°~4°小迎角、0°~4°小侧滑角。
图 6给出了刚性与弹性机翼的纵向气动特性的对比。由图可知,相比刚性机翼,在弯扭变形作用下,弹性机翼的升力系数CL下降,升力线斜率基本不变,阻力系数CD稍有下降,升阻比K显著下降,俯仰力矩导数Cmα有一定程度下降。巡航状态下升力系数下降5.2%,阻力系数下降2%,升阻比下降3.2%。
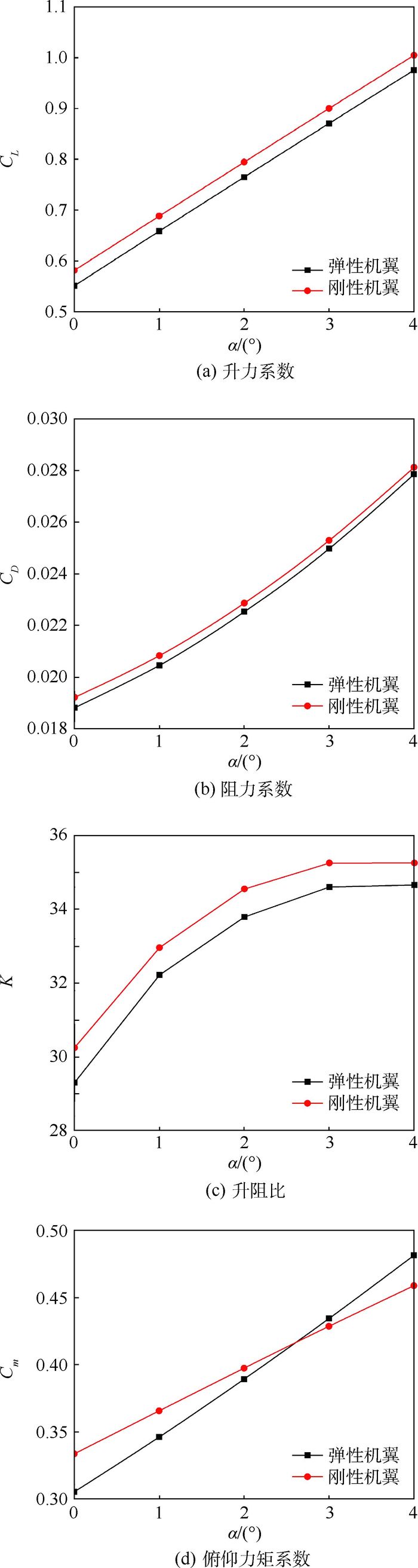 |
| 图 6 刚性与弹性机翼的纵向气动特性对比 Fig. 6 Comparison of longitudinal aerodynamic characteristics for rigid and elastic wings |
| 图选项 |
事实上,弯曲变形使翼面沿展向的曲率发生变化,导致升力损失;扭转变形产生负扭转角,降低了机翼的有效迎角,使升力系数进一步降低;而有效迎角减小,也同时使升致阻力下降。故而,升阻力的综合作用使机翼的升阻比K下降。
图 7为刚性与弹性机翼的横侧向力矩特性的对比。由图可知,弹性变形使机翼的滚转力矩系数Cl和偏航力矩系数Cn绝对值明显增大。
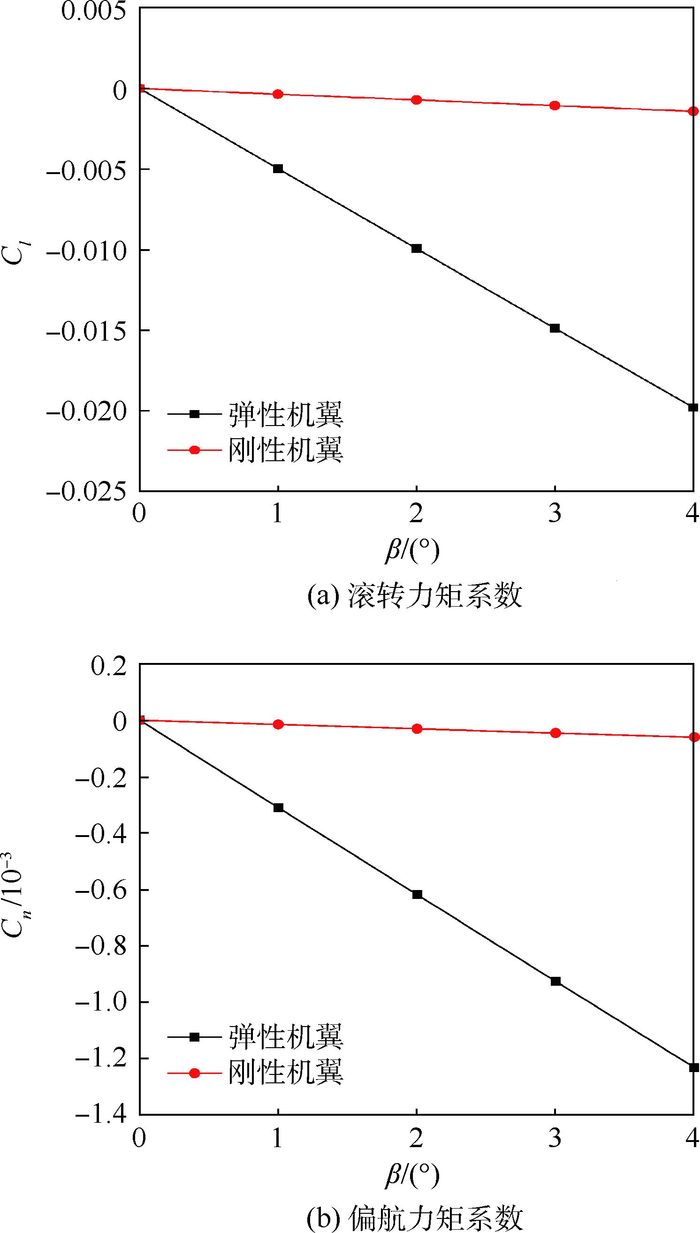 |
| 图 7 刚性与弹性机翼的横侧向力矩特性的对比 Fig. 7 Comparison of directional-lateral moment characteristics for rigid and elastic wings |
| 图选项 |
图 8为刚性与弹性机翼沿展向的升力系数CL和侧力系数CZ的对比(4°侧滑角)。由图可知,弹性变形加剧了小侧滑角下机翼升力及侧力的左右不对称性;同时弹性变形使得机翼展向曲率变化,气动力的侧向分量大幅增加,而侧力关于纵轴的力臂也显著增大。在这些因素的综合作用下,机翼的滚转及偏航力矩明显增大。
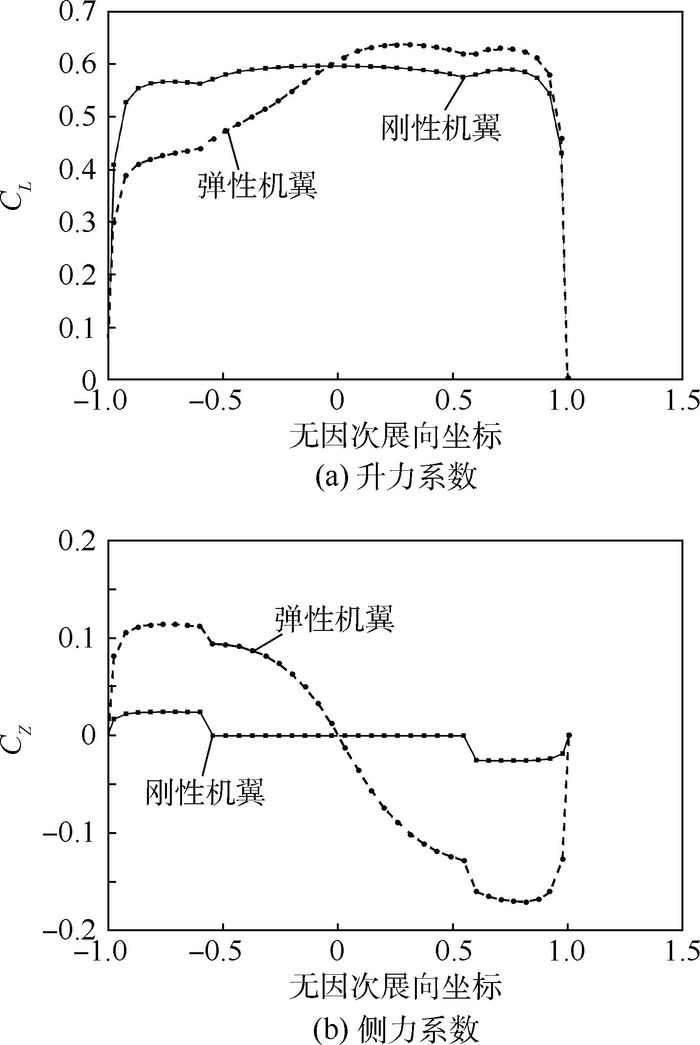 |
| 图 8 刚性与弹性机翼沿展向升力系数和侧力系数的对比 Fig. 8 Comparison of lift and side force coefficient along spanwise for rigid and elastic wings |
| 图选项 |
滚转力矩导数(Clβ)和偏航力矩导数(Cnβ)对比如表 1所示;弹性机翼的滚转力矩导数增大13倍,偏航力矩导数增大19.67倍。在实际飞行过程中,机翼受载后变形严重,导致滚转力矩及偏航力矩均大幅增加,使得飞机偏离初始设计点,可能造成横侧向不匹配。
表 1 横侧向力矩导数对比 Table 1 Comparison of directional-lateral moment derivatives
| 机翼类型 | Clβ | Cnβ |
| 刚性机翼 | -0.000 35 | -0.000 015 |
| 弹性机翼 | -0.004 9 | -0.000 31 |
表选项
3 机翼气动力弹性修正 弹性变形对机翼纵向和横侧向气动特性都有很大的影响,但利用强耦合方法求解静气弹特性,建模和求解过程需要花费大量时间,并且方法也不易掌握。为了高效地求解大展弦比机翼的弹性气动力,提出了一种弹性效应下的气动力修正分析方法,来对刚性机翼的气动计算结果进行修正。该方法为一种刚性计算+弹性修正的方法(“刚性+修正”方法,简称RC法)。展弦比是氢动力无人机大展弦比机翼最主要的特征参数,为提高方法的适应性,在修正中将展弦比引入作为一个特征量。利用第2节所建立的静气弹分析方法,对不同展弦比的氢动力无人机大展弦比机翼进行了静气弹计算,对计算结果进行如下分析。
机翼的升力系数和阻力系数可以表述为
 | (8) |
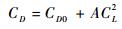 | (9) |
式中:CLα、α0、CD0和A分别为升力线斜率、零升迎角、零升阻力系数和升致阻力因子。
由图 6(a)可知,机翼发生弹性变形后,升力线斜率CLα基本不变,可认为只有零升迎角α0发生改变,对本文方案的升力系数进行修正,其结果为
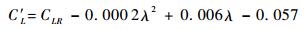 | (10) |
对于阻力系数修正,零升阻力系数CD0与浸润面积相关,可认为变形后不发生改变,将式(10) 代入式(9),略去小量常数项,得到阻力系数修正公式:
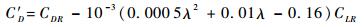 | (11) |
由图 7可知机翼发生弹性变形后,相当于产生了较大的机翼上反角,显著增加了平直机翼的横侧向力矩导数,可用式(12) 和式(13) 进行修正:
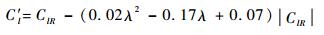 | (12) |
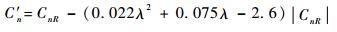 | (13) |
式中:λ、CLR、CDR、ClR和CnR分别为机翼展弦比、刚性机翼的升力系数、阻力系数、滚转力矩系数及偏航力矩系数;C′L、C′D、C′l和C′n分别为CLR、CDR、ClR和CnR的修正结果。
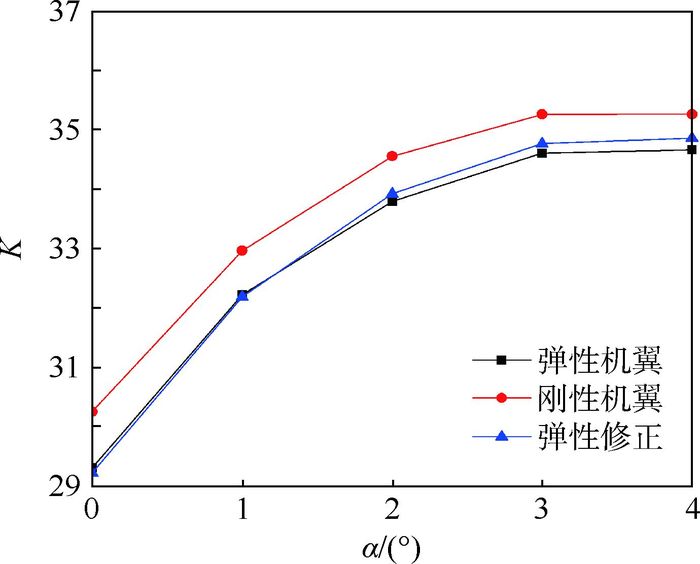
图 9给出了本文方案升阻比的修正结果。由图可知,修正计算与弹性计算结果吻合较好。
 |
| 图 9 升阻比修正结果 Fig. 9 Correction results of lift-drag ratio |
| 图选项 |
表 2给出了不同方法的气动分析效能对比。表中常用频域法指采用涡格分析气动力的方法。由表 2可知,强耦合分析需要约46 h计算机时(i7-4 790 CPU,8G内存,8核并行);而RC方法仅需约0.5 h(与刚性计算相近);RC方法的效率、精度和精细化水平都较好。
表 2 不同方法的气动效能对比 Table 2 Comparison of aerodynamic efficiency among different methods
| 方法 | 时间/h | 精度 | 精细化水平 |
| 常用频域方法 | <0.1 | 一般(预计) | 一般 |
| CFD/CSD强耦合方法 | 46 | 好 | 好 |
| RC方法 | 0.5 | 较好 | 较好 |
表选项
综合图 9和表 2可知,RC方法对氢动力飞机大展弦比机翼进行分析是有效的。
4 结论 应用静气弹计算分析方法求解了氢动力飞机大展弦比机翼的几何非线性静气弹问题,得出如下结论:
1) CFD/CSD强耦合方法可以有效地分析氢动力飞机超大展弦比机翼的静气弹特性。
2) 机翼受载后产生弯扭变形,翼面的弯度和有效迎角减小,其升力和阻力系数均减小,升阻比也随之降低(降低3.2%)。
3) 机翼的弯扭变形对横侧向气动性能影响明显,弹性机翼的滚转和偏航力矩导数将显著增大。
4) 针对氢动力飞机大展弦比轻质弹性机翼,“刚性+修正”方法提供了一种有效的快速气动分析策略。
参考文献
| [1] | OKAYA S.Aerospace fuel cell rapid prototyping power system concept[C]//12th International Energy Conversion Engineering Conference.Reston:AIAA, 2014:22-36. |
| [2] | LIM D T Y.A methodological approach for conducting a business case analysis (BCA) of the global observer joint capability technology demonstration (JCTD)[D].Monterey:Naval Postgraduate School, 2007:17-20. |
| [3] | PATIL M J, HODGES D H, CESNIK C E S.Characterizing the effects of geometrical nonlinearities on aeroelastic behavior of high-aspect-ratio wings[C]//International Forum on Aeroelasticity and Structural Dynamics.Reston:AIAA, 1999:22-25. |
| [4] | WANG Z, CHEN P C, LIU D D.Nonlinear aeroelastic analysis for a HALE wing including effects of gust and flow separation[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston:AIAA, 2007. |
| [5] | DOWELL E H.Some recent advances in nonlinear aeroelasticity:Fluid-structure interaction in the 21st century:AIAA-2010-3137[R].Reston:AIAA, 2010. |
| [6] | 杨国伟. 计算气动弹性若干研究进展[J].力学进展, 2009, 39(4): 406–420. YANG G W. Recent progress on computational aeroelaticity[J].Advances in Mechanics, 2009, 39(4): 406–420.DOI:10.6052/1000-0992-2009-4-J2009-046(in Chinese) |
| [7] | 王文全, 张立翔. 计算流固耦合动力学及其应用[M].北京: 中国水利水电出版社, 2015: 2-12. WANG W Q, ZHANG L X. Computational fluid-structure interaction dynamics and applications[M].Beijing: China Water & Power Press, 2015: 2-12.(in Chinese) |
| [8] | ALLEN C B, RENDALL T E S.Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions:AIAA-2007-3804[R].Reston:AIAA, 2007. |
| [9] | GARCIA J A. Numerical investigation of nonlinear aeroelastic effects on flexible high-aspect-ratio wings[J].Journal of Aircraft, 2005, 42(2): 1025–1036. |
| [10] | CARNIE G, QIN N.Fluid-structure interaction of HALE wing configuration with an efficient moving grid method:AIAA-2008-309[R].Reston:AIAA, 2008. |
| [11] | HEINRICH R, KROLL N.Fluid-structure coupling for aerodynamic analysis and design a DLR perspective:AIAA-2008-561[R].Reston:AIAA, 2008. |
| [12] | 马铁林, 马东立, 张华. 大展弦比柔性机翼气动特性分析[J].北京航空航天大学学报, 2007, 33(7): 781–784. MA T L, MA D L, ZHANG H. Aerodynamic characteristic analysis of high aspect ratio elastic wing[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(7): 781–784.(in Chinese) |
| [13] | 张华, 马东立, 马铁林. 弹性变形对柔性机翼气动特性影响分析[J].北京航空航天大学学报, 2008, 34(5): 487–490. ZHANG H, MA D L, MA T L. Analysis of aerodynamic characteristic of flexible wing caused by deflection[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5): 487–490.(in Chinese) |
| [14] | 聂雪媛, 黄程德, 杨国伟. 基于CFD/CSD耦合的结构几何非线性静气动弹性数值方法研究[J].振动与冲击, 2016, 35(8): 48–53. NIE X Y, HUANG C D, YANG G W. Numerical analysis for aeroelastic with structural geometrical nonlinearity using a CFD/CSD coupled method[J].Journal of Vibration and Shock, 2016, 35(8): 48–53.(in Chinese) |
| [15] | DUKOWICZ J K, KODIS J W. Accurate conservative remapping(rezoning) for arbitrary Lagrangian-Eulerian computations[J].Journal on Scientific and Statistical Computing, 1987, 8(3): 305–321.DOI:10.1137/0908037 |
| [16] | BENSON D J, HALLQUIST J O. A single surface contact algorithm for the post-buckling analysis of shell structures[J].Computer Methods in Applied Mechanics and Engineering, 1990, 78(2): 141–163.DOI:10.1016/0045-7825(90)90098-7 |
| [17] | JANSEN K, SHAKIB F, HUGHES T J R. Fast projection algorithm for unstructured meshes[J].Computational Nonlinear Mechanics in Aerospace Engineering, 1992, 146(5): 175–204. |
