综上所述,刚弹耦合动力学在民用经济建设和国防建设中有着广阔的应用前景,是国内外****不断探索的重要课题,且诸多****做出了重要的贡献,但是目前还没有完全成熟的理论研究成果,理论研究工作还任重而道远[19-21]。变分原理是从总体上把握事物,对于这类交叉学科,特别适于应用变分原理进行研究[22]。而在工程实际中,又不可避免地会涉及到初值问题,Gurtin[23]利用卷积理论提出了与弹性动力学初值-边值问题等价的变分原理,中国****罗恩在这一学科领域做出重要贡献[24-25]。本文将其推广应用于刚弹耦合动力学初值问题的研究中,首先建立刚弹耦合动力学初值问题拟变分原理然后推导出其控制方程,最后给出应用算例。
1 建立拟变分原理 首先给出刚体动力学初值问题拟变分原理以及弹性动力学初值问题拟变分原理,以此为基础,考虑耦合效应,进而建立出刚弹耦合动力学初值问题拟变分原理。
1.1 刚体动力学初值问题拟变分原理 一类变量刚体动力学初值问题拟变分原理表示为
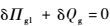 | (1) |
式中:
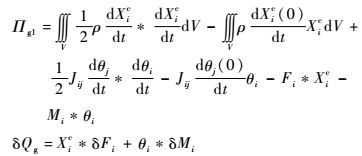 |
其中:ρ为质量密度;V为体积;
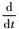
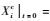
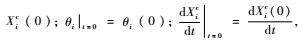
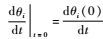
研究表明[22, 26],上述拟变分原理的拟驻值条件正是刚体动力学微分控制方程。这便说明,拟变分原理所描述系统与系统的动力学微分方程具有等价性。
1.2 弹性动力学初值问题拟变分原理 一类变量非保守弹性动力学初值问题拟变分原理表示为
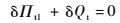 | (2) |
式中:
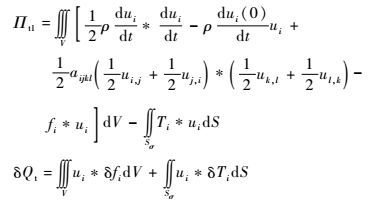 |
其中:ui为弹性位移;fi为体积力;Ti为面积力;aijkl为刚度系数;S为面积;Sσ为应力边界面。在位移边界面Su上,ui-ui=0(ui为边界位移)。初值条件为
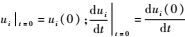
研究表明[22, 27],上述拟变分原理的拟驻值条件正是弹性动力学微分控制方程。这便说明,拟变分原理所描述系统与系统的动力学微分方程具有等价性。
1.3 刚弹耦合动力学初值问题拟变分原理 值得注意的是,刚弹耦合动力学初值问题拟变分原理的建立不是刚体动力学和弹性动力学初值问题拟变分原理的简单叠加,关键还要考虑耦合效应,即确定其刚弹耦合项,包括域中耦合项和初值耦合项。
文献[27]在时间边值问题的刚弹耦合动力学拟变分原理的研究中,通过应用功能转换原理和能量守恒定律,合理地确定了刚弹耦合动力学边值问题拟变分原理的耦合项为
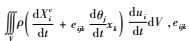
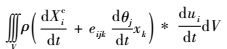 | (3) |
应用Laplace卷积理论,可进一步推断导出与式(3) 相应的初值耦合项为
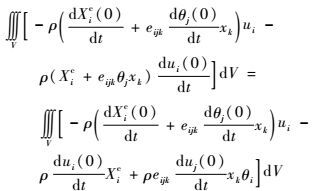 | (4) |
结合式(1)、式(2),引入式(3)、式(4),进而建立一类变量刚弹耦合动力学初值问题拟变分原理:
 | (5) |
其中:
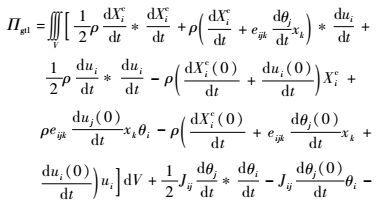 |
 |
初值条件为ui-ui=0
初值条件为

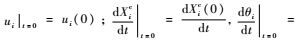
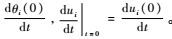
应用对合变换,将式(5) 变换为两类变量刚弹耦合动力学初值问题拟变分原理:
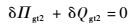 | (6) |
式中:
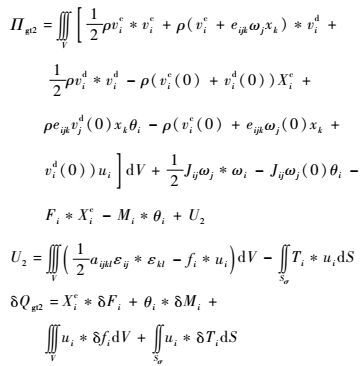 |
其中:vic为把刚弹耦合系统视为刚体时质心速度;ωi为把刚弹耦合系统视为刚体时转动角速度;vid为刚弹耦合系统变形时的速度;εij为弹性应变。其先决条件为

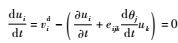
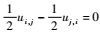
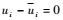
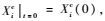
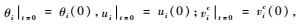
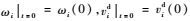
2 推导控制方程 2.1 两类变量刚弹耦合动力学控制方程 将式(6) 写成展开形式,可得
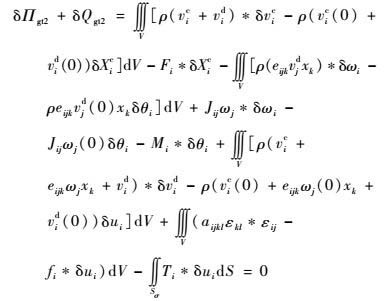 | (7) |
将运动学条件式和几何条件式代入式(7),可得
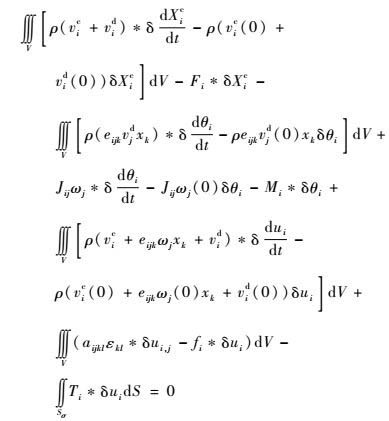 | (8) |
应用Laplace变换中的卷积理论:
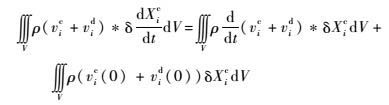 | (9) |
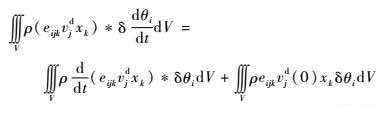 | (10) |
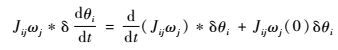 | (11) |
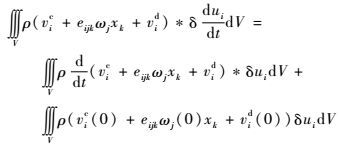 | (12) |
应用Green定理:
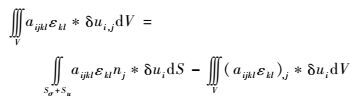 | (13) |
式中:ni为表面法线方向数。
将式(9) ~式(13) 代入式(8),并考虑到位移边界条件,可得
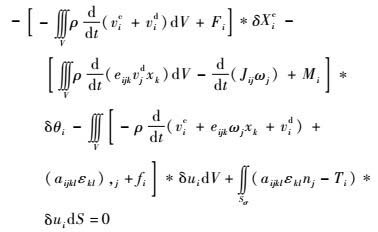 | (14) |
由于δXic、δθi、δui的任意性,可得两类变量刚弹耦合动力学初值问题拟变分原理的拟驻值条件为
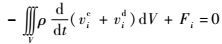 | (15) |
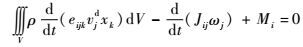 | (16) |
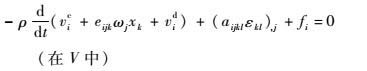 | (17) |
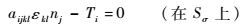 | (18) |
式(15) ~式(18) 即为刚弹耦合动力学的控制方程,与其先决条件一起构成封闭的微分方程组。
2.2 一类变量刚弹耦合动力学控制方程 应用对合变换,由式(15) ~式(18) 得到一类变量刚弹耦合动力学初值问题拟变分原理的拟驻值条件(控制方程)为
 | (19) |
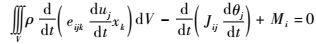 | (20) |
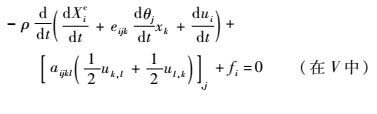 | (21) |
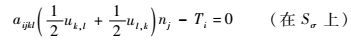 | (22) |
3 算例 对于结构的约束振动问题,目前已经有了较为成熟的理论和方法[28-29]。在航天、航空、航海和机器人动力学中,广泛存在无约束自由体的振动问题[30-31]。需要注意,无约束梁的振型是绕振动中心轴作往复振动,而不是梁的中性轴,且梁的中性轴与振动中心轴之间不仅有刚体平动位移D,还有刚体转动位移C,多部专著[32-33]及文献[34]均给出这类刚性位移的表达式:
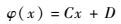 | (23) |
式中:x为空间变量。
刚体平动位移与刚体转动位移和横向弯曲振动叠加,从而使振动时的平衡位置相对于梁的中性轴有某个偏移。这类自由体的振动问题即属于刚弹耦合动力学问题。
下面应用刚弹耦合动力学初值问题的拟变分原理来研究自由梁的振动问题。这类研究一般有2种途径:一是应用推导刚弹耦合动力学初值问题的拟变分原理的拟驻值条件,得到刚弹耦合动力学初值问题的控制方程,应用求解微分方程(或其他类型的方程)的方法,求得问题的精确的或者近似的解析解或者数值解,3.1节算例便是应用刚弹耦合动力学初值问题的控制方程来求解;二是应用变分直接方法,例如Ritz方法,求得问题的近似的解析解或者数值解,3.2节算例便是借助刚弹耦合动力学初值问题的拟变分原理,应用变分直接方法Ritz方法来求解。
3.1 自由梁奇数阶振型 无约束梁的自由振动的奇数阶振型是对称弯曲振型,三阶振型φ3如图 1所示。
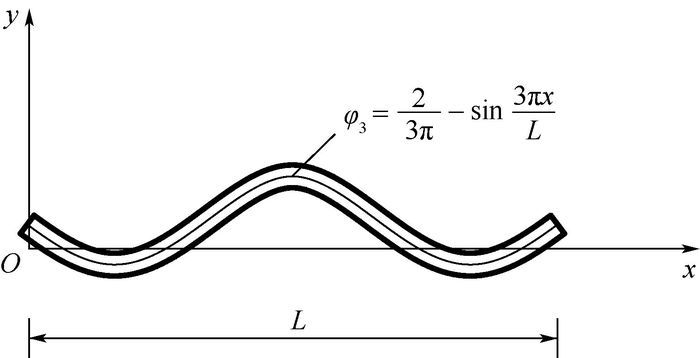 |
| 图 1 无约束梁自由振动的三阶振型 Fig. 1 Third-order vibration mode of unrestrained beam in a free vibration |
| 图选项 |
假设振动的奇数阶振型引起的广义位移为
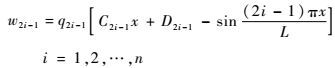 | (24) |
式中:q2i-1=A2i-1sin ω2i-1t,A2i-1为振幅,ω2i-1为角频率;x、y坐标如图 1所示;C2i-1和D2i-1为待定常数;L为梁的长度。
这里,研究的是无约束梁自由振动的情形。自由梁被激振后,仅有由梁的振动加速度导致的惯性力,且惯性力自相平衡。对于这类自由梁奇数阶振型(对称弯曲振型),研究小位移理论的情况,因此可将控制方程式(19) 变换为
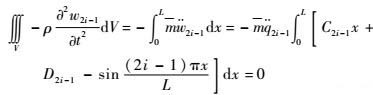 | (25) |
式中:m为单位长度梁的质量。
对式(25) 进行积分,并约去不为零的因子,可得
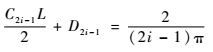 | (26) |
控制方程式(20) 变换为
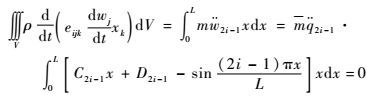 | (27) |
经过积分,并约去不为零的因子,可得
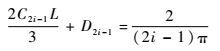 | (28) |
由式(26) 和式(28) 可解得
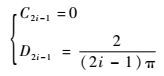 | (29) |
代入式(24) 可得广义位移为
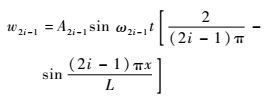 | (30) |
将控制方程式(21) 变换为积分形式,即为一个Lagrange算子:
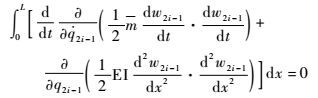 | (31) |
式中:EI为剖面刚度系数。
为了确定奇数阶振型的频率,将式(30) 代入式(31),整理可得
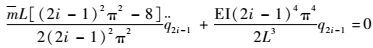 | (32) |
故得奇数阶振型的自振频率为
 | (33) |
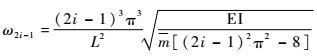 | (34) |
鉴于角频率的标准形式为
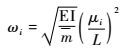 | (35) |
式中:μi为频率参数。
式(35) 是一个重要的关系式, 已经得到实验的验证[28-29]。将式(34) 变换为类似式(35) 的标准形式为
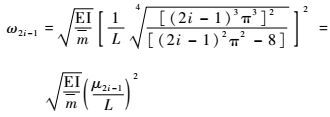 | (36) |
式中:
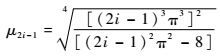 | (37) |
由上述分析可知,自由梁的奇数阶振型是绕振动中心轴作往复振动,而不是梁的中性轴。因此,若自由梁被激振前为水平等速直线运动,则由于自由振动的奇数阶振型的作用,可使自由梁的运动轨迹产生微小的扰动。
3.2 自由梁偶数阶振型 选取自由梁偶数阶振型的振型函数为Ritz方法的坐标函数,应用刚弹耦合动力学初值问题的拟变分原理寻求自由梁偶数阶振型的解析解。
无约束梁的自由振动的偶数阶振型是反对称弯曲振型,二阶振型φ2如图 2所示。
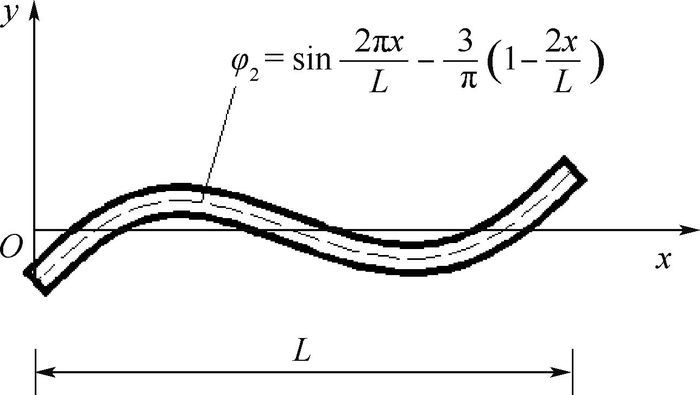 |
| 图 2 无约束梁自由振动的二阶振型 Fig. 2 Second-order vibration mode of unrestrained beam in a free vibration |
| 图选项 |
假设振动的偶数阶振型引起的广义位移为
 | (38) |
式中:q2i=A2isin ω2it,A2i为振幅,ω2i为角频率;C2i和D2i为待定常数。
将振型函数式(38) 作为Ritz方法的坐标函数,代入刚弹耦合动力学初值问题的拟变分原理的泛函式(5) 中,经过类似求拟驻值条件的推导过程,可以求得1个联立方程组,包括3个方程。
方程1:
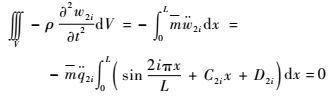 | (39) |
对式(39) 进行积分,并约去不为零的因子,可得
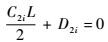 | (40) |
方程2:
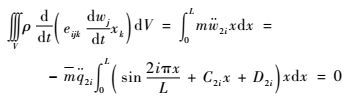 | (41) |
对式(41) 进行积分,并约去不为零的因子,可得
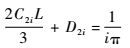 | (42) |
由式(40) 和式(42) 可解得
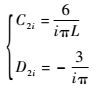 | (43) |
代入式(38) 可得广义位移为
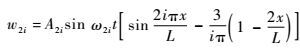 | (44) |
方程3:
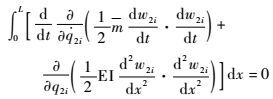 | (45) |
为了确定偶数阶振型的频率,将式(44) 代入式(45),整理可得
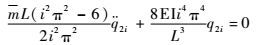 | (46) |
故得偶数阶振型的自振频率为
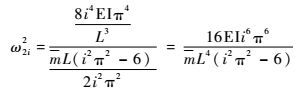 | (47) |
 | (48) |
将式(48) 变换为类似式(35) 的标准形式:
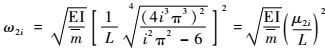 | (49) |
式中:
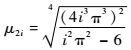 | (50) |
由上述分析可知,自由梁的偶数阶振型是绕振动中心轴作往复振动,而不是梁的中性轴,且梁的中性轴与振动中心轴之间有一个角度。因此,若自由梁被激振前为水平等速直线运动,则由于自由振动的偶数阶振型的作用,可使自由梁的运动姿态产生微小的扰动。
3.3 两点探讨 1) 3.1节和3.2节算例给出的是一般情况。当i取2时,由奇数阶振型可知广义位移为
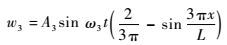 | (51) |
三阶振型如图 1所示。当i取1时,由偶数阶振型可知广义位移为
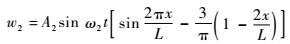 | (52) |
二阶振型如图 2所示。
2) 考虑刚弹耦合效应的计算结果,根据式(37) 和式(50) 计算可得
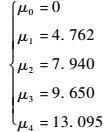 | (53) |
不考虑刚弹耦效应的计算结果为
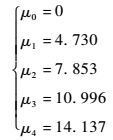 | (54) |
可见二者之间有一定的误差,建议从事理论和实验研究****给予应有的重视。
4 结论 1) 结合刚体动力学初值问题拟变分原理和非保守弹性动力学初值问题拟变分原理,经过确定耦合项和相应的初值项,建立刚弹耦合动力学初值问题拟变分原理。为建立有限元计算模型提供了依据。
2) 应用变分方法,借助于Laplace变换中的卷积理论及Green定理,推导出刚弹耦合动力学控制方程。
3) 应用刚弹耦合动力学初值问题拟变分原理解决自由梁的振动问题,得到问题的近似的解析解。
参考文献
| [1] | 蒋建平, 李东旭. 航天器挠性附件刚柔耦合动力学建模与仿真[J].宇航学报, 2015, 26(3): 270–274. JIANG J P, LI D X. Modeling and simulation for the rigid-flexible coupling[J].Journal of Astronautics, 2015, 26(3): 270–274.(in Chinese) |
| [2] | 戈庆明, 郭军. 作大范围运动刚柔混合体的动力学建模与仿真[J].北京航空航天大学学报, 2011, 37(9): 1110–1114. GE Q M, GUO J. Dynamical modeing and simulaion of rigid-flexible hybrids in large overall motions[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1110–1114.(in Chinese) |
| [3] | 陆毓颖, 刘铸永, 洪嘉振. 挠性航天器系统动力学耦合特性研究[J].空间科学学报, 2012, 32(4): 550–554. LU Y Y, LIU Z Y, HONG J Z. Study on dynamic coupling characteristic of flexible spacecraft[J].Chinese Journal of Space Science, 2012, 32(4): 550–554.DOI:10.11728/cjss2012.04.550(in Chinese) |
| [4] | 游斌弟, 温建民, 张广玉, 等. 航天器薄壳柔性附件展开耦合行为特性研究[J].宇航学报, 2015, 36(6): 640–647. YOU B D, WEN J M, ZHANG G Y, et al. Study on coupling behavior of spacecraft deployment with flexible appendages of shell structure[J].Journal of Astronautics, 2015, 36(6): 640–647.(in Chinese) |
| [5] | 韩清鹏, 高培鑫. 大范围运动条件下的刚柔混合机械臂动力学分析[J].机械设计, 2013, 30(2): 27–31. HAN Q P, GAO P X. Dynamic analysis of rigid-flexible manipulators undergoing a large overall motion condition[J].Journal of Machine Design, 2013, 30(2): 27–31.(in Chinese) |
| [6] | 车仁炜, 陆念力, 薛渊. 基于EFEM的5R机械臂刚柔耦合动力学分析[J].哈尔滨工程大学学报, 2015, 36(11): 1504–1508. CHE R W, LU N L, XUE Y. Dynamic analysis on the rigid-flexible coupled multi-boby system of 5R manipulator based on EFEM[J].Journal of Harbin Engineering University, 2015, 36(11): 1504–1508.(in Chinese) |
| [7] | 张清华, 张宪民. 平面3-RRR柔性并联机器人动力学建模与分析[J].振动工程学报, 2013, 26(2): 239–245. ZHANG Q H, ZHANG X M. Dynamic modeling and analysis of planar 3-RRR flexible parallel robots[J].Journal of Vibration Engineering, 2013, 26(2): 239–245.(in Chinese) |
| [8] | 凌云, 宋爱国, 卢伟. 一种刚、柔机械臂组合的月壤取样器动力学分析[J].宇航学报, 2014, 35(7): 770–776. LING Y, SONG A G, LU W. Dynamics analysis of a rigid-flexible combined lunar sampler[J].Journal of Astronautics, 2014, 35(7): 770–776.(in Chinese) |
| [9] | 梁立孚, 宋海燕, 郭庆勇. 应用Lagrange方程研究刚弹耦合动力学[J].哈尔滨工程大学学报, 2015, 36(4): 456–460. LIANG L F, SONG H Y, GUO Q Y. Research on rigid-flexible coupling dynamics using Lagrange equation[J].Journal of Harbin Engineering University, 2015, 36(4): 456–460.(in Chinese) |
| [10] | WASFY T M, NOOR A K. Computational strategies for flexible multi-body systems[J].Applied Mechanics Review, 2003, 56(6): 553–613.DOI:10.1115/1.1590354 |
| [11] | 钟杭, 王耀南, 李玲, 等. 旋翼飞行机械臂建模及动态重心补偿控制[J].控制理论与应用, 2016, 33(3): 311–320. ZHONG H, WANG Y N, LI L, et al. Rotor-flying manipulator modeling and control with dynamic compensation for gravity offset[J].Control Theory & Applications, 2016, 33(3): 311–320.(in Chinese) |
| [12] | KOJIMA Y, TANIWAKI S, OKAMI Y. Dynamic simulation of stick-slip motion of a flexible solar array[J].Control Engineering Practice, 2008, 16(6): 724–735.DOI:10.1016/j.conengprac.2006.11.014 |
| [13] | 李发宗, 童水光, 王相兵, 等. 船用挖掘机机械臂刚柔耦合动力学及特性研究[J].振动与冲击, 2014, 33(20): 157–163. LI F Z, TONG S G, WANG X B, et al. Rigid-flexible coupling dynamics and characteristics of marine excavator's mechanical arm[J].Journal of Vibration and Shock, 2014, 33(20): 157–163.(in Chinese) |
| [14] | 朴明伟, 杨晶, 赵强, 等. 高铁车辆刚柔耦合仿真奇异性及其处理对策[J].计算机集成制造系统, 2015, 21(9): 2458–2466. PIAO M W, YANG J, ZHAO Q, et al. Rigid-flexible coupling simulation singularity of high-speed rolling stocks and transaction strategy[J].Computer Integrated Manufacturing Systems, 2015, 21(9): 2458–2466.(in Chinese) |
| [15] | 刘莉, 陈树霖, 周思达, 等. 脉冲子结构与有限元刚-弹混合连接的子结构方法[J].航空学报, 2015, 36(8): 2670–2680. LIU L, CHEN S L, ZHOU S D, et al. A substructure method for coupling impulse response functions with finite element models via rigid-elastic joints[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2670–2680.(in Chinese) |
| [16] | 谢琴, 吴运新. 液压挖掘机刚柔耦合动力学分析[J].机械传动, 2016, 40(5): 101–104. XIE Q, WU Y X. Rigid-flexible coupling dynamics analysis of hydraulic excavator[J].Journal of Mechanical Transmission, 2016, 40(5): 101–104.(in Chinese) |
| [17] | 杨丽, 孙志礼, 柴小冬, 等. 供弹机虚拟样机刚柔耦合动力学特性[J].中国工程机械学报, 2014, 12(5): 377–383. YANG L, SUN Z L, CHAI X D, et al. Feeder virtual prototyping on rigid-flexible coupling dynamical properties[J].Chinese Journal of Construction Machinery, 2014, 12(5): 377–383.(in Chinese) |
| [18] | BASHER H A.Modeling and simulation of flexibe robot manipulator with a prismatic joint[C]//Proceedings of IEEE Southeast Conference.Piscataway, NJ:IEEE Press, 2007:255-260. |
| [19] | 马兴瑞, 王本利, 苟兴宇. 航天器动力学——若干问题进展及应用[M].北京: 科学出版社, 2001. MA X R, WANG B L, GOU X Y. Spacecraft dynamics—Development and application in a few problems[M].Beijing: Science Press, 2001.(in Chinese) |
| [20] | 黄文虎, 曹登庆, 韩增尧. 航天器动力学与控制的研究进展与展望[J].力学进展, 2012, 42(4): 367–394. HUANG W H, CAO D Q, HAN Z Y. Advances and trends in dynamics and control of spacecrafts[J].Advances in Mechanics, 2012, 42(4): 367–394.DOI:10.6052/1000-0992-11-171(in Chinese) |
| [21] | 岳宝增, 宋晓娟. 具有刚-柔-液-控耦合的航天器动力学研究进展[J].力学进展, 2013, 43(1): 162–172. YUE B Z, SONG X J. Advances in rigid-flexible-liquid-control coupling dynamics of spacecraft[J].Advances in Mechanics, 2013, 43(1): 162–172.(in Chinese) |
| [22] | 梁立孚, 宋海燕, 樊涛, 等. 非保守系统的拟变分原理及其应用[M].北京: 科学出版社, 2015: 62-70, 137-138. LING L F, SONG H Y, FAN T, et al. Quasi-variational principles of non-conservative system and Their applications[M].Beijing: Science Press, 2015: 62-70, 137-138.(in Chinese) |
| [23] | GURTIN M E. Variationnal principles for elastodynamics[J].Archive for Rational Mechanics and Analysis, 1964, 16(1): 34–50. |
| [24] | 罗恩. 关于线弹性动力学中各种Gurtin型变分原理[J].中国科学:A辑, 1987(9): 936–948. LUO E. Gurtin-type variational principles in linear elastodynamics[J].Science in China(Series A), 1987(9): 936–948.(in Chinese) |
| [25] | 罗恩, 朱慧坚. 有限变形弹性动力学的非传统Gurtin型变分原理[J].固体力学学报, 2003, 24(1): 1–7. LOU E, ZHU H J. Unconventional Gurtin-type variational principles for finite deformation elastodynamics[J].Acta Mechanica Solida Sinica, 2003, 24(1): 1–7.(in Chinese) |
| [26] | 梁立孚, 周平, 刘宗民. 刚体动力学初值问题的拟变分原理及其应用[J].哈尔滨工程大学学报, 2009, 30(10): 1091–1096. LING L F, ZHOU P, LIU Z M. Quasi-variational principles of the initial value problem in rigid-body dynamics and their applications[J].Journal of Harbin Engineering University, 2009, 30(10): 1091–1096.(in Chinese) |
| [27] | 梁立孚, 宋海燕, 李海波. 航天分析动力学[M].北京: 科学出版社, 2016: 125-128. LING L F, SONG H Y, LI H B. Analytical dynamics of aerospace systems[M].Beijing: Science Press, 2016: 125-128.(in Chinese) |
| [28] | 克拉夫R W, 彭津J. 结构动力学[M]. 王光远, 等译. 北京: 高等教育出版社, 2006: 294-306. CLOUGH R W, PENZIEN J.Dynamics of structures[M].WANG G Y, et al, translated.Beijing:Higher Education Press, 2006:294-306(in Chinese). |
| [29] | 诸德超, 邢誉峰. 工程振动基础[M].北京: 北京航空航天大学出版社, 2004: 168-277. ZHU D C, XING Y F. Engineering vibration foundation[M].Beijing: Beihang University Press, 2004: 168-277.(in Chinese) |
| [30] | 姚熊亮. 舰船结构振动冲击与噪声[M].北京: 国防工业出版社, 2007: 168-178. YAO X L. Vibration ahock and noise of warship structure[M].Beijing: National Defend Industry Press, 2007: 168-178.(in Chinese) |
| [31] | 邱吉宝, 张正平, 李海波. 航天器与运载火箭耦合分析相关技术研究进展[J].力学进展, 2012, 42(4): 416–434. QIU J B, ZHANG Z P, LI H B. Progresses in research on coupled analysis technology for space vehicle and launch vehicles[J].Advances in Mechanics, 2012, 42(4): 416–434.DOI:10.6052/1000-0992-11-203(in Chinese) |
| [32] | 李东旭. 高等结构动力学[M].北京: 科学出版社, 2010: 319-329. LI D X. Advanced atructural dynamics[M].Beijing: Science Press, 2010: 319-329.(in Chinese) |
| [33] | 史密斯M S. 结构动力学[M]. 五〇四翻译小组, 译. 北京: 国防工业出版社, 1976: 71-75. SMITH M S.Structural dynamics[M].504 Translation Group, translated.Beijing:National Defend Industry Press, 1976:71-75(in Chinese). |
| [34] | 李海波, 宋海燕, 梁立孚. 确定无约束梁耦合振型的一种途径[J].强度与环境, 2011, 38(2): 6–12. LI H B, SONG H Y, LING L F. An approach of coupled vibration mode determined of unrestrained beam[J].Structure & Environment Engineering, 2011, 38(2): 6–12.(in Chinese) |
