为便于装配或减小工作状态变化对转子系统动力特性的不利影响,在支承结构中设计合理的间隙是有效的技术途径,称为支承松动设计。支承松动设计可以有效减小多支点转子系统支承不同心的影响,即利用转子与支承之间的间隙,消除支承不同心对转子的附加约束,但支承松动引起的支承刚度非连续特征,对高速柔性转子动力特性有着极其不利的影响,所以为了保障采用支承松动设计的高速柔性转子动力特性良好,有必要研究支承松动力学特征及其对柔性转子动力特性的影响。
国内外****对转子结构系统支承松动的研究主要分为2个方面:一方面是对支承刚度分段线性转子系统动力学求解方法的研究。Kim等[1]提出利用光滑函数代替分段函数的方法研究分段线性转子系统的频响特性;Karpenko等[2]创建了单点法和多点法对带有隔振环的分段线性转子系统进行数值求解;Ji[3]和Lee[4]等分别采用多尺度法和改造的传递矩阵法求解非线性方程,研究支承松动转子系统振动特性;闫政涛等[5]利用多项式拟合改造刚度分段线性系统恢复力表达式,采用多尺度法对非线性方程进行求解。另一方面是对支承松动故障形成机理及动力学特征的研究,供振动检测和故障诊断时参考。Tiwari等[6]的研究表明松动间隙增加时,支承松动转子会出现复杂的非线性响应;Ehrich[7-8]通过实验证明转子复杂的非线性响应特征是由松动间隙导致的;Goldman和Muszynska[9-11]考虑了支承刚度和阻尼及切向摩擦的影响,研究表明支承松动转子存在同步及次同步振动成分,并伴有高次谐波振动成分,一定条件下可能产生混沌运动;Mevel和Guyader[12]通过实验研究了类似支承松动的滚珠轴承支承转子产生混沌的途径,研究结果表明转子可通过次谐波和拟周期运动的途径产生混沌运动;李振平等[13]通过研究轴心轨迹频谱图等识别松动故障特征,发现转子松动端轴心轨线图呈“柱状”结构; 姚红良等[14]研究表明松动故障降低了转子固有频率,使共振区提前到来,松动故障转子呈“软式”非线性特性,在响应谱图上2倍频3倍频谱线较明显。
综上,国内外****在支承松动转子系统动力学求解方法及其动力学特征等方面开展了研究工作,对支承松动引起的支承刚度非连续特征及其对柔性转子系统动力特性影响的研究较少,而这正是多支点柔性转子动力特性优化设计亟需的理论方法。本文根据支承松动的结构特征,探索结构松动引起支承刚度非连续变化的产生机理,基于支承松动的结构特征和力学特征,建立支承松动转子系统动力学模型,分析支承松动转子存在混沌运动的条件。根据多支点转子系统动力学特性与支承结构位置、刚度的相关性,采用优化支承位置和支承刚度的方法,降低转子动力特性对非连续支承刚度的敏感性,从而提高多支点柔性转子系统动力特性的稳健性,为多支点高速柔性转子系统的动力学优化设计提供理论方法。
1 支承松动及动力学模型 1.1 支承松动结构特征 如图 1所示,轴承弹支以一定的间隙装入轴承机匣中,间隙中引入润滑系统的压力滑油形成一定厚度的挤压油膜。当油膜受到挤压,在液体动力特性作用下,为转子提供油膜刚度,而当转子振幅增加使轴承弹支间隙很小或为零时,支承结构刚度起主导作用。同时,限幅环为典型支承松动结构,当中介支点振动过大,中介轴承弹支会与限幅环接触,对转子产生突变的约束作用,使中介支点的支承刚度产生阶跃变化。对于轴承而言,由于轴与外壳的散热条件不同,为防止内圈和外圈之间温度差造成滚动体卡滞,在轴承内部设计较大的轴承游隙,会使转子产生支承松动引起支承刚度改变。
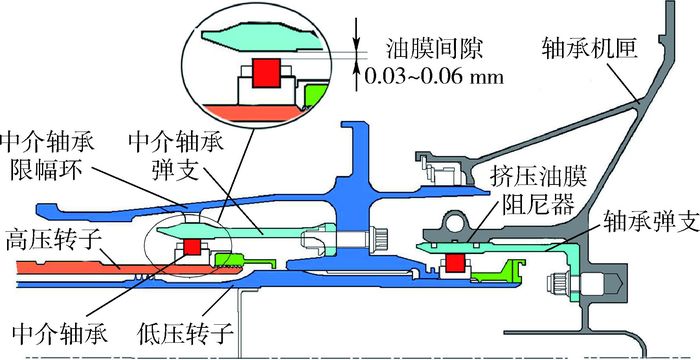 |
| 图 1 航空发动机涡轮支点结构 Fig. 1 Supporting structure of aero-turbine |
| 图选项 |
1.2 支承松动力学特征 支承松动的力学特征是使转子结构系统产生阶跃非连续支承刚度。如图 2所示,对于支承松动转子结构系统,当转子在间隙内微幅振动时,支承不起约束作用,为转子提供的支承刚度为零;当转子振幅增加超过间隙时,支承会对转子横向位移产生约束,为转子提供支承刚度。从而在支承约束作用产生或消失的瞬间,支承刚度会随振幅变化产生阶跃,其导数不连续,故具有非连续特征。
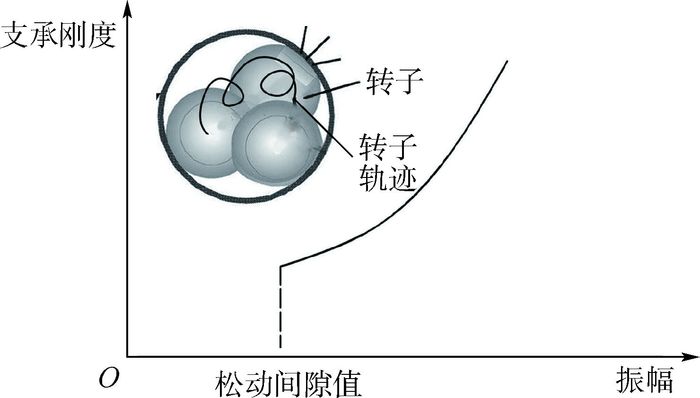 |
| 图 2 支承松动处支承刚度随振幅变化特征 Fig. 2 Change of stiffness of supporting structure with amplitude at position of bearing with looseness |
| 图选项 |
支承刚度的阶跃变化,会导致支承松动转子系统支反力随转子振幅呈非线性变化,支承对转子产生约束的瞬间为转子提供支反力,并且根据图 2所示支承刚度变化情况,支反力会随振幅增加迅速增大,使支承松动转子系统具有强非线性特征。同时,转子在不平衡力作用下可在支承内冲击、滚动、滑动、反弹,其运动轨迹具有明显的随机性,从而转子系统支承松动处的支承刚度会产生非确定性变化,使转子系统具有非确定性特征。
1.3 支承松动转子系统动力学模型 采用支承刚度随振幅变化具有阶跃特征的支承模型模拟支承松动,建立力学特征等效的支承松动转子系统的力学模型如图 3所示,两端由滚动轴承支承,转子与支承之间为无质量弹性轴,在弹性轴中间安装一个带有质量偏心薄圆盘,O、O′为支承中心,O1为轮盘形心,Kf和Df分别为松动处支承的刚度系数和径向阻尼,M和K分别为转子的模态质量和模态刚度,R为转子振幅,Rr为转轴的半径,c为静止时转子与支承之间的间隙,ω为转子自转速度,Oe为质量偏心位置,m、e和δ分别为转子质量、偏心距及初始相位角。
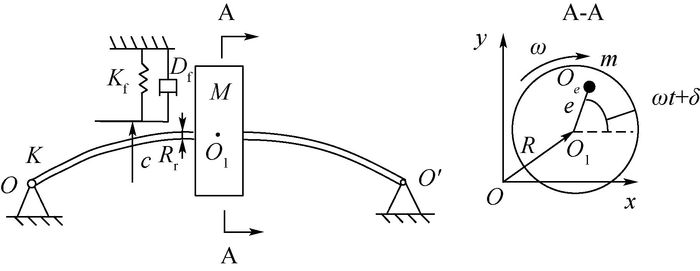 |
| 图 3 支承松动转子系统力学模型 Fig. 3 Mechanical model of rotor system supported by bearing with looseness |
| 图选项 |
如图 4所示为支承松动处转子的受力图,N=Df(dR/dt)+Kf(R-c)为松动处转子和支承之间的径向力,Ft为支承约束转子时产生的切向力,由黏性摩擦力和干摩擦力组成。对于产生支承松动的转子,其运动状态分为2个阶段:松动处的支承不约束转子,支反力为零阶段;支承约束转子横向位移,为转子提供支反力阶段。
 |
| 图 4 支承松动转子受力图 Fig. 4 Force diagram of rotor supported by bearing with looseness |
| 图选项 |
当支承松动处转子振幅小于间隙时,支承不起约束作用。此时,转子运动微分方程为
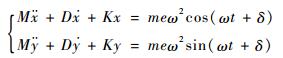 | (1) |
式中:x和y为转子在正交方向上的横向位移分量;D为转子的模态阻尼。
为考虑支承起约束作用阶段转子的运动,将方程式(1) 改写为极坐标形式。根据转换关系x=R(t)cos ?(t),y=R(t)sin ?(t),其中?(t)为转子振幅R(t)和x轴的夹角。转子的运动微分方程变为
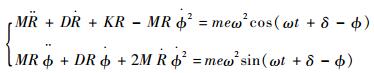 | (2) |
当支承松动处转子振幅超过间隙时,支承约束转子横向位移,根据Yamamoto等[15]提出的轴承支反力拟合公式,得到松动处支承起约束作用时的支反力表达式为F=Kf1(R-c)+Kf3(R-c)3,其中Kf1、Kf3分别为支承的线性和非线性刚度系数。此时,考虑松动处转子与支承之间的作用力,并将式(2) 第2个方程两边同乘R,将其变为转子的力矩平衡方程,得到转子运动微分方程:
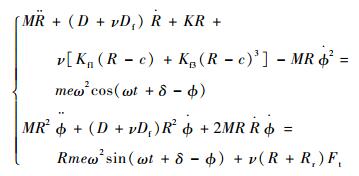 | (3) |
式中:
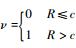
 | (4) |
式(4) 中等号右边的两项分别代表转子与支承之间的黏性摩擦力和干摩擦力,其中
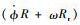
根据得到的支承松动转子系统动力学模型,转子振幅R的变化对运动方程的模态刚度有直接影响,根据力学特征分析结果,在振幅达到间隙值c时,松动处支承刚度会产生阶跃,从而引起转子系统模态刚度阶跃变化。根据运动微分方程式(3),受非线性支承刚度系数影响,随振幅继续变化,模态刚度会呈非线性变化。而系统模态刚度会直接影响转子系统固有频率,从而转子系统固有频率会随支承刚度阶跃而改变,进而转子系统共振点会产生突变,引起转子系统复杂的振动响应。尤其对于工作在多阶临界转速之上的高速柔性转子,工作转速以下存在多阶共振稳定点。根据对支承松动力学特征的分析,支承松动转子系统具有高度非线性和非确定性特征,受支承刚度阶跃的影响,转子系统振动会在多个具有突变特征的共振稳定点之间随机跳变,因此当转子动力特性对支承刚度变化敏感时,支承松动会引起混沌运动产生,使转子振动剧烈无法正常运转。
Goldman和Muszynska[11]对支承松动转子的动力学行为进行了数值和实验研究,其研究结果表明:当松动处支承对转子约束作用在一个转动周期内多次突变时,支承松动引起支承刚度阶跃变化,会使共振状态下转子的运动轨迹呈现复杂无规则特征,验证了当转子动力特性对支承刚度变化敏感时,支承松动可使转子产生混沌运动。
2 支承松动对高速柔性转子动力特性影响 2.1 多支点柔性转子系统动力学设计 航空发动机中,工作转速在弯曲临界转速之上的转子为高速柔性转子,如涡轴发动机的动力涡轮转子。由于该类转子弯曲临界转速低,工作在多阶临界转速之上,在启动过程中通过临界转速时会产生较大的振动,为防止振动变形过大,影响叶轮机效率,因此采用多支点支承方案设计,以加强转子局部刚度。但多支点支承对制造及装配工艺要求极高,往往不能满足设计要求,多个支点的中心不能精确地在一条直线上,从而在支点约束作用下,转子的轴线会发生相对偏移或变形,造成转子轴线不能精确地在一条直线上,进而引起支承不同心激励问题,如图 5所示。
 |
| 图 5 多支点柔性转子支承不同心力学模型 Fig. 5 Mechanical model of bearing misalignment on multi-supported flexible rotor |
| 图选项 |
支承松动设计可以有效减小支承不同心的影响,利用转子与支承之间的间隙,可以消除装配时支承不同心对转子的附加约束。如图 6所示,当利用其中2个支点确定转子轴线位置,如1、3号支点,其余支点采用支承松动设计时,由于支承和转子之间存在间隙,产生支承不同心时,松动处的支承在转子静止时不起约束作用,因此,装配时转子轴线仍可以与1、3号支点确定的直线重合,从而减小支承不同心对多支点柔性转子动力特性的不利影响。
 |
| 图 6 采用支承松动设计的多支点柔性转子力学模型 Fig. 6 Mechanical model of multi-supported flexible rotor using bearing with loosening design |
| 图选项 |
由于高速柔性转子会因支承松动而具有高度非线性和非确定性特征,支承刚度的非连续变化,可能会引起转子产生混沌运动,使转子振动剧烈无法正常运转。所以,为得到多支点柔性转子支承松动设计的方法,需研究支承松动位置及支承刚度变化范围,对转子动力特性的影响规律,以保证多支点柔性转子采用支承松动设计具有良好的动力特性。
2.2 支承刚度突变对柔性转子系统固有特性影响 如图 7所示,为典型多支点高速柔性转子结构,在轴的前后两端各放置2个支点,使整根轴两端近似形成固支约束,以增加两端的局部刚度,使功率输出稳定,同时增加涡轮的角向刚度,减小涡轮漏气损失,从而改善动力涡轮转子工作性能。各支点刚度设计值如表 1所示。高速柔性转子前4阶模态振型如图 8所示。
 |
| 图 7 多支点高速柔性转子结构 Fig. 7 Structure of multi-supported high-speed flexible rotor |
| 图选项 |
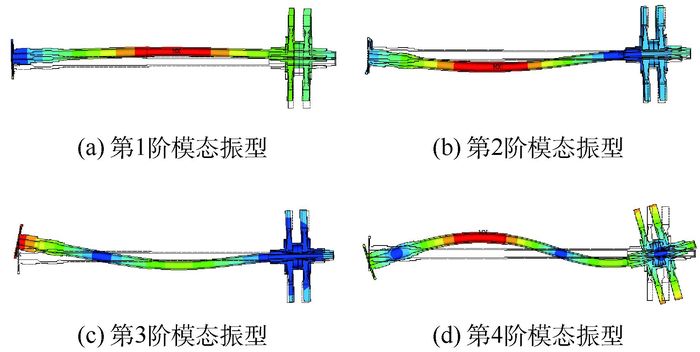 |
| 图 8 高速柔性转子前4阶模态振型 Fig. 8 Four preceding modal shapes of high-speed flexible rotor |
| 图选项 |
表 1 高速柔性转子各支点支承刚度设计值 Table 1 Designed bearing stiffness value of supporting structures of high-speed flexible rotor
| 支点编号 | 1号(滚珠) | 2号(滚棒) | 3号(滚棒) | 4号(滚棒) |
| 支承刚度/ (106N·m-1) | 5.0 | 1.4 | 3.5 | 2.8 |
表选项
2.2.1 支承位置对柔性转子系统固有特性影响 对于两端简支的等截面圆轴,其中间位置处等效刚度为
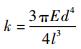 | (5) |
式中:l为支点跨度; d为轴的直径; E为轴的弹性模量。
由于松动处支点在转子振幅小于松动间隙时不起约束作用,会直接影响转子的支点跨度,根据式(5) 支点跨度减小时,转子等效刚度会增强,有利于转子抗变形能力提高。而支承松动支点位置与叶轮之间距离越大,松动间隙对叶轮角向刚度的削弱作用越小。所以设计支承松动时,需对支承松动位置进行权衡选取,使支点跨度既能保证转子的局部刚度和角向刚度较强,又能令支承松动对转子动力特性影响较小,以保证转子动力特性良好。
为简化计算,取支承刚度突变的极限状态进行比较,即将松动位置处的支承刚度取为0及设计值进行计算,进而分析支承松动对转子的影响。
对于涡轮端,3、4号支点与涡轮距离相同,因此3、4号支点松动对涡轮角向刚度影响相同,并且3、4号支点分别采用支承松动设计时,涡轮处等效刚度分别为2.48×105 N/m、2.33×105 N/m,相差不大。这是因为3号支点松动会使转子支点跨度增大,而4号支点松动会使涡轮产生悬臂结构,对涡轮处等效刚度均有较大的削弱作用。
如图 9所示,为采用有限元法计算得到不同位置支点采用支承松动设计对转子系统临界转速的影响情况。可以看出,不同位置支点松动对转子系统各阶临界转速的影响不同,4号支点松动对前2阶临界转速影响较大,3号支点松动仅对第1阶临界转速有影响且影响较大。
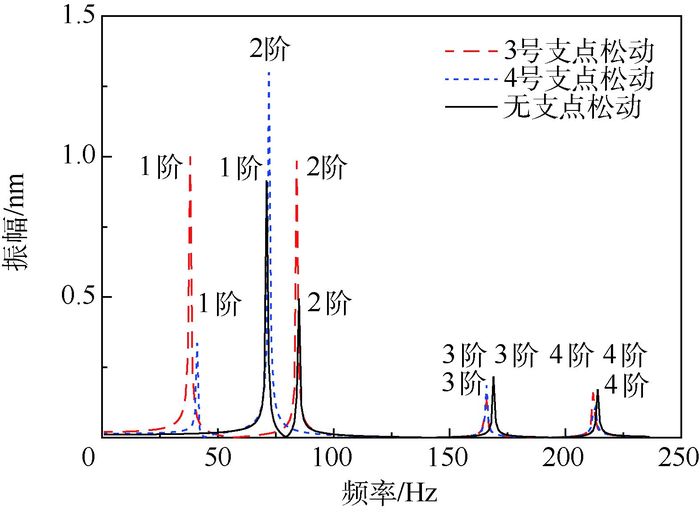 |
| 图 9 不同位置支点支承松动对柔性转子临界转速影响 Fig. 9 Influence of different positions of bearing with looseness on flexible rotor's critical speed |
| 图选项 |
可以采用同样的方法,选取转子前端的支承松动位置,但考虑1号支点靠近输出端,为保证功率输出稳定,1号支点不宜采用支承松动设计,因此令2号支点采用支承松动设计。
2.2.2 支承刚度对柔性转子系统固有特性影响 对于转子系统而言,支承刚度的非连续变化很可能会使转子系统动力特性发生巨大变化。因此确定松动支承位置后,还需对松动处支承刚度变化范围进行优化,令其变化范围位于对转子系统动力特性影响不敏感的区域内,保证柔性转子的动力特性稳定。在设计时,可根据模态频率和振型随支承刚度变化的规律,分析支承刚度对转子模态频率和振型的敏感性,进而指导松动处支承刚度变化范围的设计选取。
为了减少轴的材料、尺寸和弯曲刚度不同的影响,在计算分析转子支承刚度对其动力学特性影响时,支承刚度采用相对关键截面弯曲刚度的当量支承刚度表示,当量支承刚度定义为
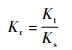 | (6) |
式中:Ks为转子系统支点位置处的等效刚度; Kt为支承刚度。
如图 10所示,以4号支点为例,计算得到4号支点当量支承刚度变化对转子系统临界转速的影响规律。从图中可以看出,当设计松动处当量支承刚度变化范围位于[0, 100]内时,支承松动引起支承刚度的非连续变化基本不会引起转子各阶临界转速的改变,转子系统的动力特性较稳定。
 |
| 图 10 4号支点当量支承刚度对柔性转子共振频率影响 Fig. 10 Influence of equivalent supporting stiffness of the fourth supporting structure on flexible rotor's resonant frequency |
| 图选项 |
由以上计算分析可知,为保证采用支承松动设计的高速柔性转子动力学性能较优,首先需对支承松动位置进行优化,使其既能保证转子有足够的局部刚度和角向刚度,又能保证支承松动对转子动力特性影响较小。然后对松动处支承刚度变化范围进行优化设计,使其位于对转子系统动力特性影响不敏感的区域内,使高速柔性转子动力特性对支承刚度非连续变化不敏感,保证采用支承松动设计的高速柔性转子动力特性稳定。
2.3 多支点柔性转子系统动力学设计流程 通过动力学模型的分析和计算结果,总结得到多支点转子支承松动设计需遵循以下流程:首先,在充分考虑发动机转子动力特性、转静子间隙控制以及结构间振动隔离等多方面因素的基础上,设计转子的支承方案、支承刚度。然后为减小多支点不同心的影响,从中选取采用支承松动设计的支点,选取时不仅需要满足支承松动对转子动力特性的影响较小的要求,而且还要求转子具有较强局部刚度,因此需要优选支承松动位置。确定支承松动支点位置后,为使柔性转子动力特性对支承刚度非连续变化不敏感,需对支承刚度变化范围进行优化设计,使其位于对转子系统动力特性影响不敏感的区域内,保证采用支承松动设计的高速柔性转子动力特性稳定。
3 结论 1) 分析了转子支承结构松动引起支承刚度非连续变化的产生机理,即支承的约束作用可随转子振幅变化产生突变,这种突变的约束作用使支承刚度产生阶跃,其导数不连续,故具有非连续特征。
2) 基于支承松动的结构特征和力学特征,建立了支承松动转子动力学模型,进而通过分析支承松动转子动力特性稳定性,得到当转子产生支承松动而具有强非线性和非确定性特征时,转子动力特性对支承刚度变化敏感时,受支承刚度阶跃影响,支承松动转子系统会产生混沌运动。
3) 研究内容为多支点高速柔性转子系统的动力学优化设计提供了设计方法:对支承松动位置及支承刚度进行优化设计,并选择合适的设计参数,使转子动力特性对支承刚度非连续变化不敏感,可以减小支承不同心影响,并保证采用支承松动设计的高速柔性转子动力特性稳定。
限于篇幅,支承松动对柔性转子系统振动响应影响将在后续工作中研究。
参考文献
| [1] | KIM T C, ROOK T E, SINGH R. Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity[J].Journal of Sound & Vibration, 2003, 263(3): 665–678. |
| [2] | KARPENKO E V, WIERCIGROCH M, PAVLOVSKAIA E E, et al. Piecewise approximate analytical solutions for a Jeffcott rotor with a snubber ring[J].International Journal of Mechanical Sciences, 2002, 44(3): 475–488.DOI:10.1016/S0020-7403(01)00108-4 |
| [3] | JI Z, ZU J W. Method of multiple scales for vibration analysis of rotor shaft systems with non-linear bearing pedestal model[J].Journal of Sound & Vibration, 1998, 218(218): 293–305. |
| [4] | LEE A C, KANG Y, LIU S L. Steady-state analysis of a rotor mounted on nonlinear bearings by the transfer matrix method[J].International Journal of Mechanical Sciences, 1993, 35(6): 479–490.DOI:10.1016/0020-7403(93)90037-U |
| [5] | 闫政涛, 翁雪涛, 朱石坚, 等. 刚度分段线性系统的自由振动解析研究[J].噪声与振动控制, 2010, 30(6): 18–22. YAN Z T, WENG X T, ZHU S J, et al. Analytical solution of free vibration of systems with piecewise linear stiffness[J].Noise and Vibration Control, 2010, 30(6): 18–22.(in Chinese) |
| [6] | TIWARI M, GUPTA K, PRAKASH O. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J].Journal of Sound & Vibration, 2000, 238(5): 723–756. |
| [7] | EHRICH F F. High order subharmonic response of high speed rotors in bearing clearance[J].Journal of Vibration & Acoustics, 1988, 110(1): 9–16. |
| [8] | EHRICH F F. Subharmonic virbration of rotors in bearing clearance[J].Journal of Engineering for Industry, 1967, 89(3): 381–389.DOI:10.1115/1.3610057 |
| [9] | GOLDMAN P, MUSZYNSKA A. Chaotic behavior of rotor-stator systems with rubs[J].Journal Engineering for Gas Turbines and Power, 1994, 116(3): 692–701.DOI:10.1115/1.2906875 |
| [10] | GOLDMAN P, MUSZYNSKA A. Dynamic effects in mechanical structures with gap and impacting:Order and chaos[J].Journal of Vibration and Acoustics, 1994, 116(3): 541–547. |
| [11] | MUSZYNSKA A, GOLDMAN P. Chaotic response of unbalanced rotor/bearing/stator systems with looseness or rubs[J].Chaos, Solitons & Fractals, 1995, 5(9): 1683–1704. |
| [12] | MEVEL B, GUYADER J L. Experiments on routes to chaos in ball bearings[J].Journal of Sound & Vibration, 2008, 318(3): 549–564. |
| [13] | 李振平, 罗跃纲, 姚红良, 等. 转子系统支承松动的非线性动力学及故障特征[J].东北大学学报(自然科学版), 2002, 23(11): 1048–1051. LI Z P, LUO Y G, YAO H L, et al. Dynamics and fault characteristics of rotor-bearing system with pedestal looseness[J].Journal of Northeastern University (Natural Science), 2002, 23(11): 1048–1051.DOI:10.3321/j.issn:1005-3026.2002.11.008(in Chinese) |
| [14] | 姚红良, 刘长利, 张晓伟, 等. 支承松动故障转子系统共振区动态特性分析[J].东北大学学报(自然科学版), 2003, 24(8): 798–801. YAO H L, LIU C L, ZHANG X W, et al. Dynamics of pedestal looseness rotor system near the critical speed region[J].Journal of Northeastern University (Natural Science), 2003, 24(8): 798–801.(in Chinese) |
| [15] | YAMAMOTO T, ISHIDA Y, IKEDA T. Summed-and-differential harmonic oscillations of an unsymmetrical shaft[J].Bulletin of JSME, 1981, 24(187): 183–191.DOI:10.1299/jsme1958.24.183 |
