为了揭示此类分离流动的非定常特性及其对于气动、结构的影响,国内外****进行了许多研究工作。Valkov和Tan[2]通过数值模拟捕捉到了压气机叶片叶背流向旋涡的结构,并研究了其对于流场性能的影响。Gbadebo等[3]进行了有关三维分离区的实验和数值研究,对分离流的结构做了分类与展示,指出基于三维时均Navier-Stokes方程的定常CFD计算可以较好地模拟转子附近的分离区流动。Mailach等[4]利用非定常CFD对转子通道内叶尖泄漏涡和分离流的传播过程进行了数值计算,并探讨了上游尾迹对其影响。Hah等[5]对转子叶片排近失速状态进行了全周非定常计算,证明了近失速流场受叶尖附近分离流动的影响很大,并进一步采取了大涡模拟技术, 更加细致地捕捉到了旋涡的非定常结构与特性。Kielb等[6]研究了叶轮机在周向流动不稳定状态下的叶片非同步振动响应问题,指出叶背分离的脱落是造成非同步振动的重要原因之一。Mailach和Vogeler[7]通过实验对旋转失速过程中压气机叶片表面气动力对于分离流的瞬态响应进行了研究。Holzinger等[8]通过实验研究了跨声速压气机转子上发生的2类自激振动现象,旋转不稳定诱导自激振动和颤振,并通过非轴对称处理机匣成功地抑制了颤振的发生,全面总结了发生在跨声速压气机转子上的不同类型的叶片振动,通过研究振动现象的内在机理,对理解流动诱发叶片振动做出了贡献。
随着计算机及计算技术的快速发展,利用数值求解流固耦合的方法来研究流动诱发振动问题逐渐成为可能[9-11]。笔者在前期工作中[12]通过数值和实验方法研究了低速轴流压气机旋转失速对叶片振动响应的影响,证明了这种双向迭代流固耦合计算方法在研究压气机旋转失速诱发叶片振动响应方面的可行性与辨识能力。
本文以某无进口导叶的高压压气机首级为研究对象,针对低转速大攻角流动条件,对近失速状态和近最高效率点状态进行非定常数值模拟,详细分析了叶背分离流在近失速状态下的非定常特性和演化过程。针对转子叶片对于叶背分离流的瞬态动力响应问题,利用流固耦合求解技术,探究叶背分离流对叶片气弹特性的影响,加深对流动诱发叶片振动机理的理解。
1 数值方法和计算模型 1.1 数值方法 本文使用商用软件CFX进行非定常流场求解,使用CFX/ANSYS迭代模式,实现流体域与固体域的迭代耦合数值计算。采用非定常时间推进方法对全周流场的演化进行非定常数值研究。控制方程为非定常雷诺平均Navier-Stokes方程,湍流模型采用k-ε模型,综合考虑了计算准确性[13]及计算时间等因素的影响。空间离散采用迎风格式,时间上采用带双时间步的二阶后差格式。
利用双向迭代流固耦合方法研究脱落的叶背分离流对叶片振动的影响。流体域求解采用了与非定常数值计算相同的求解方法,微分形式的非定常流动质量守恒方程、动量守恒方程及能量守恒方程可写为
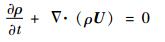 | (1) |
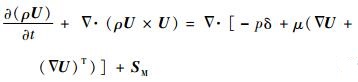 | (2) |
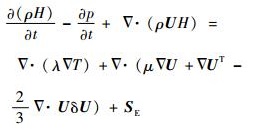 | (3) |
式中:U为速度矢量;H为总焓;ρ为密度;p为压力;δ为克罗内克符号;T为温度;μ为动力黏性系数;λ为导热系数;SM和SE分别为动量源项和能量源项。
状态方程为
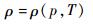 | (4) |
标准k-ε湍流模型包括湍动能k和耗散率ε的输运方程,即
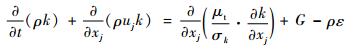 | (5) |
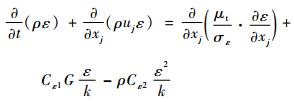 | (6) |
式中:
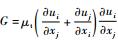
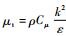
固体域叶片的瞬态响应通过求解结构动力学方程获得。假设转子各个叶片的力学特性相同,其有限元形式的固体模型结构控制方程为
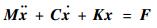 | (7) |
式中:x为位移向量;M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为气动载荷向量。
流固耦合计算中,采用守恒插值法将气动载荷、网格变形等信息在两域之间传递,在流固耦合交界面上,两域分别满足运动学及动力学条件,即法向速度及法向压力保持一致。
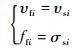 | (8) |
式中:υfi为流体侧法向速度;υsi为固体侧法向速度;ffi为流体侧法向压力;σsi为固体侧法向压力。
同时,在流固交界面上满足载荷的一致性和能量的守恒性。有限单元面上的节点力合力等于流体域对应面上压力的积分;有限单元面上的节点力对节点位移所做功等于流体域对应面上的压力对位移所做的功。
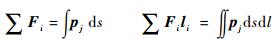 | (9) |
式中:Fi为有限单元面上的节点力;pj为流体域对应面上压力;li为节点位移。
在耦合迭代过程中,流体域和固体域分别进行各域控制方程求解,在耦合交界面上,将位移及压力依据协调条件进行转换,相互交换、反馈信息并反复求解,直至结果趋于稳定,从而达到求解整体耦合场的目的。
1.2 计算模型与边界条件 本文的研究对象为某跨声速压气机级。该模型转子16片,静子56片。转子为宽弦叶片,叶尖弦长为50mm,进口轮毂比为0.58,出口轮毂比为0.71,叶尖尖部直径为102mm,叶尖稠度为2.6,设计叶尖间隙为0.2mm。
在进行非定常流场计算时,采用转-静全周模型,如图 1(a)所示,出口边界条件在静子出口给定。在进行流固耦合模拟时,基于计算时间的考虑,简化模型由2个转子流道与对应7个静子流道组成,如图 1(b)所示。其中,简化模型转-静交界面两侧的面积,每个通道网格与全周模型的单通道网格保持一致。在有限元结构模型中,固体域为2片转子叶片,固体网格采用全六面体网格,单片叶片的节点总数为4500左右。
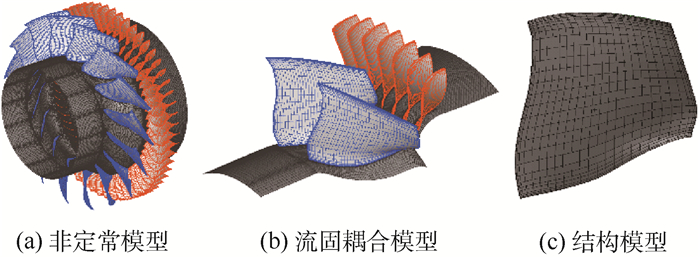 |
| 图 1 压气机计算模型与计算网格 Fig. 1 Computational model and mesh of compressor |
| 图选项 |
本文针对地面低转速状态(80%设计转速)进行计算,计算使用的转速为29250r/min。在低转速状态下,转子叶尖处于明显的大攻角流动状态。进口给定总温为288.15K,总压为101325Pa,轴向进气。出口给定平均半径处的静压,按径向平衡方程计算出压力沿叶高的分布。流固耦合计算中,流体域进出口边界条件与非定常计算的情形相同。固体域2片转子叶片作为弹性体进行计算,材料为某合金钢,物性参数如表 1所示。叶片叶背、叶盆和叶顶设置为流固耦合交界面,叶片底面设置为固支边界条件。
表 1 转子叶片材料属性 Table 1 Material property of rotor blades
| 参数 | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 数值 | 120 | 0.32 | 4370 |
表选项
采用图 1(c)中叶片结构网格,计算转子叶片在给定转速下的固有频率。计算所得的前4阶固有频率和对应的振型如表 2所示。
表 2 叶片固有频率与振型 Table 2 Natural frequency and vibration mode of blade
| 阶数 | 固有频率/Hz | 振型 |
| 1 | 1840 |  |
| 2 | 3011 |  |
| 3 | 4865 |  |
| 4 | 5341 |  |
表选项
2 大攻角状态下分离流特性 本文首先对非定常计算和流固耦合计算的流体网格进行网格无关性验证,并对非定常时间步长也进行了无关性验证,确保数值计算的精度与准确性。之后针对不同工作状态进行非定常和流固耦合分析。Case1为非定常近失速状态,Case2为接近最高效率点的一个流动状态。本文将着重对比这2个状态下的叶背分离流演化情况,并探讨其中的物理机制。通过流固耦合模拟技术研究叶背分离流对于自身转子叶排的激励作用。
2.1 流体网格无关性与时间步长无关性验证 为了避免网格疏密对计算结果的影响,首先进行流体网格无关性验证。为了节省计算量,本文针对图 1(b)中的简化模型进行网格无关性验证。全周模型与简化模型的区别仅为计算通道数不同,而每个通道的计算网格完全相同,所以简化模型的网格无关性也适用于全周模型。本文设计了粗、中、细3套网格,网格量分别为30万、75万和120万。针对每套网格进行定常计算,通过对比3套网格计算的特性线来分析网格数量对计算结果的影响,如图 2所示。
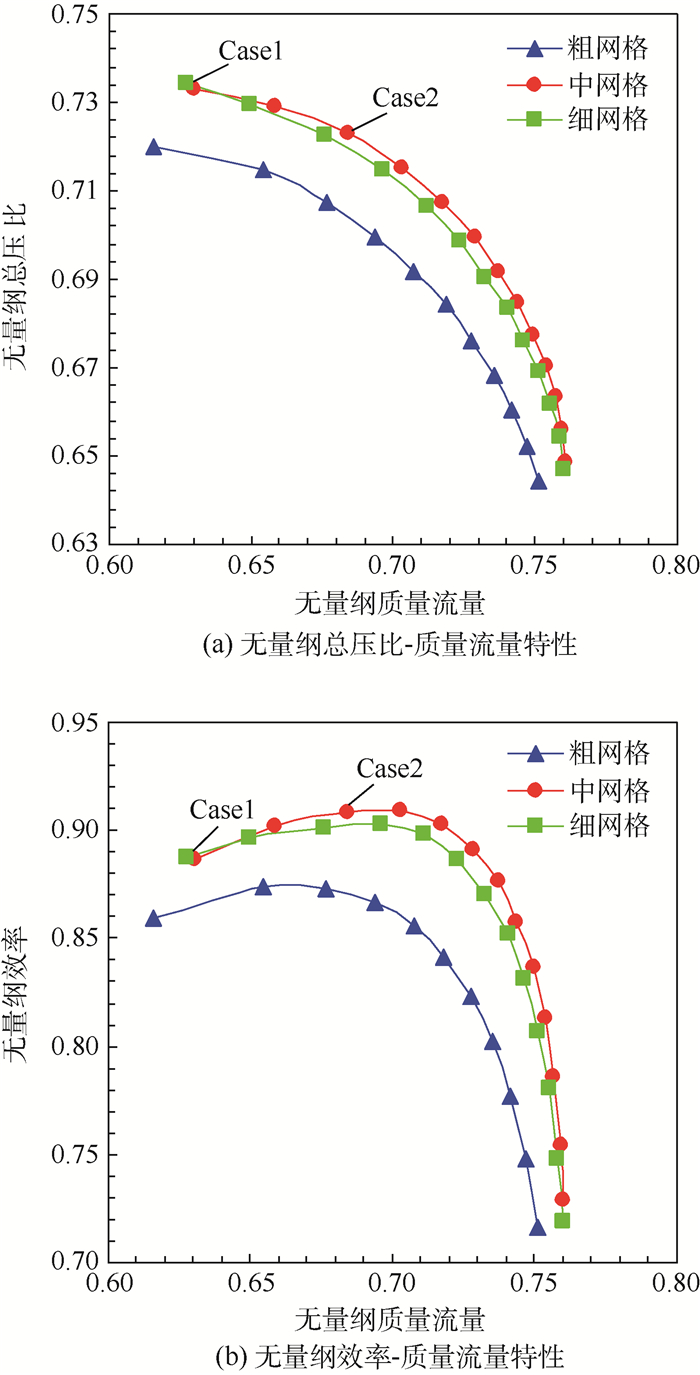 |
| 图 2 流体网格无关性分析 Fig. 2 Fluid mesh independence analysis |
| 图选项 |
从图 2可以看出,基于粗网格的压气机性能计算值普遍低于中、细网格的计算结果。而中、细网格对于性能的预估较为接近,因此可认为采用中网格计算即可满足精度要求。本文所有的计算模型均基于中网格的网格密度做出。
为了减小时间步长对于非定常结果的影响,本节选取了3个不同的时间步长进行非定常计算,来考察时间步长对计算结果的影响程度。图 3给出了利用3个不同的时间步长得到的出口质量流量随时间的变化。结果显示,3个结果基本一致,说明在取定的范围内,时间步长对计算结果影响不大。考虑到节约计算成本,故本文中的非定常计算和流固耦合计算的时间步长都取为1.3×10-5s。
 |
| 图 3 时间步长无关性分析 Fig. 3 Time step independence analysis |
| 图选项 |
2.2 压气机非定常分离流场特性分析 为了展现不同工况下叶片通道内的流动状况,图 4给出了2个分析状态下全周模型90%叶高截面的相对马赫数分布。可以看出,Case2状态转子叶片叶背有较大的分离区,且周向每个流道内的分离区大小、位置、强度都较为一致。Bohne和Niehuis[14]在针对低转速压气机的试验中曾捕捉到这类分离,并认为低转速下的大攻角是产生此类分离的原因。与Case2状态相比,Case1状态流道内虽然有明显的分离区存在,但流动情况与相邻流道完全不同,却与相隔流道的流动情况比较相似。这说明随着压气机状态向喘点逼近,转子叶尖流场结构发生了根本性变化。
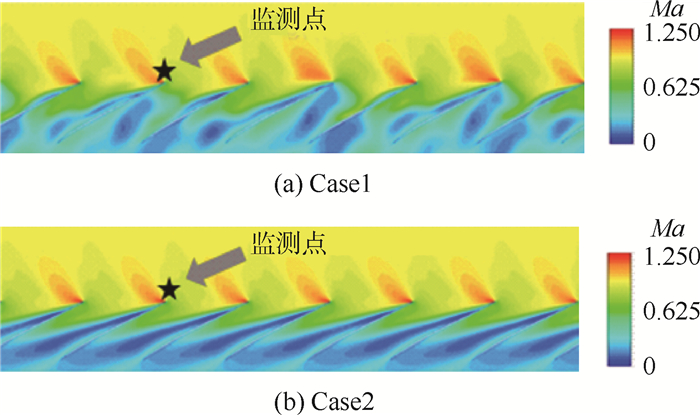 |
| 图 4 90%叶高位置的相对马赫数分布云图 Fig. 4 Relative Mach number distribution contour at 90% spanwise location |
| 图选项 |
选取图 4中标注的叶尖前缘监测点,分析相对马赫数的时域变化,并对Case1状态的相对马赫数时域曲线进行频谱分析,如图 5所示。
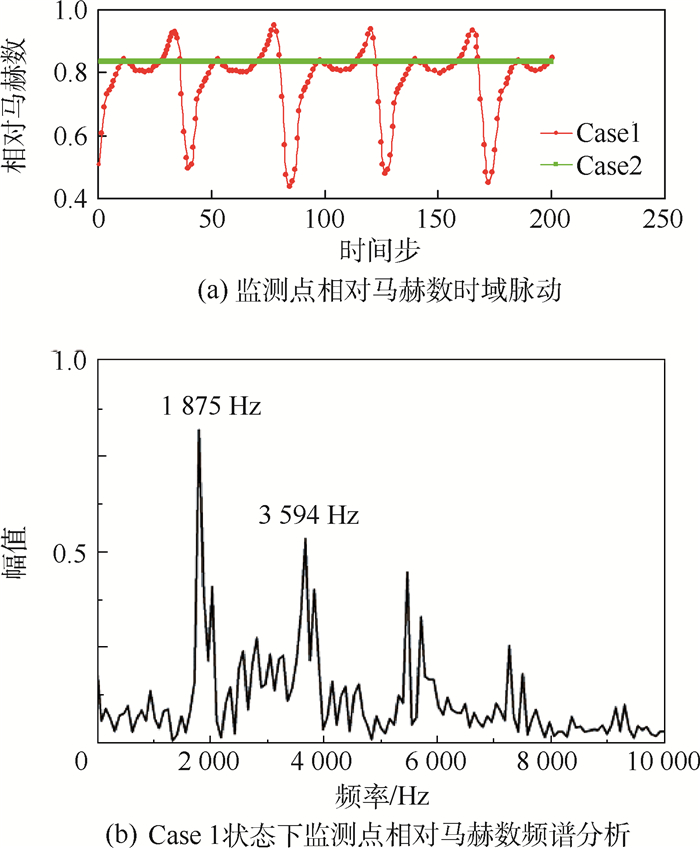 |
| 图 5 监测点相对马赫数时域脉动与频谱分析 Fig. 5 Relative Mach number time domain fluctuation and frequency spectrum analysis at monitoring point |
| 图选项 |
从图 5可以看出,Case2状态的流场细节气动参数(相对马赫数)随时间的脉动很小,说明虽然叶背区域存在较大分离(见图 4(b)),但是此分离区基本不随时间而变化,表现出了定常特征。而Case1状态的参数则脉动很大,非定常性显著,且存在明显的时间周期性。从频谱分析中可以看出,相对马赫数的最占优的频率为1875Hz。
为了揭示Case1状态下叶尖流场叶背分离区的非定常演化过程,取频谱分析中占优频率(1875Hz)所对应的周期作为一个研究周期,并将这一周期细分成9个时刻进行细致研究,研究不同的流场参数在这一时间周期内的演化过程。
按照时刻1~9先后取转子域90%叶高流面的相对马赫数分布,如图 6所示。叶尖马赫数非定常演化特征明显,叶背分离区的结构也不再稳定,而是呈现出明显的周期性脱落和传播特征。从时刻1至时刻4,2号叶片吸力面前缘存在明显分离区,并且其分离区的强度和范围都随时间的推进不断增大。直至时刻5, 一团低速分离区从2号叶片叶背表面脱落,并在流道内大致沿轴向传播,称其为“轴向传播分离区”。值得注意的是,在这一时间段内,2号叶片叶背只有一部分分离区产生了脱落现象,此时仍然有一团狭长的低速分离区紧贴叶背,没有脱落。但从时刻7开始,先前没有脱落的分离区也开始从叶背脱落下来,而在这一时间段内脱落的低速分离区却表现出了周向的传播特征,称其为“周向传播分离区”。该“周向传播分离区”呈现出的特性与旋转不稳定[15]中“叶顶泄漏涡每隔一个通道重复一次”的特性很相似,该流动现象很可能与旋转不稳定流动存在关联。
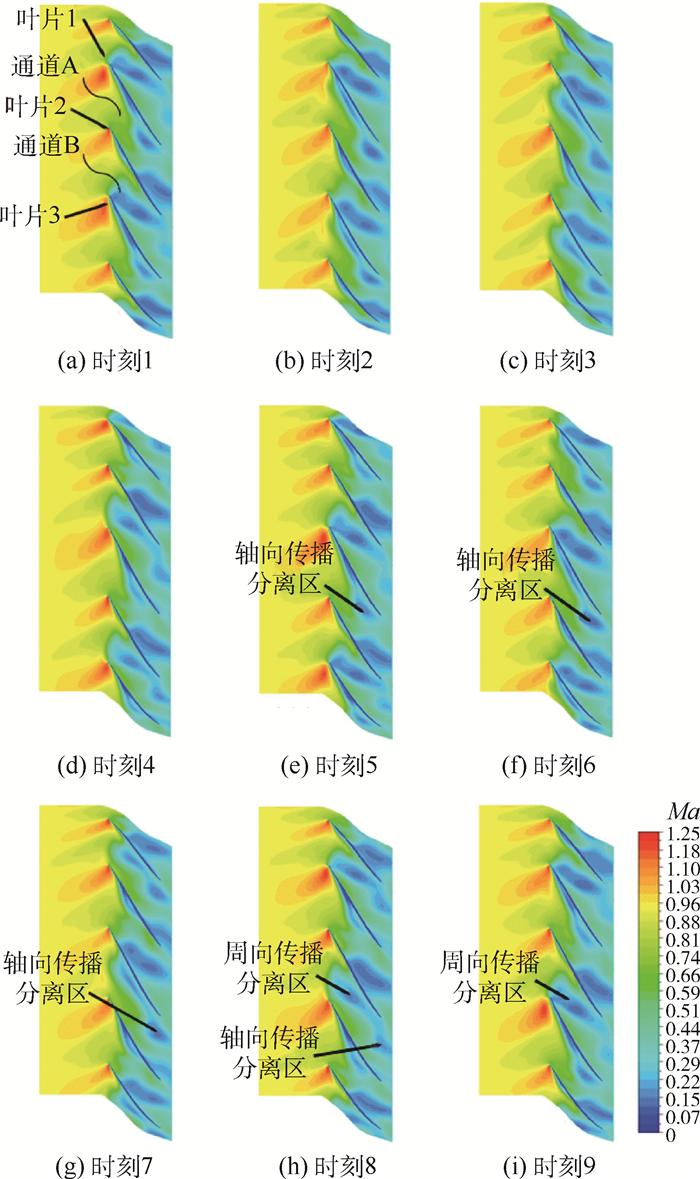 |
| 图 6 不同非定常时刻的相对马赫数分布云图 Fig. 6 Relative Mach number distribution contours at different unsteady time points |
| 图选项 |
Case1状态下叶尖流场的演化过程比较复杂,在一个周期(对应频率1875Hz)内,有2次叶背分离区的脱落过程。从叶片的进口气流角变化来看,在时刻3~时刻5,1号叶片吸力面脱落的“周向传播分离区”到达2号叶片前缘,导致叶片前缘进口气流角急剧增大(见图 7),攻角相应增大,使得激波强度增大。大攻角状态结合激波/泄漏涡、激波/附面层的相互作用,促使原本紧贴叶背的分离区发生脱落,并沿叶背向叶片尾缘传播,即“轴向传播分离区”脱落。这与Lee等[16]的工作中所描述的现象相似,这类分离区在大攻角的情况下产生,并向下游脱落,对下游流场产生影响。与此同时,“周向传播分离区”在到达2号叶片前缘之后会逐渐贴向叶片压力面,并沿着压力面向叶片尾缘移动。从图 6(f)的时刻6可知,沿2号叶片吸力面传播的“轴向传播分离区”与沿3号叶片压力面传播的“周向传播分离区”同时到达各自叶片尾缘,对叶片流道造成了堵塞,使流道通流能力下降,迫使附着在2号叶片吸力面的低速分离区再次发生脱落并向周向传播,即为“周向传播分离区”,如时刻7~时刻9所示,形成周期性脱落和传播特性。
 |
| 图 7 不同非定常时刻的气流角变化 Fig. 7 Variation of flow angle at different unsteady time points |
| 图选项 |
由于相隔叶片附近的流场情况相似,流场有近似2个相邻通道为一组的周期性流动存在,所以在Case1状态下,周向可以认为存在8个低速分离区。在取定的一个研究周期内,一个转子转过的距离为drotor=0.26圈;而周向分离区经历一个周期,相当于转过了2个通道,即转过的距离为dstall=2/B=0.125圈,B=16,为转子叶片数。故周向分离区的转速vstall=0.48vrotor,vrotor为转子的转速,即周向分离区以0.48倍的转子转速进行周向旋转。
“轴向传播分离区”在流道内进行轴向传播,对相邻转子叶片影响很小。而“周向传播分离区”会作用在逆转速方向的相邻转子叶片的压力面,这是造成叶尖前缘马赫数脉动的主要原因。每当“周向传播分离区”到达相邻叶片前缘时,位于该叶片吸力面靠近前缘处的激波会明显增强,即该叶片前缘马赫数同步增大。可见,“周向传播分离区”的脱落频率与马赫数脉动的占优频率1875Hz一致。“周向传播分离区”在转子叶背产生、发展、脱落,并与相邻转子相互影响,可能会对转子叶片表面压力分布产生不良影响。
图 8给出了不同非定常时刻2号叶片的叶盆面压力分布。可以看出,低速分离区使叶盆面叶尖前缘附近的压力脉动明显。在时刻3,叶尖前缘附近的压力开始快速下降。在时刻4,叶尖前缘角区形成了明显的低压区域,且在较小的角区内压力梯度很大。随后低压区域向后传播,且在叶片表面的强度有所减弱。至时刻9,基本完成一个非定常周期。在时刻2~时刻6之间,叶尖前缘的角区附近完成了由相对高压—低压—高压的变化过程,变化幅值大,作用区域小,压力梯度大,考虑到叶尖前缘很薄且带有一定的前掠型,这样剧烈的压力变化可能会对叶片的结构强度产生不利影响。
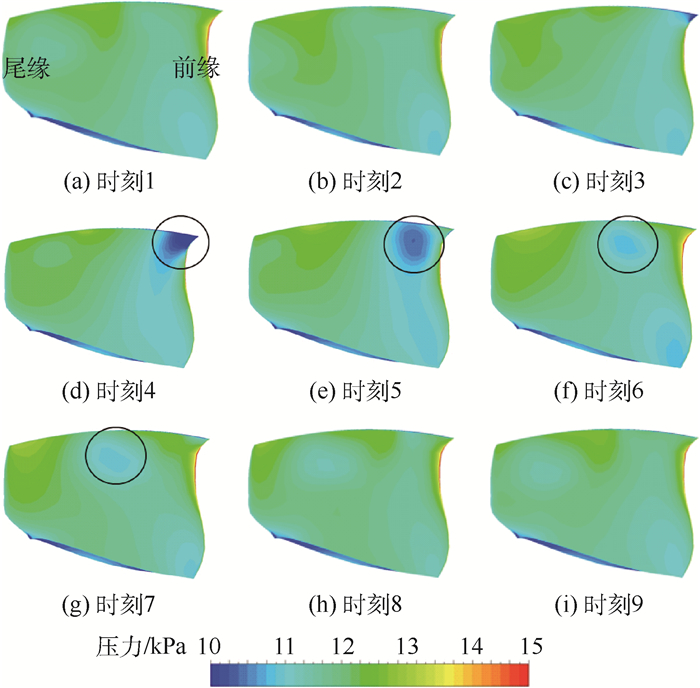 |
| 图 8 不同非定常时刻叶片叶盆面的压力云图 Fig. 8 Pressure contour of pressure side of blade at different unsteady time points |
| 图选项 |
图 9给出了2号叶片在时刻1、4、6、9的90%叶高表面压力分布。分析可知,叶片的叶背压力变化相对不明显,而叶盆前缘角区是压力脉动最显著的区域。时刻4时,叶尖前缘的负荷明显降低。
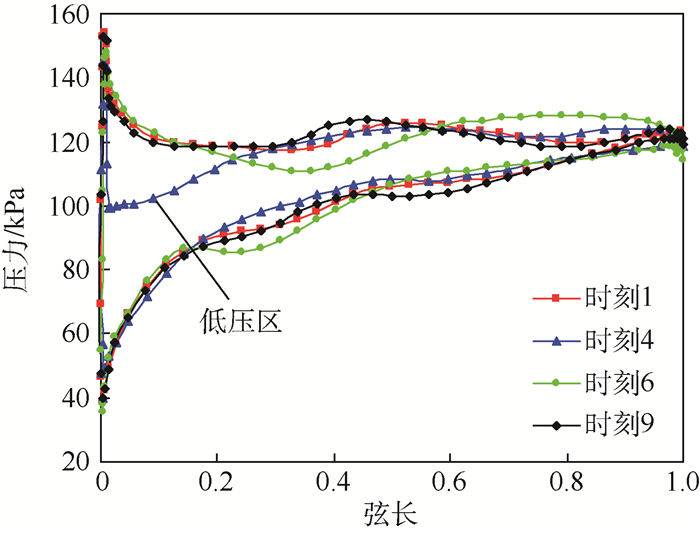 |
| 图 9 90%叶高位置的叶片表面压力分布 Fig. 9 Blade surface pressure distribution at 90% spanwise location |
| 图选项 |
由以上一系列分析可知,Case1状态下叶尖流场非定常脉动十分明显,并发生了叶背分离区的脱落和传播现象。借鉴文献[15]对低速轴流压气机中旋转不稳定流动现象起始原因的描述,本文在跨声速轴流压气机内部发现的上述非定常流动现象的起始原因可能是:随着运行工况向近失速边界靠近,压气机转子叶片叶尖泄漏流的强度逐渐增大,流场受到某个小扰动的影响后,激波与泄漏涡发生了周期性的相互干涉,泄漏涡在传播过程中再次与相邻叶片发生了周期性相互作用。
压气机转子叶背分离区的周期性脱落和传播,尤其“周向传播分离区”的周期性脱落和传播,会对相邻转子叶片表面的压力分布产生显著影响,特别是叶尖前缘附近的压力脉动十分剧烈,有可能对叶片振动产生不利影响。
3 大攻角状态下叶片动力响应特性 为了进一步揭示“周向传播分离区”对转子叶片振动的影响,本节采用流固耦合迭代计算技术分析叶片的结构瞬态响应。从2.2节的结果可以看出,在空间上,Case2状态每个通道内的流场情况相似,有良好的重复性,理论上可以简化为单转子模型进行计算;Case1状态叶尖周向非均匀性虽然较强,但仍然大致存在2个通道为一组的周向流场周期性。故为了节省计算时间,在进行流固耦合计算时,对计算模型进行合理简化,选取2个转子叶片通道,静子数量进行相应约化,组成转-静双通道简化计算模型。模型保证转-静交界面两侧面积相等,满足非定常转-静交界面的算法要求。
从不同状态下转子叶片气动力的时域变化来看(见图 10),Case1叶片表面的气动力脉动幅值要明显高于Case2状态,说明2.2节展示的叶背分离区脱落、传播现象使叶片表面气动力脉动更加剧烈。Case2状态下相邻叶片的气动力基本同步脉动;而Case1状态下相邻叶片的气动力脉动相位相反,周向传播的分离区在其中起到了明显作用。
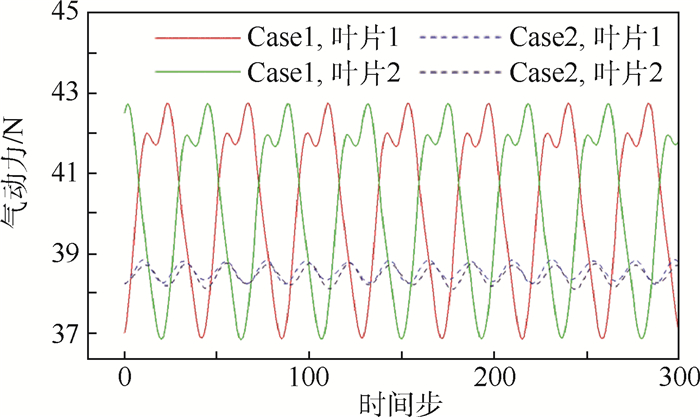 |
| 图 10 转子叶片气动力随时间的变化 Fig. 10 Variation of aerodynamic force of rotor blade with time |
| 图选项 |
图 11给出了不同状态下转子叶尖前缘点位移的时域变化曲线。结果显示,虽然在不同状态下转子叶片叶尖前缘均围绕平衡位置做等幅的类简谐运动,并且振动平衡位置基本相同,但Case1状态下叶片振动的脉动幅值要显著增大,叶片振动更加剧烈。
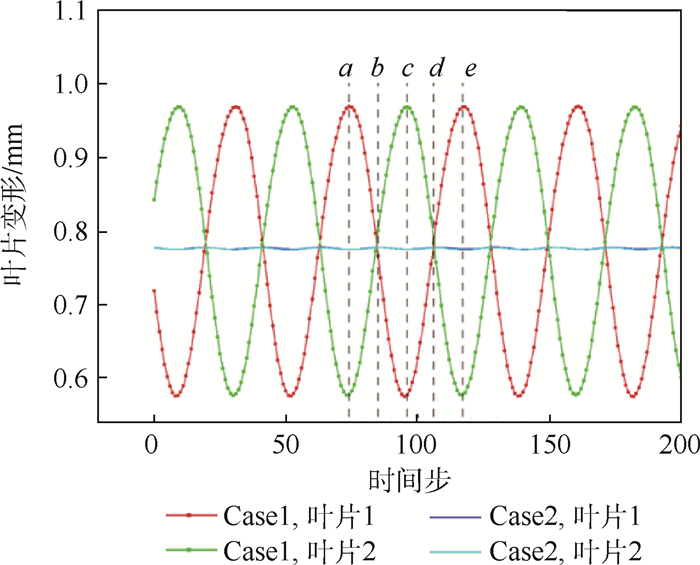 |
| 图 11 叶片振动时域曲线 Fig. 11 Blade vibration time domain curves |
| 图选项 |
从振动相位来看,Case2相邻叶片振动是基本同步的,而Case1状态下相邻叶片的振动相位存在明显的相位差。对一个叶片振动周期进行时刻划分,进一步描述相邻叶片在振动周期内的动态响应行为,如图 12所示。结果显示,在Case1状态下,从时刻a至时刻e相邻2个转子叶片在各自的叶尖前缘处交替成为振动位移最大的区域。
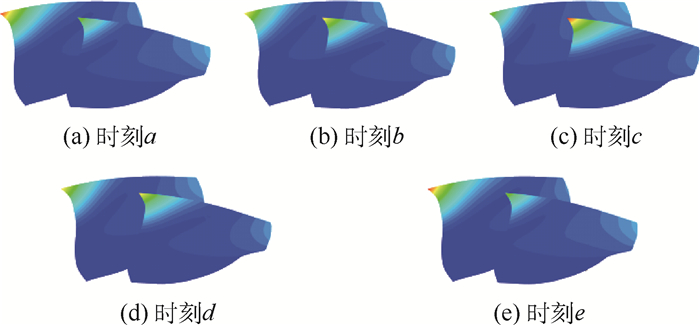 |
| 图 12 叶片振动位移云图 Fig. 12 Blade vibration displacement contours |
| 图选项 |
从频域角度看,Case1状态下叶片振动存在明显的占优频率1875Hz,如图 13所示,这与2.2节中的“周向传播分离区”的脱落频率一致。
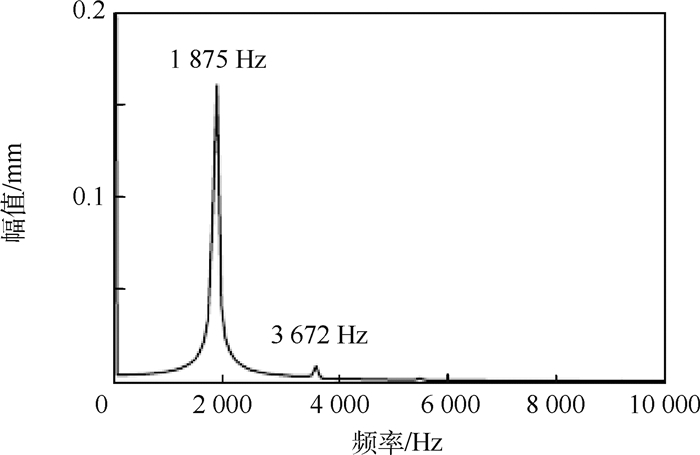 |
| 图 13 叶片振动频谱图 Fig. 13 Frequency spectrum analysis of blade vibration |
| 图选项 |
综合以上结果,“周向传播分离区”的脱落和叶片振动频率一致,且叶片振动基本呈等幅振动,故可以判断,在Case1状态下,叶片振动形式主要是由“周向传播分离区”的脱落和传播激起的强迫响应,非定常激振源是周向传播的非定常分离区,叶片的响应频率与激振源的激振频率一致。
从Case1转子叶片变形云图可以看出,虽然叶片各点变形量时刻在变化,但变形的基本形式不变,呈现叶片一阶弯曲振型。一方面,“周向传播分离区”的周期性脱落和传播使叶片前缘角区承受较大的动载荷,加大了叶片振动幅度,也改变了相邻叶片的振动相位。并且叶片的大变形区集中在前缘角区附近,叶片变形的梯度也较大,可能会存在叶片叶尖前缘疲劳甚至断裂的风险。另一方面,叶片的振动频率(1875Hz)与表 2所示的叶片一阶固有频率(1840Hz)非常接近。基于以上2点考虑,叶片在这一状态下有发生共振的危险。
工程中常常使用Campbell图对共振现象进行预测,有助于在叶片的动力特性设计中高效地分析并规避潜在的低阶共振风险,但由于流场中气流激励源的多频性和复杂性, 仅依靠分析频率避开全部叶片固有振型的气动激振源是很困难的。本文中Case1状态展现的此共振激励源是转子自身的非定常流动激励,流场结构的变化是激励源产生的原因。所以非定常激励能否产生,何时产生,强度多大,频率多少,位置如何,这些都和具体的流场状态有关,很难通过理论分析事先得知。这说明在设计阶段仅仅利用Campbell图进行共振分析是不全面的。虽然开展非定常/流固耦合计算会耗费计算资源,增加时间成本,但是这对研究复杂流动引发的共振问题具有明显的意义。利用非定常/流固耦合手段可以较为全面地预测复杂气动环境中激励源的大小、频率和位置,从而为设计者进行叶片调频等工作提供理论支持,最大可能地避免共振、颤振等振动问题的发生。从另一角度来看,即便共振现象不会发生,周向脱落的叶背分离区造成转子叶片振动响应十分明显,叶片的振动幅值明显增大。这种强烈的强迫响应同样会对叶片疲劳强度造成威胁,在工程中也应引起重视。
4 结论 本文对低转速大攻角状态转子通道内分离区的传播过程及其对转子叶片气弹特性的影响进行了全三维数值研究。
1) 在近失速状态,叶尖流场表现出了很强的非定常特征。转子叶尖同一流道中会脱落2个低速分离区。第1个分离区主要呈现轴向传播的特性,其会对下游流场产生影响;第2个分离区主要呈现周向传播的特性,其作用于周向相邻转子的叶盆,造成了叶尖表面压力分布的剧烈脉动。
2) 在近失速状态,转子叶片呈现出剧烈的振动,其振动频率与“周向传播的分离区”的脱落频率一致。转子叶片的振动体现为“周向传播的分离区”作用下的非定常强迫响应。转子振动频率与叶片一阶固有频率接近,转子叶片有发生共振的可能。“周向传播的分离区”的脱落和传播扮演着周期性作用力的角色,对转子叶片的气弹特性产生了重要的影响。
3) 对于复杂非定常流引发的共振问题,Campbell图难以进行全面的预测。利用非定常/流固耦合计算手段可以有效捕捉由于复杂非定常流形成的非定常激励源,从而预测叶片共振和结构响应问题。当压力、马赫数(速度)和其他气动信号被用来建立压气机转子内部非定常分离流和叶片气弹特性的关系时,这对于深入认识非定常流动诱发叶片振动问题具有积极的意义,值得开展进一步的研究工作,也应在设计阶段对这类预测工作予以重视。
参考文献
| [1] | 夏联, 崔健, 顾扬. 可调静叶对压气机低速性能影响的试验研究[J].燃气涡轮试验与研究, 2005, 18(1): 31–34. XIA L, CUI J, GU Y. An experimental investigation on the effect of variable stator vane angle on compressor performance at low speed[J].Gas Tirbine Experiment and Reasearch, 2005, 18(1): 31–34.(in Chinese) |
| [2] | VALKOV T V, TAN C S. Effect of upstream rotor vortical disturbances on the time-averaged performance of axial compressor stator.Part 2:Rotor tip vortex/streamwise vortex-stator blade interactions[J].Journal of Turbomachinery, 1999, 121(3): 387–397.DOI:10.1115/1.2841331 |
| [3] | GBADEBO S A, CUMPSTY N A, HYNES T P. Three-dimensional separations in axial compressors[J].Journal of Turbomachinery, 2005, 127(2): 331–339.DOI:10.1115/1.1811093 |
| [4] | MAILACH R, LEHMANN I, VOGELER K. Periodical unsteady flow within a rotor blade row of an axial compressor.Part 2:Wake-tip clearance vortex interaction[J].Journal of Turbomachinery, 2008, 130(4): 041005.DOI:10.1115/1.2812330 |
| [5] | HAH C, BERGNER J, SCHIFFER H P.Tip clearance vortex oscillation, vortex shedding and rotating instabilities in an axial transonic compressor rotor[C]//ASME Turbo Expo 2008.New York:ASME, 2008:57-65. |
| [6] | KIELB R E, BARTWE J W, THOMAS J P, et al.Blade excitation by aerodynamic instabilities—A compressor blade study[C]//ASME Turbo Expo 2003.New York:ASME, 2003:399-406. |
| [7] | MAILACH R, VOGELER K.Unsteady aerodynamic blade excitation at the stability limit and during rotating stall in an axial compressor[C]//ASME Turbo Expo 2006.New York:ASME, 2006:1701-1711. |
| [8] | HOLZINGER F, WARTZEK F, JUNGST M, et al. Self-excited blade vibration experimentally investigated in transonic compressors:Rotating instabilities and flutter[J].Journal of Turbomachinery, 2015, 138(4): 041006-1–041006-9. |
| [9] | 张章. 风扇/压气机气动弹性动力响应的机理与应用研究[D]. 北京: 北京航空航天大学, 2013. ZHANG Z.Investigation on the mechanism and application of aeroelastic dynamic respones in fan/compressor[D]. Beijing:Beihang University, 2013(in Chinese). |
| [10] | 张明明. 轴流压气机气动弹性失稳机理研究[D]. 北京: 北京航空航天大学, 2012. ZHANG M M.Investigation on the mechanism of aeroelasticity instability in axial compressor[D]. Beijing:Beihang University, 2012(in Chinese). |
| [11] | YANG X D.Flow field and vibration behavior of the rotor due to mistuning IGV in a transonic compressor[C]//Proceeding of ASME 2012 International Mechanical Engineering Congress & Exposition.New York:ASME, 2012:267-274. |
| [12] | ZHANG M M, HOU A P, LI J X, et al. Analysis of blade vibration response induced by rotating stall in axial compressor[J].Journal of Aerospace Power, 2012, 27(10): 2269–2277. |
| [13] | 杜鹃. 跨音压气机/风扇转子叶顶泄漏流动的非定常机制研究[D]. 北京: 中国科学院工程热物理研究所, 2010. DU J.Investigation on the unsteady mechanism of tip leakage flow in transonic compressor/fan rotors[D]. Beijing:Institute of Engineering Thermalphysics, Chinese Academy of Sciences, 2010(in Chinese). |
| [14] | BOHNE A, NIEHUIS R.Experimental off-design investigation of unsteady secondary flow phenomena in a three stage axial compressor at 68% nominal speed[C]//ASME Turbo Expo 2004.New York:ASME, 2004:857-866. |
| [15] | MAILACH R, LEHMANN I, VOGELER K. Rotating instabilities in an axial compressor originating from the fluctuating blade tip vortex[J].Journal of Turbomachinery, 2000, 123(3): 453–463. |
| [16] | LEE S, RUNEHAL A K, KIM H J, et al. Large eddy simulation of unsteady flows in turbomachinery[J].Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2006, 218(7): 463–475. |
