目前,单发停车爬升梯度的计算方法主要是根据飞机爬升状态下的动力学方程推导出爬升梯度的计算公式,将爬升梯度表示为以飞机重量、发动机推力、飞机升阻比和加速因子等为自变量的函数,通过代入上述自变量的数值最终确定飞机爬升梯度的大小[2-4]。关键发动机停车后可用推力减小,起飞加速过程受到影响;不对称推力将导致飞机在发动机停车后的一段时间内偏离预定的起飞航迹和姿态,甚至出现机头下沉等现象[5]。采用数学公式的计算方法难以反映单发停车后飞机飞行参数的动态过程和纠偏过程中驾驶员的操纵程序,以及上述因素对于起飞爬升性能的影响。
本文建立了飞机本体动力学模型、起落架运动模型以及基于起飞任务的驾驶员操纵模型,构成了人机闭环数学仿真模型。在此基础上,结合民用航空规章的要求提出了适航符合性评估指标,最终建立了基于人机闭环数学仿真计算的民机单发停车起飞爬升梯度适航符合性评估方法,并以某型飞机为算例完成了仿真计算验证。
1 适航条款的要求与理解 CCAR-25R4第25.121条(a)~(c)款对民机在单发停车情况下起飞飞行航迹不同阶段的最小爬升梯度做出了规定[6]。单发停车爬升梯度的适航符合性验证需要考虑起落架位置、起飞重量以及结冰条件等因素。其中,起落架的位置应按照CCAR-25R4第25.111条的规定形态进行设置,起飞重量应选为最大起飞重量,在民机的方案设计阶段可主要针对非结冰条件进行适航符合性验证。CCAR-25R4第25.121(a)条规定的验证状态为:飞机在离地速度VLOF时,起落架在放下位置,关键发动机停车且其余发动机处于开始收起落架时的可用功率状态;第25.121(b)条规定的验证状态为:飞机在起飞安全速度V2时,起落架在收起位置,关键发动机停车且其余发动机处于开始收起落架时的可用功率状态;第25.121(c)条规定的验证状态为:飞机在起飞航迹末端的航路形态,关键发动机停车且其余发动机处于可用的最大连续功率状态。
在各个验证状态下,根据发动机数量的不同,飞机需满足不同的最小爬升梯度要求,具体数值如表 1所示。
表 1 单发停车起飞的最小爬升梯度值 Table 1 Minimum climb gradients for takeoff with one engine inoperative
| 发动机数 | 最小爬升梯度/% | ||
| 离地速度VLOF | 起飞安全速度V2 | 起飞航迹末端 | |
| 双发 | > 0 | 2.4 | 1.2 |
| 三发 | 0.3 | 2.7 | 1.5 |
| 四发 | 0.5 | 3.0 | 1.7 |
表选项
在对民机单发停车起飞爬升梯度的数学仿真计算过程中,起飞仿真任务必须保证在起飞航迹的每一点满足相应的速度要求。CCAR-25R4第25.107条对起飞过程中的关键速度做出了明确的规定,各个速度的定义及详细确定方法可参阅文献[6]。图 1表示了部分起飞参考速度的名称及彼此间的大小关系。
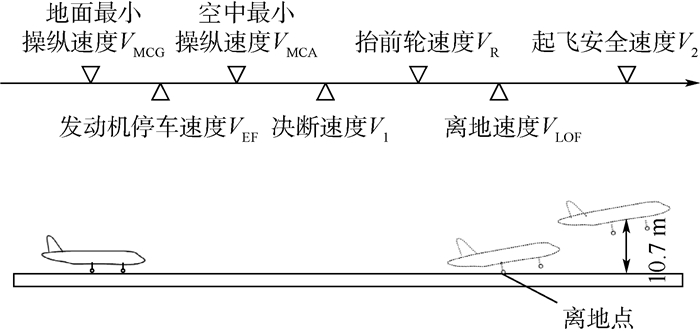 |
| 图 1 起飞参考速度关系 Fig. 1 Relationship of reference speeds during takeoff |
| 图选项 |
单侧发动机失效产生不对称推力,不平衡的力和力矩会导致飞机向发动机停车一侧偏航和滚转,从而产生航向偏离。此外,由图 1可知,起飞过程中的抬前轮速度VR应大于空中最小操纵速度VMCA;发动机停车速度VEF应大于地面最小操纵速度VMCG。综合上述原因,数学仿真过程中应保证单发停车后驾驶员的纠偏操纵合理,对飞机的姿态和航迹偏离进行限制。根据CCAR-25R4第25.149条对于最小操纵速度的规定,适航符合性验证需满足以下限制条件:①在单侧发动机停车后的整个纠偏过程中,航迹偏角的最大改变量不超过20°,并且在恢复直线飞行后能保持滚转角不大于5°[6];②单侧发动机停车后飞机偏离跑道中心线的横向距离不超过9 m[6]。
综合上述分析,民机单发停车起飞爬升梯度的适航符合性评估应包含两方面内容:①在适航条款规定的各验证状态下,飞机的爬升梯度大小是否满足要求;②数学仿真任务是否符合规定的起飞程序以及纠偏过程中飞机的飞行参数是否满足限制条件。
2 飞机数学仿真计算模型 2.1 飞机本体动力学模型 为模拟单发停车情况下的起飞过程,需建立飞机的六自由度全量运动方程组。地面运动过程的建模考虑起落架对飞机的作用力和力矩。在机体坐标系下,机体质心平移的动力学方程为[7]
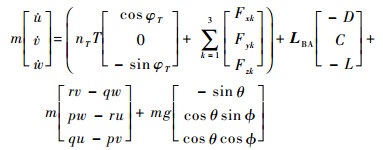 | (1) |
式中:m为飞机质量;u、v和w分别为空速在机体坐标系三轴上的分量;D、C和L分别为阻力、侧力和升力;p、q和r分别为滚转、俯仰和偏航角速度;g为重力加速度;θ和?分别为俯仰角和滚转角;T为单台发动机的推力;nT为工作发动机的台数;φT为发动机安装角;Fxk、Fyk和Fzk分别为第k个起落架作用于机体的力在机体坐标系x、y和z三轴方向的分量;LBA为气流轴坐标系到机体坐标系的坐标转换矩阵[7]。
对式(1)进行一次积分和二次积分即可得到机体质心的速度和位移。
在机体坐标系内,考虑起落架作用力和力矩的刚性机体的转动动力学方程为[7]
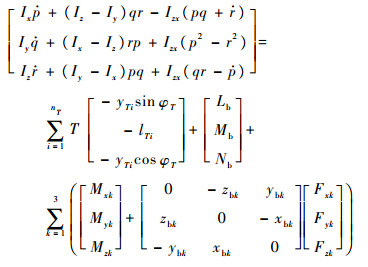 | (2) |
式中:Ix、Iy和Iz分别为绕x、y和z轴的转动惯量;yTi为第i台发动机的推力作用点在机体坐标系的y轴坐标;lTi为第i台发动机的俯仰力臂,推力线在飞机重心之上为正;Lb、Mb和Nb分别为气动力矩在机体坐标系上的分量;Mxk、Myk和Mzk分别为第k个起落架作用于机体的力矩在机体坐标系x、y和z三轴方向的分量;xbk、ybk和zbk分别为起落架在机身上安装点的机体坐标系三轴坐标分量。
机体的姿态运动学方程为[7]
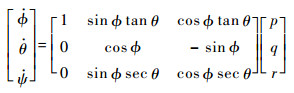 | (3) |
式中:ψ为偏航角。
2.2 起落架运动模型 支柱式起落架模型主要包括缓冲支柱模型和轮胎模型。建模过程中将起落架支柱等效为悬臂梁,可沿轴向平动,同时可发生侧向弯曲变形,不考虑扭转变形[8]。缓冲器运动方程、机轮轴线平动运动方程和机轮转动运动方程共同构成了起落架运动模型。具体建模方法可参阅文献[9-10]。
飞机在地面滑行过程中,轮胎与跑道发生相互作用引起轮胎的弹性变形。轮胎径向作用力Fgz、纵向作用力Fgx、侧向摩擦力Fgy和滚阻力矩Mr表示为[11-12]
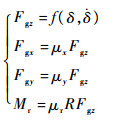 | (4) |
式中:δ为轮胎的径向压缩量;μx为滑动摩擦阻力系数;μy为轮胎侧向摩擦系数;μr为轮胎的纯滚动摩擦系数;R为轮胎的滚动半径。
2.3 发动机模型 为模拟发动机的推力响应特性,发动机的推力与油门偏度的关系可表示为[13]
 | (5) |
式中:Ti为第i台发动机的推力;Tp为发动机时间常数;Timax为发动机最大推力;δpi为油门偏度,取值范围为0~1。
发动机停车可以采用突然关闭或减小油门的方法来模拟[13],因此发动机停车后推力的响应特性由时间常数Tp决定。
2.4 驾驶员操纵模型 单发停车后,飞机驾驶员的操纵策略与全发工作时有所不同。在方向舵效能允许的情况下,通常可选择带侧滑的飞行姿态。但是在起飞阶段,需要尽可能减小飞行阻力,不宜存在侧滑角,因此应采用无侧滑、略带一定坡度的飞行状态[7]。在驾驶员发现发动机停车后的最初一段时间内,应立即蹬舵使方向舵满偏,以平衡不对称推力引起的偏航力矩。同时,驾驶员需要操纵副翼,一方面用以平衡方向舵偏转、发动机推力不对称和侧滑引起的滚转力矩;另一方面使飞机向发动机正常工作一侧适当滚转以平衡蹬舵产生的侧力。飞机的滚转角?应保持在期望的范围内,并且在恢复直线飞行后不大于5°。
单发停车起飞过程的人机闭环仿真控制结构如图 2所示[14],其操纵过程通过内外2个闭环实现。图中:χ为航迹偏角;χc为航迹偏角指令;yc为飞机质心在地面坐标系的y轴坐标指令;?err、θerr和ψerr为姿态控制指令误差信号;Gpθ(s)、Gp?(s)和Gpψ(s)为驾驶员操纵模型;δa、δr和δe分别为副翼、方向舵和升降舵偏度。
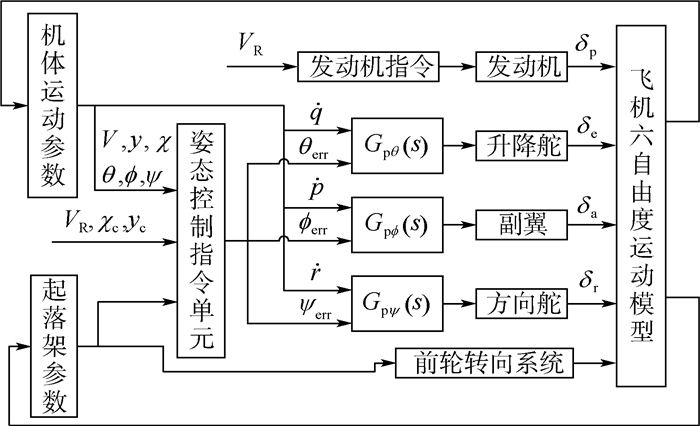 |
| 图 2 起飞任务仿真控制结构框图[14] Fig. 2 Structure block diagram of model for pilot-in-loop takeoff control simulation[14] |
| 图选项 |
外环控制依据起飞操纵程序跟踪飞机起飞过程中的质心运动参考轨迹并生成相应的俯仰、偏航和滚转姿态指令作为内环控制的输入,这部分任务由图 2中的姿态控制指令单元完成。
在升降舵通道中,俯仰姿态指令单元根据飞机抬前轮时刻tR和离地时刻tLOF生成俯仰轴姿态控制指令θc。其中,tR和tLOF可分别根据飞机地面加速滑跑速度是否达到预定的抬前轮速度VR和离地速度VLOF来确定。θc的表达式如下:
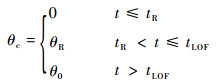 | (6) |
式中:θR为飞机两轮滑跑阶段的目标俯仰角;θ0为飞机离地后起飞爬升段的目标俯仰角。
在副翼通道中,滚转姿态指令单元根据飞机质心与跑道中心线的位置偏差(yc-y)和航迹偏角的偏差(χc-χ)生成滚转轴姿态控制指令?c:
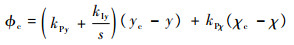 | (7) |
式中:kPy和kPχ分别为驾驶员根据飞机质心侧向偏差(yc-y)和航迹偏角偏差(χc-χ)进行操纵的增益;kIy为驾驶员消除稳态误差环节的增益。
在方向舵通道中,偏航姿态指令单元生成偏航轴姿态控制指令ψc:
 | (8) |
式中:kPyng和kχ分别为驾驶员根据起落架前轮位置偏差(yngc-yng)和航迹偏角偏差(χc-χ)进行操纵的增益;kIyng为驾驶员消除稳态误差环节的增益;ψ0为飞机爬升过程中的目标偏航角;kPψ为驾驶员根据偏航角偏差进行操纵的增益;kIψ为驾驶员消除稳态误差环节的增益;yngc为起落架前轮在地面坐标系的y轴坐标指令;yng为起落架前轮在地面坐标系的y轴坐标。
内环控制的任务是依据姿态控制指令误差形成实际的三轴操纵输入,由数字驾驶员完成对飞机的操纵。
图 2中的Gpθ(s)、Gp?(s)和Gpψ(s)均采用一种改进的McRuer驾驶员操纵模型。该模型除包含驾驶员依据视觉信息调节其自身的操纵策略与行为模型外,还引入了人体生理器官对运动感觉的反应,其结构框图如图 3所示。图中:Fa、Fe和Fr分别为驾驶杆(盘)/脚蹬力大小;δac、δec和δrc分别为副翼、升降舵和方向舵指令。该驾驶员操纵模型以姿态控制指令误差和角加速度作为输入信号,输出驾驶员操纵杆(盘)力和脚蹬力。驾驶杆(盘)和脚蹬指令再通过杆力-杆位移模型和杆位移-舵偏量模型最终生成舵面偏转指令。
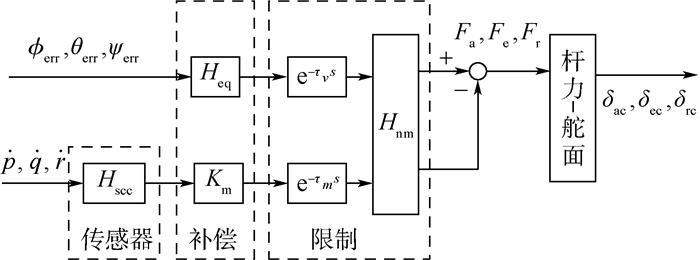 |
| 图 3 驾驶员操纵模型结构图 Fig. 3 Structure chart of pilot control model |
| 图选项 |
图 3中,Hscc为人体内耳前庭器官系统用于感知角运动变化的半规管模型,其数学描述为[15]
 | (9) |
Heq为视觉补偿项,其数学描述为[16-17]
 | (10) |
式中:TL为驾驶员对操纵过程的预测而需要的超前补偿时间常数,约为0~1.0 s,该值反映了驾驶员精神负荷的大小;TD为中枢信息的传递和加工过程的时滞,约为0~1 s,该值反映了驾驶员体力负荷的大小;Kv为驾驶员操纵增益,取值范围为1~100[18]。
Km为运动补偿增益,取值范围为1~100。
驾驶员操纵模型中的“限制”项e-τvs和e-τms表示驾驶员对信息反应的神经传导时延,τv和τm的取值范围约为0.06~0.20 s。Hnm(s)表示人体的肌肉作动延迟,其数学描述为自然频率ωn=9.0 rad/s、阻尼比ζ=0.7的二阶环节:
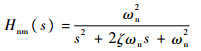 | (11) |
杆力-杆位移模型可根据适航条款中对于杆力梯度和最大杆力等指标的规定进行设计。杆位移-舵偏量模型则由飞机的操纵系统决定。
特别地,驾驶员油门通道采用开环操纵,在飞机速度未达到发动机停车速度VEF之前,关键发动机的油门偏度确定为最大可用起飞功率,否则取为停车功率。
3 数学仿真计算与评估方法 3.1 适航符合性评估流程 民机单发停车起飞爬升梯度的数学仿真计算与适航符合性评估分为以下几个步骤:①根据适航条款的要求确定量化评估指标,并设计考核飞行任务;设置大气条件及飞行条件,包括飞机飞行高度、起飞过程中各个关键速度值、重量与重心位置、起落架收放状态及发动机功率等。②通过人机闭环数学仿真,模拟飞机完成考核任务的起飞过程,并采集相关数据。③根据适航条款及相关准则的要求,对飞机的爬升梯度和起飞过程中的重要飞行参数进行评估。具体评估流程如图 4所示。
 |
| 图 4 单发停车起飞爬升性能评估流程 Fig. 4 Assessment process of climb performance during takeoff with one engine inoperative |
| 图选项 |
3.2 飞行仿真任务设计 数学仿真验证的飞行任务和驾驶员操纵程序制定如下:
1)?飞机采用起飞构型,起飞前飞机静止停在跑道上,机体纵轴线与跑道中心线对齐。将油门杆推至起飞功率位置,前轮对准跑道中心线。
2)?飞机从起始点加速至VEF,此时关键发动机停车,1 s后飞机加速至V1,并且飞行员意识到关键发动机停车,操纵方向舵平衡偏航力矩并维持飞机起飞姿态继续加速至抬前轮速度VR。
3)?速度达到VR后,飞行员拉杆抬前轮,在速度达到离地速度VLOF时飞机离地,开始爬升,并同时开始收起起落架。
4)?飞机离地后继续起飞,直至飞行速度达到V2,起落架完全收上。
5)?飞机以预定的姿态继续爬升,距离地面高度达到120 m之前,襟翼位置不变,速度保持表速不变;高度达到120 m以后,襟翼收上,等表速爬升至高450 m。
3.3 关键速度计算 在飞机完成起飞的整个过程中,各阶段的速度均需满足适航条款的规定。其中,决断速度V1、抬前轮速度VR和起飞安全速度V2是执行起飞任务前需要确定的性能参数。表 2列出了部分关键速度之间需满足的数值关系。
表 2 部分参考速度间的数值关系 Table 2 Numerical relationship of reference speeds
| 速度 | 数值条件 |
| VEF | VEF≥VMCG |
| V1 | V1≥1.05VMCG,V1≤VR |
| VR | VR≥1.05VMCA |
表选项
从表 2可以看出,地面最小操纵速度VMCG和空中最小操纵速度VMCA的大小限制了其他速度的取值范围,这2个速度值可事先计算获得[13]。V1的大小也受到起飞跑道长度的限制,而V1由VEF和驾驶员反应时间(通常取1 s)共同决定,因此在仿真过程中应保证VEF的取值合理。VEF限制值VEFmax的确定步骤如图 5所示,其中加速停止距离的计算流程和方法可参阅文献[6],Lp为可用跑道长度。
 |
| 图 5 VEF限制值的确定流程 Fig. 5 Determination process of maximum value of VEF |
| 图选项 |
VR的取值将影响飞机离地前的地面滑跑距离[19]。较小的VR会导致离地起飞所需的升力不足,飞机继续两轮滑跑加速的过程中会产生更大的阻力,延长了离地的时间,同时增加了滑跑距离。较大的VR则意味飞机抬前轮时间较晚,也会增大滑跑距离。因此,在满足表 2要求的前提下,应综合多次数字飞行仿真计算的结果确定VR的取值以尽量缩短起飞距离。
3.4 爬升梯度计算 飞机起飞爬升过程中任意时刻的爬升梯度为该时刻爬升角的正切值:
 | (12) |
式中:CGi和γi分别为第i个验证状态点对应的爬升梯度和爬升角。
适航条款规定的3个验证状态点分别为飞机离地点、速度达到起飞安全速度V2时以及起飞航迹末端。因此,可根据仿真结果输出的爬升角时间历程曲线计算得到各验证状态点的爬升梯度值。
4 算例及结果分析 以某型四发飞机为例,对单发停车起飞过程进行人机闭环数学仿真。飞机在海平面高度以最大起飞重量起飞,最右侧发动机停车,发动机停车速度VEF=49 m/s(tEF=19.3 s), VR=55 m/s,V2=59 m/s,升降舵预置量为-2.5°。
图 6为飞行状态参数及舵面偏转时间历程曲线。可知,t=28.6 s时,飞机速度达到起飞安全速度V2,并在之后等速爬升。在t=30.5 s时飞机达到起飞安全高度10.5 m,之后继续爬升到起飞航迹末端450 m。整个起飞任务过程中,飞机质心相对于跑道中心线的侧向偏差最大值为8 m。
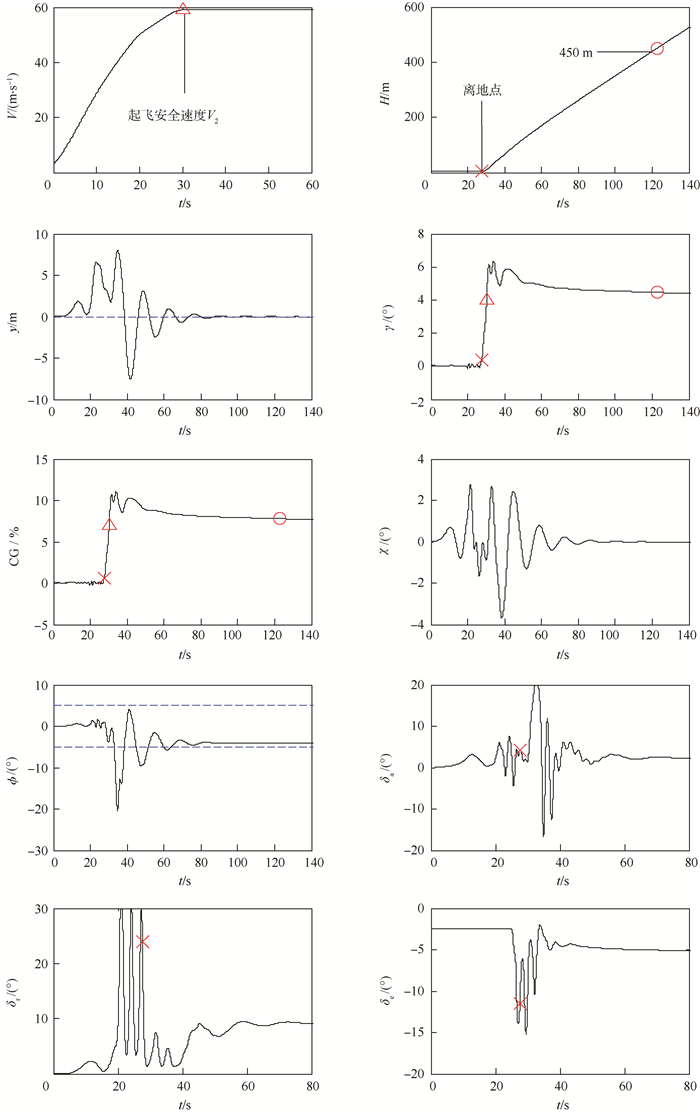 |
| 图 6 飞行状态参数及舵面偏转时间历程曲线 Fig. 6 Time histories of airframe state parameters and deflections of control surfaces |
| 图选项 |
在关键发动机停车后至飞机离地前的地面加速滑跑过程中,驾驶员操纵方向舵偏转以平衡不对称推力引起的偏航力矩。由图 7(a)可知,起落架轮胎与地面之间产生侧向摩擦力以平衡方向舵偏转产生的侧力,从而抑制了飞机的侧向偏离。副翼主要用于平衡滚转力矩,尽量保持机翼水平,飞机离地前的滚转角最大值为1.7°。飞机离地后,轮胎与地面作用力消失(见图 7(a)、图 7(b)),驾驶员操纵副翼使飞机向发动机正常工作一侧滚转以平衡侧力,副翼偏度增大并达到满偏20°,同时升降舵负偏角度增大以保持爬升姿态,防止升力的垂直分量减小引起机头下沉。随着飞机恢复平衡,副翼和方向舵的偏度逐渐减小并趋于稳定。
 |
| 图 7 起落架参数时间历程曲线 Fig. 7 Time histories of landing gear state parameters |
| 图选项 |
由图 6可知,整个纠偏过程中航迹偏角χ的最大改变量为3.7°,飞机最终恢复平衡并维持-3°的滚转角继续爬升。飞机在离地速度VLOF、起飞安全速度V2和起飞航迹末端(H=450 m)处的爬升角γ分别为0.4°、1.9°和4.5°。飞机起飞爬升过程中的爬升梯度为爬升角的正切值,根据仿真输出的爬升角计算得到上述验证状态下的爬升梯度分别为0.7%、3.3%和7.9%。对比表 1中的规定值可知,飞机在单发停车起飞过程中的爬升梯度满足适航条款的要求。
5 结论 1)?针对适航条款对于民机单发停车起飞爬升梯度的要求和起飞程序的规定,建立了包含飞机本体动力学模型、起落架运动模型和驾驶员操纵模型的人机闭环数学仿真模型;设计了飞行仿真任务和驾驶员操纵程序,并最终建立了基于人机闭环数学仿真计算的单发停车起飞爬升梯度适航符合性评估方法。
2)?基于人机闭环数学仿真的起飞爬升梯度计算方法考虑了关键发动机停车后非对称推力对飞机起飞姿态和航迹的影响,以及飞机离地前起落架对于驾驶员纠偏操纵的影响。该方法可以反映飞行过程中飞机的动态响应特性,能够更精确地对各验证状态下的爬升梯度进行适航符合性评估。
3)?在单发停车起飞的过程中,飞机离地前主要依靠起落架轮胎与地面之间的摩擦力平衡侧力并控制侧向偏离,副翼偏度较小以保持机翼水平。飞机离地后,驾驶员操纵副翼和方向舵使飞机恢复预定爬升姿态。
4)?在民机的方案设计阶段可采用本文方法对其单发失效的起飞爬升性能进行适航符合性评估,为飞机的设计和起飞重量的确定等提供依据,并为其适航符合性试飞验证提供理论参考。
参考文献
| [1] | 黄太平. 飞机性能工程[M].北京: 科学出版社, 2005: 37-43.HUANG T P. Aircraft performance engineering[M].Beijing: Science Press, 2005: 37-43.(in Chinese) |
| [2] | 李旭, 臧志恒, 魏志强. 民用飞机起飞第2爬升段爬升梯度计算分析[J].交通与计算机, 2006, 24(5): 85–87.LI X, ZANG Z H, WEI Z Q. Climb gradient calculation for the second segment in airplane takeoff[J].Computer and Communications, 2006, 24(5): 85–87.(in Chinese) |
| [3] | JOHNSON S C, GLOVER H.Method for determining a currently obtainable climb gradient of an aircraft:U.S.Patent 6, 691, 004[P].2004-02-10. |
| [4] | FILIPPONE A. Theoretical framework for the simulation of transport aircraft flight[J].Journal of Aircraft, 2010, 47(5): 1679–1696.DOI:10.2514/1.C000252 |
| [5] | 韩丰波, 于新江, 樊丹. 某大型运输机不对称推力飞行初探[J].飞行力学, 1997, 15(3): 82–85.HAN F B, YU X J, FAN D. Discussion on non-symmetric thrust flight for a certain type of the large transporter[J].Flight Dynamics, 1997, 15(3): 82–85.(in Chinese) |
| [6] | 中国民用航空局.中国民用航空规章第25部:运输类飞机适航标准:CCAR-25R4[S].北京:中国民用航空局, 2011.Civil Aviation Administration of China.China civil aviation regulations part 25:Airworthiness standards of transport category aircraft:CCAR-25R4[S].Beijing:Civil Aviation Administration of China, 2011(in Chinese). |
| [7] | ETKIN B. Dynamics of flight:Stability and control[M].New York: John Wiley & Sons, 1995. |
| [8] | 刘海良, 王立新. 基于数字虚拟飞行的民用飞机纵向地面操稳特性评估[J].航空学报, 2015, 36(5): 1432–1441.LIU H L, WANG L X. Assessment of longitudinal ground stability and control for civil transport aircraft based on virtual flight testing methodology[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1432–1441.(in Chinese) |
| [9] | PI W S, YAMANE J R, SMITH M J C.Generic aircraft ground operation simulation:AIAA-1986-0989[R].Reston:AIAA, 1986. |
| [10] | KHAPANE P D. Simulation of asymmetric landing and typical ground maneuvers for large transport aircraft[J].Aerospace Science and Technology, 2003, 7(8): 611–619.DOI:10.1016/S1270-9638(03)00066-X |
| [11] | SMILEY R F, HORNE W B.Mechanical properties of pneumatic tires with special reference to modern aircraft tires:NASA TR-64[R].Hampton:NASA, 1960. |
| [12] | WOOD G, BLUNDELL M, SHARMA S. A low parameter tyre model for aircraft ground dynamic simulation[J].Materials & Design, 2012, 35: 820–832. |
| [13] | 贾重任, 黄成涛, 王立新. 空中最小操纵速度的人机闭环数学仿真计算[J].北京航空航天大学学报, 2013, 39(5): 580–584.JIA Z R, HUANG C T, WANG L X. Mathematical simulation method to calculate air minimum control speed[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 580–584.(in Chinese) |
| [14] | LIU F, WANG L, TAN X. Digital virtual flight testing and evaluation method for flight characteristics airworthiness compliance of civil aircraft based on HQRM[J].Chinese Journal of Aeronautics, 2015, 28(1): 112–120.DOI:10.1016/j.cja.2014.12.013 |
| [15] | HOSMAN R, VAN DER GEEST P, VAN DER ZEE J.Development of a pilot model for the manual balked landing maneuver:AIAA-2009-5818[R].Reston:AIAA, 2009.http://arc.aiaa.org/doi/pdfplus/10.2514/6.2009-5818 |
| [16] | POOL D M, ZAAL P M T, DAMVELD H J, et al.Pilot equation in manual control of aircraft dynamics[C]//Proceedings of the 2009 IEEE International Conference on Systems, Man, and Cybernetics.San Antonio:[s.n.], 2009. |
| [17] | ROBINSON J, BARNES S, WEBB M, et al.The use of pilot modeling in aviation regulatory affairs:AIAA-2009-5825[R].Reston:AIAA, 2009. |
| [18] | 高金源, 李陆豫, 冯亚昌, 等. 飞机飞行品质[M].北京: 国防工业出版社, 2003: 139-142.GAO J Y, LI L Y, FENG Y C, et al. Aircraft handling qualities[M].Beijing: National Defend Industry Press, 2003: 139-142.(in Chinese) |
| [19] | OHME P.A model-based approach to aircraft takeoff and landing performance assessment:AIAA-2009-6154[R].Reston:AIAA, 2009.http://www.oalib.com/references/16436343 |
