基于Yule-Walker方程的AR参数估计,已经较为完善[4-6]。文献[4]提出重复计算观测数据自协方差以抑制观测噪声的影响并提高AR参数估计精度。文献[5-6]通过对噪声补偿修正Yule-Walker (Noise-Compensated Modified Yule-Walker,NCMYW)方程求解特征值和特征向量,同时得到观测噪声方差和AR参数的估计值。
MA参数估计可分为2种:①等效为高阶AR模型,MA参数估计精度与等效AR模型的阶次和AR参数估计精度有关,从理论上看这种估计是有偏的,常见的有Durbin方法[7];②直接估计,根据采用的序列统计量不同衍生出不同的方法。
在基于1阶统计量的MA参数估计方法中,以序列估计值与真实值之差最小作为目标,常见形式有条件平方和或非条件平方和[8],该目标函数非线性度较高,且一般适用于无观测噪声的模型。文献[9-10]使用非条件平方和作为指标函数,分别使用遗传算法和共轭梯度法求解包括MA参数在内的模型参数,算法精度高但耗时长。
在基于2阶统计量的MA参数估计方法中,以序列自协方差估计值与理论值之差最小作为目标,适用于有观测噪声的模型。文献[11-12]对Gevers-Wouters (GW)算法在应用上加以推广,该算法收敛快精度高;文献[13]利用AR参数和序列倒频谱递推求解MA参数。这些方法的参数估计精度与自协方差估计值的精度密切相关。基于更高阶统计量估计MA参数需要的样本数较长,且估计精度不高[14]。
目前,MA序列的自协方差估计值一般取为样本自协方差,而该估计值的方差较大,导致MA参数估计的方差较大,单次估计结果可靠性低。本文推导了一种方差小的自协方差估计值,作为GW算法的输入,仿真纯MA过程的参数估计,并实际应用到陀螺仪的随机漂移补偿中,2组结果均验证了改进算法能提高参数估计精度。
1 MA参数估计新方法 MA(q)的一般形式为
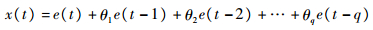 | (1) |
式中:{e(t)}为白噪声序列,均值为0,方差为σe2;q为MA过程的阶次;θi(i=1, 2, …, q)为MA过程的参数。
假设特征方程1+θ1z-1+θ2z-2+…+θqz-q=0的根在单位圆内,保证MA(q)的可逆性。已知数据序列{x(t)}t=1N,求解θi(i=1, 2, …, q)和σe2的过程即为MA参数估计。
记θ0=1,MA(q)的理论自协方差为
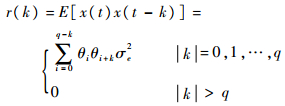 | (2) |
设有一零均值平稳序列{x(t)}t=1N,由序列可得样本自协方差为
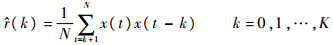 | (3) |
实际上,为了得到自协方差函数的有效估计,至少需要50个观测值,待估的自协方差函数中,K一般不超过N/4[8]。
当数据长度N由变差系数法[15]确定时,估计式(3)可认为是无偏的。自协方差估计值的协方差阵在文献[16]中有详细推导,下面直接给出结论。设变量σkp用于近似表示?(k)和?(p)的协方差,其定义为
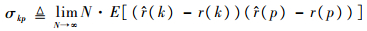 | (4) |
式中:0≤k,p < ∞。
假设{x(t)}为高斯过程,则有
 | (5) |
并且?(k)和?(p)的协方差近似为
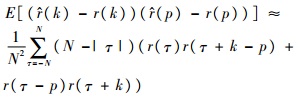 | (6) |
式中:k, p=0, 1, …, 且k, q?N。
假设{x(t)}为线性过程,即有

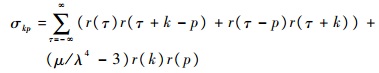 | (7) |
MA过程作为线性过程的特例,其σkp符合式(7)。式(7)中涉及驱动噪声的二阶矩和四阶矩,在参数估计前无法使用,可用于事后分析自协方差估计值和参数估计值的精度。如果MA过程满足高斯假设,则自协方差估计值的协方差采用式(6)近似;如果不满足高斯假设,由于式(7)与式(5)相差(μ/λ4-3)r(k)r(p),为较小的数[17],也可近似使用式(6)衡量自协方差估计值的估计精度。
根据MA(q)理论自协方差的结构,即大于q阶延迟的为0,将式(6)简化为
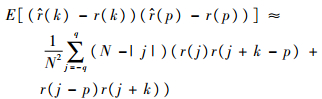 | (8) |
实际上,对于给定的MA(q)序列{x(t)}t=1N,根据式(3)可计算直到K阶的自协方差估计值。记
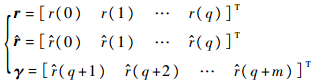 | (9) |
样本自协方差的前q阶?并不包含数据{x(t)}t=1N中所有关于未知MA参数的信息,q阶延迟以后的m个样本自协方差γ通过与?的协方差不为0影响前q阶自协方差估计精度。数据长度有限时,高阶延迟的自协方差估计精度低且计算量变大,m不宜取过高;低阶延迟的自协方差估计与?的相关度高,m不宜取过低;一般取m≈5q。
取直到q+m阶延迟的自协方差估计值[?TγT],其协方差矩阵?为(m+q+1)×(m+q+1)维,根据式(8)第k+1行p+1列元素近似为
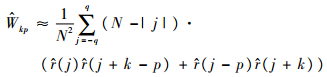 | (10) |
根据加权最小二乘的一般形式,权矩阵取为协方差阵的逆矩阵,则MA(q)参数估计的目标函数为
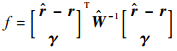 | (11) |
将矩阵行列按1→q+1和q+2→m+q+1分块,即得
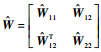
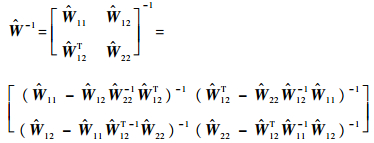 | (12) |
将式(12)代入式(11)并化简,与r无关的项视为常数项,目标函数转化为
 | (13) |
式中:
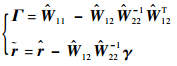 | (14) |
由于E[?12?22-1γ]=0,E[?]=E[?]=r,故和?都是r的无偏估计。根据式(13),的协方差阵为Γ=?11 -?12?22-1?12T,比?的协方差阵?11小,故作为自协方差估计值精度高于?。
根据式(3)、式(9)、式(10)和式(14)计算自协方差估计值,作为GW算法的输入。自协方差估计值简写为ACF,后文称使用?的GW算法为传统ACF-GW算法,使用的为改进ACF-GW算法。
2 随机漂移建模及补偿 2.1 数据预处理 随机漂移可建模为带观测噪声的ARMA模型。ARMA建模要求观测数据符合平稳性假设,其中平稳性检验可采用轮次法或单位根检验,若不满足可以对原始数据做差分或对数差分处理,具体可参考文献[8]。使用样本方差变差系数法确定建模所需的数据长度[16]。采用文献[17]提出的定阶方法确定ARMA(p, q)模型的阶次p和q,其优点是不需要预先计算模型参数。
设系统状态为x,观测输出为y,并设观测输出y是在系统状态x上叠加一个白噪声v,x符合ARMA(p, q)模型,且平稳可逆,离散表达式为
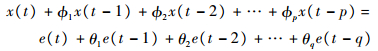 | (15) |
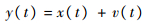 | (16) |
式中:?i(i=1, 2, …, p)为AR部分的参数;v(t)为观测白噪声,均值为0,方差为σv2;e(t)与v(t)不相关。
2.2 ARMA参数估计 ARMA参数估计分为2步:先估计AR参数和观测噪声方差σv2;再估计MA参数和驱动噪声方差σe2。参考文献[6],对AR参数和σv2同时估计。记ry为观测数据的自协方差,列写NCMYW方程为
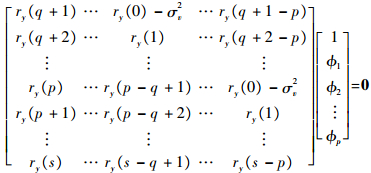 | (17) |
基于式(17)的变形方程,使用广义Schur正交分解(也称为QZ)方法求解特征值和对应的特征向量,其中特征值矩阵对角线元素绝对值最小的即可近似为观测噪声方差的估计值v2,其对应的特征向量将首系数归一化即得AR参数估计值
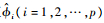
定义z-1为延迟算子,即z-τx(t)=x(t-τ),式(15)可改写为
 | (18) |
式中:A(z)=1+?1z-1+?2z-2+…+?pz-p; B(z)=1+θ1z-1+θ2z-2+…+θqz-q。
将式(18)代入式(16)得
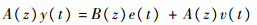 | (19) |
式中:设fy(t)=A(z)y(t),fe(t)=B(z)e(t),fv(t)=A(z)v(t),则fe(t)为MA(q)过程,fv(t)为MA(p)过程。因为e(t)与v(t)不相关,所以fe(t)和fv(t)也不相关,在式(19)两边同时乘以fy(t-τ)并求期望可得
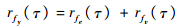 | (20) |
在求得AR参数估计值
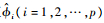
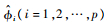
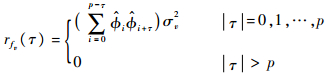 | (21) |
将式(21)代入式(20),结合残余序列的自协方差估计值,求出MA(q)过程fe(t)的0~q+m阶的自协方差估计值为
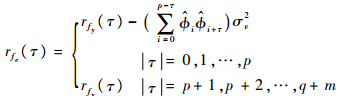 | (22) |
式(22)计算出的自协方差估计值rfe等价于第1节中由观测数据计算所得的[???γ],再根据式(10)和式(14)得到协方差阵小的自协方差估计值,将求得的作为GW算法的输入,估计MA参数和驱动噪声方差。
2.3 ARMA预测 将ARMA过程式(15)和式(16)用状态空间模型表示:
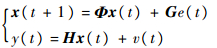 | (23) |
式中:状态变量选为x(t)=[x1(t)x2(t)…xp(t)]T,x1(t)对应ARMA过程的状态,系统噪声方差为Q=σe2,观测噪声方差为R=σv2;系统矩阵Φ、测量矩阵H和驱动噪声系数矩阵G由ARMA参数构成,如下:
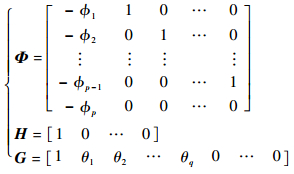 | (24) |
ARMA预测,对于状态空间模型式(24)来说,就是在有限过去时段观测值y(t), y(t-1), …, y(1)的基础上,确定状态向量x(t+l)(l>0)的有限样本最优估计,即确定出

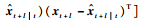
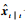
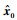
3 MA过程仿真验证 3.1 传统ACF-GW算法与改进ACF-GW算法 本节旨在仿真验证本文提出的改进ACF-GW算法相比传统ACF-GW算法的参数估计精度高。使用传统与改进ACF-GW算法分别对MA(1)、MA(2)和MA(3)进行仿真,每种情况仿真n=50次,发生序列时设其长度l=6 000,利用变差系数法确定求解参数所需最小样本长度N,驱动噪声方差均设为σe2=1。
选择的评价指标有如下3个:
1)?单位圆中特征方程1+θ1z-1+θ2z-2+…+θqz-q=0根的分布图中多次仿真结果的分散程度。
2)?参数估计平均误差e,定义为n次参数估计平均值与参数真实值之差的平方平均数,即
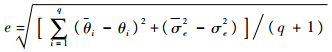 | (25) |
3)?参数估计均方根误差d,定义为每次参数估计值与参数真实值之差的平方平均数,参数θi的估计均方根误差为
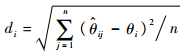 | (26) |
式中:
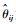
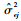
1)? MA(1)。系数θ1=-0.539 0。仿真结果如表 1和图 1所示。
表 1 MA(1)传统与改进ACF-GW算法参数估计误差 Table 1 Error of traditional and improved ACF-GW algorithm parameter estimation for MA(1)
| 算法 | 参数 | 参数估计均值 | 参数估计平均误差e | 参数估计均方根误差d |
| 传统ACF- | θ1 | -0.542 0 | 0.002 59 | 0.037 1 |
| GW算法 | σ2 | 0.998 0 | 0.031 9 | |
| 改进ACF- | θ1 | -0.540 2 | 0.000 84 | 0.019 4 |
| GW算法 | σ2 | 1.001 2 | 0.025 9 |
表选项
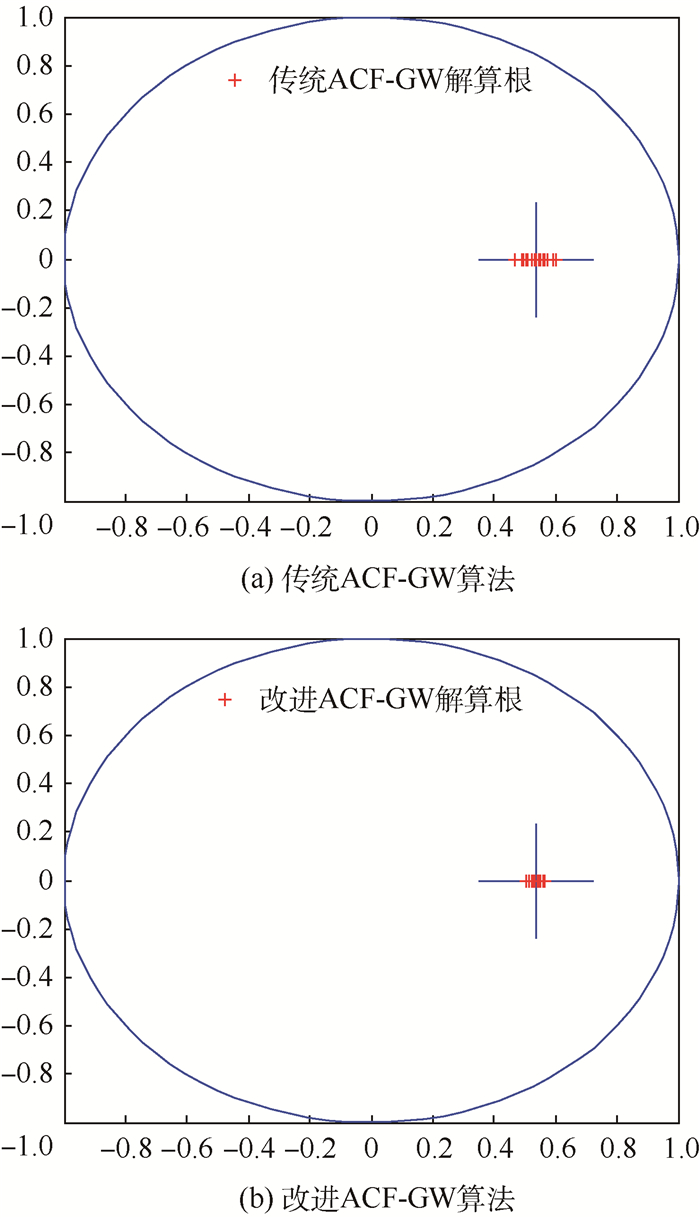 |
| 图 1 MA(1)特征方程的根 Fig. 1 Roots of characteristic equation for MA(1) |
| 图选项 |
2)? MA(2)。系数θ1=-0.494 4,θ2=0.297 1。仿真结果如图 2和表 2所示。
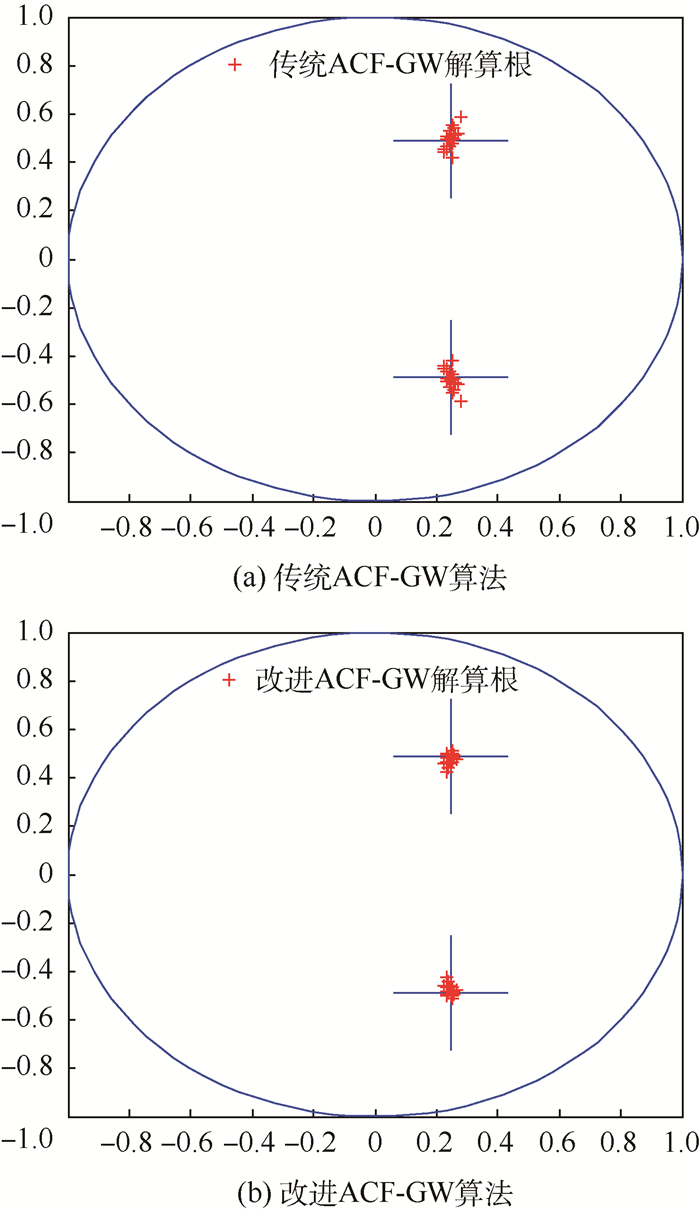 |
| 图 2 MA(2)特征方程的根 Fig. 2 Roots of characteristic equation for MA(2) |
| 图选项 |
表 2 传统与改进ACF-GW算法参数估计误差 Table 2 Error of traditional and improved ACF-GW algorithm parameter estimation for MA(2)
| 算法 | 参数 | 参数估计均值 | 参数估计平均误差e | 参数估计均方根误差d |
| 传统 | θ1 | -0.495 2 | 0.005 0 | 0.030 0 |
| ACF-GW | θ2 | 0.305 6 | 0.041 6 | |
| 算法 | σ2 | 0.998 8 | 0.034 7 | |
| 改进 | θ1 | -0.492 4 | 0.001 8 | 0.026 0 |
| ACF-GW | θ2 | 0.297 1 | 0.020 7 | |
| 算法 | σ2 | 1.002 4 | 0.032 6 |
表选项
3)? MA(3)。系数θ1=-0.531 9,θ2=0.219 6,θ3=-0.416 5。仿真结果如图 3和表 3所示。
 |
| 图 3 MA(3)特征方程的根 Fig. 3 Roots of characteristic equation for MA(3) |
| 图选项 |
表 3 传统与改进ACF-GW算法参数估计误差 Table 3 Error of traditional and improved ACF-GW algorithm parameter estimation for MA(3)
| 算法 | 参数 | 参数估计均值 | 参数估计平均误差e | 参数估计均方根误差d |
| 传统ACF-GW算法 | θ1 | -0.548 6 | 0.020 2 | 0.029 3 |
| θ2 | 0.218 5 | 0.016 6 | ||
| θ3 | -0.438 7 | 0.033 5 | ||
| σ2 | 0.970 7 | 0.037 7 | ||
| 改进ACF-GW算法 | θ1 | -0.530 5 | 0.004 5 | 0.009 4 |
| θ2 | 0.221 2 | 0.012 7 | ||
| θ3 | -0.417 3 | 0.011 9 | ||
| σ2 | 0.991 3 | 0.020 3 |
表选项
从所给3个指标对比传统ACF-GW算法和改进ACF-GW算法:
1)? 图 1、图 2和图 3分别对应传统ACF-GW算法和改进ACF-GW算法求解MA(1)、MA(2)和MA(3)参数所得特征方程的根的分布情况,其中“十”字表示理论根。可以得出,传统ACF-GW算法和改进ACF-GW算法对应的特征根都分布在理论根周围,说明用这2种算法求解MA参数的正确性;直观上可以看出,改进ACF-GW算法对应的特征根分布更为集中。
2)? 表 1、表 2和表 3分别列出使用传统ACF-GW算法和改进ACF-GW算法求解MA(1)、MA(2)和MA(3)参数时的平均误差和均方根误差。对比参数估计平均误差项,该项表征参数估计值与参数真值的平均偏差,传统ACF-GW算法约为改进ACF-GW算法的3倍,说明改进ACF-GW算法的参数估计值更接近真值,精度更高。对比参数估计均方根误差项,该项表征参数估计值与参数真值的偏差,或单次估计结果的可靠性,传统ACF-GW算法约为改进ACF-GW算法的2~3倍,说明改进ACF-GW算法的参数估计值波动小,单次估计可靠性高。
3.2 自协方差估计中m的选取 以第3.1节中的MA(2)为例,求得样本长度N=2 318,自协方差估计精度与m的关系如图 4所示。图 4(d)为r(0)、r(1)和r(2)的误差的代数和。可以看出,当m=5q=10时,自协方差估计已趋于稳定,且估计误差小。
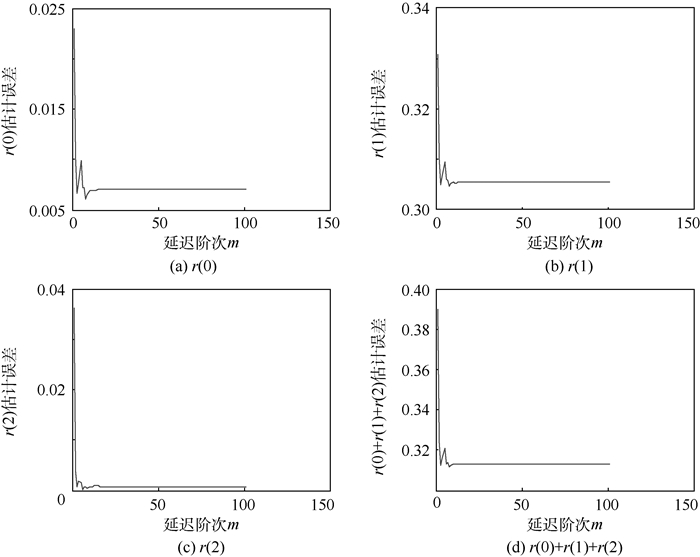 |
| 图 4 自协方差估计误差随延迟阶次m变化 Fig. 4 Estimation error of autocovariances versus lag order m |
| 图选项 |
4 MEMS陀螺仪随机漂移补偿 选用芯片ADIS16375作为待进行误差补偿的MEMS-IMU,该陀螺仪的零偏稳定性为12 (°)/h。惯性传感器的测量误差包括确定性误差和随机漂移。首先,基于实验室现有的双轴转台对MEMS-IMU进行动静态标定试验,补偿确定性误差,包括零偏和标度因数等。然后,对确定性误差补偿后剩余的随机数据进行ARMA建模。最后,利用得到的ARMA模型和经确定性误差补偿之后的随机数据进行Kalman滤波,并对滤波估计得到的随机信号与确定性误差补偿之后的随机数据作差,即为随机漂移补偿后的结果。
在30℃恒温箱中静置测量MEMS-IMU的输出,时间为4 h。陀螺仪三轴随机漂移经检验为平稳序列,ARMA模型阶次分别为(1, 1)、(2, 1)和(2, 1),本文中参数估计方法仅适用于p>q,故对X轴陀螺仪的模型升阶,设其为(2, 1),本节最后将论证这种做法的合理性。在MA参数估计部分分别采用传统ACF-GW算法和改进ACF-GW算法。由于ARMA模型只是对实际过程的近似,模型真实参数未知,故选择衡量指标为随机漂移补偿前和补偿后陀螺仪输出的均值和标准差,如表 4所示。
表 4 陀螺仪误差补偿后的均值和标准差 Table 4 Mean and standard deviation of compensated gyros
| 陀螺仪 | MA参数估计 | 均值/((°)·s-1) | 标准差/((°)·s-1) |
| X | 原始观测 | -0.182 2 | 0.238 6 |
| 确定性误差补偿 | 0.000 1 | 0.238 7 | |
| 传统ACF-GW算法 | 0.000 1 | 0.066 5 | |
| 改进ACF-GW算法 | 0.000 1 | 0.052 2 | |
| Y | 原始观测 | 0.012 9 | 0.265 4 |
| 确定性误差补偿 | -0.002 0 | 0.265 0 | |
| 传统ACF-GW算法 | -0.002 0 | 0.096 3 | |
| 改进ACF-GW算法 | -0.002 0 | 0.059 6 | |
| Z | 原始观测 | -0.095 7 | 0.212 9 |
| 确定性误差补偿 | 0.007 8 | 0.212 7 | |
| 传统ACF-GW算法 | 0.007 8 | 0.054 5 | |
| 改进ACF-GW算法 | 0.007 8 | 0.037 3 |
表选项
以均值和标准差为衡量指标,对比表 4中各项可以看出:
1)?转台标定主要用于补偿确定性误差,确定性误差被补偿掉后均值接近0,但标准差基本不变。
2)?随机漂移建模后滤波补偿可有效降低输出的标准差。AR参数估计方法相同,MA参数估计分别采用传统ACF-GW算法和改进ACF-GW算法,X、Y、Z轴输出标准差降低到0.066 5,0.096 3,0.054 5和0.052 2,0.059 6,0.037 3。对比可看出, 改进ACF-GW算法对应的标准差更小,补偿效果更好。使用改进ACF-GW算法补偿后的标准差降低至补偿前的1/5左右。
以X轴陀螺仪为例,在所有测量数据中随机选择6 000 s的陀螺仪数据,画出其静态时的原始观测输出、确定性误差补偿后的输出和随机漂移补偿后的输出,如图 5所示。其中随机漂移补偿中的ARMA参数估计采用改进ACF-GW算法。从图 5中可直观看出,确定性误差补偿主要修正输出均值,随机漂移补偿主要修正标准差。
 |
| 图 5 X轴陀螺仪误差补偿结果 Fig. 5 Results after error compensation of X gyro |
| 图选项 |
ARMA定阶时曾对X轴陀螺仪的模型升阶,下面通过残差检验的方法说明ARMA(2, 1)的合理性。滤波残差理论上为白噪声,然而,事实上我们并不知道真正的参数值,只有估计值,参考文献[8],以1/N作为滤波残差自相关函数的标准差会低估低阶延迟的自相关明显偏离零值的统计显著性,但通常可以应用于一般和较高的延迟。图 6为使用ARMA(2, 1)模型对X轴陀螺仪随机误差滤波的滤波残差的自相关函数,延迟大于5的自相关函数基本在一倍标准差范围内,可认为ARMA(2, 1)模型的假设合理。
 |
| 图 6 X轴陀螺仪补偿残差的自相关函数 Fig. 6 Autocorrelation function of X gyro's residual signal after error compensation |
| 图选项 |
5 结论 本文在分析了现有MA参数估计方法的基础上,提出了一种方差小的自协方差估计值,然后将该估计值作为GW算法的输入得到改进ACF-GW算法,解决了MA参数估计结果波动大、单次估计精度低的问题。通过仿真和MEMS陀螺随机漂移补偿验证得出以下结论:
1)?与传统ACF-GW算法对比,改进ACF-GW算法对应的MA过程的特征根分布更为集中;参数估计值的平均偏差,改进ACF-GW算法约为传统ACF-GW算法的1/3,改进ACF-GW算法精度更高;参数估计值的均方根误差,改进ACF-GW算法约为传统ACF-GW算法的1/3~1/2,改进ACF-GW算法的参数估计值波动小,单次估计可靠性高。
2)?对陀螺仪输出中的随机漂移建模补偿可有效降低补偿后数据的标准差,改进ACF-GW算法对应的补偿后标准差更小,补偿后的标准差降低至补偿前的1/5左右。
理论仿真和实际应用均表明本文提出的MA参数估计方法是有效的。
参考文献
| [1] | 曾庆化, 黄磊, 刘建业, 等. 基于ARMA模型的光纤陀螺随机噪声滤波方法[J].中国惯性技术学报, 2015, 23(1): 120–124.ZENG Q H, HUANG L, LIU J Y, et al. Real-time filtering methods of FOG random noise based on ARMA model[J].Journal of Chinese Inertial Technology, 2015, 23(1): 120–124.(in Chinese) |
| [2] | STEBLER Y, GUERRIER S, SKALOUD J, et al.Improving modeling of MEMS-IMUs operating in GNSS-denied conditions[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2011).Washington, D.C.:INST Navigation, 2011:2417-2426. |
| [3] | 袁赣南, 梁海波, 何昆鹏, 等. MEMS陀螺随机漂移在线补偿技术[J].北京航空航天大学学报, 2010, 36(12): 1448–1452.YUAN G N, LIANG H B, HE K P, et al. On-line compensation technique for micro mechanical gyroscope random error[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(12): 1448–1452.(in Chinese) |
| [4] | FATTAH S A, ZHU W P, AHMAD M O.An identification technique for noisy ARMA systems in correlation domain[C]//IEEE International Symposium on Circuits and System.Piscataway, NJ:IEEE Press, 2007:349-352. |
| [5] | FATTAH S A, ZHU W P, AHMAD M O.Identification of autoregressive moving average systems from noise-corrupted observations[C]//Joint IEEE North-East Workshop on Circuits and Systems/TAISA Conference.Piscataway, NJ:IEEE Press, 2008:69-72. |
| [6] | FATTAH S A, ZHU W P, AHMAD M O. Identification of autoregressive moving average systems based on noise compensation in the correlation domain[J].IET Signal Processing, 2011, 5(3): 292–305.DOI:10.1049/iet-spr.2009.0240 |
| [7] | BROERSEN P M T. Modified Durbin method for accurate estimation of moving-average models[J].IEEE Transactions on Instrumentation and Measurement, 2009, 58(5): 1361–1369.DOI:10.1109/TIM.2008.2009183 |
| [8] | BOX G E P, JENKINS G M, REINSEL G C. Time series analysis:Forecasting and control[M].Hoboken: John Wiley & Sons, 2011: 140-145. |
| [9] | ABO-HAMMOUR Z S, ALSMADI O M K, AL-SMADI A M, et al. ARMA model order and parameter estimation using genetic algorithms[J].Mathematical and Computer Modelling of Dynamical Systems, 2012, 18(2): 201–221.DOI:10.1080/13873954.2011.614068 |
| [10] | 范菁.ARMA模型的两种共轭梯度参数估计法及ARIMAX模型的应用[D].秦皇岛:燕山大学, 2009:23-34.FAN J.The two methods of conjugate gradient parameters estimation of ARMA model and the application of the ARIMAX model[D].Qinhuangdao:Yanshan University, 2009:23-34(in Chinese). |
| [11] | 邓自立, 王欣, 高媛. 建模与估计[M].北京: 科学出版社, 2007: 260-271.DENG Z L, WANG X, GAO Y. Modeling and estimation[M].Beijing: Science Press, 2007: 260-271.(in Chinese) |
| [12] | TAO G L, DENG Z L. Self-tuning fusion Kalman filter for multisensor single-channel ARMA signals with coloured noises[J].IMA Journal of Mathematical Control and Information, 2015, 32(1): 55–74.DOI:10.1093/imamci/dnt027 |
| [13] | KADERLI A, KAYHAN A S. Spectral estimation of ARMA processes using ARMA-cepstrum recursion[J].IEEE Signal Processing Letters, 2000, 7(9): 259–261.DOI:10.1109/97.863151 |
| [14] | MENDEL J M. Tutorial on higher-order statistics (spectra) in signal processing and system theory:Theoretical results and some applications[J].Proceedings of the IEEE, 1991, 79(3): 278–305.DOI:10.1109/5.75086 |
| [15] | 王可东, 熊少锋. ARMA建模及其在Kalman滤波中的应用[J].宇航学报, 2012, 33(8): 1048–1055.WANG K D, XIONG S F. An ARMA modeling method and its application to Kalman filtering[J].Journal of Astronautics, 2012, 33(8): 1048–1055.(in Chinese) |
| [16] | SODERSTROM T, STOICA P. System identification[M].London: Prentice Hall, 1989: 570-575. |
| [17] | 肖创柏, 罗晖, 李衍达. 基于OIVPM的特征值确定ARMA模型的结构[J].自动化学报, 1996, 22(1): 68–73.XIAO C B, LUO H, LI Y D. ARMA model order determination based on the eigenvalues of the overdetermined instrumental variable produce moment[J].Acta Automatica Sinica, 1996, 22(1): 68–73.(in Chinese) |
