再入制导方法按照其生成指令的不同方式可大致分为两大类:即预测-校正制导和轨迹跟踪制导[2]。就应用角度而言,虽然后者的制导精度和鲁棒性略逊于前者,但由于其计算量较小,因此在目前的再入飞行中往往更受青睐。
历史上,航天飞机采用的阻力加速度制导方法就属于一种典型的轨迹跟踪制导方法(以下简称轨迹跟踪方法)[3-4]。近年来,为了进一步提高轨迹跟踪方法的自主性和鲁棒性,国内外****对这类制导方法进行了深入研究。其中,文献[5-6]从不同角度对阻力加速度制导方法进行了改进,进而避免了该方法在离线规划参考剖面时的繁琐过程;文献[7]则利用拟平衡滑翔条件(Quasi-Equilibrium Glide Condition,QEGC)对再入问题进行了简化,从而使再入轨迹的在线快速规划成为可能;文献[8]提出了一种应用线性二次型调节器(Linear Quadratic Regulator,LQR)的轨迹跟踪方法,拥有较高的鲁棒性;文献[9]提出了一种封闭形式的近似滚动时域控制(Receding Horizon Control,RHC)方法,避免了在线积分和显式的增益调度;文献[10]则提出了一种基于轨迹线性化控制(Trajectory Linearization Control,TLC)理论的再入轨迹跟踪制导律,减少了制导指令的解算时间。
尽管上述各类方法在仿真测试中均表现出了不错的精度和鲁棒性[7-8],但要在实际飞行中成功实施这些方法,仍依赖于高精度的导航信息。然而,“黑障”区等复杂因素的存在使得再入飞行器的导航精度在相当长的一段时间内难以得到保证[11]。此时,由于轨迹跟踪方法对导航信息的误差及不连续性的适应性较差,再入飞行往往面临失败的风险。
针对上述情况,本文提出了一种新型的自适应制导方法。该方法依据实时飞行状态对参考高度-速度剖面进行在线拟合、迭代,并解算出满足终端约束的制导指令,从而有效地消除“黑障”区内累计的导航误差以及飞离“黑障”区时导航信息跳变对制导产生的影响。各类仿真结果显示,该方法较传统轨迹跟踪制导方法拥有更高的自主性和适应性,在干扰情况下也能保持更高的制导精度。此外,该方法拥有较高的运算效率,具备在线实时规划参考剖面的应用潜力。
1 再入制导问题描述 1.1 再入动力学方程 考虑地球自转因素,建立基于北天东坐标系的三自由度无量纲运动方程如下[12]:
 | (1) |
式中:r为被地球半径R0无量纲化的地心距;V为被第一宇宙速度
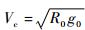
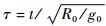
 | (2) |
式中;ρ为大气密度;Sref为参考面积;m为质量;CL和CD为升力系数和阻力系数,它们均为攻角α、马赫数和高度的函数。
在再入轨迹规划问题中,攻角是根据航程、热防护及配平等要求预先给定的,一般为马赫数的函数:
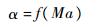 | (3) |
1.2 再入轨迹约束条件 再入轨迹约束条件包括过程约束和终端约束。常见的过程约束包括热流率约束、过载约束和动压约束:
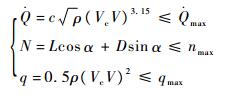 | (4) |
式中:c为与飞行器头部驻点半径有关的常数;nmax为最大方向过载。
再入轨迹的终端约束一般包括飞行器进入末端能量管理段(Terminal Area Energy Management, TAEM)时的高度约束、速度约束和待飞航程约束:
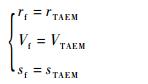 | (5) |
式中:rTAEM、VTAEM和sTAEM分别为末端能量管理段高度、速度和待飞航程。
1.3 导航系统模型 在再入飞行段,飞行器一般采用惯性导航系统(Inertial Navigation System,INS)和全球定位系统(Global Positioning System,GPS)的组合导航方式[13]。其中,INS拥有自主性高和抗干扰能力强的优势,但其导航误差会随时间积累;GPS则通过接受卫星信号解算出高精度的速度与位置信息,从而对INS的导航误差进行校正。
INS的导航误差是由惯性元件的随机噪声、系统的安装误差和刻度因数等因素引起的。本文按文献[14]中近空间飞行器INS误差的仿真结果,对式(1)中的各状态变量x=
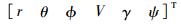
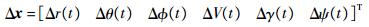 | (6) |
对于轨道再入飞行,“黑障”区一般存在于45~80km的范围内[13]。此时,GPS接收的无线电信号被屏蔽,飞行器只能依赖INS进行导航,故在这一阶段制导系统的输入信号为xnavi=x+Δx。而在“黑障”区以外,由于GPS能够精确地解算飞行器的速度和位置信息,因此导航误差可忽略不计,即xnavi=x。制导系统在接收到导航信息xnavi后,再计算出跟踪参考状态xc所需的制导指令。整个系统的结构图如图 1所示。
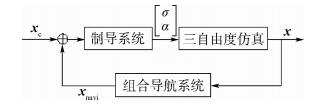 |
| 图 1 考虑导航误差的再入飞行结构 Fig. 1 Configuration of reentry flight with navigation error |
| 图选项 |
1.4 再入飞行剖面 结合1.3节中组合导航系统的特点,本文按飞行器是否飞离“黑障”区并重新捕获GPS信号作为分界点,将再入轨迹分为轨迹跟踪段和在线更新段,如图 2所示。
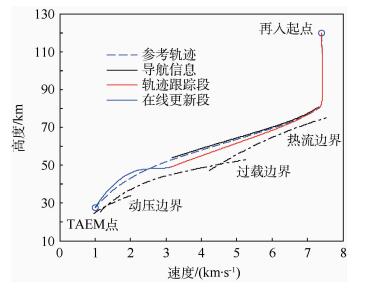 |
| 图 2 再入飞行高度-速度剖面 Fig. 2 Altitude-versus-velocity profile of reentry flight |
| 图选项 |
轨迹跟踪段覆盖再入初期到飞行器飞离“黑障”区的飞行阶段。在整个轨迹跟踪段,飞行器都能较好地满足“拟平衡滑翔”条件,轨迹倾角的变化较为缓慢。因此,该段中仍可采用传统的轨迹跟踪制导方法。尽管“黑障”区内不断累积的导航误差会使飞行器的真实飞行状态不断偏离参考轨迹,但此时飞行器尚能较好地维持平稳飞行。
相比于轨迹跟踪段,在线更新段中制导方法面临的考验更为严峻:一方面,飞行器已不能很好地满足“拟平衡滑翔”条件,再入轨迹的力学特性发生了较大变化;另一方面,尽管存在导航信息的融合技术[13],但是当GPS消除“黑障”区内积聚的导航误差后,导航信息仍可能出现跳变。此时,导航信息的误差及不连续性会致使传统轨迹跟踪方法出现控制饱和及能量耗散不均等状况。而在该段实时采用基于轨迹迭代的在线更新方法,可以有效地避免该类风险的发生。
2 制导方法设计 2.1 轨迹跟踪段制导方法
2.1.1 参考轨迹的离线规划 本文中所使用的参考轨迹按文献[7]提出的“拟平衡滑翔”方法进行设计。该方法的核心是认为再入飞行轨迹的一大部分满足轨迹倾角γ较小且变化较缓慢的假设,即cosγ=1和
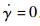
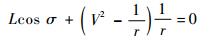 | (7) |
在初始下降段,由于大气密度稀薄,不需考虑各类约束的影响,因此飞行器在此段采用常值倾侧角|σ0|飞行。飞行从初始下降段过渡到拟平衡滑翔段的条件为
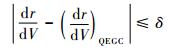 | (8) |
式中:δ>0为预先选定的常数;
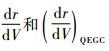
飞行进入拟平衡滑翔段后,则可按文献[7]中的方法确定满足式(4)和式(5)中约束条件的倾侧角剖面σ(V),并进一步确定高度、速度、轨迹倾角和待飞航程等纵向状态变量的参考值,即
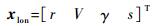
为了增强轨迹跟踪控制的鲁棒性,并降低状态变量的维数,这里可引入能量e作为自变量,代替对制导问题不太关键的自变量时间t。能量e可表示为
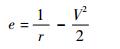 | (9) |
至此,由“拟平衡滑翔”方法确定的纵向参考轨迹状态量和控制量可按均匀选取的能量节点eN为自变量进行存储,即
 | (10) |
对于式(10)所存储的参考轨迹,每个节点的参考速度可直接由
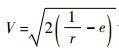
2.1.2 轨迹在线跟踪 按照文献[8],在使用LQR方法前,需先对由式(10)存储的参考轨迹按式(11)进行小扰动线性化。
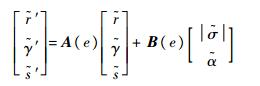 | (11) |
式中:
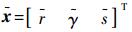
在线跟踪轨迹时,制导系统通过导航系统输出的导航信息xnavi计算出当前的能量ei,并对由式(10)记录的数表进行插值,获取纵向参考状态量xc=rc(ei)γc(ei)sc(ei)T和参考控制量uc=|σc(ei)|αc(ei)T。相应地,也可通过插值确定反馈增益K(ei)。依据上述参考量和反馈增益,可计算出跟踪轨迹所需的反馈控制量:
 | (12) |
式中:δxlon=xnavi/lon-xc,其中xnavi/lon=[rnaviγnavisnavi]T为导航系统输出的当前纵向状态变量。轨迹跟踪段最终的制导指令为u=[|σc+δσ|αc+α]T,倾侧角的符号由航向角误差漏斗逻辑确定。
2.2 在线轨迹更新段制导方法
2.2.1 高度-速度剖面的多项式拟合 考虑到再入过程中速度V具有良好的单调性,并为了方便施加终端约束,本文选择以速度为自变量拟合参考高度-速度剖面,并进一步解算相应的制导指令。为了兼顾制导精度、状态变量的连续性以及算法的效率,在线轨迹更新段的高度-速度剖面由四次多项式进行拟合,即
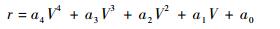 | (13) |
剖面的起点可记为点T, 该点的高度、速度和轨迹倾角由当前的导航信息确定,记为rT、VT和γT。相应地,此时的制导指令为σT和αT。换言之,对于每个制导周期,高度-速度剖面的起点T由飞行器的实时飞行高度和速度确定。而高度-速度剖面的终点始终由TAEM点的高度约束rTAEM与速度约束VTAEM确定。
通过研究式(1)中再入飞行三自由度动力学方程组的第1式和第4式,可知在忽略地球自转影响的前提下,有
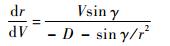 | (14) |
因此,式(14)可根据导航信息rT、VT和γT确定高度-速度剖面在点T处的斜率(dr/dV)T。
求解式(13)中5个系数ai所需的拟合条件至此确定了3项: [VT?rT]、[VT?(dr/dVT)]以及[VTAEM?rTAEM]。因此,还需要再选取2个拟合条件,才能完全确定上述5个拟合系数。
在确定第4个拟合条件时,应当选择对航程调节能力强的参数作为节点,以使式(13)中的参考剖面在不同飞行状态下均能满足终端航程约束sTAEM。
注意到对于待飞航程有
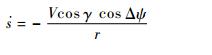 | (15) |
式中:Δψ为航向角误差。通常情况下,可认为飞行器近似沿地球大圆飞行,即cosΔψ≈1。那么,结合式(1)中的第4式,有
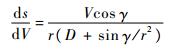 | (16) |
对于再入轨迹,无量纲化高度r≈1,因此式(16)表明阻力加速度D对待飞航程的变化起主导作用。通过式(2)则容易发现特定飞行器所受阻力加速度D主要受到大气密度的影响。换言之,式(13)中参考剖面的高度分布规律直接决定了飞行器航程的远近。
基于上述特点,这里可引入点T和TAEM点之间的速度中点C,即
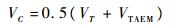 | (17) |
选取点C对应的飞行中点高度rC作为第4个节点,则第4项拟合条件为[VC?rC]。
由于前4个拟合条件已经基本确定了参考剖面的几何特征,因此最后一个拟合条件的选择具有一定的自由度。本文在此主要考虑以下两类情况。
第一类情况中,制导的首要目标是保证倾侧角在起点T处的连续性。对式(14)求导可得
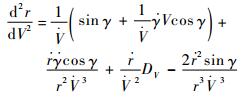 | (18) |
式中:
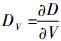
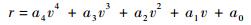 | (19) |
式中:v=V-VTAEM。此处定义ΔV=VT-VTAEM,fT=(dr/dV)T,gT=(d2r/dV2)T,则式(19)中相应的拟合系数为
 | (20) |
另一类情况中,为优先保证制导精度,需将终端轨迹倾角约束在某一特定值γTAEM。此时,参考高度-速度剖面的终端斜率可由式(14)确定。则第5个拟合条件相应地取为[VTAEM?(dr/dV)TAEM]。参考高度-速度剖面此时则可记为
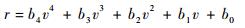 | (21) |
此处定义fTAEM=(dr/dV)TAEM,则相应的拟合系数为
 | (22) |
图 3中分别绘制了由式(19)和式(21)确定的参考高度-速度剖面以及相应的倾侧角指令。由图 3可见,式(19)确定的剖面在起点T处变化更为平缓,对应倾侧角指令的连续性也较好。但其在中后段的变化加剧,倾侧角指令迅速逼近下边界,不利于轨迹跟踪;相反,式(21)确定的剖面在起点T附近较为陡峭,相应的倾侧角指令发生了突变。但其在中段以后的变化逐渐放缓,倾侧角指令也较平滑。
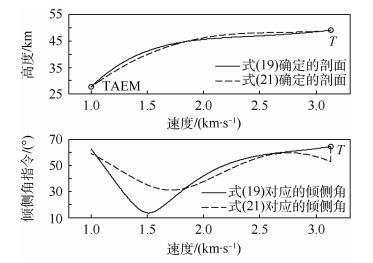 |
| 图 3 参考高度-速度剖面及倾侧角指令 Fig. 3 Reference altitude-versus-velocity profile and bank angle command |
| 图选项 |
基于以上特点,制导方法可在飞行器刚进入在线更新段时选用式(19)进行参考剖面的拟合,从而保证倾侧角指令的连续性;而当飞行进入在线更新段的中段时,制导方法可选取合适的时机切换到式(21)的剖面拟合,从而更好地保证终端制导精度。
具体的切换时机可如下选取:对于第i个制导周期,若假设与参考由式(19)确定的剖面和式(21)确定的剖面对应的倾侧角指令分别为|σ1(i)|和|σ2(i)|,则当两组指令之差|Δσ(i)|=|σ1(i)|-|σ2(i)|不再减小时:
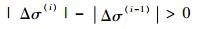 | (23) |
制导便可由式(19)确定的剖面切换到由式(21)确定的剖面。从图 3可见,在线更新段的前半段中,与式(19)确定的剖面对应的倾侧角指令的变化速率在不断增快,而与式(21)确定的剖面对应的倾侧角指令则正好与之相反,即σ1(i)一直处于追逐|σ2(i)|的状态。因此条件式(23)一般在在线更新段的中段得到满足。
需要指出的是,在一些导航误差较小的情况下,式(21)确定的剖面所对应的倾侧角指令只发生5°以内的跳变。在这种情况下,在线更新段可以始终采用式(21)确定的剖面进行制导,而无需引入式(19)确定的剖面的应用。
2.2.2 高度-速度剖面的迭代 为使式(19)和式(21)拟合的剖面满足终端航程约束,需要对中点高度rC进行迭代求解。
通过研究发现,在迭代时将能量e作为自变量,并将终端待飞航程sf作为迭代指标可以提高算法的效率和收敛性。这是由于待飞航程s相对于能量e有很好的单调性,且终端航程误差sf-sTAEM的符号有明确的物理意义:当其为正时,表明飞行器航程过近;反之,则说明航程过远。
由式(9)可知,对于能量e有
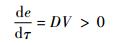 | (24) |
即整个再入过程中能量e单调递增(能量e是无量纲化的机械能的负值)。结合式(15),可知:
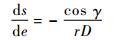 | (25) |
对于第k步迭代以及高度rC(k),通过式(9)和式(19)(或式(21))很容易求出当前能量e对应的速度V和高度r。对式(19)(或式(21))求导一次并结合式(14)则可求得相应的轨迹倾角γ。至此,式(25)的右半部分完全确定。将待飞航程s从起点eT积分至终点eTAEM便可得到终端待飞航程sf(k)。
第k+1步迭代所用的中点高度rC(k+1)可由割线法进行更新:
 | (26) |
若第k步迭代的终端待飞航程sf(k)满足条件:
 | (27) |
则对应的中点高度rC(k)所确定的高度-速度剖面即为最终的参考剖面,迭代过程结束。
值得注意的是,虽然以终端待飞航程sf为迭代指标时,迭代过程对初值rC(0)和rC(1)并不敏感,但在中点速度VC所对应的再入走廊中点±2~3km的范围内选取初值仍可在一定程度内提高迭代速度。此外,选取ε=10-5便可保证良好的制导精度。
2.2.3 制导指令的生成 一旦中点高度rC(k)得以确定,则对于当前速度V,通过式(14)和式(19)(或式(21))很容易求得相应的参考高度r和参考轨迹倾角γ。通过式(3)给定的攻角剖面,则易求得相应的攻角指令α。而结合式(1)中的第1、第4和第5式以及式(18)便可求得倾侧角指令|σ|。倾侧角的符号仍由航向角误差漏斗逻辑确定。
值得注意的是,由式(20)和式(22)可见,当ΔV随着飞行不断减小时,多项式拟合的效果将逐渐变差。就物理意义而言,ΔV对应着飞行器的剩余能量。当ΔV较大时,飞行器具有更多的剩余能量,高度-速度剖面也就具备了更大的调节范围;而当剩余能量较少时,高度-速度剖面的调节范围将会减小,而剖面的高度调节范围又直接对应飞行器的航程范围,因此此时终端航程精度也会随之降低。针对本文中的飞行器,通过仿真验证表明,当2000m/s≤V≤3200m/s时,在线更新方法拥有良好的制导精度。因此,算法在满足飞行速度V≤2000m/s时将进行最后一次参考剖面的规划,并求解整个剖面的纵向参考状态和制导指令。上述信息将以式(10)的格式进行存储。随后的飞行中,制导系统通过式(12)对上述剖面进行在线跟踪。
3 在线应用及仿真验证 3.1 在线调整策略 在线应用过程中,在导航误差过大或升阻力所受干扰较强的情况下,上述在线更新方法可能会解算出超过飞行器能力范围的制导指令。此时,需要对拟合参数进行适当调节。
对于特定飞行器,参考高度-速度剖面的变化范围主要受倾侧角σ的限制(0°<σ< 90°),故由式(18)可见,对于确定的r、V、γ和α,适当地对剖面各点的d2r/dV2值进行调节,便能解算出合理的倾侧角指令σcmd。
结合文献[15]中的结论,对于本文中规划的高度-速度剖面式(19)和式(21), 由于点T和TAEM点处的倾侧角指令σcmd均较大,故只需对中点C附近的d2r/dV2进行调节以便保证倾侧角指令σcmd在飞行器的能力范围之内。结合式(20)和式(22),并对式(19)和式(21)求导2次,有
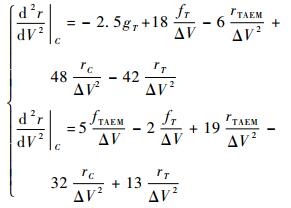 | (28) |
由式(28)可知,当式(19)确定的剖面超出飞行器能力范围时,可牺牲一定的制导精度,通过放宽终端航程约束sTAEM来调节中点高度rC,进而减小d2r/dV2,从而保证相应倾侧角指令σcmd在限制范围内。针对本文中的飞行器,仿真结果表明,sTAEM每放宽5km,σcmd的最小值将增加4°左右,且sTAEM的放宽量一般不必超过10km;对于式(21)确定的剖面,则可采用减小γTAEM的策略调节d2r/dV2的值,进而保证相应的倾侧角指令σcmd得以实现。针对本文中的飞行器,仿真结果表明,γTAEM每减小0.5°,σcmd的最小值将增加2°左右,γTAEM的调节范围一般在-12.0°~-14.0°之内。需要指出的是,由于参考剖面处于实时更新的状态,因此,除最后一次更新参考剖面外,单个制导周期只需保证起点T处对应的倾侧角指令不至于过小(|σ|≥5°), 便可认为参考剖面满足飞行器的能力范围。
3.2 仿真验证 本文的仿真采用航天飞机模型,再入飞行任务的初始状态参数和过程约束设置分别如表 1和表 2所示。
表 1 仿真初始状态参数 Table 1 Initial state parameters of simulations
| 参数 | 高度/ km | 速度/ (m·s-1) | 经度/ (°) | 纬度/ (°) | 轨迹倾角/ (°) | 航向角/ (°) |
| 数值 | 120.0 | 7400.0 | 175.5 | 0 | -1.1 | 74.2 |
表选项
表 2 仿真过程约束 Table 2 Process constraints of simulations
| 参数 | 最大热流率/(MW·m-2) | 最大过载/g | 最大动压/ kPa |
| 数值 | 760 | 2.5 | 20 |
表选项
所有飞行任务的目标点航向对准锥(HAC)的经、纬度坐标分别为255.55°和12.50°。终端航程约束sTAEM=110.0km,高度约束rTAEM=27.5km,速度约束VTAEM=1000.0m/s。所有仿真的截止条件均取为V≤1000.0m/s。
3.2.1 常规导航误差下的仿真结果 本文按照文献[14]中的数据对捷联式惯性导航系统的误差进行拟合,并将其折合为三自由度动力学方程组(1)中各状态变量的导航误差。本文中INS的误差参数如下:陀螺仪安装误差为10″,标度因数误差1.0×10-4,随机零偏0.01(°)/h,一阶马尔可夫过程相关时间3600s,驱动白噪声方差0.01(°)/h;加速度计安装误差为600″,标度因数误差1.5×10-3,高斯白噪声0.01(°)/h,一阶马尔可夫过程相关时间1800s,驱动白噪声方差10-4g。其1000s时各状态变量的导航误差如表 3所示。
表 3 惯性导航系统1000s时的导航误差 Table 3 Navigation error of INS at 1000th second
| 参数 | 高度/ km | 速度/ (m·s-1) | 经度/ (″) | 纬度/ (″) | 轨迹倾角/ (″) | 航向角/ (″) |
| 数值 | 3.5 | 30 | 32.3 | 32.3 | 35.0 | 80.0 |
表选项
按上述参数设置导航误差,并对传统轨迹跟踪方法和在线更新方法分别进行仿真,可得到表 4以及图 4~图 6中的结果。
表 4 常规导航误差下的终端制导误差 Table 4 Terminal guidance error under normal navigation error
| 方法 | 高度/km | 航程/km |
| 轨迹跟踪方法 | -0.010 | 2.63 |
| 在线更新方法 | 0.182 | -0.77 |
表选项
 |
| 图 4 高度-速度剖面仿真结果 Fig. 4 Simulation results of altitude-versus-velocity profile |
| 图选项 |
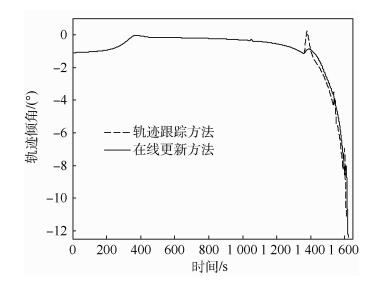 |
| 图 5 轨迹倾角历程 Fig. 5 Flight-path angle history |
| 图选项 |
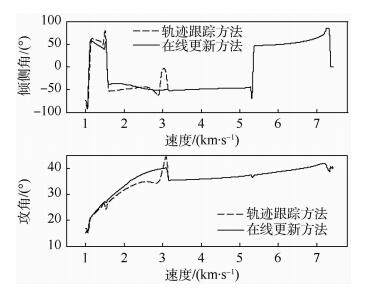 |
| 图 6 制导指令历程 Fig. 6 Guidance command history |
| 图选项 |
由表 4可见,轨迹跟踪方法与在线更新方法的终端高度精度均较好,而在线更新方法的终端航程精度要高于轨迹跟踪方法。
由图 4和图 5可见,在满足终端高度约束的情况下,在线跟踪方法可以有效地避免再入轨迹的剧烈变化,保证飞离“黑障”区后飞行过程的平稳过渡。而传统的轨迹跟踪方法则难以达到此目标。
由图 6可见,通过实时规划参考剖面,在线更新方法有效避免了传统轨迹跟踪方法中出现的倾侧角剧烈振荡现象。此外,两种方法的攻角指令均在离开“黑障”区时发生了跳变。这是由于在轨迹跟踪段内,LQR方法需要同时对参考高度和参考航程进行追踪。而由于导航误差的存在,飞行器的实际飞行高度低于参考高度,在此情况下,制导逻辑只能通过逐渐减小攻角来降低阻力,进而跟踪参考航程。
3.2.2 极端导航误差下的仿真结果 由于再入过程中的高超声速气流扰动以及高频动态飞行环境等因素可能会使INS的导航误差进一步显著增加,因而有必要检验在线更新方法在此类恶劣飞行环境下的适应性。为此,本文针对3.2.1节中的INS设置了其极端情况下的导航误差量,如表 5所示。
表 5 极端情况下惯性导航系统1000s时的导航误差 Table 5 Navigation error of INS at 1000th second under extreme conditions
| 参数 | 高度/ km | 速度/ (m·s-1) | 经度/ (″) | 纬度/ (″) | 轨迹倾角/ (″) | 航向角/ (″) |
| 数值 | 5.0 | 50 | 48.5 | 48.5 | 50.0 | 120.0 |
表选项
按以上参数设置对在线更新方法进行仿真,可得到表 6、图 7和图 8中的结果。
表 6 极端导航误差下的终端制导误差 Table 6 Terminal guidance error under extreme navigation error
| 方法与条件 | 高度/km | 航程/km |
| 轨迹跟踪方法 | -0.014 | 11.74 |
| 未考虑倾侧角连续条件 | -0.139 | 1.56 |
| 考虑倾侧角连续条件 | -0.131 | -0.26 |
表选项
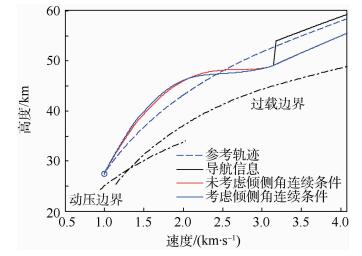 |
| 图 7 极端导航误差下的高度-速度剖面仿真结果 Fig. 7 Simulation results of altitude-versus-velocity profile under extreme navigation error |
| 图选项 |
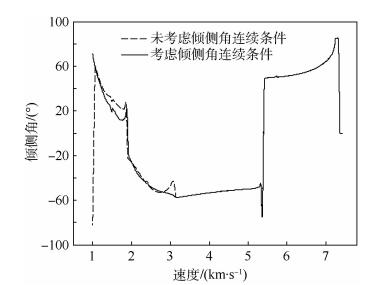 |
| 图 8 极端导航误差下的倾侧角指令历程 Fig. 8 Bank angle command history under extreme navigation error |
| 图选项 |
由表 6可见,3种情况下的终端高度精度均较好,但在线更新方法的终端航程精度要远高于轨迹跟踪方法。此外,考虑倾侧角连续条件时的在线更新方法的终端航程精度要略优于不考虑倾侧角连续条件的情况。
由图 7可见,相对于未考虑倾侧角连续条件的情况,当在线更新方法引入式(19)确定的剖面时,再入轨迹在在线更新段的起点处拥有更加平滑的过渡段。而在再入轨迹的末端,由于考虑倾侧角连续条件的在线更新方法已经切换到了式(21)确定的剖面,因此两种情况下的末端轨迹具有相似的形态。
由图 8可见,相较于提高制导精度,考虑倾侧角连续条件更大的作用在于通过引入式(19)确定的剖面抑制倾侧角突变。从仿真结果来看,未考虑倾侧角连续条件时,倾侧角出现了10°的跳变。同时,倾侧角速率已经接近15(°)/s的限制值;相比之下,考虑倾侧角连续条件时,倾侧角速率小于1(°)/s。在实际飞行中,倾侧角的连续性对应着飞行器姿态角的连续性,因此通过制导方法主动消除不必要的倾侧角突变比起被动地限制倾侧角速率,对降低飞行器姿态控制的难度有着更积极的作用。
3.2.3 气动拉偏情况下的仿真结果 本文挑选了表 7中的4种典型气动拉偏情况,对传统轨迹跟踪方法和在线更新方法分别进行了仿真。仿真中的导航误差按表 3设置。
表 7 气动拉偏参数 Table 7 Aerodynamic dispersion parameters
| 案例 | 阻力拉偏/% | 升力拉偏/% |
| 案例1 | -10 | +10 |
| 案例2 | -5 | +5 |
| 案例3 | +3 | -3 |
| 案例4 | +5 | -5 |
表选项
按上述参数进行仿真可得如表 8、图 9和图 10所示的结果。
表 8 气动拉偏情况下的终端制导误差 Table 8 Terminal guidance error under aerodynamic dispersion conditions
| 案例 | 轨迹跟踪方法 | 在线更新方法 | |||
| 高度/km | 航程/km | 高度/km | 航程/km | ||
| 案例1 | -0.450 | -28.8 | -0.223 | -12.23 | |
| 案例2 | -0.087 | -14.7 | 0.184 | -4.8 | |
| 案例3 | 0.262 | 8.0 | -0.018 | -1.4 | |
| 案例4 | -0.199 | 16.4 | 0.313 | 7.3 | |
表选项
 |
| 图 9 气动拉偏情况下的高度-速度剖面仿真结果 Fig. 9 Simulation results of altitude-versus-velocity profile under aerodynamic dispersion conditions |
| 图选项 |
 |
| 图 10 气动拉偏情况下的倾侧角指令历程 Fig. 10 Bank angle command history under aerodynamic dispersion conditions |
| 图选项 |
由表 8可见,在拉偏的情况下,两种方法的高度误差近似;而在线更新方法的终端航程误差则
远远低于传统的轨迹跟踪方法,体现出了其具备更强的航程适应性。值得注意的是,案例4已接近飞行器的性能极限(升阻比减少10%),在线更新方法不适用于更加恶劣的拉偏情况;而对于升阻比增加的情况(案例1和案例2),在线更新方法表现出了更强的适应性。
图 9和图 10分别绘制了极端拉偏情况下两种方法的高度-速度剖面及相应倾侧角指令。可见,在线更新方法可针对不同的升阻力情况灵活改变参考剖面和倾侧角指令,从而满足航程要求。而传统轨迹跟踪方法则在所用情况中均沿同一参考剖面飞行,进而难以对航程实现调节。这也是其终端航程精度远低于在线更新方法的原因。此外,由图 10可见案例4中的倾侧角指令在在线更新段的中段已接近飞行器倾侧角调节范围的下边界。即在线更新方法将难以应对比此更为恶劣的拉偏情况。
4 结论 本文结合再入飞行中“黑障”区造成的导航信息误差与跳变等实际问题,提出了一种基于轨迹迭代的自适应在线更新方法。理论分析研究以及与轨迹跟踪方法的对比仿真结果表明:
1)在线更新方法能够结合实时飞行状态快速拟合、迭代出满足终端高度、速度与航程约束的参考高度-速度剖面,并生成相应制导指令。在常规和极端的导航信息误差及跳变情况下均具有良好的自适应性和终端精度。
2)在线更新方法在拟合参考剖面时充分考虑了各状态量与控制量的连续性,有效避免了传统轨迹跟踪制导方法在飞行器离开“黑障”区时出现的倾侧角剧烈振荡及飞行轨迹骤变等高风险飞行状态,提高了飞行过程的平稳性。
3)与轨迹跟踪方法相比,在线更新方法在存在气动拉偏的情况下能够更灵活地调节飞行器的飞行状态,从而使其具备更高的航程适应能力和制导精度。
4)在线更新方法具有较高的运算效率。在普通计算机(2.40GHz处理器)上运行时,完成单次高度-速度剖面的规划所需的运算时间在25~50ms范围内。而完成整个在线更新段100次左右的高度-速度剖面规划仅需3.2s。故该方法具备在线实时规划再入轨迹的应用潜力。
因此,本文提出的自适应在线更新方法能够有效应对再入飞行中制导系统输入信息存在的误差及跳变,对提高制导的自主性、适应性和精度具有一定的工程应用价值。
参考文献
| [1] | LU P. Entry guidance:A unified method[J].Journal of Guidance, Control and Dynamics, 2014, 37(3): 713–728.DOI:10.2514/1.62605 |
| [2] | WINGROVE R C. Survey of atmosphere re-entry guidance and control methods[J].AIAA Journal, 1963, 1(9): 2019–2029.DOI:10.2514/3.1987 |
| [3] | HARPOLD J C, GRAVES C A. Shuttle entry guidance[J].Journal of Astronautical Sciences, 1979, 37(3): 239–268. |
| [4] | HARPOLD J C, GAVERT D E. Space shuttle entry guidance performance results[J].Journal of Guidance, Control, and Dynamics, 1983, 6(6): 442–447.DOI:10.2514/3.8523 |
| [5] | ROENNEKE A J.Adaptive on-board guidance for entry vehicle:AIAA-2001-37343[R].Reston:AIAA, 2001.http://arc.aiaa.org/doi/pdfplus/10.2514/6.2001-4048 |
| [6] | MEASE K D, CHEN D T, TEUFE P, et al. Reduced-order entry trajectory planning for acceleration guidance[J].Journal of Guidance, Control, and Dynamics, 2002, 25(2): 257–266.DOI:10.2514/2.4906 |
| [7] | SHEN Z J, LU P. On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111–121.DOI:10.2514/2.5021 |
| [8] | DUKEMAN G A.Profile-following entry guidance using linear quadratic regulator theory[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit 2002.Reston:AIAA, 2002.http://arc.aiaa.org/doi/abs/10.2514/6.2002-4457 |
| [9] | LU P. Regulation about time-varying trajectories:Precision entry guidance illustrated[J].Journal of Guidance, Control, and Dynamics, 1999, 22(6): 784–790.DOI:10.2514/2.4479 |
| [10] | 朱国栋, 沈作军. 基于轨迹线性化控制的再入轨迹跟踪制导[J].北京航空航天大学学报, 2015, 41(11): 1975–1982.ZHU G D, SHEN Z J. Trajectory linearization control based tracking guidance design for entry flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 1975–1982.(in Chinese) |
| [11] | 李瑾.跨大气层可重复使用运载器再入段自主导航研究[D].北京:北京航空航天大学, 2007:4.LI J.Study of the autonomous navigation of spanning aerosphere reusable launch vehicle[D].Beijing:Beihang University, 2007:4(in Chinese).http://mall.cnki.net/magazine/article/hkgx200704002.htm |
| [12] | VINH N X, BUSEMANN A, CULP R D. Hypersonic and planetary entry flight mechanics[M].Ann Arbor, MI: University of Michigan Press, 1980. |
| [13] | 杨峰, 程承, 张共愿. 一种亚轨道飞行器再入段组合导航方法[J].宇航学报, 2010, 31(3): 729–733.YANG F, CHENG C, ZHANG G Y. Simulation research of sub-orbital vehicle re-entry flight segment navigation technology[J].Journal of Astronautics, 2010, 31(3): 729–733.(in Chinese) |
| [14] | 彭慧.近空间飞行器惯性导航系统误差建模及修正关键技术[D].南京:南京航空航天大学, 2014:25-28.PENG H.The key technology research on error modeling and compensation of the INS for the HCV[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2014:25-28(in Chinese).http://www.doc88.com/p-7857627752585.html |
| [15] | SHEN Z J, LU P. On-board entry trajectory planning for sub-orbital flight[J].Acta Astronautica, 2005, 56(6): 573–591.DOI:10.1016/j.actaastro.2004.10.005 |
