通航飞行器垂直飞行轨迹规划就是通过构建规划空间 Ω ,将复杂多约束条件结合到航迹代价函数中,最终搜索得到满足约束限制的通航垂直剖面规划航迹。目前针对航迹规划问题的方法很多,常见的方法包括:A*算法、Dijkstra算法、Voronoi图法、人工势场法、遗传算法、蚁群算法以及神经网络等[1-5]。航迹规划方法的分类方法多种多样,通常可以按照规划方法的特征分为传统规划算法和智能规划算法,也可以按照规划空间的特征分为栅格规划空间算法和图形规划空间算法。目前,复杂多约束条件下的航迹规划大量集中在对相关数学问题的研究上,通常采用目标加权函数以构建评价指标,选取合适的智能算法,以搜索到的数学“最优点”构建规划的最优航迹[6]。然而目前的航迹规划多针对无人机、导弹以及军用飞行器展开[7],其与通航飞行器的作业区域、飞行性能存在较大差异,使得上述航迹规划方法不能简单类推到通航领域。通航是使用民用航空器从事一般运输航空以外的民用航空活动,虽然从事通航的飞行器与一般运输航空有可能相同,但通航中使用更多的是小型飞行器,因此本文主要针对机动、灵活的通航小型飞行器展开航迹规划研究,同时考虑到一般运输航空飞行高度高,飞行航迹要求必须在固定航路内,但通航可在开放空域内自由选取飞行航迹,因此一般运输航空垂直飞行轨迹规划方法与通航也不同,目前尚没有专门针对通航飞行器复杂多约束条件下的垂直飞行轨迹规划方法。
本文综合考虑飞行任务、地形信息和飞行器性能参数等约束条件,对基于栅格的A*算法进行简化和改进,算法简单易实现,搜索速度快,克服了A*算法在通航垂直飞行轨迹规划问题中应用的局限性,实验分析表明改进A*算法生成的通航垂直剖面规划航迹优于传统路径规划方法。
1 问题描述 通航飞行器垂直剖面航迹规划问题可以被描述为以通航飞行器所在垂直剖面为 Ω ,利用起点 S 、终点 T 位置信息确定 Ω 大小,已知执行任务的预设航迹点以及其他限制条件,最终计算得到一条在航迹代价模型度量下的垂直剖面最优或可行轨迹。通航飞行器垂直剖面规划航迹需要满足2个方面限制:①不超出飞行器的物理极限;②满足飞行任务要求(例如飞行高度要求、经过预设航迹点要求等)。针对上述通航垂直剖面约束限制条件,具体说明如下:
1) 最大爬升/下降角:属于通航飞行器的物理极限指标,其可约束通航飞行器在Ω内垂直方向上爬升、下降的角度范围。
2) 最小航迹段长度:在Ω内,通航飞行器保持飞行姿态不变的最短距离,其由飞行器的机动性能决定。
3) 飞行高度限制:其由最大限制高度、最低安全高度组成,中国目前限定通航各类低空空域垂直范围原则为真高1 000 m以下[8],同时最大限制高度可根据不同飞行任务(例如科学实验、航空摄影等)做出调整,但飞行高度不得超过最大限制高度且不得低于最低安全高度。
4) 预设航迹点:在执行飞行计划过程中,为通航飞行器预先设定且要求必须经过的航迹位置点。
5) 垂直机动次数:飞行器执行飞行任务过程中,在垂直方向上改变飞行姿态的次数,垂直机动次数越多,驾驶员的操作代价越大,越容易疲劳,油耗也会随之增加。
通航飞行过程中可能存在临时性的机动飞行,考虑到其属于飞行中变更航迹的范畴,而航迹规划的目的在于预先给出一条在航迹代价模型度量下的规划航迹,临时性机动飞行的存在并不影响航迹规划的有效性,则将上述诸多约束条件结合到A*算法中去,即可通过约束建模简化通航飞行器垂直剖面航迹规划问题。
2 垂直剖面航迹规划 2.1 A*算法 A*算法是当前广泛应用的经典启发式路径寻优算法之一。该算法的基本思路是通过约束建模将约束条件和启发函数相结合,以通向目标点的最小代价路径为最优结果,代价函数由2个部分组成,其定义为[9]
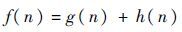 | (1) |
式中: g(n) 为由当前节点 n 至起点 S 的完成路径代价函数; h(n) 为启发函数,也就是由当前节点 n 至终点 T 的估计代价函数; f(n) 为由起点 S 出发经历当前节点 n 最终至终点 T 的航迹代价函数。A*算法就是将候选节点中对应 f(n) 值最小的节点作为后续待扩展节点。
A*算法可以在构建的静态栅格中搜索最优或可行路径,一般在算法执行过程中需构建2个动态表:OPEN表和CLOSE表,OPEN表存储搜索完成但未发生扩展的节点,CLOSE表存储已发生扩展的节点。在每轮搜索过程中,首先从OPEN表中获取“代价值最小”的节点,将其存入CLOSE表以完成本轮扩展。对扩展后的各节点进行分析,参照分析结果更新OPEN表、CLOSE表内容,并将合适的扩展节点存入CLOSE表,若搜索到目标节点,则终止扩展,否则不断重复以上过程,若最终OPEN表为空并且未能找到目标节点,则采用当前代价函数的算法不存在最优航迹。
对通航垂直剖面飞行轨迹规划问题而言,A*算法能将图的搜索问题转化为树的搜索问题,以启发信息来引导算法的搜索决策,既可提高搜索效率,又可保证得到垂直剖面规划航迹最优性[10]。通常代价函数、搜索策略和启发函数是影响A*算法性能的3个主要因素,A*算法的规划时间、精确性与Ω栅格的数目、大小相关。
2.2 规划空间构建 在利用改进A*算法对通航垂直剖面航迹进行规划之前,首先需要构建一个合理的Ω,设 (x,y) 为Ω内的坐标点, x 为飞行距离, y 为海拔高度,在已知起点 S 、终点 T 的位置信息之后,就可以确定Ω大小,设 Xmax 为Ω对应飞行距离的最大值,以 Ymax 为Ω对应海拔高度的最大值,综上Ω可以表示为集合 {(x,y)|0≤x≤Xmax,0≤y≤Ymax} 。
通航Ω以划分的单个栅格为基本单元,其所有栅格单元对应的代价值构成代价矩阵,将飞行任务、地形信息和飞行器性能参数等约束条件表示成符号信息,采用不同数据结构表示不同的环境信息,并将其导入构建的代价矩阵,便于计算机处理,使用从当前节点到目标节点航迹的最小累积代价作为每个栅格单元的最佳代价[11],最终完成对通航Ω的构建。
2.3 约束条件建模 为保证在复杂多约束条件下规划出满意的航迹,综合考虑通航飞行器垂直剖面航迹规划的各项约束条件,就约束建模具体实现过程进行详细说明:
针对最大爬升/下降角的限制条件,该约束是通航飞行器的物理极限指标之一,其限制了通航飞行器在Ω爬升或者下降的最大角度。设第 i 段垂直剖面航迹的水平投影长度为 xi-xi-1 ,其对应垂直投影长度为 yi-yi-1 ,设置最大爬升/下降角为 θ ,则最大爬升/下降角约束建模可表示为[12]
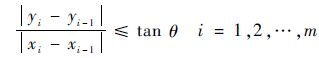 | (2) |
设置Ω栅格中各航迹节点航向,A*算法是对当前节点的所有相邻节点计算航迹代价,从 i 点出发可能的运动方向为图 1中所标1~8,而在Ω中由于运动方向和最大爬升/下降角 θ 的限制,不可能向相邻的任意方向飞行,假设飞行器从 i 点出发从左向右飞,则 i 点的扩展航迹节点为图中所标2、3和4这3个方向,上述方法不仅解决了最大爬升/下降角的限制问题,而且对搜索空间进行了化简,提高了搜索算法的执行效率。
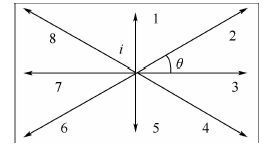 |
| 图 1 节点扩展方向 Fig. 1 Expanding directions of a node |
| 图选项 |
针对最小航迹段长度的限制条件,设飞行航迹由 {li|i=1,2,…,m} 组成,对通航飞行器Ω划分栅格,考虑最大爬升/下降角 θ 的约束限制,Ω栅格可设置为长方形,以长方形长为最小航迹段长度 lmin ,则针对最小航迹段长度的约束条件建模可表示为[13]
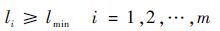 | (3) |
针对飞行高度约束限制条件,设置最大限制高度 htop 和最低安全高度 hlow 。根据中国低空开放政策通航飞行最大限制高度 htop 可以设置为1 000 m,同时其也可根据不同飞行任务需求(例如科学实验、航空摄影等)做出调整。根据飞行模式、作业区域和飞行阶段的最低安全高度要求,设置通航垂直剖面航迹最低安全高度 hlow ,降低飞行器与地面相撞的风险。
针对通航飞行器飞行计划执行中预设航迹点的限制条件,若存在 k 个预设航迹点,则按照其到终点 T 的距离远近进行编号,具体编号为 1,2,…,k ,将起点 S 、终点 T 分别标号为 0 和 k+1 ,再按照编号依次分段规划航迹,并连接分段规划的航迹,得到符合约束限制的垂直剖面规划航迹。
针对垂直机动次数的限制条件,将垂直机动代价因子 M(i) 引入评估函数,飞行器在某航迹节点发生一次垂直机动,则垂直机动代价增加,否则保持不变,通过对 M(i) 权重系数的控制实现对通航飞行器垂直机动次数的限制。
为了获得满足复杂多约束条件的垂直剖面规划航迹,通过约束建模将上述不同的约束条件与A*算法相结合,最终得到一种适用于通航飞行器垂直剖面航迹规划的方法,方法能对搜索空间进行有效简化,从而使搜索效率得到提高。
2.4 航迹代价建模 为保证通航飞行器的安全,提高运营效率,通航飞行器不仅需要满足飞行器自身性能条件的限制,而且需要应对飞行任务的约束,因此代价函数中必须兼顾上述两方面的各影响因素,采用建立代价函数的策略,可构造出针对扩展节点的评估机制,以筛选航迹代价值最小,即在上述航迹代价函数评价体系下的最优航迹。综上,设置由起点 S 出发至当前节点 n 已完成路径的代价函数:
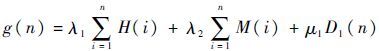 | (4) |
式中: H(i) 为第 i 个航迹节点飞行上界限制高度 hmax(i) 与该航迹节点真高 hreal(i) 的差值代价,即 H(i)=hmax(i)-hreal(i) ,其中 H(i) 越小,表示通航飞行器越接近飞行任务最大限制高度; M(i) 为从第 i-1 到第 i 个航迹节点垂直机动代价,其对应式(4)中的第2项代价值越小,表示通航飞行器机动次数越少,驾驶员的操作负担越小; D1(n) 为由当前节点 n 至起点 S 的规划路径长度代价,若 D1(n) 值越小,则表示通航飞行器航迹越短; λ1、λ2 和 μ1 为式(4)中各影响因素对应的权重系数。
本文的启发函数选用从当前节点 n 至终点 T 的曼哈顿距离 D2(n) 表示,此处也就是在Ω内从当前节点 n 至终点 T 的绝对轴距总和[14]。设Ω中当前节点 n 的坐标为 (xn,yn) ,终点 T 的坐标为 (xT,yT) ,则两点的曼哈顿距离可以表示为
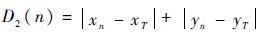 | (5) |
与计算由当前节点 n 至起点 S 的规划路径长度 D1(n) 的欧式距离相比,该启发函数既可保障包含足够的启发信息量,又可有效改善算法搜索效率,于是由启发函数构成的估计代价函数为
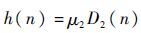 | (6) |
式中: μ2 为启发函数D2(n)对应权重系数。
综上,垂直剖面航迹代价函数可写为
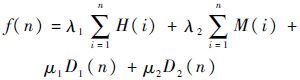 | (7) |
改进A*算法的基本原则是优先扩展 f(n) 值小的节点,当前节点 n 的 f(n) 值在同时候选的多个节点的 f(n) 值中为最小时, n 就是这些候选节点中的最优点,该启发式算法搜索过程实质上就是一个节点不断地生成和扩展的过程[15]。利用改进A*算法计算通航飞行器垂直剖面规划轨迹时,首先需在垂直剖面构建栅格规划空间,本文中搜索栅格即为航迹垂直剖面要素栅格,以飞行距离 l 和飞行高度 h 为横、纵坐标的Ω中,为通航飞行器 V 规划出满足复杂多约束条件的垂直剖面飞行轨迹。
2.5 确定权重系数 为使通航飞行任务顺利完成,各权重系数 λ1、λ2、μ1 和 μ2 应根据通航飞行器的性能、飞行任务要求以及飞行环境特征而做出相应变化。
各权重系数的求解是一种多目标决策问题,具有结构复杂、变量繁多、定性分析与定量计算混杂等特征,考虑到层次分析法具有以定性和定量相结合的方式处理各种复杂决策因素的优点,适用于解决类似本文中各权重系数确定的多目标决策问题,因此本文采用层次分析法[16]来确定各权重系数,式(7)中权重系数 λ1、λ2、μ1 和 μ2 分别对应影响因素1~4,构建一种无结构的多准则决策策略,将通航航迹规划专家的思维过程层次化、数量化,具体实现步骤如下:
1) 构造判断矩阵A,将影响因素1~4进行两两比较,确定层次中各个因素的相对重要程度之比 aij ,之后以定量的方式表示出来,其相对重要性一般采用1~9的数字及其倒数的标度来表示[17],随着 aij 值不断增加,因素 i 相对于因素 j 的重要性也不断增加。例如, aij=1 表示因素 i 与因素 j 重要性相同, aij=5 表示因素 i 与因素 j 相比明显重要。综上,本文的4阶判断矩阵为
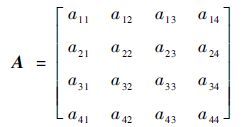 | (8) |
2) 计算各权重系数,利用特征值法求解航迹代价函数中的各权重系数,方程为
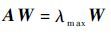 | (9) |
式中: λmax 为判断矩阵 A 的最大特征值; W 为 A 对应的特征向量,对 W 各项归一化处理就可得到航迹代价函数各权重系数。
3) 检验一致性,判断矩阵 A 的一致性指标通常可以表示为
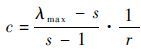 | (10) |
式中: s 为判断矩阵的阶数; r和c 分别为层次分析法中的平均随机一致性指标和一致性比例,其中 r 与判断矩阵阶数有关,经查询平均随机一致性指标表[17],得到当判断矩阵阶数 s=4 时,对应 r=0.89 ,计算 c 值, c 值越小判断矩阵 A 的一致性越好,当 c <0.1 时,判断矩阵 A 的一致性可以接受,否则需对判断矩阵 A 中的各项进行调整。
2.6 算法具体流程 基于改进A*算法的通航飞行器垂直剖面航迹规划方法具体步骤如下,其对应流程图见图 2。
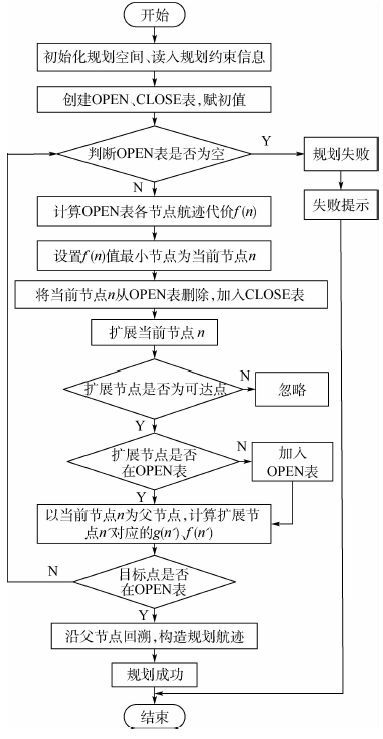 |
| 图 2 算法流程图 Fig. 2 Algorithm flowchart |
| 图选项 |
步骤 1 初始化规划空间,对规划空间Ω划分栅格,将起点 S 、终点 T 的位置信息输入规划空间,读入规划约束信息。
步骤 2 创建OPEN表和CLOSE表,并将起点 S 导入OPEN表,同时将CLOSE表置空,此时OPEN表中只有起点 S 。
步骤 3 遍历OPEN表,以最小 f(n) 值的节点作为当前节点 n ,同时删除OPEN表中的当前节点 n ,并将其导入CLOSE表,完成对OPEN、CLOSE表的更新。
步骤 4 扩展当前节点 n 的相邻节点,按顺序执行下述步骤:① 如果该扩展节点不满足约束条件、不可通行或者该节点已经在CLOSE表中,则设置其为不可达点,忽略不可达点,对其不做任何操作,继续检测下一个节点。②如果OPEN表不含该扩展节点,则在OPEN表中加入该扩展节点,同时设置当前节点 n 为其父节点,并计算扩展节点 n′ 对应的 g(n′) 和 f(n′) 值。③如果OPEN表含该扩展节点,则计算以当前节点 n 为父节点的扩展节点 n′ 对应的 g(n′) 是否小于原有 g(n) 值,若小于,则更新扩展节点 n′ 的父节点为当前节点 n ,并更新扩展节点 n′ 对应的g(n′)和 f(n′) 值,若不小于,则不更新。
步骤 5 重复步骤3和步骤4直到满足循环结束条件,也就是当终点 T 被导入OPEN表作为待查节点时,表示得到满足条件垂直剖面规划航迹,此时可结束循环操作;若OPEN表最终为空,即已经没有新的节点可以添加,同时CLOSE表中没有终点 T ,此时也结束循环,且最终未找到规划航迹。
步骤 6 从终点 T 沿存储的父节点开始回溯,最终经遍历所得的节点就构成了要求的垂直剖面规划航迹。
3 实验结果与分析 本文采用改进A*算法,对通航垂直剖面航迹展开规划实验,实验使用计算机主频为2.5 GHz,内存为4 G,实验环境为MATLAB,针对机动灵活的小型飞行器展开研究,以经典Cessna 172机型为例,实验涉及飞机性能参数都取自Cessna 172飞行员操作手册[18]。Ω大小由空间起点 S 和空间终点 T 确定,设置起点 S 纬度、经度和高度为(34.37°,109.39°,0 m),终点 T 为(34.28°,110.09°,0 m),3个需经过的预设航迹点依次为P1(34.14°,109.53°,750 m)、P2(34.36°,109.58°,750 m)和P3(34.26°,110.03°,750 m),根据Cessna 172飞行性能模型,Ω被划分为长方形栅格,栅格长度根据最小航迹段长度 lmin 限制设置为500 m,栅格高度根据最大爬升/下降角 θ 限制设置为50 m。
式(11)为结合实际飞行数据、飞行任务要求和飞行限制条件等影响因素确定的判断矩阵 A ,判断矩阵 A 中各元素取值大小参照航迹代价评估函数中各个影响因素的相对重要程度。
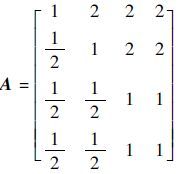 | (11) |
按2.5节方法计算航迹代价评估函数各权重系数大小为: λ1=0.395 2,λ2=0.278 1,μ1=0.163 4,μ2=0.163 4, 最大特征值为: λmax=4.060 6 ,一致性检验 c=0.022 7 ,满足 c <0.1 条件。
为了验证改进A*算法的优越性,在相同的规划空间Ω条件下,不但将其与传统A*算法进行比较,还将其与应用广泛且与A*算法具有相似框架的传统Dijkstra算法、改进Dijkstra算法(具有边界跟随特性)比较,分别规划出从相同的起点 S 到相同的终点 T 的垂直剖面航迹,分析上述3种算法所规划出航迹的飞行高度、机动次数、燃油消耗和扩展节点个数等相关指标。
图 3为传统A*算法、传统Dijkstra算法、改进Dijkstra算法(具有边界跟随特性)和改进A*算法的垂直剖面规划航迹。图中青色区域为航迹垂直方向地形剖面,红色区域为通航飞行最低安全高度限制区,其参照目视飞行条件下巡航速度小于250 km/h的最低安全高度设置为距地面真高100 m以下区域,红色曲线为飞行作业区域上边界,其参照低空开放政策及不同飞行任务而设定,此处设置为真高1 000 m,蓝色曲线为算法规划的通航飞行器垂直剖面航迹。
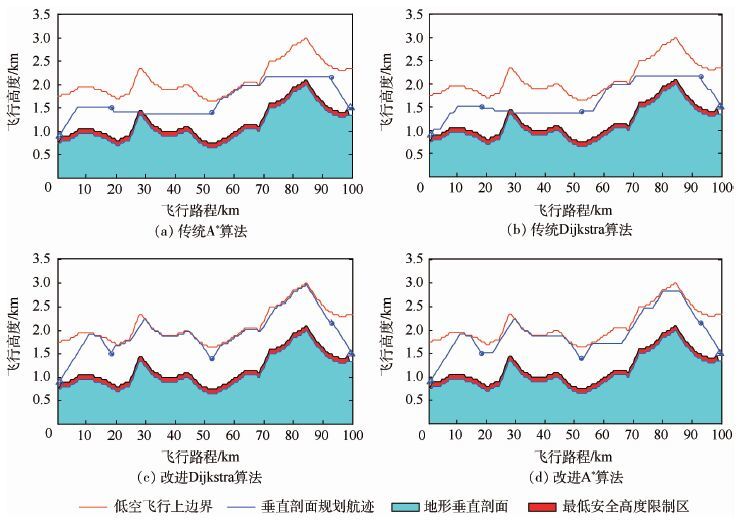 |
| 图 3 采用传统A*算法、传统Dijkstra算法、改进Dijkstra算法和改进A*算法的垂直剖面规划航迹 Fig. 3 Vertical profile of planned trajectory obtained by traditional A-star algorithm,traditional Dijkstra algorithm,improved Dijkstra algorithm and improved A-star algorithm |
| 图选项 |
图 3(a)和图 3(b)分别是路径规划中常用的传统A*算法和传统Dijkstra算法结果,两者规划结果相近,虽然其均实现了在相应航迹代价函数下的规划路径最短,但是在地形起伏较为剧烈的地区规划出的航迹距离地面高度有可能出现过低的状况,影响飞行安全。如图 3(c)所示,改进Dijkstra算法虽然对低空飞行上边界具有很好的跟随效果,避免了出现飞行高度过低的情况,然而机动次数过多,增加了飞行员的操作负担。如图 3(d)所示,改进A*算法不仅可避免出现图 3(a)和图 3(b)中飞行高度过低的情况,机动次数与图 3(c)中所示改进Dijkstra算法相比也大大减少,有效减轻飞行员工作负担。
图 4为传统A*算法、传统Dijkstra算法、改进Dijkstra算法(具有边界跟随效果)以及改进A*算法4种算法规划航迹与飞行上边界距离对比效果图,从图中可以看出传统A*算法、传统Dijkstra算法规划航迹与飞行上边界间距相近,改进A*算法与飞行上边界的距离介于传统Dijkstra算法和改进Dijkstra算法之间,也就是说巡航段最小离地高度较传统Dijkstra算法和A*算法有明显提高,其可在低空开放高度层内明显增加飞行安全系数。
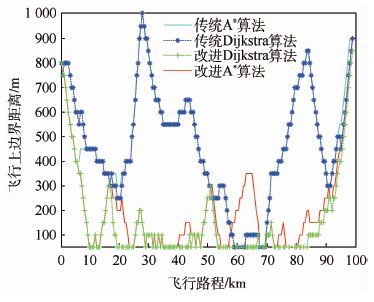 |
| 图 4 规划航迹与飞行上边界距离 Fig. 4 Interval between planned trajectory and upper boundary of permitted flight region |
| 图选项 |
表 1为4种算法规划航迹所涉及重要结果指标的比较,其中采用上述4种算法可分别规划出各航迹节点飞行距离和飞行高度确定的计划航迹,由航迹代价函数中的距离相关项可计算得到如表 1中总的飞行距离,由飞行上边界确定的垂直方向作业范围为1 km,其相较于水平方向作业范围100 km非常小,使得上述4种以最短路径为主要准则的规划算法虽然在垂直方向的航迹差异较大,但飞行距离仍比较接近。
表 1 种算法规划航迹所涉及重要结果指标的比较 Table 1 Important indexes compare of the results obtained by 4 trajectory planning algorithms
| 算法 | 平均飞行高度/m | 飞行高度方差/m | 最小离地高度/m | 机动次数/次 | 飞行距离/km | 燃油消耗/L | 扩展节点数目/个 |
| 传统A* | 551 | 24 | 50 | 24 | 101.12 | 15.72 | 693 |
| 传统Dijkstra | 533 | 22 | 50 | 24 | 101.11 | 15.71 | 6 409 |
| 改进Dijkstra | 851 | 13 | 700 | 69 | 101.32 | 17.85 | 6 365 |
| 改进A* | 803 | 13 | 650 | 30 | 101.28 | 17.42 | 2 584 |
表选项
表 1中的燃油消耗是按照Cessna 172飞行手册[18]计算得到,即根据计划航迹在各个高度层爬升、巡航等的实际飞行距离以及对应高度层飞行单位距离的燃油消耗可以计算出航迹总燃油消耗。由于Cessna 172飞行手册[18]忽略了下降阶段的燃油消耗,即其燃油消耗主要由爬升、巡航段决定,而机动飞行包括向下、向上机动2种,使得表 1中出现传统A*算法、传统Dijkstra算法与改进A*算法的机动次数相差不多,但燃油消耗相差较多,而改进Dijkstra算法与改进A*算法的机动次数相差较多,但燃油消耗相差不多的情况。
表 1中的改进A*算法虽然简化了搜索空间,但由于将航迹代价模型导入搜索策略,使得扩展节点个数多于传统A*算法,但其与传统A*算法、传统Dijkstra算法相比平均飞行高度更高,飞行高度方差明显减小,最小离地高度显著增加,可以在低空开放高度层内明显增加飞行安全系数,其与改进Dijkstra算法相比扩展节点个数明显减少,算法执行效率更高,机动次数明显降低,飞行员工作负担减轻,在具备上述优势的情况下保证飞机燃油消耗与其他3种方法相近,合理控制飞行运营成本。
4 结 论 本文在综合分析复杂多约束条件下通航飞行器垂直剖面航迹规划问题的基础上提出了一种新的解决方法,经实验验证表明:
1) 算法综合考虑飞行任务、地形信息和飞行器性能参数等约束条件,构造合理的规划空间,通过约束建模将复杂多约束条件结合到规划算法中去,克服了传统路径规划方法在通航垂直剖面飞行轨迹规划问题中应用的局限性。
2) 算法采用目标加权函数来建立航迹代价模型,以曼哈顿距离作为启发函数,将约束模型引入航迹代价函数从而量化各项指标,建立了符合通航垂直剖面航迹规划特性的航迹评价方法。
3) 算法与传统A*算法、传统Dijkstra算法相比,飞行高度更高,飞行高度方差明显减小,最小离地高度显著增加,使得在低空开放高度层内飞行安全系数明显增加,其与改进Dijkstra算法相比扩展节点个数明显减少,算法执行效率更高,机动次数明显降低,飞行员工作负担减轻。在具备上述优势的情况下改进A*算法保证飞机燃油消耗与其他3种方法相近,合理控制飞行运营成本,能够更为有效地解决复杂多约束条件下通航飞行器垂直剖面航迹规划问题。
参考文献
| [1] | OK K,ANSARI S,GALLAGHER B,et al.Path planning with uncertainty: Voronoi uncertainty fields[C]//2013 IEEE International Conference on Robotics and Automation (ICRA).Piscataway,NJ:IEEE Press,2013:4596-4601. |
| Click to display the text | |
| [2] | GOMEZ E,MARTINEZ S.A comparative study of geometric path planning methods for a mobile robot:Potential field and voronoi diagrams[C]//2013Ⅱ International Congress of Engineering Mechatronics and Automation (CⅡMA).Piscataway,NJ:IEEE Press,2013:1-6. |
| Click to display the text | |
| [3] | CHENG C T, FALLAHI K, LEUNG H, et al. A genetic algorithm-inspired UUV path planner based on dynamic programming[J]. IEEE Transactions on System,2012, 42(6): 1128–1134. |
| Click to display the text | |
| [4] | CUI C,WANG N,CHEN J.Improved ant colony optimization algorithm for UAV path planning[C]//20145th IEEE International Conference on Software Engineering and Service Science(ICSESS).Piscataway,NJ:IEEE Press,2014:291-295. |
| Click to display the text | |
| [5] | GAUTAM S A,VERMA N.Path planning for unmanned aerial based on genetic algorithm & artificial neural network in 3D[C]//2014 International Conference on Data Mining and Intelligent Computing(ICDMIC).Piscataway,NJ:IEEE Press,2014:1-5. |
| Click to display the text | |
| [6] | 郑昌文, 严平, 丁越明, 等. 飞行器航迹规划研究现状和趋势[J]. 宇航学报,2007, 28(6): 1441–1446.ZHENG C W, YAN P, DING Y M, et al. Research status and trend of route planning for flying vehicles[J]. Journal of Astronautics,2007, 28(6): 1441–1446.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 宋建梅, 李侃. 基于A*算法的远程导弹三维航迹规划算法[J]. 北京理工大学学报,2007, 27(7): 613–617.SONG J M, LI K. 3D route planning algorithm for long range missiles based on A-star algorithm[J]. Transactions of Beijing Institute of Technology,2007, 27(7): 613–617.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 关于深化我国低空空域管理改革的意见[EB/OL].北京:国务院,中央军委,2010(2010-09-05)[2015-05-17].http://www.gov.cn/jrzg/2010-11/14/content_1745143.html. Opinions on deepening the reform of China’s low-altitude airspace management[EB/OL].Beijing:the State Council,Central Military Commission,2010(2010-09-05)[2015-05-17].http://www.gov.cn/jrzg/2010-11/14/content_1745143.html.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 占伟伟, 王伟, 陈能成, 等. 一种利用改进A*算法的无人机航迹规划[J]. 武汉大学学报(信息科学版),2015, 40(3): 315–320.ZHAN W W, WANG W, CHEN N C, et al. Path planning strategies for UAV based on improved A-star algorithm[J]. Geomatics and Information Science of Wuhan University,2015, 40(3): 315–320.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | SZCZERBA R J, GALKOWSKI P, GLICKTEIN I S, et al. Robust algorithm for real-time route planning[J]. Aerospace and Electronic Systems,2000, 36(3): 869–878. |
| Click to display the text | |
| [11] | 孟中杰, 黄攀峰, 闫杰. 基于改进稀疏A*算法的高超声速飞行器航迹规划技术[J]. 西北工业大学学报,2010, 28(2): 182–186.MENG Z J, HUANG P F, YAN J. Exploring trajectory planning for hypersonic vehicle using improved sparse A-star algorithm[J]. Journal of Northwestern Polytechnical University,2010, 28(2): 182–186.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | 刘琼昕, 王景, 高春晓, 等. 基于引导点的无人机三维航迹规划方法[J]. 北京理工大学学报,2014, 34(11): 1163–1168.LIU Q X, WANG J, GAO C X, et al. The UAV 3D route planning method based on the guide points[J]. Transactions of Beijing Institute of Technology,2014, 34(11): 1163–1168.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | DE FILIPPIS L, GUGLIERI G, QUAGLIOTTI F. Path planning strategies for UAVs in 3D environments[J]. Journal of Intelligent & Robotic Systems,2012, 65(1): 247–264. |
| Click to display the text | |
| [14] | |
| [15] | 王红卫, 马勇, 谢勇. 基于平滑A*算法的移动机器人路径规划[J]. 同济大学学报(自然科学版),2010, 38(11): 1647–1650.WANG H W, MA Y, XIE Y. Mobile robot optimal path planning based on smoothing A* algorithm[J]. Journal of Tongji University (Natural Science),2010, 38(11): 1647–1650.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | 常建娥, 蒋太立. 层次分析法确定权重的研究[J]. 武汉理工大学学报(信息与管理工程版),2007, 29(1): 153–156.CHANG J E, JIANG T L. Research on the weight of coefficient through analytic hierarchy process[J]. Journal of Wuhan University of Technology (Information & Management Engineering),2007, 29(1): 153–156.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [17] | 邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识,2012, 42(7): 93–100.DENG X, LI J M, ZENG H J, et al. Research on computation methods of AHP wight vector and applications[J]. Mathematics in Practice and Theory,2012, 42(7): 93–100.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [18] | Pilot’s operating handbook:Cessna model 172[EB/OL].KANSAS,Kansas:Cessna Aircraft Company,1978(2005-06-16)[2015-05-17].http://www.skywarriorinc.com/downloads/POH%20BOOKS/172N%20POH.pdf. |
| Click to display the text | |
