基于视觉导航的无人机自主飞行主要利用装配在无人机上的摄像头获得着陆场附近的图像,并采用视觉技术估计无人机的位置和姿态信息,同时感知着陆场周围环境,辅助无人机完成自主飞行。视觉导航作为一种完全自主的导航方式,并不依赖于其他地面和空中设备,故在提高无人机自主性方面有着很大的优越性^[1]。相比于传统的INS/GPS等导航方式,视觉导航因完全自主且无源等特点得到了广泛而深入的研究,但基于视觉导航的航迹规划技术仍然存在很大的研究发展空间。
将已经相对成熟的地面机器人视觉导航技术应用于无人机自主飞行中会遇到很大困难,飞行器的动态不稳定、高动态以及多自由度对视觉导航的数据更新率提出了更高层次的要求,然而导航参数的获取需要经过一系列复杂的视觉算法,同时视觉算法本身的测量误差、收敛能力和收敛速度仍是很难攻破的研究难题^[1]。最终,这些问题会通过视觉导航反馈回路引进整个系统,严重影响系统性能甚至导致系统发散,故基于视觉的控制算法必须对这些问题具有较好的鲁棒性。
20世纪80年代,Zames^[2]首次提出了H_∞优化控制的概念,从而为解决系统的鲁棒稳定性问题奠定了基础。H_∞控制针对模型不确定性下的鲁棒稳定性问题交出了满意的答卷,但其解决其他性能问题的能力也是有限的。为了有效改善系统的调节性能,ernstein和Haddad^[3]在989年首先提出了H₂/H_∞混合控制的概念。近年来,越来越多的理论研究^[4]证明了H₂/H_∞混合控制在多目标优化问题上的优势,同时这方面的应用研究也取得了很大的进展^[5-6]。其中,文献[7-8]分别从数值仿真和实时仿真的角度实现了无人机自主着陆和地面目标监视,并验证了系统优异的鲁棒性能。
1 视觉位置测量模型不确定性 为了从理论上研究视觉导航系统的特性,分析视觉导航系统输入/输出之间的关系,本文引入建模理论构造视觉位置测量模型。实际的视觉导航系统以真实的三维场景为输入,解算后的位姿估计为输出,整个过程涉及光学、图像处理和投影几何等众多学科的知识。为了提高控制理论研究对计算机视觉算法研究的指导意义,本文将视觉导航系统划分为传感器(摄像头、激光测距仪)和视觉处理计算机2个物理部分,对视觉处理计算机建立视觉位置测量模型。可见,视觉位置测量模型本质上即是摄像机成像模型求逆^[9]:

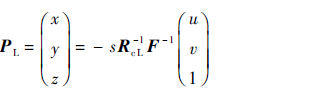(1)

式中:P_L为无人机在着陆坐标系下的位置坐标;s为尺度变换因子;R_cL为着陆坐标系与摄像机坐标系之间的旋转矩阵;F为本文定义的视觉位置测量模型内矩阵。
根据以上理论推导的非线性模型以及实际视觉导航系统的工作原理,本文将视觉位置测量模型的输入/输出规范化。输入为:O_L在像素坐标系下的坐标(u,v),尺寸变换因子s,以及着陆坐标系和摄像机坐标系之间的旋转欧拉角(Φ,θ,ψ);输出为:无人机(忽略摄像头光心与无人机质心之间的位置关系)在着陆坐标系下的位置(x,y,z)。
一般来说,理论模型与实际系统之间总是存在偏差,实际系统很难被准确建模,即存在不确定性。通常,不确定性按照来源不同可以分为2类^[10]:①系统内部不可预计的动态,如系统参数误差、线性化后缺失的系统动态等;②未知或不可预计的外部不确定性,如干扰、测量噪声等。依据以上分析,研究视觉位置测量模型的模型不确定性,并将模型表示为以下形式:

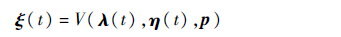(2)

式中:V为灵敏度函数;因变量为ξ=(x,y,z)^T；自变量包括表示成像原理的坐标和尺度变换因子λ=(u,v,s)^T；标示坐标旋转关系的欧拉角η=(Φ,θ,ψ)^T；以及部分时不变参数p=(u₀,v₀,f_z,f_y,γ)^T,γ为航迹角。
接下来,本文将从灵敏度的方面对模型不确定性进行研究分析。
研究不同自变量对因变量的影响的第步即是定性分析不同自变量对因变量的影响程度,或是视觉位置估计对参数不确定性和输入误差的敏感程度,本文将此问题定义为因变量对自变量的灵敏度研究。借鉴梯度的定义,利用函数在某点(基准点)的摄动百分比来表示因变量对自变量的灵敏度:

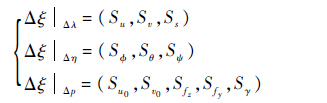(3)

式中:(Δλ,Δη,Δp)为各因变量在基准点(λ₀,η₀,p₀)附近的摄动百分比;Δξ为自变量在基准点ξ₀由因变量摄动所产生的摄动百分比。
例如:

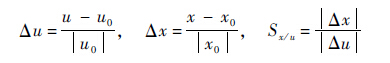(4)

式中:S_x/u为自变量x对因变量u的灵敏度。
根据灵敏度的定义,将自变量摄动限制在基准点附近,并假设摄动百分比范围为(-5，5)。随机选择摄动百分比和基准点,即6个不同的随机条件分别为(-7 892,-3 90,500),(-6 803,-3 89,487),(-2 000,0,28),(-6 570,-3 673,407),(-7 863,-3 872,438)和(- 984,-5,92),分析相同条件下的所有灵敏度。图 1对比了4个不同灵敏度在6个随机条件下的数值。其中S_z/θ相较于其他灵敏度可以忽略;S_y/u和S_y/ψ依据因变量摄动和基准点不同而变化,大部分情况下S_y/u略大于S_y/ψ(除随机条件5外);S_z/s与因变量摄动和基准点无关,与视觉位置测量模型的解析式相符。根据灵敏度的定义,灵敏度数值大小反映了自变量(λ,η,p)误差变化对因变量ξ=(x,y,z)¹摄动的影响程度,即视觉测量算法对不同参数不确定性和输入误差的敏感程度。通[CM(9*8/9]过大量对比实验分析可以得出以下结论:{S_z/(λ,p)∪S_y/(λ,η,p)∪S_ξ/s}所包含的灵敏度应该被重点关注。另外,无人机飞行控制中,高度z的估计一般融合了辅助传感器的信息,故S_z/(λ,p)数值的参考意义不大。综合理论分析与实际情况,S_y/λ、S_y/ψ和S_y/p所表征的敏感性最强。

图 1 相同条件下不同灵敏度的比较 Fig. 1 Comparison of different sensitivities under the same conditions

图选项

因为本文主要研究视觉位置测量模型存在误差的鲁棒控制,故可以考虑将非线性视觉位置测量模型线性化,对线性模型设计鲁棒控制律。首先将非线性视觉位置测量模型ξ(t)=V(λ(t),η(t),p)表示为如下线性形式:

(5)

然后利用小扰动定理(small-disturbance theory),将非线性模型等式两边按泰勒级数展开并保留次项^[11],再采用全量表示形式:

(6)

结合式(5)可求得雅可比矩阵V₁和V₂。
显然,雅可比矩阵V₁和V₂不仅会随基准点变化,还会因参数p不确定性而产生摄动。采用加法摄动^[2]的形式,则雅可比矩阵的摄动矩阵ΔV₁和ΔV₂可表述为如下形式:

(7)

选择当前基准点,仍然假设摄动百分比Δp的极值为(-5,5),并依据不同参数不确定性的灵敏度设置合理的参数不确定性加权系数,可得ΔV₁和ΔV₂均满足范数有界:

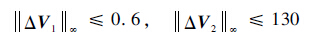(8)

2 基于H₂/H_∞的鲁棒控制 2.1 飞行器模型 本文主要研究视觉导航下的航迹跟踪,因此不需要考虑具体实际的飞行器非线性模型。根据质点运动在惯性坐标系和航迹坐标系下的关系,可以得到无人机的运动学方程^[3]:

(9)

式中:V_a和χ分别为飞行速度和航向角。
为减少优化算法的计算量,仅考虑无人机的部分动力学约束,并且假设无人机做无侧滑飞行,同时忽略侧力,可得其在航迹坐标系下的动力学方程^[3]为

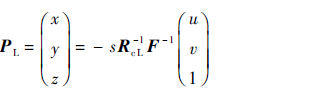(10)

式中:m为飞机质量；g为重力加速度；α和Φ分别为迎角和滚转角;T、L和D分别为无人机所受推力、升力和阻力,其表达式如下^[4]:

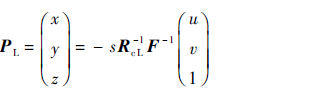(11)

其中:η_t为油门开度；_max为最大推力;S为参考翼面面积;ρ、C_L和C_D分别为大气密度、升力系数和阻力系数,具体表达式如下^[3]:

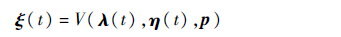(12)

其中:ρ_s为海平面的大气密度;h为飞机所在高度；l₀、l₁、l₂、l₃、l₄、d₀、d₁、d₂、d₃和d₄为随迎角变化的系数。
2.2 广义控制对象构造 为了同时保证系统的鲁棒稳定性和跟踪性能,并有效利用H₂/H_∞混合控制解决由视觉位置测量模型所引入的参数不确定性和输入干扰问题,本文设计了适于H₂/H_∞多性能指标分析的被控系统。

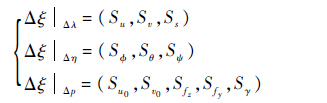(13)

式中:A、为控制系统矩阵；u为控制输入矩阵；z₁和z₂分别为H_∞和H₂性能的评价输出;$y={{\left( \tilde{x},\tilde{y},\tilde{z},{{V}_{a}},\gamma ,\chi \right)}^{T}}$为测量输出,观测量中飞机的坐标${{\left( \tilde{x},\tilde{y},\tilde{z} \right)}^{T}}$由视觉位置测量模型提供;w代表所有外部输入信号，包括航迹跟踪参考输入r=(x,y,z,V_a,γ,χ)^T,视觉位置测量模型干扰输入d,以及视觉位置测量模型辅助输入$v={{\left( \lambda ,\eta \right)}^{T}};\Delta {{{\tilde{D}}}_{3}}$为视觉位置测量模型引入被控系统的不确定性。
依据第节的线性模型分析,可得不确定性$\Delta {{{\tilde{D}}}_{3}}$为

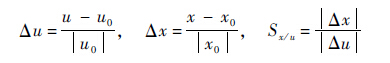(14)

作为H_∞性能的评价输出,z₁表征了系统对模型不确定性的鲁棒性;第1节对视觉位置测量模型干扰输入的分析研究表明,S_y/u和S_y/ψ所表征的灵敏度最强,故$\Delta {{{\tilde{D}}}_{21}}$主要体现了(λ,ψ)摄动的影响;z₂₂表征了系统的参考跟踪性能;而C、E分别为状态变量和控制输入对评价输出的加权矩阵。依据上述评价输出的物理含义,外部输入信号w可以划分为辅助输入w₁、干扰输入和参考输入w₂,即

(15)

则广义被控对象G可表示为以下形式:

(16)

式中:${{{\tilde{D}}}_{3p}}={{{\tilde{D}}}_{3}}+\Delta {{{\tilde{D}}}_{3}}$;F_d为干扰输入对测量输出的加权矩阵。
针对上述广义被控对象G设计控制律u=K_∞/2y,采用下线性分式变换(Low Linear Fractional ransformation,LLF)^[5],可以得到w₁到z₁的闭环实现为^[7-6]

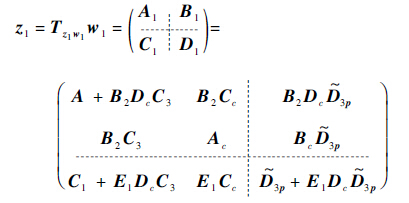(17)

同理,可得w₂到z₂的闭环实现。
H_∞控制问题的线性矩阵不等式(Linear Matrix Inequality,LMI)形式^[7]对于形如K_∞/2的闭环系统,A₁渐近稳定且$\left\| {{T}_{z1w1}} \right\|<{{\gamma }_{1}}$的充要条件为存在实对称矩阵X₁满足：

(18)

H₂控制问题的LMI形式^[7]对于闭环系统K_∞/2,A₂渐近稳定且$\left\| {{T}_{z2w2}} \right\|<{{\gamma }_{2}}$的充要条件为存在实对称矩阵X₂和Z满足

(19)

式中：γ₁、γ₂为控制系统需要达到的控制性能指标要求。
至此,多目标的H₂/H_∞优化控制问题即转换为LMI形式,从而可以利用成熟的LMI工具箱,例如MALA软件的LMI工具箱。
3 结果分析 在进行详尽的鲁棒性分析之前,本文首先以无人机跑道跟踪段为例对系统性能做一个简要的分析。图 2所示航迹初始位置为(-8 000,-3 000,600)m,并假设初始时刻目标出现在摄像头视野内,航迹终止时无人机以对准跑道的姿态抵达(-3 000,0,500)m。图 3所示为无人机航迹跟踪的误差,其中0~30 s左右无人机主要跟踪直线航迹,而0~0 s和30~40 s之间无人机出现较大机动,跟踪误差也相应增大。

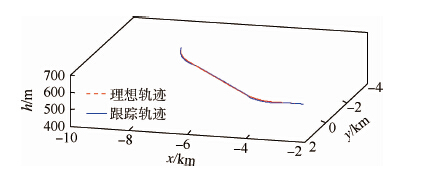图 2 航迹跟踪 Fig. 2 rajectory tracking

图选项

图 3 航迹跟踪误差 Fig. 3 rajectory tracking errors

图选项

为了更直观地分析各种不确定性对系统性能的影响,将未加任何不确定性的跟踪误差作为基准误差,下面所有跟踪误差分析都建立在与基准误差比较的基础上。
延续第2节中的分析,先将视觉位置测量模型的不确定性分为参数不确定性和输入干扰,对应的控制输入分别为图 4(a)和图 4(b)。图 5为模型不确定性下的航迹跟踪。可见,无人机在航迹跟踪过程中,由于摄像机标定误差等原因,视觉位置测量模型的输出值与标准值始终存在一定的误差。假定由于摄像机标定误差等原因,参数不确定性中的(u₀,v₀)相对于真值出现了(2,4)%的摄动。从图 5中可以看出,控制器在(u₀,v₀)存在误差的情况下仍然可以保证系统的稳定性,但是因为设计H₂/H_∞控制器时并未引入全局模型,跟踪误差一直存在。

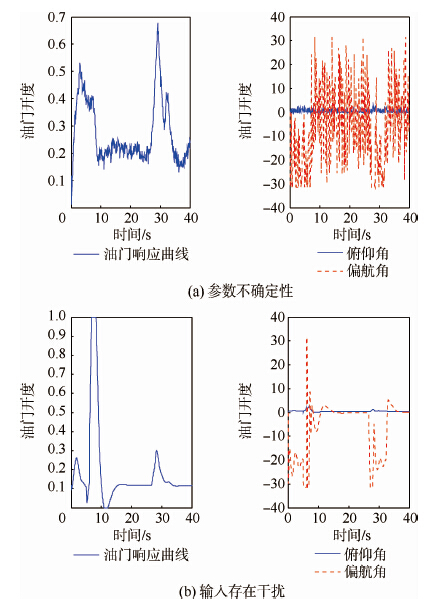图 4 模型不确定性下的控制输入 Fig. 4 Control inputs under model uncertainties

图选项

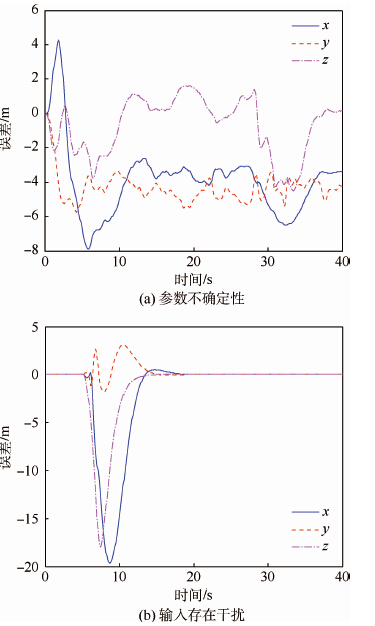图 5 模型不确定性下的航迹跟踪误差 Fig. 5 rajectory tracking errors under model uncertainties

图选项

图 5(b)所示为无人机在航迹跟踪过程中,由于视觉处理算法误差等原因,(u,v)的解算出现了较大的误差,亦即视觉测量模型受到一个短暂而剧烈的干扰:假定在航迹跟踪的5~0 s之间,(u,v)的测量出现了(3,4)%的摄动。从图 5中可以看出,跟踪误差随干扰变化后迅速恢复到原来的跟踪能力,并且干扰的抑制效果也很理想。
通过大量仿真实验分析,一般合理范围内的参数不确定性和输入干扰并不会对系统的稳定性造成威胁,但是为了保证较为满意的跟踪性能,两者应该满足以下条件:
) 模型本身摄动范围最好不超过(－15,5)%,而引起参数不确定性的参数摄动最好不要超过(－8,8)%。2) 短时间5 s内的输入干扰,对于模型不确定影响较大的变量(u,v,w),其摄动范围不应该超过(－7,7)%。
3) 对于持续时间较长(20 s以上)的输入干扰,(u,v,w)的摄动范围最好不超过(－2,2)%,否则跟踪误差会持续累加,甚至可能会导致系统的发散。
4 结 论 为了在理论上研究视觉位置估计误差,本文首先建立了视觉位置测量模型,然后根据非线性模型的特点将不确定性分为参数不确定性和输入干扰2种。视觉估计对不同模型不确定性的敏感程度的理论分析和仿真表明,S_y/λ、S_y/ψ和S_y/p所表征的敏感性最强。
在设计H₂/H_∞鲁棒控制的过程中,为了保证系统对视觉位置估计误差的鲁棒稳定性和跟踪性能,模型本身的摄动范围不超过(－15,5)%,引起参数不确定性的参数摄动不超过(－8,8)%;5 s以内的短时间输入干扰,变量(u,v,w)摄动范围不超过(－7,7)%;20 s以上的长时间输入干扰,应保证摄动范围低于(－2,2)%;否则会导致跟踪误差的累加,最终可能引起系统的发散。

参考文献

[1]	STEPANYAN V.Vision based guidance and flight control in problems of aerial tracking[D].Blacksburg:Virginia Polytechnic Institute and State University,2006:1-78.
	Click to display the text
[2]	ZAMES G. Feedback and optimal sensitivity:Model reference transformations,multiplicative seminorms,and approximate inverses[J]. IEEE Transactions on Automatic Control,1981, 26(2): 301–320.
	Click to display the text
[3]	BERNSTEIN D S, HADDAD W M. LQG control with an H∞ performance bound:A Riccati equation approach[J]. IEEE Transactions on Automatic Control,1989, 34(3): 293–305.
	Click to display the text
[4]	SCHERER C W. Multiobjective H2/H∞ control[J]. IEEE Transactions on Automatic Control,1995, 40(6): 1054–1062.
	Click to display the text
[5]	HWANG C L, CHANG L J. Trajectory tracking and obstacle avoidance of car-like mobile robots in an intelligent space using mixed H2/H∞ decentralized control[J]. IEEE/ASME Transactions on Mechatronics,2007, 12(3): 345–352.
	Click to display the text
[6]	NAG A,PATEL S S,KISHORE K,et al.A robust H-infinity based depth control of an autonomous underwater vehicle[C]//International Conference on Advanced Electronic Systems.Piscataway,NJ:IEEE Press,2013:68-73.
	Click to display the text
[7]	WANG R,ZHOU Z,SHEN Y.Flying-wing UAV landing control and simulation based on mixed H2/H∞[C]//IEEE International Conference on Mechatronics and Automation.Piscataway,NJ:IEEE press,2007:1523-1528.
	Click to display the text
[8]	LI Z,DING J.Ground moving target tracking control system design for UAV surveillance[C]//2007 IEEE International Conference on Automation and Logistics.Piscataway,NJ:IEEE Press,2007:1458-1463.
	Click to display the text
[9]	SONKA M, HLAVAC V, BOYLE R. Image processing,analysis,and machine vision[M].London: Thomson West, 2008: 775-786.
	Click to display the text
[10]	王德进. >H2和H∞优化控制理论[M].哈尔滨: 哈尔滨工业大学出版社, 2001: 2-3.WANG D J. H2 & H∞ optimal control theory[M].Harbin: Harbin Industrial University Press, 2001: 2-3.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[11]	吴森堂, 费玉华. 飞行控制系统[M].北京: 北京航空航天大学出版社, 2005: 64-67.WU S T, FEI Y H. Flight control system[M].Beijing: Beihang University Press, 2005: 64-67.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[12]	Measurement and Control Group.Robust control[Z].[S.l.]:Eindhoven University of Technology,2002.
	Click to display the text
[13]	HORIE K, CONWAY B A. Optimization for fighter aircraft vertical-plane maneuvering using poststall flight[J]. Journal of Aircraft,2000, 37(6): 1017–1021.
	Click to display the text
[14]	KHADEMI I,MALEKI B,MOOD A N.Optimal three dimensional Terrain following/Terrain avoidance for aircraft using direct transcription method[C]//201119th Mediterranean Conference on Control & Automation.Piscataway,NJ:IEEE Press,2011:254-258.
	Click to display the text
[15]	GU D W, PETKOV P, KONSTANTINOV M. Robust control design with MATLAB[M].Berlin: Springer, 2005: 20-22.
	Click to display the text
[16]	SCHERER C W. An efficient solution to multi-objective control problems with LMI objectives[J]. Systems & Control Letters,2000, 40(1): 43–57.
	Click to display the text
[17]	HINDI H A,HASSIBI B,BOYD S P.Multi-objective H2/H∞ optimal control via finite dimensional Q-parameterization and linear matrix inequalities[C]//Proceedings of the 1998 American Control Conference.Piscataway,NJ:IEEE Press,1998:3244-3249.
	Click to display the text