传统的航路规划方法可大致分为4类。第1类是基于拓扑图[2]的方法(如Voronoi图、Laguerre图等)。该方法属于对环境的几何建模,解析过程直观简单,计算复杂度受障碍数量影响较大。第2类是人工势场[3],属于一种拟物算法,算法的固有特点造成了诸如:落入势场平衡“陷阱”区域、由于相邻障碍间强势场影响造成搜索盲区等一系列问题。第3类是栅格法[4](如A*、D*算法等),可以通过代价地图计算可行路径,计算代价较大,且仅限于低维离散空间。第4类是智能优化算法[5-6](如遗传算法、蚁群算法等),这些寻优方法在解决路径规划问题方面有着优良的性能,其解与迭代次数有很大关系,且易陷入局部最优。近年来提出了一些基于物理学原理的优化算法,如万有引力算法[7]、拟态物理学方法[8-9]、类电磁算法[10]、中心力算法[11]等。这些算法利用物理规律表征规划要素间的关系,在解决包括航路规划问题在内的优化问题中表现出一定的优势。但算法复杂度大,计算代价高,对于复杂环境和高维空间的快速安全航路规划问题并不适用。
以快速扩展随机树(Rapidly exploring Random Tree,RRT)算法[12-13]为代表的基于采样的方法为解决高维航路规划的效率和可行性问题提供了一种有效方案。但由于缺少启发要素,基础RRT算法的路径生成带有很大的随机性。文献[14]利用A*算法的代价函数改进RRT算法,但无法避免局部最小问题。文献[15-16]用地形代价函数和几何方法优化RRT算法生成的路径。文献[17]从减小计算代价角度对算法进行了改进。Karaman和Frazzoli[18]证明了RRT算法得到最优解的概率为0,并提出改进的RRT*算法可解出最优结果。文献[19]提出用滤波方法优化路径生成。由于这些改进方法没有考虑环境威胁的强度分布,且未综合考虑航路规划的效率和安全性。为此,本文将电势场理论引入飞行环境的威胁建模,建立基于电势威胁场引导的航路点生成机制,进而构建基于拟态电势能导向的随机采点扩展式航路规划方法,探索基于航路点导向扩展来提高航路规划效率和安全性的新机理。
1 基于拟态电势场的飞行环境建模 飞行航路规划的主要目的是为飞行器确定出从起始点到目标点的安全可飞航路,需要考虑的主要问题是对航路上威胁的规避、航路规划的快速性等问题,以确保规划的航路能够满足任务的实时性和飞行安全性等方面的要求。建立有效描述飞行区域中威胁情况的环境模型,是实现高效航路规划的基础。
飞行环境中的威胁障碍主要有:高炮、防空导弹、高山、建筑物、禁飞区等。非攻击性障碍可根据其特性划定界限,以防止飞行器进入。对于攻击性威胁,传统环境建模方法常把威胁模型简单建为以火力范围确定半径的圆形或球形,或建立高斯随机威胁场等。这些方法均无法有效描述威胁强度的变化。防空武器的探测杀伤概率与目标距离有关,同时考虑到飞行器物理限制和不确定客观因素,越靠近威胁障碍,威胁性越大,即飞行威胁度与相对距离呈正相关。基于这种特性,可引入模拟电势场来表征威胁强度。
根据电势叠加原理,在二维坐标直角坐标系中,设P点坐标为(x, y),电荷qi的坐标为(xi, yi),则电荷qi在点P处的电势为
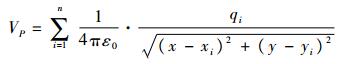 | (1) |
式中:ε0为真空电容率。
电场强度为
 | (2) |
式中:ΔV为电势梯度;ax和ay分别表示沿x和y轴的正方向。
电场强度是描述电场强弱和电场力的性质的物理量。电场强度的大小取决于激发电场的电荷,与电场中的受力电荷无关[20]。模拟电场分布,设各威胁源为同种正电荷,坐标为(xi, yi),威胁源o在P点形成的电势为
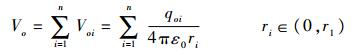 | (3) |
式中:ri为第i个防空阵地与某一点的距离。
由于防区外火力杀伤概率为零,设0 < ri < r1为火力覆盖区。设飞行器为受力试探电荷,不影响电势场分布。引入目标点后,电势场变化为
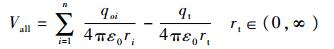 | (4) |
2 基于拟态电势能引导的航路扩展方法 基于快速扩展随机树思想的航路规划方法,虽然具有快速向未知区域的搜索倾向,但随机扩展必然带有很大盲目性,生成的路径随机性较强。根据拟态电势场的飞行环境建模,通过引入基于拟态电势能的节点引导机制,可有效启发路径节点选择,有效解决随机性带来的盲目扩展问题。
2.1 拟态电势能引导的航路点概率选择原理 飞行器在威胁势场中飞行,在一定区域范围内受威胁和目标电势的叠加影响。即试探电荷在电场中移动,受电场力作用而做功,引起电势能变化。根据电势定义,对于叠加电场,在威胁势场某一路径上任意两点i、j间有
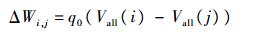 | (5) |
库仑定律表明,静电力做功与路径无关,是保守力,所以静电场是保守场。如图 1所示,做功大小由起点xinit和终点xgoal相对电势值决定,电势差为ΔV,且
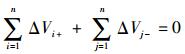
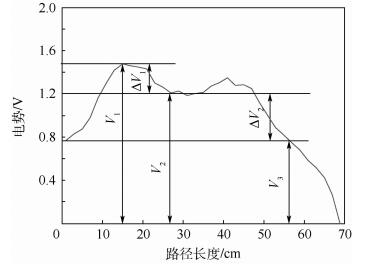 |
| 图 1 电势与路径长度示意图 Fig. 1 Schematic diagram of electric potential and path length |
| 图选项 |
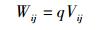 | (6) |
因此,电场力做功问题只限于对起点和终点的反映而缺乏对路径的准确描述。基于此,为有效表示路径与功之间的联系,只考虑电势能改变量为正的节点,并引入δ为路径比例小量,保证做功相等情况下取最短的路径。设路径长度为l,做功为w(p),则一条路径的机械功表示为
 | (7) |
高斯核函数[21]可以被认为是在正态分布假设条件下,同类信息间度量距离的工具,在数据挖掘等算法中应用广泛。在威胁势场中,本文将高斯核函数与电势能特性相结合,建立航路节点选择机制,有效启发路径趋向目标点生成。为防止出现局部最小现象,以一定概率保留背离目标方向的点。具体如下:
对于高斯核函数
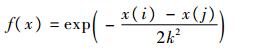 | (8) |
式中:k为指定参数;设x(i)-x(j)为Vall(i)-Vall(j)。当x(i)-x(j)>0,概率按式(8)计算;当x(i)-x(j)≤0时,表明下一状态点朝向目标点生成,概率为1。
设随机生成n条路径,每条路径有m个节点。对于第i条路径的生成概率pi有
 | (9) |
式中:pj_randi为随机生成点的概率;pj_select i为选择概率。对于n条路径来说,每个父结点能随机扩展出下一节点的概率是相同的,都为1/n,则
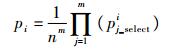 | (10) |
代入式(8)得
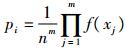
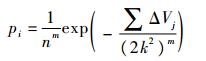 | (11) |
将式(7)代入式(11),路径比例小量忽略不计,则
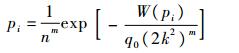 | (12) |
那么可以得出以下结论:W(pi)越小,则概率pi越大。即具有最少电势能增量的路径搜索到目标点的概率最大。
2.2 简化运动模型描述 为使规划的路径基本符合飞行器运动约束的要求,本文将位姿点信息融入规划算法。设飞行器的位姿为
 | (13) |
在速度方向上姿态角θk表示为
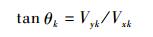 | (14) |
下一相邻位姿点
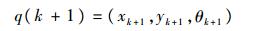 | (15) |
设速度V不变,单位步长为ρ,则时间周期为Δk=ρ/V,下一步位置坐标为
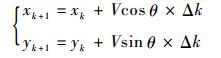 | (16) |
2.3 算法描述 根据式(12)的结论,本文提出基于电势能引导进行节点概率选择,即在航路扩展时,按RRT算法模式以一定步长在父节点周围生长,当势能递减时,将其作为子节点并加入搜索树中,当搜索趋近威胁时,认为树向前扩展失败,以选择概率接受新节点,并累乘概率。重复上述过程,以确保路径趋向目标点扩展,根据路径比例小量选取最优分支。为保证改进算法向未知区域搜索,同时保留距随机生成点单位步长范围内最近的子节点。
首先,对于任务区域C进行定义。设在飞行环境中存在若干威胁源,飞行器为单位正电荷,威胁源为负电荷,同一威胁类型电量相同,根据火力覆盖范围确定电场影响范围。设目标点为电量较大的正电荷,电场覆盖任务区域。设Cfree为非威胁区,设Tk为一个具有K个节点的扩展树,x为Tk的节点,且TK∈Cfree。xinit为起点,xgoal为终点,xrand为非威胁区空间中一随机电势点,即xrand∈Cfree。
然后,进行采点选取新节点。用xrand与K个节点进行距离计算对比,设xnear为树中与xrand距离最小的节点。设p, q∈Cfree,令Dis(p, q)为状态点的几何距离,这里采用欧氏距离,则Dis(xnear, xrand)≤Dis(x, xrand)。在xrand与xnear两点直线间取xnew,xnew∈Cfree,并满足Dis(xnear, xrand)=ρ,其中ρ>0,为树生长的最小单位长度,称为步长。如满足条件,考虑运动约束,保证路径平滑,令α=π-θ,以α>3π/4条件筛选节点。
最后,进行电势能概率选择。计算xnear与新增节点xnew的电势差ΔV(xnear, xnew),如果ΔV(xnear, xnew)≤0,则树新增一个节点xnew,否则以选择概率接受新节点。令Tk+1为扩展后的树,Tk+1=Tk+xnew。否则重新选取xrand,循环上述步骤。
3 仿真实验分析 本节通过仿真实验对比,从规划算法的效率、航路代价和安全性等方面,对基于拟态电势能的航路规划方法的性能进行分析。仿真实验环境为:软件MATLAB7.0;计算机配置:Windows XP操作系统、CPU为Inter Core i3、主频3.3GHz。飞行威胁场大小为50km×50km,设θ为常数1,δ=0.01,
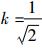

首先,在同等条件下与RRT算法、A*算法对比规划时间、航路长度等指标。仿真条件:设定13处威胁点,威胁强度由电量大小确定,电量为+1C和+2C,目标点电量为-10C;飞行器为元电荷,电量为+1C。
如图 2和图 3所示,(x, y)表示位置坐标。表 1列出了各算法性能对比。平均曲率的计算方法为:将路径做近似平滑逼近,按曲率公式对每个节点进行计算求均值得出。根据式(7),目标导向性表示目标点引力对电荷沿路径从起点移动到终点所做的功。由于在RRT算法中节点的选取带有很大的随机性,产生的节点都是建立盲目搜索的基础上的。这种方式带来的最大好处就在于有极大的未知空间搜索优势,但也会因为大面积无效搜索导致计算成本急剧增加,而且产生的路径并非最优。如图 3所示。目标导向性表示路径上节点的电势之和,描述路径向目标点的趋向性,其值的绝对值越小,则越能以正确方向趋近目标点,且节点数越少。其数据通过位置坐标对应电势大小按路径节点累加取得。可见,A*算法(以Manhattan距离为启发函数)能以最短路径找到目标点,但在复杂环境下计算时间最长,且路径未考虑运动约束;本文提出的算法节点选择收敛性明显增强,扩展树指向较为单一,路径较为平滑,且计算时间较小。
表 1 算法性能对比 Table 1 Algorithm performance comparison
| 算法 | 计算时间/s | 路径长度/km | 平均曲率 | 目标导向性/J |
| 本文 | 0.9 | 78 | 0.74 | -27.0476 |
| A* | 9.4 | 76 | 0.71 | -26.3611 |
| RRT | 4.3 | 92 | 1.63 | -31.8905 |
表选项
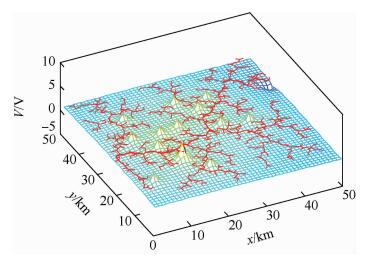 |
| 图 2 RRT算法生成路径 Fig. 2 Path generated by RRT algorithm |
| 图选项 |
 |
| 图 3 本文算法与A*算法生成路径对比 Fig. 3 Comparison of paths generated by proposed algorithm and A* algorithm |
| 图选项 |
其次,进行路径安全性评价。根据以上的仿真实验结果,对比3种方法的路径安全性。基于电势场拟态的威胁环境建模有效表征了威胁强度与距离之间的关系。考虑到飞行器机动性及环境未知因素,路径紧贴威胁边界飞行也存在极大的危险性。因此,综合考察全域内所有威胁对每一飞行节点的影响十分必要。基于此,这里将环境威胁模型拓展为评价指标,即
 | (17) |
设以原点为中心,不同威胁源拟态电荷沿梯度方向的电势线对比如图 4所示。距威胁源距离越近,威胁度越大。在威胁源中心威胁度急剧增大,距离中心5个单位以上时威胁度渐近为0。
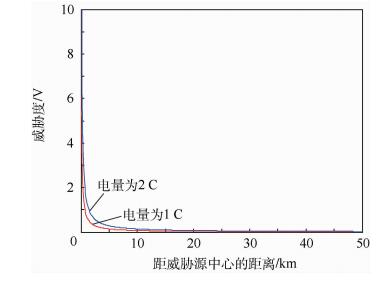 |
| 图 4 不同威胁的威胁度对比 Fig. 4 Comparison of threat levels of different threats |
| 图选项 |
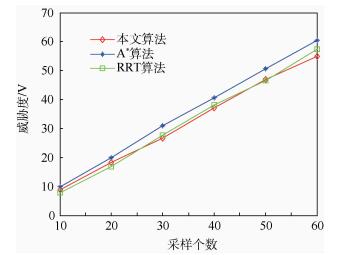
因为扩展树节点数和路径长度有很大关系,而不能直接表示威胁度的强弱。为在同一条件下对比3种算法生成的路径的威胁度,本文以目标点xgoal为圆心,分别以等差递增数列为半径作圆,确定与路径交点的位置坐标。根据威胁度的定义,对每一采样点进行计算,并累加求和。
如图 5所示,采样点个数与威胁度大致呈线性关系,采点数对威胁度影响不大。本文算法与RRT算法路径威胁度相似,且均小于A*算法,表明路径距离威胁源较远,路径安全性更佳。
 |
| 图 5 3种算法的威胁度对比 Fig. 5 Comparison of three algorithms' threat levels |
| 图选项 |
最后,对算法适用性进行对比。通过局部最小测试,与RRT-A*算法进行对比,分析算法的适用性。仿真条件:在任务环境中,设6处威胁源呈反C形排列。起始点坐标(1, 22),目标点坐标(30, 20)。威胁源和目标点电量分别为1C和-10C。
图 6为未考虑运动约束条件α,生成的路径与图 7相比平滑度更差。对算法进行局部最小测试表明:RRT-A*算法虽然运用A*算法的启发函数改进了RRT算法,航路扩展趋向性更强,但并没有很好地解决A*算法启发后引入的局部最小问题(见图 8)。基于拟态电势能启发的算法通过节点概率选择,有效解决了局部最小问题。
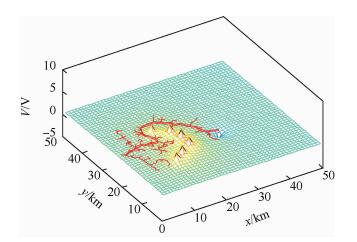 |
| 图 6 本文算法在未考虑约束条件下的局部最小测试 Fig. 6 Proposed algorithm's local minimum test without constraint condition |
| 图选项 |
 |
| 图 7 本文算法在考虑约束条件下的局部最小测试 Fig. 7 Proposed algorithm's local minimum test with constraint condition |
| 图选项 |
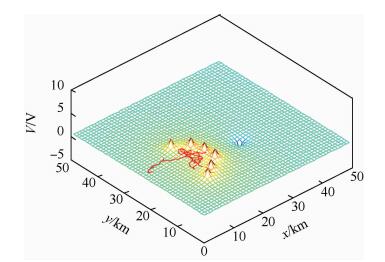 |
| 图 8 RRT-A*算法的局部最小测试 Fig. 8 RRT-A* algorithm's local minimum test |
| 图选项 |
4 结论 本文依据电势场分布特性进行威胁环境建模,从概率选择的角度建立了基于拟态电势能的航路扩展方法。
1)该方法改善了复杂环境和高维空间下航路规划算法的计算效率和适用性, 突出体现了计算成本低、速度快以及航路安全性高等特点。
2)本文的研究表明,基于电场力做功的物理原理可为飞行器航路规划问题提供新的机理,但对于动态威胁的实时规划等问题,还需要进一步研究。
参考文献
| [1] | 茹常剑, 魏瑞轩, 沈东. 多无人机协同的稳定控制机理研究[J].物理学报, 2014, 63(22): 220202–1.RU C J, WEI R X, SHEN D. Study on stability control mechanism of multiple unmanned aerial vehicle cooperative system[J].Acta Physica Sinica, 2014, 63(22): 220202–1.(in Chinese) |
| [2] | LUGO-CARDENAS I, FLORES G, SALAZAR S, et al.Dubins path generation for a fixed wing UAV[C]//International Conference on Unmanned Aircraft Systems (ICUAS).Piscataway, NJ:IEEE Press, 2014:339-346. |
| [3] | CHEN T B, ZHANG Q S.Robot motion planning based on improved artificial potential field[C]//3rd 2013 International Conference on Computer Science and Network Technology (ICCSNT).Piscataway, NJ:IEEE Press, 2013:1208-1211.http://opus.bath.ac.uk/view/divisions/dept=5Fmech=5Feng.type.html |
| [4] | SZCZERBA R J, GALKOWSKI P, GLICKTEIN I S, et al. Robust algorithm for real-time route planning[J].IEEE Transactions on Aerospace and Electronic System, 2000, 36(3): 869–878.DOI:10.1109/7.869506 |
| [5] | TUNCER A, YILDIRIM M. Dynamic path planning of mobile robots with improved genetic algorithm[J].Computers & Electrical Engineering, 2012, 38(6): 1564–1572. |
| [6] | CHAARI I, KOUBAA A, BENNACEUR H, et al.SmartPATH:A hybrid ACO-GA algorithm for robot path planning[C]//Proceedings 2012 IEEE Congress on Evolutionary Computation (CEC 2012).Piscataway, NJ:IEEE Press, 2012:1-8. |
| [7] | SHAMSUDIN H C, ABIDIN A F Z, IRAWAN A, et al.A fast discrete gravitational search algorithm[C]//4th International Conference on Computational Intelligence, Modelling and Simulation.Piscataway, NJ:IEEE Press, 2012: 24-28. |
| [8] | SPEARS W M, SPEARS D F, KERR W, et al. An overview of physicomimetics[J].Lecture Notes in Computer Science, 2005, 3342: 84–97.DOI:http://html.rhhz.net/BJHKHTDXXBZRB/10.1007/b105069 |
| [9] | 柴争义, 王秉, 李亚伦. 拟态物理学优化的认知无线电网络频谱分配[J].物理学报, 2014, 63(22): 228802–1.CHAI Z Y, WANG B, LI Y L. Spectrum allocation of cognitive radio network based on artificial physics optimization[J].Acta Physica Sinica, 2014, 63(22): 228802–1.(in Chinese) |
| [10] | BIRBIL S I, FANG S C. An electromagnetism-like mechanism for global optimization[J].Journal of Global Optimization, 2003, 25(3): 263–282.DOI:10.1023/A:1022452626305 |
| [11] | RICHARD A, FORMATO J D. Central force optimization:A new nature inspired computational framework for multidimensional search and optimization[J].Nature Inspired Cooperative Strategies for Optimization, 2008, 129: 221–238.DOI:10.1007/978-3-540-78987-1 |
| [12] | DAVE F, ANTHONY S.Anytime RRTs[C]//Proceedings of IEEE/RSJ International Conference on Intelligent, Robots and System.Piscataway, NJ:IEEE Press, 2006:5798-5803. |
| [13] | OREN S, DAN H.Asymptotically near-optimal RRT for fast, high-quality, motion planning[C]//IEEE International Conference on Robotics & Automation (ICRA).Piscataway, NJ:IEEE Press, 2014: 4680-4685. |
| [14] | LI J, LIU S, ZHANG B.RRT-A* motion planning algorithm for non-holonomic mobile robot[C]//SICE Annual Conference 2014.Piscataway, NJ:IEEE Press, 2014: 1833-1838. |
| [15] | LEE D, SHIM D H.Spline-RRT* based optimal path planning of terrain following flights for fixed-wing UAVs[C]//The 11th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI 2014).Piscataway, NJ:IEEE Press, 2014:257-261. |
| [16] | LEE D, SONG H, SHIM D H.Optimal path planning based on spline-RRT* for fixed-wing UAVs operating in three-dimensional environments[C]//International Conference on Control, Automation, and Systems.Piscataway, NJ:IEEE Press, 2014:22-25. |
| [17] | VIEIRA H L, GRASSI V.Improving RRT's efficiency through motion primitives generation optimization[C]//2014 Joint Conference on Robotics: SBR-LARS Robotics Symposium and Robocontrol.Piscataway, NJ:IEEE Press, 2014: 37-42. |
| [18] | KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning[J].International Journal of Robotics Research, 2011, 30(7): 846–894.DOI:10.1177/0278364911406761 |
| [19] | RATLIFF N, ZUCKER M, BAGNELL J, et al.CHOMP:Gradient optimization techniques for efficient motion planning[C]//Proceedings of IEEE International Journal Conference on Robotics and Automation (ICRA).Piscataway, NJ:IEEE Press, 2009:489-494. |
| [20] | 马文蔚. 物理学[M].5版北京: 高等教育出版社, 2006: 149-186.MA W W. Physics.Physics[M].5th edBeijing: Higher Education Press, 2006: 149-186.(in Chinese) |
| [21] | JUNGHUN S, SONGHWAI O.A cost-aware path planning algorithm for mobile robots[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ:IEEE Press, 2012:4724-4729. |
