采用单传感器的雷达三维重构技术中,如文献[8]对自旋和进动目标进行散射点三维信息提取,文献[9]对转台目标进行三维重构,这类方法均是目标相对于雷达运动信息已知情况下的三维重构,无法适用于实际情况中目标运动未知的三维重构。文献[10]从单部雷达获得的ISAR序列中提取目标散射中心二维位置,然后采用卡尔曼滤波和最近邻数据关联准则实现不同姿态下二维散射中心关联,完成目标三维坐标数据提取。由于散射中心在雷达视线上几何投影得到的一维信息提取方法已经成熟,利用多个不同姿态下的一维散射中心距离数据进行关联后完成目标的三维重构是一种有效可行的方法,得到了广泛应用[11],但是由于实际中目标的三维运动,散射中心在不同雷达视角下投影位置会发生变化,不同散射中心运动轨迹会发生重叠或遮挡等情况,因此目标散射中心的正确关联是从目标散射中心数据得到目标三维成像的关键步骤。
现有的实现目标散射中心关联的方法可以分为2类:
第1类是基于已知姿态下投影的几何约束方法。文献[12-13]分别利用Hough变换和广义Radon变换(GRT Radon)变换得到了目标三维像,这2种方法都是基于图像域的变换方法,通过分析三维空间网格中的能量分布获得了目标的三维成像结果,但该结果只是目标真实尺寸的投影,而不是目标的空间真实尺寸。文献[14]提出了一种基于目标运动姿态已知的散射中心关联的三维成像方法,采用随机抽样一致性方法,通过判断各关联样本反投影内点数量剔除错误的关联样本,相比于三维点云进行聚类[15]的方法,该方法具有更高的可靠性和重建精度,但利用穷举所有姿态下一维散射中心的任意关联组合来提取真实三维散射中心的空间位置,其工作量和消耗的资源很大,一旦散射点数量增大,要求的视角数量也要大量增加。
第2类散射点关联方法不需要投影几何约束条件,根据姿态变化的连续性对散射中心位置进行跟踪,利用辅助信息如散射中心的幅度、类型等信息进行关联。文献[16]综述了近年来基于目标特征辅助的数据关联方法。如传统的最近邻(Nearest Neighbor,NN)法建立在统计距离基础之上,而概率数据关联(Probabilistic Data Association,PDA)和多假设跟踪(MHT)则用关联概率来定义。这些方法在信噪比高于12 dB时能够取得较好的效果。但信噪降低时,关联效果很差。
基于以上的问题分析,本文提出了一种基于强度信息辅助的MHT散射点关联方法,此方法基于卡尔曼滤波和幅度信息辅助的最佳分配方案,在传统的基于强度信息辅助的MHT方法基础上,推导了一种相对幅度似然函数辅助的MHT方法,实现不同姿态下一维散射中心关联,对关联后的数据应用序贯因式分解法实现散射点三维坐标的提取。最后,通过仿真实验,验证了该方法的有效性。
1 雷达目标三维重构模型 雷达传感器与具有任意三维转动的刚体目标空间几何关系如图 1所示,传感器位于坐标系的原点 O ,对目标进行连续视角的观测。
 |
| θ—雷达视线与z轴的夹角;φ—雷达视线在xy平面的投影与x轴的夹角;ω—目标在转动时候的角速度;ρ—雷达视线方向上的距离投影;X—散射点位置向量;c^—雷达的视线单位向量。 图 1 空间目标运动模型 Fig. 1 Spatial target motion model |
| 图选项 |
设刚体目标由 N 个不共面的散射中心构成,这些散射中心的位置配置矩阵 X 可以表示为
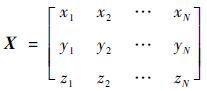 | (1) |
在 tk 时刻沿着视角方向单位向量 (tk)=[c1,c2,c3] 得到的一维距离特征信息可以表示为
 | (2) |
式中:||c(tk)||=1;ρ 的维数为 1×N;τ(tk)∈R3,τ(tk) 为目标质心的位置矢量; 1N 为 1×N 的各元素为1的向量。
对式(2)去除平动信息后有
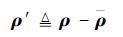 | (3) |
 | (4) |
去除平动信息后的配置矩阵为
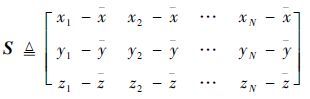 | (5) |
式中:
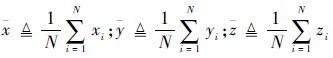
此时投影方程可以表示为
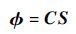 | (6) |
式中:
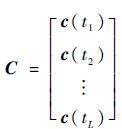
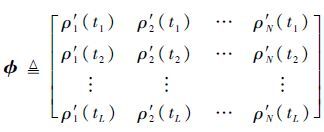
2 幅度信息辅助的MHT关联方法 根据前面的分析可知,正确的量测矩阵?是三维重构方法实现的基础。但在实际中,目标的三维运动会导致目标各散射中心投影到各视角上的投影位置序列发生改变。对一维散射中心进行正确关联是三维成像的关键步骤。鉴于上述问题,本文构建了一种基于幅度信息辅助的MHT关联方法,用于雷达目标三维运动未知情况下的散射中心关联。以下对该关联方法以及具体实施方法进行详细阐述。
2.1 MHT关联方法 MHT关联方法采用标准卡尔曼滤波模型进行估计和预测,本文采用匀加速(CA)模型。其状态方程可表示为
 | (7) |
式中: F(k) 为状态转移方程; X(k) 为状态向量; V(k) 为零均值、白色高斯过程噪声序列,其协方差为
 |
式中:δkj为高斯过程的方差。
一步预测的协方差为
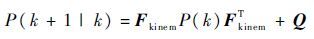 | (8) |
式中:Q为正交矩阵;
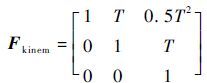 |
其中:T为相邻量测间的时间间隔。
在卡尔曼滤波中,第 i 个量测相对于第 j 个目标预测位置的新息为
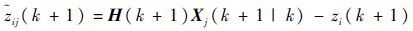 | (9) |
式中: H(k+1)=[Hkinem(k+1)0];Hkinem(k+1)=[100];Xj=[RR·R¨Am]T ,R、R·、R¨和Am分别为散射点位置、速度、加速度和散射点强度。
第 i 个量测相对于第 j 个目标预测位置的新息协方差为
 | (10) |
式中: Pj(k+1|k) 为一步预测协方差矩阵; σ2r 为量测协方差。
定义量测 i 相对于第 j 个目标预测位置的马氏距离为
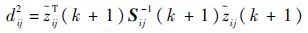 | (11) |
在MHT中,新量测可能来自于已有目标、新目标和虚警,对每次接收到的量测,需要分别计算其属于3种来源的对数似然矩阵 Ω∈
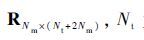
当量测 i 来源于第 j 个目标时,则此关联的对数概率为
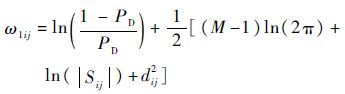 | (12) |
式中:PD为检测概率; M 为状态向量的维数; Sij 为信息协方差; ω1ij 为矩阵 Ω1∈RNm×Nt的第 i 行第 j 列的元素, ω1ij 的数值越小表示量测-目标的关联概率越高。
2.2 相对幅度辅助的MHT关联方法 文献[17-19]将关联目标幅度作为目标的一个固定特征,包含在状态向量中,与运动信息共同对关联概率计算发生作用;文献[20]将目标幅度信息以幅度似然函数形式直接对关联概率计算发生作用。前一种方法对跟踪性能的影响不如后者直观,同时将幅度与运动信息结合在一起可能会存在未知的影响;后一种方法的逻辑是量测的幅度越大,被关联的概率越高,这在目标的幅度波动不大而杂波的幅度波动较大的情况下将基本无法使用。为了克服上述2种幅度辅助方法中的缺点,在2.1节MHT关联方法的基础上,提出一种相对幅度似然函数辅助的MHT方法。不同于幅度似然函数法需要找到最强幅度去进行关联,相对幅度法选择幅度相似的散射点进行关联。
在对数似然矩阵中引入散射点相对幅度似然函数 Λij :
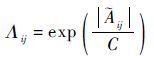 | (13) |
式中: C 为常数,用来控制滤波过程中对幅度差异大小的容忍度, C 值越大,表示对相对幅度差异的容忍度越大; ij 为第 i 个量测的幅度相对于第 j 个目标的幅度的新息:
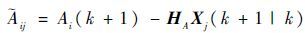 | (14) |
式中:
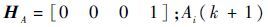
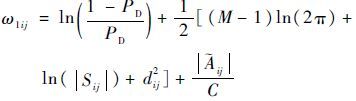 | (15) |
当量测 i 来源于新目标时,有
 | (16) |
式中: ρN 为新目标的密度; ω2ii 为矩阵 Ω2∈RNm×Nm的第 i 行第 i 列的元素。
当量测 i 来源于虚警时,有
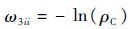 | (17) |
式中: ρC 为杂波密度; ω3ii 为矩阵 Ω3∈RNm×Nm的第 i 行第 i 列的元素。
基于上述原理,本文提出的基于散射点幅度信息辅助的MHT散射点关联方法主要步骤如下。
步骤 1 将散射点视为要跟踪的目标,选取第1次回波得到的所有一维散射点位置和强度信息进行卡尔曼滤波,利用系统的状态方程预测下一次回波散射点状态,计算新息,由滤波方程得到当前状态的估计值,更新协方差矩阵。
步骤 2 生成对数似然矩阵,设置阈值 C ,按照式(11)引入相对幅度似然函数 Λij=
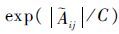
这里先对幅度大小进行统计,根据统计结果, C 的大小选择在幅度中心值附近。
步骤 3 采用Murty方法生成 M 个最佳分配。将步骤2得到的代价矩阵 Ω 所有元素取其绝对值,如果 Ω 中最小元素为正,则不进行操作,采用Murty分配方法[21]从代价矩阵中找出 M 个最佳分配,生成最佳分配细胞矩阵{分配 i ,代价 pi }( i=1,2,…,M ),这里每个分配是 Nm×1 的矩阵,其各个元素对应量测所分配的目标号。
步骤 4 对步骤3得到的每个最佳分配进行更新,生成假设树,假设树深度设置为 N 。当前假设矩阵中假设 i 包含的目标个数记为 nt ,令 p2=-nt·lb(1-PD) ,找出此分配中目标号大于假设 i 中最大目标号与当前量测数目之和的目标号,设置为0,将分配中目标号大于假设 i 中最大目标号的目标号按照最大目标号依次进行重新编号,分配代价增加 pi+p2 ,完成上述更新,包含 M 个最佳分配的细胞矩阵作为一个新元素存入新假设矩阵。
步骤 5 利用新假设对目标状态进行更新,若新假设中目标标号大于当前目标最大标号则归为新目标。当前目标生命值为0,则目标状态维持不变,否则将当前目标的编号与新假设所包含的目标标号进行匹配,匹配成功的目标根据量测值进行状态更新,生命值保持不变,没有匹配的目标生命值减1。
步骤 6 设定假设树的深度最大为 N ,当假设树小于 N 时,正常循环生成新假设,当大于等于 N 时,剪除假设矩阵和目标矩阵中低概率的假设和对应的目标状态。图 2给出了一个示例,
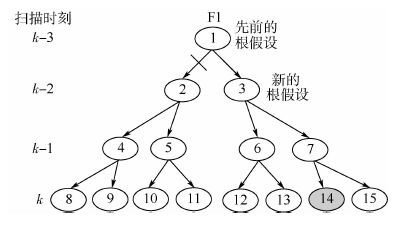 |
| 图 2 N-扫描剪枝假设结构树 Fig. 2 Track tree structure of N-scan pruning hypothesis |
| 图选项 |
对低概率假设进行剪除过程为:首先找出 k 时刻的代价最小的假设,比如“假设14”的代价最小,则在假设矩阵中设置“假设3”为新的根假设,并将“假设3”的假设分支(编号分别为:3,6,7,12,13,14,15)都保留下来,而“假设2”的假设分支则完全删除。
综上所述,本节中基于散射点强度信息辅助的MHT有效关联方案方法流程如图 3所示。
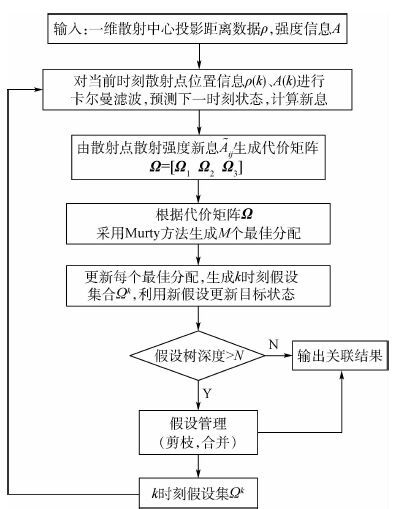 |
| 图 3 强度信息辅助的MHT散射中心关联流程图 Fig. 3 Flowchart of MHT scatterers association based on scattering intensity |
| 图选项 |
3 目标散射中心三维重构 基于因式分解的三维重构包括2个步骤[22]。首先,量测矩阵?通过奇异值分解得到2个秩为3的矩阵。假设投影次数 L≥N ,通过计算?∈RL×N 矩阵的奇异值分解,可以得到正交矩阵 U∈RL×3 和 V∈RN×3, 有
 | (18) |
采用因式分解法需要先将所有观测视角下的数据存储在量测矩阵?中,然后才能进行奇异值分解得到目标的形状和视角矩阵,其运算量为 O(LN2) ,导致其实时性不强。而且当投影次数 L 较大时,数据存储量很大,式(18)的奇异值分解速度会变慢。文献[23]将序贯因式分解的方法应用到二维图像序列中,运算量将变为 O(N2) ,提升了运算速度。本文结合一维散射中心距离像序列,给出了散射点一维距离像序列序贯因式分解的三维成像方法。
重建过程如下。
步骤 1 计算迭代特征向量。首先给定一个 N×3 的各列互相正交矩阵 Q0 和一个空矩阵 Z0∈RN×N ,计算矩阵 Ql∈RN×3 的算法如下。
算法1 for l=1,2,…
 |
(QR分解)
end
步骤 2 计算形状空间的固定基。根据步骤1产生的矩阵 Ql 定义一个range(Ql)上的投影矩阵 Hl=QlQlT ,给定一个各列互相正交的 N×3 的矩阵 0 。计算形状空间固定基矩阵 l∈RN×3 算法如下。
算法 2 for l=1,2,…
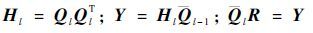 |
end
步骤 3 仿射变换。获得形状空间固定基矩阵 l 后,计算出目标在第 l 帧的视角向量 l 和对称矩阵 Wl。l 是正交矩阵,所以

算法 3 for l=1,2,…
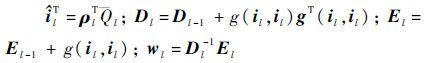 |
end
对 Wl 的特征分解可以产生仿真变换矩阵 Al ,从而可以获得视角向量和形状矩阵:
 | (19) |
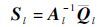 | (20) |
4 仿真实验分析 本节通过仿真实验对本文提出的散射点关联和重构方法进行验证分析。仿真实验中设置了9个分散的散射点,散射点位置和相对散射强度如表 1所示,图 4给出了散射点在三维坐标系中的位置。
表 1 散射点位置和相对散射强度 Table 1 Location of scatterers and relative scattering intensity
| 散射点位置/m | 相对散射强度 | ||
| x | y | z | |
| 1 | 0 | 0 | 1 |
| -1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | -1 | 0 | 1 |
| 1 | 0 | 1 | 2 |
| -1 | 0 | 1 | 2 |
| 0 | 1 | 1 | 2 |
| 0 | -1 | 1 | 2 |
| 0 | 0 | 2 | 4 |
表选项
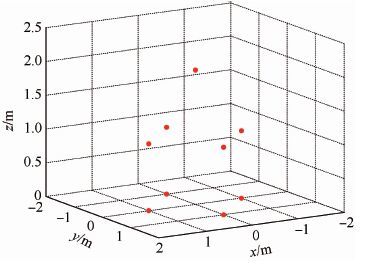 |
| 图 4 目标三维散射点模型 Fig. 4 Target 3D scatterers model |
| 图选项 |
对以上模型,设置目标三维运动过程中参数如下:姿态角 θ 初始值设置为15°,变化周期Tθ=10 s,状态角φ初始值设置为60°,变化周期Ts=8 s。
4.1 一维散射点关联仿真 假设目标平动已经得到了精确补偿,采用文献[24]的二维状态空间方法提取出目标散射点的一维距离像。仿真中采用步进频信号,起始频率为8 GHz,频率步进间隔为Δ f=20 MHz,频率点数为101个,脉冲重复周期设置为0.001 s,脉冲数为200,回波信号中加入高斯白噪声。图 5给出了信噪比为15 dB时的各散射点时间-距离投影-幅度图。从图中可以看出一维散射点存在重叠缺失还有虚假点等情况。
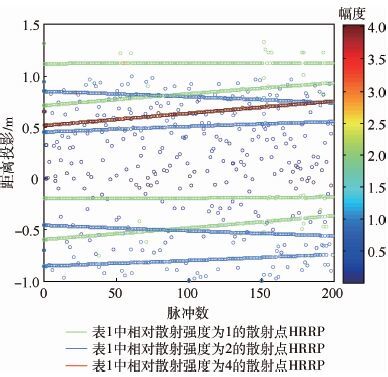 |
| 图 5 散射点的距离投影和幅度 Fig. 5 Scatterers projected range and relative scatter intensity |
| 图选项 |
针对以上得到的一维投影距离,分别采用传统的聚类方法、几何约束方法、MHT方法和本文提出的基于幅度信息辅助的MHT方法对一维散射点位置进行关联。这里设置检测概率PD=0.999,新目标密度ρN=2,杂波密度ρC=3,考虑到MHT方法最优分配方案数和树深太大时会增加运算量,太小又会影响关联效果,这里最优分配方案数设置为M=5,假设树深度H=3,最大生命点数为4,噪声功率谱密度为1 000,量测噪声标准差为0.06,初始协方差为0.01。各种方法关联后的航迹结果如图 6所示。
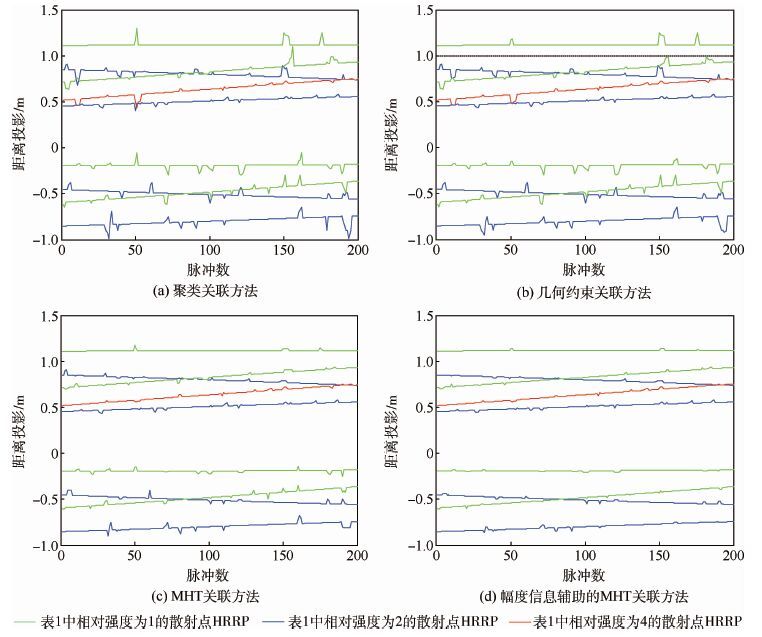 |
| 图 6 一维散射点关联结果 Fig. 6 Result of 1D scatterers centers association |
| 图选项 |
图 6(a)和图 6(b)分别是采用聚类方法和几何约束方法[11]关联的结果,图 6(c)和图 6(d)分别是采用MHT方法和幅度信息辅助的MHT方法关联的结果。通过仿真结果可以看出前2种方法较容易受到虚假散射点的影响,关联过程中,航迹关联会因为虚假散射点而产生错误。而MHT方法关联结果较前2种方法关联结果有了明显提升,能够较有效地抑制虚假散射中心的影响,实现正确的航迹关联。同时对比图 6(c)和图 6(d)可以发现,采用幅度信息辅助的MHT关联方法相比于无幅度信息辅助的MHT关联方法能够进一步提高关联效果,更好地降低关联时的错误率。可见,基于幅度信息辅助的MHT关联方法,可以实现散射中心距离数据的正确关联,为目标散射中心的三维重构奠定了基础。
4.2 散射点三维重构仿真 采用强度信息辅助的多目标跟踪方法关联散射点后,利用序贯因式分解方法重构出散射点的三维位置。图 7给出了已有几何约束关联方法和本文提出的方法重构后的结果。本文方法得出的重建结果与真实坐标之间的平均欧式误差为0.09 m,文献[11]中已有的几何约束关联方法平均欧式误差为0.29 m,可以看出本文重建效果更加接近目标散射点的真实位置。
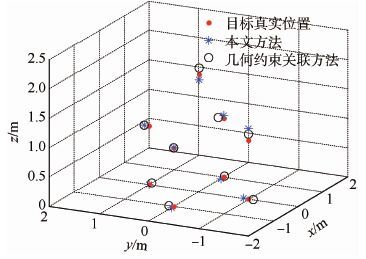 |
| 图 7 目标三维重构结果 Fig. 7 Results of target 3D reconstruction |
| 图选项 |
仿真实验对文献[11, 15]中的方法和本文的重建结果进行了误差分析。在一维散射中心投影数据中加入方差0~0.5 m的高斯噪声,采用本文方法和现有方法进行了100次重建实验,计算出散射点重建结果和真实值间的平均欧式距离误差。图 8给出了上述3种重建结果的重建误差曲线,纵坐标为100次门托卡罗实验结果的平均值。由图 8可以看出,本文方法相比于文献[11]中的几何约束方法和文献[15]中的聚类方法具有更高的重建精度。
 |
| 图 8 平均欧式距离误差结果 Fig. 8 Results of Euclidean distance error |
| 图选项 |
5 结 论 本文在MHT关联方法的基础上提出了一种基于散射点相对幅度信息辅助的散射点关联方法。
1) 在MHT方法的对数似然矩阵中引入散射点相对幅度似然函数,从而利用散射点幅度信息对未知视角下的目标多个散射点的一维距离像序列进行关联。
2) 相比于以往的幅度信息辅助的MHT方法,该关联方法能够有效解决目标运动未知情况下的散射点关联鲁棒性差问题。
3) 在完成目标散射点一维距离像数据正确关联后,采用序贯因式分解的方法重构出了散射点三维位置,相比于传统的因式分解法,该方法减小了数据存储量,提高了三维重构的实时性能。
4) 仿真实验表明该方法对未知三维运动的目标散射点重构有很好的效果,实际中散射点的类型信息也可以作为辅助信息进行散射点关联。
参考文献
| [1] | SKOLNIK M. Introduction to radar systems[M].New York: McGraw-Hill, 2001: 320-333. |
| Click to display the text | |
| [2] | HONG C L, BO J, HONG W L, et al. Superresolution ISAR imaging based on sparse Bayesian learning[J]. IEEE Transaction on Geoscience and Remote Sensing,2014, 52(8): 5005–5013. |
| Click to display the text | |
| [3] | NOVIELLO C, FORNARO G, MARTORELLA M. Focused SAR image formation of moving targets based on Doppler parameter estimation[J]. IEEE Transaction on Geoscience and Remote Sensing,2015, 53(6): 3460–3470. |
| Click to display the text | |
| [4] | 梁必帅, 张群, 娄昊, 等. 基于微动特征关联的空间非对称自旋目标雷达三维成像方法[J]. 电子与信息学报,2014, 36(6): 1381–1388.LIANG B S, ZHANG Q, LOU H, et al. A method of three-dimensional imaging based on micro-motion feature association for spatial asymmetrical spinning targets[J]. Journal of Electronics and Information Technology,2014, 36(6): 1381–1388.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | MARTORELLA M, STAGLIANO D, SALVETTI F, et al. 3D interferometric ISAR imaging of noncooperative targets[J]. IEEE Transaction on Aerospace and Electronic Systems,2014, 50(4): 3102–3114. |
| Click to display the text | |
| [6] | 刘承兰.干涉逆合成孔径雷达(InISAR)三维成像技术研究[D].长沙:国防科学技术大学,2012:15-20. LIU C L.Research on interferometric inverse synthetic aperture radar three-dimensional imaging[D].Changsha:National University of Defense Technology,2012:15-20(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 梁必帅, 张群, 娄昊, 等. 基于微动特征关联的空间自旋目标宽带雷达三维成像[J]. 电子与信息学报,2013, 35(9): 2132–2140.LIANG B S, ZHANG Q, LOU H, et al. Three-dimensional broadband radar imaging of space spinning targets based on micro-motion parameter correlation[J]. Journal of Electronics and Information Technology,2013, 35(9): 2132–2140.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | MAYHAN J T.Phase-enhanced 3D snapshot ISAR imaging and interferometric SAR:ESC-TR-2007-067[R].Lexington:Lincoln Laboratory,2009. |
| Click to display the text | |
| [9] | KEMPF T,PEICHL M,DILL S.3D tower-turntable ISAR imaging[C]//Proceedings of the 4th European Radar Conference.Munich:Wiley Press,2007:114-117. |
| Click to display the text | |
| [10] | 王昕, 郭宝锋, 尚朝轩. 基于二维ISAR图像序列的雷达目标三维重建方法[J]. 电子与信息学报,2013, 35(10): 2475–2480.WANG X, GUO B F, SHANG C X. 3D reconstruction of target geometry based on 2D data of inverse synthetic aperture radar images[J]. Journal of Electronics and Information Technology,2013, 35(10): 2475–2480.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | 张颖康, 肖扬, 胡绍海. 非合作雷达目标散射中心关联和三维重建算法[J]. 电子与信息学报,2011, 33(9): 2076–2082.ZHANG Y K, XIAO Y, HU S H. Method of scattering centers association and 3D reconstruction for non-cooperative radar target[J]. Journal of Electronics and Information Technology,2011, 33(9): 2076–2082.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | LI J, PI Y M. Research on the 3D imaging algorithm of spin target based on the Hough transform[J]. Eurasip Journal on Wireless Communications and Networking,2013, 2013(1): 503–504. |
| Click to display the text | |
| [13] | WANG Q, XING M D, LU G Y, et al. High-resolution three-dimensional radar imaging for rapidly spinning targets[J]. IEEE Transaction on Geoscience and Remote Sensing,2008, 46(1): 22–30. |
| Click to display the text | |
| [14] | 张颖康, 肖扬, 胡绍海. 基于散射中心关联的三维成像方法[J]. 系统工程与电子技术,2011, 33(9): 1988–1994.ZHANG Y K, XIAO Y, HU S H. New method of 3D imaging based on scattering centers association[J]. Systems Engineering and Electronic,2011, 33(9): 1988–1994.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | 任双桥, 刘永祥, 黎湘, 等. 基于多姿态角下一维距离像的雷达目标三维成像[J]. 电子学报,2005, 33(6): 1088–1090.REN S Q, LIU Y X, LI X, et al. Radar target 3D imaging based on multi-aspect range profiles[J]. Acta Electronica Sinica,2005, 33(6): 1088–1090.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | ZHANG R H, ZHANG J. Feature-aided data association:A survey[J]. Engineering and Electronics,2011, 33(1): 35–41. |
| Click to display the text | |
| [17] | 薛锋, 刘忠, 曲毅. 结合幅度信息的粒子滤波机动目标被动跟踪[J]. 电光与控制,2008, 15(6): 13–17.XUE F, LIU Z, QU Y. Amplitude information based particle filtering for passive tracking of maneuvering target[J]. Electronics Optics and Control,2008, 15(6): 13–17.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [18] | DAVEY S J.Extensions to the probabilistic multi-hypothesis tracker for improved data association[D].Adelaide:The University of Adelaide,2003:68-72. |
| Click to display the text | |
| [19] | HAMMARBERG B, FORSTER C, TOREBJORK E. Parameter estimation of human nerve C-fibers using matched filtering and multiple hypothesis tracking[J]. IEEE Transaction on Biomedical Engineering,2002, 49(4): 329–336. |
| Click to display the text | |
| [20] | PITTON J,GANSE A,ANDERSON G.Distributed environmental inversion for multi-static sonar tracking[C]//International Conference on Information Fusion.Piscataway,NJ:IEEE Press,2006:1-6. |
| Click to display the text | |
| [21] | WERTHMANN J R.A step-by-step description of a computationally efficient version of multiple hypothesis tracking[C]//Signal and Data Processing of Small Targets Conference.Piscataway,NJ:IEEE Press,1992:288-300. |
| Click to display the text | |
| [22] | CARLO T, TAKEO K. Shape and motion from image streams under orthography:A factorization method[J]. International Journal of Computer Vision,1992, 9(2): 137–154. |
| Click to display the text | |
| [23] | MORITA T, TAKEO K. A sequential factorization method for recovering shape and motion from image streams[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1997, 9(8): 858–867. |
| Click to display the text | |
| [24] | WANG J, WEI S M, SUN J P. A GTD model and state space approach based method for extracting the UWB scattering center of moving target[J]. Science China information Sciences,2011, 54(1): 182–196. |
| Click to display the text | |
