Worthington和Cole[1]首次通过试验观测到液滴和球体的入水过程,定性地分析了入水过程所产生的喷溅、空泡和由空泡闭合产生的射流等流动现象.May和Woodhull[2, 3, 4]针对球体的密度、表面状态以及尺寸展开了试验,得到了球体入水的附加质量系数、临界速度、空泡形成与发展规律等一系列研究结果.Truscott和Techet[5, 6]针对球体旋转入水问题开展了大量的试验研究,分析了表面状态等因素对空泡发展过程的影响,得到了不同旋转角速度条件下球体入水的空泡流动特性,并估算了球体入水过程的升力和阻力.Gordillo等[7]应用势流理论对高雷诺数下的空泡最小半径和闭合点附近空泡形态随时间的变化过程进行了数值研究.
何春涛[8]采用数值模拟方法分别针对球体和圆柱体匀速垂直入水以及自由垂直过程进行了研究,得到了空泡生成和发展过程、影响因素及阻力系数变化规律等结论.同时对典型回转体进行了入水空泡试验,包括球体和圆柱体入水试验以及两圆柱体串、并联入水试验,分析了表面沾湿状态、头部形状及回转体密度对入水空泡演化过程的影响.马庆鹏等[9]对锥头圆柱体垂直自由高速入水问题进行了数值模拟研究,分析了入水后速度和入水空泡的发展规律,并分析了初始速度对空泡发展的影响.
尽管在实际情况中空气域压力是恒定的,然而在Gilbarg和Anderson[10]的试验过程中发现空气域压力对球体低速垂直入水的空泡发展影响较大.因此为了探究空气域压力对高速射弹入水过程的影响,本文对127°锥头圆柱体以500m/s的初始速度垂直入水过程进行了数值模拟,并与理论分析结果进行对比验证其合理性.在此基础上,开展不同空气域压力条件下的数值计算,分析空气域压力对入水弹道、流体动力特性、空泡形态及流场特性的影响.
1 数值计算方法 1.1 控制方程本文选取流体体积法(Volume Of Fluid,VOF)作为均质多相流模型对入水过程的气、汽、液三相流动进行描述,并假设流体为不可压缩,同时不计及入水过程中的热效应.VOF多相流模型将多相流体看作单一的流体介质混合物,各相共享同一压力场、速度场并忽略各相之间的滑移速度.在此,液相、气相及水蒸汽相的体积分数分别为αl、αg和αv,三者满足关系式αl+αg+αv=1.
混合介质的连续性方程为
式中：i=1,2,3,下同.
动量守恒方程为
式中:t为时间；ρl、ρg和ρv分别为液相、气相和水蒸汽相的密度;ρm=αlρl+αgρg+αvρv为混合介质的密度;μl、μg和μv分别为液相、气相和水蒸气相的动力黏度;μm=αlμl+αgμg+αvμv为混合介质的动力黏度；μt=ρmCμk2/ε为湍流黏性系数;Cμ为经验常数;k为湍动能;ε为湍动耗散率;ui和uj为速度分量,j=1,2,3;xi和xj为位移.
湍流模型采用Menter SST (Shear Stress Turbulence) k-ω模型[11],其表达式为
式中:ρ为流体密度;P为速度梯度引起的湍动能项;Pkb和Pω为浮力引起的湍动能项;ω为耗散率;μ为动力黏度;F1为混合函数;常数项的值分别为α=5/9，β=0.075，β*=0.09,σk=0.85,σω=0.5,σω2=0.856.
湍流动力黏度的限制方程为
式中:a1=0.31为常数;
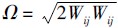为剪切应变率的不变测度;F2=tanh(arg22)为混合函数.其中,Wij和arg2定义为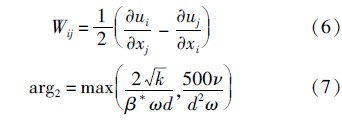
模型中混合函数F1的表达式为
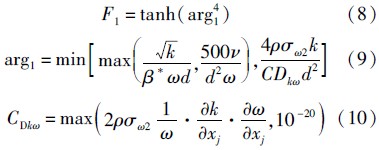
式中:ν=μ/ρ为流体运动黏度;d为流场中流体质点距离最近壁面的距离;arg1为表达式;CDkω为湍流交叉扩散项.
在对空化问题进行求解时,本文应用了基于Rayleigh-Plesset气泡方程建立的Schnerr and Sauer空化模型.该模型守恒方程的建立基于水蒸汽相,水蒸汽相的质量输运方程为
式中:RB为气核半径,其值为1μm;αnuc为不可凝结气体体积分数,其值为5×10－4;p为远场压力;pv为饱和蒸汽压;Fvap=50和Fcond=0.001为经验常数.
1.2 控制方程的求解本文选用有限体积法[12]对流体控制方程进行时间和空间上的离散,其中压力场与速度场的耦合求解选用PISO (Pressure Implicit with Splitting of Operators)算法;压力场的空间离散选取PRESTO!格式;应用CICSAM格式对各相体积率进行离散;在考虑了收敛性与计算量后,选取一阶迎风格式对动量方程进行离散.
1.3 模型建立本文的高速射弹模型采用带有一定角度圆锥头的刚性、实心圆柱体结构,其结构示意图如图 1所示,其外形参数及属性见表 1.
 |
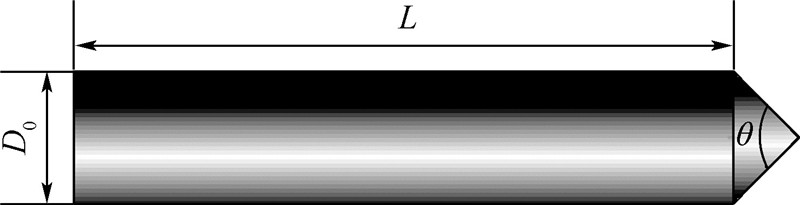| L—柱体长度；D0—柱体直径；θ—锥角.图 1 高速射弹结构示意图Fig. 1 Structure schematic of high-speed projectile |
| 图选项 |
表 1 高速射弹外形参数及属性Table 1 Configurations parameters andproperties of high-speed projectile
| L/mm | D0/mm | θ/(°) | ρs/ (g·cm-3) | CD0 | Vp/ (m·s-1) |
| 50 | 10 | 127 | 2.7 | 0.637 | 500 |
| 注：ρs—密度；CD0—空化数为0时的阻力系数；Vp—初始入水速度. | |||||
表选项
由于所选射弹为轴对称体,所以本文数值模拟采用二维轴对称模型.计算域与网格划分及边界条件的示意如图 2所示,将x轴作为对称轴,计算域深度沿x轴正方向递增,流场宽度沿y轴方向,坐标原点O取自由液面上方0.02m位置.流场空气域高度为0.32m,流场直径1m,水域深度为1.98m,弹体头部距离水面为0.02m.
 |
| 图 2 计算域与计算网格及边界条件示意图Fig. 2 Schematic of computational domain,mesh and boundary conditions |
| 图选项 |
流域顶端为压力入口边界,下方为压力出口边界,出口压力等于当地流体静压,计算环境压力p0=101325Pa,饱和蒸汽压力pv=3540Pa.对弹体附近计算区域的网格进行局部加密,以保证汽水交界面和空泡区域的计算精度.其中,沿弹体轴向前后2D0、径向6D0的范围内采用三角形网格进行加密,其余计算域采用四边形网格划分,加密区渐进过渡到外部网格,且高速射弹上方沿x轴负方向的四边形网格为等高均布,其运动方向(即x轴正方向)及流域径向方向的四边形网格采用渐疏处理.本文计算域划分的网格总量为273284.
本文对高速射弹入水过程的数值模拟引入了动网格技术,以实现射弹沿重力方向的单自由度运动.由于本文网格划分多为四边形网格,中间加密的三角形网格作为一个整体运动,且流域内所有网格节点为单自由度运动,因此,本文采用动态层法实现动网格的更新.
2 数值模拟结果验证 2.1 射弹入水结果验证考虑不可压缩流体,忽略入水过程中的热效应,根据牛顿第二定律,可以得到
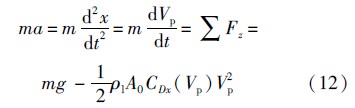
整理后得
式中:m为流体质量;x为位移;g为重力加速度;a为流体加速度;Fz为受力;A0为运动体截面积;σ为空化数;CDx为阻力系数,其数值采用Sedov[13]得到的经验公式CDx=CD0+σ来确定.从而可以得到入水速度方程:
应用第1.3节中所建立的模型进行数值模拟,并与通过式(14)得到的理论结果进行对比,得到如图 3所示的入水速度及入水深度的数值与解析结果对比.从图中可以看出,两种方法得到的入水速度及深度结果具有较高的一致性.
 |
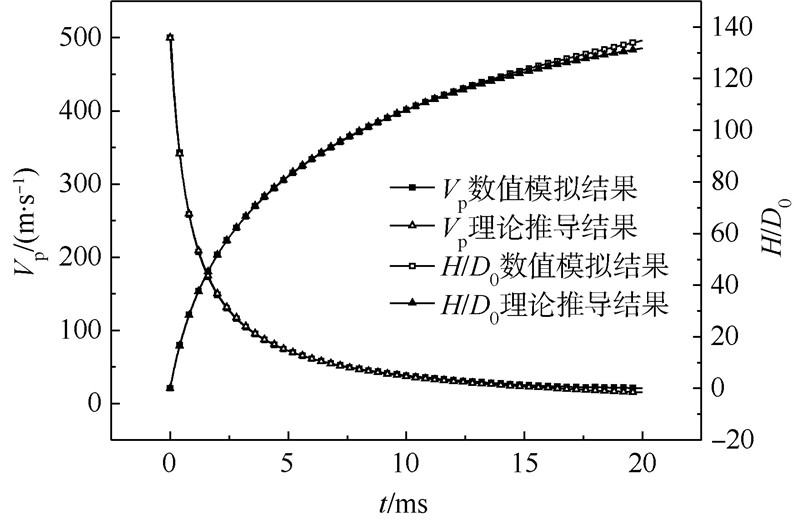| 图 3 入水速度及入水深度的数值与解析结果对比Fig. 3 Comparison of numerical and analytical results of water entry velocities and depths |
| 图选项 |
2.2 空泡形态结果验证结合文献[14]对射弹入水后的空泡形态进行理论推导.由于射弹为高速运动,可忽略重力.动能的改变量可以表达为
式中:Ep为动能;xb为射弹深度.空泡壁面各位置的扩张速度可表示为
式中:y为径向距离;ζ为源强;ξ为浸入指数.
空泡模型示意图如图 4所示.
 |
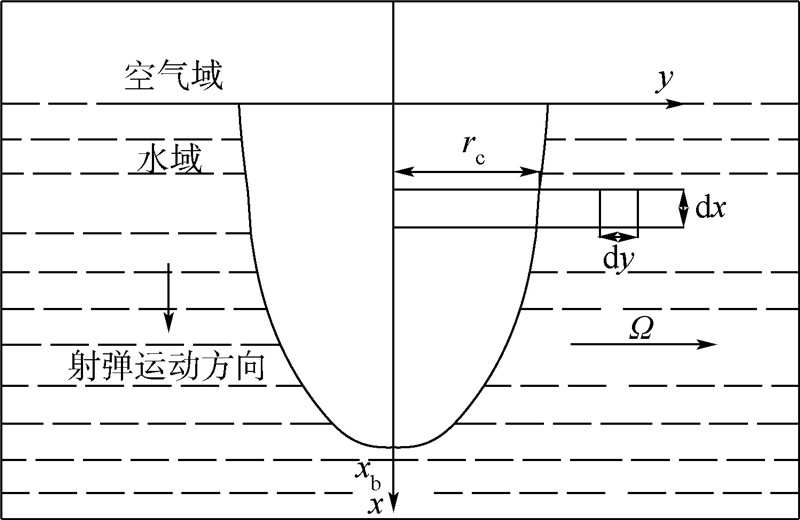| rc—空泡半径.图 4 空泡模型示意图Fig. 4 Cavity growth model |
| 图选项 |
由此可得动能dEy的表达式:
式中:N=ln(Ω/rc)为无量纲的几何参数,考虑到本文中模型速度较高故选取N=30.
对于扩张中的空泡,其势能可以表示为
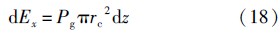
令Pg=P0(x)－Pc(x),P0(x)为液体静压,空泡内部压力Pc(x)取值为饱和蒸汽压,即Pc(x)=3540Pa.至此,由能量守恒定律就可以得到
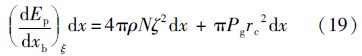
式中：
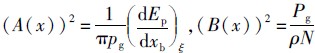则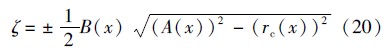
结合边界条件uy=a=r · c(x)整理后可以得到射弹入水为tb时刻的空泡轮廓为
本文分别选取了0.2及1ms时刻的空泡形态进行了对比,结果如图 5所示.可以看出,两种方法得到的结果具有较好的一致性.
 |
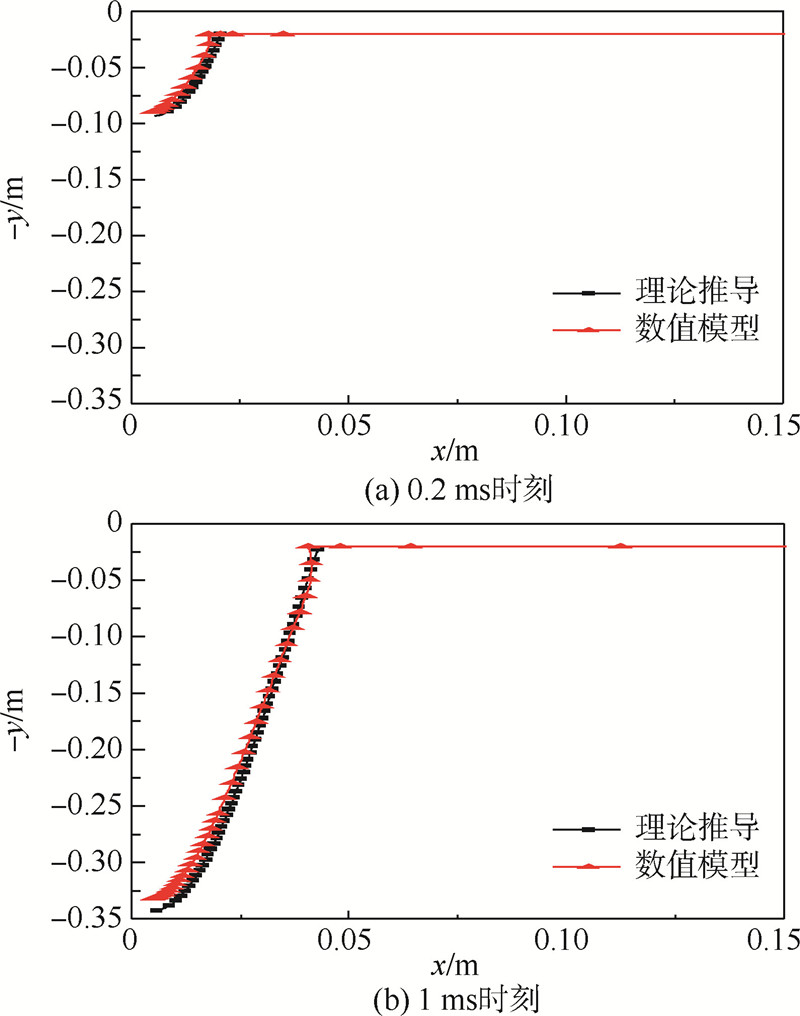| 图 5 0.2和1ms时刻空泡形态对比Fig. 5 Comparison of cavity shape when t=0.2 and 1ms |
| 图选项 |
综上所述,可以看出本文采用的数值计算方法是可信的.从而可以基于该方法针对空气域压力对入水过程进行分析研究.
3 空气域压力影响分析采用第1.3节中的模型并选取8种空气域压力(poper)数值分析空气域压力对入水空泡流场的影响,压力分别取为:poper=p0/10,p0/8,p0/4,p0/2,p0,2p0,4p0,8p0.
3.1 入水弹道及流体动力特性不同空气域压力时，入水速度对比如图 6所示.由图 6可见,不同poper状态下,射弹入水速度随时间的变化过程是一致的;从细节图中可以看到,空气域压力越高,入水速度衰减得越快.这一现象同样表现在入水深度随时间的变化规律中,空气域压力越高,入水深度越小,无量纲入水深度对比见图 7.
 |
| 图 6 入水速度对比Fig. 6 Comparison of water entry velocities |
| 图选项 |
 |
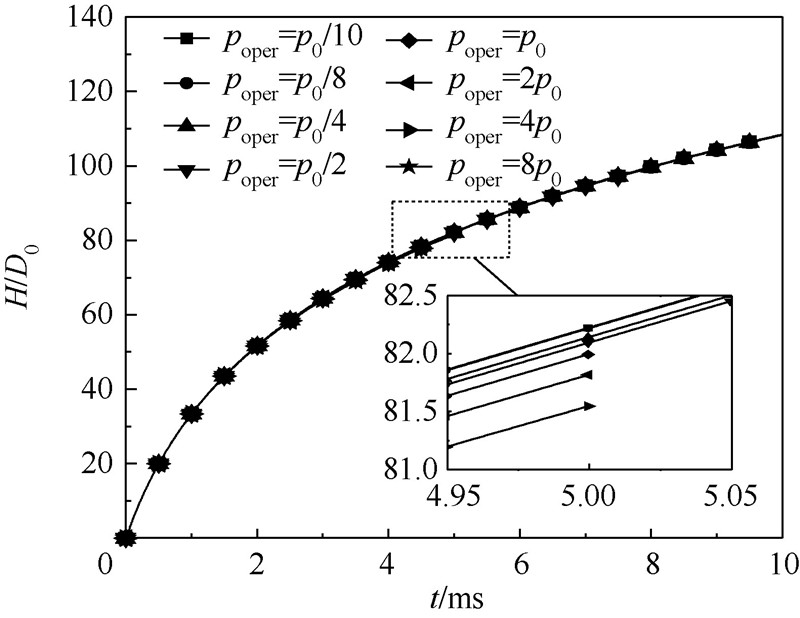| 图 7 无量纲入水深度对比Fig. 7 Comparison of non-dimensional water entry depths |
| 图选项 |
图 8给出了不同空气域压力条件下高速射弹入水初期阻力系数变化曲线,从图中可以看出,空气域压力对射弹阻力系数的影响并不明显.
 |
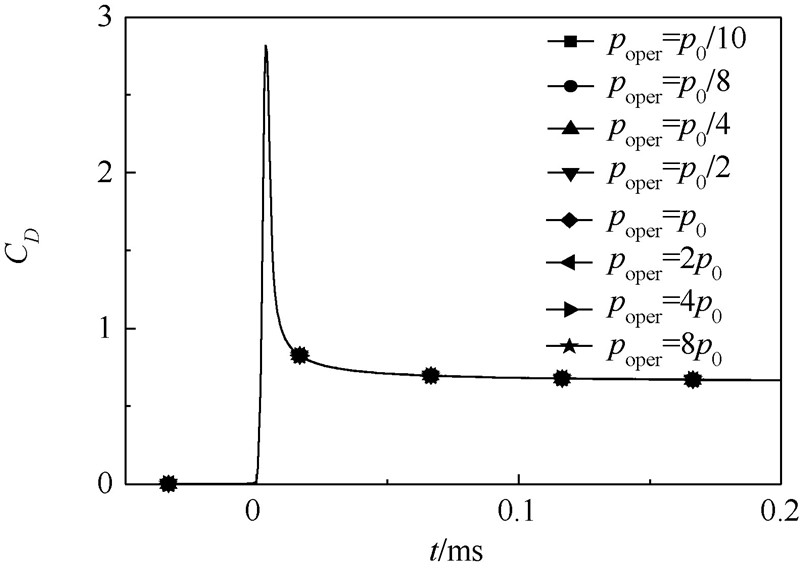| 图 8 入水初期阻力系数对比Fig. 8 Comparison of drag coefficients during initial stage of water entry |
| 图选项 |
3.2 空泡形态及流场特性分析 图 9为入水0.5ms时刻空泡处于敞开阶段的各poper状态下的空泡形态曲线,其中r/r0为无量纲半径，r为空泡半径，r0为柱体半径.由图可知,poper对于液面下空泡形态的影响很小,但对于自由液面处的空泡直径以及表面喷溅形态,其影响较为明显.通过对比可知,poper较大时,该位置空泡半径较小,自由液面上方表面喷溅的紧缩现象较为明显.
 |
| 图 9 入水0.5ms时刻空泡形态对比Fig. 9 Comparison of cavity shapes when t=0.5ms |
| 图选项 |
由于表面喷溅的状态决定了空泡的表面闭合,因此需要对不同poper条件下空泡表面闭合时间做进一步对比分析,如图 10所示.
图 10给出了poper=p0/2,p0,2p0,4p0,8p0等5种条件下的空泡表面闭合时间分布(其余3种空气域压力条件下空泡未能表面闭合).从图 10可以看出,p0/2条件下闭合时间是标准大气压时的 2倍;而当压力大于标准大气压时,闭合时间迅速缩短,随着压力不断增大,闭合时间的变化趋于平缓.
 |
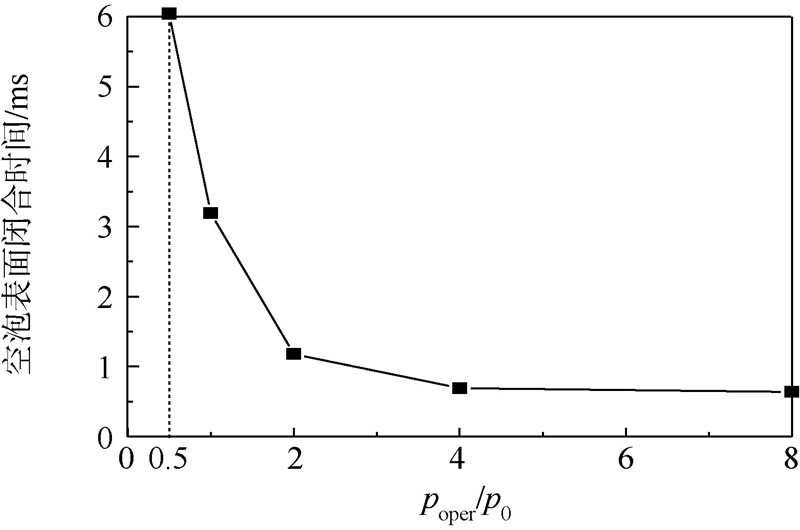| 图 10 入水空泡表面闭合时间对比Fig. 10 Comparison of time for surface closure |
| 图选项 |
各空气域压力条件下空泡表面闭合时间的具体值如表 2所示.
表 2 不同空气域压力条件下空泡闭合时间Table 2 Time of surface closure
| poper | p0/2 | p0 | 2p0 | 4p0 | 8p0 |
| 闭合时间/ms | 6.04 | 3.20 | 1.20 | 0.70 | 0.64 |
表选项
空泡发生表面闭合主要是由于喷溅两侧压力差作用的结果,射弹在以高速通过空泡口时使得该位置的流体流动速度迅速增加,从而产生低压区,同时在空气域相对高压的作用下,表面喷溅逐渐向空泡轴线靠拢.所以当poper较大时,喷溅两侧压力差则较大,从而空泡发生表面闭合的时间较提前;同理,当poper降至一定值时,其所提供的压力差无法使空泡表面闭合.
图 11给出了入水0.5ms 时刻不同空气域压力条件下,自由液面处空泡口直径上的流体速度分布曲线.由图 11可知,尽管poper有所不同,但整体趋势均为空泡口轴线附近的流体速度值最高,同时越接近空泡壁位置速度值越低;poper越大时,流体速度值也越高,当poper=8p0时,轴线位置流速甚至为900m/s.由此可见,空泡表面闭合是较为重要的.
 |
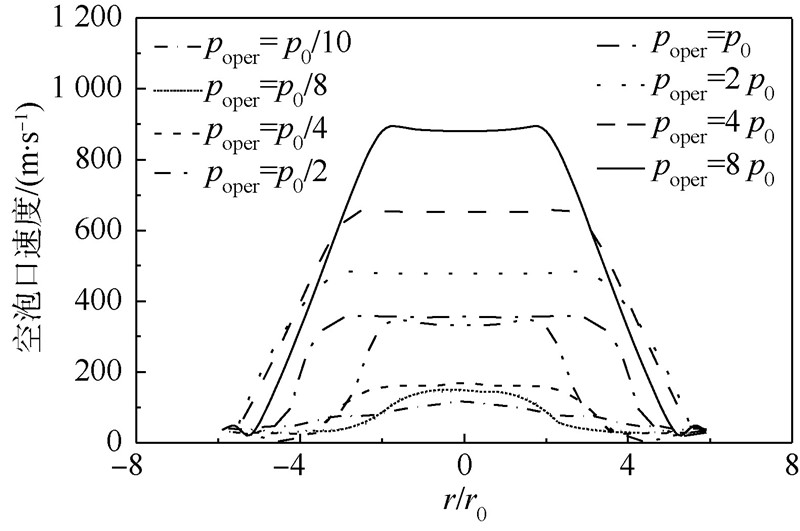| 图 11 入水0.5ms时刻自由液面高度空泡口速度分布Fig. 11 Velocity distribution inside cavity at level of free surface when water-entry time t=0.5ms |
| 图选项 |
进一步的分析可知,通过计算得到空泡附近流场速影响就是气体高速通过空泡口进入空泡内部形成的低压区与空气域压力的差值作用.
为分析0.5ms时刻的流场分布特性,绘制了流场速度V、压力p以及空化特性的分布云图,如图 12和图 13所示.
 |
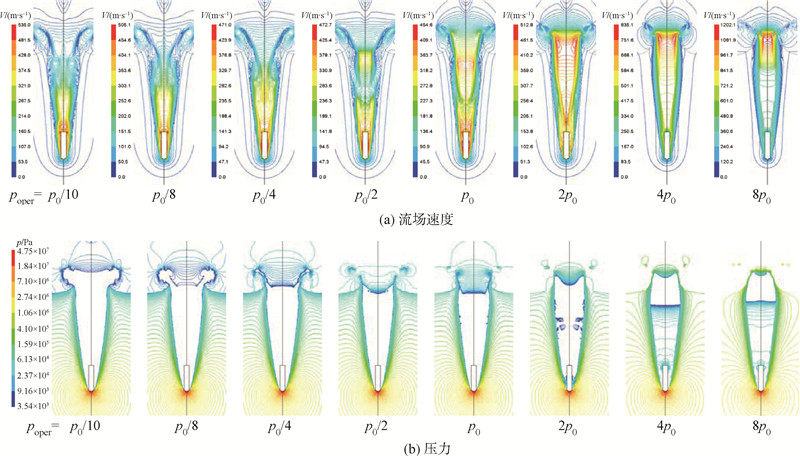| 图 12 入水0.5ms时刻空泡附近流场速度及压力等值线分布云图Fig. 12 Contours of flow field velocity and pressure isolines around cavity when water-entry time t=0.5ms |
| 图选项 |
 |
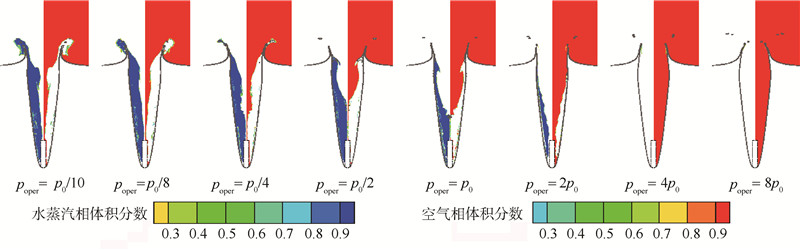| 图 13 入水0.5ms时刻空泡附近流场各相体积分数分布云图Fig. 13 Contour of volume fractions around cavity when water-entry time t=0.5ms |
| 图选项 |
图 12(a)给出了0.5ms时刻下的空泡附近流场速度等值分布云图,由图可见,不同poper条件下的空泡口位置的速度等值线分布均近似平行,且速度极值是随着poper的增大而增加的.同时,在不同poper条件下,空泡上方高速区域宽度也有所差异,在poper<p0时,能够看到空泡口下方有明显的紧缩现象,在poper=p0，2p0，4p0条件下,高速区域较宽,然而在poper=8p0条件下,高速区域的宽度反而减小.结合图 14的各相分布可以看出,各工况下空泡内部的高速区域分布以及气相区域分布基本一致.由此可见,空泡内部空气相的流动速度与空泡内水蒸汽相的分布有着紧密的联系,当水蒸汽相较厚时,则空气相流动截面较小,速度也较高.当水蒸汽相较厚时,则空气相流动截面较小,速度也较高.当时,由于此时空泡口已处于收缩阶段,高速区域的宽度缩减显著,此时速度极值可以达到1200m/s.
图 12(b)给出了空泡附近流场压力的等值线分布云图,从图中可以看到,各poper条件下的射弹头部及空泡壁面外侧的压力等值线的分布规律是较为一致的.当poper≤2p0时,空泡内部达到饱和蒸汽压力,而当poper=4p0，poper=8p0时,空泡已接近表面闭合,空泡口附近高速区仍为饱和蒸汽压力,但空泡下部的低速区压力值较大.同时,通过对比各工况下的喷溅位置压力可以看出,随着poper值的增大,喷溅的外表面压力值也随之增大,但内表面的压力值是一致的,从而上下压力差也越大,由此也证明了前文空气域压力对空泡表面闭合时间的影响性分析.
图 13给出了各相体积分数分布云图,各poper条件下的图示左侧为水蒸气相体积分数云图,右侧为空气相体积分数云图.通过该图可以看出,在空泡敞开阶段,poper越低,空泡内部水蒸汽相的体积越大,空化效应越明显;而在poper=4p0、poper=8p0条件下,由于空气相以较快的速度进入空泡内,而且此时空泡内压力较高,则水蒸汽相基本没有产生.即当空泡处于敞开阶段时,较高的空气域压力对空泡内部的空化效应抑制得较为明显.
4 结 论本文对锥角为127°的锥头圆柱体射弹高速入水过程开展了数值模拟研究,分析了空气域压力对入水过程弹道、空泡形态、流体动力特性以及流动分布特性的影响,得到:
1) 入水弹道及空泡形态的理论结果与数值模拟结果均具有较高的一致性,验证了本文所应用的数值模拟方法的正确性与可靠性.
2) 在空泡敞开阶段,同一时刻空气域压力对自由液面下方的空泡大小影响很小,但对自由液面上方的喷溅形态影响较大.压力较高时,空泡口处空泡半径较小,自由液面上方喷溅的紧缩现象较为明显.
3) 空气域压力对空泡表面闭合时间有较大的影响.压力越高,空泡发生表面闭合时间越早;但当压力低于 1 4 标准大气压时,无法产生足够的压力差使喷溅向轴线靠拢,空泡无法表面闭合.
4) 在空泡闭合之前,空气域压力对空泡内部的空化效应影响较大.压力越高,通过空泡口进入空泡内部的空气相越多,对空化效应的抑制越明显.
参考文献
| [1] | Worthington A M, Cole R S.Impact with a liquid surface studied by the aid of instantaneous photography[J].Philosophical Transactions of the Royal Society,1900,194(252):175-200. |
| Click to display the text | |
| [2] | May A, Woodhull J C.The virtual mass of a sphere entering water vertically[J].Journal of Applied Physics,1950,21(12):1285-1289. |
| Click to display the text | |
| [3] | May A. Effect of surface condition of a sphere on its water-entry cavity[J].Journal of Applied Physics,1951,22(10):1219-1222. |
| Click to display the text | |
| [4] | May A. Vertical entry of missiles into water[J].Journal of Applied Physics,1952,23(12):1362-1372. |
| Click to display the text | |
| [5] | Truscott T T, Techet A H.A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres[J].Physics of Fluids,2009,21(12):1-4. |
| Click to display the text | |
| [6] | Truscott T T, Techet A H.Water entry of spinning spheres[J].Journal of Fluid Mechanics,2009,625(1):135-165. |
| Click to display the text | |
| [7] | Gordillo J M, Sevilla A,Martinez-Bazan C.Bubbling in a co-flow at high Reynolds numbers[J].Physics of Fluids,2007,19(7):077102. |
| Click to display the text | |
| [8] | 何春涛. 典型运动体入水过程多相流特性研究[D].哈尔滨:哈尔滨工业大学,2012. He C T.Study on multiphase flow of typical body during water entry.[D].Harbin:Harbin Institute of Technology,2012(in Chinese). |
| Cited By in Cnki | |
| [9] | 马庆鹏,魏英杰, 王聪,等.锥头圆柱体高速入水空泡数值模拟[J].北京航空航天大学学报,2014,40(2):204-209. Ma Q P,Wei Y J,Wang C,et al.Numerical simulation of high-speed water-entry cavity of cone cylinder[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(2):204-209(in Chinese). |
| Cited By in Cnki (0) | |
| [10] | Gilbarg D, Anderson R A.Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water[J].Journal of Applied Physic,1948,19(2):127-139. |
| Click to display the text | |
| [11] | Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605. |
| Click to display the text | |
| [12] | Versteeg H K, Malalasekera W.An introduction to computational fluid dynamics.The finite volume method[M].New York:Pearson Education,2007:168-190. |
| Click to display the text | |
| [13] | Sedov L I. Two-dimensional problems in hydrodynamics and aerodynamics[M].New York:John Wiley & Sons Inc.,1965:221-231. |
| [14] | Lee M, Longoria R G,Wilson D E.Cavity dynamics in high-speed water entry[J].Physics of Fluids,1997,9(3):540-550. |
| Click to display the text |
