传统的阵风响应分析一般针对刚性飞机进行,但对于大展弦比飞机,刚性假设不再适用,必须考虑飞机的弹性振动以及非定常气动力的影响.Tang等通过试验和解析的方法研究了大展弦比柔性机翼的阵风响应问题[1, 2];Patil和Taylor基于二维准定常气动力结合Peters二维入流理论建立非定常气动力模型,进行连续阵风的频域和时域响应分析[3];Su和Cesnik综合考虑了结构非线性和刚体自由度的影响,建立了一套低阶气动弹性方程,针对翼身融合体构型的大展弦比飞机进行了离散阵风响应分析[4];Ricciardi和Patil评估了准静态Pratt方法应用于高空长航时大展弦比飞机阵风响应计算中的准确性,发现该方法适用于连翼布局飞机但不适用于飞翼布局飞机[5];国内王立新等利用直接力方法开展了大展弦比飞翼构型飞机的阵风载荷减缓控制研究[6];北京航空航天大学气弹室先后于2009年和2011年开展了中等展弦比机翼和弹性飞机的阵风减缓控制风洞试验研究[7, 8].然而多数研究都是针对连续阵风开展并在频域内进行分析,而且往往没有考虑由于弹性振动以及阵风干扰,飞机局部出现瞬时攻角超过翼型失速攻角的情况,因此,针对大展弦比飞机,亟需发展一种可以考虑弹性效应以及大攻角情况下气动力非线性的阵风响应分析方法,本文基于上述需求,针对离散阵风,综合考虑了弹性影响和大攻角非线性情况,详细分析了大展弦比飞机的阵风响应特性.
1 气动力非线性气弹系统建模为解决上述大展弦比飞机阵风响应问题,针对研究对象的特点,首先提出以下2点假设:①本文所考虑的气动力非线性是指由弹性振动以及阵风干扰所引起的飞机局部瞬时攻角过大,超过了升力系数的线性范围;②假设弹性飞机的振动仍是在平衡位置附近线性范围内的振动,因此模态理论仍然适用.
1.1 修正的Theodorsen方法对于展弦比大于4的飞机,由于机翼各部分间的展向影响较小可以忽略,因此可采用片条理论计算非定常气动力[9 ,10].针对单个气动片条,作用于其上的升力和力矩可以采用Theodorsen方法求解[9].然而,传统Theodorsen气动力为线性气动力,无法应用于大攻角情况,因此,为了在阵风引起局部攻角超过线性范围的情况下应用Theodorsen气动力,需要将传统的Theodorsen方法向非线性范围进行延拓.
基于上述考虑,需对Theodorsen气动力进行如下3点修正:①加入阵风干扰项;②考虑升力系数随攻角的非线性特性;③将传统的频域Theodorsen气动力转化为时域形式.
根据Theodorsen非定常气动力理论,二元翼段以频率ω作简谐振动时,单位展长上的升力L(向上为正)和对刚心的俯仰力矩M(抬头为正)分别为[9]
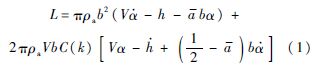
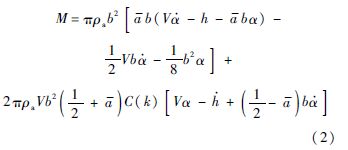
式中:V为飞行速度;ρa为大气密度;h为刚心的沉浮位移(向上为正);α为绕刚心的转角(抬头为正);a为二元翼段刚心距中点的无量纲距离；b为半弦长;
为减缩频率;C(k)为Theodorsen函数.根据Theodorsen理论,二元翼段的气动力(矩)由环量部分和非环量部分组成,其中环量部分包含升力线斜率2π、等效攻角
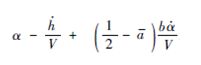和Theodorsen函数C(k)的乘积.为满足大展弦比柔性飞机阵风响应计算的需要,以下对传统Theodorsen气动力进行3方面修正.1.1.1 加入阵风干扰项本文采用1-cos型离散阵风模型,阵风方向垂直于飞行轨迹,如图 1所示.
 |
| wg—阵风速度幅值;lg—阵风尺度.图 1 1-cos型阵风剖面Fig. 1 Profile of 1-cos gust |
| 图选项 |
1-cos型阵风的速度剖面可表示为
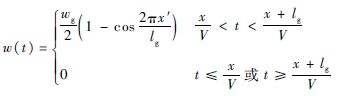
阵风干扰对系统的影响表现为阵风速度w(t)产生的附加等效攻角
因此考虑阵风干扰后,原等效攻角变为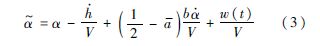
1.1.2 考虑非线性升力系数传统Theodorsen气动力之所以为线性的,是因为其环量部分使用了不可压流中二维平板的理论升力线斜率2π,且用升力系数斜率2π与等效攻角相乘的形式来获得升力系数CL,但在实际情况中,片条的升力系数斜率CLα较2π会有小幅偏差,而且考虑大攻角情况下气动力的非线性特性后,片条升力系数的线性表达式CL=CLα·?不再适用,因此考虑采用非线性函数CL=CL(?)代替传统Theodorsen气动力中用线性表达的CL.值得注意的是,真实的CL=CL(?)曲线可通过风洞试验获得,在阵风响应时域仿真分析中可通过非线性查表算法实现.
此时,综合上述两步,可将考虑阵风干扰的Theodorsen线性气动力延拓到非线性区域,其表达式为
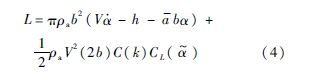
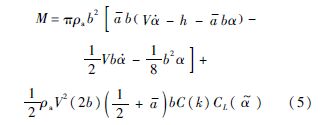
1.1.3 Theodorsen方法的时域化传统Theodorsen气动力为频域形式的气动力,其中的C(k)代表了气动力的非定常特性,如式(6)所示,它是减缩频率k的函数,无法直接用于时域的非线性求解过程,这里i为虚数单位.
根据Jones近似公式,可将C(k)写为时域传递函数形式[10],即
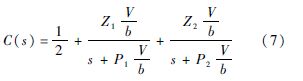
式中:Z1=0.0075;Z2=0.1005;P1=0.0455;P2=0.300;s为Laplace变量.在进行非线性阵风响应时域仿真时,利用传递函数环节C(s)代替Theodorsen函数C(k).
将修正的Theodorsen方法与片条理论相结合,即可建立同时考虑阵风干扰以及局部攻角失速时的非线性时域非定常气动力模型.设片条均匀分布,宽度为Δl,则作用于每个片条上的升力Li(向上为正)和绕刚轴的俯仰力矩Mi(抬头为正)分别为
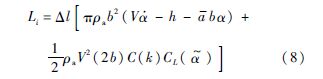
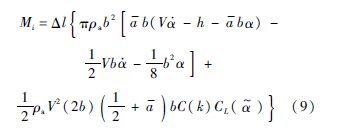
1.2 非线性阵风响应系统建模本部分以上述非线性气动力为基础,建立大展弦比柔性飞机的阵风响应系统模型.如图 2所示为典型大展弦比柔性飞机示意图.按照片条理论,将全机主要升力面划分为若干气动片条,其中机翼片条编号从左至右为1~m,尾翼片条编号从左至右为m+1~n.
 |
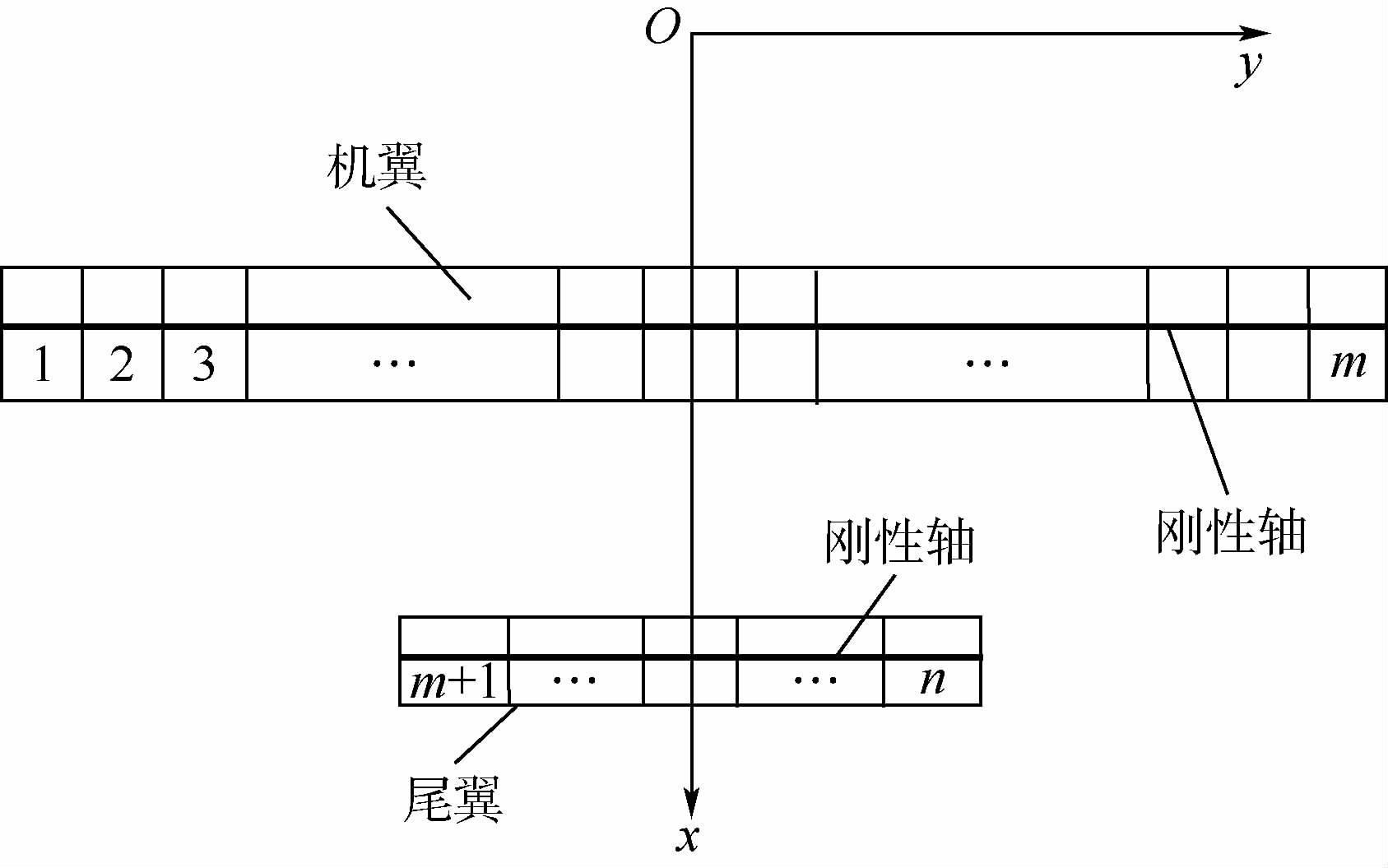| 图 2 大展弦比飞机片条划分示意图Fig. 2 Schematic diagram of strip definition of high aspect ratio aircraft |
| 图选项 |
设飞机总质量为m,绕质心的俯仰惯量为I,h和L均向上为正,俯仰自由度α和绕质心的俯仰力矩M均抬头为正,飞机的运动状态可由二阶刚体模态(h和α)以及前p阶弹性模态表示,模态坐标系下弹性飞机的运动方程[11]为
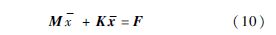
式中:广义质量阵M=diag(m，I，1，…，1)；广义刚度阵K=diag(0，0，ω12，…，ωp2)；[ω1…ωp]为弹性模态的固有频率；广义力F=[φ]TL+[φ]TM,[φ]和[φ]分别为系统模态矩阵的平移分量和转动分量,系统模态矩阵由飞机刚体运动模态和弹性模态共同组成,L=[L1L2…Li…Ln]T(i=1,2,…,n)和M=[M1M2…Mi…Mn]T(i=1,2,…,n)分别为全机所有n个片条上的升力和俯仰力矩向量,第i个片条上的升力和力矩的表达式Li和Mi分别参见式(8)、式(9).状态变量x=[hαq1…qp]T,其中qj(j=1,2,…,p)为第j阶弹性模态的广义坐标.
由式(10)可得柔性飞机环节的状态空间方程为
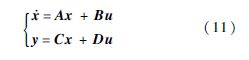
式中:
根据模态叠加法,所有片条上的沉浮位移h=[h1h2…hi…hn]T(i=1,2,…,n)和俯仰角α=[α1α2…αi…αn]T(i=1,2,…,n)可表达为
接下来,将L=[L1L2…Li…Ln]T和M=[M1M2…Mi…Mn]T(i=1,2,…,n)展开为如下形式:
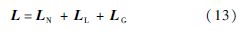
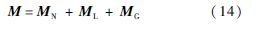
式中：
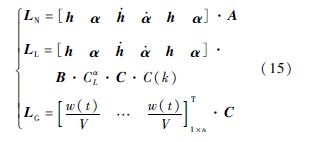
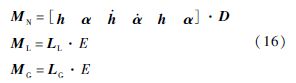
其中：下标N、L、G分别代表气动力(矩)中的非环量部分、环量部分以及阵风部分；系数分别为
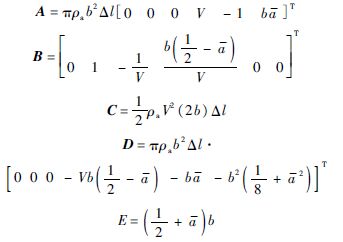
综上所述,将式(11)和式(12)描述的柔性飞机动力学模块与式(13)~式(16)描述的非线性时域气动力求解模块相耦合,即组成了大展弦比柔性飞机阵风响应模型.
2 离散阵风时域响应分析基于以上理论方法,通过MATLAB/Simulink建立大展弦比柔性飞机非线性阵风响应仿真模型.将柔性飞机环节的状态空间模型与非线性时域非定常气动力计算模块相连接,并加入阵风干扰输入,即可组成如图 3所示的考虑攻角非线性的阵风响应分析系统模型并进行时域仿真分析.
 |
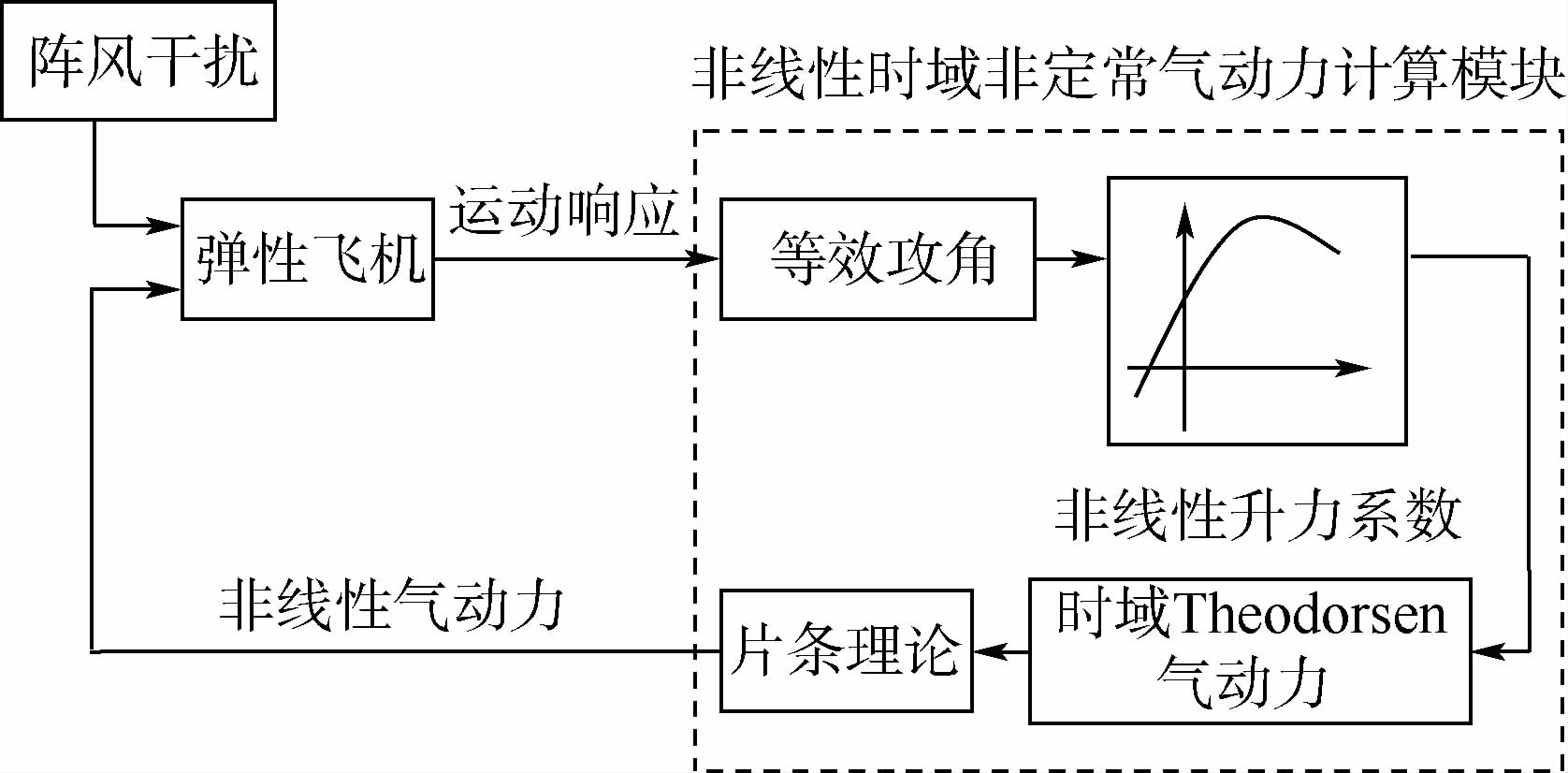| 图 3 考虑气动力非线性的柔性飞机阵风响应原理图Fig. 3 Schematic gust response diagram of flexible aircraft with aerodynamic nonlinearity |
| 图选项 |
3 算例及结果分析针对某大展弦比飞机模型,按照本文方法建立非线性阵风响应计算模型,并对其在1-cos型离散阵风作用下的响应进行仿真分析,考察飞机柔性、攻角非线性等因素对飞机不同部位阵风响应的影响规律.
3.1 模型描述图 4描述了某大展弦比飞机简化的有限元模型,该飞机的主要参数如表 1所示.全机共划分为26个气动片条,其中机翼21个片条,编号从左至右为1~21,尾翼5个片条,编号从左至右为22~26,片条均匀划分,宽度为3m.
 |
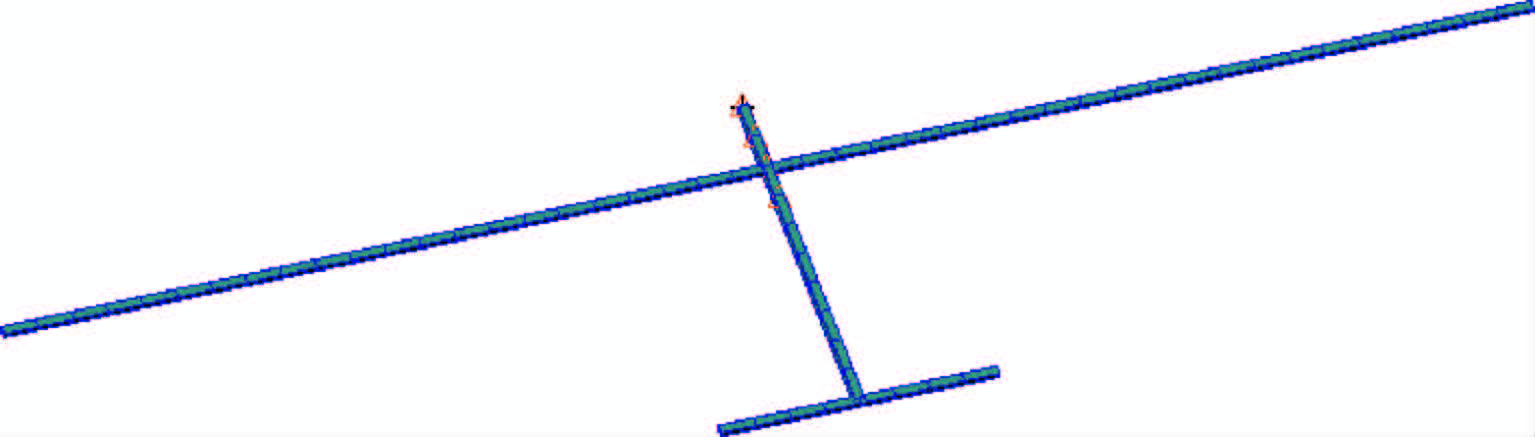| 图 4 大展弦比飞机有限元模型Fig. 4 Finite element model of high aspect ratio aircraft |
| 图选项 |
表 1 大展弦比飞机主要参数Table 1 Major parameters of high aspect ratio aircraft
| 参数 | 数值 | 参数 | 数值 |
| 全机质量/kg | 1738 | 翼展/m | 63 |
| x向质心/m | 4.966 | 弦长/m | 3 |
| 俯仰惯量/(kg·m2) | 3.24×104 | 展弦比 | 21 |
表选项
首先对该模型进行模态分析,结果表明机身及尾翼模态频率较高,与机翼相比刚度较大,可以认为其弹性阵风响应较小,因此本文分析中仅选取机翼的低阶弹性模态,而忽略机身及尾翼的弹性响应.图 5和图 6分别给出了机翼的对称一弯模态和对称二弯模态,模态频率分别为0.35Hz和1.92Hz.
 |
| 图 5 机翼一弯模态Fig. 5 First bending mode of wing |
| 图选项 |
 |
| 图 6 机翼二弯模态Fig. 6 Second bending mode of wing |
| 图选项 |
飞机飞行高度为6km,大气密度为0.652kg/m3,飞行速度为21m/s,定直平飞状态下配平攻角为3.8°.计算飞机在1-cos型离散阵风作用下的阵风响应,选取阵风速度幅值为7m/s,阵风尺度为25~100m.
3.2 弹性效应的影响首先研究弹性效应对飞机阵风响应的影响.图 7给出了阵风尺度为50m时机翼翼尖处瞬时攻角的对比结果,可以看出,刚体假设下翼尖瞬时攻角(Angle of Attack,AOA)峰值约为13.0°,在考虑弹性影响后,翼尖瞬时攻角峰值增加为13.8°左右.图 8给出了刚体假设和考虑弹性效应时,飞机翼尖处以及质心(Center of Gravity,CG)处附加过载的对比结果,可以看出考虑弹性效应后,质心处附加过载峰值变化较小,而机翼翼尖处的附加过载峰值则由3.1g(g为重力加速度)增加为4.8g,由于弹性效应引起的阵风附加过载较刚体情况增加约55%.针对不同阵风尺度的分析结果表明:对于大展弦比飞机,弹性效应对飞机的阵风响应有较大影响,一般将引起机翼翼尖处过载显著增加,影响趋势与国外相关理论研究及风洞试验结果相一致[3, 12, 13, 14].
 |
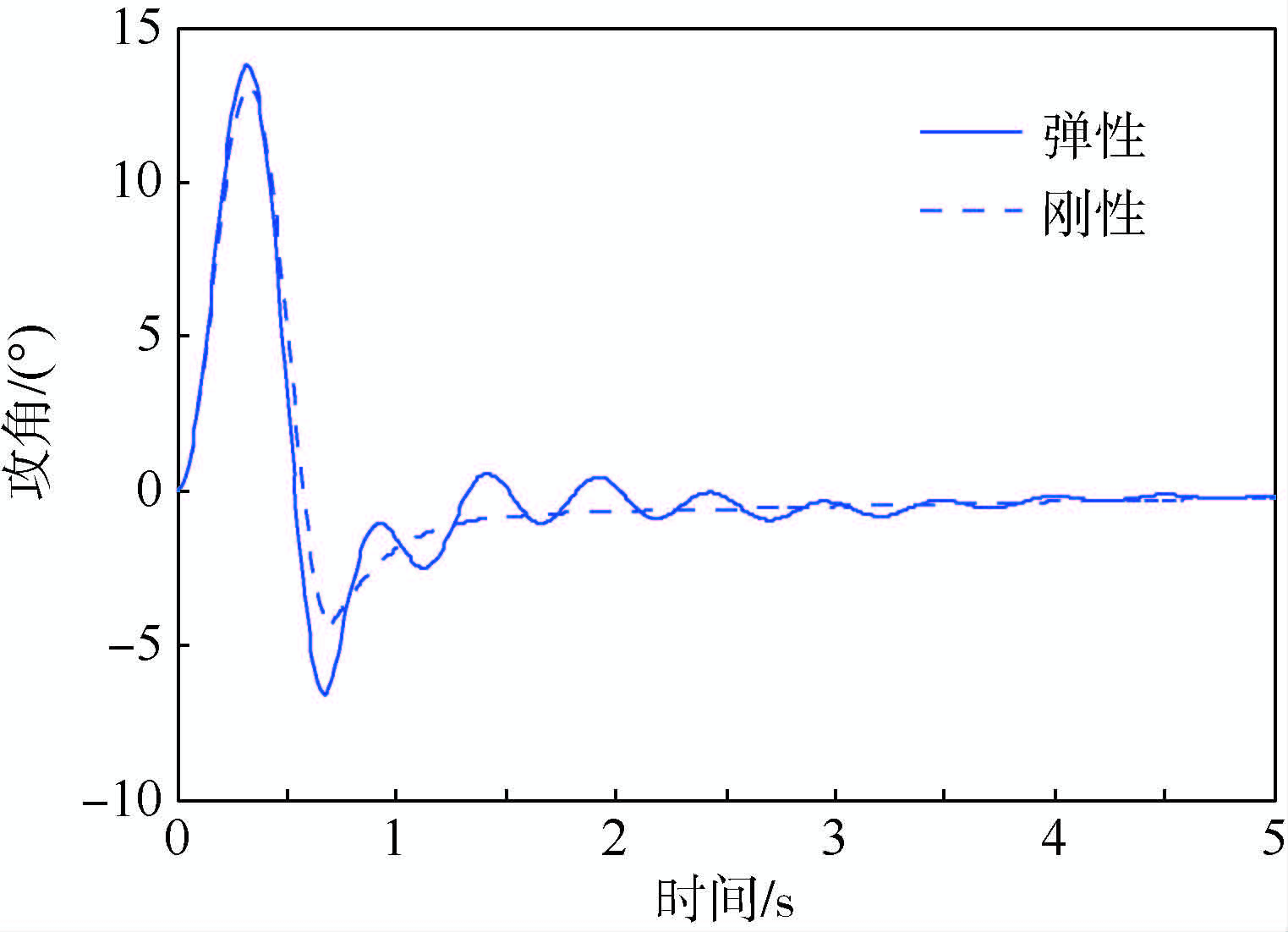| 图 7 刚性和弹性情况下翼尖的瞬时攻角对比Fig. 7 Comparison of transient AOA at wingtip between rigid and flexible cases |
| 图选项 |
 |
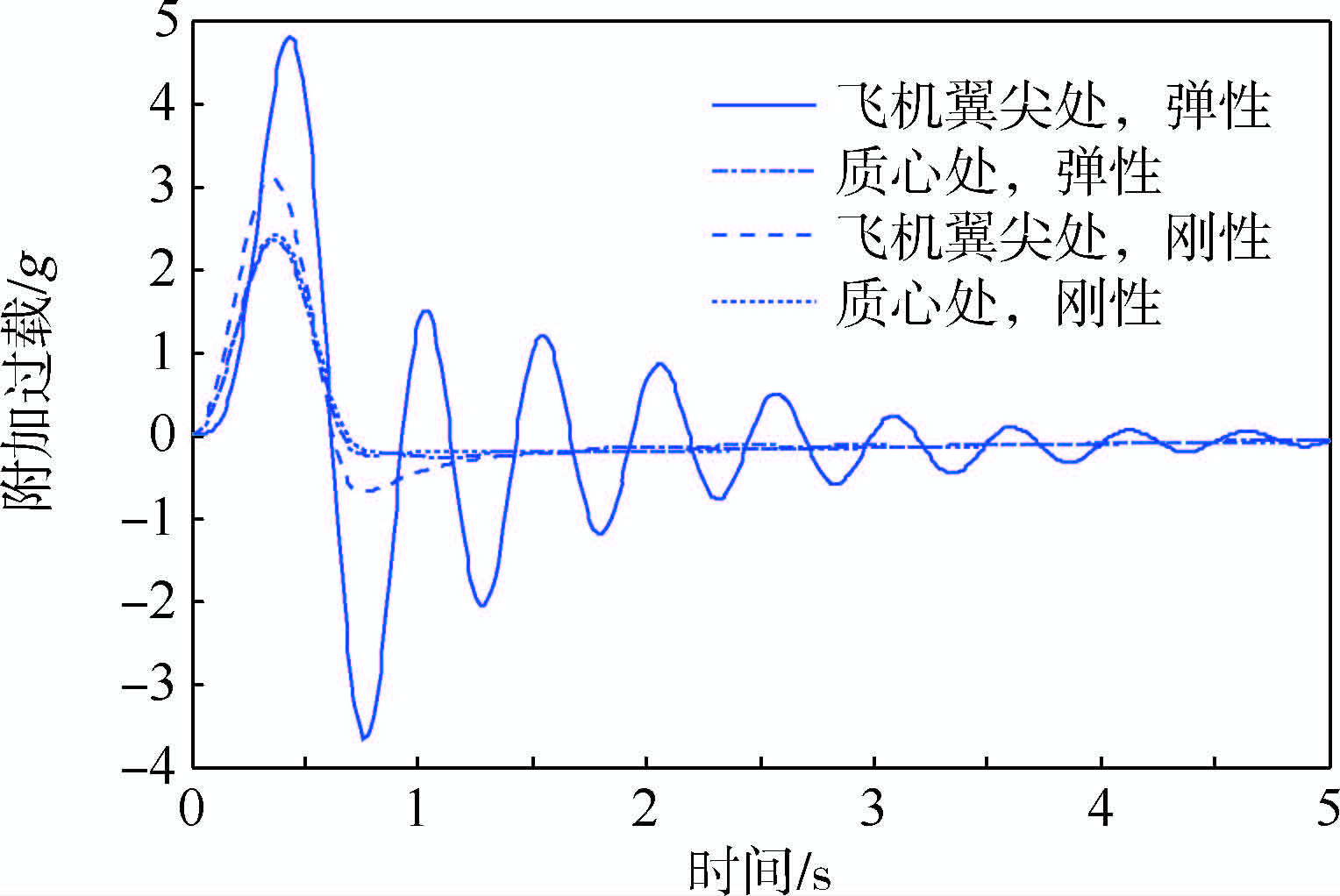| 图 8 刚性和弹性情况下附加过载对比Fig. 8 Comparison of gust additional induced load between rigid and flexible cases |
| 图选项 |
3.3 气动力非线性的影响本节研究攻角的非线性效应对弹性飞机阵风响应的影响.图 9给出了分析时所采用的线性和非线性的升力系数对比曲线,其中升力系数随攻角非线性变化的曲线代表了模型的大攻角失速特性.图 10给出了两种升力系数情况下,计算模型不同位置处瞬时攻角的对比曲线.图 11描述了攻角线性与非线性对飞机不同位置处附加过载的影响.由图 11可知,考虑攻角非线性的影响后,质心处附加过载峰值由原来的2.72g减小为2.16g,翼尖处的附加过载峰值由3.15g减小为2.91g.针对不同阵风尺度的分析结果表明:考虑攻角非线性效应,对飞机各部位的阵风附加过载均有一定的卸载作用,对结构设计有利.
 |
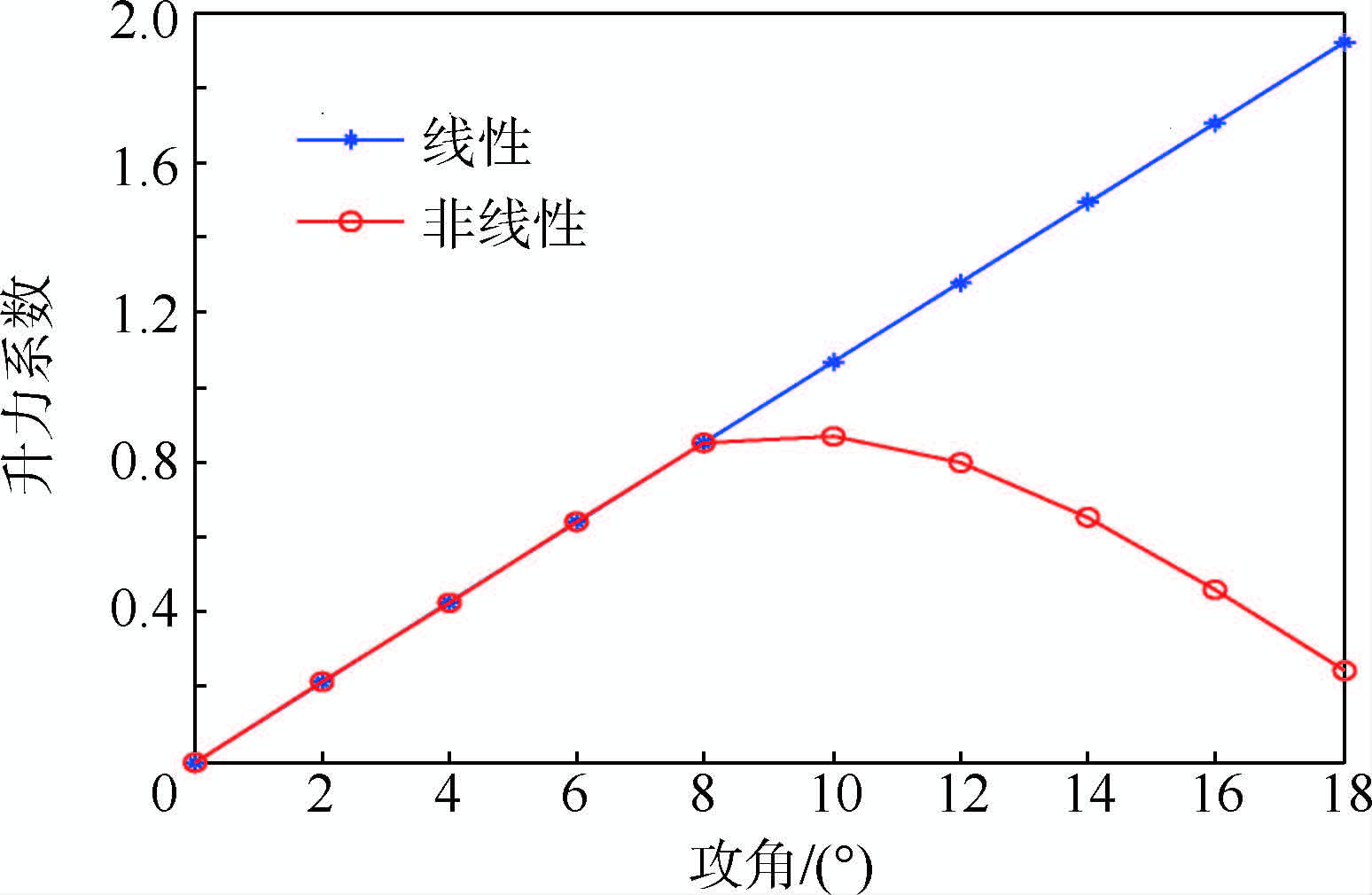| 图 9 线性和非线性情况下升力系数对比Fig. 9 Lift coefficient comparison of linear and nonlinear cases |
| 图选项 |
 |
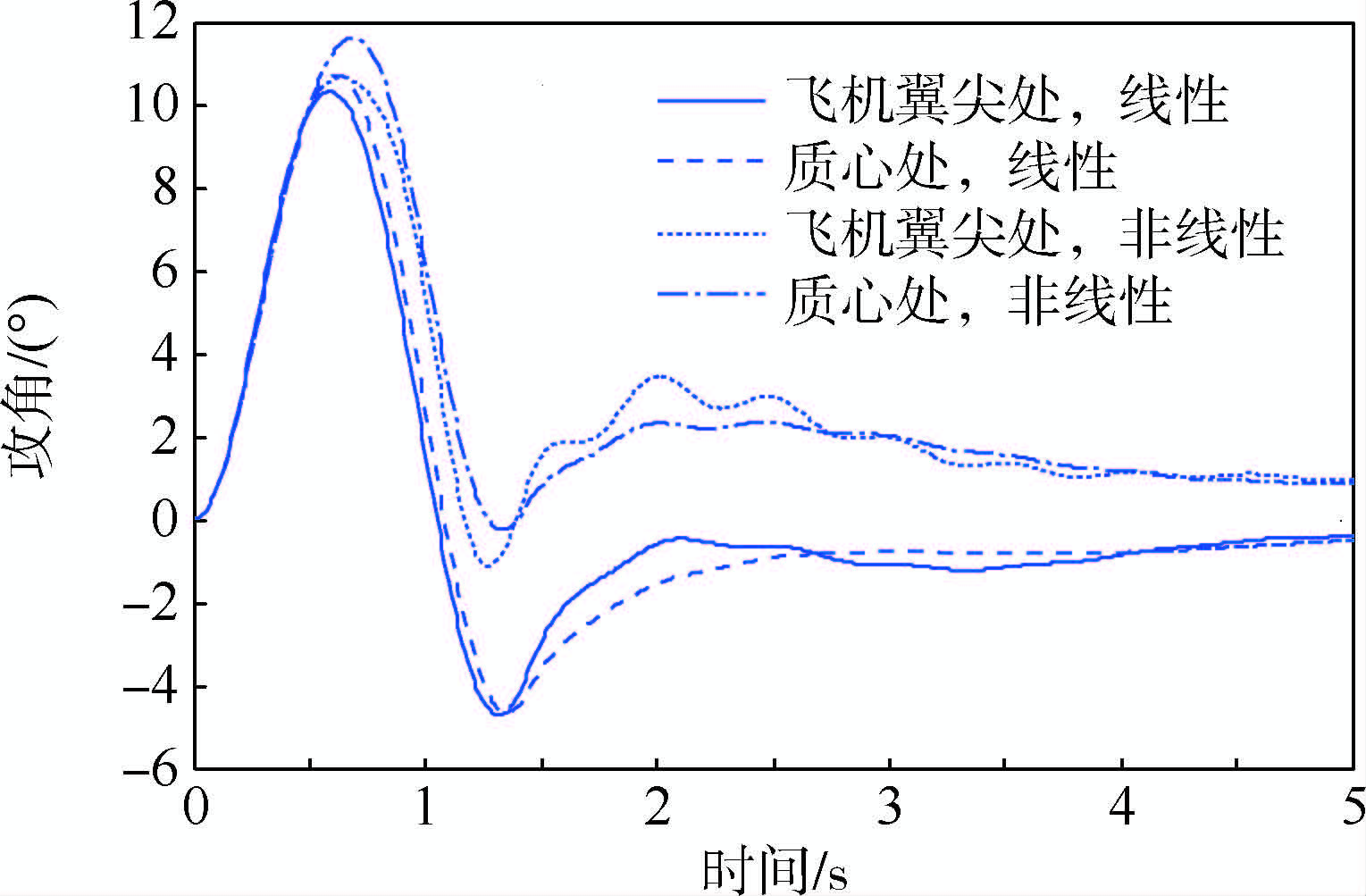| 图 10 线性与非线性情况下瞬时攻角对比Fig. 10 AOA comparison of linear and nonlinear cases |
| 图选项 |
 |
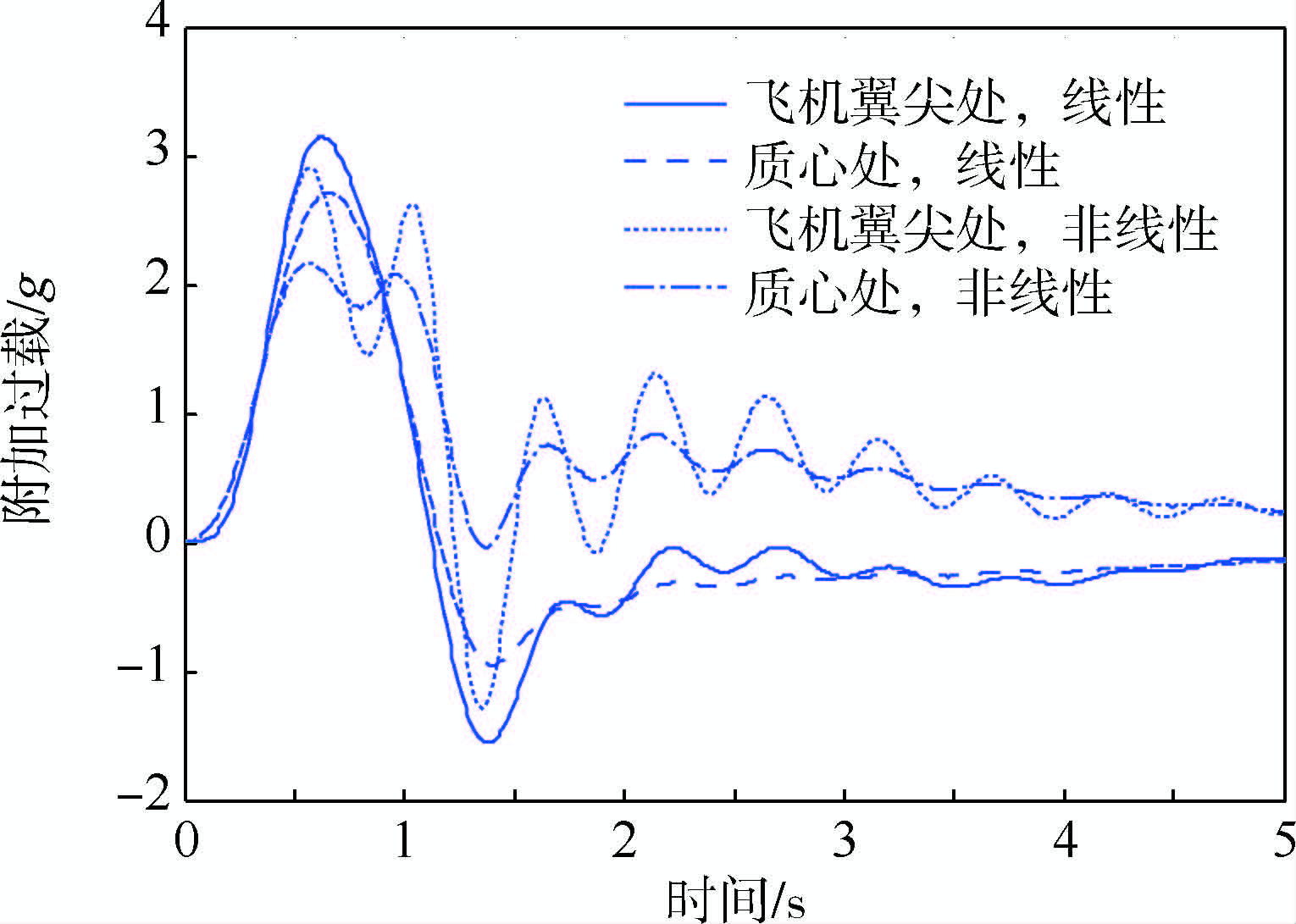| 图 11 线性与非线性情况下附加过载对比Fig. 11 Comparison of gust additional induced load between linear and nonlinear cases |
| 图选项 |
3.4 阵风尺度的影响阵风尺度是描述阵风干扰的重要参数,根据飞机强度规范要求,需要进行一系列阵风尺度下的阵风响应分析.图 12分别给出了在攻角线性和非线性两种情况下,质心和翼尖处的附加过载随阵风尺度的变化情况,由图可知,随着阵风尺度变大,翼尖及质心处的阵风附加过载均逐渐减小,攻角非线性效应对各部位过载均表现为卸载作用,在分析的阵风尺度范围内,由于攻角非线性效应引起的阵风附加过载降低最多可到41.7%.
 |
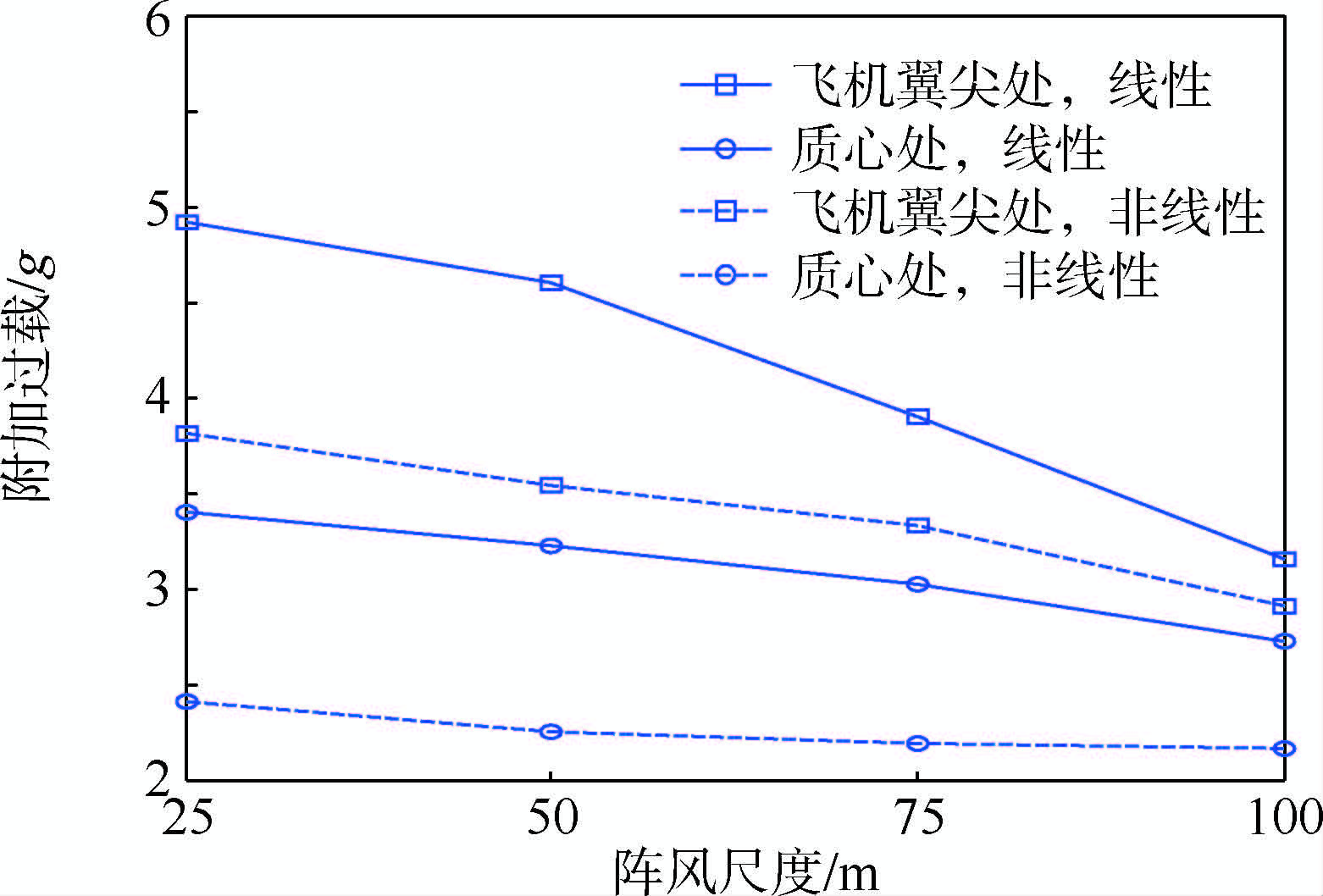| 图 12 不同阵风尺度下的附加过载对比Fig. 12 Comparison of gust additional induced load under various gust scales |
| 图选项 |
4 结 论本文针对大展弦比柔性飞机,考虑大攻角情况下的气动力非线性效应,通过将修正的Theodorsen气动力理论与片条理论相结合,计算得到非线性的时域非定常气动力;在此基础上,建立阵风干扰下的大展弦比柔性飞机气动弹性仿真模型,发展了一种可考虑攻角非线性影响的大展弦比柔性飞机阵风响应分析方法.根据本文算例结果可得出如下结论:
1) 对于大展弦比飞机,弹性效应对其阵风响应分析结果影响显著,不可忽略.
2) 气动力的大攻角非线性特性对飞机不同位置处的附加过载均有较明显的影响,一般表现为卸载作用.
3) 不同阵风尺度对大展弦比柔性飞机的阵风响应结果有一定影响,随着阵风尺度增加,阵风响应减小.
参考文献
| [1] | Tang D, Dowell E H.Experimental and theoretical study of gust response for high-aspect-ratio wing[J].AIAA Joural, 2002, 40(3): 419-429. |
| Click to display the text | |
| [2] | Tang D, Grasch A.Gust response for flexibly suspended high-aspect ratio wings[J].AIAA Journal, 2010, 48(10): 2430-2444. |
| Click to display the text | |
| [3] | Patil M J, Taylor D J.Gust response of highly flexible aircraft[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Reston: AIAA, 2006, 1: 456-468. |
| [4] | Su W H, Cesnik C E S.Nonlinear aeroelasticity of a very flexible blended-wing-body aircraft[J].Journal of Aircraft, 2010, 47(5): 1539-1553. |
| Click to display the text | |
| [5] | Ricciardi A P, Patil M J.Evaluation of quasi-static gust loads certification methods for high-altitude long-Endurance aircraft[J].Journal of Aircraft, 2013, 50(2): 457-468. |
| Click to display the text | |
| [6] | 高洁, 王立新, 周堃. 大展弦比飞翼构型飞机阵风载荷减缓控制[J].北京航空航天大学学报, 2008, 34(9): 1076-1079. Gao J, Wang L X, Zhou K.Gust load alleviation control of aircraft with large ratio flying wing configuration[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(9): 1076-1079(in Chinese). |
| Click to display the text | |
| [7] | 陈磊. 弹性飞机阵风减缓控制与风洞试验方法研究[D].北京: 北京航空航天大学, 2011. Chen L.Studies on flexible aircraft gust alleviation control and wind tunnel test[D].Beijing: Beijing University of Aeronautics and Astronautics, 2011(in Chinese). |
| Click to display the text | |
| [8] | 谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J].北京航空航天大学学报, 2003, 29(12): 1087-1090. Xie C C, Wu Z G, Yang C.Aeroelastic analysis of flexible large aspect ratio wing[J].Journal of Beijing University of Aeronautics and Astronautics, 29(12): 1087-1090(in Chinese). |
| Click to display the text | |
| [9] | 陈桂彬, 邹丛青, 杨超. 气动弹性设计基础[M].北京: 北京航空航天大学出版社, 2010: 65-73. Chen G B, Zou C Q, Yang C.Aeroelastic design basis[M].Beijing: Beihang University of Press, 2010: 65-73(in Chinese). |
| [10] | 赵永辉. 气动弹性力学与控制[M].北京: 科学出版社, 2007: 323-324. Zhao Y H.Aeroelasticity and control[M].Beijing: Science Press, 2007: 323-324(in Chinese). |
| [11] | 金长江, 肖业伦. 大气扰动中的飞行原理[M].北京: 国防工业出版社, 1992: 5-7. Jin C J, Xiao Y L.Flight theory in atmospheric disturbances[M].Beijing: National Defence Industry Press, 1992: 5-7(in Chinese). |
| [12] | Tang D, Dowell E H.Experimental and theoretical study of gust response for high-aspect-ratio wing[J].AIAA Journal, 2002, 40(3): 419-429. |
| Click to display the text | |
| [13] | Karpel M, Moulin B, Chen P C.Dynamic response of aeroservoelastic systems to gust excitation[J].Journal of Aircraft, 2005, 42(5): 1264-1272. |
| Click to display the text | |
| [14] | Azoulay D, Karpel M.Characterization of methods for computation of aeroservoelastic response to gust excitation[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Reston: AIAA, 2006, 6: 4138-4152. |
| Click to display the text |
