虚拟手术模拟的对象一般是三维软组织,研究者通常使用有限元法或质点弹簧法作为计算模型模拟变形,但有限元法计算量较大,不易满足实时性的要求,而质点弹簧法容易产生抖动,降低了系统的稳定性和真实性.位置动力学模型[1](position based dynamics)是一种模拟可变对象的新方法,这种方法最初用于模拟衣服、布料等二维对象,目前已被NVIDIA公司封装在物理引擎PhysX[2]中用于模拟三维对象.该方法的计算量远远小于有限元法,而真实性和可操作性比质点弹簧法要高.但该方法目前不支持拓扑结构改变的情况,因此还没有研究者在支持切割操作的虚拟手术系统中使用这种方法.
本文提出了一种采用位置动力学模型模拟三维软组织变形的方法.为了模拟切割操作,本文改进了原有的位置动力学模型,使其支持拓扑改变的情况.此外,实现了力反馈设备的应用,增加了切割过程中的触觉模拟,提高了手术过程仿真的真实性.
本文的创新点有:①软组织模拟一般使用质点弹簧模型或者有限元作为物理模型,目前没有使用位置动力学的例子,本文采用了这种方法并和其他物理模型进行了比较,结果说明采用的物理模型有更好的变形效果;②本文改进了位置动力学模型,使之适用于拓扑改变的情况;③本文完善了切割方法,一方面对四面体分裂方法进行了扩展,避免了切口边缘的裂缝问题,另一方面对四面体网格增加纹理信息,使其能产生细节丰富的切口.1 相关工作切割模拟在虚拟手术中非常关键,尽管前人进行了深入的研究,但切割模拟到目前为止仍然是一个很有挑战性的问题.文献[3]从物理模型角度将切割模拟划分为3类:
1) 基于有限元的方法.这种方法使用有限单元模拟组织内部的生物力学属性,易于并行处理,但计算量较大.Sela等在文献[4]中设计了一种使用不连续自由形态变形的切割算法,这种方法通过改变潜在几何的拓扑结构实现切割操作.文献[5]提出了一种基于混合模型的层次化切割算法,并已被应用在腹腔镜手术模拟器中.Sifakis等使用基于四面体网格的有限元方法模拟皮瓣修复手术[6].文献[7]提出的算法通过从多精度体数据图片中删除最精细体素来实现切割操作.Dick等提出了一种基于六面体的切割算法[8],这种算法使用多网格求解器计算变形.文献[9]提出了一种基于有限元的切割算法,并给出了相应的碰撞检测算法.
2) 基于几何规则的方法.这种方法使用几何原理模拟组织的物理属性,和有限元方法相比,这种方法计算速度快,但变形和切割真实性有所降低.文献[10]以表面模型描述软组织,并使用质点弹簧模型模拟变形,该方法利用解剖刀的深度信息产生切口和软组织的内部结构.Steinemann等设计了一种基于四面体网格的体模型切割算法[11],该方法通过定义一个切割平面来避免产生退化三角形,该算法应用于息肉切除手术模拟器中.文献[12]提出了一种基于三角网格的实时切割算法,并被应用在白内障切除手术中.文献[13]提出了一种基于表面模型的切割算法,该算法在处理切割时,能产生较少的拓扑改变.为了提高计算效率,该方法使用了层次化数据库来控制网格细分.
3) 无网格方法.这种方法适合处理大形变的情况,是有限元方法的一种扩展,但需要存储表面网格以表现切口信息.Steinemann等提出了一种基于无网格离散化变形场的切割算法[14],该方法使用可见性图来进行形状更新.Pietroni等提出了切割立方体来模拟切割操作[15].
保持物理性质的变形方法是虚拟手术的一个重要研究内容.和上述方法不同,本文使用了Müller等提出的位置动力学模型[1]作为物理模型.这种方法是一种基于几何的方法,和有限元方法与无网格方法相比计算量更小,和质点弹簧方法相比,提供了更好的稳定性,并且可以直接控制模型的位置,因此在游戏领域得到了广泛应用.最近,Macklin和Müller又将位置动力学模型应用到液体仿真[16].但到目前为止,位置动力学模型还不能直接应用到拓扑改变的情况下,而拓扑改变是切割模拟的关键内容.
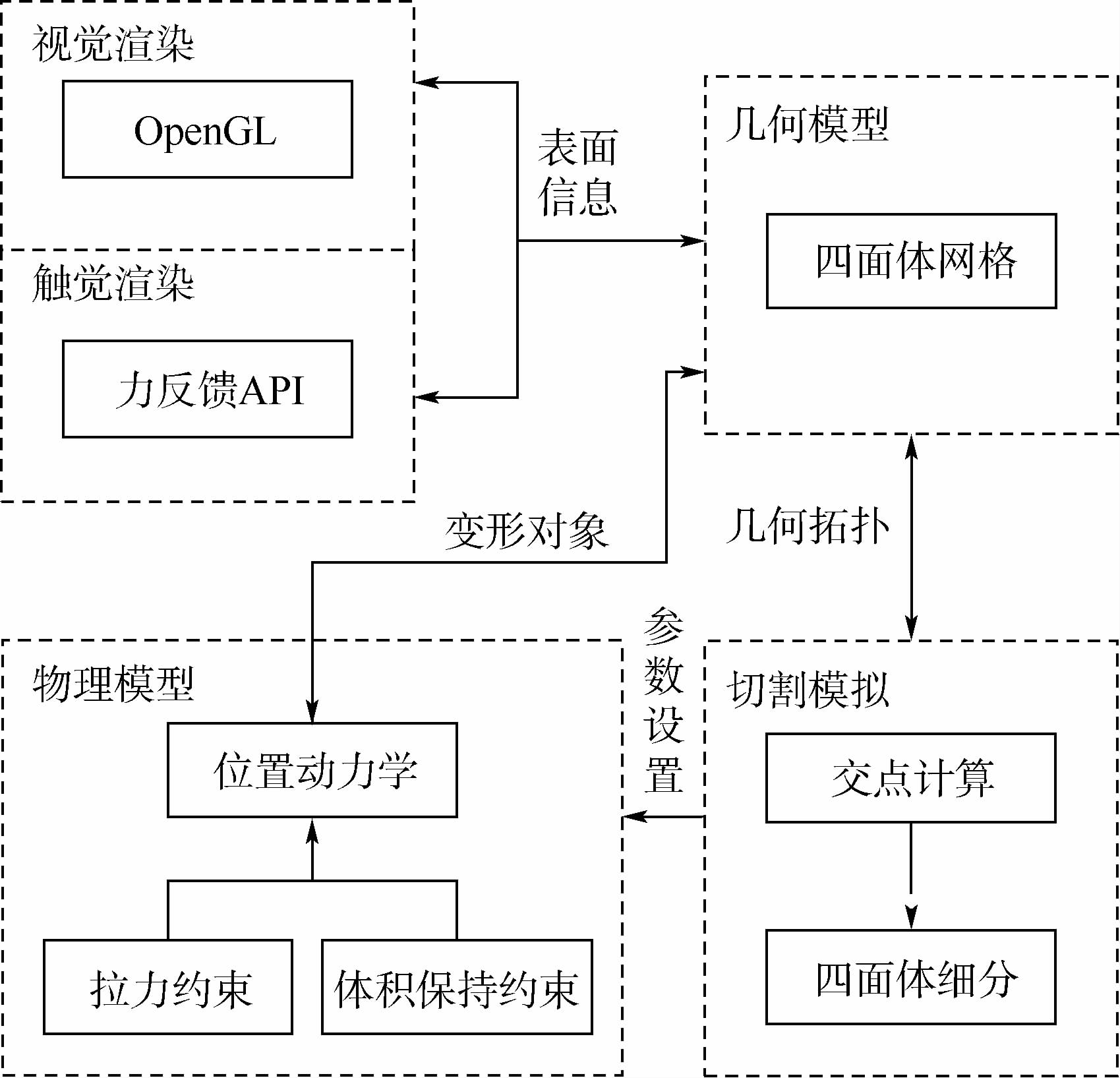
除了上文提到的文献外,有不少研究者开发了特定的虚拟手术模拟器.文献[17]设计了基于体绘制的训练模拟器,该模拟器可以模拟肺、肝等器官的切割手术.Paloc等设计了一种网格可实时合并的模拟器[18],该模拟器根据Delaunay准则对网格进行合并或分裂,从而提供合适的网格精度.文献[19]设计的模拟器支持肝脏切除手术、脑肿瘤切除手术.文献[20, 21]设计了基于PhysX的手术模拟器,分别支持腹腔镜胃束带手术和胆囊切除手术.2 框架概述本文的系统框架如图 1所示.
虚拟手术系统可分为几何模型、物理模型、切割模拟、视觉渲染和触觉渲染5部分.每部分的具体内容如下.
几何模型:软组织模型的组织方法.使用四面体网格表示软组织.四面体网格的凸包构成软组织的外表面,视觉渲染和触觉渲染只绘制外表面.
物理模型:物理形变的计算方法.以四面体网格为变形对象,使用位置动力学实现物理变形.不同于服装模拟,软组织模拟包含两种约束:拉力约束和体积保持约束.
切割模拟:包括交点计算和单元细分.切割时,要更新物理模型的约束条件和连接信息.
视觉渲染:以网格的外表面为渲染对象,使用OpenGL进行渲染.
触觉渲染:以网格的外表面为触觉对象,使用Geomagic Touch和OpenHaptics进行触觉模拟.当手术器械挤压软组织时,系统会产生相应的力反馈效果.
 |
| 图 1 手术模拟系统框架Fig. 1 System framework of surgery simulator |
| 图选项 |
几何模型和物理模型两部分实现软组织的变形.切割模拟需要计算四面体的交点,得到交点后一方面修改几何模型的拓扑结构,另一方面修改物理模型的设置参数.触觉渲染提供了系统的人机交互接口,该部分和几何模型形成力反馈,并为手术器械提供位置、方向、受力等信息.3 软组织对象的表示使用四面体网格表示软组织对象.使用四面体网格而不是表面三角网格的一个优点是四面体网格能够在物理仿真时描述变形对象的内部结构.
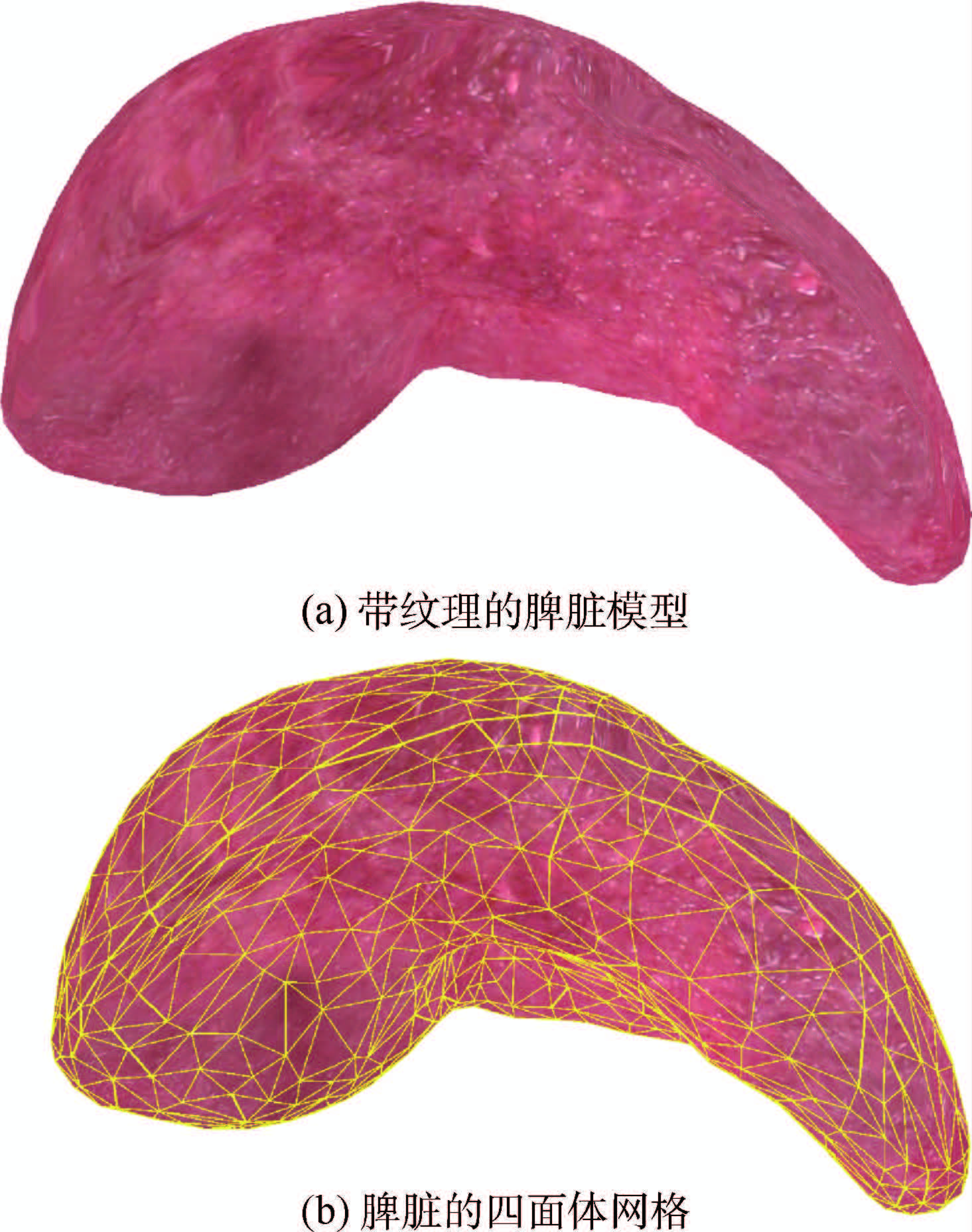
脾脏、肝脏的模型是从3dscience.com上购买得到的.模型是obj格式的表面三角网格,并不包含四面体网格.使用PhysX Viewer生成四面体网格,但该网格不包含纹理信息.
在初始化时,通过比较每个三角面片被共享的次数判断该面片是否为四面体网格外表面(共享次数为1的面片为网格的外表面).为了使四面体网格包含纹理信息,采用了如下的方法:遍历外表面上的每个顶点,寻找距离该顶点最近的三角网格顶点,并将三角网格顶点的纹理坐标赋值给四面体网格的顶点.四面体的内部网格一方面描述软组织的物理结构,另一方面在切割时形成切口.
图 2所示是使用四面体网格表示的脾脏模型.图 2 (a)渲染了带纹理的脾脏模型,图 2 (b)渲染了脾脏模型的纹理和四面体网格.
 |
| 图 2 使用四面体网格表示脾脏Fig. 2 Spleen using tetrahedral mesh |
| 图选项 |
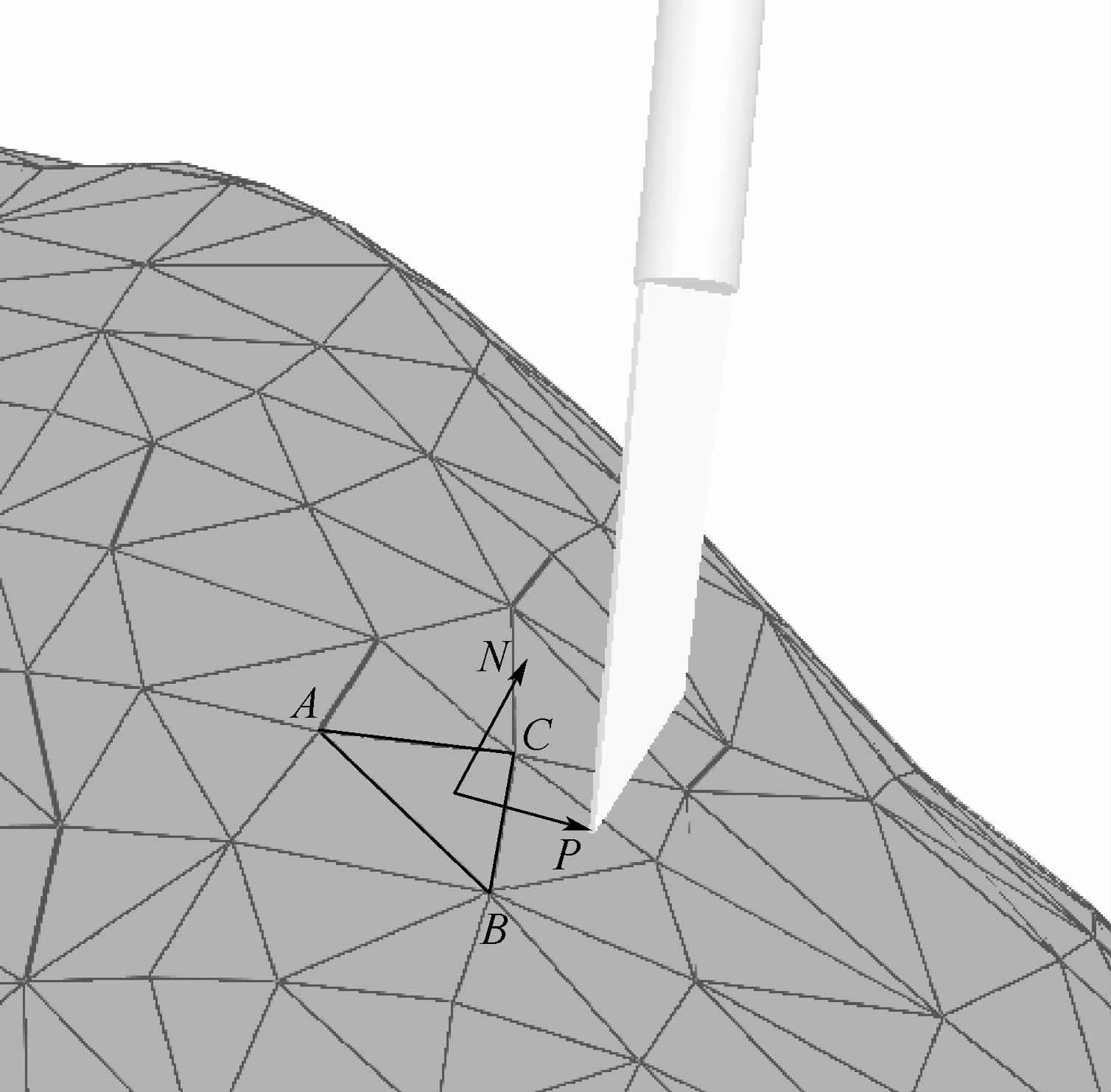
4 物理仿真4.1 碰撞检测碰撞检测用于判断解剖刀是否和软组织接触.设计了一种基于点的方法.方法如图 3所示,其中P是解剖刀的刀尖,三角形面片ABC是距离P最近的四面体凸包上的面片,O是ABC的重心,ON是ABC的法向.判断解剖刀和软组织是否接触,只需判断P是否和最近三角形面片接触.最近三角形ABC是按照下面的方法搜索的:
1) 搜索点P为内部投影点的三角形,计算点P到每个三角形平面的欧式距离.
2) 对全部距离进行排序,选择具有最短欧式距离的三角形作为最近三角形.
找到最近三角形面片ABC后,用下面的方法判断解剖刀刀尖是否和三角形接触.

如果式(1)成立,则OP与ON的夹角大于90°,解剖刀穿过三角形面片ABC所在的平面,否则解剖刀没有穿过面片所在平面.
当解剖刀和网格相接触并开始移动时,算法记录接触点,并开始计算解剖刀与四面体网格边和面的交点.
 |
| 图 3 碰撞检测示意图Fig. 3 Illustration of collision detection |
| 图选项 |
4.2 位置动力学模型介绍位置动力学是一种直接由位置计算变形的启发式算法.在进行变形迭代时,不需要通过外力计算加速度,进而得到位置改变量.初始化时算法对模型施加几何约束,当模型中顶点的位置改变时,算法根据约束函数将每个点投影到合适的位置,从当前位置到下一位置的位置改变量可以用约束函数的梯度表示.其中,常用的几何约束包括:两个点的距离应保持不变、两个三角形面片的角度应保持不变、组成模型的每个四面体单元的体积应保持不变等.
每个约束可以表示成Cj(x1,x2,…,xn)=0的形式,j为约束的序号,xi为受约束点的位置,n为受该约束影响点的数量.对于每个点P和位置改变量ΔP,约束函数C(P+ΔP)可以展开为
式中:ΔP为点P位置改变量;ΔPC(P)为点P约束函数的梯度;O(|ΔP|2)为ΔP的二阶无穷小.
为了保证动量守恒,限定ΔP和ΔPC(P)的方向相同,从而得到位置改变量为
式中:λ为拉格朗日乘子.
4.3 变形计算流程使用位置动力学主要有两个原因:①操作者可以直接控制模型的顶点位置;②位置动力学模型解决了质点弹簧模型不稳定的特点.上述两点使得位置动力学模型在虚拟手术中变得更加有吸引力[20].位置动力学模型的计算过程包含5步.
1) 初始化四面体每个顶点的位置Pi和速度Vi.
2) 在每个时间间隔Δt中,按照式(4)更新顶点的速度Vnewi:
式中:F为外力;wi=1/mi,mi为该顶点的质量;Damp(*)为阻尼函数.
然后预测顶点位置,如式(5)所示.
3) 以预测位置Pnewi为参数,遍历所有约束条件,并通过迭代方法求解动态系统,得到更新后的位置信息Psoli.
4) 按照式(6)和式(7)更新最终的位置Pfini和速度Vfini:
5) 开始下一时间间隔的计算,返回第2步,更新顶点的速度并预测位置.
位置动力学是一种基于几何的模拟方法,通过添加几何约束条件模拟物理变形现象.模拟软体变形时,考虑了两种约束条件:一种是拉力约束,另一种是体积保持约束.此外,式(3)可以细化为
式中:C(P1,P2,…,Pn)为以所有顶点位置为输入的约束函数;▽PiC(P1,P2,…,Pn)为函数关于顶点Pi的梯度.Müller在文献[1]中给出了拉力约束改变量的推导,本文在下面给出了体积保持约束改变量的推导.4.4 拉力约束拉力约束用于模拟两个点之间的拉力和弹力.当两个点的距离在外力作用下发生变化时,施加在这两个点上的拉力约束使其恢复到原始距离.图 4是两个点产生拉力约束的示意图,拉力约束的公式为
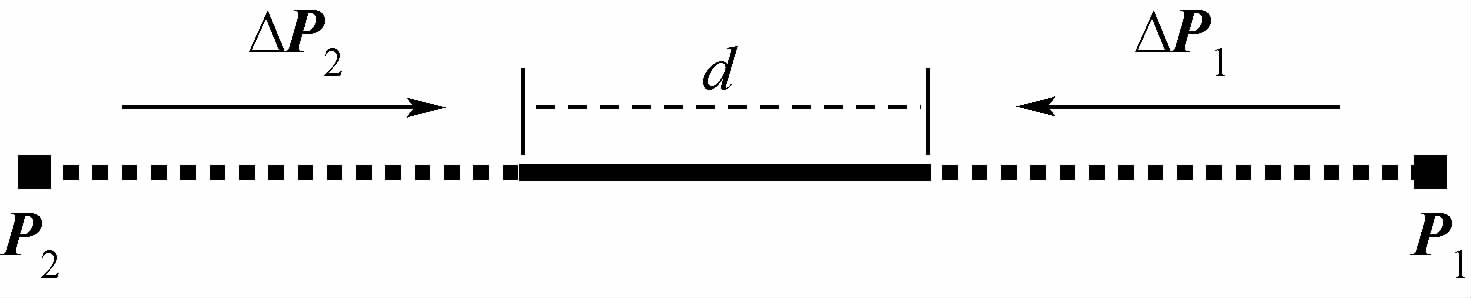 |
| 图 4 两个点的拉力约束Fig. 4 Stretching constraint between two vertices |
| 图选项 |
式中:d为P1和P2的静止距离.P1和P2的梯度分别为
式(11)~式(12)代入式(8),得到
4.5 体积保持约束体积保持约束用于保持四面体单元的体积不变,从而保持软组织的体积不变.图 5为体积保持约束的示意图.图 5 (a)为单个四面体的静止状态,当拖拽P4成图 5 (b)时,P4产生改变量ΔP4使其恢复为静止状态,其他顶点也产生对应的改变量.
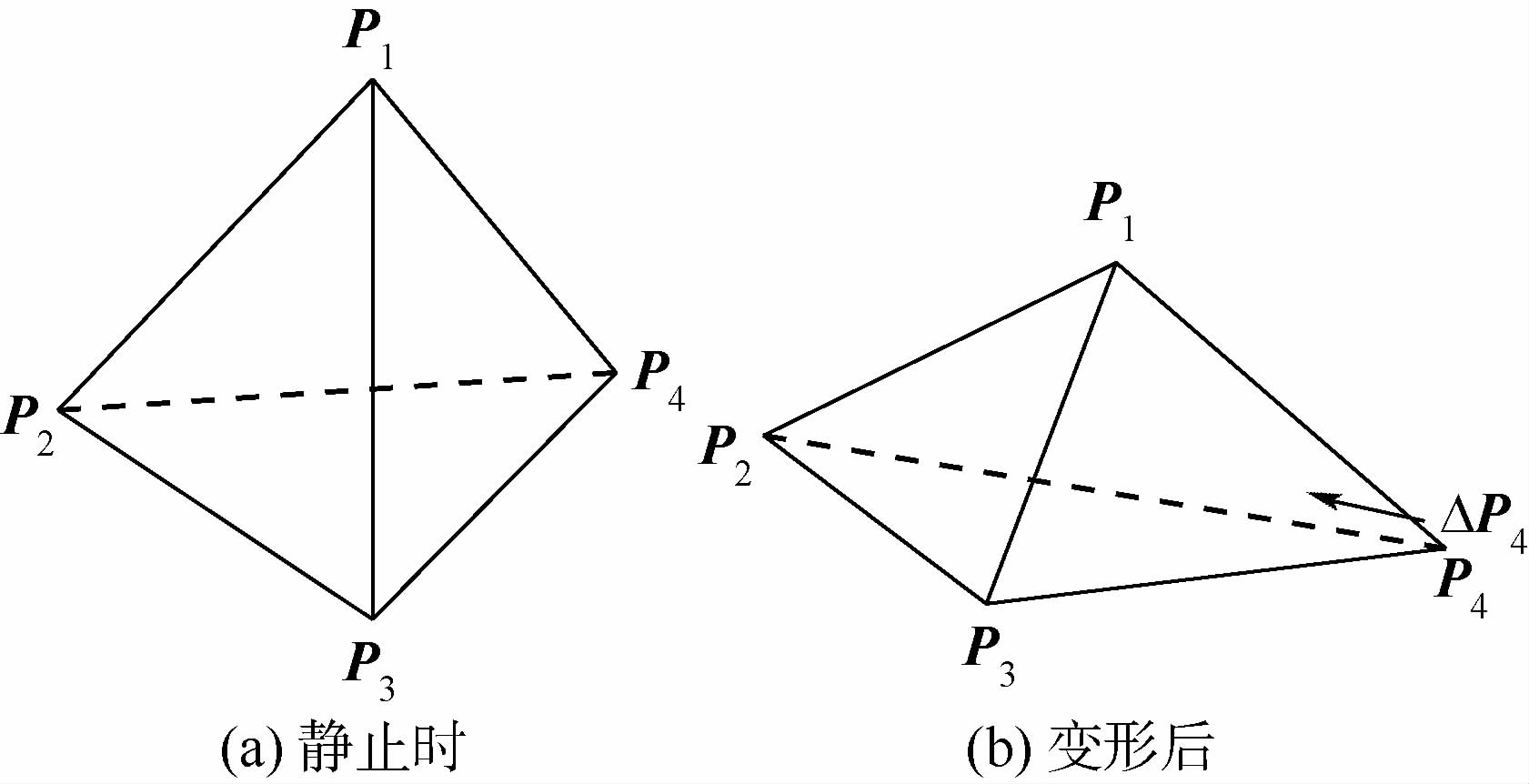 |
| 图 5 四面体的体积保持约束Fig. 5 Volume conservation constraint in a tetrahedron |
| 图选项 |
体积保持的约束函数为
式中:V0为四面体变形之前的静止体积.根据式(14),得到3个梯度:
由于∑iΔPiC=0,可以得到

代入到式(8)中,得到
5 交互式切割算法5.1 算法流程图图 6为一个时间间隔内的切割算法流程图.
5.2 四面体的渐进式切割分裂四面体网格时,解剖刀被抽象为一条只有长度没有厚度的直线段.每一时刻的刀尖位置和刀柄位置均被记录下来,相邻时刻的对应端点连接形成切割平面,算法使用切割平面计算解剖刀和四面体的交点.图 7表示的是时间间隔为Δt时的切割平面PtPt+1Qt+1Qt.使用4.1节的算法判断解剖刀是否和四面体网格接触.如果接触,开始计算四面体网格的所有边和面与解剖刀的交点.
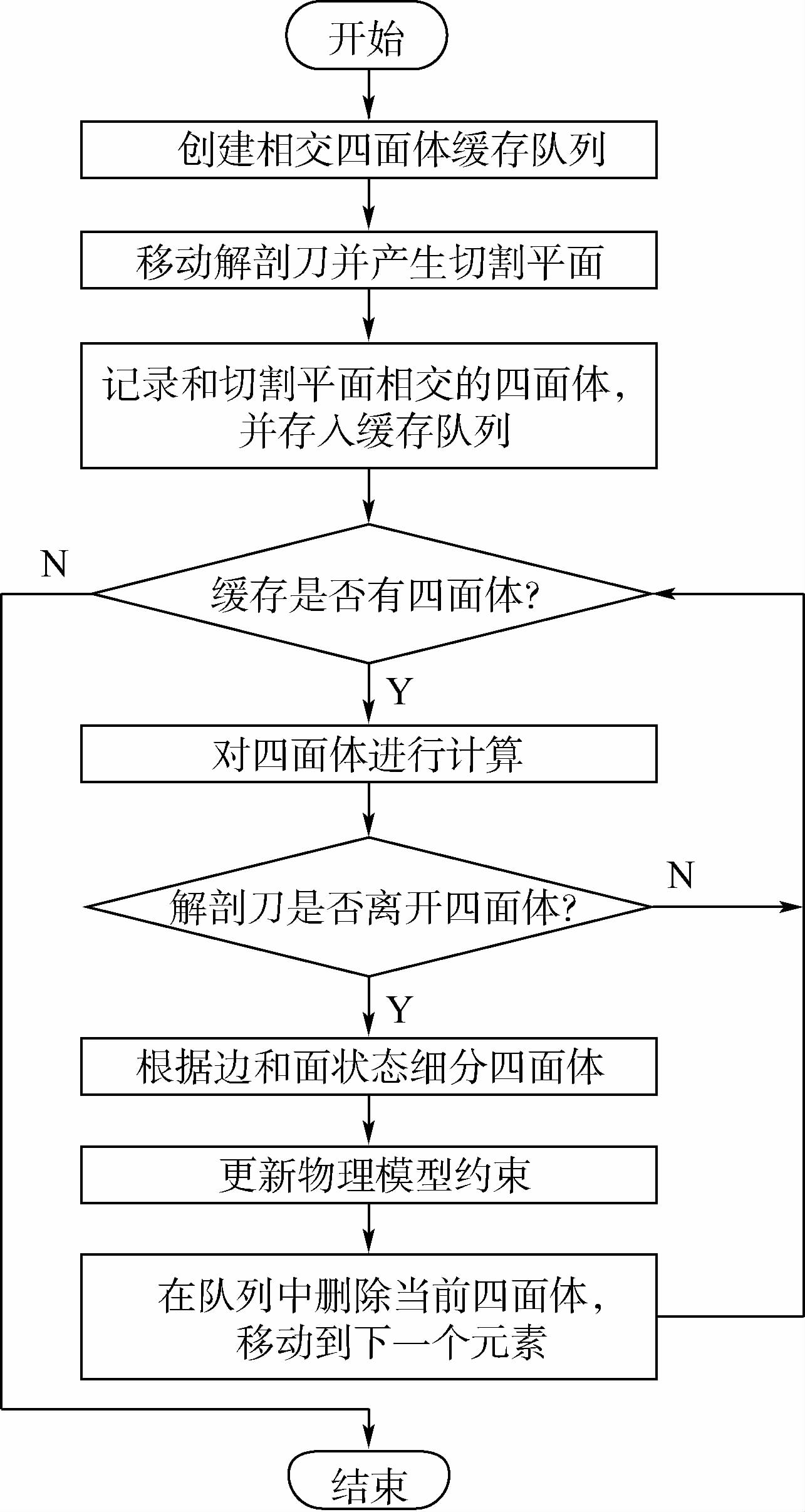 |
| 图 6 切割算法流程图Fig. 6 Flowchart of cutting algorithm |
| 图选项 |
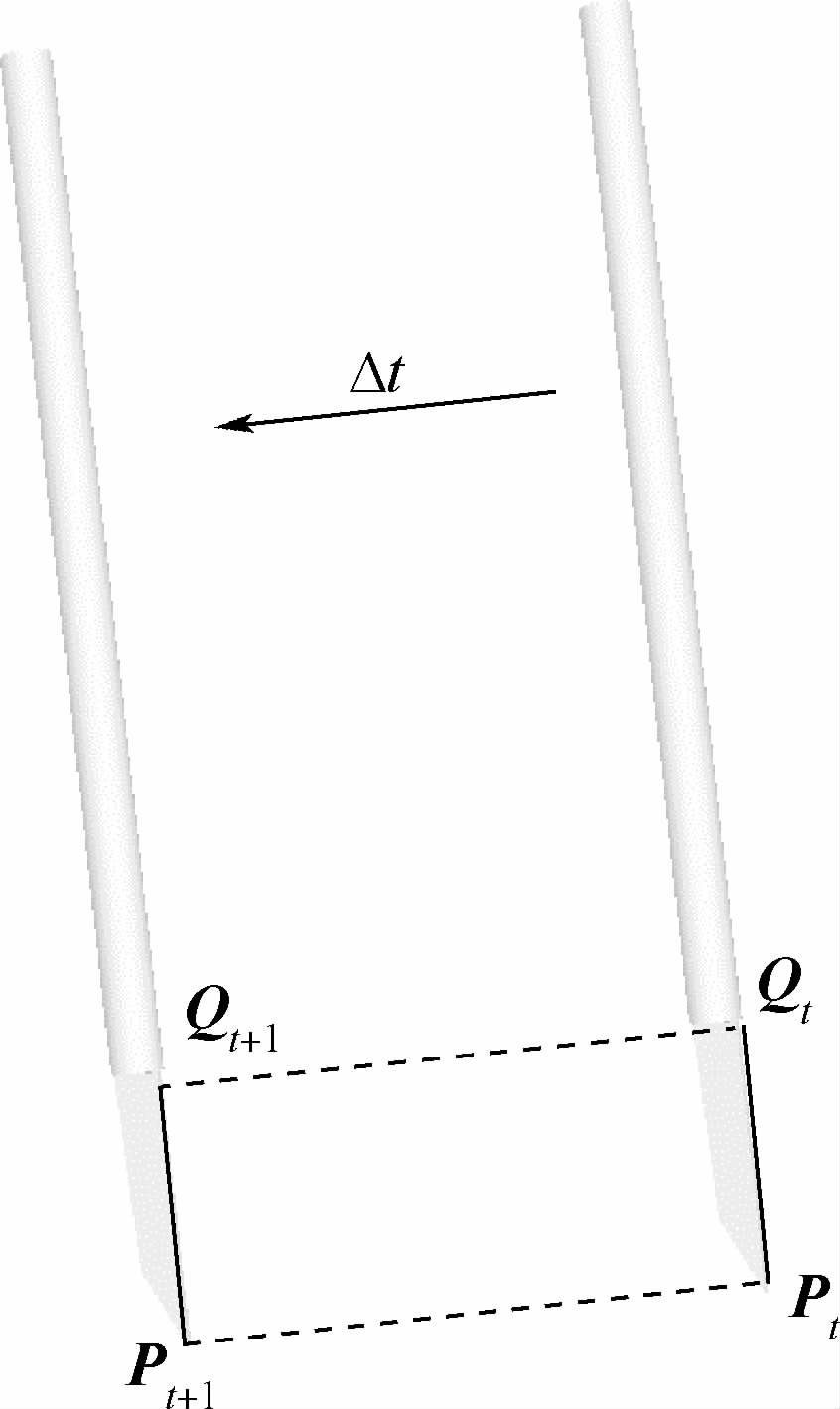 |
| 图 7 时间间隔为Δt时的切割平面Fig. 7 Sweep surface between time interval Δt |
| 图选项 |
计算交点时,需要计算出切割平面与四面体的边交点和面交点,算法将交点信息保存下来.四面体的边分裂状态和面分裂状态组成一张查找表,当解剖刀离开四面体时,算法按照查找表进行分裂,并更新和当前四面体有公共边或公共面的四面体.除了进行几何拓扑改变外,算法还需要更新物理模型的约束条件.当解剖刀离开表面网格时,四面体的切割过程也同时结束.
切割平面和单个四面体相交有5种情况,如图 8所示,细分的方法参考最少生成原则[22].
切割的首尾四面体可能会有不完全分裂的情况,为了避免软组织表面出现“T”型裂缝,又提出了3种分裂方式,如图 9所示.状态1时,解剖刀和四面体的一条边有交点.状态2时,解剖刀和四面体的两条边相交.状态3时,四面体的3条边V1V2,V1V3和V3V4和解剖刀相交于点E1、E2和E3,深色区域是形成的切口,分裂后的结果如图 10所示.
 |
| 图 8 四面体的普通分裂方法Fig. 8 General subdivisions for a tetrahedron |
| 图选项 |
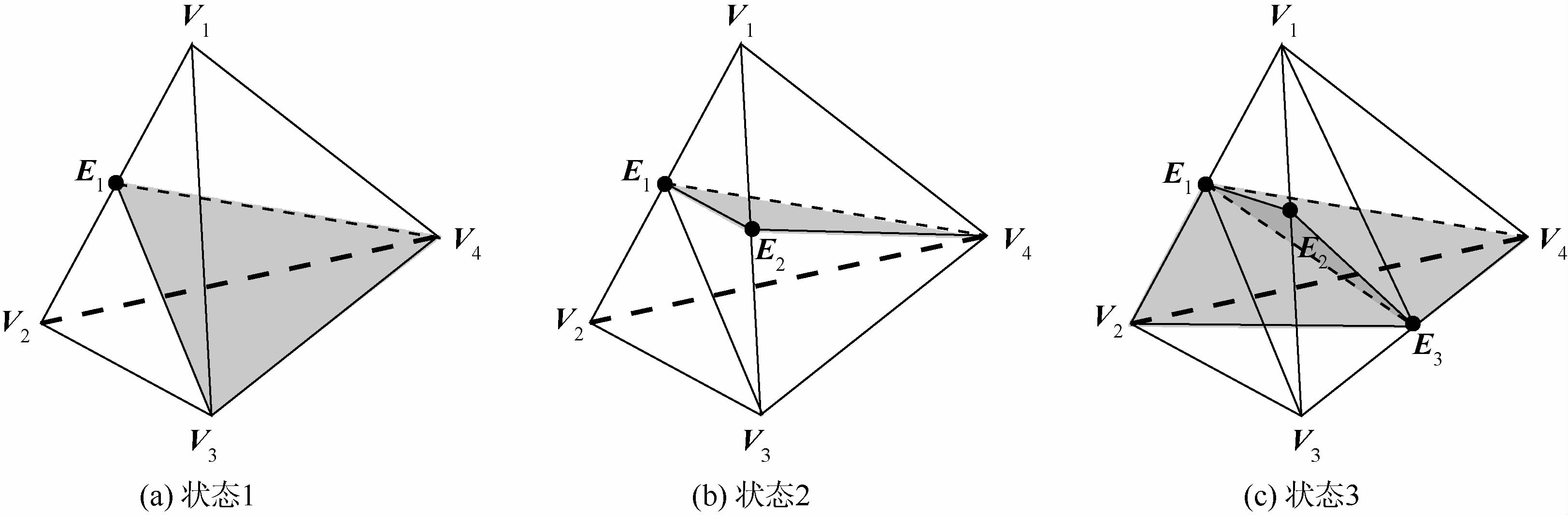 |
| 图 9 四面体的特殊分裂方法Fig. 9 Special subdivisions for a tetrahedron |
| 图选项 |
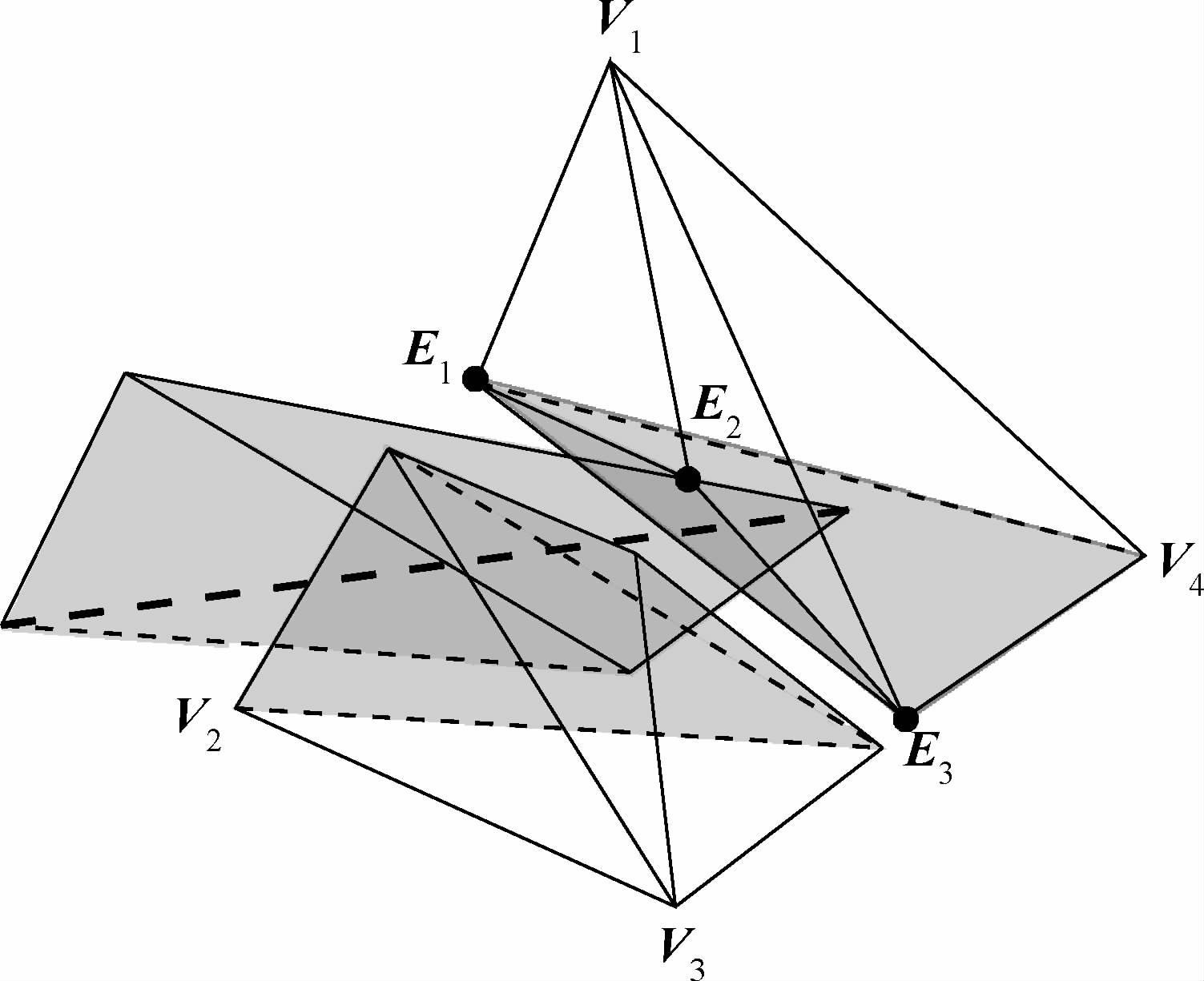 |
| 图 10 状态3特殊分裂后的结果Fig. 10 Special subdivision result for condition 3 |
| 图选项 |
当分裂结束后,内部网格沿着切割平面分离,被切割平面切开的四面体单元的内表面三角面片形成切口.由于四面体单元的体积比较大,在一次切割模拟时不会产生退化四面体,因此可以避免小四面体的合并.5.3 拓扑改变时的位置动力学切割操作会改变网格的原始拓扑,位置动力学模型并不支持拓扑改变的情况.因此,改进了原始的位置动力学模型.
切割发生时会生成子四面体,因此需要对原有的约束进行更新:①删除被切割四面体的拉力约束和体积保持约束;②产生子四面体拉力约束和体积保持约束.
子四面体的拉力约束需要获得子边的静止距离.边交点产生子边的静止距离为
式中:dAP为顶点A到交点P的静止距离;lAP为顶点A到交点P的当前距离;lPB为交点P到顶点B的当前距离;d为线段AB的静止距离.
对于面交点P,以计算子边AP的静止距离dAP为例.首先计算P在三角形ABC内的重心坐标(λ1,λ2,λ3).然后计算静止时的情况,如图 11所示,射线AP与边相交于点D.
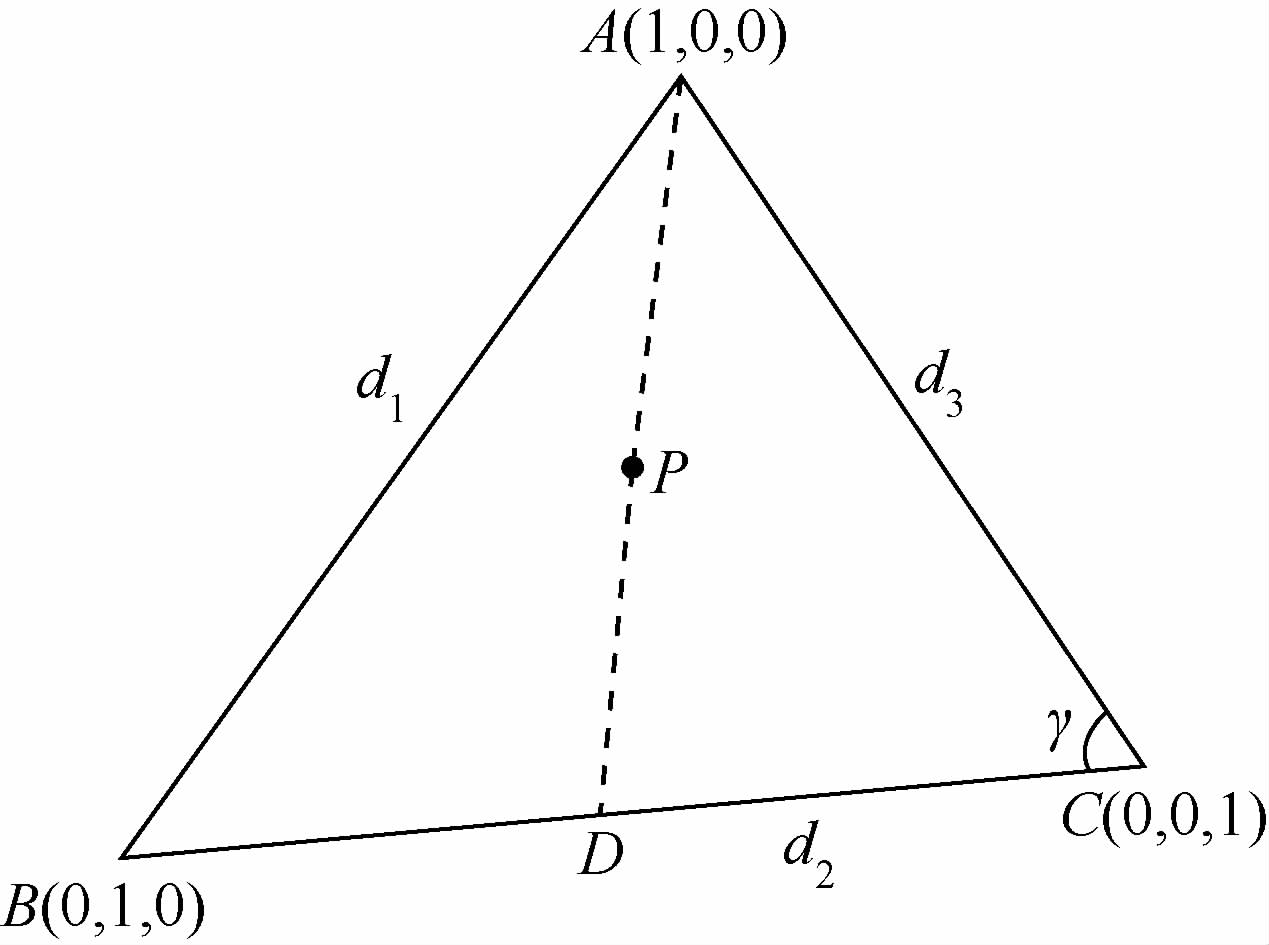 |
| 图 11 重心坐标示意图Fig. 11 Illustration of barycentric coordinates |
| 图选项 |
由余弦定理可知,夹角γ的余弦函数可表示为

式中:d1为AB边边长;d2为BC边边长;d3为AC边边长.
由重心坐标相关知识得到线段DC的长度为
将式(21)和式(22)代入余弦定理,可得到线段AD的长度为
线段AP的长度为
子四面体的体积保持约束需要计算子四面体的体积,根据4个顶点的位置直接计算获得.尽管子四面体的体积可能不是静止体积,但在变形程度不大的情况下,这种近似方法也可以模拟切割操作.6 触觉渲染触觉渲染可以使手术模拟器更接近真实手术环境.当力反馈设备的触笔在触觉空间中碰到物体时,设备会产生相应的接触效果.此外,可以对力反馈设备增加外设(剪式握柄、电刀式握柄),进一步提高真实性.
使用一台Geomagic Touch力反馈设备和OpenHaptics HLAPI进行触觉渲染.该设备具有6个自由度(x、y、z、roll angle、pitch angle、yaw angle),工作空间为16cm×12cm×7cm,3个轴的刚度分别为1.26,2.31,1.02N/mm.OpenHaptics使用双线程机制,一个主线程负责通用计算,另一个线程负责触觉渲染,因此可以保证1kHz的刷新率.
本文使用HLAPI提供的接口进行触觉渲染,因此作用力的计算不在本文的讨论范围.当解剖刀或抓钳挤压软组织时,设备会根据虎克定律产生反弹力,如果解剖器械在软组织表面移动时,设备会产生摩擦力.解剖刀和抓钳的位置可以通过设备获得.系统的设备和环境如图 12所示.
使用OpenHaptics时,需通过3步建立触觉渲染:
1) 初始化力反馈设备并创建上下文.
2) 定义触觉帧,并在触觉帧内指定软组织对象.
3) 指定对象的形状并渲染对象.
在渲染时需要注意,该接口认为按顺时针定义的面是正向面.
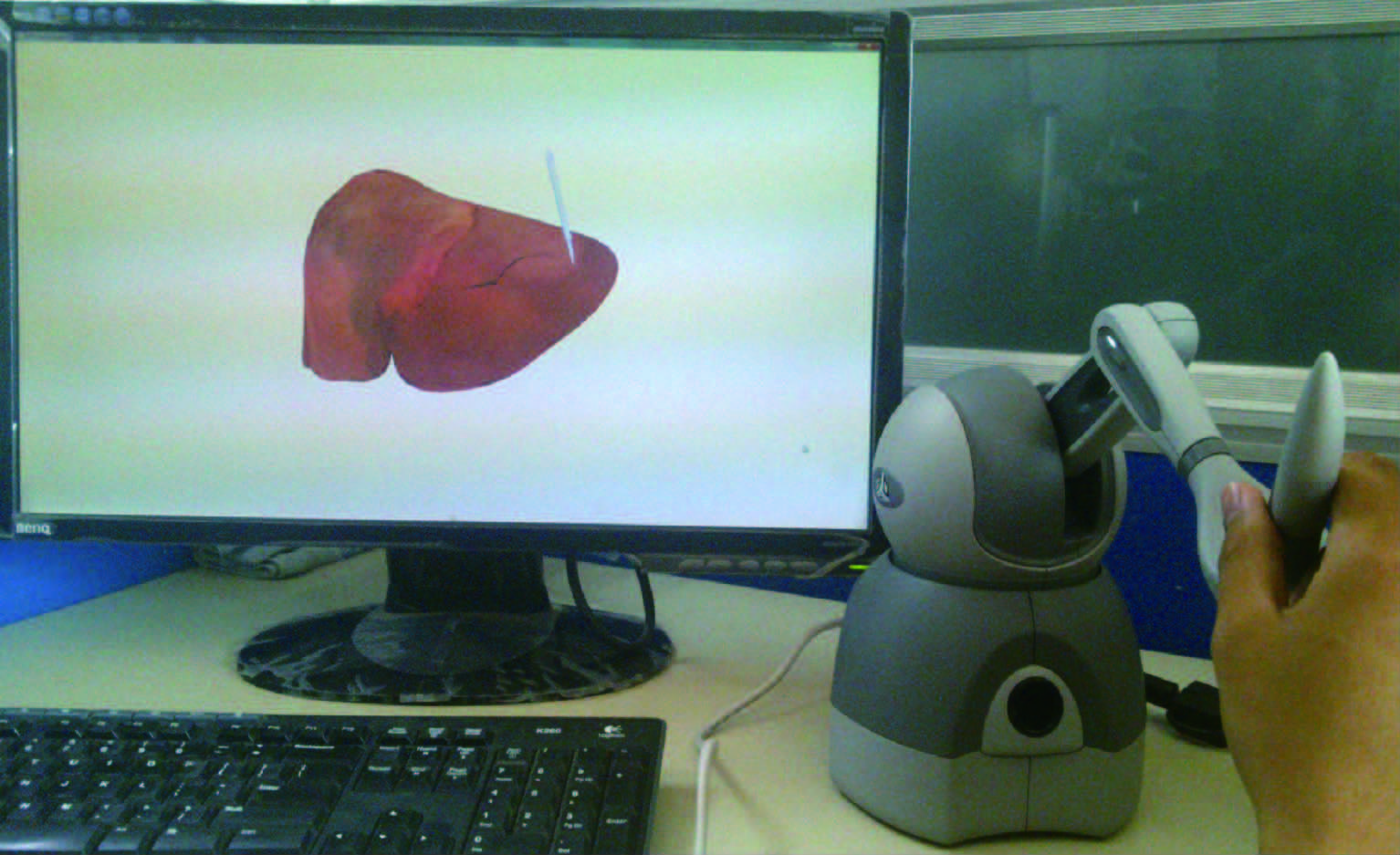 |
| 图 12 模拟系统的设备和环境Fig. 12 Environment and equipment of the simulator system |
| 图选项 |
7 实验结果和讨论系统使用C++、OpenGL、CUDA和OpenHaptics实现,实验平台为NVIDIA GeForce GTX 580、Intel(R) Xeon(R) CPU (2.53GHz,8核)和12GB RAM.进行了4组实验:脾脏、肝脏、手臂和马.手臂和马模型来自3dlinks.com.第1组是脾脏模型的实验,图 13是变形的实验结果,图 14和
 |
| 图 13 完整脾脏变形的模拟Fig. 13 Deformation of an integrated spleen model |
| 图选项 |
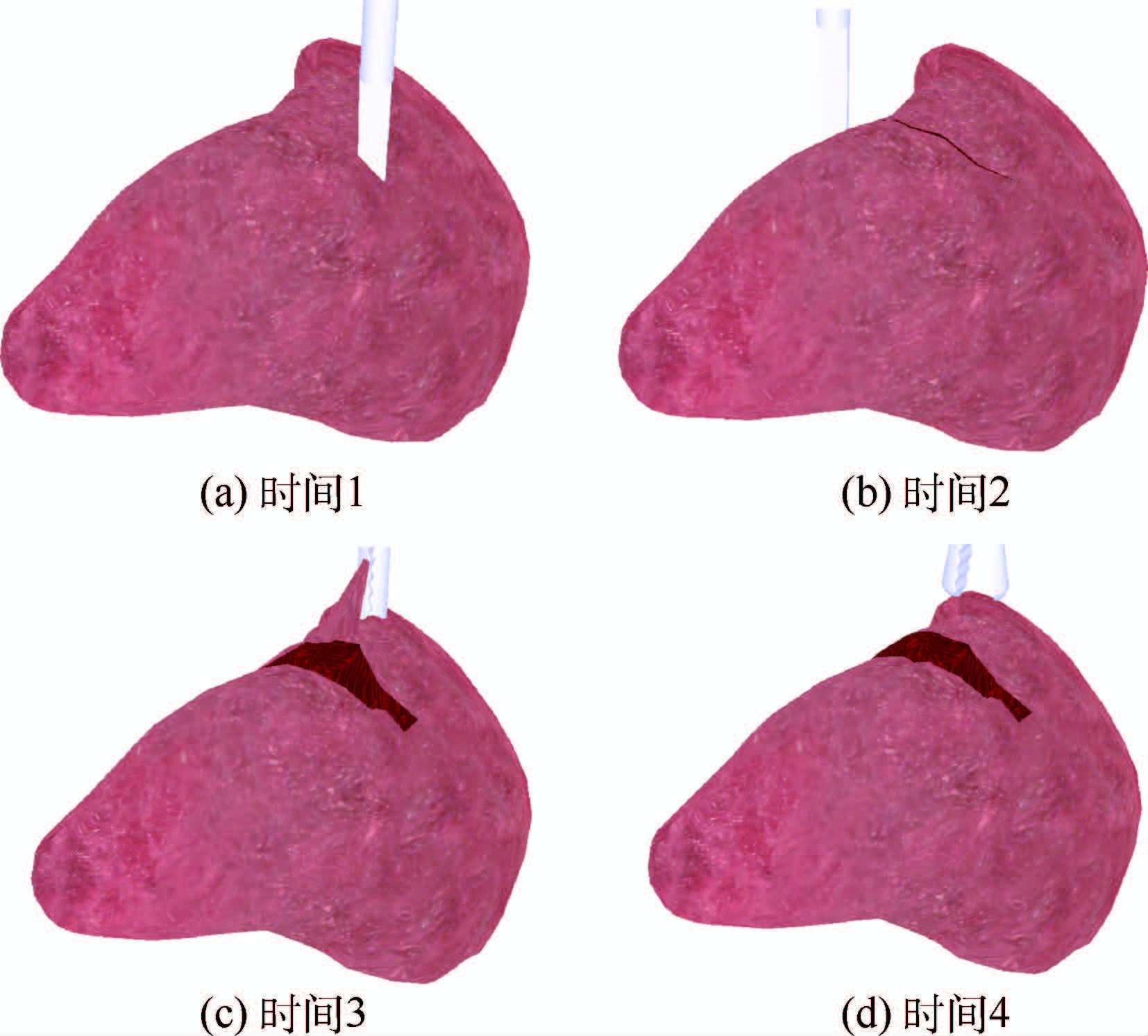 |
| 图 14 切割脾脏的模拟Fig. 14 Simulation of cutting a spleen model |
| 图选项 |
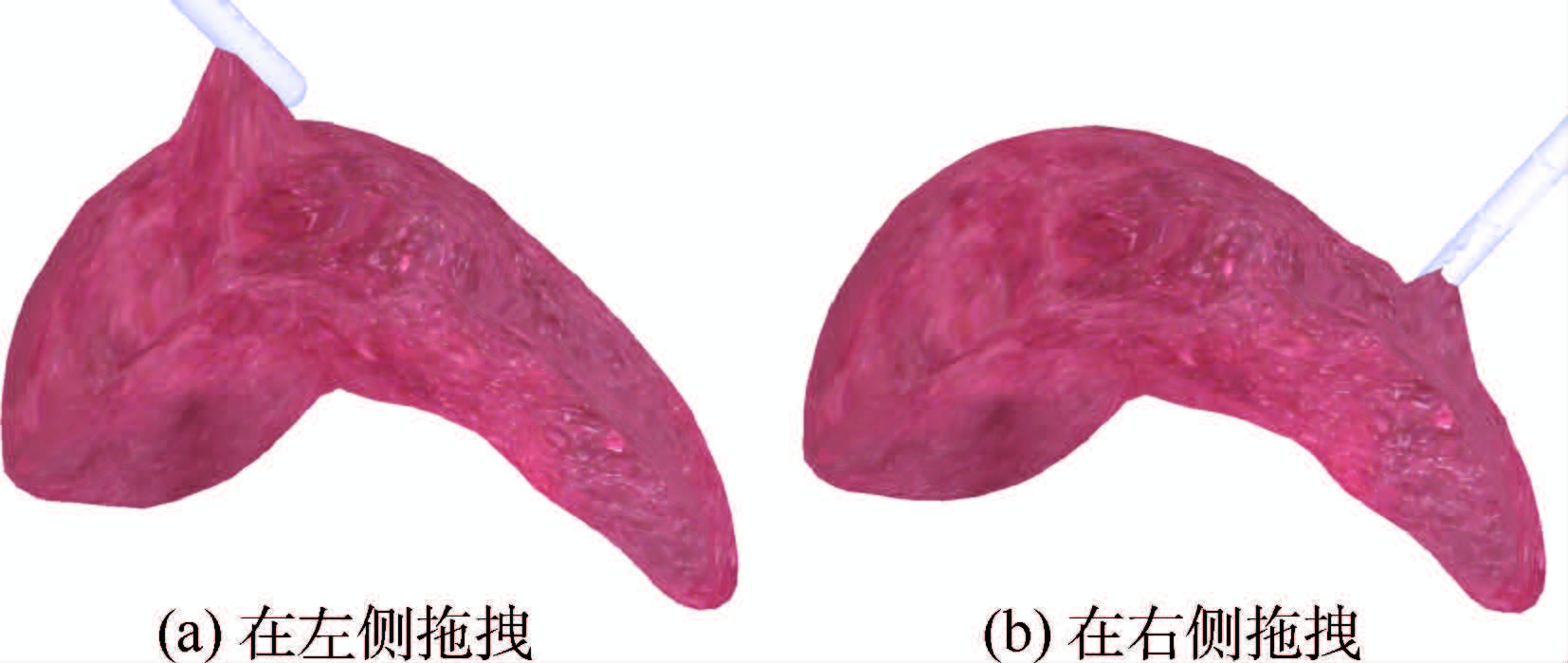
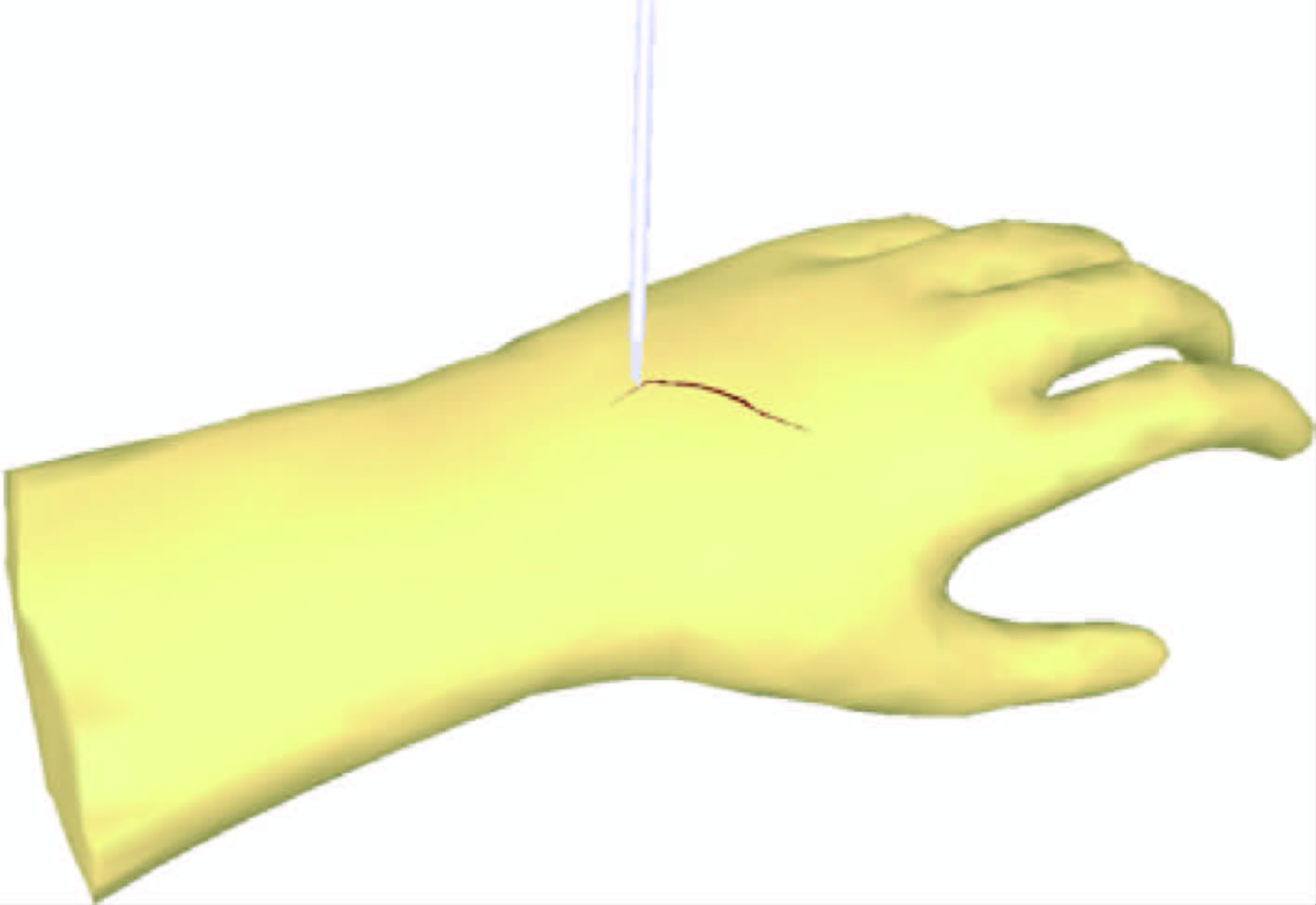
图 15是切割的实验结果.图 14模拟了在脾脏表面切开一个小口的情况,在重力的作用和相邻单元的约束下,切口开始出现.使用抓钳拖拽脾脏,可以看见生成的切口.图 15模拟了切断脾脏并拖拽的情况.第2组是肝脏模型的实验,实验结果如图 16和图 17所示.第3组是手臂模型的实验,实验结果如图 18所示.第4组是马模型的实验,实验结果如图 19所示.
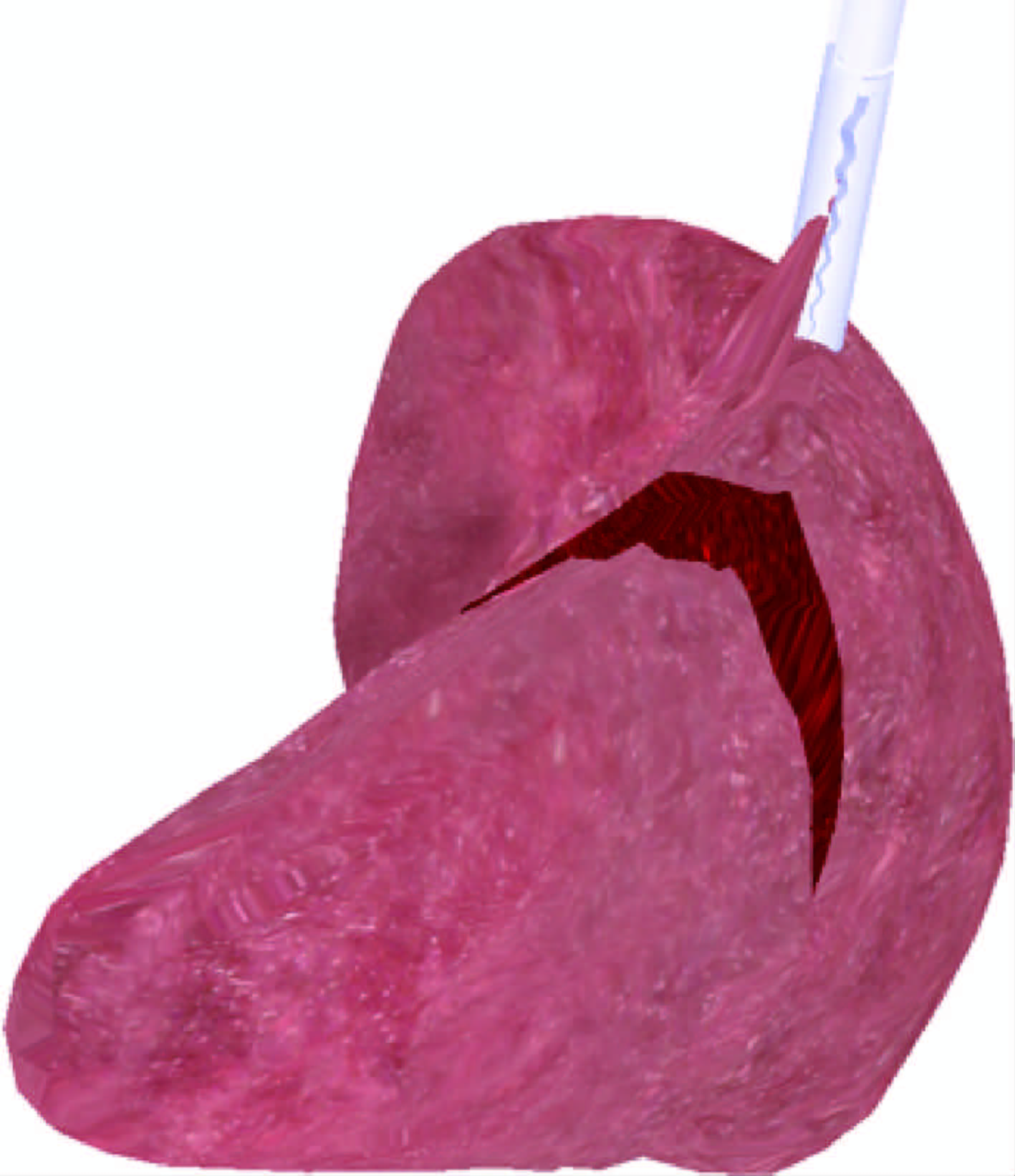 |
| 图 15 切断脾脏后的变形模拟Fig. 15 Deformation after cutting spleen model |
| 图选项 |
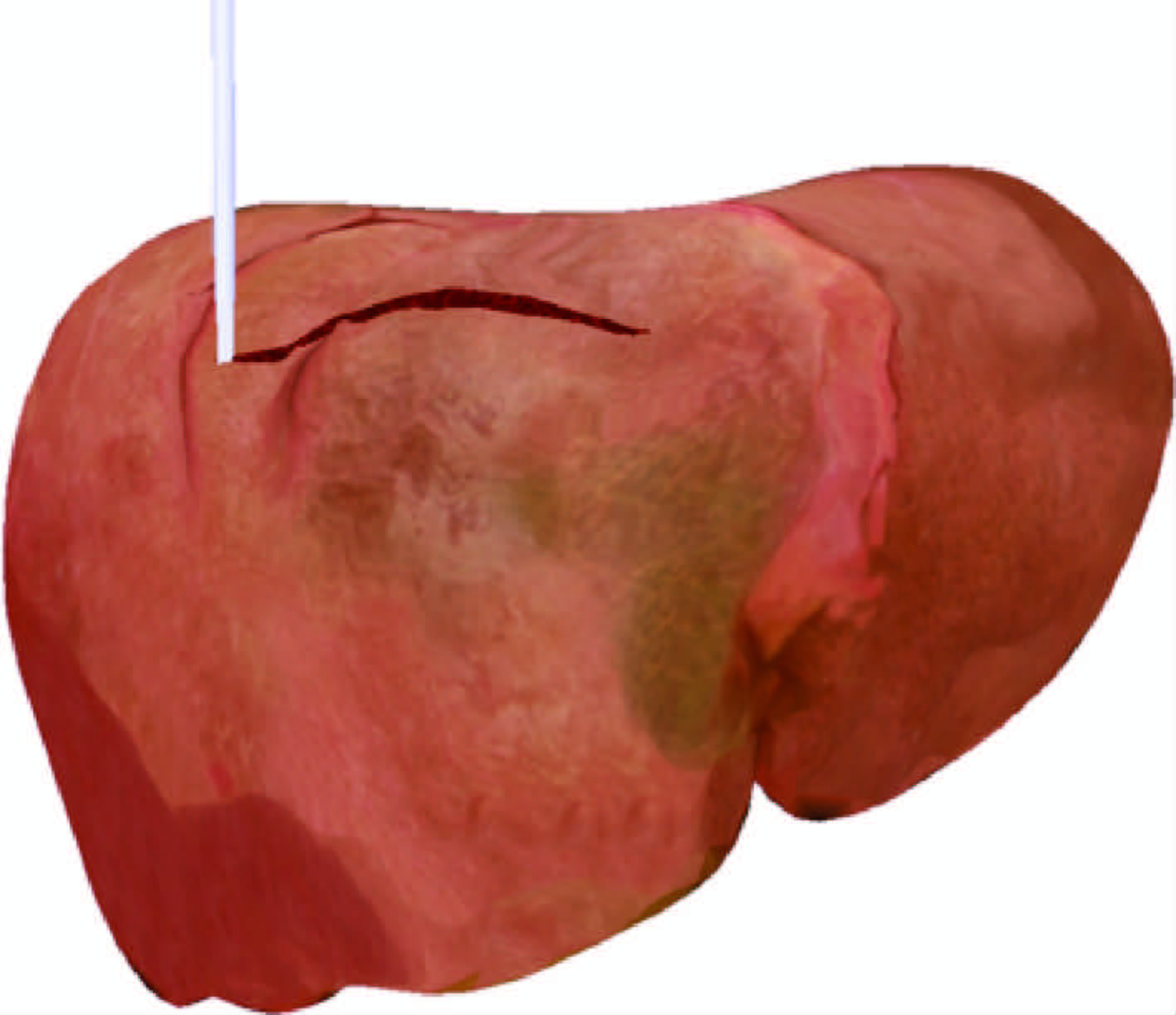 |
| 图 16 切割肝脏后的模拟Fig. 16 Simulation of cutting a liver model |
| 图选项 |
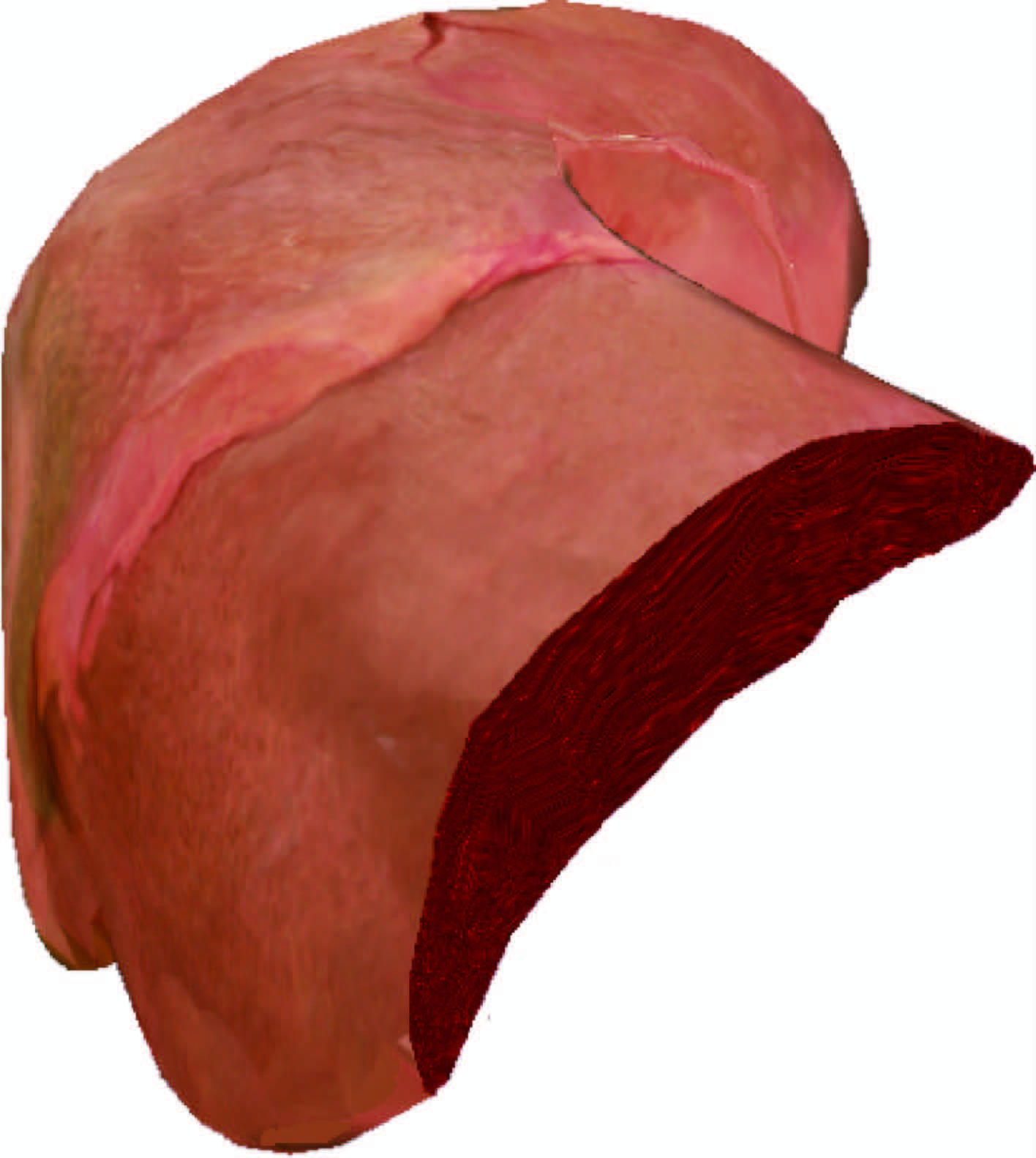 |
| 图 17 肝脏切口的模型Fig. 17 Incision of liver model |
| 图选项 |
 |
| 图 18 切割手臂的模拟Fig. 18 Simulation of cutting a hand model |
| 图选项 |
 |
| 图 19 切割马后的变形模拟Fig. 19 Deformation after cutting a horse model |
| 图选项 |
由图 14~图 19可得,本文算法能很好地模拟切割操作,并且切口比较真实.
在时间上,针对不同的模型,本文算法均能保证帧率在60帧/s以上.本文进一步分析了时间性能,对上述实验进行了统计.表 1记录了不同模型四面体顶点数量、四面体数量和对应的时间开销.
表 1中,拓扑更新的时间包括相交计算.由表 1中可得,物理变形时间与四面体的数量有关,减少四面体的数量可以减小物理变形的时间.拓扑更新的时间与切割区域的单元密度有关,因此会出现单元数量少的马模型比手臂模型更耗时的情况.
表 1 不同模型的时间效率Table 1 Time efficiency for different models
| 模型 | 顶点 | 单元 | 物理变形/ms | 几何渲染/ms | 拓扑更新/ms | 相交计算/ms |
| 脾脏 | 711 | 2385 | 1.2 | 11.9 | 3.2 | 2.9 |
| 肝脏 | 813 | 2739 | 2.1 | 9.8 | 4.7 | 3.6 |
| 手臂 | 1283 | 4523 | 2.2 | 10.2 | 2.9 | 2.8 |
| 马 | 1266 | 3992 | 1.9 | 10.6 | 6.6 | 6.2 |
表选项
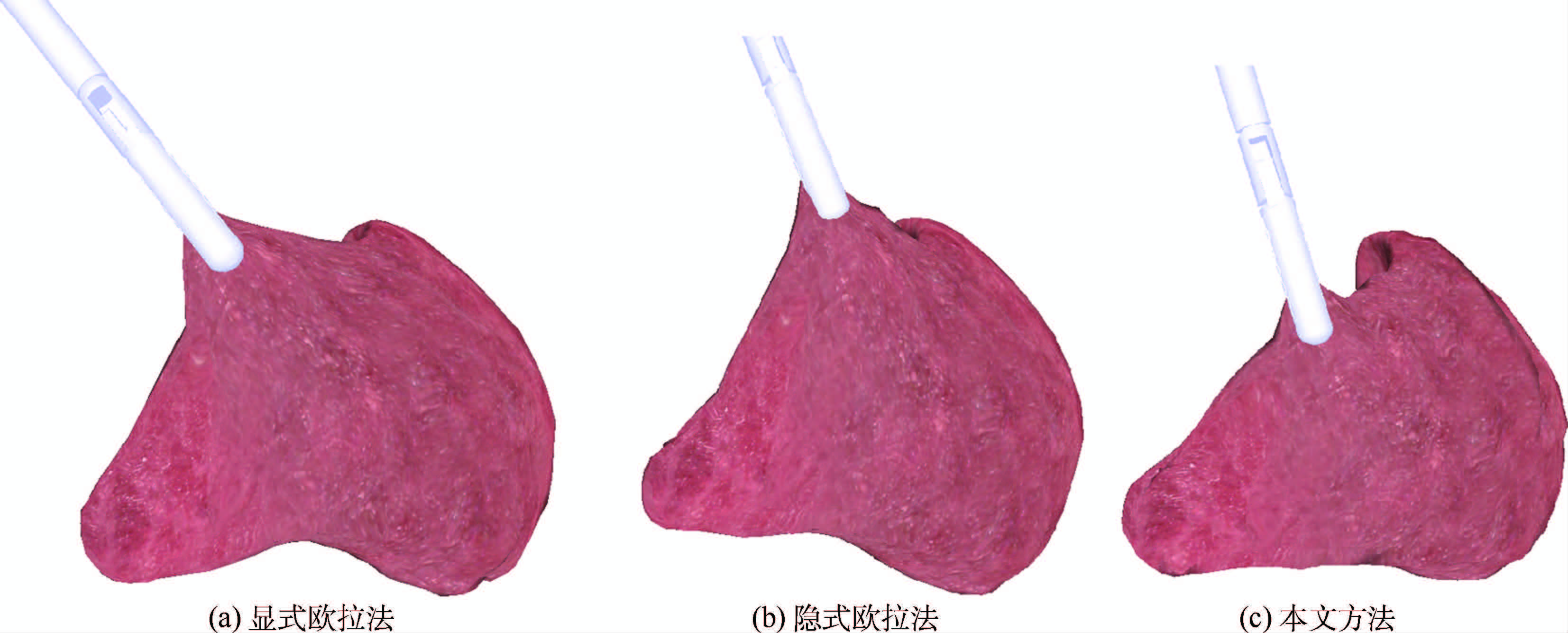
传统的虚拟手术模拟器一般采用质点弹簧模型作为物理模型,但其不能直接描述体积保持约束,为了证明本文使用的物理模型有更好的变形效果,本文对比了基于显式欧拉法的质点弹簧模型和基于隐式欧拉法的质点弹簧模型.图 20 (a)和图 20 (b)分别使用的是显式欧拉法和隐式欧拉法,图 20 (c)是本文使用的位置动力学.由于质点弹簧模型不能直接增加体积保持约束,因此在变形时缺乏软组织内部的影响,如图 20 (a)和图 20 (b)
 |
| 图 20 不同物理模型的变形效果Fig. 20 Deformation effect among different physical methods |
| 图选项 |
所示,而本文使用的位置动力学包含体积保持约束,因此变形时能体现软组织内部的影响.
8 结 论本文提出一种基于位置动力学的软组织实时切割算法,并得到以下结论:
1) 对位置动力学进行了改进与扩展,使其支持拓扑改变的情况.
2) 使用改进的位置动力学模型能快速地模拟软组织的物理变形,使其能保证手术过程模拟的实时性.
3) 通过实验对比,扩展后的位置动力学模型可以更准确地描述软组织的形变特点,保证模拟器的真实性及稳定性.
参考文献
| [1] | Müller M, Heidelberger B, Hennix M, et al.Position based dynamics[J].Journal of Visual Communication and Image Representation, 2007, 18(2): 109-118. |
| Click to display the text | |
| [2] | NVIDIA Corporation. NVIDIA? PhysX? SDK Documentation[EB/OL].Santa Clara, CA: San Tomas Expressway, 2014[2014-10-25].http: //docs.nvidia.com/gameworks/content/gameworkslibrary/physx/guide/Index.html. |
| [3] | Wu J, Dick C, Westermann R.Physically-based simulation of cuts in deformable bodies: A survey[C]//Eurographics 2014 State-of-the-Art Report.Strasbourg: Eurographics Association, 2014: 1-19. |
| Click to display the text | |
| [4] | Sela G, Subag J, Lindblad A, et al.Real-time haptic incision simulation using FEM-based discontinuous free form deformation[J].Computer Aided Design, 2007, 39(8): 685-693. |
| Click to display the text | |
| [5] | Choi C, Kim J, Han H, et al.Graphic and haptic modelling of the oesophagus for VR-based medical simulation[J].The International Journal of Medical Robotics and Computer Assisted Surgery, 2009, 5(3): 257-266. |
| Click to display the text | |
| [6] | Sifakis E, Hellrung J, Teran J, et al.Local flaps: A real-time finite element based solution to the plastic surgery defect puzzle[C]//Studies in Health Technology and Informatics.Amsterdam: IOS Press, 2009: 313-318. |
| [7] | Jerabkova L, Bousquet G, Barbier S, et al.Volumetric modeling and interactive cutting of deformable bodies[J].Progress in Biophysics and Molecular Biology, 2010, 103(2-3): 217-224. |
| Click to display the text | |
| [8] | Dick C, Georgii J, Westermann R.A hexahedral multigrid approach for simulating cuts in deformable objects[J].IEEE Transactions on Visualization and Computer Graphics, 2011, 17(11): 1663-1675. |
| Click to display the text | |
| [9] | Wu J, Dick C, Westermann R.Efficient collision detection for composite finite element simulation of cuts in deformable bodies[J].Visual Computer, 2013, 29(6-8): 739-749. |
| Click to display the text | |
| [10] | Zhang H, Payandeh S, Dill J.On cutting and dissection of virtual deformable objects[C]//Proceedings-IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2004: 3908-3913. |
| Click to display the text | |
| [11] | Steinemann D, Harders M, Gross M, et al.Hybrid cutting of deformable solids[C]//Proceedings of the IEEE Virtual Reality Annual International Symposium.Piscataway, NJ: IEEE Press, 2006: 35-42. |
| Click to display the text | |
| [12] | Choi K S, Soo S, Chung F L.A irtual training simulator for learning cataract surgery with phacoemulsification[J].Computers in Biology and Medicine, 2009, 39(11): 1020-1031. |
| Click to display the text | |
| [13] | Pan J J, Chang J, Yang X S, et al.Graphic and haptic simulation system for virtual laparoscopic rectum surgery[J].International Journal of Medical Robotics and Computer Assisted Surgery, 2011, 7(3): 304-317. |
| Click to display the text | |
| [14] | Steinemann D, Otaduy M, Gross M.Fast arbitrary splitting of deforming objects[C]//Proceedings of the 2006 ACM SIGGRAPH/Eurographics Symposium on Computer Animation.Aire-la-Ville: Eurographics Association, 2006: 63-72. |
| Click to display the text | |
| [15] | Pietroni N, Ganovelli F, Cignoni P, et al.Splitting cubes: A fast and robust technique for virtual cutting[J].Visual Computer, 2009, 25(3): 227-239. |
| Click to display the text | |
| [16] | Macklin M, Müller M.Position based fluids[J].ACM Transactions on Graphics, 2013, 32(4): 104. |
| Click to display the text | |
| [17] | Nakao M, Minato K.Physics-based interactive volume manipulation for sharing surgical process[J].IEEE Transactions on Information Technology in Biomedicine, 2010, 14(3): 809-816. |
| Click to display the text | |
| [18] | Paloc C, Faraci A, Bello F.Online remeshing for soft tissue simulation in surgical training[J].IEEE Computer Graphics and Applications, 2006, 26(6): 24-34. |
| Click to display the text | |
| [19] | Courtecuisse H, Allard J, Kerfriden P, et al.Real-time simulation of contact and cutting of heterogeneous soft-tissues[J].Medical Image Analysis, 2014, 18(2): 394-410. |
| Click to display the text | |
| [20] | Maciel A, Halic T, Lu Z H, et al.Using the PhysX engine for physics-based virtual surgery with force feedback[J].International Journal of Medical Robotics and Computer Assisted Surgery, 2009, 5(3): 341-353. |
| Click to display the text | |
| [21] | Ahn W, Dargar S, Halic T, et al.Development of a virtual reality simulator for natural orifice translumenal endoscopic surgery cholecystectomy procedure[J].Studies in Health Technology and Informatics, 2014, 196: 1-5. |
| Click to display the text | |
| [22] | Mor A, Kanade T.Modifying soft tissue models: Progressive cutting with minimal new element creation[C]//Medical Image Computing and Computer-Assisted Intervention-MICCAI 2000.Berlin: Springer, 2000: 598-607. |
| Click to display the text |
