经典的太沙基固结理论将固结过程划分为主固结和次固结,忽略了黏性变形对主固结过程的影响,也未考虑应力状态、应力历史对黏性变形的影响.一些****尝试在土的本构关系中考虑流变特性并与固结理论结合,得到了主、次固结耦合的理论[1, 2, 3, 4].一种方法是引入元件理论来考虑土的流变变形[5],然而土的变形为非线性并与应力历史有关,综合考虑这些效应往往导致元件理论过于复杂,参数也很难确定[6];另一种方法是建立黏弹塑性本构模型来反映土变形的时间效应,殷建华等[7, 8, 9]引入了“等效时间”的概念,建立了软土与时间相关的应力-应变关系,该模型与固结理论结合在加载初期得到孔压升高的结果,殷建华等对这一现象做出了定性解释.目前这一现象只在多维固结的实际工程中观测得到,在室内一维固结试验中并未出现.
姚仰平等[10]引入Bjerrum[11]的瞬时压缩线概念,将固结过程分为瞬时压缩与延时压缩,提出相对瞬时压缩线的蠕变公式并推导出老化时间与超固结度的关系,进而结合超固结土统一硬化(Unified Hardening,UH)模型[12],得到考虑时间效应的UH模型.该模型采用非线性压缩和蠕变公式,可以综合考虑应力及时间效应引起的变形,合理反映了荷载的率效应、蠕变引起的土体的硬化以及应力历史、蠕变历史对蠕变变形的影响,模型参数物理意义明确,可通过室内试验获得,能够方便地应用于有限元软件进行工程分析[13].
本文结合考虑时间效应的UH模型对一维固结问题进行分析,得到可以反应主、次固结全过程的模型,探讨了影响固结规律的因素.加载初期,部分条件下的模拟结果可能出现孔压升高的现象,类似于所谓的“曼德尔”效应[14],但产生机理却不相同,本文对出现这一结果的原因进行了分析,给出了这一现象未能通过室内一维固结试验证实的原因,并通过模拟一维固结试验对模型及分析结果进行验证.此外,工程中通常采用预压固结的方法来处理软土地基,然而目前确定固结时间的方法主要是做图法(
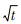法和标准曲线法),所得结果可能因人而异,本文基于固结控制微分方程推导了固结度与时间的关系,可以用于预测固结基本完成需要的时间,希望为预压固结法的工期确定提供参考.1 固结控制微分方程1.1 软土的一维应力-应变关系采用文献[15]的方法可将考虑时间效应的UH模型[10]拓展至一维固结,得到考虑时间效应的一维体积应变增量:
式(1)可以统一计算超固结土和正常固结土应力和蠕变引起的变形. 式中:Cc为压缩指数;Cs为回弹指数;Cα为次固结系数;σ′z为竖向有效应力;e0为初始孔隙比;t为时间；ta为老化时间,为相对瞬时压缩线确定的状态量;t0为单位时间,根据分析的问题取1s、1min等;dt为真实时间增量;M为临界状态应力比;Mf为潜在破坏应力比：
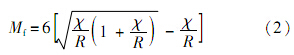
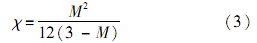
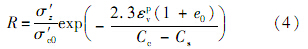
其中:R为超固结参数,反应土体超固结程度的演化;εpv为塑性体积应变;σ′ c0类似于前期固结压力,为回弹线与瞬时压缩线交点的竖向应力.若不考虑时间效应,σ′ c0即为前期固结压力,初始超固结参数R0为超固结度的倒数.天然的软土由于蠕变变形,相对于瞬时压缩线会存在一定的“超固结度”,瞬时压缩线和R0的确定可参考文献[7].超固结参数与老化时间的关系为
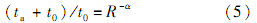
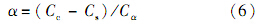
1.2 固结控制方程推导由连续性条件和Darcy定律,可得固结方程:
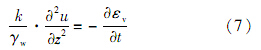
式中:k为土的渗透系数;γw为水的重度,取10kN/m3;u为孔压.
经典固结理论认为土的次固结变形不会引起孔压的改变.但不排水持荷剪切蠕变试验[16, 17]表明,蠕变同样会引起土体的孔压变化.本文将变形分为瞬时压缩和延时压缩,瞬时压缩为荷载引起的变形,延时压缩为时间效应产生的蠕变变形.这两部分变形同时存在于主、次固结过程中,其产生的体积应变均会引起土体孔压的变化,在固结的不同阶段,两部分变形所占的比重不同,从而使土体表现出主固结或次固结的特性.
将式(1)所得变形代入式(7),结合有效应力原理u=σz－σ′z,其中,σz为竖向总应力,荷载施加完成后可视为定值.推导得
考虑加卸载准则,当dσ′z<0时
2 预测及分析2.1 预测条件平均固结度的计算公式为
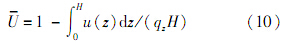
式中:qz为竖向施加荷载；H为模型高度.采用差分法对式(8)和式(9)求解,模型沿深度方向N等分，并对时间进行离散，差分计算的示意图如图 1所示(其中j为标记网格数),对应的边界条件为
 |
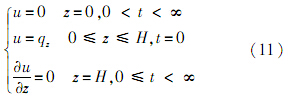
| 图 1 差分方法计算示意图Fig. 1 Sketch of calculation of differential method |
| 图选项 |
首先探讨模型预测规律,计算参数见表 1.初始应力p0=10kPa,qz=90kPa,渗透系数k=3.63×10-7m/min,H=1.0m.
表 1 分析选用参数Table 1 Parameters used in analysis
| 参数 | Cc | Cs | Cα | R0 | M | e0(p0=10kPa) |
| 数值 | 0.0217 | 0.0131 | 0.0108 | 0.95 | 1.112 | 0.53 |
表选项
2.2 孔压升高现象探讨图 2为本文模型得到的孔压随深度的分布规律.在上述条件下,加载初期,本文模型会出现孔压升高、有效应力减小的现象.
 |
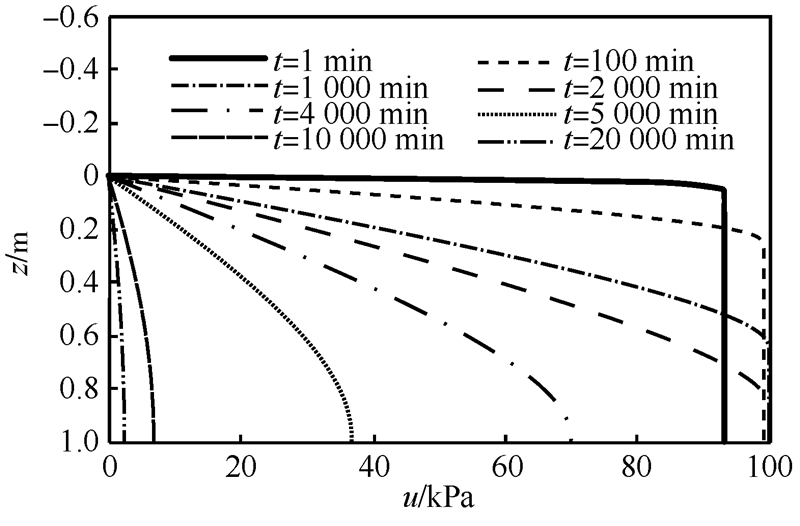| 图 2 孔压随深度分布规律Fig. 2 Distribution law of pore-water pressure in different depths |
| 图选项 |
殷建华等[7, 8, 9]也曾得到相似的结果,他们认为远离排水面的土体会因为排水不畅而产生应力松弛,从而导致孔压升高.松弛现象在土中是客观存在的,Hicher[18]采用蒙脱石进行三轴不排水试验,在恒定应变速率下观测到偏应力降低的现象.1.1节也曾提到在不排水持荷剪切蠕变试验中,也会因蠕变而导致孔压升高并引起土体破坏[16, 17].对于一维固结,若排水条件较差,是有可能因蠕变而导致孔压上升的,其产生机理与“曼德尔”效应显然不同.下面将对这一过程进行理论分析.加载初期,底部孔压难以即时消散,可以认为不透水层处,有
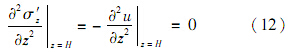
松弛过程中,有效应力减小,属于卸载过程,故采用式(9)进行分析.将式(12)代入式(9),得
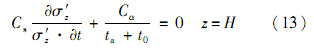
当荷载改变较小,dt≈dta,分离变量求解得
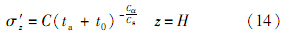
式中:C为积分常数;老化时间ta由固结所用时间及初始老化时间ta0组成,ta0一定程度上反应了土的历史沉积时间,可由初始超固结参数结合式(5)求出.当t=0,σ′ z=σ′z0(σ′z0为竖向初始有效应力):
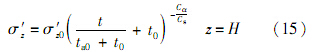
由式(15)可得,Cα/Cs越大,底部有效应力减小越快,Cα/Cs一定程度上反映了主次固结变形的相对大小;ta0越大,有效应力减小越慢.
图 2的结果基于较为理论的初始状态,没有考虑土体的沉积历史,计算模型所取的参数相当于重塑土,ta0较小,故模拟结果出现了明显的有效应力减小现象.而对于天然的土,均存在一定的沉积或等效的沉积过程,ta0较大,加载后,土体蠕变变形较小,可能无法观察到松弛的现象.这可能是“曼德尔”效应没有在一维固结试验中观测到的一个重要原因.此外,室内一维固结试验采用双面排水,排水距离则只有1cm,不透水层处孔隙水一旦排出,式(12)便不再成立,孔压升高持续时间较短,仪器较难监测得到.后文采用本文模型对室内固结试验进行了模拟,模拟结果没有出现孔压升高的现象并且与试验结果较为一致.2.3 模型预测规律探讨下文将对固结规律进行探讨,所用参数在表 1的基础上进行调整.
图 3(a)反映了次固结系数对固结的影响,次固结系数越大,前期的孔压升高更为显著,而次固结变形的增大也使整体孔压消散速率较慢,相同时刻平均固结度较小.
图 3(b)反映了超固结度(OCR)对固结的影响,超固结度越大,初始老化时间越大,由2.2节分析,初期孔压上升情况得到减弱,计算结果也正是如此.而超固结度的增大会使相同时间主、次固结变形均有所减小,因而整体孔压消散较快,平均固结度更大.这些结果也符合太沙基固结理论的压缩系数越小,土体固结越快的结论,这里的压缩系数是考虑主次固结变形的“等效压缩系数”.
有****指出在经历一定的预固结时间后,软基固结前期可能存在次固结系数越大、孔压消散越快、固结度越大这一与直觉相反的固结现象[2],采用本文模型很容易对其做出解释.由于蠕变变形的存在,自然状态的土会产生老化而成为超固结土.经受相同时间的预固结后,次固结系数较大的土蠕变变形也较大,老化产生的超固结度更大.由图 3(a)、图 3(b)得到的规律可知,超固结度和次固结系数的增加对土固结变形的影响规律恰好相反.若预固结时间足够长而使超固结度的增大成为影响土固结的主导因素时,其初期孔压消散可能比次固结系数小的土更快.
图 3(c)反映了压缩指数Cc及回弹指数Cs对土体固结的影响,若Cc、Cs以相同的倍数增加,加载初期孔压升高现象得到减弱,而后期孔压消散时间却大大增加.后期孔压消散规律很容易得出压缩系数越大、孔压消散越慢的结论.然而加载初期的结果与压缩系数越大固结度越大这一结论相矛盾.而采用式(15)则可以对其进行解释,Cs的增大使Cα/Cs值减小,前期孔压升高现象减弱,从而前期平均固结度更大.
 |
| 图 3 平均固结度随时间变化曲线Fig. 3 Variation curves of mean degree of consolidation changing with time |
| 图选项 |
无论是主固结还是次固结变形的增加,都会使孔压消散速率减慢,固结完成时间延长.加载初期孔压升高的程度受Cα/Cs值及初始超固结参数的影响,这与式(15)结论一致.3 试验验证文献[19]基于GDS(Global Digital Systems)先进固结试验系统对萧山软土进行了试验.分别采用本文模型和太沙基固结理论对800~1600kPa加载区间进行预测分析(见图 4),得到了孔压u(见图 4(a))与沉降变形s(见图 4(b))随时间变化的结果,并与试验结果进行了对比.文献[19]给出了表 2中的参数.
 |
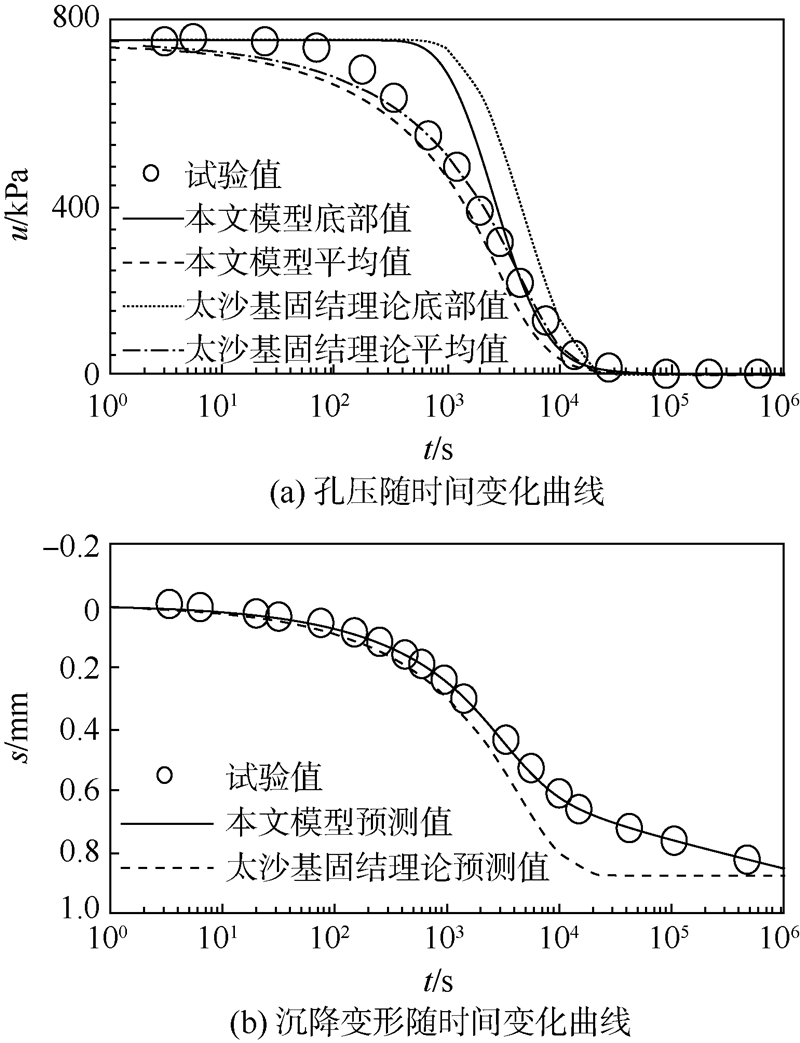| 图 4 800~1600kPa加载实测与模型预测结果对比Fig. 4 Comparison between test and model prediction results when loading ranges from 800kPa to 1600kPa |
| 图选项 |
表 2 试验所得参数Table 2 Parameters of test
| 参数 | Cc | Cs | a/kPa-1 | e0(p0=800kPa) | H/mm |
| 数值 | 0.356 | 0.0733 | 1.34×10-4 | 0.82 | 14.8 |
表选项
本文根据图 4(b)中次固结段试验结果,拟合得到Cα值为0.011,渗透系数k在试验过程中会发生改变,本文近似取1.5×10-11m/s.文献[19]未给出有效内摩擦角,为了定性分析模型规律,根据经验摩擦角取25°,计算得临界状态应力M=0.984,考虑沉积作用,R0取0.575.由于部分试验参数不全,本文模型只能定性预测土的孔压和变形随时间变化的规律.
文献[19]采用GDS先进固结试验系统测试了试样底部的孔压值(见图 4(a)),本文模型和太沙基固结理论的预测结果发现,计算得到的平均孔压值与试验测得的孔压值规律更为接近.严格来说,试验中测得的底部孔压也并不是某一物理点的值,而应是一定范围内土体孔压的均值.当控制最终变形基本相同时,UH模型得到的孔压消散会快于太沙基固结理论的结果.而地基基础工程中也发现,地基中实测固结度会大于太沙基固结理论的计算值.图 4(b)结果表明,本文模型较好地反映了变形随时间的发展规律.而对于太沙基固结理论,即使调整压缩系数也无法合理反映变形随时间发展的全过程.4 固结时间的确定采用差分法求解控制方程具有一定的难度,工程中往往更关心土体固结基本完成所需的时间,本文对式(7)进一步简化分析以方便于工程应用.4.1 固结时间理论推导主固结过程包括了瞬时压缩变形和部分延时压缩变形,直接分析主固结段具有一定难度.而对于软土,当主固结基本完成后,可以认为,次固结变形主要由延时压缩产生,即
,代入式(7)得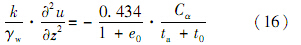
由式(16)可知,对于某个确定的时刻,可知孔压沿深度分布为抛物线型.若不透水层距透水层深度为H,某时刻,该处孔压为u(H),根据边界条件式(11),可以确定抛物线方程:
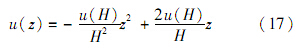
将式(17)代入式(10),可求出不透水层处的孔压u(H)与平均固结度U的关系：
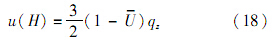
将式(18)代入式(17)求出
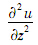并代入式(16),可得
ta由ta0与t组成.由式(5)老化时间与超固结参数的关系,可得
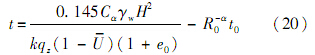
由于假定变形全部由次固结变形产生,式(20)可用于计算固结基本完成所用的时间.4.2 公式验证及讨论为了验证近似解析式(20)的正确性,将其结果与1.2节所得偏微分方程的数值解进行比较.由图 5可以看出,当t足够大时,近似解析解式(20)表示的曲线与模型预测得到的曲线重合.
由式(20)可以得到当初始超固结参数接近1时,若Cα/k比值恒定,固结完成所需时间基本相同,采用本文模型数值解对这一结论进行验证.从图 6可以看出Cα/k比值相同的两组数据,固结度随时间变化曲线基本一致,固结最终完成时间也基本相同,这与式(20)的结论基本一致.
 |
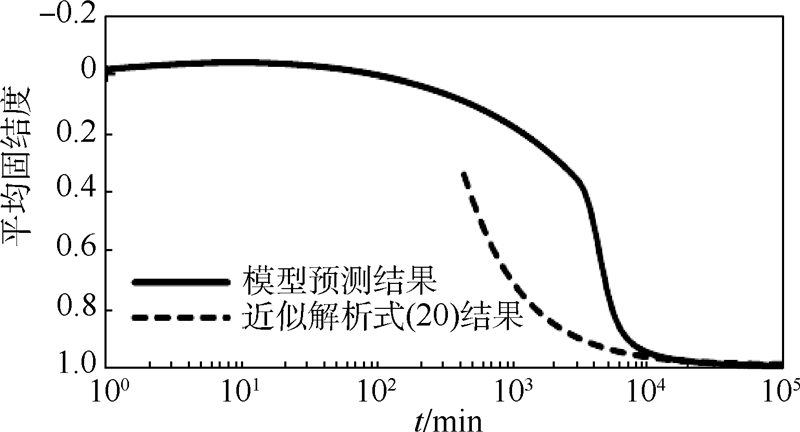| 图 5 近似解析式(20)与模型预测结果对比Fig. 5 Comparison between results of approximate analytic solution Eq.(20) and model prediction |
| 图选项 |
 |
| 图 6 Cα/k值对平均固结度的影响Fig. 6 Influence of Cα/k on mean degree of consolidation |
| 图选项 |
5 结 论基于本文的假定,可以得到统一考虑主、次固结变形的模型,反应各个土性参数对固结规律的影响,对一维固结问题进行分析.
1) 加载初期,模型预测结果可能存在孔压上升、有效应力减小的松弛现象,推导了有效应力随时间减小的表达式,给出了出现这一结果的原因.
2) 次固结系数、超固结度、压缩、回弹指数等参数对固结度与沉降变形均有影响,引起土体变形增大的参数往往导致固结时间增加.
3) 通过室内试验验证了本文模型的预测结果,在最终变形相同的情况下,本文模型所得孔压消散快于太沙基固结理论.本文模型可以合理地预测变形随时间发展的规律.
4) 对次固结变形段进行解析分析,推导出固结时间与固结度的关系,可以用于计算固结基本完成需要的时间,方便确定预压固结所需的时间.
参考文献
| [1] | 高彦斌. 饱和软粘土一维非线性流变——固结耦合分析[J].工程力学,2006,23(8):116-121. Gao Y B.One-dimensional nonlinear creep-consolidation analysis of saturated clay[J].Engineering Mechanics,2006,23(8):116-121(in Chinese). |
| Cited By in Cnki (12) | |
| [2] | 胡亚元,江涛. 次固结系数对准超固结土固结特性的影响[J].浙江大学学报:工学版,2011,45(6):1088-1093. Hu Y Y,Jiang T.Impact of secondary consolidation coefficient on consolidation characteristics of quasi over-consolidated clay[J].Journal of Zhejiang University:Engineering Science,2011,45(6):1088-1093(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 仇玉良,丁洲祥. 一维小变形主、次固结耦合理论模型分析[J].岩土力学,2012,33(7):1957-1964. Qiu Y L,Ding Z X.Study of coupling theory of one-dimensional small-strain primary and secondary consolidation model[J].Rock and Soil Mechanics,2012,33(7):1957-1964(in Chinese). |
| Cited By in Cnki (0) | |
| [4] | 刘忠玉,冯桂云, 王喜军.考虑流变特性的正常固结土一维固结分析[J].郑州大学学报:理学版,2013,45(2):110-114. Liu Z Y,Feng G Y,Wang X J.One-dimensional consolidation of normally consolidated soils considering their rheological behaviors[J].Journal of Zhengzhou University:Natural Science,2013,45(2):110-114(in Chinese). |
| Cited By in Cnki (2) | |
| [5] | Ma B N, Muhunthan B,Xie X Y.Stress history effects on 1-D consolidation of soft soils:A rheological model[J].International Journal for Numerical and Analytical Methods in Geomechanics,2013,37(16):2671-2689. |
| [6] | 袁静,龚晓南, 益德清.岩土流变模型的比较研究[J].岩石力学与工程学报,2001,20(6):772-779. Yuan J,Gong X N,Yi D Q.Comparison study on rheological constitutive models[J].Chinese Journal of Rock Mechanics and Engineering, 2001,20(6):772-779(in Chinese). |
| Cited By in Cnki (168) | |
| [7] | 殷建华,Clark J I. 土体与时间相关的一维应力-应变性状、弹粘塑性模型和固结分析[J].岩土力学,1994,15(3):65-80. Yin J H,Clark J I.One-dimensional time dependent stress-strain behavior of soil,elastic visco-plastic modeling,and consolidation analysis[J].Rock and Soil Mechanics,1994,15(3):65-80(in Chinese). |
| [8] | 殷建华,Clark J I. 土体与时间相关的一维应力-应变性状、弹粘塑性模型和固结分析(续)[J].岩土力学,1994,15(4):65-75. Yin J H,Clark J I.One-dimensional time dependent stress-strain behavior of soil,elastic visco-plastic modeling,and consolidation analysis(continuation)[J].Rock and Soil Mechanics,1994,15(4):65-75(in Chinese). |
| [9] | Yin J H,Graham J, Clark J I,et al.Modelling unanticipated pore-water pressures in soft clays[J].Canadian Geotechnical Journal,1994,31(5):773-778. |
| Click to display the text | |
| [10] | Yao Y P, Kong L M,Hu J.An elastic-viscous-plastic model for overconsolidated clays[J].Science China Technological Sciences,2013,56(2):441-457. |
| Click to display the text | |
| [11] | Bjerrum L. Engineering geology of Norwegian normally-consolidated marine clays as related to settlements of buildings[J].Geotechnique,1967,17(2):83-118. |
| Click to display the text | |
| [12] | Yao Y P, Hou W,Zhou A N.UH model:Three-dimensional unified hardening model for overconsolidated clays[J].Geotechnique,2009,59(5):451-469. |
| Click to display the text | |
| [13] | Luo T, Qin Z H,Feng X,et al.A symmetrisation method for non-associated unified hardening model[J].Computers and Geotechnics,2013,52:38-45. |
| Click to display the text | |
| [14] | Mandel J. Consolidation des sols(étude mathématique)[J].Geotechnique,1953,3(7):287-299. |
| Click to display the text | |
| [15] | 姚仰平,侯伟. K0超固结土的统一硬化模型[J].岩土工程学报,2008,30(3):316-322. Yao Y P,Hou W.A unified hardening model for K0 consolidated clays[J].Chinese Journal of Geotechnical Engineering,2008,30(3):316-322(in Chinese). |
| [16] | Arulanandan K, Shen C K,Young R B.Undrained creep behaviour of a coastal organic silty clay[J].Geotechnique,1971,21(4):359-375. |
| Click to display the text | |
| [17] | Sekiguchi H. Theory of undrained creep rupture of normally consolidated clay based on elasto-viscoplasticity[J].Soils and Foundations,1984,24(1):129-147. |
| Click to display the text | |
| [18] | Hicher P Y. Comportement mécanique des argiles saturées sur divers chemins de sollicitations monotones et cycliques:Application à une modélisation élastoplastique et viscoplastique[D].Paris:Université Paris,1985. |
| [19] | 李西斌. 软土流变固结理论与试验研究[D].杭州:浙江大学,2005. Li X B.Theoretical and experimental studies on rheological consolidation of soft soil[D].Hangzhou:Zhejiang University,2005(in Chinese). |
| Cited By in Cnki (16) |
