 )
) 1四川师范大学脑与心理科学研究院, 成都 610066
2应用实验心理北京市重点实验室
3北京师范大学心理学部, 北京 100875
收稿日期:2020-10-23发布日期:2021-07-22通讯作者:刘红云E-mail:hyliu@bnu.edu.cn基金资助:国家自然科学基金项目(32071091)Mixture Model Method: A new method to handle aberrant responses in psychological and educational testing
LIU Yue1, LIU Hongyun2,3( )
) 1Institute of Brain and Psychological Sciences, Sichuan Normal University, Chengdu 610066, China
2Beijing Key Laboratory of Applied Experimental Psychology, Beijing Normal University, Beijing 100875, China
3Faculty of Psychology, Beijing Normal University, Beijing 100875, China
Received:2020-10-23Published:2021-07-22Contact:LIU Hongyun E-mail:hyliu@bnu.edu.cn摘要/Abstract
摘要: 混合模型方法(Mixture Model Method)是近年来提出的, 对心理与教育测验中的异常作答进行处理的方法。与反应时阈值法, 反应时残差法等传统方法相比, 混合模型方法可以同时完成异常作答的识别和模型参数估计, 并且, 在数据污染严重的情况下仍具有较好的表现。该方法的原理为根据正常作答和异常作答的特点, 针对分类潜变量(即作答层面的分类)的不同类别, 在作答反应和(或)反应时部分建立不同的模型, 从而实现对分类潜变量, 以及模型中其他题目和被试参数的估计。文章详细介绍了目前提出的几种混合模型方法, 并将其与传统方法比较分析。未来研究可在模型前提假设违背, 含有多种异常作答等情况下探索混合模型方法的稳健性和适用性, 通过固定部分题目参数, 增加选择流程等方式提高混合模型方法的使用效率。
图/表 2
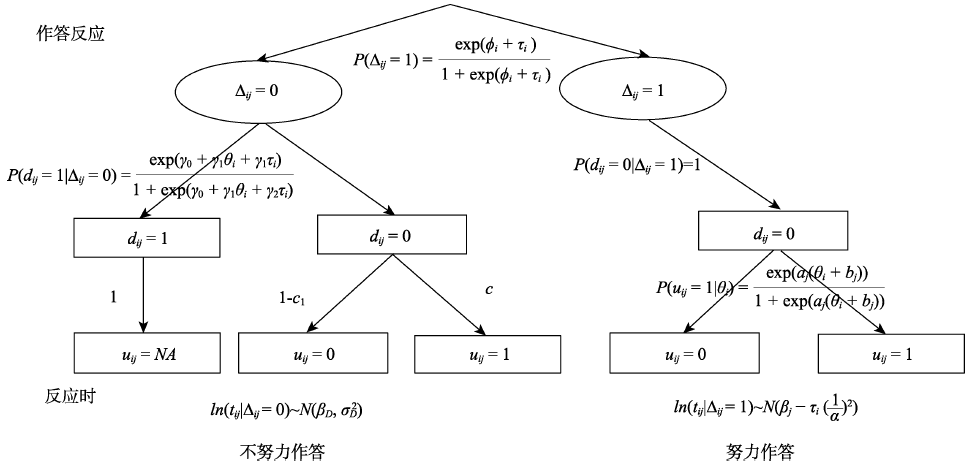
图1考虑了缺失的混合模型示意图
 图1考虑了缺失的混合模型示意图
图1考虑了缺失的混合模型示意图表1本文中所有方法的主要局限性总结
| 方法 类型 | 具体方法 | 没有综合利用反应时和作答反应的信息 | 没有基于理论分布 | 偶有例外, 无法批量应用 | 包含有关异常作答的强假设 | 对高比例异常作答 敏感 | 异常作答比例低时容易出现问题 | 计算复杂耗时长 | 识别结果不一定是异常作答 | 只能用于已知异常作答答对概率的情境 | 只能用于识别快速异常作答 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 反应时 阈值法 | 统一阈值法 | × | × | × | |||||||
| 根据题目特征求阈值法 | × | × | × | ||||||||
| 双峰分布交点求阈值法 | × | × | × | × | |||||||
| 常模阈值法 | × | × | |||||||||
| 基于信息求阈值法 | × | × | × | ||||||||
| 条件分布法 | × | × | × | × | |||||||
| 反应时 残差法 | 标准化反应时残差法 | × | × | × | |||||||
| 贝叶斯残差法 | × | × | × | ||||||||
| 混合 模型法 | 等级分组的反应时模型 | × | × | × | |||||||
| 半参数化的混合模型 | × | × | × | × | × | ||||||
| 基于反应时的混合作答反应模型 | × | × | × | × | × | ||||||
| 基于反应时和作答反应的混合多层模型 | × | × | × |
表1本文中所有方法的主要局限性总结
| 方法 类型 | 具体方法 | 没有综合利用反应时和作答反应的信息 | 没有基于理论分布 | 偶有例外, 无法批量应用 | 包含有关异常作答的强假设 | 对高比例异常作答 敏感 | 异常作答比例低时容易出现问题 | 计算复杂耗时长 | 识别结果不一定是异常作答 | 只能用于已知异常作答答对概率的情境 | 只能用于识别快速异常作答 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 反应时 阈值法 | 统一阈值法 | × | × | × | |||||||
| 根据题目特征求阈值法 | × | × | × | ||||||||
| 双峰分布交点求阈值法 | × | × | × | × | |||||||
| 常模阈值法 | × | × | |||||||||
| 基于信息求阈值法 | × | × | × | ||||||||
| 条件分布法 | × | × | × | × | |||||||
| 反应时 残差法 | 标准化反应时残差法 | × | × | × | |||||||
| 贝叶斯残差法 | × | × | × | ||||||||
| 混合 模型法 | 等级分组的反应时模型 | × | × | × | |||||||
| 半参数化的混合模型 | × | × | × | × | × | ||||||
| 基于反应时的混合作答反应模型 | × | × | × | × | × | ||||||
| 基于反应时和作答反应的混合多层模型 | × | × | × |
参考文献 70
| [1] | 黄美薇, 潘逸沁, 骆方. (2020). 结合选择题与主观题信息的两阶段作弊甄别方法. 心理科学, (1), 75-80. |
| [2] | 简小珠, 焦璨, Steven P Reise, 彭春妹. (2010). 四参数模型对被试作答异常现象的拟合与纠正. 心理科学进展, 18(3), 537-544. |
| [3] | Baer R. A., Ballenger J., Berry D. T. R., & Wetter M. W. (1997). Detection of random responding on the MMPI-A. Journal of Personality Assessment, 68(1), 139-151. pmid: 16370774 |
| [4] | Berry D. T. R., Wetter M. W., Baer R. A., Larsen L., Clark C., & Monroe K. (1992). MMPI-2 random responding indices: Validation using a self-report methodology. Psychological Assessment, 4(3), 340-345. doi: 10.1037/1040-3590.4.3.340URL |
| [5] | Bolsinova M., & Tijmstra J. (2019). Modeling differences between response times of correct and incorrect responses. Psychometrika, 84(4), 1018-1046. doi: 10.1007/s11336-019-09682-5pmid: 31463656 |
| [6] | Bolt D. M., Cohen A. S., & Wollack J. A. (2002). Item parameter estimation under conditions of test speededness: Application of a mixture Rasch model with ordinal constraints. Journal of Educational Measurement, 39(4), 331-348. doi: 10.1111/jedm.2002.39.issue-4URL |
| [7] | Borghans L., & Schils T. (2012). The leaning tower of PISA: Decomposing achievement test scores into cognitive and noncognitive components (Unpublished doctorial dissertation). Maastricht University. |
| [8] | Bridgeman B., & Cline F. (2004). Effects of differentially time-consuming tests on computer-adaptive test scores. Journal of Educational Measurement, 41(2), 137-148. doi: 10.1111/jedm.2004.41.issue-2URL |
| [9] | Clark M. E., Gironda R. J., & Young R. W. (2003). Detection of back random responding: Effectiveness of MMPI-2 and personality assessment inventory validity indices. Psychological Assessment, 15(2), 223-234. doi: 10.1037/1040-3590.15.2.223URL |
| [10] | Cousineau D. (2009). Fitting the three-parameter Weibull distribution: Review and evaluation of existing and new methods. IEEE Transactions on Dielectrics and Electrical Insulation, 16(1), 281-288. doi: 10.1109/TDEI.2009.4784578URL |
| [11] | Custer M., Sharairi S., & Swift D. (2012,April). A comparison of scoring options for omitted and not-reached items through the recovery of IRT parameters when utilizing the Rasch model and joint maximum likelihood estimation. Paper presented at the annual meeting of the National Council of Measurement in Education, Vancouver, BC, Canada. |
| [12] | Dolan C. V., van der Maas H. L. J., & Molenaar P. C. M. (2002). A framework for ML estimation of parameters of (mixtures of) common reaction time distributions given optional truncation or censoring. Behavior Research Methods, Instruments & Computers, 34, 304-323. doi: 10.3758/BF03195458URL |
| [13] | Feinberg R., & Jurich D. (2018, April). Using rapid responses to evaluate test speededness. Paper presented at the meeting of the National Council of Measurement in Education (NCME), New York, NY. |
| [14] | Goldhammer F., Martens T., Christoph G., & Lüdtke O. (2016). Test-taking engagement in PIAAC (OECD Education Working Papers, No. 133). Paris, France: OECD Publishing. |
| [15] | Guo H., Rios J. A., Haberman S., Liu O. L., Wang J., & Paek I. (2016). A new procedure for detection of students’ rapid guessing responses using response time. Applied Measurement in Education, 29(3), 173-183. doi: 10.1080/08957347.2016.1171766URL |
| [16] | Hauser C., & KingsburyG. G.(2009). Individual score validity in a modest-stakes adaptive educational testing setting. Paper presented at the annual meeting of the National Council on Measurement in Education, San Diego, CA. |
| [17] | Hauser C., Kingsbury G. G., & Wise S. L. (2008). Individual validity: Adding a missing link. Paper presented at the annual meeting of the American Educational Research Association, New York, NY. |
| [18] | Hong M. R., & Cheng Y. (2019a). Robust maximum marginal likelihood (RMML) estimation for item response theory models. Behavior Research Methods, 51(2), 573-588. doi: 10.3758/s13428-018-1150-4URL |
| [19] | Hong M. R., & Cheng Y. (2019b). Clarifying the effect of test speededness. Applied Psychological Measurement, 43(8), 611-623. doi: 10.1177/0146621618817783URL |
| [20] | Köhler C., Pohl S., & Carstensen C. H. (2017). Dealing with item nonresponse in large-scale cognitive assessments: The impact of missing data methods on estimated explanatory relationships. Journal of Educational Measurement, 54(4), 397-419. doi: 10.1111/jedm.2017.54.issue-4URL |
| [21] | Kong X. J., Wise S. L., & Bhola D. S. (2007). Setting the response time threshold parameter to differentiate solution behavior from rapid-guessing behavior. Educational and Psychological Measurement, 67(4), 606-619. doi: 10.1177/0013164406294779URL |
| [22] | Lee Y. H., & Jia Y. (2014). Using response time to investigate students’ test-taking behaviors in a NAEP computer-based study. Large-scale Assessments in Education, 2(8), 1-24. |
| [23] | Liu Y., Cheng Y., & Liu H. (2020). Identifying effortful individuals with mixture modeling response accuracy and response time simultaneously to improve item parameter estimation. Educational and Psychological Measurement, 80(4), 775-807. doi: 10.1177/0013164419895068URL |
| [24] | Lu J., Wang C., Zhang J., & Tao J. (2020). A mixture model for responses and response times with a higher-order ability structure to detect rapid guessing behaviour. British Journal of Mathematical and Statistical Psychology, 73(2), 261-288. doi: 10.1111/bmsp.v73.2URL |
| [25] | Ma L., Wise S. L., Thum Y. M., & Kingsbury G. (2011, April). Detecting response time threshold under the computer adaptive testing environment. Paper presented at the annual meeting of the National Council of Measurement in Education, New Orleans, LA. |
| [26] | Masters G. N. (1982). A Rasch model for partial credit scoring. Psychometrika, 47, 149-174. doi: 10.1007/BF02296272URL |
| [27] | Meyer J. P. (2010). A mixture Rasch model with item response time components. Applied Psychological Measurement, 34(7), 521-538. doi: 10.1177/0146621609355451URL |
| [28] | Michaelides M. P., Ivanova M., & Nicolaou C. (2020). The relationship between response-time effort and accuracy in PISA science multiple choice items. International Journal of Testing, 20(3), 187-205. doi: 10.1080/15305058.2019.1706529URL |
| [29] | Molenaar D., Bolsinova M., & Vermunt J. K. (2018). A semi-parametric within-subject mixture approach to the analyses of responses and response times. British Journal of Mathematical and Statistical Psychology, 71(2), 205- 228. doi: 10.1111/bmsp.2018.71.issue-2URL |
| [30] | Molenaar D., Bolsinova M., Rozsa S., & de Boeck P.,(2016). Response mixture modeling of intraindividual differences in responses and response times to the Hungarian WISC- IV block design test. Journal of Intelligence, 4(3), 10-29. doi: 10.3390/jintelligence4030010URL |
| [31] | Molenaar D., Oberski D., Vermunt J., & de Boeck P., (2016). Hidden Markov item response theory models for responses and response times. Multivariate Behavioral Research, 51(5), 606-626. doi: 10.1080/00273171.2016.1192983pmid: 27712114 |
| [32] | Molenaar D., & de Boeck P.,(2018). Response mixture modeling: Accounting for heterogeneity in item characteristics across response times. Psychometrika, 83(2), 279-297. doi: 10.1007/s11336-017-9602-9pmid: 29392567 |
| [33] | Morgenthaler S. (2007). A survey of robust statistics. Statistical Methods and Applications, 15, 271-293. doi: 10.1007/s10260-006-0034-4URL |
| [34] | Partchev I., & de Boeck P.,(2012). Can fast and slow intelligence be differentiated? Intelligence, 40(1), 23-32. doi: 10.1016/j.intell.2011.11.002URL |
| [35] | Patton J. M., Cheng Y., Hong M. R., & Diao Q. (2019). Detection and treatment of careless responses to improve item parameter estimation. Journal of Educational and Behavioral Statistics, 44(3), 309-341. doi: 10.3102/1076998618825116URL |
| [36] | Pohl S., Haberkorn K., Hardt K., & Wiegand E. (2012). NEPS technical report for reading? Scaling results of starting cohort 3 in fifth grade. NEPS Working Paper No.15. Bamberg: Otto-Friedrich-Universitt, Nationales Bildungspanel. |
| [37] | Pokropek A. (2016). Grade of membership response time model for detecting guessing behaviors. Journal of Educational and Behavioral Statistics, 41(3), 300-325. doi: 10.3102/1076998616636618URL |
| [38] | Qian H., Staniewska D., Reckase M., & Woo A. (2016). Using response time to detect item preknowledge in computer-based licensure examinations. Educational Measurement: Issues and Practice, 35(1), 38-47. |
| [39] | Ranger J., & Kuhn J. T. (2017). Detecting unmotivated individuals with a new model-selection approach for Rasch models. Psychological Test and Assessment Modeling, 59(3), 269-295. |
| [40] | Ranger J., Wolgast A., & Kuhn J. T. (2019). Robust estimation of the hierarchical model for responses and response times. British Journal of Mathematical and Statistical Psychology, 72(1), 83-107. doi: 10.1111/bmsp.2019.72.issue-1URL |
| [41] | Rios J. A., Guo H., Mao L., & Liu O. L. (2017). Evaluating the impact of careless responding on aggregated-scores: To filter unmotivated examinees or not?. International Journal of Testing, 17(1), 74-104. doi: 10.1080/15305058.2016.1231193URL |
| [42] | Rose N. (2013). Item nonresponses in educational and psychological measurement (Unpublished doctorial dissertation). Friedrich-Schiller-University, Jena. |
| [43] | Rose N., von Davier M., & Nagengast B. (2017). Modeling omitted and not-reached items in IRT models. Psychometrika, 82(3), 795-819. doi: 10.1007/s11336-016-9544-7URL |
| [44] | Samejima F. (1969). Estimation of latent ability using a response pattern of graded scores (Psychometric Monograph Supplement No. 17). Richmond, VA: Psychometric Society. |
| [45] | Schnipke D. L., & Scrams D. J. (1997). Modeling item response times with a two-state mixture model: A new method of measuring speededness. Journal of Educational Measurement, 34(3), 213-232. doi: 10.1111/jedm.1997.34.issue-3URL |
| [46] | Schnipke D. L. & Scrams D. J. (2002). Exploring issues of examinee behavior: Insights gained from response-time analyses. In C. N. Mills, M.T. Potenza, J.J. Fremer, & W. C. Ward (Eds.), Computer-based testing: Building the foundation for future assessments (pp. 237-266). Mahwah, NJ: Lawrence Erlbaum. |
| [47] | Setzer J. C., Wise S. L., van den Heuvel J. R., & Ling G. (2013). An investigation of examinee test-taking effort on a large-scale assessment. Applied Measurement in Education, 26(1), 34-49. doi: 10.1080/08957347.2013.739453URL |
| [48] | Shao C., Li J., & Cheng Y. (2016). Detection of test speededness using change-point analysis. Psychometrika, 81(4), 1118-1141. pmid: 26305400 |
| [49] | Silm G., Must O., & Täht K. (2013). Test-taking effort as a predictor of performance in low-stakes tests. TRAMES: A Journal of the Humanities & Social Sciences, 17(4), 433- 448. |
| [50] | Sinharay S., & Johnson M. S. (2019). The use of item scores and response times to detect examinees who may have benefited from item preknowledge. British Journal of Mathematical and Statistical Psychology, 73(3), 397-419. doi: 10.1111/bmsp.v73.3URL |
| [51] | Ulitzsch E., von Davier M., & Pohl S. (2020). A hierarchical latent response model for inferences about examinee engagement in terms of guessing and item-level non- response. British Journal of Mathematical and Statistical Psychology, 73(S1), 83-112. doi: 10.1111/bmsp.v73.s1URL |
| [52] | van der Linden W. J.(2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), 181-204. doi: 10.3102/10769986031002181URL |
| [53] | van der Linden W. J.(2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 72, 287-308. doi: 10.1007/s11336-006-1478-zURL |
| [54] | van der Linden W. J., & Guo, F. (2008). Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Psychometrika, 73, 365-384. doi: 10.1007/s11336-007-9046-8URL |
| [55] | Wang C., Chang H. H., & Douglas J. A. (2013). The linear transformation model with frailties for the analysis of item response times. British Journal of Mathematical and Statistical Psychology, 66(1), 144-168. doi: 10.1111/j.2044-8317.2012.02045.xURL |
| [56] | Wang C., Fan Z., Chang H. H., & Douglas J. A. (2013). A semiparametric model for jointly analyzing response times and accuracy in computerized testing. Journal of Educational and Behavioral Statistics, 38(4), 381-417. doi: 10.3102/1076998612461831URL |
| [57] | Wang C., & Xu G. (2015). A mixture hierarchical model for response times and response accuracy. British Journal of Mathematical and Statistical Psychology, 68(3), 456-477. doi: 10.1111/bmsp.2015.68.issue-3URL |
| [58] | Wang C., Xu G., & Shang Z. (2018). A two-stage approach to differentiating normal and aberrant behavior in computer based testing. Psychometrika, 83(1), 223-254. doi: 10.1007/s11336-016-9525-xURL |
| [59] | Wang C., Xu G., Shang Z., & Kuncel N. (2018). Detecting aberrant behavior and item preknowledge: A comparison of mixture modeling method and residual method. Journal of Educational and Behavioral Statistics, 43(4), 469-501. doi: 10.3102/1076998618767123URL |
| [60] | Weirich S., Hecht M., Penk C., Roppelt A., & Böhme K. (2017). Item position effects are moderated by changes in test-taking effort. Applied Psychological Measurement, 41(2), 115-129. doi: 10.1177/0146621616676791URL |
| [61] | Wise S. L. (2015). Effort analysis: Individual score validation of achievement test data. Applied Measurement in Education, 28(3), 237-252. doi: 10.1080/08957347.2015.1042155URL |
| [62] | Wise S. L. (2017). Rapid-guessing behavior: Its identification, interpretation, and implications. Educational Measurement: Issues and Practice, 36(4), 52-61. doi: 10.1111/emip.2017.36.issue-4URL |
| [63] | Wise S. L. (2019). An information-based approach to identifying rapid-guessing thresholds. Applied Measurement in Education, 32(4), 325-336. doi: 10.1080/08957347.2019.1660350URL |
| [64] | Wise S. L., & DeMars C. E. (2006). An application of item response time: The effort-moderated IRT model. Journal of Educational Measurement, 43(1), 19-38. doi: 10.1111/jedm.2006.43.issue-1URL |
| [65] | Wise S. L., & DeMars C. E. (2010). Examinee noneffort and the validity of program assessment results. Educational Assessment, 15(1), 27-41. doi: 10.1080/10627191003673216URL |
| [66] | Wise S. L., & Kingsbury G. G. (2016). Modeling student test-taking motivation in the context of an adaptive achievement test. Journal of Educational Measurement, 53(1), 86-105. doi: 10.1111/jedm.12102URL |
| [67] | Wise S. L., & Ma L. (2012, April). Setting response time thresholds for a CAT item pool: The normative threshold method. Paper presented at the annual meeting of the National Council on Measurement in Education, Vancouver, Canada. |
| [68] | Wright B. D., & Stone M. H. (1979). Best test design. Rasch measurement. Chicago, IL: MESA Press. |
| [69] | Yan T., & Tourangeau R. (2008). Fast times and easy questions: The effects of age, experience and question complexity on web survey response times. Applied Cognitive Psychology, 22(1), 51-68. doi: 10.1002/(ISSN)1099-0720URL |
| [70] | Yu X., & Cheng Y. (2019). A change-point analysis procedure based on weighted residuals to detect back random responding. Psychological Methods, 24(5), 658-674. doi: 10.1037/met0000212URL |
相关文章 13
| [1] | 陈冠宇, 陈平. 解释性项目反应理论模型:理论与应用[J]. 心理科学进展, 2019, 27(5): 937-950. |
| [2] | 赵晓宁, 胡金生, 李松泽, 刘西, 刘琼阳, 吴娜. 基于眼动研究的孤独症谱系障碍早期预测[J]. 心理科学进展, 2019, 27(2): 301-311. |
| [3] | 王孟成, 毕向阳. 回归混合模型:方法进展与软件实现[J]. 心理科学进展, 2018, 26(12): 2272-2280. |
| [4] | 施霖. 短波长敏感视锥细胞适应水平与颜色对比度检测阈值的相关性[J]. 心理科学进展, 2017, 25(suppl.): 24-24. |
| [5] | 郭磊;尚鹏丽;夏凌翔. 心理与教育测验中反应时模型应用的优势与举例[J]. 心理科学进展, 2017, 25(4): 701-712. |
| [6] | 张阳;李艾苏;张少杰;张明. 微眼动的识别技术[J]. 心理科学进展, 2017, 25(1): 29-36. |
| [7] | 陈宇帅;温忠麟;顾红磊. 因子混合模型:潜在类别分析与因子分析的整合[J]. 心理科学进展, 2015, 23(3): 529-538. |
| [8] | 王力;张栎文;张明亮;陈安涛. 视觉运动Simon效应和认知Simon效应的影响因素及机制[J]. 心理科学进展, 2012, 20(5): 662-671. |
| [9] | Ernst Poeppel;包燕;周斌. “时间窗”—— 认知加工的后勤基础[J]. 心理科学进展, 2011, 19(6): 775-793. |
| [10] | 冯成志;贾凤芹 . 双眼竞争研究现状与展望[J]. 心理科学进展, 2008, 16(2): 213-221. |
| [11] | 李明;杜建政. 基于反应时的人格内隐测量及其方法学的思考[J]. 心理科学进展, 2008, 16(1): 184-191. |
| [12] | 彭正敏,林绚晖,张继明,车宏生. 情绪智力的能力模型[J]. 心理科学进展, 2004, 12(6): 817-817~823. |
| [13] | 陈玲丽,吴家舵. 序列学习是否是内隐学习?[J]. 心理科学进展, 2004, 12(4): 500-504. |
PDF全文下载地址:
http://journal.psych.ac.cn/xlkxjz/CN/article/downloadArticleFile.do?attachType=PDF&id=5577
