摘要:为解决一类典型工程摆的工作性能参数优选, 抽象该类系统为“受垂直激励和水平约束”的物理单摆模型. 运用多尺度法解析系统的亚谐共振响应, 明确了系统参数对幅值共振带宽、多值性的作用规律. 利用Melnikov函数法, 求解得到系统的同宿轨和Smale意义上混沌的阈值条件. 通过数值法解析系统单参分岔、最大Lyapunov指数、双参分岔及吸引域流形转迁等动力特性, 揭示了这类摆系统的亚谐共振分岔、周期吸引子倍增、周期与混沌吸引子共存等全局特性的运动规律, 进一步明确了相关参数改变对系统运动形态转化、能量分布与演变规律的作用机理, 得到了相关参数对工程系统工作性能的影响和作用机制. 研究结果对工程中该类典型物理系统的工作性能参数调整, 及其对实际工况中系统的减振抑振提供了理论依据.
关键词: 单摆/
亚谐共振/
分岔/
混沌

English Abstract

全文HTML

--> --> -->

不同于简单的单摆, 受垂直激励和水平约束的单摆系统, 是工程弹簧摆的典型物理抽象. 单摆具有运动的等时性, 起重机吊重系统^[1,2]以及人体行走系统可简化为单摆模型^[3], 并且单摆原理应用于减振装置也具有良好的效果^[4,5]. 伽利略^[6]和惠更斯^[7]都是单摆研究的奠定者. 单摆模型基础上延伸出的弹簧摆、复摆、倒立摆等系统的物理特性, 本质上往往不能简单等同于单摆, 所以得到****们的广泛研究^[8-10], 对复杂摆系统的响应解析、稳定性、分岔和混沌的研究, 也就成为摆类系统的研究重点^[11-13].
萧寒等^[14]和张丽娟等^[15]研究了一类外激励作用下的弹簧摆系统的分岔和周期稳定性, 明确了系统的拟周期环面破裂和阵发性进入混沌的路径. Bek等^[16]解析出阻尼弹簧摆的二阶近似非线性响应; Butikov等^[17]研究了一类具有黏性阻尼和干摩擦阻尼作用的弹簧摆, 获得了系统干摩擦阻尼确定的极限环及对称的非黏性强迫振荡的稳态周期性. Zhou等^[18]和Franco等^[19]研究倒立摆的亚谐分岔、混沌运动及平衡控制, 获得异宿轨临界条件和系统参数的鲁棒性. Najdecka等^[20]研究了参数激励的双摆动力特性, 明确了同步与旋转稳定性间的关系.
对实际应用中特定工程摆悬挂点的激励响应的研究, 也引发了****的关注^[21,22]. Kholostova^[23]研究了悬挂点受水平激励的单摆, 解析出系统周期运动中稳定性和不稳定周期运动的边界条件; Jallouli等^[24]研究了谐波激励和参数激励作用的非线性摆的零吸引子孤子解转换为周期稳定解的条件; Brzeski等^[25]研究了强迫Dufffing振荡摆的动力分岔、旋转周期解及参数空间中的共存吸引子条件.
实际工程中的船用起吊机^[26]、绳系航天器^[27]及水下极端环境球形机器人重摆^[28], 以及轧制工艺系统中工作辊偏心于支撑辊的轧制状态, 都可通过力学分析转化为受垂直激励和水平约束的单摆^[29]. 可见, 受垂直激励和水平约束的摆系统是单摆物理模型的进一步延伸, 工程应用广泛. 对此类问题的研究文献较少, 使用现有单摆物理系统的研究结论, 无法明确对这类多参量作用下的工程弹簧摆的物理属性及工作性能的优选评估. 因此深入研究这类摆系统的基本物理问题和动力学机制是提升这类工程摆广泛优化应用的关键.
本文较系统地研究了“受垂直激励和水平约束的单摆系统”的基本物理问题. 通过理论解析和数值计算, 深入研究了该类典型工程摆系统的亚谐共振、幅频特性、混沌、单参和双参分岔及吸引域流形转迁等特性, 揭示了这类摆系统的工作参数变化诱发能量改变对系统动特性和工作性能的影响.

图1为受垂直激励和水平约束的单摆模型. 其中, x和y分别表示水平方向和垂直方向, o为悬挂点, 摆球悬挂点受到垂直激励y₁(t), 摆球等效质量为m, 不计悬挂点处质量, 重力加速度为g, 摆球与垂直方向夹角为u(t), 摆长为l. 摆球在运动过程中受到水平方向的约束作用, 表现为弹性回复力和阻尼力形式, 其刚度系数和阻尼系数分别为k和c.
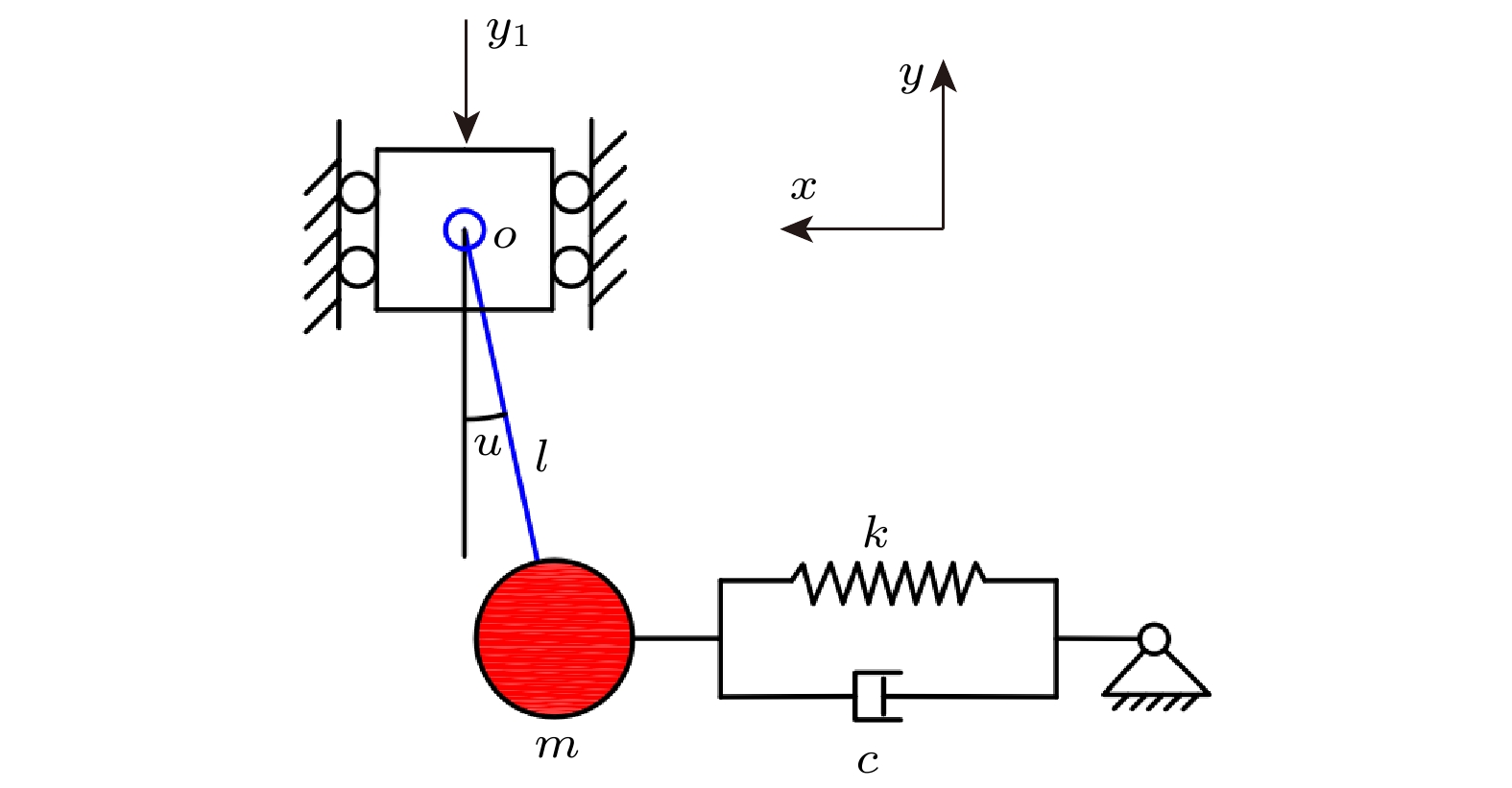图 1 受垂直激励和水平约束的单摆模型
Figure1. Simple pendulum model with vertical excitation and horizontal constraint.

摆球的水平位移x_p和垂直位移y_p可以表示为: $x_{\rm{p}} = l\sin u,\; y_{\rm{p}} = y_1－l\cos u$. 摆球的水平速度和垂直速度可写为: $ {\dot x_{\rm{p}}} = l\dot u\cos u $, $ {\dot y_{\rm{p}}} = {\dot y_1} + l\dot u\sin u $. 取摆球悬挂点位置为重力零势能位置, 单摆系统动能为T, 势能为V, 耗散能为D, 图1所示的受垂直激励和水平约束的单摆系统Lagrange方程为

$ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial T}}{{\partial \dot u}}} \right) - \frac{{\partial T}}{{\partial u}} + \frac{{\partial V}}{{\partial u}} + \frac{{\partial D}}{{\partial \dot u}} = 0 , $

式中,

$ \left\{ \begin{aligned}& T = \frac{1}{2}m\left[ {{l^2}{{\dot u}^2}{{\cos }^2}u + {{\left( {{{\dot y}_1} + l\dot u\sin u} \right)}^2}} \right], \\& V = mg\left( {{y_1} - l\cos u} \right) + \frac{1}{2}k{l^2}{\sin ^2}u, \hfill \\& D = \frac{1}{2}c{l^2}{{\dot u}^2}{\cos ^2}u. \end{aligned} \right. $

将(2)式代入(1)式, 整理化简, 考虑摆角u较小时令$\sin u\cos u \approx u,\; \cos 2u \approx 1$, 整理得到受垂直激励和水平约束的单摆运动方程为

$ m{l^2}\ddot u + m\left( {{{\ddot y}_1} + g} \right)l\sin u + k{l^2}u + c{l^2}\dot u = 0 . $

把水平刚度系数k进一步表达为非线性形式:

$ k = - {k_1} + {k_3}{\left( {ul} \right)^2} , $

式中, k₁, k₃分别是一次方刚度和三次方刚度系数.
y方向垂直位移激励型式为简谐激励, 可表示为

$ {y_1} = - a\cos (\omega t) , $

式中a, ω分别为垂直位移激励幅值和激励频率.
把(4)式和(5)式代入(3)式, 并进行无量纲化处理, 令ω₁ = (k₁/m)^1/2, τ = ω₁t, ω_b = ω/ω₁, u = x, 整理得到

$\begin{split} &\ddot x + {c_{11}}\dot x - x + {k_{33}}{x^3} + {g_1}\sin x \\& + b \omega _b ^2\cos {\omega _b}\tau \sin x = 0 , \end{split}$

式中, $c_{11} = c/(m \omega_1),\; k_{33} = k_3l^2/(m\omega_1^2), \; b = a/l, \; g_1 = $$ g/(l \omega_1^2)$. 其中, c₁₁为无量纲化后的阻尼系数, k₃₃为无量纲化后的三次方刚度系数, b为无量纲化后的垂直位移激励幅值, ω_b为无量纲化后的垂直位移激励频率, 即频率比. (6)式是受垂直激励和水平约束单摆的非线性系统动力学方程, 是进一步分析其亚谐共振分岔和混沌行为的基础.

受垂直激励和水平约束的单摆系统, 是工程弹簧摆的典型物理抽象. 单摆悬挂点处垂直方向的位移激励作为激励源, 会关联水平约束摆的水平振动输出, 很多可以抽象成受垂直激励和水平约束单摆的工程问题^[30,31], 更多关注于系统中非线性共振, 尤其是实际的亚谐共振导致多个响应谐波迭加引发的系统响应跳跃增减甚至混沌对实际系统工作性能的影响.
2

-->

3.1.受垂直激励和水平约束单摆系统的1/2次亚谐共振响应

采用多尺度法^[32]对系统求解. 考虑到振动位移x为小量, 令sinx ≈ x, 引入小参数ε, (6)式可化为

$ \begin{split}\ddot x + x =\;& \varepsilon ( - {c_{11}}\dot x - {k_{33}}{x^3} + 2x \\&- {g_1}x + b{\omega _b^2}x\cos {\omega _b}\tau ),\end{split} $

(7)式的一次近似解可记为

$ x(\tau ,\varepsilon ) = {x_0}({T_0},{T_1}) + \varepsilon {x_1}({T_0},{T_1}) + o({\varepsilon ^2}) . $

设置时间尺度为

$T_{0}=\tau, \quad T_{1}=\varepsilon \tau.$

时间微分为

$ \frac{{\rm{d}}}{{{\rm{d}}\tau }} = {D_0} + \varepsilon {D_1} + {\varepsilon ^2}{D_2} + \cdots , $

$ \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{\tau ^2}}} = {D_0^2} + 2\varepsilon {D_0}{D_1} + {\varepsilon ^2}\left( {2{D_0}{D_2} + {D_1^2}} \right) + \cdots , $

式中, ${D_n} = {\partial / {\partial {T_n}}}, ~ n = 0, \; 1, \; 2, \cdots$.
将(8)—(11)式代入(7)式, 比较ε同幂次系数, 得到

$ {D_{{0}}^{\rm{2}}}{x_{\rm{0}}} + {x_{\rm{0}}} = 0 , $

$ \begin{split}{D_0^2}{x_1} + {x_1} = \;&- 2{D_0}{D_1}{x_0} - {c_{11}}{D_0}{x_0} + (2 - {g_1}){x_{\rm{0}}} \\&- {k_{33}}{x_0^3} - b{x_0}{\omega _b^2}\cos ({\omega _b}{T_0}) ,\\[-10pt]\end{split} $

根据(12)式可得

$ {x_0}({T_0},{T_1}) = A({T_1}){{\rm{e}}^{{\rm{i}}{T_0}}} + \bar A({T_1}){{\rm{e}}^{ - {\rm{i}}{T_0}}}, $

将(14)式代入(13)式得

$ \begin{split} &{D_0^2}{x_1} + {x_1} \\ =& ( - 2{\rm{i}}\dot A - {\rm{i}}{c_{11}}A - 3{k_{33}}{A^2}\bar A -{g_1}A + 2A){{\rm{e}}^{{\rm{i}}{T_0}}} \\ &+ (2{\rm{i}}\dot {\bar A} + {\rm{i}}{c_{11}}\bar A - 3{k_{33}}A{{\bar A}^2} + 2\bar A - {g_1}\bar A){{\rm{e}}^{ - {\rm{i}}{T_0}}} \\ & - {k_{33}}{{\bar A}^3}{{\rm{e}}^{ - 3{\rm{i}}{T_0}}} - {k_{33}}{A^3}{{\rm{e}}^{3{\rm{i}}{T_0}}} \\ &- \frac{b}{{\rm{2}}}A{\omega _b^2} \cdot {{\rm{e}}^{{\rm{i}}{T_0} + {\rm{i}}{\omega _b}{T_0}}} - \frac{b}{{\rm{2}}}\bar A{\omega _b^2 }\cdot {{\rm{e}}^{ - {\rm{i}}{T_0} + {\rm{i}}{\omega _b}{T_0}}} \\&- \frac{b}{{\rm{2}}}A{\omega _b^2} \cdot {{\rm{e}}^{{\rm{i}}{T_0} - {\rm{i}}{\omega _b}{T_0}}} - \frac{b}{{\rm{2}}}\bar A{\omega _b^2} \cdot {{\rm{e}}^{ - {\rm{i}}{T_0} - {\rm{i}}{\omega _b}{T_0}}}. \\[-15pt]\end{split} $

观察(15)式, 发现ω_b ≈ 2时, 系统会发生1/2次亚谐共振. 令:

$\omega_{b}=2+\varepsilon \sigma,$

式中, σ为调谐参数, 与频率有关.
将(16)式代入(15)式, 消去久期项得

$ - 2{\rm{i}}\dot A - {\rm{i}}{c_{11}}A - 3{k_{33}}{A^2}\bar A - {g_1}A + 2A - 2b\bar A{{\rm{e}}^{{\rm{i}}\sigma {T_1}}} = 0, $

令

$ \left\{ \begin{aligned} &A = \frac{1}{2}{a_x}{{\rm{e}}^{{\rm{i}}\beta }},\;\;\bar A = \frac{1}{2}{a_x}{{\rm{e}}^{ - {\rm{i}}\beta }}, \\ &\dot A = \frac{1}{2}{{\dot a}_x}{{\rm{e}}^{{\rm{i}}\beta }} + \frac{1}{2}{\rm{i}}\dot \beta {a_x}{{\rm{e}}^{{\rm{i}}\beta }},\end{aligned} \right. $

代入(17)式可得

$ \begin{split} & - {\rm{i}}{{\dot a}_x} + \dot \beta {a_x} - \frac{1}{2}{\rm{i}}{c_{11}}{a_x} - \frac{3}{8}{k_{33}}{a_x^3} + {a_x} - \frac{1}{2}{g_1}{a_x} \\ =\;&{a_x}b\left[ {\cos \left( { - 2\beta + \sigma {T_1}} \right) + {\rm{i}}\sin \left( { - 2\beta + \sigma {T_1}} \right)} \right]. \\[-10pt]\end{split} $

分开实部和虚部, 令

$\varphi=-2 \beta+\sigma T_{1},$

于是得到

$ {a_x}\dot \varphi = {a_x}\sigma - \frac{3}{4}{k_{33}}{a_x^3} + 2{a_x} - {g_1}{a_x} - 2{a_x}b\cos \varphi , $

$ {\dot a_x} = - \frac{1}{2}{c_{11}}{a_x} - {a_x}b\sin \varphi . $

在系统稳态工作时, 令

$ {a_x}\dot \varphi = {\dot a_x} = 0 , $

可得

$ {a_x}\sigma - \frac{3}{4}{k_{33}}{a_x^{\rm{3}}} + 2{a_x} - {g_1}{a_x} = 2{a_x}b\cos \varphi, $

${c_{11}}{a_x} = - 2{a_x}b\sin \varphi ,$

于是近似解为

$ \begin{split} & x(\tau ,\varepsilon ) \\ =\;& \frac{1}{2}{a_x}\cos \left( {\tau + \frac{{\sigma \varepsilon }}{{\rm{2}}}\tau - \frac{\varphi }{2}} \right) \\ &+ \frac{1}{{64}}\varepsilon {k_{33}}{a_x^3}\cos \left( {3\tau + \frac{{3\sigma \varepsilon }}{{\rm{2}}}\tau - \frac{{3\varphi }}{2}} \right) \\&+ \frac{{b{{\left( {2 + \varepsilon \sigma } \right)}^2}}}{{{\rm{4}}{{( {3 + \varepsilon \sigma } )}^2} - {\rm{4}}}}\varepsilon {a_x}\cos \left( {3\tau + \frac{{3\sigma \varepsilon }}{{\rm{2}}}\tau - \frac{\varphi }{2}} \right).\end{split} $

将(24)式和(25)式左右两边平方相加, 可得

$ {\left( {\sigma - \frac{3}{4}{k_{33}}{a_x^2} + 2 - {g_1}} \right)^2} + {c_{11}^2} = 4{b^2}, $

$ \varphi = \arctan \left( {\frac{{ - {c_{11}}}}{{\sigma - {{3{k_{33}}{a_x^2}} / 4} + 2 - {g_1}}}} \right) , $

(27)式即为幅频特性方程, (28)式为相频特性方程.
通过数值解析, 得到幅频响应曲线. 图2反映了b (激励幅值a和摆长l )变化时, 系统随调谐值σ变化的幅频响应. 调谐值σ相同时, b增大, 系统共振区带宽增加; 沿纵坐标方向共振曲线, 左侧幅值a_x与b呈正相关, 右侧幅值a_x与b呈负相关; 沿横坐标方向共振曲线, 左侧b与调谐值σ呈负相关, 右侧呈正相关. 图3反映了k₃₃取不同值时, 系统随调谐值σ变化的幅频响应. 调谐值σ相同时, 随k₃₃增大, 系统共振区带宽减小; 沿纵坐标方向, 左右两侧的共振曲线幅值a_x与k₃₃呈负相关; 沿横坐标方向, 在相同振幅值a_x前提下, k₃₃与调谐值σ呈正相关. 图4反映了c₁₁取不同值时, 系统随调谐值σ变化的幅频响应曲线. 在相同调谐值前σ提下, 随c₁₁增大, 系统共振区带宽变窄; 沿纵坐标方向共振曲线, 左侧a_x与c₁₁呈负相关, 右侧a_x与c₁₁呈正相关; 沿横坐标方向, 在相同振幅值a_x前提下, c₁₁与调谐值σ在左侧呈正相关, 在右侧呈负相关.
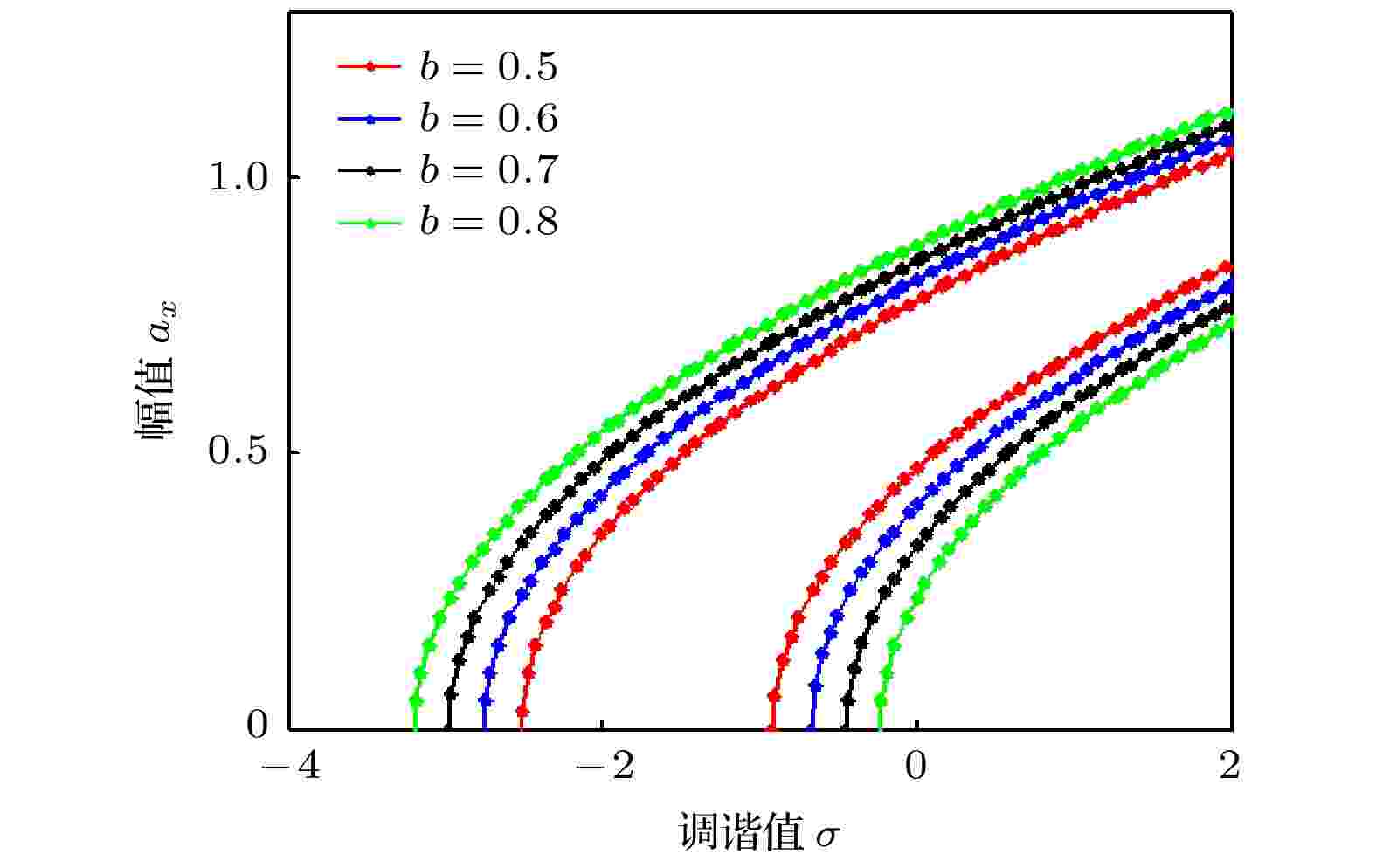图 2 σ变化下改变b的幅频响应曲线
Figure2. Amplitude-frequency response curves with different σ and b.

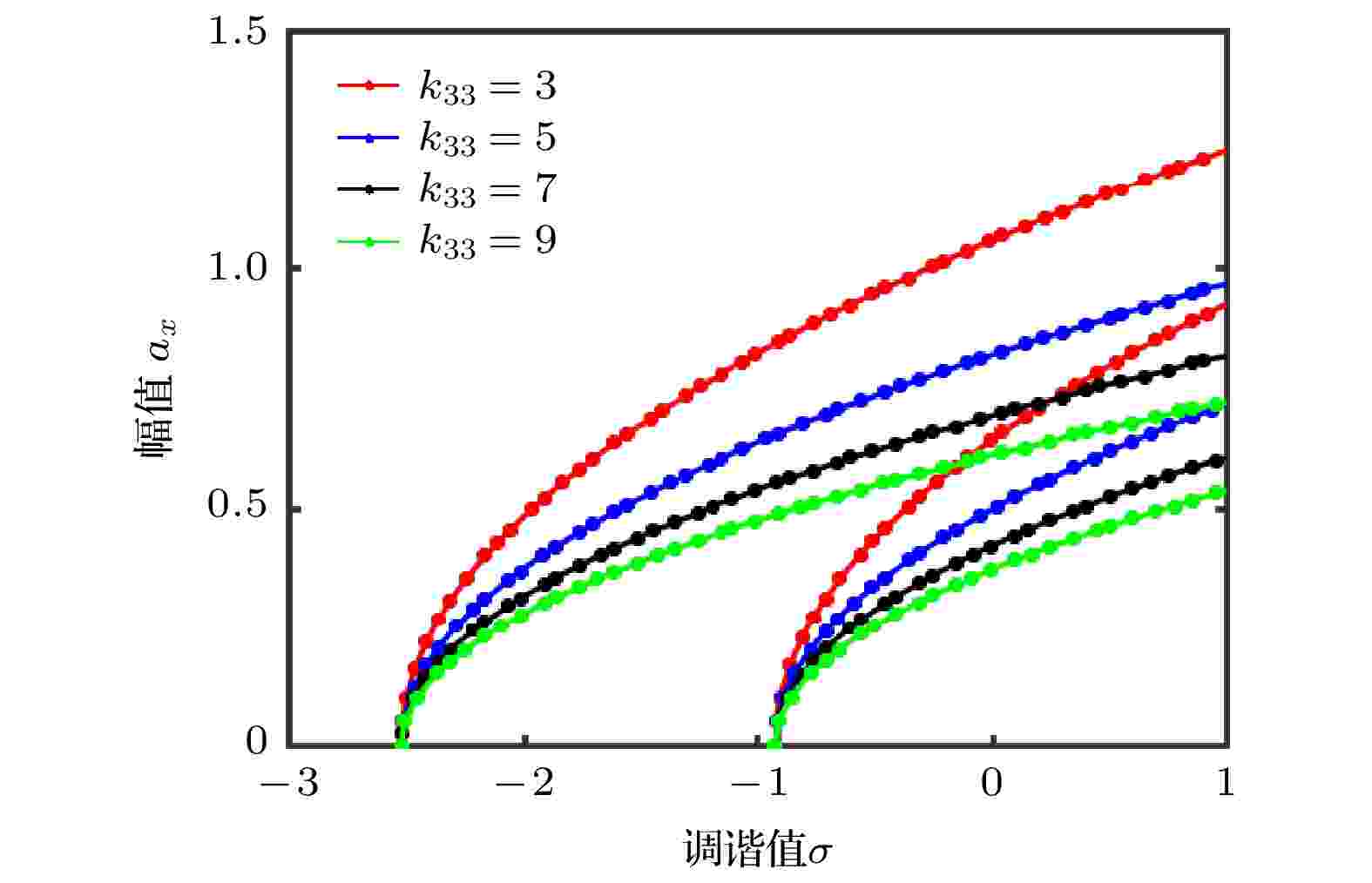图 3 σ变化下改变k₃₃的幅频响应曲线
Figure3. Amplitude-frequency response curves with different σ and k_33.

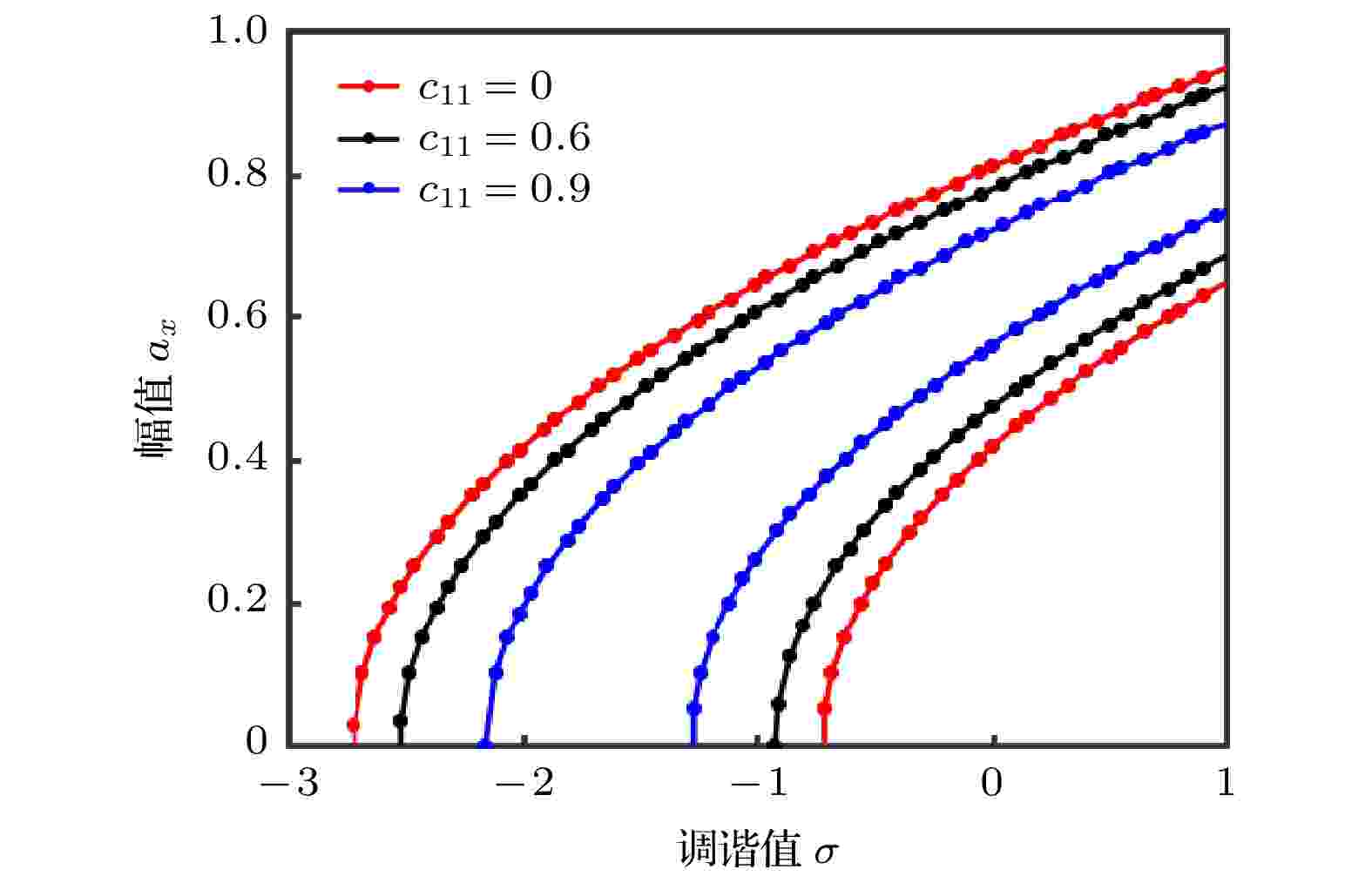图 4 σ变化下改变c₁₁的幅频响应曲线
Figure4. Amplitude-frequency response curves with different σ and c₁₁.

图5反映了调谐值σ变化时, 系统随c₁₁变化的幅频响应曲线. 相同调谐值σ时, 曲线关于c₁₁ = 0对称, 随调谐值σ绝对值增大, 系统振动共振幅值减小; 沿纵坐标方向共振曲线, a_x与σ呈负相关; 沿横坐标方向, 在相同振幅值a_x前提下, c₁₁与调谐值σ呈正相关; 随调谐值σ绝对值增大, 系统振动共振区带宽由封闭曲线转化为开口的缩颈曲线, 系统能耗的增大使共振幅值降低; 且随σ增大, 振幅死亡的开口度增宽, 有利于系统参数的优化阈调控. 图6反映了调谐值σ取不同值时, 系统随k₃₃变化的幅频响应曲线. 随调谐值σ绝对值增大, 共振区域向k₃₃绝对值减小的方向移动; 沿纵坐标方向共振曲线, 左侧a_x与σ呈负相关, 右侧a_x与σ呈正相关; 沿横坐标方向, 在相同振幅值a_x前提下, 共振曲线左侧k₃₃与调谐值σ呈正相关, 右侧k₃₃与调谐值σ呈负相关.
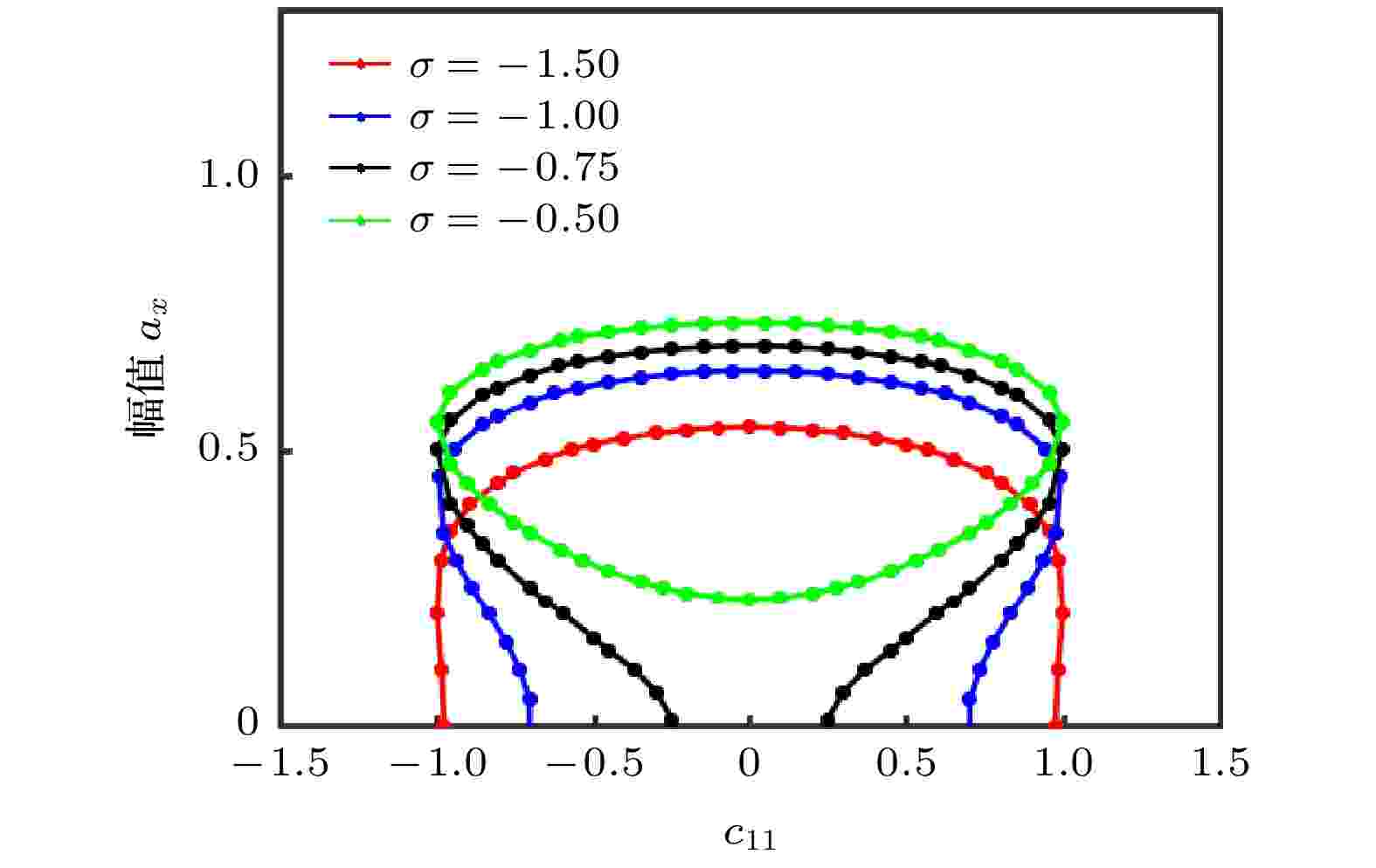图 5 c₁₁变化下改变σ的幅频响应曲线
Figure5. Amplitude-frequency response curves with different c₁₁ and σ.

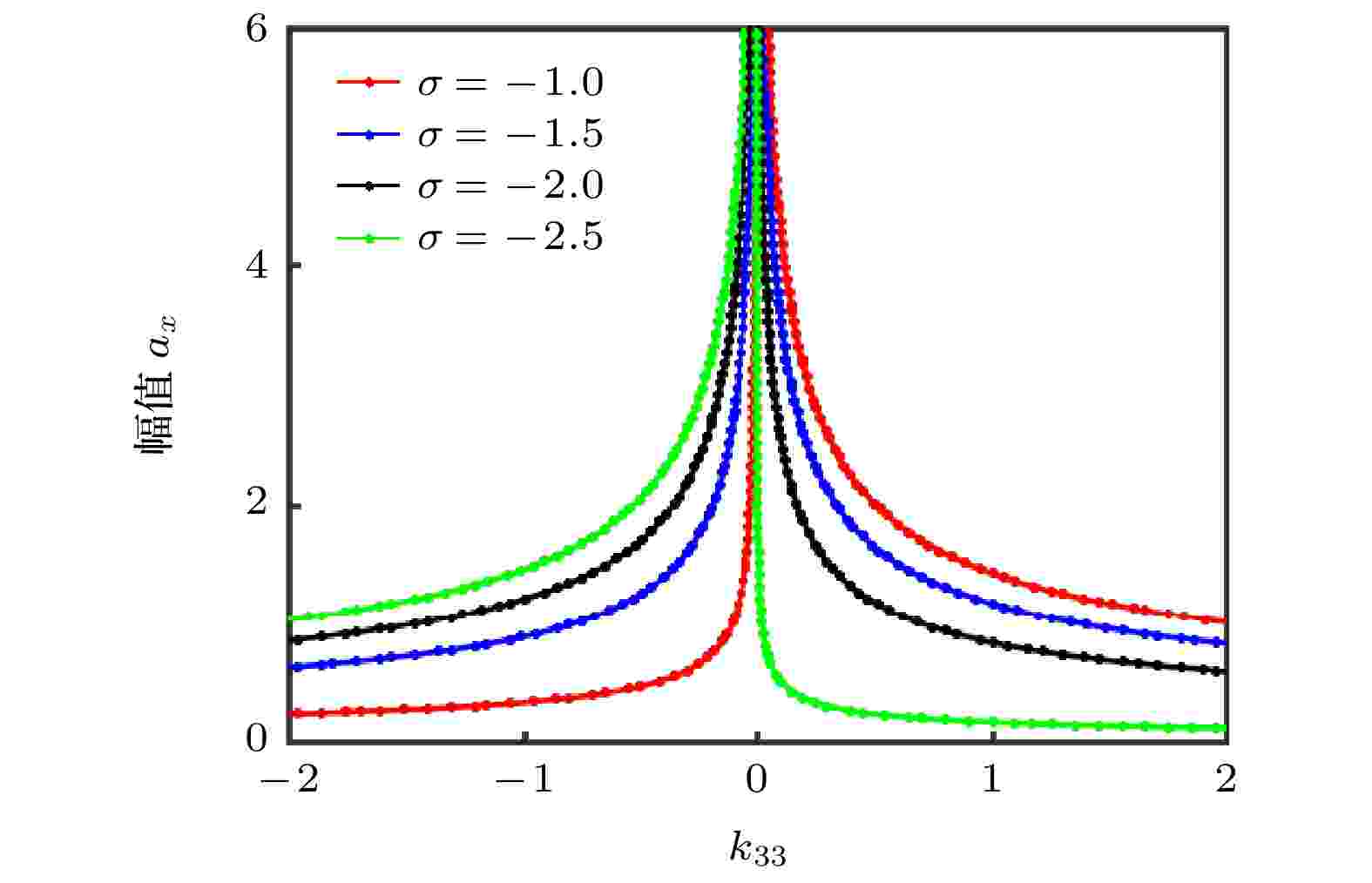图 6 k₃₃变化下改变σ的幅频响应曲线
Figure6. Amplitude-frequency response curves with different k₃₃ and σ.

实际工程中受垂直位移激励和水平约束的抽象单摆, 往往在水平约束方向的小振幅输出下, 可获得良好的工作性能. 通过上述对系统的1/2次亚谐共振幅频特性分析, 得到参数b, k₃₃, c₁₁以及调谐值σ对系统幅频特性的影响规律. 由b = a/l可知, 增大垂直位移激励幅值a或减小等效摆长l, 将导致单摆系统共振区域带宽增大、共振幅值增大; 参数$k_{33}=k_3l^2/(mw^2_1) $, k₃₃的大小和水平约束的三次方刚度成正比, 增大三次方刚度能够减小单摆亚谐共振振幅; 参数$c_{11} =c/(mw_1)$, c₁₁的大小和水平约束的阻尼系数成正比, 通过增大阻尼系数能够使单摆亚谐共振区域变窄和共振幅值减小. 实际工程摆中, 涉及工作性能的结构参数可依据上述分析结果进行调整.
2 -->

3.2.受垂直激励和水平约束单摆系统的1/2次亚谐共振的分岔结构

由奇异性理论定常解的局部稳定性分析, 结合系统幅频特性方程(27)得到

$ {r^2} - {q_1}r + {q_2} = 0 , $

式中,

$ \left\{ \begin{aligned} &r = {a_x^2}, \\& {q_1} = {{{\rm{8}}\left( {2 - {g_1} + \sigma } \right)} / {{\rm{3}}{k_{33}},}} \\ &{q_2} = 16\big[ (2 - g_1 + \sigma)^2 + c_{11}^2 - 4 b^2 \big] / (9k_{33}^2). \end{aligned} \right. $

在(29)式中, 令

$Q(y)= y^{2}-\lambda^{2}+\alpha_{1}=0,$

式中, y = r－q₁/2, λ = q₁/2, α₁ = q₂.
结合普适开折理论, (31)式能够视为Golubitsky-Schaeffer范式^[33] Q(y, λ) = y²－λ²的普适开折, 奇异点即为余维1的临界点. 受垂直激励和水平约束的单摆系统1/2次亚谐共振分岔拓扑结构如下:
a)分岔点集:

$B=\left\{\alpha_{1}=0\right\}.$

b)滞后点集:

$H=\phi.$

c)双极限点:

$D=\left\{\alpha_{1}>0\right\}.$

d)转迁集:

$\varSigma = B \cup H \cup D.$

因此α₁取不同值时, 受垂直激励和水平约束单摆系统1/2次亚谐共振分岔拓扑结构如图7所示. 当α₁ ≥ 0时, 使α₁发生变化的微小扰动都会使系统分岔结构发生变化, 不利于单摆运动的稳定性; 而当参数满足α₁ < 0时, 系统分岔是持久的, 利于保证单摆运动的稳定性.
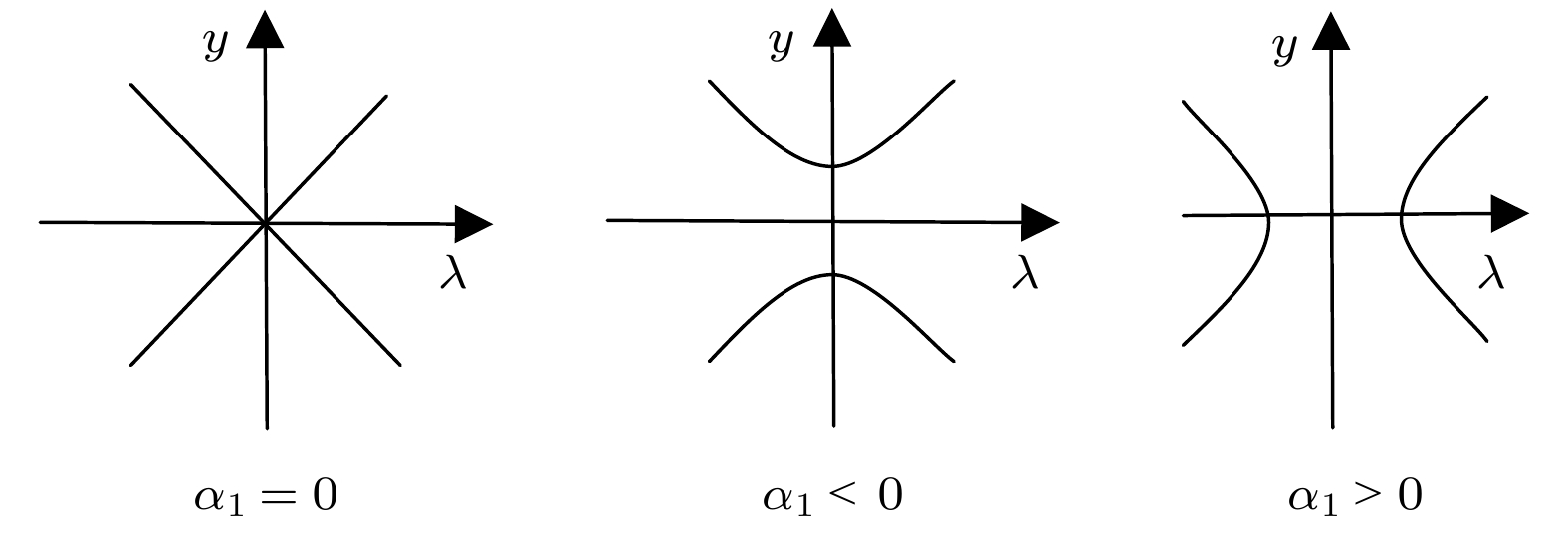图 7 受垂直激励和水平约束单摆系统1/2次亚谐共振分岔拓扑结构
Figure7. Bifurcation topology of 1/2-order subharmonic resonance of a simple pendulum system with vertical excitation and horizontal constraint.

2

-->

4.1.受垂直激励和水平约束单摆系统的势阱

运用Melnikov方法, 对受垂直激励和水平约束的单摆非线性系统进行混沌运动分析与预测. 令$ \sin x \approx x $, 引入小参数δ, 受垂直激励和水平约束的单摆系统的运动方程(6)在δ = 0时的Hamilton系统为

$ \left\{ \begin{aligned} &\frac{{{\rm{d}}x}}{{{\rm{d}}\tau }} = z, \\ &\frac{{{\rm{d}}z}}{{{\rm{d}}\tau }} = (1 - {g_1})x - {k_{33}}{x^3}. \end{aligned} \right. $

令dx/dτ = dz/dτ = 0, 当g₁ < 1, k₃₃ > 0时, 得到系统的3个平衡点分别是

$ \left\{ \begin{aligned} &{A_{\rm{1}}}\left( { - \sqrt {{{\left( {1 - {g_1}} \right)} / {{k_{33}}}}} ,\; 0} \right), \\ &{A_{\rm{2}}}\left( {\sqrt {{{\left( {1 - {g_1}} \right)} / {{k_{33}}}}} ,\; 0} \right), \\ &O\left( {0 ,\; 0} \right). \end{aligned} \right. $

对平衡点O(0, 0), 其特征值λ₁和λ₂是实数; 对于平衡点A₁和A₂, 其特征值λ₁和λ₂是共轭纯虚根, 所以平衡点O是不稳定的鞍点, 而平衡点A₁和A₂是稳定的中心. 令Hamilton函数为H(x, z), 得到受垂直激励和水平约束的单摆系统的Hamilton函数为

$ H\left( {x,z} \right) = \frac{1}{2}{z^2} - \frac{1}{2}\left( {1 - {g_1}} \right){x^2} + \frac{1}{4}{k_{33}}{x^4} . $

令其Hamilton量为

$ H\left( {x,z} \right) = h , $

式中, h为常数.
由(38)式和(39)式, 得到相轨线方程:

$ {z^2} - \left( {1 - {g_1}} \right){x^2} + \frac{1}{2}{k_{33}}{x^4} = 2h . $

势能函数U(x)可表示为

$ U\left( x \right) = - \frac{1}{2}\left( {1 - {g_1}} \right){x^2} + \frac{1}{4}{k_{33}}{x^4} . $

Hamilton系统(38)的势阱曲线和相轨线分别如图8(a)和图8(b)所示. 图8(a)中, 对称的双势阱W₁和W₂分别对应于稳定中心点, 势垒对应于不稳定鞍点. 当把系统中的质点运动理解为孤立振子或振子群型式的运动时: 一方面, 对称势阱W₁和W₂之间的势垒为系统稳定的周期运动提供了过渡平台, 当系统振子运动能量较小而不能穿越势垒时, 振子在W₁或W₂势阱内做小幅值的稳定周期运动, 对应于图8(b)中的封闭椭圆相轨线, 最后将稳定于中心点; 另一方面, 当系统振子获得越过势垒的足够能量后, 会在势阱W₁和W₂之间大范围运动, 个别能量高的活跃振子在势阱壁和势垒平台间发生碰撞、反弹、折回和冲击, 使系统运动复杂化, 对应于图8(b)中的O点或其他相轨线. 系统能量变化, 会引发系统运动相轨线的拓扑结构改变, 系统的运动状态随之改变. 图8(a)中, 随摆长l增大, 势阱的开口宽度和深度都减小, 说明系统的摆动运动能量更多的转移到振动运动能量上, 能量在运动形态间交换, 在图8(b)的局部放大结构图8(c)中, 摆长l增大时, 系统从O点出发的相轨线会在不同摆长的运动路径间发生跃迁和跌落的路径转迁, 使得系统运动复杂化. 这种受垂直激励和水平约束的单摆系统, 是工程弹簧摆的典型物理抽象. 例如机构中的两个弹性接触辊在服役状态下发生动态弹性形变, 即1个工作循环中, 两辊间的弹性形变(摆长)的动态连续变化引起的能量转迁会使系统的运动路径在不同的相轨线之间切换, 使得系统运动复杂化.
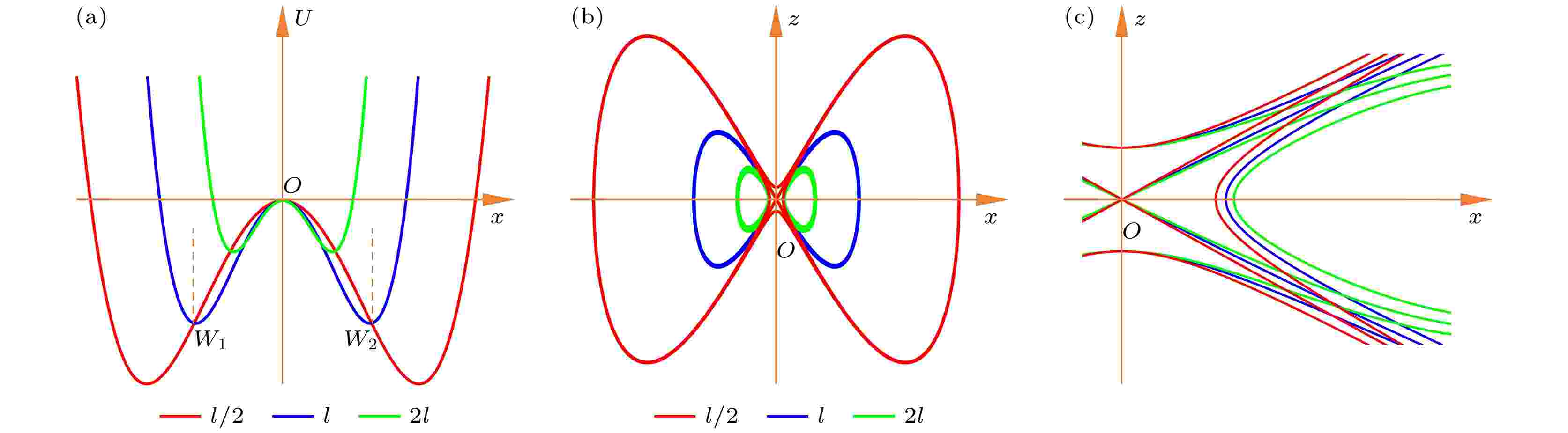图 8 (a)势阱曲线; (b), (c)相轨线及其局部放大图
Figure8. (a) Potential well curve; (b), (c) phase track and its enlarged view.

2 -->

4.2.受垂直激励和水平约束单摆系统的同宿轨与混沌预测

当h = 0时, 可得(38)式同宿轨道为

$ z = \pm \sqrt {(1 - {g_1}){x^2} - \frac{1}{2}{k_{33}}{x^4}}. $

取τ = 0, z = 0可解得

$ {x_0} = \pm \sqrt{ \dfrac{2(1 - {g_1})}{{k_{33}}}}, $

因dx/dτ = z, 对(42)式积分并整理得

$ {x^ \pm }(\tau ) = \pm \sqrt {\frac{{2(1 - {g_1})}}{{{k_{33}}}}} {\rm{sech}} \sqrt {1 - {g_1}} \tau, $

由此得系统的同宿轨道参数方程为

$ \begin{split}&\left( {\begin{array}{*{20}{c}}{{x^ \pm }(\tau )}\\{{z^ \pm }(\tau )}\end{array}} \right)=\\\;& \left( \begin{array}{c} \pm \sqrt {\dfrac{{2(1 - {g_1})}}{{{k_{33}}}}} {\rm{sech}}\sqrt {1 - {g_1}} \tau \\ \mp \sqrt {\dfrac{2}{{{k_{33}}}}} (1 - {g_1}) {\rm{sech}}\sqrt {1 - {g_1}} \tau {\rm{tanh}}\sqrt {1 - {g_1}} \tau \end{array} \right) .\end{split}$

可把受垂直激励和水平约束的单摆系统的Melnikov函数表示为

$ {M_ \pm }(\tau {}_0) = \int_{ - \infty }^{ + \infty } {f({x^ \pm }(\tau )) \wedge g({x^ \pm }(\tau ),\tau + {\tau _0})} {\rm{d}}\tau . $

利用(45)式可得

$ \begin{split}&f({x^ \pm }(\tau )) \wedge g({x^ \pm }(\tau ),\;\tau + {\tau _0}) = - {c_{11}}{\left[ {{z^ \pm }(\tau )} \right]^2} \\ \;& \qquad - b{\omega _b^2}\cos {\omega _b}(\tau + {\tau _0}){x^ \pm }(\tau ){z^ \pm }(\tau ), \end{split}$

将(47)式代入系统Melnikov函数(46)得到

$\begin{split}&{M_ \pm }(\tau {}_0) = \int_{ - \infty }^{ + \infty } {\left[ { - {c_{11}}{{({z^ \pm }(\tau ))}^2}} \right]} {\rm{d}}\tau \\&- \int_{ - \infty }^{ + \infty } {\left[ {b{\omega _b^2}\cos {\omega _b}(\tau + {\tau _0}){x^ \pm }(\tau ){z^ \pm }(\tau )} \right]} {\rm{d}}\tau ,\end{split}$

计算得到系统发生混沌运动的Melnikov阈值为

$ \begin{split}{M_ \pm }(\tau {}_0) =\;& \frac{{{\rm{4}}{c_{11}}{{(1 - {g_1})}^{{3 / 2}}}}}{{3{k_{33}}}}\pm 8{\rm{\pi }}b{\omega _b^4}\frac{{{{(1 - {g_1})}^{{3 / 2}}}}}{{{k_{33}}}} \\&\times\sin {\omega _b}{\tau _0}{\mathop{\rm csch}\nolimits} (2\sqrt {1 - {g_1}} {\rm{\pi }}{\omega _b}).\\[-10pt]\end{split}$

由Melnikov理论可知, 当(49)式存在简单零点时, 系统(6)存在Smale马蹄意义上的混沌. 因此系统在1/2次亚谐共振情况下, 当满足

$\left\{ \begin{aligned}&\sup \left( {{M_ \pm }\left( {\tau {}_0} \right)} \right) > 0, \\&\inf \left( {{M_ \pm }\left( {\tau {}_0} \right)} \right) < 0,\end{aligned} \right.$

即:

$\begin{split}&\mathop {\min }\limits_{{\tau _0} \in \left( {0,{{2{\rm{\pi }}} / {{\omega _b}}}} \right)} \bigg[ { \pm 8{\rm{\pi }}b{\omega _b^4}\frac{{{{(1 - {g_1})}^{{3 / 2}}}}}{{{k_{33}}}}\sin {\omega _b}{\tau _0}{\mathop{\rm csch}\nolimits} (2\sqrt {1 - {g_1}} {\rm{\pi }}{\omega _b})} \bigg] < - \frac{{{\rm{4}}{c_{11}}{{(1 - {g_1})}^{{3 / 2}}}}}{{3{k_{33}}}} \\ &< \mathop {\max }\limits_{{\tau _0} \in \left( {0,{{2{\rm{\pi }}} / {{\omega _b}}}} \right)} \bigg[ { \pm 8{\rm{\pi }}b{\omega _b^4}\frac{{{{(1 - {g_1})}^{{3 / 2}}}}}{{{k_{33}}}}\sin {\omega _b}{\tau _0}{\mathop{\rm csch}\nolimits} (2\sqrt {1 - {g_1}} {\rm{\pi }}{\omega _b})} \bigg],\end{split}$

存在${M_ \pm }(\tau {}_0) = 0$且${{\partial {M_ \pm }(\tau {}_0)} \mathord{\left/ {\vphantom {{\partial {M_ \pm }(\tau {}_0)} {\partial \tau {}_0}}} \right. } {\partial \tau {}_0}} \ne 0$, 系统可发生Smale马蹄意义的混沌.
图9直观反映了系统发生混沌的临界参量b, c₁₁, ω_b之间的制约关联条件. 曲面的上部空间参数组合引发系统混沌运动, 当c₁₁接近0.5时, b值越大, 越易引发系统混沌. 根据Melnikov函数预测条件, 选取符合混沌临界参数c₁₁ = 0.5, k₃₃ = 1.5, g₁ = 0.8, b = 0.6, ω_b = 2, 计算单摆系统的混沌吸引子空间结构, 如图10所示. 图10中混沌吸引子呈现中心对称分布, 蓝色与红色分别代表单摆系统顺时针和逆时针运动的混沌吸引子, 运动过程中系统参数改变, 导致系统能量的交替变化, 使系统运动复杂化. 图11对应系统摆长变化的分岔, 随摆长l增大, 系统历经二周期、单周期、二周期、四周期到混沌运动的演化过程. 结合图10与图11, 系统在ω_b = 2时的混沌吸引子是成对的两个旋转对称分岔点的余维.
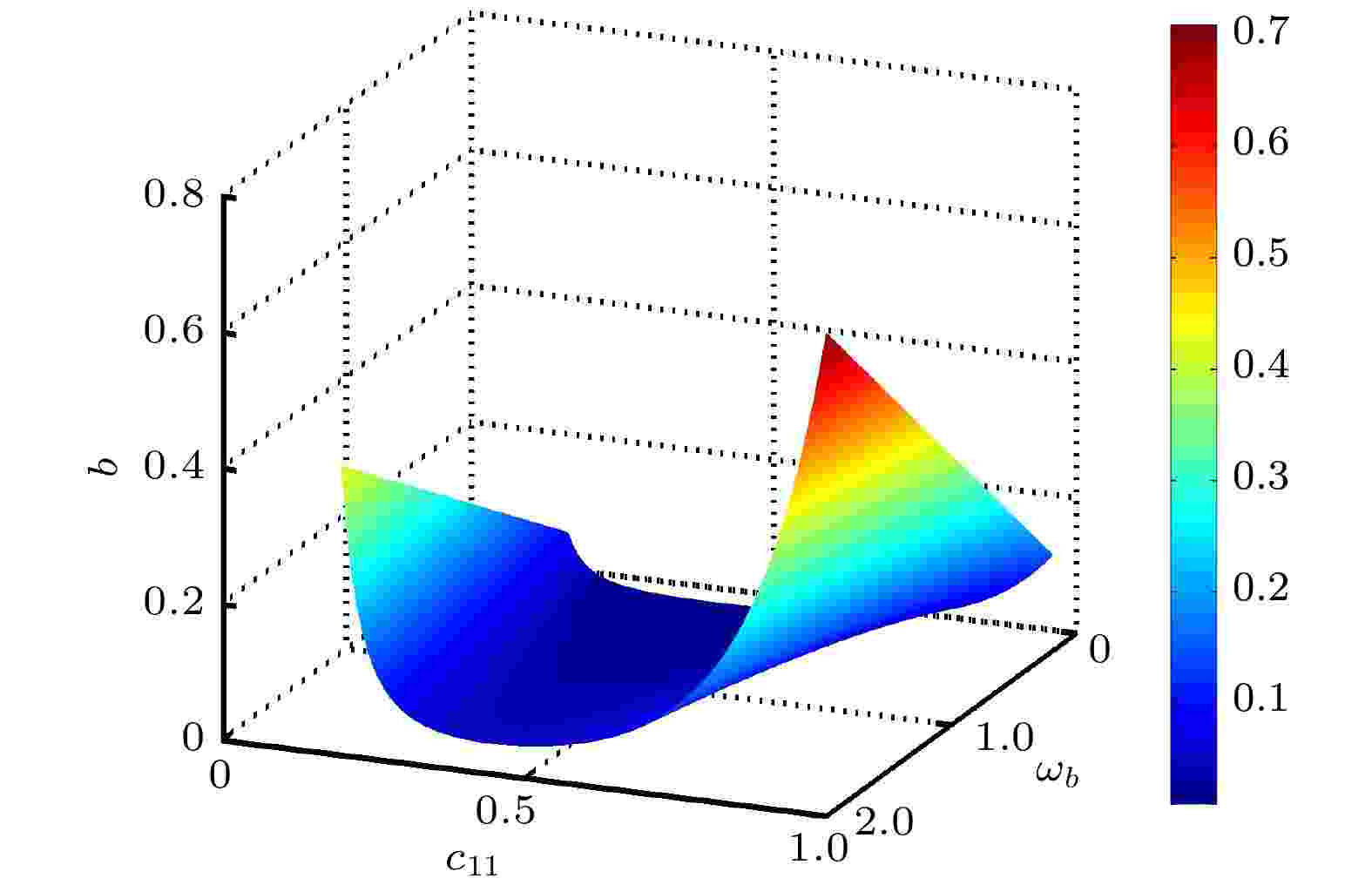图 9 系统混沌运动的参数条件
Figure9. Parameter conditions for chaotic motion of the system

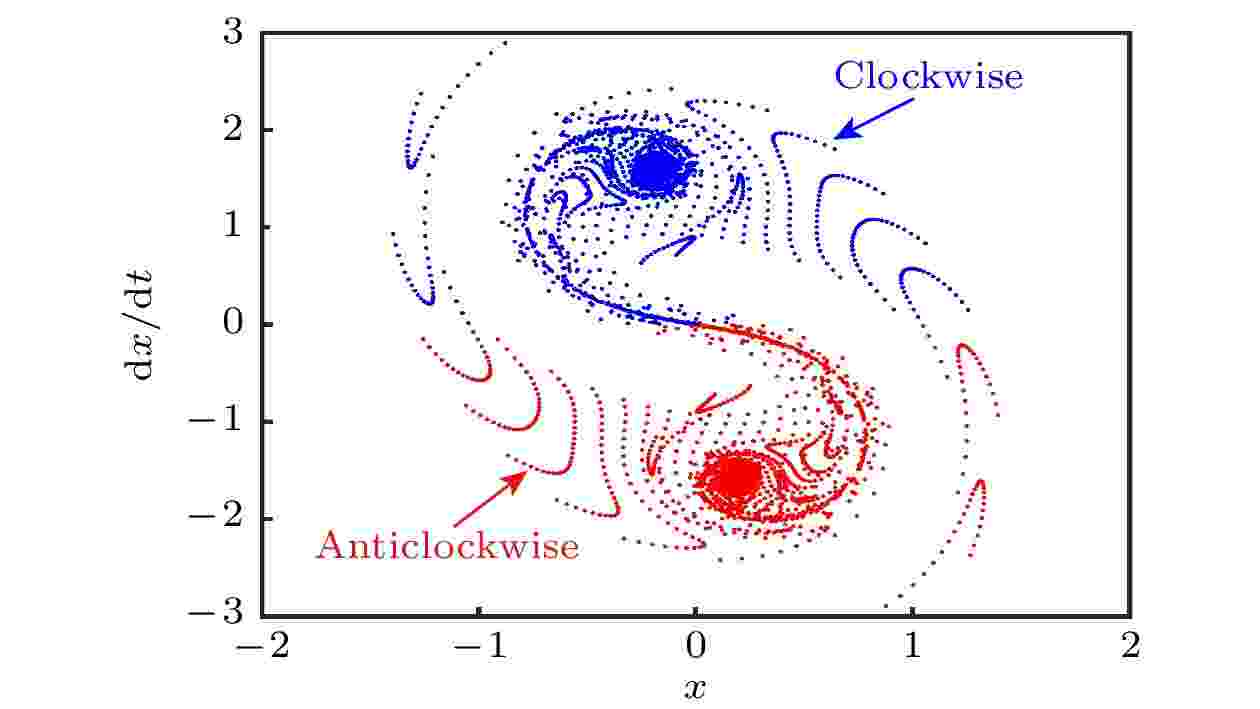图 10 单摆系统亚谐共振在ω_b = 2时的混沌吸引子
Figure10. Chaotic attractor of simple pendulum system when ω_b = 2.

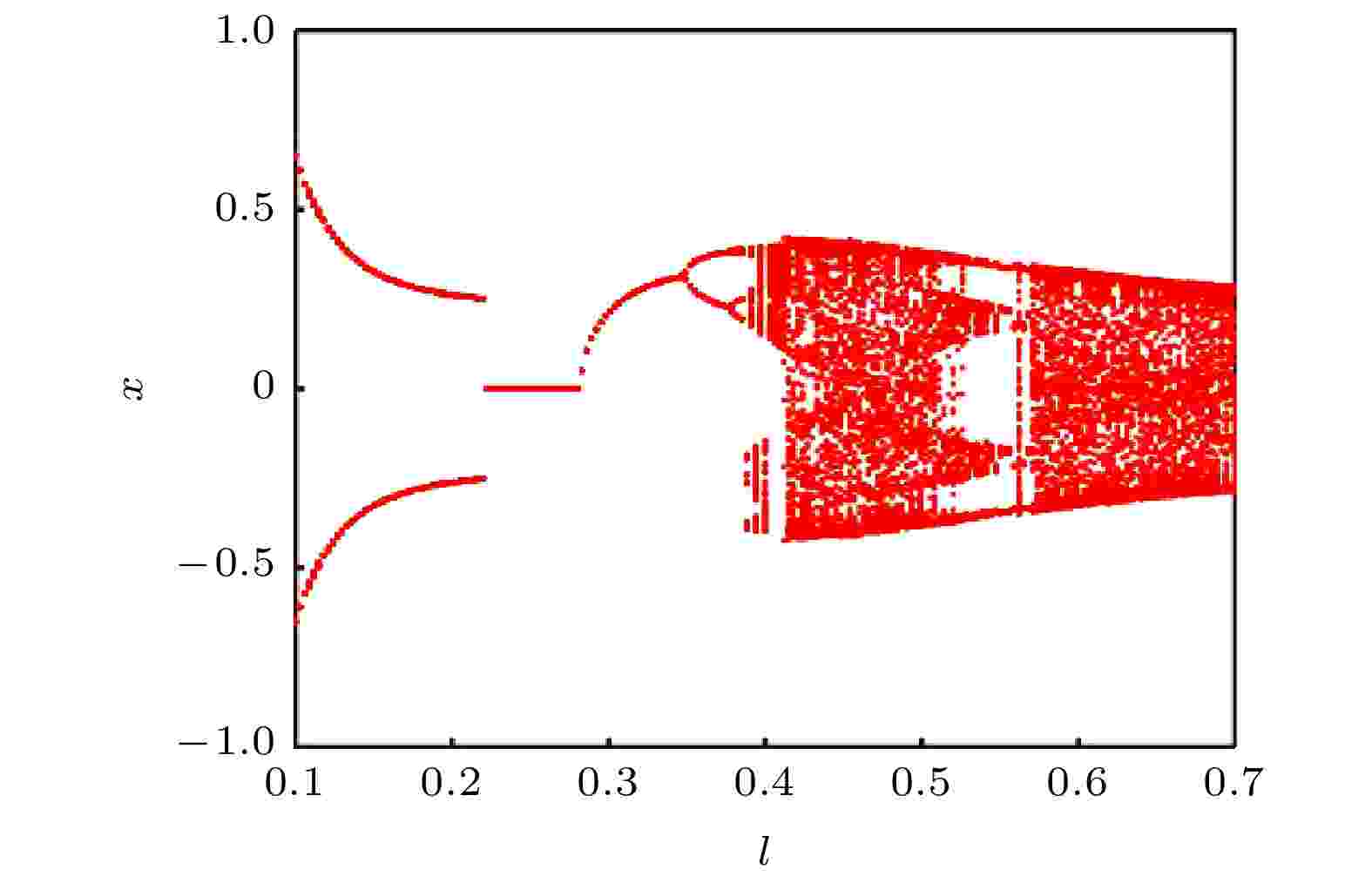图 11 摆长l变化下的分岔图
Figure11. Bifurcation diagram with different l.

对受垂直激励和水平约束的单摆系统(6)进行数值仿真, 如无特殊说明, 参数如下: c₁₁ = 0.618, k₃₃ = 1.3, g₁ = 0.28, b = 0.48. 通过仿真分岔、最大Lyapunov指数和双参耦合分岔等系统特性, 研究单摆系统亚谐共振与混沌的演化机制.
2

-->

5.1.受垂直激励和水平约束单摆系统的亚谐共振分岔与混沌

3 -->

5.1.1.ω_b对单摆系统分岔的影响

随ω_b变化的单摆系统的运动分岔及最大Lyapunov指数如图12(a)和图12(b)所示. 可见, 随ω_b增大, 单摆系统历经“单周期-二周期-四周期-混沌-四周期-混沌-二周期-混沌-四周期-二周期-单周期”的系列复杂运动变化, 且中间交替发生多次的倍周期分岔.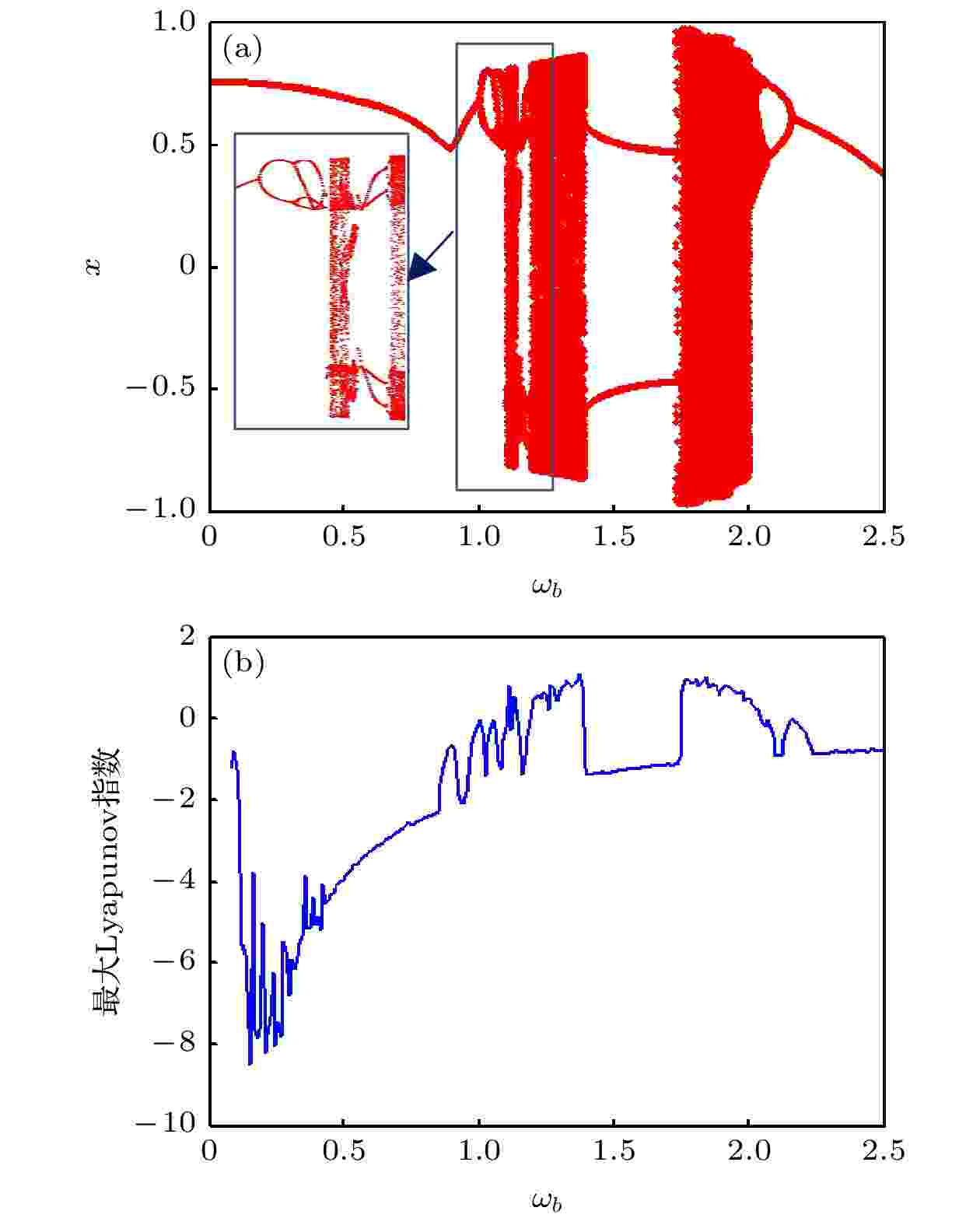
图 12 ω_b变化下的(a)分岔和(b)最大Lyapunov指数
Figure12. (a) Bifurcation and (b) maximum Lyapunov exponent with different ω_b.

ω_b变化的相图和时间历程如图13(a)—(f)所示. ω_b = 0.5, 1.02, 1.8时, 系统分别处于单周期、二周期、混沌运动状态; 且ω_b = 1.8的时间历程图(图14(a)—(c))显示出系统运动中较明显的交叠拍振共振行为, 伴随b (垂直位移激励幅值或摆长)变化, 系统能量也不断交替改变, 系统共振频次和振幅带宽都发生变化. 比较图13(d)—(f)发现, ω_b变化改变了单摆的运动周期, 其变化过程与系统动力学行为(图13(a)—(c))相一致.
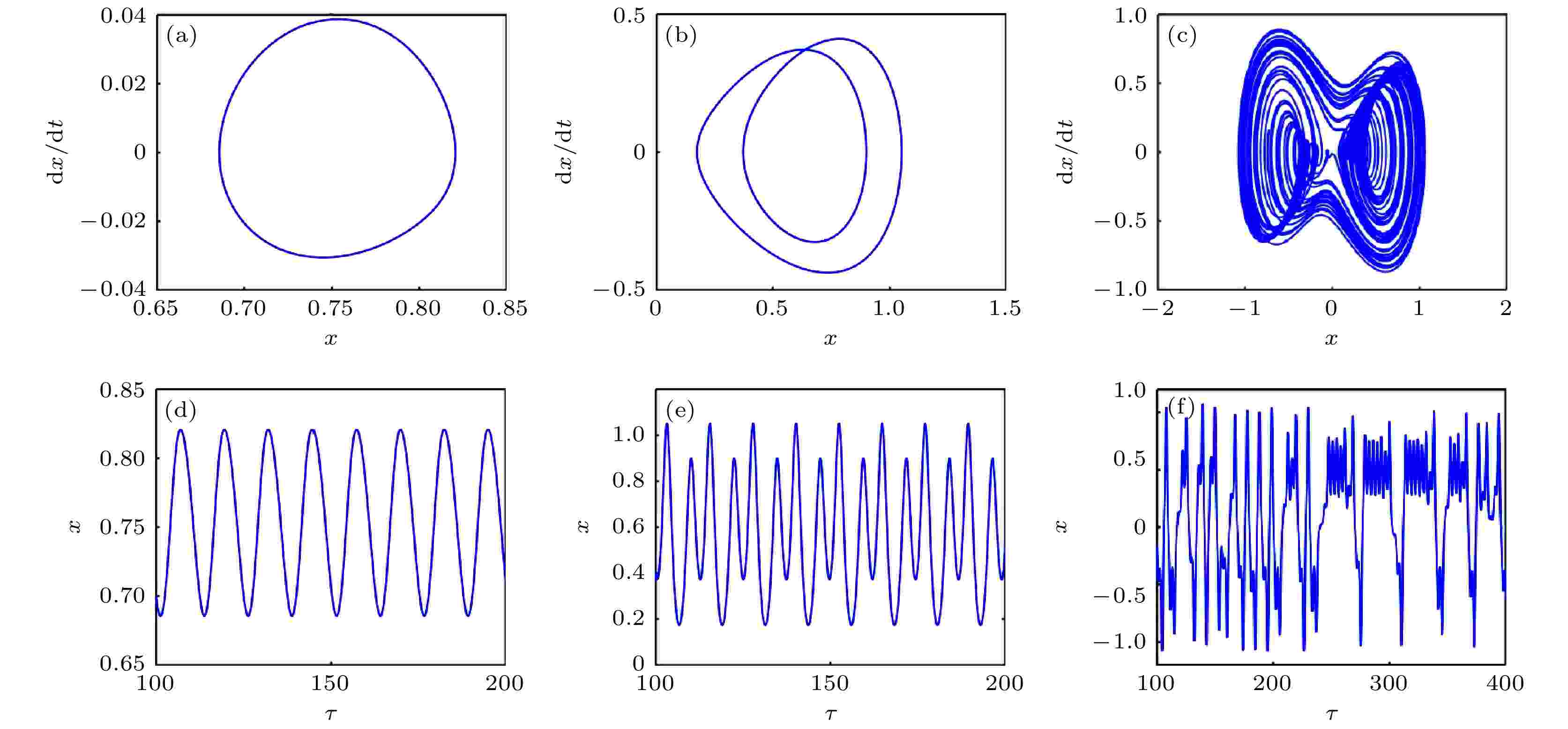图 13 ω_b变化下的(a)?(c)相图和(d)?(f)时间历程图　(a), (d) ω_b = 0.5; (b), (e) ω_b = 1.02; (c), (f) ω_b = 1.8
Figure13. (a)?(c) Phase diagram and (d)?(f) time history diagram with different ω_b : (a), (d) ω_b = 0.5; (b), (e) ω_b = 1.02; (c), (f) ω_b = 1.8

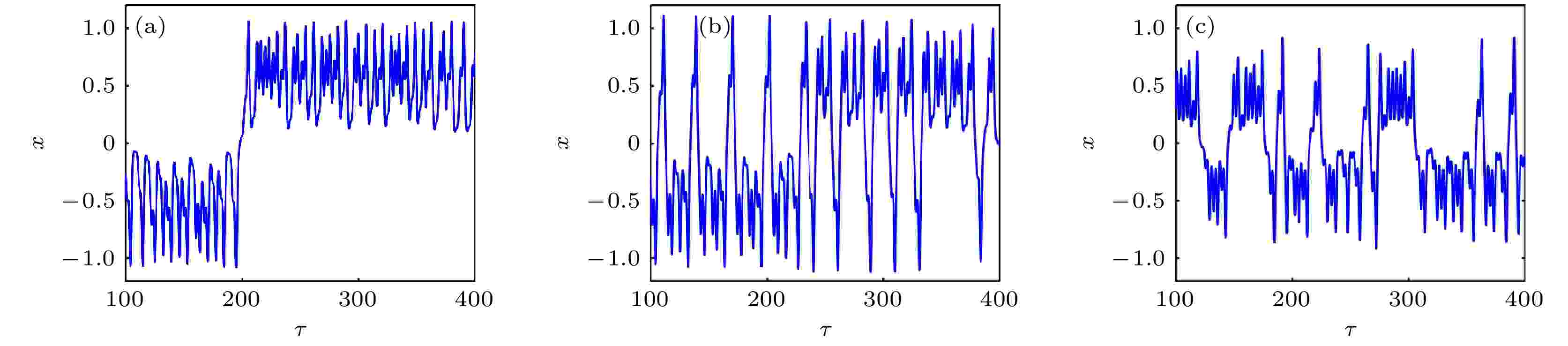图 14 当ω_b = 1.8时b变化下的时间历程图　(a) b = 0.28; (b) b = 0.38; (c) b = 0.58
Figure14. Time history diagram when b changes and ω_b = 1.8: (a) b = 0.28; (b) b = 0.38; (c) b = 0.58.

3 -->

5.1.2.c₁₁对单摆系统分岔的影响

随c₁₁变化的系统分岔和最大Lyapunov指数如图15(a)和图15(b)所示. 可见, 随水平约束阻尼系数c₁₁增大, 系统历经“混沌-四周期-二周期-混沌-八周期-四周期-二周期-单周期”的系列复杂运动变化过程.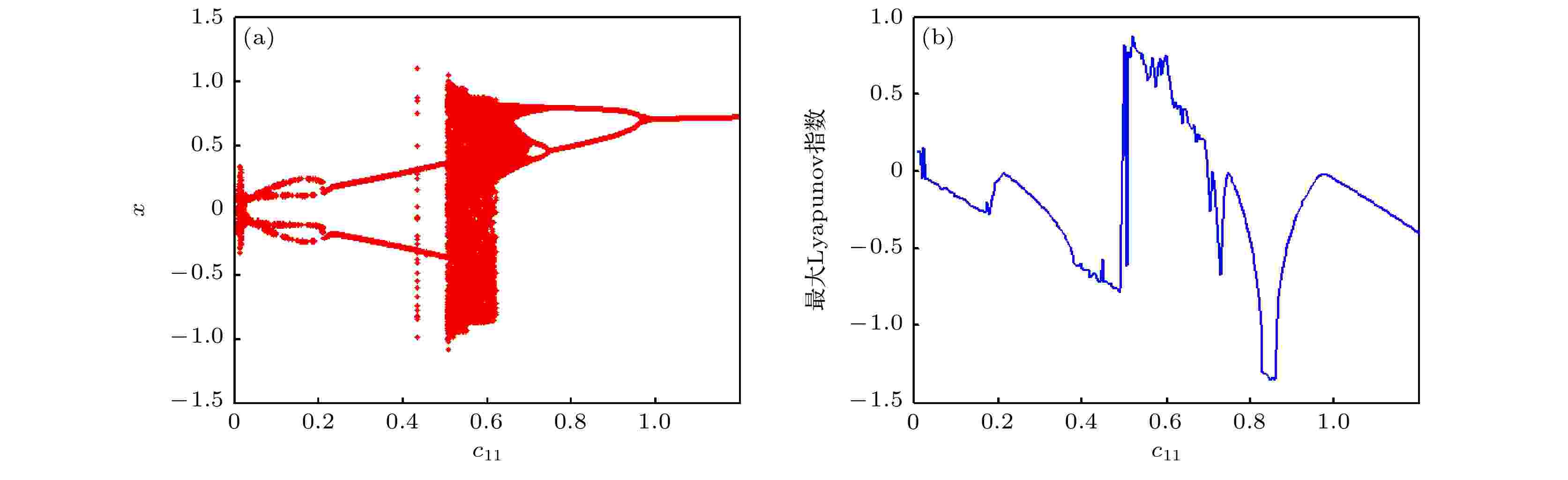
图 15 c₁₁变化下的(a)分岔和(b)最大Lyapunov指数
Figure15. (a) Bifurcation and (b) maximum Lyapunov exponent with different c₁₁.

c₁₁变化的相图和时间历程如图16(a)—(f)所示. 其中图16(a)—(f)中, c₁₁ = 0.6, 0.63, 1.2时, 系统分别处于双曲混沌、混沌、单周期运动状态; c₁₁ = 0.6, 系统表现为左右两中心的相轨迹被鞍点所吸引的双曲混沌; c₁₁ = 0.63, 系统表现出对称性降低, 有序性增加的混沌态. 随c₁₁继续增大, 系统由倒倍周期分岔发展为c₁₁ = 1.2的单周期运动. 比较图16(d)—(f)发现, c₁₁变化改变了水平约束单摆系统的运动周期, 其变化过程与系统动力学行为(图16(a)—(c))相一致.
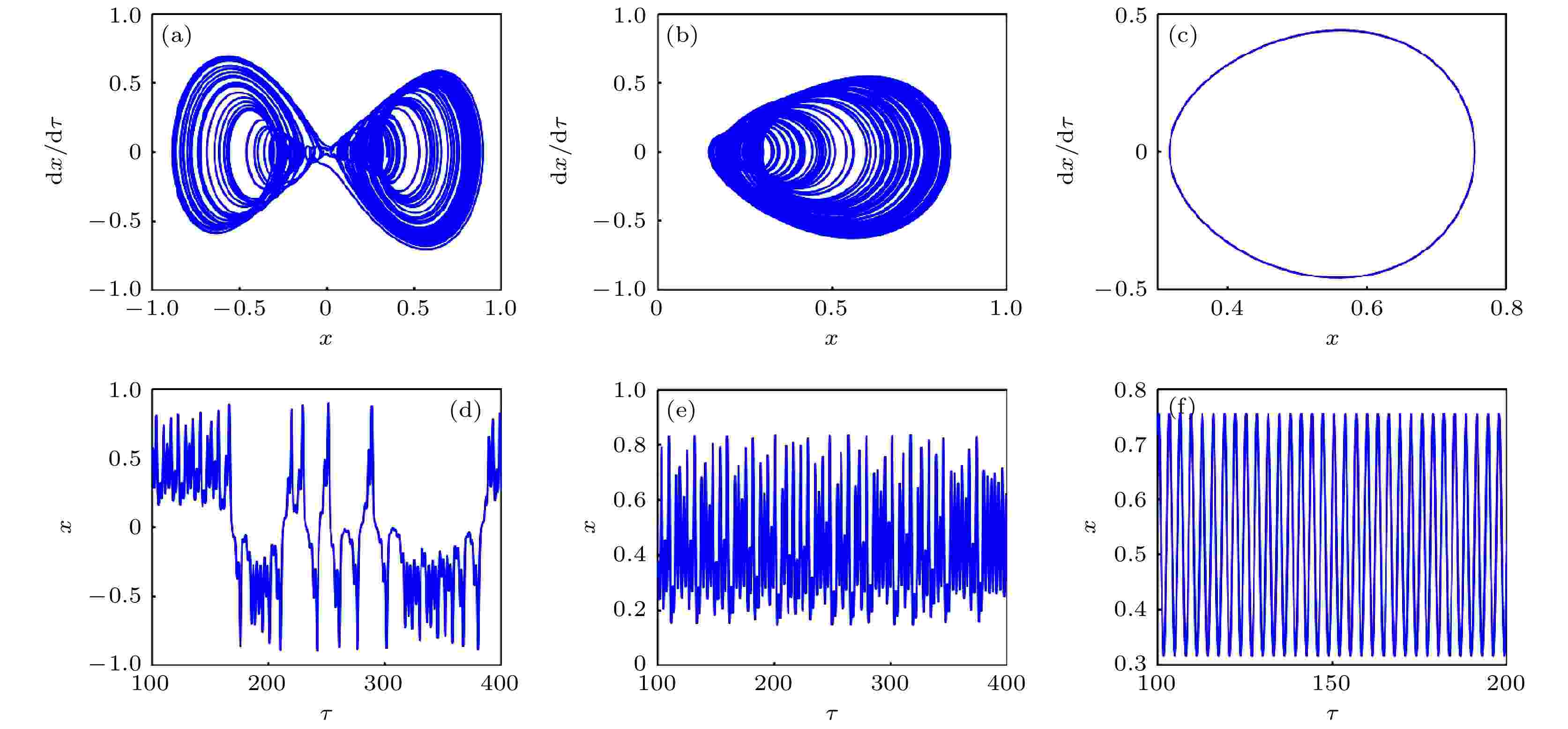图 16 c₁₁变化下的(a)?(c)相图和(d)?(f)时间历程图　(a), (d) c₁₁ = 0.6; (b), (e) c₁₁ = 0.63; (c), (f) c₁₁ = 1.2
Figure16. (a)?(c) Phase diagram and (d)?(f) time history diagram with different c₁₁: (a), (d) c₁₁ = 0.6; (b), (e) c₁₁ = 0.63; (c), (f) c₁₁ = 1.2.

3 -->

5.1.3.g₁对单摆系统分岔的影响

随g₁变化的系统分岔图及最大Lyapunov指数曲线如图17(a)和图17(b)所示. 可见, 随g₁增大, 单摆系统历经“混沌-四周期-二周期-单周期”的运动状态改变. g₁取不同值的相图和时间历程如图18所示. 其中图18(a)—(c), 随系统历经双曲混沌、混沌、二周期等运动状态的改变, 这与图18(d)—(f)中, g₁变化引起的系统动力学行为相一致.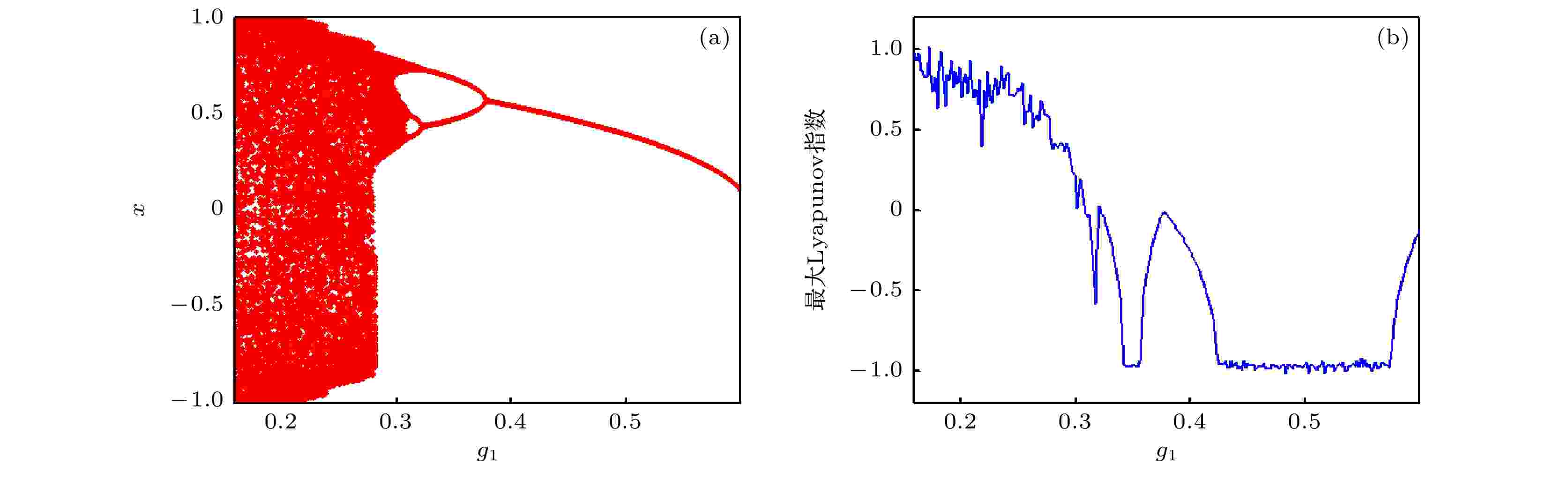
图 17 g₁变化下的(a)分岔和(b)最大Lyapunov指数
Figure17. (a) Bifurcation and (b) maximum Lyapunov exponent with different g₁.

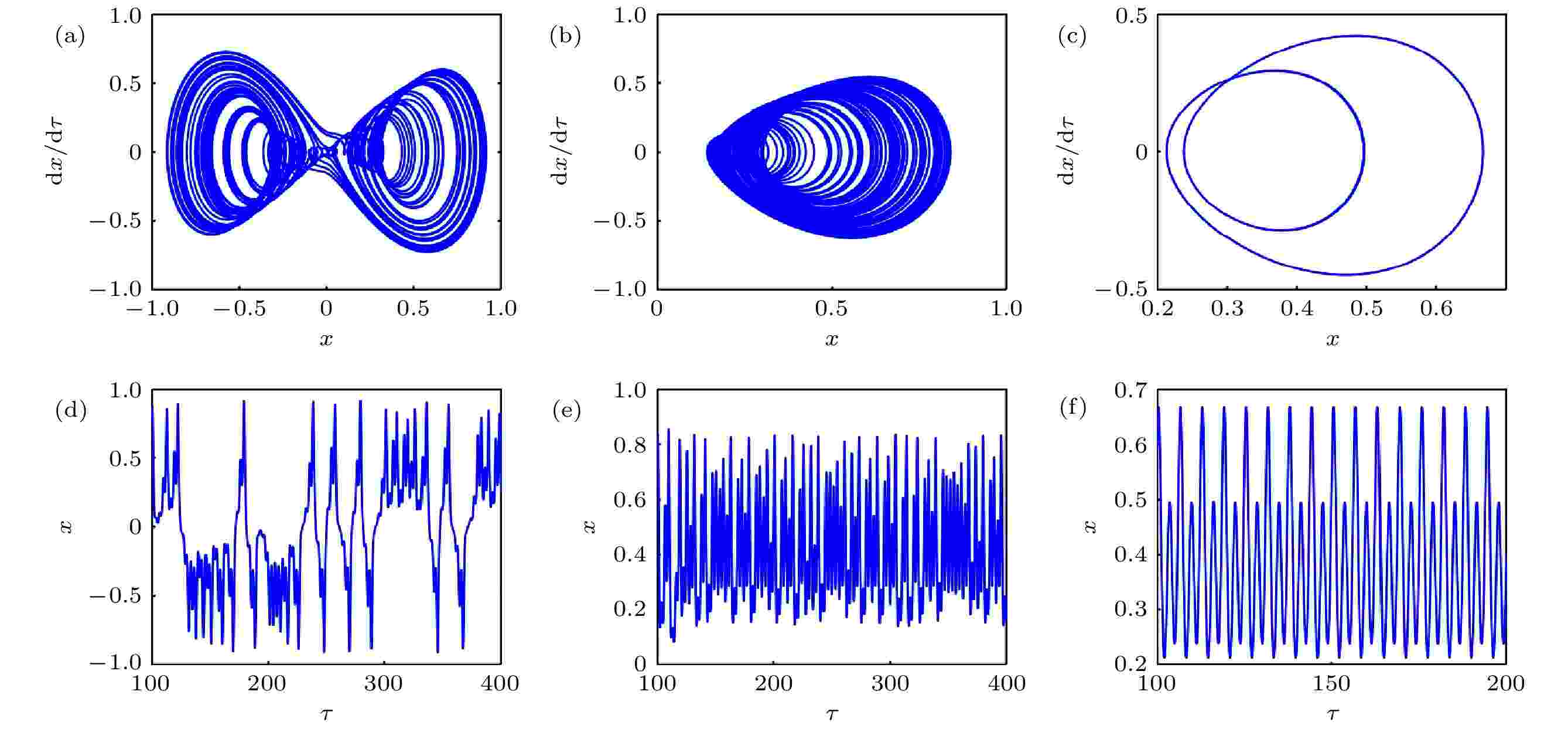图 18 g₁变化下的(a)?(c)相图和(d)?(f)时间历程图　(a), (d) g₁ = 0.27; (b), (e) g₁ = 0.28; (c), (f) g₁ = 0.36
Figure18. (a)?(c) Phase diagram and (d)?(f) time history diagram with different g₁: (a), (d) g₁ = 0.27; (b), (e) g₁ = 0.28; (c), (f) g₁ = 0.36.

3 -->

5.1.4.k₃₃对单摆系统分岔的影响

随k₃₃变化的系统分岔及最大Lyapunov指数曲线如图19(a)和图19(b)所示. 随k₃₃增大, 系统历经“单周期-二周期-四周期-八周期-混沌”系列运动状态的改变过程. 随k₃₃变化的相图和时间历程如图20所示. 其中图20(a)—(c), k₃₃ = 0.6, 1.2, 1.4时, 系统分别处于四周期、混沌、双曲混沌运动. 随k₃₃变化, 单摆的周期性也发生改变如图20(d)—(f), 其变化过程与系统动力学行为(图20(a)—(c))相一致.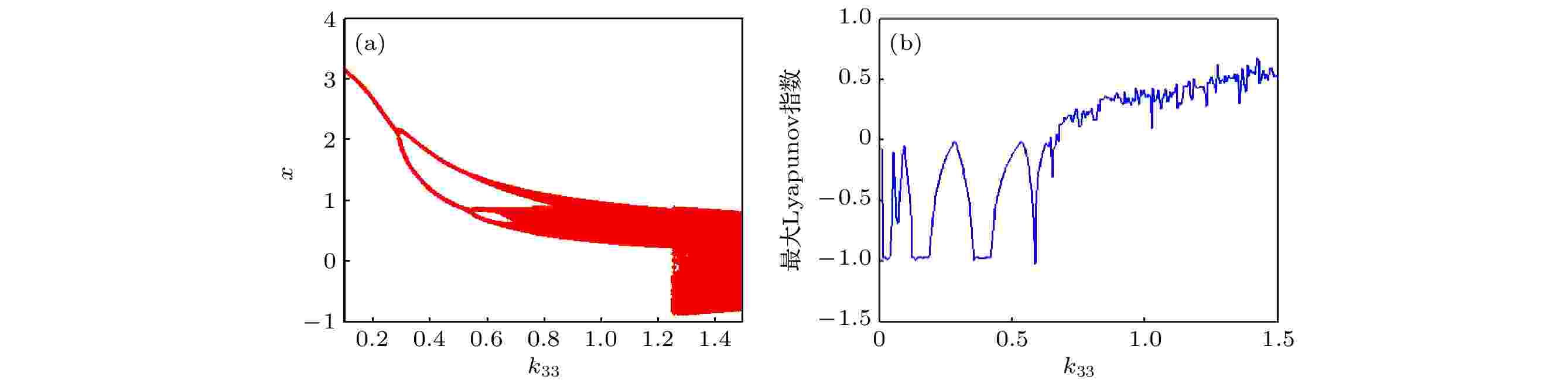
图 19 k₃₃变化下的(a)分岔和(b)最大Lyapunov指数
Figure19. (a) Bifurcation and (b) maximum Lyapunov exponent with different k_33..

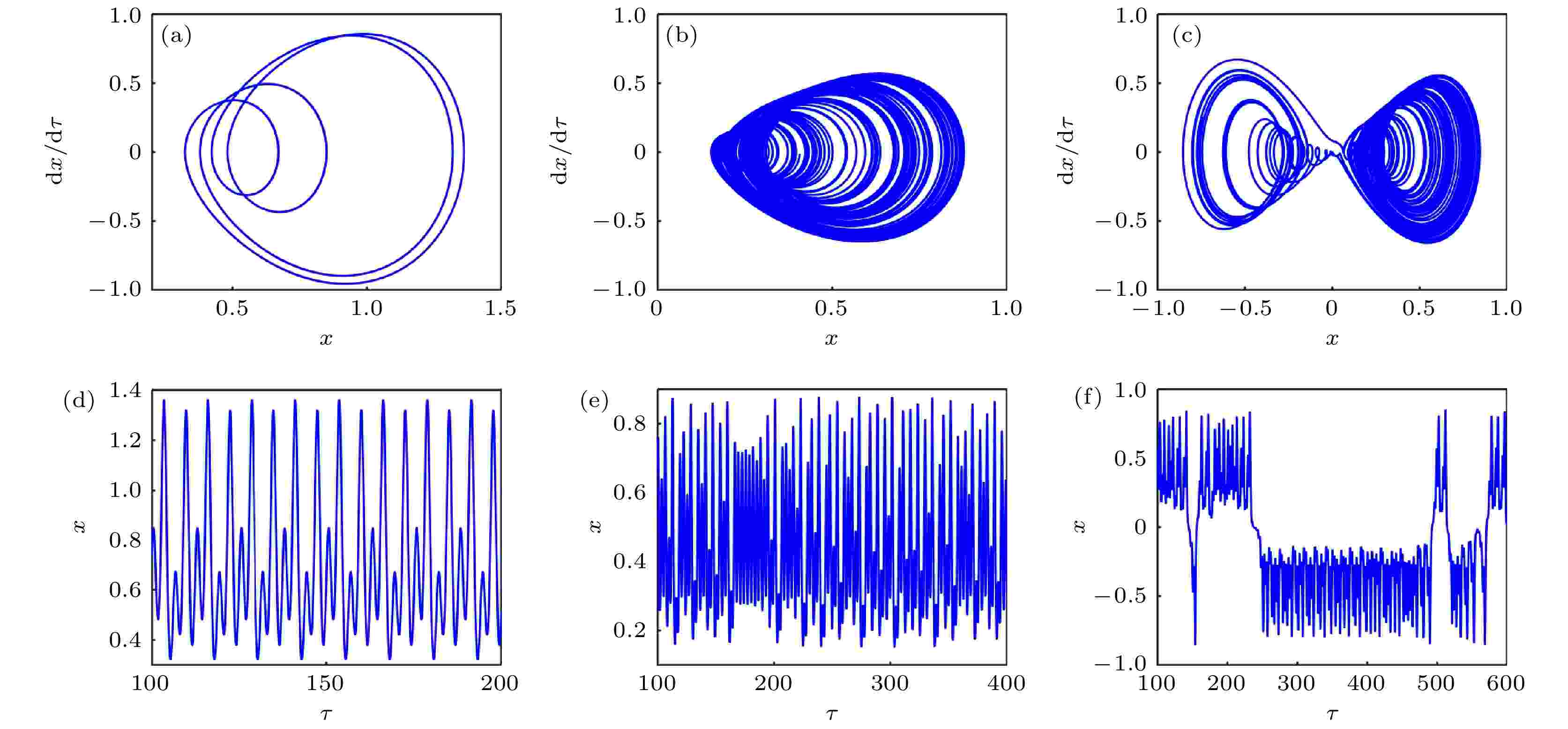图 20 k₃₃变化下的(a)?(c)相图和(d)?(f)时间历程图　(a), (d) k₃₃ = 0.6; (b), (e) k₃₃ = 1.2; (c), (f) k₃₃ = 1.4
Figure20. (a)?(c) Phase diagram and (d)?(f) time history diagram with different k₃₃: (a), (d) k₃₃ = 0.6; (b), (e) k₃₃ = 1.2; (c), (f) k₃₃ = 1.4

3 -->

5.1.5.b对单摆系统分岔的影响

随b变化单摆系统的运动分岔及最大Lyapunov指数如图21(a)和图21(b)所示. 可见, 随b增加, 单摆系统历经“单周期-二周期-四周期-混沌-四周期-二周期-单周期”的系列复杂运动变化.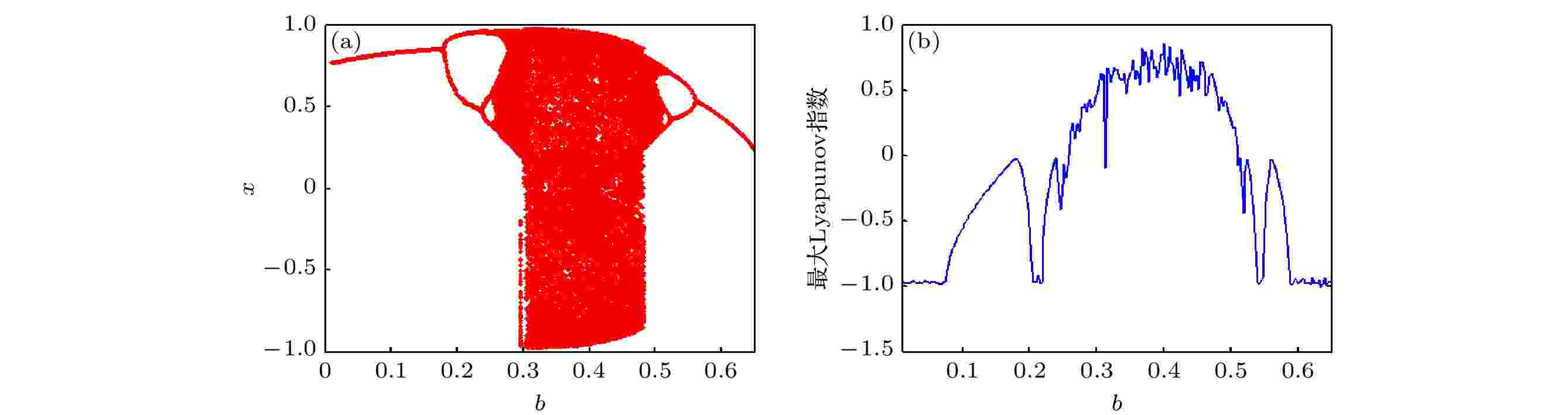
图 21 b变化下的(a)分岔和(b)最大Lyapunov指数
Figure21. (a) Bifurcation and (b) maximum Lyapunov exponent with different b.

b变化的相图和时间历程如图22(a)—(f)所示. 其中图22(a)—(f)中, b = 0.19, 0.28, 0.36系统分别处于二周期、混沌、双曲混沌的运动状态. b = 0.36的时间历程图(图23(a)—(c))显示出系统运动中较明显的交叠拍振共振行为, 伴随ω_b变化, 系统能量也不断交替改变, 系统共振频次和振幅带宽都发生变化. 比较图22(d)—(f)发现, b变化改变了单摆的运动周期, 其变化过程与系统动力学行为(图22(a)—(c))相一致.
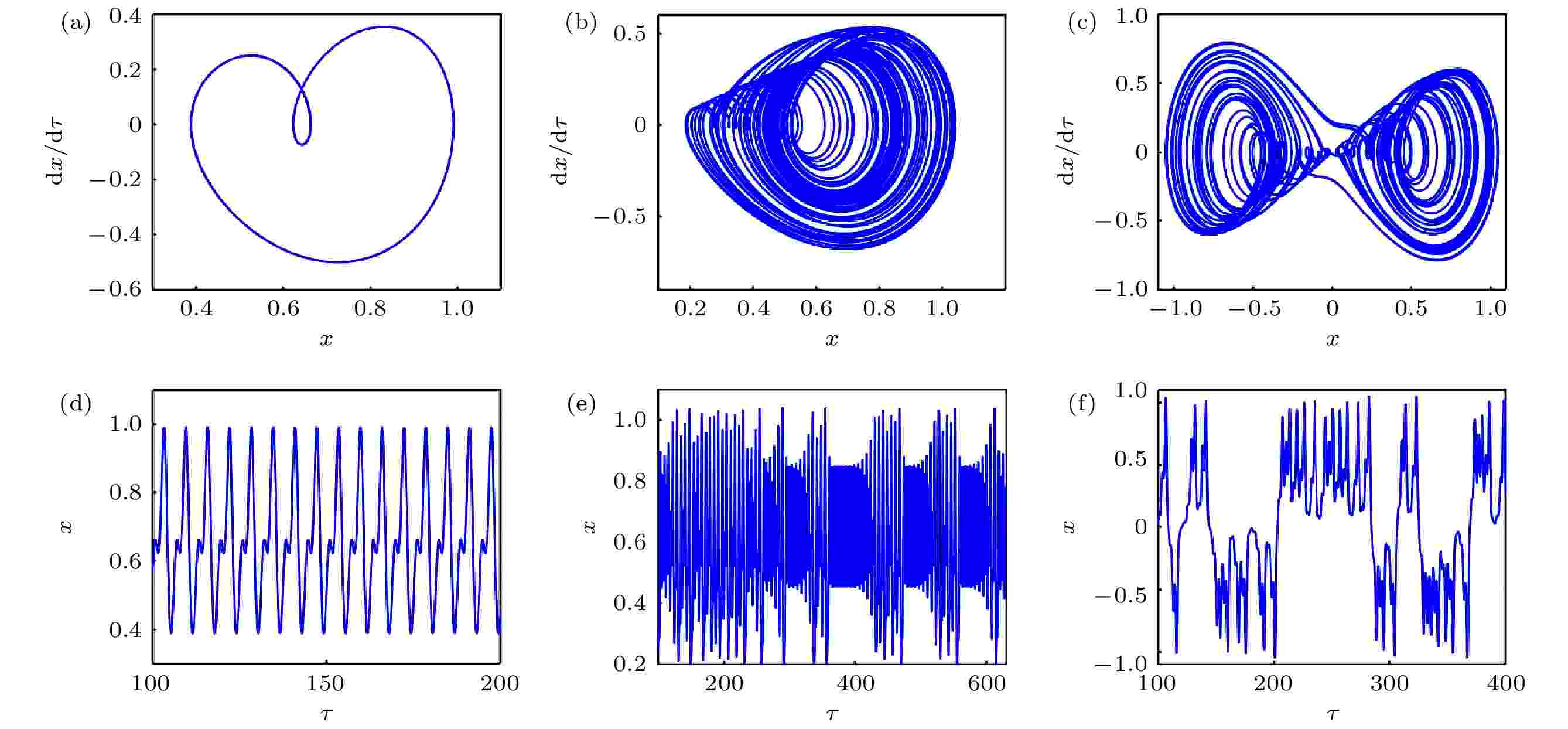图 22 b变化下的(a)?(c)相图和(d)?(f)时间历程图　(a), (d) b = 0.19; (b), (e) b = 0.28; (c), (f) b = 0.36
Figure22. (a)?(c) Phase diagram and (d)?(f) time history diagram with different b: (a), (d) b = 0.19; (b), (e) b = 0.28; (c), (f) b = 0.36

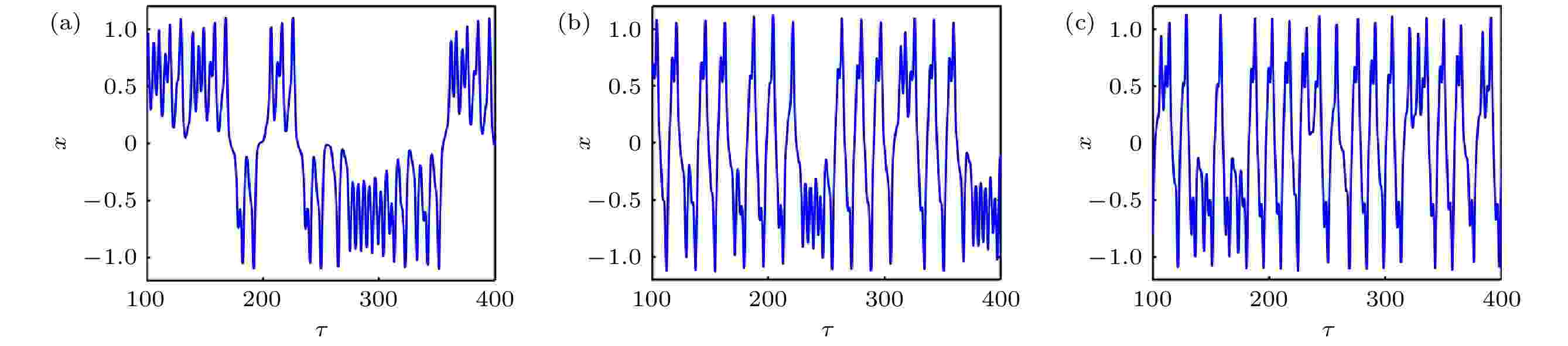图 23 当b = 0.36时ω_b变化下的时间历程图　(a) ω_b = 1.3 (b) ω_b = 1.5; (c) ω_b = 1.7
Figure23. Time history diagram when ω_b changes and b = 0.36: (a) ω_b = 1.3; (b) ω_b = 1.5; (c) ω_b = 1.7.

2 -->

5.2.受垂直激励和水平约束单摆系统的亚谐共振双参分析

通过分析方程(6)随相关变量的双参组合, 研究受垂直激励和水平约束的单摆系统在双参量耦合变化下的动力行为演化, 映射双参域变化下的单摆系统分岔运动特性.
参数ω_b耦合c₁₁的系统运动特性如图24(a)所示. 在区域“Ch1”, “Ch2”和“Ch3”的组合取值, 反映系统运动做混沌运动; 其他区域组合取值, 系统做周期运动. 图24(a)中, 考虑参量的一维变化, 沿“L1”路径变化参数ω_b, 系统运动状态变化过程与图12一致; 沿着“L2”路径变化参数c₁₁, 系统运动状态变化过程与图15一致, 这也在一定程度上佐证了单参数分岔对系统运动改变的结果.
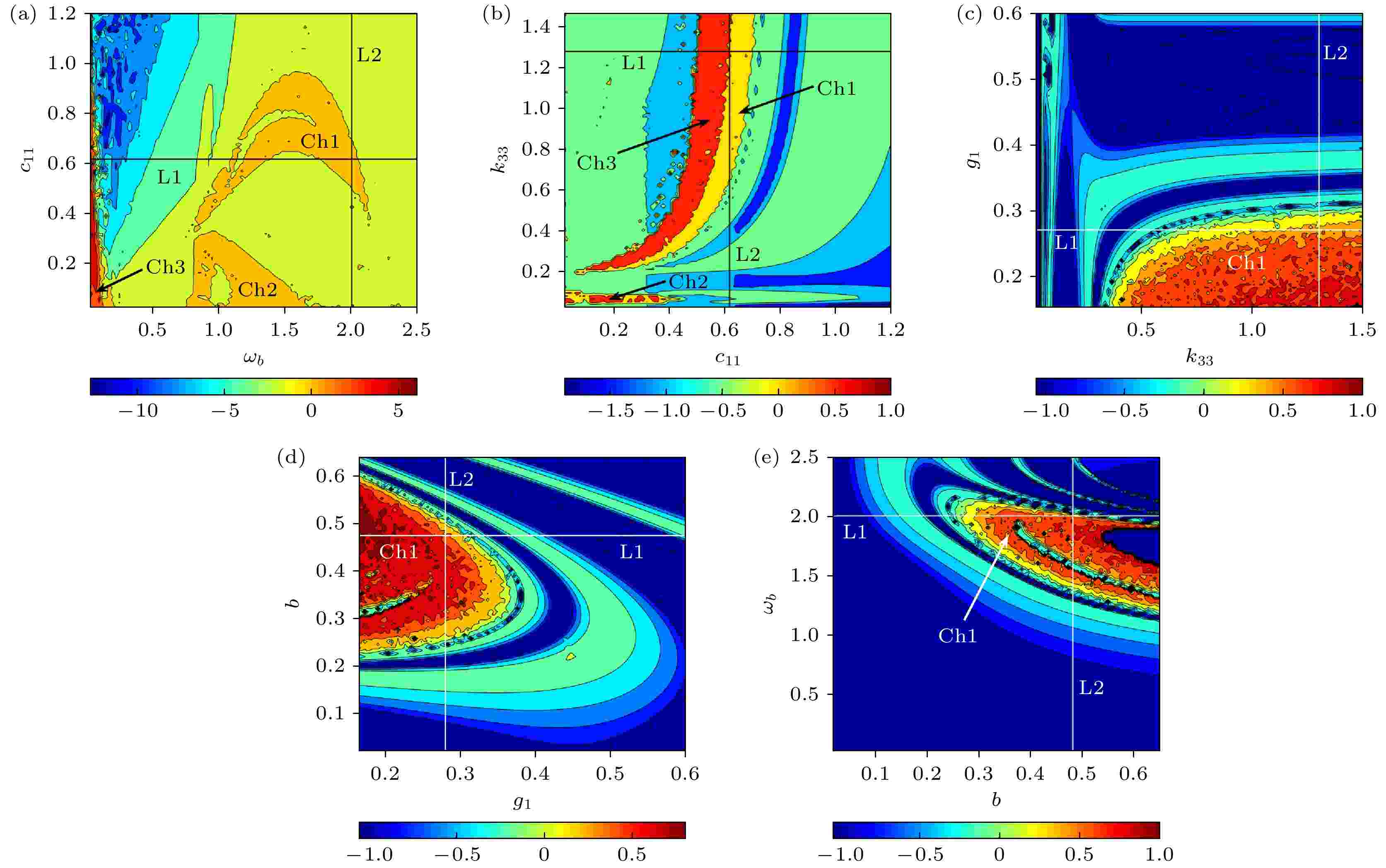图 24 单摆非线性系统在双参数域上的运动　(a) ω_b-c₁₁; (b) c₁₁-k₃₃; (c) k₃₃-g₁; (d) g₁-b; (e) b-ω_b
Figure24. Motion of a simple pendulum nonlinear system in the bi-parameter domain: (a) ω_b-c₁₁; (b) c₁₁-k₃₃; (c) k₃₃-g₁; (d) g₁-b; (e) b-ω_b

参数c₁₁耦合k₃₃的系统运动特性如图24(b)所示. 区域“Ch3”组合取值会导致系统运动的不稳定性比区域“Ch1”, “Ch2”大; 当c₁₁, k₃₃在“Ch1”, “Ch2”和“Ch3”区域边缘组合取值时, 会导致系统运动由混沌转向周期运动.
参数k₃₃耦合g₁的系统运动特性如图24(c)所示. 区域“Ch1”内组合取值, 最大Lyapunov指数为正, 系统做混沌运动. 参数g₁耦合参数b的系统运动特性如图24(d)所示. 区域“Ch1”内组合取值, 系统最大Lyapunov指数大于零, 系统做混沌运动, 当g₁和b在其他区域内组合取值时, 最大Lyapunov指数为负, 系统做周期运动.
参数b耦合参数ω_b组合的系统运动特性如图24(e)所示. 区域“Ch1”内组合取值, 系统最大Lyapunov指数为正, 系统做混沌运动; 当b和ω_b的组合取值在“Ch1”区域边界时, 系统最大Lyapunov指数在0附近变动, 系统发生混沌和周期运动的转换.
上述对受垂直激励和水平约束的单摆系统在双参数域上的运动特性分析, 明确了参数ω_b, c₁₁, k₃₃, g₁和b的组合取值对系统运动状态的影响, 系统发生周期运动与混沌运动的转换边界, 系统最大Lyaounov指数发生穿越0的突变, 系统动力特性也变得复杂.

分析受垂直激励和水平约束的单摆系统亚谐共振分岔与混沌等运动状态转换, 能量变化是本质驱动内因. 动力系统运动过程吸引子、吸引域的流形转迁所表现出的能量演化机制, 决定了系统的运动特性.
研究参数b改变对受垂直激励和水平约束的单摆非线性系统的吸引子、吸引域的影响, 揭示单摆系统运动过程中能量变化影响下的全局动力特性. 参数b变化引发的单摆系统吸引子、吸引域的转迁如图25所示.
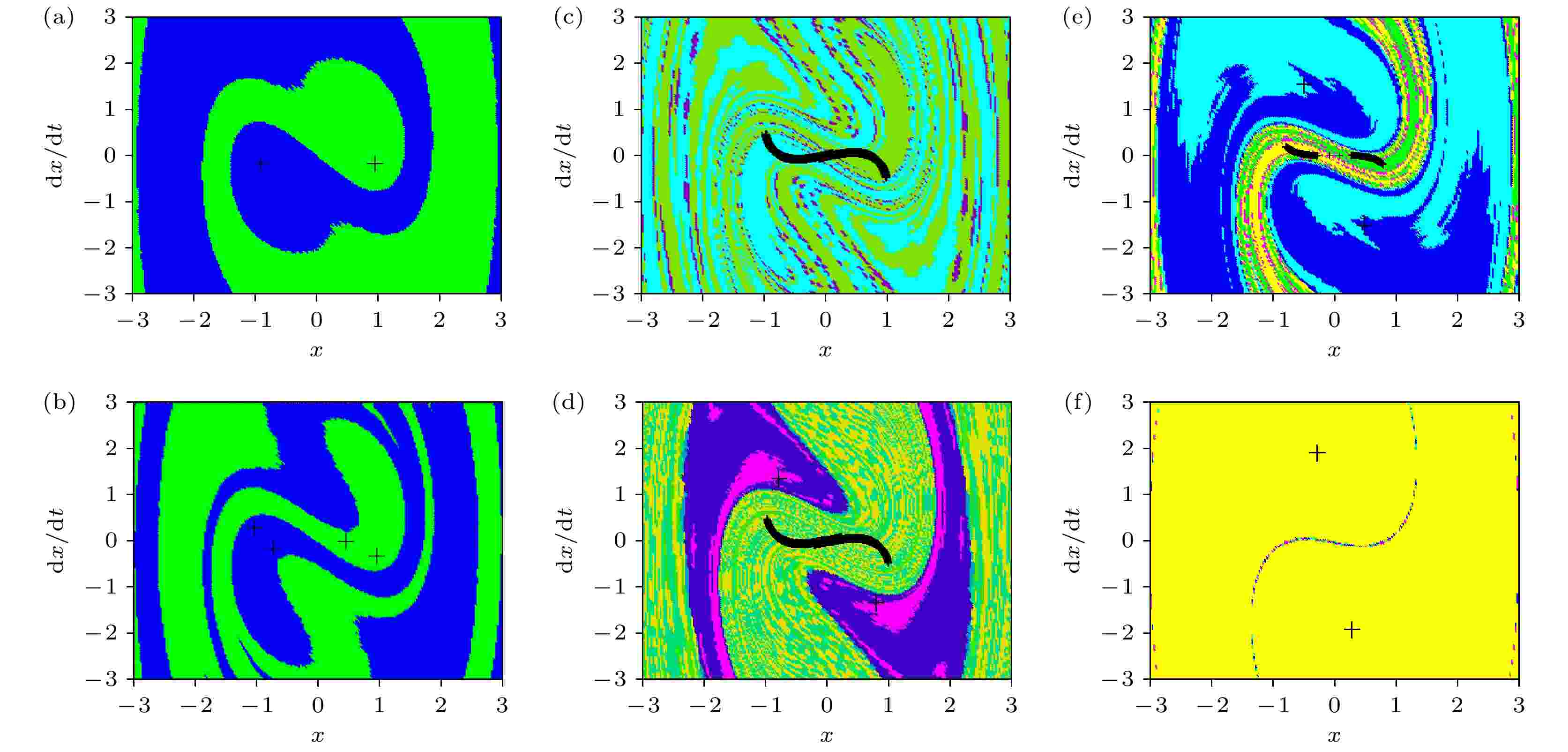图 25 系统在参数b变化时的吸引子、吸引域　(a) b = 0.11; (b) b = 0.23; (c) b = 0.32; (d) b = 0.35; (e) b = 0.49; (f) b = 0.81
Figure25. Attractor and attraction domain of the system when the parameter b changes: (a) b = 0.11; (b) b = 0.23; (c) b = 0.32; (d) b = 0.35; (e) b = 0.49; (f) b = 0.81.

b = 0.11的吸引域如图25(a)所示. 此时系统存在两个周期吸引子, 且每个吸引子所在的吸引域(蓝色和绿色)边界清晰, 二者相互缠绕, 系统处于稳定运动状态; 如图25(b)所示, 随b增大至b = 0.23时, 周期吸引子倍增, 存在4个周期吸引子, 每两个周期吸引子所在吸引域(蓝色和绿色)边界清晰, 吸引域带宽变窄, 还有进一步稀疏的演化趋势, 这些都在一定程度上反映出b的改变会诱发单摆系统内部稳定域的变化.
b = 0.32的吸引域如图25(c)所示. 系统历经倍周期分岔运动的极限位置到达边界, 系统的运动状态发生激变, 出现混沌吸引子, 系统能量的改变导致单摆的运动失稳. 如图25(d)所示的b = 0.35, 系统内部继续激变, 混沌吸引子所在的吸引域区域减少, 出现周期吸引子, 并且两个周期吸引子及其所在的吸引域中心对称分布, 反映出垂直激励引发的能量改变激发出单摆系统的周期吸引子与混沌吸引子共存, 系统所表现出的运动形式则取决于初始状态.
b = 0.49的吸引域如图25(e)所示. 混沌吸引子分散, 所在的吸引域变窄, 密集程度降低, 并且周期吸引子和混沌吸引子共存, 两个周期吸引子所在的吸引域面积增大, 该条件下垂直激励引发的能量变化激发出单摆系统的周期吸引子聚集, 系统所表现出的运动形式依然与初始状态密切相关. b = 0.81的吸引域如图25(f)所示, 系统存在两个周期吸引子, 且两个周期吸引子所在的吸引域相互环绕, 呈中心对称分布, 系统处于周期运动状态, 反映出垂直激励所引起的能量变化引起单摆系统周期吸引子能量增大, 系统主要表现为周期运动.
可见, 参数b变化改变了系统中的能量分布, 导致系统周期吸引子倍增, 混沌吸引子出现, 系统经历倍周期分岔通向混沌; 当系统在周期吸引子和混沌吸引子共存条件下, 各自吸引域边界会因系统能量变化, 不断发生边界的侵蚀、融合的复杂过程. 在混沌吸引子消失后, 周期吸引子及其吸引域中心对称分布, 这都在一定程度上反映出单摆系统能量影响下的全局动力特性.

受垂直激励和水平约束的单摆系统, 是工程弹簧摆的典型物理抽象. 本文系统地研究了这类工程摆的物理特性, 研究结果对实际工程应用中涉及工作性能的参数调整, 奠定了理论依据. 通过对该系统的亚谐共振分岔和混沌分析, 结论如下:
1)增大水平约束阻尼系数和三次方刚度系数, 有利于减小单摆系统共振幅值; 增大水平约束阻尼系数可减小单摆系统共振区域带宽; 增大垂直位移激励幅值将增大系统共振幅值、增加共振区域带宽.
2)对该系统的单参分岔研究表明, 垂直位移激励幅值、激励频率、水平约束阻尼系数和三次方刚度系数等参数变化, 都将导致系统运动特性的改变, 这与传统单摆中的阻尼对运动过程无影响结论不同. 上述参量变化, 本质上改变了系统中的能量分布, 使得单摆系统发生倍周期分岔、倒倍周期分岔、周期运动和混沌运动等动力学行为.
3)对系统在不同参量条件下的相轨迹和时间历程的分析, 表明方程(6)中的g₁相当于关联了系统摆长和运动周期的耦合项, 无论摆长还是运动周期使得系统能量降低, 系统都会通过参数g₁的耦合, 使得能量发生转换, 维持系统振动.
4)对该系统的双参数域分岔研究表明, 通过合适选择系统参数, 可有效控制该系统的振动行为, 并且通过参数的匹配优选能有效避免混沌的发生. 进一步通过对系统吸引子、吸引域的分析, 揭示了系统能量变化对运动形态的演化机理.
上述结论为受垂直激励和水平约束的单摆模型的工程应用提供重要理论依据, 同时对实际工况下的减振抑振提供了理论参考.