摘要: Lyapunov指数是识别系统非线性动力学特征的重要标志, 但是目前的算法通用性不足且计算流程复杂. 本文在经典的Lyapunov指数算法的基础上, 基于摄动理论提出了一种适用于不连续系统的Lyapunov指数计算方法. 首先, 以系统状态参数初始值和沿相空间每个基本矢量的扰动量为初始条件, 确定相轨迹. 其次, 采取差商近似导数法, 获得Jacobi矩阵的近似矩阵. 然后, 对Jacobi矩阵进行特征值提取, 得到系统的Lyapunov指数谱. 最后, 将新算法应用到二自由度干摩擦冲击振荡器系统实例中, 并将计算结果与同步方法的计算结果进行对比, 对新算法的有效性进行验证. 该算法不仅适用于离散系统和连续时间系统, 而且能够快速计算复杂不连续系统的Lyapunov指数, 为确定复杂不连续系统的动力学行为提供了新思路.
关键词: Lyapunov指数 /
不连续系统 /
摄动理论 English Abstract Lyapunov exponent algorithm based on perturbation theory for discontinuous systems Ma Zhao-Zhao 1 ,Yang Qing-Chao 2 ,Zhou Rui-Ping 1 1.School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 51579242, 51839005) and the Natural Science Foundation of Hubei Province, China (Grant No. 2018CFB182).Received Date: 13 March 2021Accepted Date: 17 August 2021Available Online: 25 August 2021Published Online: 20 December 2021Abstract: Lyapunov exponent is a significant symbol to identify the nonlinear dynamic characteristics of the system. However, most of algorithms are not universal enough and complex. According to the classic Lyapunov exponent algorithm and perturbation theory, in this paper we propose a new algorithm which can be used to compute Lyapunov exponents for discontinuous systems. Firstly, the initial value of the system state parameter and the disturbance of each basic vector along the phase space are taken as initial conditions to determine the phase trajectory. Secondly, the method of difference quotient approximate derivative is adopted to obtain the Jacobi matrix. Thirdly, the eigenvalues of the Jacobi matrix are calculated to obtain the Lyapunov exponent spectrum of the system. Finally, the algorithm in a two-degree-of-freedom system with impacts and friction is used, showing its effectiveness and correctness by comparing its results with the counterparts from the synchronization method. The algorithm can not only be used for discrete systems and continuous-time dynamic systems, but also quickly calculate the Lyapunov exponent of complex discontinuous systems, which provides a new idea for determining the dynamic behavior of complex discontinuous systems.Keywords: Lyapunov exponent /discontinuous system /perturbation theory 全文HTML --> --> --> 1.引 言 Lyapunov指数是在局部和全局稳定性准则下确定系统稳定性的数值, 它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率[1 ] . 从数学角度, Lyapunov指数是状态转移矩阵的特征值, 决定了系统吸引子上轨迹无穷小扰动的演化进程. 因此, Lyapunov指数被认为是衡量系统对初始条件敏感性的重要指标. 所有Lyapunov指数值的和决定了系统在相空间中体积的发散度, 所有Lyapunov指数值的和为负值是存在全局稳定吸引子的充要条件, 并且表明系统是耗散的; 若所有Lyapunov指数均为负值, 则吸引子为稳定点; 对于n 维系统, 如果前m 个Lyapunov指数等于零而另外n – m 个Lyapunov指数均为负值, 则吸引子为m 维环面; 若最大Lyapunov指数为正值, 则为混沌运动, 若存在不止1个Lyapunov指数为正值, 则为超混沌运动. 对于保守系统, 所有Lyapunov指数值的和为零, 若所有Lyapunov指数值的和为正值, 则表明系统是全局不稳定的, 相轨迹呈指数发散.[2 ] 及Shimada和Nagashima[3 ] 首先提出了1个基于Oseledets定理[4 ] 计算Lyapunov指数谱的有效算法, 文献[5 -8 ]对算法进行了改进. 近年来, 提出了基于系统扰动的数量积和导数计算Lyapunov指数的方法[9 -13 ] , 该算法可以计算连续系统的Lyapunov指数谱, 但是如果系统中存在不连续性则会出现较大误差或数值溢出现象.[14 ] 、最小二乘阴影法[15 ] 和伪轨道法[16 ] 消除状态扰动矢量的不连续性等方法, 虽然不需要重构相空间和Jacobi矩阵, 但容易引起系统动力学特性的质变. Takens[17 ] 和Wolf等[18 ] 根据时间序列信号重构系统吸引子, 提出了计算不连续系统最大Lyapunov指数的算法. 多年以来, 文献[19 -27 ]针对该类方法的数据量、稳定性和计算速率等方面进行了评估改进, 该类方法的优点是物理意义明显, 便于理解, 计算结果不易受到拓扑复杂性的影响, 有一定的抗噪能力. 近年来, 部分****又提出了映射法[28 -30 ] 、补偿矩阵法[31 ] 、完全同步法[32 -36 ] 、克隆动力学法[37 ] 等, 这些方法对一些特性类型的不连续系统具有较高的准确性, 但算法通用性不强且计算流程较为复杂.2.方 法 为了克服现有Lyapunov指数算法的不足, 以一般性的理论为依据, 使得新算法适用于更多的系统并更具通用性; 另一方面, 以经典的数值算法为基础, 对广泛应用的Jacobi法进行改进, 保证新算法计算的准确性.2.1.算法理论 2.1.算法理论 以常微分方程(ODE)形式描述一种n 维自治连续时间系统:$ {\boldsymbol{x}} \in {{\boldsymbol{R}}^n} $ 为状态向量, $ t \in {\boldsymbol{R}} $ 为时间, f $ {{\boldsymbol{R}}^n} \to {{\boldsymbol{R}}^n} $ 上的连续可微函数. 假设$ {S_t}({{\boldsymbol{x}}_0}) $ 为满足ODE(1)初始条件$ {{\boldsymbol{x}}_0} $ 的解(轨迹), 则有2 )式对$ {{\boldsymbol{x}}_0} $ 进行微分获得如下变分方程:$ {{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 显示了初始条件$ {{\boldsymbol{x}}_0} $ 的无穷微扰对轨迹$ {S_t}({{\boldsymbol{x}}_0}) $ 的影响:$ \Delta {\boldsymbol{s}}(t) $ 是由初始扰动量$ \Delta {{\boldsymbol{x}}_0} $ 引起$ {S_t}({{\boldsymbol{x}}_0}) $ 的扰动, 即: $ \Delta {\boldsymbol{s}}(t) = {S_t}({{\boldsymbol{x}}_0} + \Delta {{\boldsymbol{x}}_0}) - {S_t}({{\boldsymbol{x}}_0}) $ . 向量$ \Delta {\boldsymbol{s}}(t) $ 的长度可以从下式中求得$ {u}_{i}(t), i=1, \cdots, n $ 为$ {{\boldsymbol{U}}_t}{({{\boldsymbol{x}}_0})^{\text{T}}}{{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 的特征值. $ {{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 是1个实矩阵, 所以$ {{\boldsymbol{U}}_t}{({{\boldsymbol{x}}_0})^{\text{T}}}{{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 是实对称的. 因此, $ {u_i}(t) \in {\boldsymbol{R}} $ 和对应的特征向量可以构成正交基$ {\boldsymbol{v}}_{i}(t), i=1, \cdots, n $ . 由于任意1个$ \Delta {{\boldsymbol{x}}_0} \in $ $ {{\boldsymbol{R}}^n} $ , 都有$ {\left| {\Delta {\boldsymbol{s}}(t)} \right|^2} \geqslant 0 $ , 可得到矩阵$ {{\boldsymbol{U}}_t}{({{\boldsymbol{x}}_0})^{\text{T}}}{{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 为半正定, 且$ {u_i}(t) \geqslant 0 $ . 因此, 如果$ \Delta {{\boldsymbol{x}}_0} $ 与$ {{\boldsymbol{v}}_i}(t) $ 平行, 则$ \left| {\Delta {\boldsymbol{s}}(t)} \right| = \left| {\Delta {{\boldsymbol{x}}_0}} \right|\sqrt {{u_i}(t)} $ . 可以得到: 若初始扰动量$ \Delta {{\boldsymbol{x}}_0} $ 的1个分量与$ {{\boldsymbol{v}}_i}(t) $ 平行, 则其轨迹长度的影响因子为$ \sqrt {{u_i}(t)} $ . 可用以下公式表示:$ \left[ {{\boldsymbol{a}}, {\boldsymbol{b}}} \right] $ 表示向量$ {\boldsymbol{a, b}} $ 之间的数量积.8 )式可以得到, 在时间t 足够长的情况下, $ \sqrt {{u_i}(t)} \approx {{\text{e}}^{{\lambda _i}t}} $ .$ {\lambda _i} $ , 在相空间中都存在1个对应的方向, 使得初始扰动量$ \Delta {{\boldsymbol{x}}_0} $ 在该方向上的投影长度乘以$ {{\text{e}}^{{\lambda _i}t}} $ 作为系统在时间t 内的演化. 可用以下公式表示:$ \Delta {{\boldsymbol{x}}_0} $ 的分量沿相空间某个方向的平均指数收缩率(如果$ {\lambda _i} < 0 $ )或扩展率(如果$ {\lambda _i} > 0 $ ).t , 使用(4 )式计算Jacobi矩阵$ {{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ ; 然后, 计算$ {{\boldsymbol{U}}_t}{({{\boldsymbol{x}}_0})^{\text{T}}}{{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 的特征值$ {u_i} $ ; 最后, 应用(8 )式计算每个Lyapunov指数值.2.2.连续系统经典算法 -->2.2.连续系统经典算法 基于以上推导公式建立了一种连续系统的经典算法[8 ] . 该算法利用了最大的扰动子空间$ {W_i} $ 中的每个初始扰动均以$ {{\text{e}}^{{\lambda _i}t}} $ 的速度变化这一特点, 即平行于$ {{\boldsymbol{v}}_i} $ 的初始扰动量$ \Delta {{\boldsymbol{x}}_0} $ 分量的长度在时间t 上以因数$ {{\text{e}}^{{\lambda _i}t}} $ 进行扩展或收缩.n 维系统的Lyapunov指数${\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant $ $ {\lambda _n}$ , 几乎任意1个初始扰动量$ \Delta {{\boldsymbol{x}}_0} $ 都具有与$ {{\boldsymbol{v}}_1} $ 平行的分量, 则该分量长度的变化因数为$ {{\text{e}}^{{\lambda _1}t}} $ . 如果$ {\lambda _1} $ 是最大Lyapunov指数, 则其分量将成为主导量. 由于扰动量$ \Delta {{\boldsymbol{x}}_0} $ 的方向与$ {{\boldsymbol{v}}_1} $ 对齐, 则$ \Delta {{\boldsymbol{x}}_0} $ 的长度以近似指数速率$ {\lambda _1} $ 变化, 即$ \left| {\Delta {\boldsymbol{s}}(t)} \right| \approx \left| {\Delta {{\boldsymbol{x}}_0}} \right|{{\text{e}}^{{\lambda _1}t}} $ . 这意味着$ {\lambda _1} $ 决定了几乎所有初始扰动改变其长度的平均指数速率. 为了计算n 个Lyapunov指数谱, 通过Gram-Schmidt正交归一化获得相互正交的初始扰动量$ \Delta {\boldsymbol{x}} $ , 减少扰动量之间对齐的影响. 为了计算$ {\lambda _2} $ , 当$ \Delta {{\boldsymbol{x}}_0} $ 与$ {{\boldsymbol{v}}_1} $ 对齐时, 必须计算另1个与$ \Delta {{\boldsymbol{x}}_1} $ 正交的新扰动, 且该扰动的长度以近似指数速率$ {\lambda _2} $ 变化, 并与$ {{\boldsymbol{v}}_2} $ 对齐, 如图1 所示.图 1 两个扰动量$ \Delta {\boldsymbol{x}} $ , $ \Delta {{\boldsymbol{x}}_0} $ 的正交归一化Figure1. Orthonormalization of two perturbations$\Delta {\boldsymbol{x}} , ~ \Delta {{\boldsymbol{x}}_0}$ .$ {\lambda _3} $ , 必须计算1个与前面两个扰动量正交的新扰动, 则其与$ {{\boldsymbol{v}}_1} $ 和$ {{\boldsymbol{v}}_2} $ 正交, 以近似指数速率$ {\lambda _3} $ 变化, 并与$ {{\boldsymbol{v}}_3} $ 对齐. 总的来说, 若计算n 个Lyapunov指数谱, 必须计算n 个不同的扰动, 第1个是根据等式(5 )自由演化的, 其他第i 个新扰动都与第$ 1, \cdots, (i - 1) $ 个扰动量保持正交.$ {{\boldsymbol{U}}_t}({{\boldsymbol{x}}_0}) $ 在时间t 较长的情况下变得计算困难, 甚至无法计算, 使得该经典算法在实践中效果不佳.2.3.不连续系统Lyapunov指数的算法 -->2.3.不连续系统Lyapunov指数的算法 32.3.1.算法思想 -->2.3.1.算法思想 在连续系统Lyapunov指数经典算法[8 ] 的基础上, 基于算法理论详述利用差商近似导数法获得Jacobi矩阵计算不连续系统Lyapunov指数的具体算法.$ {{\boldsymbol{x}}_0} $ 和计算参数; 然后求解系统, 得到充分接近实际系统吸引子的轨迹; 再利用差商近似倒数方法计算不连续系统的Jacobi矩阵; 利用Gram-Schmidt正交归一化获得相互正交的初始扰动量, 并将不同的扰动量用于求解相应的Lyapunov指数, 进而得到系统的Lyapunov指数谱.2.3.2.算法实现的具体方法 -->2.3.2.算法实现的具体方法 下面详述该算法在不连续系统中实现的具体方法.1 )中的矢量场f x [8 ] 可以得出系统Lyapunov指数. 否则, 不能直接从变分方程(4 )获得Jacobi矩阵$ {{\boldsymbol{U}}_t}({{\boldsymbol{x}}_j}) $ . 针对不连续系统, 进行适应性修改. 首先考虑连续时间不连续系统, 系统(1 )的解$ {S_t}({\boldsymbol{x}}) $ 实际上是将初始状态x t 之后系统(1 )状态的映射. $ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 为在点x $ {S_t} $ 的Jacobi矩阵:$ {{\boldsymbol{e}}_1}, \cdots, {{\boldsymbol{e}}_n} $ 是$ {{\boldsymbol{R}}^n} $ 中的标准基, $ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 的列是$ {S_t}({\boldsymbol{x}}) $ 关于后续状态变量的偏导数. 根据导数定义, (10 )式中的偏导数可以表示为Δ → 0时差商的极限. 因此, 可通过以下方式估算矩阵$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ :Δ 值时, 需要在与Δ 成比例的截断误差和取决于实际使用数据类型的近似误差之间取得平衡, 矩阵$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 的近似算法如图2 所示.图 2 矩阵$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 逼近算法示意图Figure2. Illustration of the algorithm of the $ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ matrix approximation.$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ , 需要利用未扰动的初始条件x Δ 值扰动的初始条件$ {\boldsymbol{x}} +\Delta {\boldsymbol{e}}_ {i}, i=1, \cdots, n $ , 确定映射$ {S_t}({\boldsymbol{x}}) $ 的值. 总之, 估算一次矩阵$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ , 需要对映射$ {S_t}({\boldsymbol{x}}) $ 进行$ n + 1 $ 次计算: ${S_t}({\boldsymbol{x}}), {S_t}({\boldsymbol{x}} + \Delta {{\boldsymbol{e}}_1}), \cdots, {S_t}({\boldsymbol{x}} + $ $ \Delta {{\boldsymbol{e}}_n})$ , 并代入(11 )式得到近似Jacobi矩阵$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ . 新算法是将上述Jacobi矩阵的估算方法与经典Lyapunov指数算法[8 ] 相结合, 其中的所有其他步骤都与经典Lyapunov指数算法相同, 主要区别在于Jacobi矩阵是从近似公式(11 )而不是(4 )式获得. 令$ {t}_{j}\in {\boldsymbol{R}}_{+}, j=0, 1, \cdots, J $ 为1个递增的时间序列, $ { {\boldsymbol{x}}^{_j}} = {\boldsymbol{x}}({t_j}) $ . 假设初始条件$ {t_0} = 0 $ 并且${ {\boldsymbol{x}}^0} = $ $ {\boldsymbol{x}}({t_0}) = {{\boldsymbol{x}}_0}$ , 则$ \Delta {t_j} = {t_j} - {t_{j - 1}} $ 和$ { {\boldsymbol{x}}^{(j - 1)}} $ 代入(11 )式中就可以得到矩阵$ {{\boldsymbol{U}}_{\Delta {t_j}}}({ {\boldsymbol{x}}^{(j - 1)}}) $ 的近似值. 这种方法的最大优点是, 不再要求轨迹上每个点的向量场f 11 )式时, 只要满足对于每个$ {t_j} $ , 轨迹$ {S_{\Delta {t_j}}}({\boldsymbol{x}}) $ 在点$ { {\boldsymbol{x}}^{(j - 1)}} $ 处对于所有状态变量是可微的, 则系统中不论存在多少不连续性或不连续的类型均能满足要求. 同时, 对时间序列$ {t_j} $ 仅要求$ {t}_{j}\in {\boldsymbol{R}}_{+}, j=0, 1, \cdots, J $ 是递增的, $ {t_j} $ 值大小没有限制. 而且, 不需要明确知道定义矢量场f $ {S_{\Delta {t_j}}}({\boldsymbol{x}}) $ 的方法就足够了. $ {S_{\Delta {t_j}}}({\boldsymbol{x}}) $ 的值无论是从轨迹$ {S_{\Delta {t_j}}}({\boldsymbol{x}}) $ 的显式定义或隐式定义, 还是从数值过程, 甚至是从实验中获得都没有关系, 该算法均有效.$ {\boldsymbol{U}}({\boldsymbol{x}}) $ 可以理解为在点x F $ {\boldsymbol{U}}({\boldsymbol{x}}) $ :$ {\boldsymbol{U}}({\boldsymbol{x}}) $ , 需要对映射F $ n + 1 $ 次计算: $ {\boldsymbol{F}}({\boldsymbol{x}}), {\boldsymbol{F}}({\boldsymbol{x}} + \Delta {{\boldsymbol{e}}_1}), \cdots, {\boldsymbol{F}}({\boldsymbol{x}} + \Delta {{\boldsymbol{e}}_n}) $ , 并代入(13 )式得到近似Jacobi矩阵$ {\boldsymbol{U}}({\boldsymbol{x}}) $ .图3 所示.图 3 不连续系统Lyapunov指数算法的示意图Figure3. Illustration of the algorithm of discontinuous system Lyapunov exponent.$ {\boldsymbol{x}} (0) = {{\boldsymbol{x}}_0} $ 为初始条件, $ \Delta {\boldsymbol{x}}_{i}^{(0)}, i=1, \cdots, n $ 为初始扰动, $\Delta \hat {\boldsymbol{x}}_i^{(0)} = {{\Delta {\boldsymbol{x}}_i^{(0)}}/{|{\Delta {\boldsymbol{x}}_i^{(0)}} |}}$ 为归一化初始扰动. 假设对于不连续系统$ {\boldsymbol{x}}^{(j)}= {\boldsymbol{x}}({t}_{j}), \Delta {\boldsymbol{x}}_{i}^{(j)}= $ $ \Delta {\boldsymbol{x}}_{i}({t}_{j}) $ , 其中$ {t_j} $ 是递增的时间序列, 使得$ {t_0} = 0 $ 和$ \Delta {t_j} = {t_j} - {t_{j - 1}} $ .$ { {\boldsymbol{x}}^{(j - 1)}} $ 在不连续系统中获得新状态$ { {\boldsymbol{x}}^{(j)}} $ .11 )式计算得Jacobi矩阵${{\boldsymbol{U}}_{\Delta {t_j}}} ({ {\boldsymbol{x}}^{(j - 1)}})$ .$ j = 1, 2, \cdots, T $ , 重复以上2)—5)过程. 然后, 使用以下公式估算不连续系统的整个Lyapunov指数谱:3.数值仿真研究 23.1.二自由度干摩擦冲击振荡器系统 3.1.二自由度干摩擦冲击振荡器系统 二自由度干摩擦冲击振荡器系统由连接到刚度为$ {k_1} $ 的弹簧的质量块M 和阻尼系数为$ {c_1} $ 的黏滞阻尼器组成, 另1个质量块m 位于质量块M 上, 其相对于M 的位置由缓冲器A 和B 限制, 质量块之间存在摩擦力$ {F_T} $ 和阻尼系数为$ {c_2} $ 的黏性阻尼力. 两自由度冲击振子是1个质量-弹簧-阻尼系统, 其中两个质量块可以相互碰撞, 并在相对运动过程中存在干摩擦, 如图4 所示.图 4 二自由度干摩擦冲击振荡器模型Figure4. Model of the two-degrees-of-freedom (2-DoF) mechanical oscillator with impacts and friction.M 和m 分别是外部和内部振动体的质量; $ {{x}_1} $ , $ {{x}_2} $ 是它们的位置; $ {k_1} $ 是弹簧刚度; $ {c_1} $ , $ {c_2} $ 是阻尼系数; $ {F_T} $ 是摩擦力; A 是强迫振幅; Ω 是谐波激励的角频率; $ {\delta _0} $ 是内部质量块m 与外部质量块M 之间的间隙; μ 是摩擦系数, R 是恢复系数; $ {t_{\text{c}}} $ 是发生碰撞的时间. 方程组(16 )定义了振荡器系统的演化, 方程组(18 )描述了在系统发生碰撞时刻$ {t_{\text{c}}} $ 处不连续性的状态转换.16 )—(18 )式转换为无量纲表示得到$ {\boldsymbol{y}}(0) $ , 使得$ \left| {{y_3} - {y_1}} \right| < {y_0} $ , 可以数值估计轨迹$ {S_\tau }({\boldsymbol{y}}(0)) $ . 唯一的限制是两个物体在碰撞过程中的速度没有定义. 此外, 还假设当$ \left| {{y_3}(0) - {y_1}(0)} \right| < {y_0} $ 和$ {y_2} \ne {y_4} $ 时, 轨迹$ {S_\tau }({\boldsymbol{y}}(0)) $ 相对于初始条件是可微的.3.2.数值仿真结果 -->3.2.数值仿真结果 为了将数值仿真结果与不同算法[35 ] 获得的结果进行比较验证, 控制参数$ \eta $ 在[1.2, 1.45]范围内变化, 并设定以下参数值: $ \gamma = 0.693 $ , $ \sigma = 0.50 $ , $ \mu = 0.02 $ , $ \beta = 0.05 $ , $ {y_0} = 0.80 $ , $ p = 1.00 $ , $ R = 0.60 $ , 初始条件为零. 采用自适应步长的龙格-库塔(Runge-Kutta)方法对二自由度冲击振荡器系统进行了数值求解. 在开始计算Lyapunov指数和将轨迹点保存到分岔图之前, 每组参数针对$ \tau = 400\dfrac{{{\rm{2\pi }}}}{\eta } $ 运行该振荡器系统, 以减少瞬态影响. 其中, Jacobi矩阵$ {{\boldsymbol{U}}_{\Delta {\tau _j}}}({ {\boldsymbol{x}}^{(j - 1)}}) $ 通过(11 )式获得, 为了保持方法的准确性, Δ 值应与变分方程(4 )的积分绝对误差处于同一阶或更低阶, 并考虑冲击振荡器系统中数据类型的近似误差, 从而确定Δ 值取10–6 .$ \Delta {{\boldsymbol{y}}_4} $ 的收缩速度过快, 导致在计算自然对数时出现了数值问题. 因此, 仅给出了该振荡器系统的3个最大的Lyapunov指数. 为了观察Lyapunov指数值的稳定性, 在估算程序的每次迭代之后, 再利用(15 )式计算结果. 在每100次迭代后, 估计最后100个$ {\lambda _1}, {\lambda _2}, {\lambda _3} $ 值的标准差. 当所有标准偏差低于阈值10–4 时, 终止计算, 并取最后100次迭代中$ {\lambda _1}, {\lambda _2}, {\lambda _3} $ 的平均值作为最终值. 图5 给出了3个最大Lyapunov指数图和系统状态分岔图. 可以观察到, Lyapunov指数值恰当地反映了系统在分岔图中的行为. 因此, 通过新算法在二自由度干摩擦冲击振荡器系统(19 )—(21 )中的应用, 证明了该Lyapunov指数新算法的有效性.图 5 二自由度干摩擦冲击振荡器系统的分叉图和3个最大Lyapunov指数图 (a) 状态变量$ {y_1} $ ; (b) 状态变量$ {y_2} $ ; (c) 状态变量$ {y_3} $ Figure5. Bifurcation diagram and the corresponding diagram of the three largest Lyapunov exponents of the 2-DoF mechanical oscillator system with impacts and friction: (a) State variable $ {y_1} $ ; (b) state variable $ {y_2} $ ; (c) state variable $ {y_3} $ .[35 ] 得到的计算结果进行比较, 可以得到, 使用两种算法获得的最大Lyapunov指数图高度一致. 从而, 两种方法也相互验证了算法的正确性.4.讨 论 在物理环境中, 具有冲击、干摩擦等因素的不连续系统, 难以直接从变分方程中获得Jacobi矩阵, 经典的Lyapunov指数算法[8 ] 变得难以实现, 因此, 本文算法基于摄动理论, 在经典Lyapunov指数算法基础上, 采用差商近似导数获得近似Jacobi矩阵的方法, 以损失一定Jacobi矩阵计算精度为代价提升算法普适性.$ n + 1 $ 个不同初始条件向量: $ {{\boldsymbol{x}}_0}, {{\boldsymbol{x}}_0} + \Delta {{e}_1}, \cdots, {{\boldsymbol{x}}_0} + \Delta {{e}_n} $ 在时间t 上对系统积分求解$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ , 因此, 求解$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 相当于求解$ n + 1 $ 阶非线性系统的计算量. 在经典算法中, 通常变分方程(4 )与系统轨迹$ {S_t}({\boldsymbol{x}}) $ 一起求解, 可以将变分方程(4 )视为n 个线性时变系统, 因此, 求解$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 相当于求解1个n 阶非线性系统和n 个线性时变系统的计算量. 只要系统状态的时间导数值的计算量不比等式(4 )中$ {{\boldsymbol{U}}_t}({\boldsymbol{x}}) $ 后续列的时间导数的计算量大很多, 则两种算法的计算量是相当的. 同时, 许多非线性系统的矢量场f [11 ] . 差商近似导数法获得近似Jacobi矩阵中所需的每个轨迹$ {S_t}({\boldsymbol{x}}), {S_t}({\boldsymbol{x}} + \Delta {{\boldsymbol{e}}_1}), \cdots, {S_t}({\boldsymbol{x}} + \Delta {{\boldsymbol{e}}_n}) $ 的积分是完全独立的, 每个轨迹都可以在使用单独处理器的独立进程中进行求解, 使得新算法非常适合于多处理器计算模式, 提升运算效率.5.结 论 本文基于经典Lyapunov指数算法和摄动理论提出了一种计算不连续系统Lyapunov指数的新算法, 在经典Lyapunov指数算法基础上, 利用相轨迹上的正交矢量型初始微扰动获得近似Jacobi矩阵. 该算法不需要知道定义矢量场或者映射的方程式, 只需要有一种获得相轨迹的方法就足够了, 并且适用于连续或不连续的离散时间和连续时间系统. 通过数值仿真分析, 验证了本文Lyapunov指数算法简单、有效和鲁棒. 本文提出的算法可以应用于包括不连续滑动振荡器和许多其他不连续系统的大量不连续系统的研究. 










































































































 图 1 两个扰动量
图 1 两个扰动量
























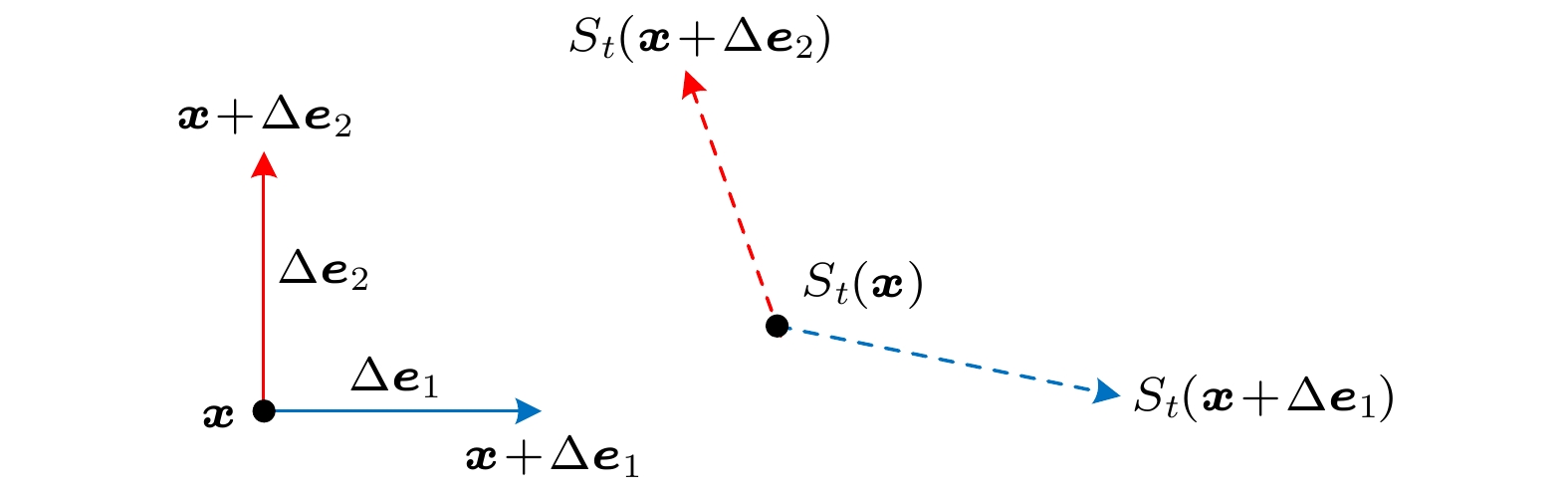 图 2 矩阵
图 2 矩阵

































































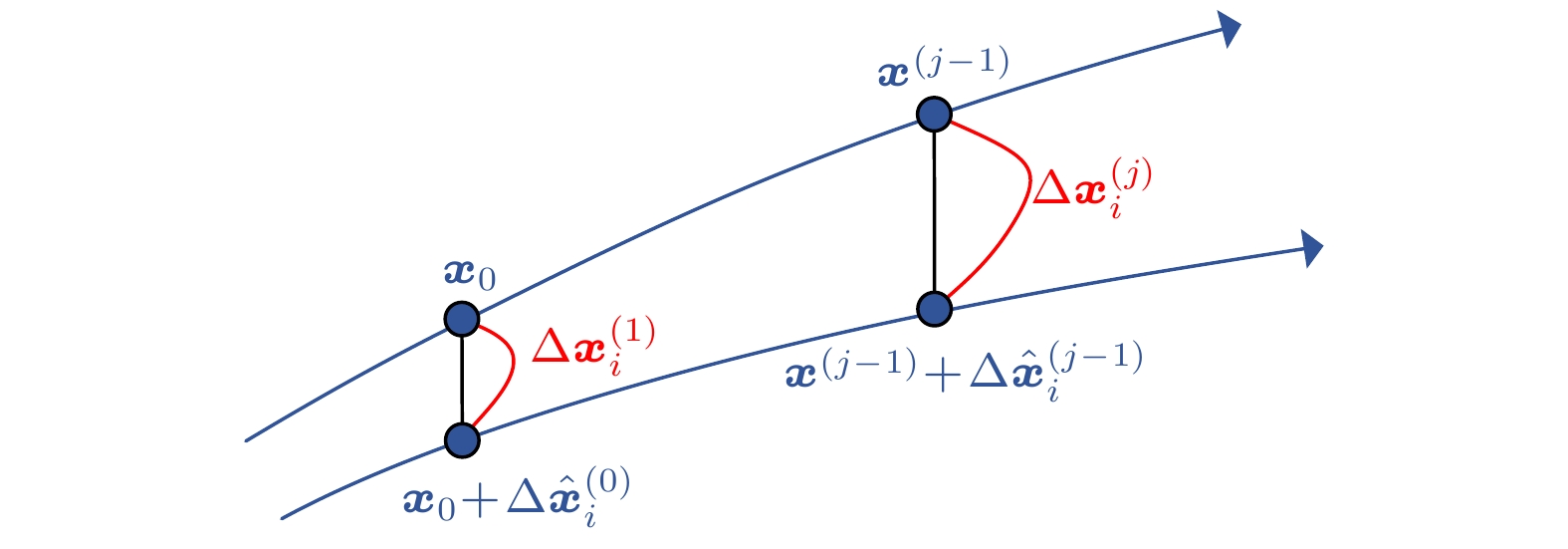 图 3 不连续系统Lyapunov指数算法的示意图
图 3 不连续系统Lyapunov指数算法的示意图















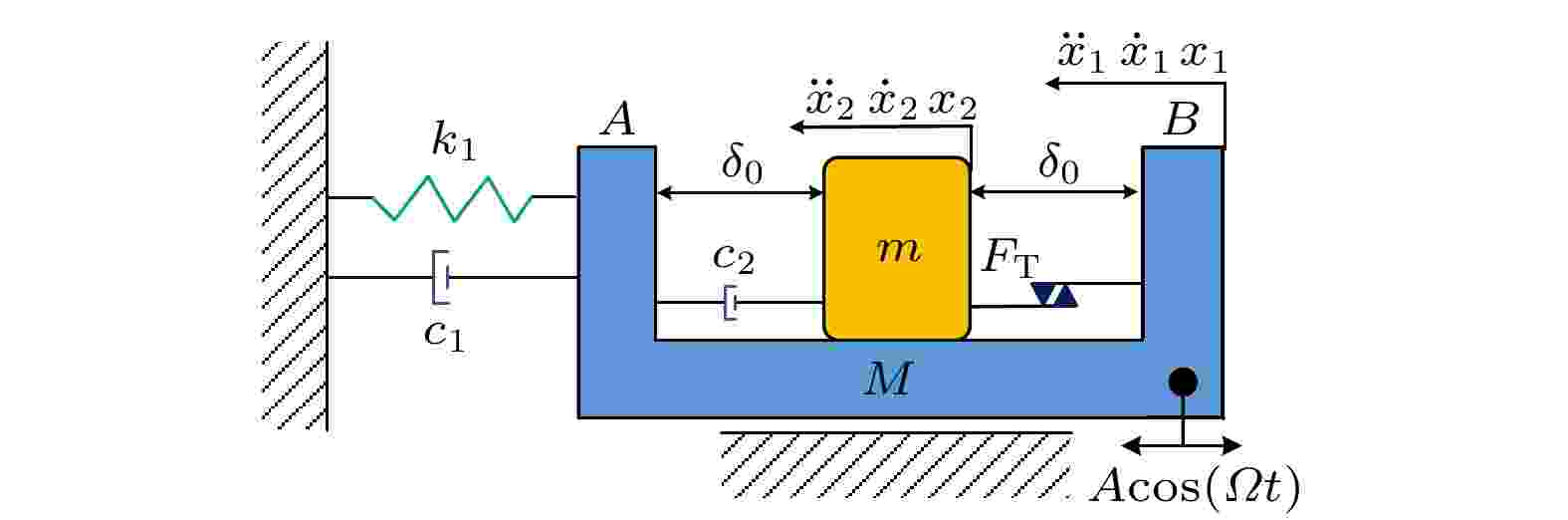 图 4 二自由度干摩擦冲击振荡器模型
图 4 二自由度干摩擦冲击振荡器模型

































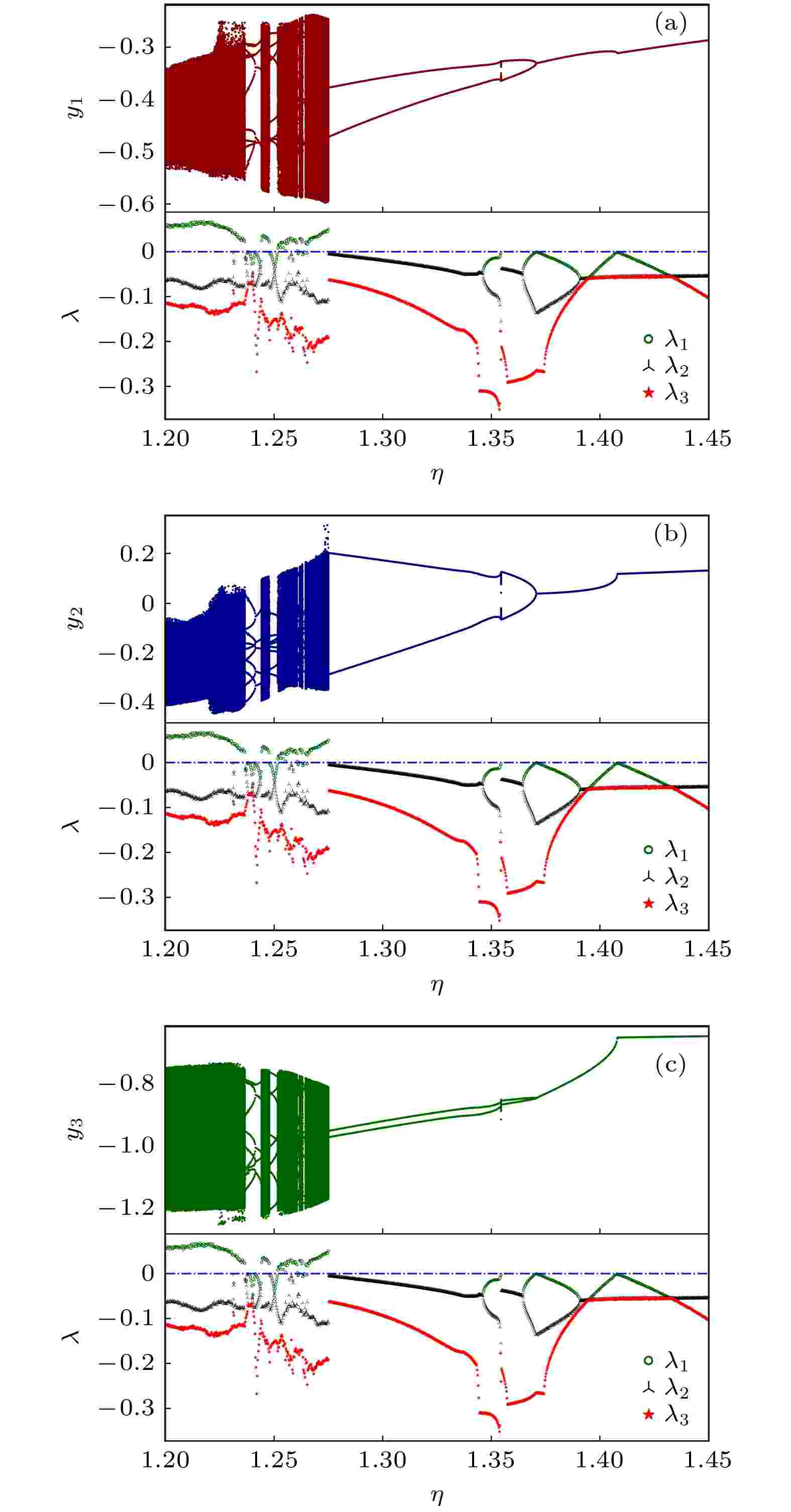 图 5 二自由度干摩擦冲击振荡器系统的分叉图和3个最大Lyapunov指数图 (a) 状态变量
图 5 二自由度干摩擦冲击振荡器系统的分叉图和3个最大Lyapunov指数图 (a) 状态变量




























