摘要: 研究了基本费米子的质量分布, 并找到一组描述基本费米子质量在特定分布模式下的经验关系式. 这启发我们对基本费米子质量等级和基本费米子具有三代的根源进行深入的思考, 提出了一种理论模型, 解释了基本费米子为什么具有三代, 并讨论了基本费米子质量等级和自旋的起源.
关键词: 质量等级 /
基本费米子 /
代 /
自旋 English Abstract Mass distribution and generation of elementary fermions Mi Li-Gong Xie Quan Zhang Li Wu Zhong-Zu College of Big Data and Information Engineering, College of Physics, Guizhou University, Guiyang 550025, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11963003), the National SKA Program of China (Grant No. 2020SKA0110300), the Youth Science & Technology Talents Development Project of Guizhou Education Department, China (Grant Nos. KY[2018]433, 119), and the Guizhou University Talent Research Fund, China (Grant No. (2018)60)Received Date: 07 May 2021Accepted Date: 26 July 2021Available Online: 20 August 2021Published Online: 05 December 2021Abstract: In this paper, we study the mass distribution of elementary fermions and find a set of empirical relations to describe the mass distribution of elementary fermions. This inspires us to investigate in depth the origin of elementary fermion mass hierarchies and generations. We present a theoretical model to explain why the elementary fermions have three generations and discuss the origin of the fundamental fermion mass hierarchies and spin.Keywords: mass hierarchies /elementary fermion /generation /spin 全文HTML --> --> --> 1.引 言 在标准模型框架下, 共有三代基本费米子, 每代基本费米子包含一对夸克和一对轻子. 三代夸克和带电轻子都具有质量. 中微子振荡实验进一步表明至少有两种中微子也具有质量[1 -3 ] . 基本费米子质量是粒子物理标准模型的基本参数. 其中, 轻子作为物理粒子能够被观测到, 因此轻子质量能够直接测量; 而夸克被禁闭在强子内部, 其质量必须通过它们对强子性质的影响而间接测定. 标准模型并没有预测夸克和轻子的质量大小, 夸克和轻子的质量值只能通过实验测得. 对于夸克, 能够根据需要选择不同的重整化方案对它的质量参数进行定义. 为了比较不同的质量测定结果, 通常采用微扰理论, 将获得的质量值转化为在$ \overline{{\rm {MS}}} $ (minimal-subtraction)方案中, 固定的重整化尺度下的跑动质量[4 ] . 本文采用的轻夸克的质量是在$ \overline{{\rm {MS}}} $ 方案中, 重整化尺度为2 GeV下定义的. c夸克和b夸克的质量是在$ \overline{{\rm {MS}}} $ 方案中定义的跑动质量. t夸克和带电轻子的质量采用直接测量的物理质量. 本文的主要工作是通过考察基本费米子的质量分布规律, 提出了一组描述基本费米子质量在特定分布模式下的经验关系式, 并提出了一种理论模型解释产生三代基本费米子的原因.2.基本费米子的质量分布 基于目前对基本费米子质量的测量[5 ,6 ] , 在表1 中, 将三代夸克与轻子依次排成三列四行, 并分别用l 和n 表示基本费米子的列数和行数. 表1 中三代基本费米子中较重的夸克和轻子分别排在$ n = 1 $ 行和$ n = 2 $ 行, 较轻的三代夸克和轻子分别排在$ n = 3 $ 行和$ n = 4 $ 行. 经过排列后, 在$ l = 1 $ 列, 基本费米子从上到下分别为下夸克、电子、上夸克、电子中微子; 在$ l = 2 $ 列, 基本费米子从上到下分别为粲夸克、$ \text{μ} $ 子、奇夸克、$ \text{μ} $ 子中微子; 在$ l = 3 $ 列, 基本费米子从上到下分别为顶夸克、$ \text{τ} $ 子、底夸克、$ \text{τ} $ 子中微子. 表1 中括号内为对应的夸克或轻子的质量, 以MeV为单位. 该质量采用Particle Data Group (2020)的推荐值[7 ] . 不难发现, 在表1 中, 从$ n = 1 $ 行到$ n = 3 $ 行, 基本费米子的质量从左到右依次增大, 且呈现一种周期性, 这暗示着三代中微子也应该遵循同样的分布规律.代 $l=1$ $l=2$ $l=3$ $n=1$ ${\rm d}\,[4.64_{-0.17}^{+0.48}]$ ${\rm c}\,[1270\pm20]$ ${\rm t}\,[172760\pm300]$ $n=2$ ${\rm e}\,[0.5109989461\pm0.0000000031]$ $\text{μ}\,[105.6583745\pm0.0000024]$ $\text{τ[}\,[1776.82\pm0.12]$ $n=3$ ${\rm u}\,[2.16_{-0.26}^{+0.49}]$ ${\rm s}\,[93_{-5}^{+11}]$ ${\rm b}\,[4180_{-20}^{+30}]$ $n=4$ $\text{ν}_ {\rm e}$ $\text{ν}_\text{μ}$ $\text{ν}_\text{τ}$
表1 基本费米子的质量分布Table1. Mass distribution of elementary fermions.表1 中, 第l 列和第n 行的基本费米子的质量记为$ m_{ln} $ , 并令$ N(n) $ 表示第n 组夸克中, 较重的基本费米子的质量与另外两个较轻的基本费米子的总质量的比值; $ L(l) $ 表示第l 代基本费米子中, 较重的基本费米子的质量与另外三个较轻的基本费米子的总质量的比值. 不妨称$ N(n) $ 和$ L(l) $ 为基本费米子质量的量子结构函数. 我们提出: 对于基本费米子, 分别存在一个量子结构函数$ N(n) $ 和$ L(l) $ 将它们的质量联系在一起.3.基本费米子质量的经验关系 采取如下的分析步骤构造量子结构函数$ N(n) $ : 首先, 设想存在一个数值区间[$ k_i, k_j $ ], 且该区间内的元素记为k , 则有$k_i\leqslant k \leqslant k_j$ , 其中, $ k_i $ 和$ k_j $ 不妨称为区间[$ k_i, k_j $ ]的界; 其次, 假设对于行数n , 总能够找到对应的$ k_i $ 和$ k_j $ , 使得$ k_i = k_i(n) $ , $ k_j = k_j(n) $ , 其中$ k_i(n) $ 和$ k_j(n) $ 不妨称为n 的界函数; 第三, 设想存在k 的一个函数$ F(k) $ , 使得当k 从$ k_i $ 依次取到$ k_j $ 时, 有$ F(k) $ 不妨称为$ N(n) $ 的结构核. $ F(k) $ 应该不是唯一的, 我们找到了$ N(n) $ 的一个好的结构核$ F(k) $ , 即$ \alpha $ 为精细结构常数. 从而有n 的一组界函数, 即$ n = 1 $ 时, $ k_j(1) = 1+0^0 $ , 其中, $ 0^0 $ 没有严格的定义, 在本文中, 我们约定: $ 0^0 = 0 $ , 从而有$ k_j(1) = 1 $ . 设$ N(n) $ 的经验值为$ N_{\rm{e}}(n) $ , 由(5 )式和(6 )式可得到$ N(n) $ 的一个经验表达式:$n = 1, \,2,\, 3$ 时, 由(7 )式可得$ N(n) $ 的观测值为$N_{\rm{o}}(n)$ . 采用Particle Data Group (2020)的推荐值, 计算可得$ n = 1, 2, 3 $ 时, $ N(n) $ 的经验值$N_{\rm{e}}(n)$ 和观测值$N_{\rm{o}}(n)$ 符合得非常好. 图1(a) 给出了$ N(n) $ 的经验值和观测值的相关图, 通过pearson相关分析, 得到两者的相关系数为0.9999, 其显著性为0.00889, 说明两者在大于99%的置信度水平上具有极强的正相关.图 1 观测值和经验值的相关性 (a) $N_{\rm{o}}(n)$ 与$N_{\rm{e}}(n)$ 的比较; (b) $L_{\rm{o}}(l)$ 与$L_{\rm{e}}(l)$ 的比较Figure1. Correlation between theoretical and observed values: (a) the correlation between $N_{\rm{o}}(n)$ and $N_{\rm{e}}(n)$ for $n = 1, 2, 3$ ; (b) the correlation between $L_{\rm{o}}(l)$ and $L_{\rm{e}}(l)$ for $l = 1, 2, 3$ .表1 中, 对于第l 代基本费米子, 设$ L(l) $ 的经验值为$L_{\rm{e}}(l)$ , 我们找到了$L_{\rm{e}}(l)$ 的一个好的经验关系式:$ l = 1,\, 2,\, 3 $ 时, 由(10 )式计算可得$ L(l) $ 的观测值为$L_{\rm{o}}(l)$ . 根据Particle Data Group (2020)推荐的夸克和轻子的质量值, 计算可得[8 ] , 在计算过程中已经将其忽略. 可见, $ L(l) $ 的经验值$L_{\rm{e}}(l)$ 和观测值$L_{\rm{o}}(l)$ 符合得非常好. 图1(b) 中绘制了$ L(l) $ 的经验值和观测值的相关图, 通过pearson相关分析, 得到两者的相关系数为0.99999, 其显著性为$0.00278,$ 说明两者在大于99%的置信度水平上具有极强的正相关.7 )式和(10 )式, 可估算得到下夸克、上夸克、粲夸克、奇夸克和底夸克的质量均值分别为$ m_{\rm d} = 4.28 \; {\rm{MeV}} $ , $m_{\rm u} = $ $ 1.96 \; {\rm{MeV}}$ , $ m_{\rm c} = 1266 \; {\rm{MeV}} $ , $ m_{\rm s} = 94.5 \; {\rm{MeV}} $ , $m_{\rm b} = 4101 \; {\rm{MeV}}$ . 将计算结果与对应的夸克质量的观测值进行比较(见表1 ), 不难发现两者符合得非常好. 进一步, 由(2 )式和(10 )式可得$\xi(l) = \dfrac{m_{l2}+m_{l3}+m_{l4}}{m_{(l-1)2}+m_{(l-1)3}+m_{(l-1)4}}$ . 同样, 使用3种带电轻子和顶夸克的质量, 忽略中微子的质量后, 估算可得$ \xi(3) = 29.37 $ , $ \xi(2) = 81 $ . 根据Particle Data Group (2020)推荐的夸克和轻子的质量值, 估算可得$ \xi(3) $ 和$ \xi(2) $ 的观测值分别为$ 29.99_{-1.67}^{+0.93} $ 和$ 74.38_{-13.11}^{+12.58} $ . 可见, 两者符合得很好.4.基本费米子代的理论解释和讨论 根据标准模型, 狄拉克场与希格斯场相耦合, 通过自发对称性破缺使费米子从希格斯场的真空期待值获得质量[9 ] . 但标准模型没能给出基本费米子的质量大小, 目前, 也很难解释基本费米子的质量等级和中微子质量的起源问题. 三代基本费米子的质量具有显著的等级, 从电子到顶夸克, 质量跨越 了5个数量级. 文献[10 ]提出了一种观点, 认为除了顶夸克, 其他质量较轻的基本费米子与希格斯场的作用都是间接的. 考虑到基本费米子的质量正比于它与希格斯场的耦合强度, 与顶夸克相比, 质量较轻的基本费米子与希格斯场的耦合强度可以忽略, 这种观点具有它的合理性. Steven 在文献[11 ]中也表达了同样的想法. 他进一步提出第三代夸克和带电轻子通过与希格斯场耦合获得质量, 然后, 质量再通过某种机制从第三代基本费米子依次传递到第二代和第一代基本费米子.U U K 对其所处的能量量子态进行表征. 令$K = 0, $ $ 1, \cdots, K_m$ , 其中, $ K_m $ 为最大的K 值, 则U $ K_m+1 $ . 当$ K = 0 $ 时, U $0 < K\leqslant K_m$ 时, U U $ \varepsilon_K $ , 则有$ \varepsilon_K > \varepsilon_{K-1} $ . U U K 的每一个取值表征的能量量子态对应着U U U $ K_m+1 $ , 我们说U $ K_m+1 $ 维量子空间. 当U U U l ($l = 1, 2, $ $ 3, \cdots$ ). 第l 代代粒子对应着 U K 存在一个最大的取值$ K_m $ , 因此, 质量量子数l 也相应地存在一个最大的取值$ l_m $ , 于是有U $ \varUpsilon $ . $ \varUpsilon $ 量子具有波粒二象性, 它的动量$ P_K $ 和波长$ \varLambda_K $ , 能量$ E_K $ 和周期$ T_K $ 的关系满足德布罗意方程:h 为普朗克常量. 当将$ \varUpsilon $ 量子视为粒子时, 它具有内禀的空间尺度和时间尺度. $ \varUpsilon $ 量子作为粒子具有的内禀的空间尺度和时间尺度分别称为空间量子尺度和时间量子尺度, 定义为U $ \varUpsilon $ 量子的空间量子尺度和时间量子尺度为零, 此时, U 16 )式代入到(15 )式, 得到$ \varUpsilon $ 量子的空间量子动量和空间量子能量分别为$\hbar = h/(2\pi)$ 为约化的普朗克常数.U $ \varUpsilon $ 量子的空间量子动量和空间量子尺度分别存在一个不确定度$ \Delta P_K $ 和$ \Delta r_K $ , 且它们满足量子力学的不确定性关系, 即U K 时, $ \varUpsilon $ 量子的空间量子动量和其不确定度, 空间量子尺度和其不确定度不能任意取值, 它们之间必须满足如下关系:19 )式可以作为量子数K 的定义.$ \varUpsilon $ 量子不仅具有内禀的动量和能量, 而且还具有内禀的自旋. $ \varUpsilon $ 量子的自旋包括两类: 一类由空间量子动量和空间量子尺度决定, 称为内自旋, 记为$ S_{\rm i} $ , 其大小定义为空间量子动量与空间量子尺度的大小的乘积; 一类由空间量子动量的不确定度和空间量子尺度的不确定度决定, 称为外自旋, 记为$ S_{\rm o} $ , 其大小定义为空间量子动量的不确 定度与空间量子尺度的不确定度的大小的乘积. 由(15 )式和(16 )式可得$ \varUpsilon $ 量子的内自旋的大小为$ \varUpsilon $ 量子的内自旋是量子化的, 且由量子数K 决定. $ \varUpsilon $ 量子的内自旋只能取$ \hbar $ 的整数倍, 因此, $ \varUpsilon $ 量子是玻色子. 由(19 )式和(20 )式可得$ \varUpsilon $ 量子的外自旋的大小为$ \varUpsilon $ 量子的外自旋由内自旋和量子数K 决定. 当$ K = 0 $ 时, $ S_{\rm i} = 0 $ , 此时, $ S_{\rm o} $ 的取值不确定, 理论上, 它应该能取满足(18 )式的任意一个数值. 当$ K > 0 $ 时, (21 )式可化为$\varUpsilon$ 量子的外自旋也是量子化的, 且由量子数K 决定. $\varUpsilon$ 量子的外自旋具有如下的特性: 基本粒子在与处于激发态的U $\varUpsilon$ 量子能够将其外自旋赋予基本粒子, 使得基本粒子获得大小为$S_{\rm o}$ 的自旋. 由(20 )式和(22 )式知, 在量子维度跃迁过程中, $\varUpsilon$ 量子的自旋将发生变化. 我们将U U U U $ K > 0 $ 时, 结合(18 )式和(22 )式立刻得到U K 只能取0, 1和2三个数值, 且$ K_m = 2 $ . 由(14 )式可得$ l_m = 3 $ . 这至少表明两点.$ \varUpsilon $ 量子(U $ K = 0, 1, 2 $ 时, 相应的3种$ \varUpsilon $ 量子(U $ \varUpsilon_0 $ (${\boldsymbol{U}_0}$ ), $ \varUpsilon_1 $ (${\boldsymbol{U}_1}$ )和$ \varUpsilon_2 $ (${\boldsymbol{U}_2}$ ). $ \varUpsilon_0 $ , $ \varUpsilon_1 $ 和$ \varUpsilon_2 $ 的内自旋分别为$ 0 $ , $ \hbar $ 和$ 2\hbar .$ $ \varUpsilon_0 $ 的外自旋不确定, 但$ \varUpsilon_1 $ 和$ \varUpsilon_2 $ 分别具有确定的外自旋$ \hbar $ 和${\hbar}/{2}$ . U U $ K = 1 $ )和基态之间的量子维度跃迁; b类, 在第一激发态和第二激发态($ K = 2 $ )之间的量子维度跃迁; c类, 在基态和第二激发态之间的量子维度跃迁. 从而, U U U U U U ${\hbar}/{2}$ 的自旋, 根据U $ {\boldsymbol{U}_2} $ 场发生作用, 这种相互作用可理解为基本费米子与$ \varUpsilon_2 $ 量子的一种耦合, 在作用过程中, $ \varUpsilon_2 $ 量子将${\hbar}/{2} $ 的外自旋赋予基本费米子. 同理, 传递强相互作用和电弱相互作用的规范玻色子具有的$ \hbar $ 自旋的来源可解释为: 规范玻色子产生时将与$ {\boldsymbol{U}_1} $ 场发生作用, 并获得$ \varUpsilon_1 $ 量子的大小为$ \hbar $ 的外自旋.U $ {\boldsymbol{U}_0} $ 场, $ {\boldsymbol{U}_1} $ 场和$ {\boldsymbol{U}_2} $ 场通过量子维度跃迁可以相互转化, 它们是U U $ {\boldsymbol{U}_1} $ 场本质上应该是一种统一的规范作用场, 具有自旋为$ \hbar $ 的$ \varUpsilon_1 $ 量子本质上是一种统一的规范玻色子. $ {\boldsymbol{U}_1} $ 场在宇宙的演化过程中将分化为电磁相互作用场、强相互作用场和弱相互作用场等3种基本相互作用场, 相应地, $ \varUpsilon_1 $ 量子也随之蜕化为传递3种基本相互作用的规范玻色子. $ {\boldsymbol{U}_2} $ 场的场量子是自旋为$ 2\hbar $ 的$ \varUpsilon_2 $ 量子. 根据无质量粒子的洛伦兹不变理论[12 ] , 自旋量子数为2的无质量粒子具有引力子最显著的动力学特征, 因此我们认为: $ {\boldsymbol{U}_2} $ 场本质上应该是一种统一的引力场, 相应地, $ \varUpsilon_2 $ 量子本质上是一种统一的引力子. 目前, 我们发现引力场只有一种, $ {\boldsymbol{U}_2} $ 场在宇宙的演化过程中是否会分化为不同种类的引力相互作用呢?已经发现宇宙中存在暗物质和暗能量, 它们之间的引力相互作用与普通物质之间的引力相互作用是否相同呢?这将是未来需要思考的一个重要问题. $ {\boldsymbol{U}_0} $ 场的场量子是自旋为0的$ \varUpsilon_0 $ 量子. 我们认为: $ {\boldsymbol{U}_0} $ 场是赋予基本粒子作用荷的场. 随着宇宙的演化, $ {\boldsymbol{U}_0} $ 场有可能分化为分别赋予基本粒子质量、电荷和色荷等作用荷的场. 已经知道赋予规范玻色子和基本费米子质量的场是希格斯场. 那么, 可以设想在宇宙中应该还分布着赋予基本粒子其他作用荷的场. 未来寻找赋予基本粒子各种作用荷的场量子将是非常有意义的工作. 











































































































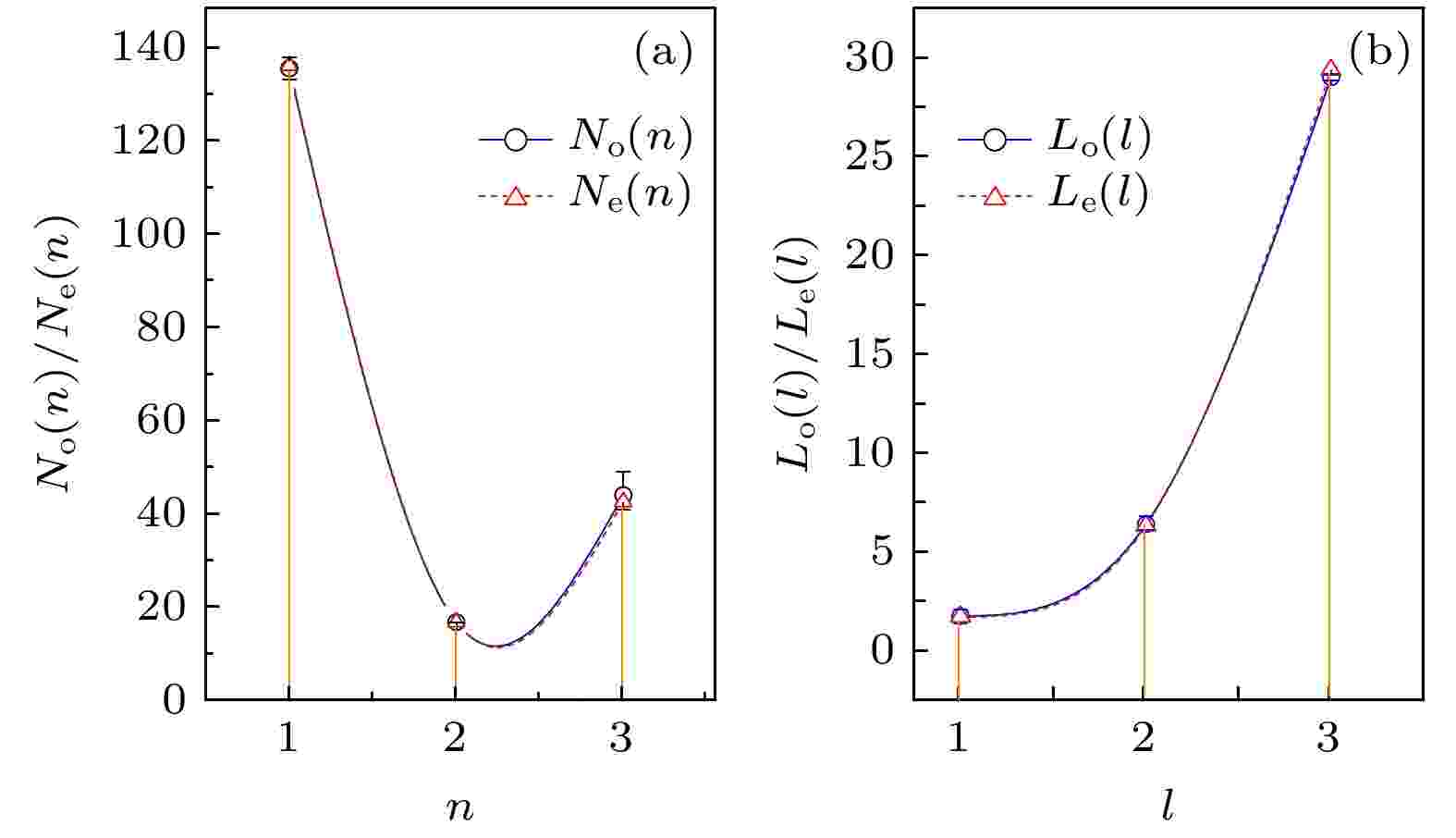 图 1 观测值和经验值的相关性 (a)
图 1 观测值和经验值的相关性 (a) 












































































































































































































































