摘要: 自从Moriya和Kaplan在自旋轨道耦合的单带哈伯德模型中发现了对称的螺旋交换作用, Shekhtman, Entin和Aharony等用这种不可忽略的对称螺旋交换作用成功地解释了
$ {\text{L}}{{\text{a}}_{\text{2}}}{\text{Cu}}{{\text{O}}_{\text{4}}} $ 的弱铁磁性. 本文应用非马尔科夫量子态扩散方法研究了具有Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用和Dzyaloshinskii-Moriya相互作用的自旋链系统中量子失协的非马尔科夫动力学演化问题, 分析了Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用在零温和有限温度下不同外加磁场时对量子失协的影响. 结果表明, 在没有磁场或仅有均匀磁场的情况下, 系统中的量子失协可以通过增加Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用而增加, 而在非均匀磁场中则相反. 更重要的是, 通过调节均匀磁场和Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用可以得到理想的失协状态. 此外, 还分别讨论了Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用在马尔科夫环境和有限温度下对量子失协的影响.
关键词: 非马尔科夫量子态扩散方法 /
量子失协 /
磁场 /
Kaplan-Shekhtman-Entin-Wohlman-Aharony相互作用 English Abstract Effects of Kaplan-Shekhtman-Entin-Wohlman-Aharony interaction on quantum discord of non-markovian dynamics under different magnetic fields Zhang Jin-Feng Arapat Ablimit Yang Fan Akbar Hamutjan Tang Shi-Sheng Ahmad Abliz School of Physics and Electronic Engineering, Xinjiang Normal University, Urumqi 830054, China Fund Project: Project supported by the Fund for Less Developed Regions of the National Natural Science Foundation of China (Grant No. 11864042).Received Date: 08 July 2021Accepted Date: 31 August 2021Available Online: 11 September 2021Published Online: 20 November 2021Abstract: Since the discovery of symmetric helical interactions in the spin-orbit coupled single-band Hubbard model by Moriya and Kaplan, Shekhtman, Entin, Aharony et al. have successfully used this non-negligible symmetric helical exchange interaction to explain the weak ferromagnetism of La2 CuO4 . By using the non-Markovian quantum state diffusion method, the quantum discord of non-Markovian dynamics in the spin chain system that has Kaplan–Shekhtman–Entin-Wohlman–Aharony interactions and Dzyaloshinskii-Moriya interactions is studied. The effects of Kaplan–Shekhtman–Entin-Wohlman–Aharony interaction on the quantum discord under different external magnetic fields at zero and finite temperatures are discussed. The results show that the quantum discord in the system can be increased via the increasing of Kaplan–Shekhtman–Entin-Wohlman–Aharony interaction in the case of zero or uniform magnetic field, while the case is opposite under the nonuniform magnetic field. More importantly, the ideal discord state can be obtained by modulating the uniform magnetic field and Kaplan–Shekhtman–Entin-Wohlman–Aharony interaction. Moreover, the Markovian case and the effect of temperature on the quantum discord are also discussed, respectively.Keywords: non-markovian quantum state diffusion method /quantum discord /magnetic field /Kaplan-Shekhtman-entin-Wohlman-Aharony interaction 全文HTML --> --> --> 1.引 言 量子关联是量子系统中的一种非经典关联, 它是量子计算和量子通信中的一种重要资源[1 -4 ] . 量子关联的表征和控制对于量子信息的应用至关重要, 量子关联最典型的度量方法是量子纠缠[5 ,6 ] . 但是, 量子纠缠并不足以描述系统中所有的量子关联[7 ,8 ] , 例如当系统中没有量子纠缠时还可以存在量子关联. 因此, Harold和Zurek [9 ] 引入了另一种关联的度量方法, 即量子失协, 量子失协被定义为量子信息与经典信息之差, 并且被证明是量子关联的一种好的度量方法[10 ] . Fanchini等[11 ] 研究了两个量子比特耦合到独立和共同的非马尔科夫环境中量子失协的动力学演化过程, 结果表明即使没有纠缠, 由环境引入的关联也会转移到两个量子比特上, 产生有限的量子失协. Daki?等[12 ] 通过研究发现, 量子失协是量子远程态制备的必要资源.[13 ] . 量子自旋系统作为一种固态系统, 由于其体积小、易于集成, 在量子态制备和存储方面具有潜在的应用价值. 作为自旋系统中最简单的模型, 海森伯自旋链模型被广泛应用于电子自旋[14 ] 、量子点[15 ] 、原子核自旋[16 ] 和模拟量子计算机的研究. 其中对Dzyaloshinskii和Moriya发现的具有Dzyaloshinskii-Moriya(DM)相互作用的自旋系统的研究已经受到了研究人员的广泛关注, 这是因为DM相互作用被认为是量子失协的有效调控参数之一. Mohammad[17 ] 研究了海森伯XY 自旋链模型中DM相互作用对量子失协和量子纠缠的影响, 结果表明在DM相互作用下量子失协比量子纠缠更稳定; Sun等[18 ] 发现, 通过增加DM相互作用可以提高两比特海森伯XYZ 自旋链模型的量子失协大小.[19 ] 发现反对称的DM相互作用时, 还发现系统中存在一个对称的螺旋各向异性相互作用. 在很长一段时间内, 与反对称的DM相互作用相比, 这种对称螺旋相互作用被认为是可以忽略的. 然而, Kaplan[20 ] 随后在自旋轨道耦合的单带哈伯德模型中发现了这种对称的螺旋作用, 然后Shekhtman等[21 ,22 ] 论证了它的重要性, 因为它可以恢复被DM相互作用打破的各向同性海森伯体系的$O(3)$ 对称性. Shekhtman等[22 ] 用这种不可忽略的对称螺旋交换作用成功地解释了$ {\text{L}}{{\text{a}}_{\text{2}}}{\text{Cu}}{{\text{O}}_{\text{4}}} $ 的弱铁磁性. 由于他们的这些发现, 对称螺旋交换相互作用被简称为KSEA相互作用[23 -25 ] . 最近, Yurischev[26 ] 发现无外磁场时KSEA相互作用可以抑制热平衡态下量子失协的局域最小值. KSEA相互作用被证明非常有助于增加热平衡态下的量子费舍尔信息和减缓系统的退相干[27 ] . 由于DM和KSEA相互作用很重要, 研究人员已经提出合成和控制DM和KSEA相互作用的方法. Liu等[28 ] 研究局域自旋, 通过具有自旋轨道耦合的传导电子系统所产生的间接磁交换相互作用发现, 当系统中只有电流没有自旋流(即仅有偏置电压)时, 可以合成和控制各项异性的海森伯相互作用和DM相互作用; 当系统中没有电流但有自旋流(即仅有自旋偏置电压)时, 不仅可以合成和控制各项异性的海森伯相互作用, 还可以合成和控制DM和KSEA相互作用. 因此在该系统中可以通过调节自旋偏置电压和偏置电压来合成和控制海森伯相互作用、DM相互作用和KSEA相互作用. 此外还可以尝试通过人工合成具有螺旋交换相互作用的材料, 通过改变材料成分、变换堆叠顺序和混合杂质来控制DM和KSEA相互作用的强度大小和方向[28 ] .[29 ] 在1998年提出的, 用于研究开放量子系统的非马尔科夫动力学演化过程. 该方法在处理开放量子体系的动力学演化过程中不受耦合强度、关联时间及库的谱密度影响[29 ] , 其提供的数学工具使我们能够精确地研究非马尔科夫过程带来的奇异性质, 在数值上处理一个随机的纯态, 能够极大地提高计算效率, 适合处理较复杂的模型. 虽然固态体系有易嵌入和可扩展等优点, 但与其他体系相比, 其环境自由度过大, 与环境存在强耦合等原因使其相干性难以长时间保持, 体系明显具有非马尔科夫特性. 例如, 自旋与自旋库相互作用体系[30 ] 和自旋玻色体系[31 ] 的非马尔科夫效应非常明显. 此类系统的动力学演化不能用Lindblad主方程(马尔科夫近似得到)准确描述, 只有考虑体系的非马尔科夫特性才能解决. 本文利用NMQSD方法研究在非马尔科夫环境下带有DM相互作用的海森伯XYZ 自旋链系统在外加磁场时, 沿z 方向的KSEA相互作用对量子失协动力学演化的影响.2.模型与方法 海森伯XYZ 自旋链模型线性耦合于一组谐振子组成的玻色库时, 该模型中系统的总哈密顿量可以表示为$\left( {\hbar = 1} \right)$ 2 )式中的$ {b_k} $ 和$ b_k^\dagger $ 分别为湮灭算符和产生算符, $ {\omega _k} $ 为玻色库中玻色子的跃迁频率; (3 )式中$L = $ $ {k_A}\sigma _ - ^A + {k_B}\sigma _ - ^B$ 是玻色环境和系统耦合的Lindblad算符, 其中${k_A}$ 和${k_B}$ 表示的是两个常量, 描述的是两个自旋链与各自环境的不同耦合强度, 本文令${k_A} = {k_B} = 1$ , $ {g_k} $ 表示系统与环境之间的耦合系数.1 )式中${H_{\text{s}}}$ 表示为含z 方向的DM相互作用、z 方向KSEA相互作用和z 方向外加磁场的海森伯自旋链哈密顿量, 可以写为$ {J_x} $ , $ {J_y} $ , $ {J_z} $ 分别为x , y , z 三个方向的耦合常数, 本文令${J_x} \ne {J_y} \ne {J_z}$ , 此时海森伯自旋链模型变为海森伯XYZ 模型, $\sigma = ({\sigma _x}, {\sigma _y}, {\sigma _z})$ 表示泡利算符, $ {B_z} $ 表示z 方向的均匀外加磁场, $ {b_z} $ 表示z 方向的磁场非均匀度, $ {D_z} $ 表示为z 方向的DM相互作用, $ {\varGamma _z} $ 表示为z 方向的KSEA相互作用.2.1.零温下非马尔科夫量子态扩散方法 2.1.零温下非马尔科夫量子态扩散方法 为了求解零温下该模型的量子失协动力学演化问题, 需要借助NMQSD方法来对其进行处理. 假设$ {\psi _{{z^*}}}(t) $ 为系统波函数, 根据NMQSD理论可以得到关于$ {\psi _{{z^*}}}(t) $ 的动力学微分方程[32 ] $\alpha (t, s) = \displaystyle\sum\nolimits_k {|{g_k}{|^2}} {{\text{e}}^{ - {\text{i}}{\omega _k}(t - s)}}$ 为环境关联系数, $z_t^* = - {\text{i}}\displaystyle\sum\nolimits_k {(g_k^*z_k^*{{\text{e}}^{{\text{i}}{\omega _k}t}})}$ 为环境噪音函数, $z_t^*$ 满足$M[{z}_{t}^{*}]=0, M[{z}_{t}{z}_{\text{s}}^{*}]=\alpha (t, s), M[\cdot]=\dfrac{1}{\text{π}}{\displaystyle \int {\text{d}}^{2}z{\text{e}}^{-|z{|}^{2}}}$ 表示环境噪声的系综平均值. 本文选取Ornstein-Uhlenbeck(OU)噪声为环境关联函数, OU噪声表达式可以写为$\alpha (t, s) = \dfrac{\gamma }{2}{{\text{e}}^{ - \gamma |t - s|}}$ , 其中γ 表示玻色库的环境记忆效应系数, 当γ 趋近于无穷大时, 系统处于马尔科夫状态; 当γ 趋近于0时, 系统处于非马尔科夫状态. 通过使用方程 $\dfrac{{\text{δ}}}{{{\text{δ}}z_t^*}}|{\psi _{{z^*}}}(t) \rangle = $ $ O(t, s, {z^*})\dfrac{{\text{δ }}}{{{\text{δ }}z_t^*}}|{\psi _{{z^*}}}(t) \rangle$ 来代替导数项, 可将(5 )式改写为$\bar O(t, {z^*}) = \displaystyle\int_0^t {\alpha (t, s)O(t, s, {z^*})} {\text{d}}s$ , 利用O 算符所满足的微分方程[32 ] 8 )式可以改写为[32 ] $\bar O(t, s) \approx {\bar O_0}(t)$ 时, 表明算符${\bar O_0}(t, z)$ 对噪声$z_t^*$ 可以忽略不计. 因此, 在零阶近似情况下两个二能级原子耦合到玻色库的主方程, 可以变为以下形式:2.2.有限温度下非马尔科夫量子态扩散方法 -->2.2.有限温度下非马尔科夫量子态扩散方法 考虑到有限温度下的热平衡态系统密度矩阵为[33 ] $Z = {\text{Tr}}[{{\text{e}}^{ - \beta {H_{{\text{bath}}}}}}]$ 是配分函数, $ \beta = 1/({k_{\text{B}}}T) $ . ${k_{\rm{B}}}$ 是玻尔兹曼常数, 假设${k_{\text{B}}} = 1$ , 则系统的总哈密顿量可以写为[33 ] $ {H_{\text{s}}} $ 和零温环境中相同, 通过波戈留玻夫变换最终可得到系统的总哈密顿量为$\overline {{n_\lambda }} = 1/\exp \left[ {\hbar {\omega _\lambda }/({k_{\text{B}}}T)} \right] - 1$ 是量子的热占有数. 在有限温度下, 量子态扩散方程包含两个相互独立的噪声$z_t^*, \omega _t^*$ $\overline {{O_i}} (i = 1, 2)$ 可定义为O 算符微分方程可以写为10 )式和(22 )式分别为整个体系在零温和有限温度下的非马尔科夫主方程, 后面的研究均基于这两个主方程进行.3.数值计算及讨论 一个给定的两体量子态的量子互信息为[9 ] ${{\boldsymbol{\rho}} ^A} = {\text{T}}{{\text{r}}_B}{{\boldsymbol{\rho}} ^{AB}}$ , ${{\boldsymbol{\rho}} ^B} = {\text{T}}{{\text{r}}_A}{{\boldsymbol{\rho}} ^{AB}}$ 分别是子系统A 和B 的约化密度矩阵, $S({\boldsymbol{\rho}}) = - {\text{Tr}}({\boldsymbol{\rho}} {\log _2}{\boldsymbol{\rho}} )$ 是系统的冯诺伊曼熵.B , 用一组完备的POVM测量基$\{ {{{B}}_k}\} $ 进行测量, 如果测量的结果为k , 条件矩阵则变为${\rho _k} = {\text{Tr}}[({{\boldsymbol{I}}_A} \otimes \{ {{\boldsymbol{B}}_k}\}){{\boldsymbol{\rho}} ^{AB}}({{\boldsymbol{I}}_A} \otimes \{ {{\boldsymbol{B}}_k}\})]$ . 对子系统进行测量之后, 相应的量子条件熵为$I({{\boldsymbol{\rho}} ^{AB}}|\{ {{{\boldsymbol{B}}}_k}\} )$ , 遍求全部的测量, 从中选择最优的一组. 这个最大值即为经典关联$C({{\boldsymbol{\rho}} ^{AB}})$ , 具体的数学形式为[9 ] [9 ] , 即28 )式和零温非马尔科夫近似主方程(10 )式以及有限温度非马尔科夫近似主方程(22 )式通过数值计算讨论环境记忆效应、外加磁场、KSEA相互作用对耦合到玻色库中的两比特海森伯XYZ 自旋链模型的量子失协随时间演化特性的影响. 本文选择最大纠缠态$\left| \psi \right\rangle = $ $ {1 / {\sqrt 2 }}(\left| {01} \right\rangle + \left| {10} \right\rangle )$ 作为初始态.图1(a) 给出了量子失协随KSEA相互作用和时间t 变化的三维投影图, 图1(b) 是在$\omega t = 5$ 时量子失协随KSEA相互作用的演化过程. 从图1 可以看出, 当KSEA相互作用强度增加时, 量子失协也随之增大, 而当KSEA相互作用强度增加到${\varGamma _z} \geqslant 2$ 之后, 系统的量子失协接近最大值的理想失协状态. 这是由于KSEA相互作用恢复了系统的$O(3)$ 对称性, 从而抑制系统的退相干, 使得系统的量子失协可以保持较高的状态.图 1 (a)量子失协随KSEA相互作用和时间的演化特性; (b) KSEA相互作用在$\omega t = 5$ 时对量子失协的影响. 其他参数${J_x} = 0.2,~ {J_y} = 0.5,~ {J_z} = 0.9, ~\gamma = 0.1,~ {B_z} = 0,~ {b_z} = 0$ , ${D_z} = 0.2,~T = 0$ Figure1. (a) Dynamics of quantum discord with KSEA interactions and time; (b) effect of KSEA interaction on quantum discord at$\omega t = 5$ . The other parameters are${J_x} = 0.2,~ {J_y} = 0.5,~ {J_z} = 0.9,~ \gamma = 0.1,~ {B_z} = 0, {b_z} = 0$ , ${D_z} = $ $ 0.2, T = 0$ .图2(a) 中给出了不加磁场时KSEA相互作用对量子失协随时间演化特性的影响. 从图中明显可以看到, ${\varGamma _z}$ 取值越大, 量子失协越大. 其次, 在图2(b) 中, 考虑了外加均匀磁场的情况. 不难看出, 当KSEA相互作用${\varGamma _z} = 0$ 时, 系统的量子失协强度大于图2(a) 中没有磁场时的情形. 显然, 均匀磁场的存在促进了量子失协的增加. 此外, 随着KSEA相互作用强度的增加, 系统的量子失协强度亦增大, 表明均匀磁场和KSEA相互作用的联合效应对量子失协强度的提升具有积极作用. 最后, 在图2(c) 中给出了非均匀磁场的情况. 有趣的是, KSEA相互作用越小, 磁场的非均匀度和KSEA相互作用的联合效应越积极, 比没有磁场或外加均匀磁场时还要明显. 甚至没有KSEA相互作用时磁场的非均匀度使得量子失协几乎能达到理想值. 通过一系列磁脉冲实现量子逻辑操作的核磁共振量子计算方案, 或不可避免的磁耦合存在时的情况都是非均匀磁场的情况. KSEA相互作用越大, 非均匀磁场下的量子失协衰减得越快. 显然, 当体系中存在KSEA相互作用时, 磁场的非均匀度抑制了KSEA相互作用恢复$O(3)$ 对称性的效果.图 2 KSEA相互作用在不同磁场环境下对量子失协的影响 (a)不加磁场${B_{{z}}} = 0,~ {b_z} = 0$ ; (b)均匀磁场${B_{ {z}}} = 1, $ $ {b_z} = 0$ ; (c)非均匀磁场${B_{ {z}}} = 1, ~{b_z} = 3$ . 其他参数${J_x} = 0.2, $ $ {J_y} = 0.5,~ {J_z} = 0.9$ , $\gamma = 0.1,~ {D_z} = 0.2, ~T = 0$ Figure2. Effects of KSEA interactions on the dynamics of the quantum discord in different magnetic field environment: (a) No magnetic field added${B_{\text{z}}} = 0,~ {b_z} = 0$ ; (b) uniform magnetic field${B_{\text{z}}} = 1,~ {b_z} = 0$ ; (c) non-uniform magnetic field${B_{\text{z}}} = 1, {b_z} = 3$ . The other parameters are${J_x} = 0.2, $ $ {J_y} = 0.5,~ {J_z} = 0.9$ , $\gamma = 0.1,~{D_z} = 0.2,~ T = 0$ .$\gamma = 3$ )KSEA相互作用对量子失协的影响, 图3 研究了马尔科夫环境下外加均匀磁场(${B_z} = 2$ )时KSEA相互作用对量子失协的影响. 结果表明, 在马尔科夫环境中, 均匀磁场和较大的KSEA相互作用的联合效应能够使得量子失协最终保持一个稳定的失协状态. 然而, 通过比较可以发现, 此时的量子失协比非马尔科夫环境中的量子失协明显要小. 这是由于马尔科夫环境中从系统流出到环境中的能量和信息不再回流到系统中, 导致此时的KSEA相互作用对系统量子失协的积极作用没有非马尔科夫环境下的作用效果好.图 3 马尔科夫环境下均匀磁场中KSEA相互作用对量子失协的影响. 其他参数${J_x} = 0.2,\; {J_y} = 0.5,\; {J_z} = 0.9$ , $\gamma = $ $ 3, \; {B_z} = 2,\; {b_z} = 0, \;{D_z} = 0.2,\; T = 0$ .Figure3. Effects of KSEA interactions on quantum discord in a uniform magnetic field in Markovian environment. The other parameters are ${J_x} = 0.2, \;{J_y} = 0.5,\; {J_z} = 0.9,\; \gamma = 3$ , ${B_z} = 2,\; {b_z} = 0,\; {D_z} = 0.2, \;T = 0$ .图4(a) 给出了量子失协随温度$T$ 和时间t 变化的三维图, 图4(b) 给出了$\omega t = 5$ 时量子失协随温度$T$ 演化的二维图. 可以看出, 随着温度$T$ 的增加量子失协逐渐减少, 最终减少到一个稳定值. 很显然, 虽然环境温度的增加使得KSEA相互作用不能再有效恢复海森伯系统的$O(3)$ 对称性, 从而导致量子失协比零温时的要小, 但是在KSEA相互作用和均匀磁场的联合效应下量子失协总能保持一定的稳态值.图 4 (a)量子失协随时间和温度的演化特性; (b)温度在$\omega t = 5$ 时对量子失协的影响. 其他参数${J_x} = 0.2, \;{J_y} = 0.5, $ $ {J_z} = 0.9$ , $\gamma = 0.1,\; {B_z} = 1,\; {b_z} = 0,\; {D_z} = 0.2,\; {\varGamma _z} = 2$ Figure4. (a) Dynamics of quantum discord with time t and temperature $T$ ; (b) effect of temperature $T$ on quantum discord at$\omega t = 5$ . The other parameters are ${J_x} = 0.2, \, {J_y} = $ $ 0.5, \,{J_z} = 0.9,\,\gamma = 0.1, \,{B_z} = 1, \,{b_z} = 0, \,{D_z} = 0.2$ , ${\varGamma _z} = 2$ 4.结 论 通过数值计算, 利用NMQSD方法研究了在非马尔科夫环境下不同的外部磁场中KSEA相互作用对量子失协的影响. 此外还分析了在马尔科夫环境下均匀磁场中KSEA相互作用对量子失协的影响并与非马尔科夫的情况进行了简单的对比. 最后, 得出了温度对非马尔科夫环境下含有KSEA相互作用的系统量子失协的影响. 基于数值结果可以得出以下结论: 当因实际需要在体系中有必要合成和调制KSEA相互作用时, 在非马尔科夫环境下外加均匀磁场时KSEA相互作用提升系统量子失协的效果最明显. 但是磁场的非均匀度会削弱KSEA相互作用的这种效应. 然而, 只要KSEA相互作用足够小, 那么通过磁场的非均匀度就可以更高效地提升量子失协. 马尔科夫环境下的量子失协和热平衡态时的量子失协都同样可以通过KSEA相互作用维持在一个稳定值上. 
























































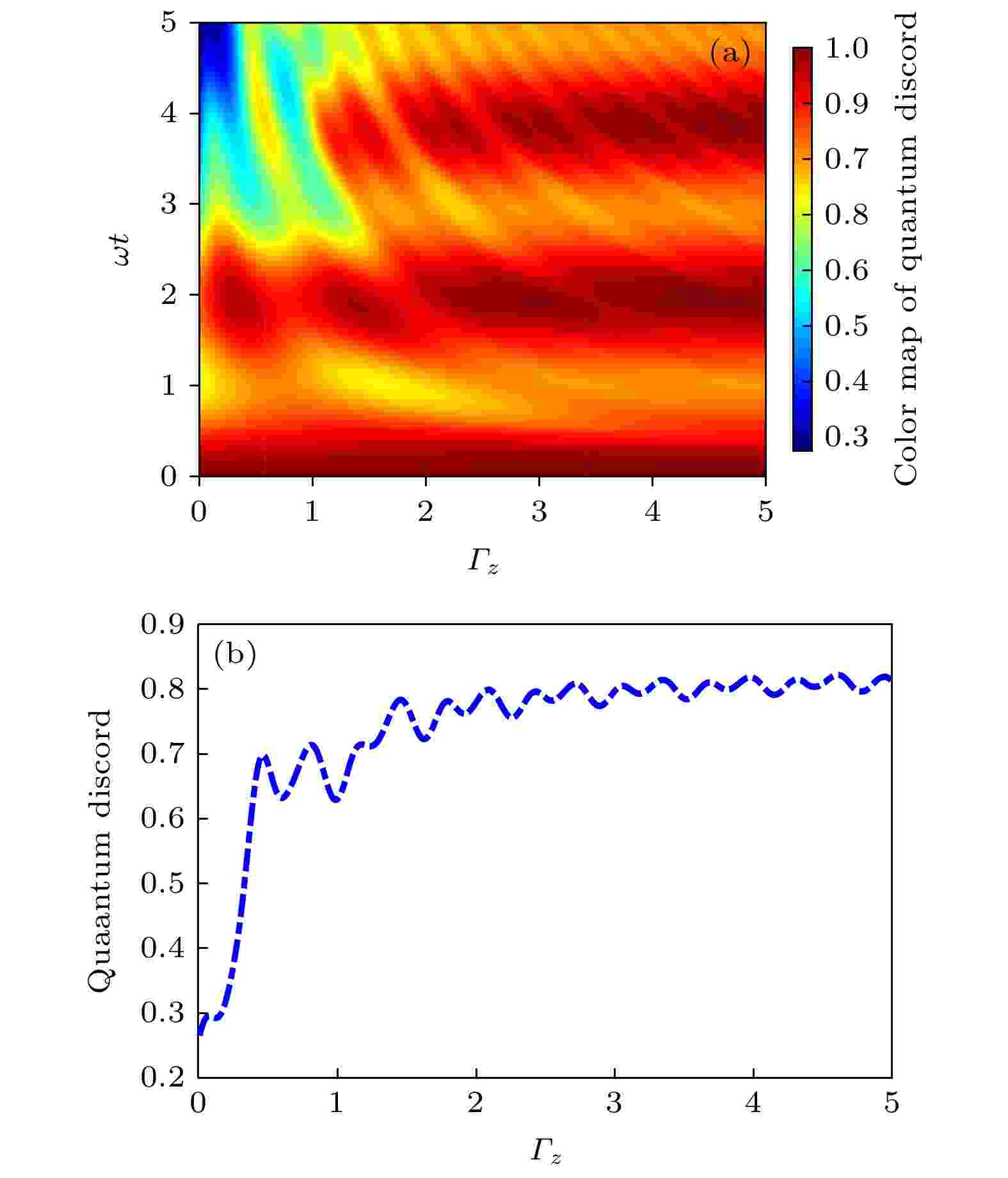 图 1 (a)量子失协随KSEA相互作用和时间的演化特性; (b) KSEA相互作用在
图 1 (a)量子失协随KSEA相互作用和时间的演化特性; (b) KSEA相互作用在









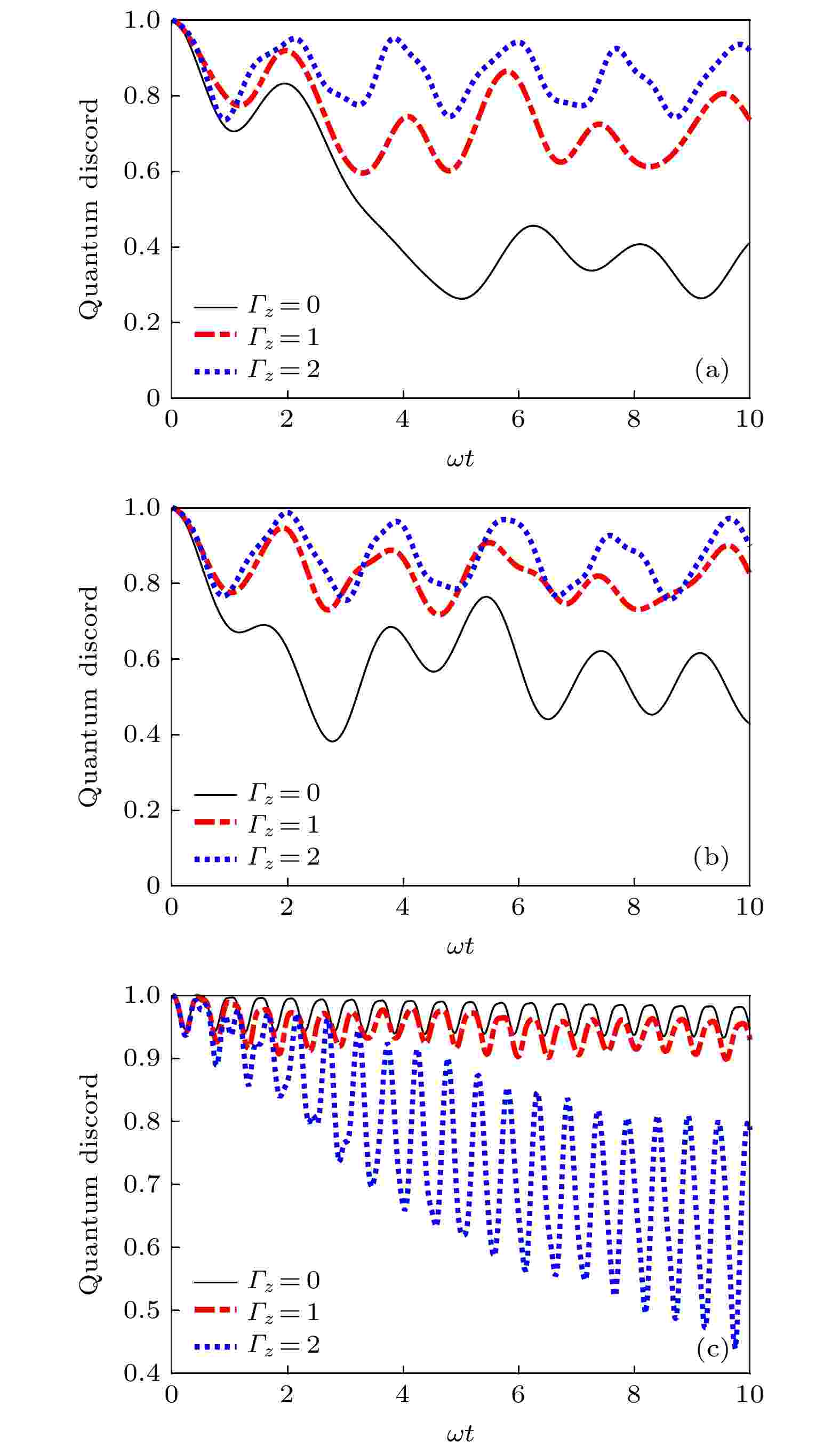 图 2 KSEA相互作用在不同磁场环境下对量子失协的影响 (a)不加磁场
图 2 KSEA相互作用在不同磁场环境下对量子失协的影响 (a)不加磁场














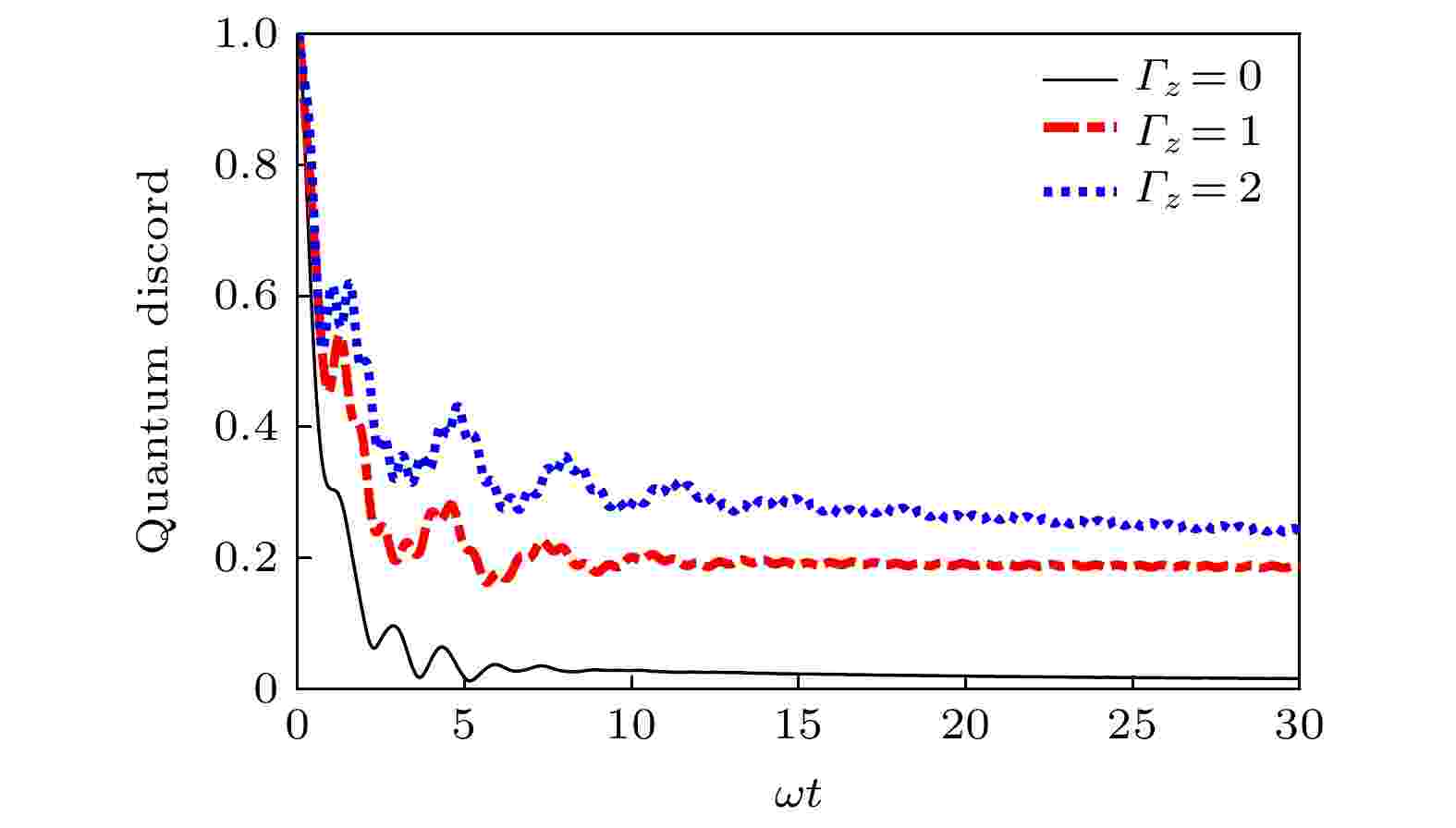 图 3 马尔科夫环境下均匀磁场中KSEA相互作用对量子失协的影响. 其他参数
图 3 马尔科夫环境下均匀磁场中KSEA相互作用对量子失协的影响. 其他参数















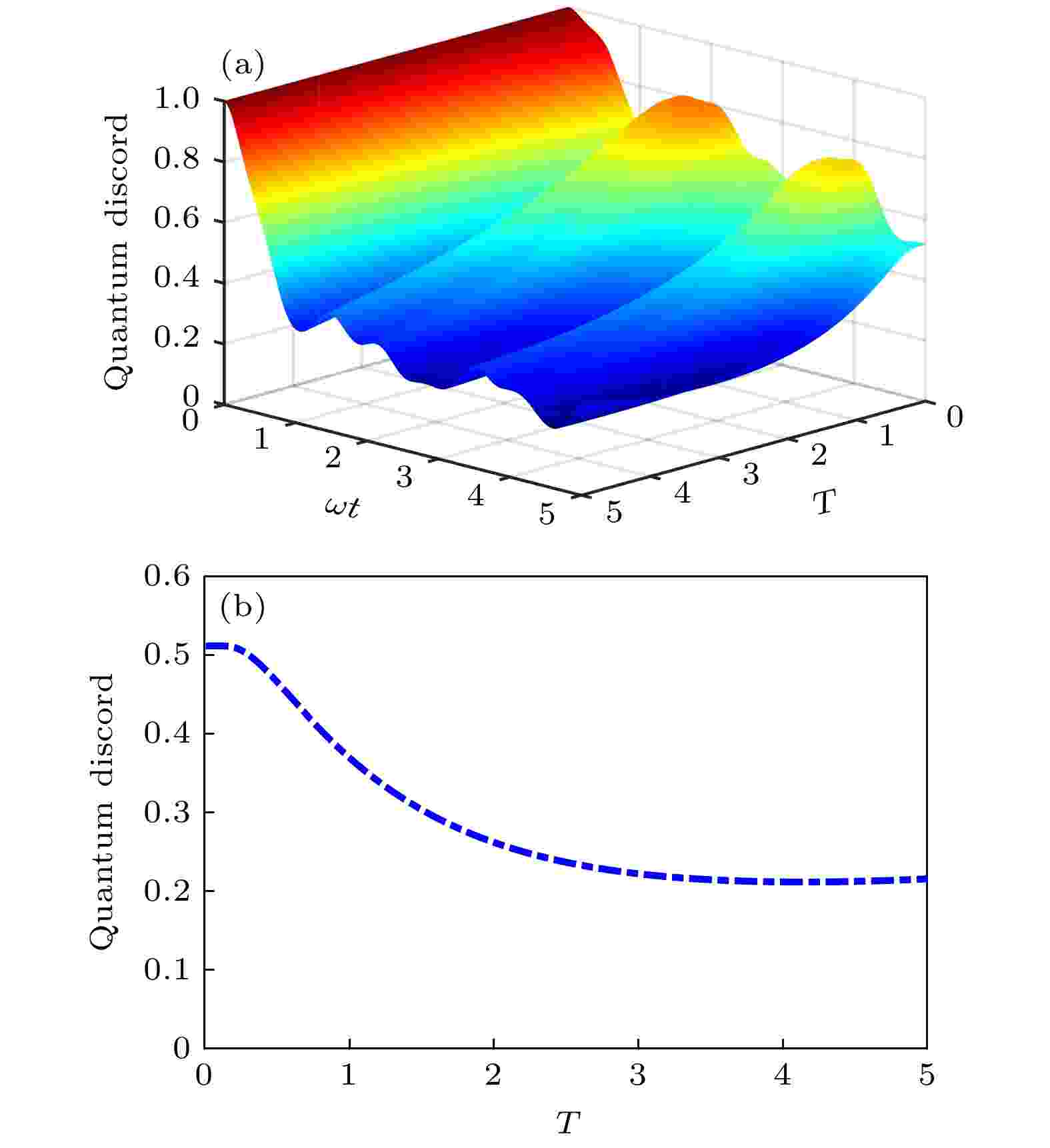 图 4 (a)量子失协随时间和温度的演化特性; (b)温度在
图 4 (a)量子失协随时间和温度的演化特性; (b)温度在












