摘要:在马赫6高超声速静风洞中针对长短轴比为4∶1的钝头椭圆锥表面横流不稳定性进行了实验研究. 综合利用温敏漆技术、基于纳米粒子的平面激光散射技术和Kulite传感器压力测试对模型表面横流区域内的温度分布、边界层流动结构以及模型表面压力进行了测试. 研究了椭圆锥表面横流控制区域边界层转捩机理, 来流单位雷诺数和攻角对边界层转捩的影响规律, 得到以下结论: 在风洞噪声模式下, 长短轴比为4∶1的椭圆锥模型表面中心线与前缘线之间横流区域的边界层转捩是由横流的行进波控制的, 未发现横流定常涡的足迹, 行进波的特征频率在20 kHz左右; 来流单位雷诺数增大时转捩位置会提前, 行进波的频率和幅值均增大; 在一定攻角范围内, 随攻角增大迎风面边界层转捩位置推迟, 行进波特征频率变化不大但能量减弱, 攻角继续增大时转捩现象消失.
关键词: 高超声速/
椭圆锥/
横流不稳定性/
边界层转捩

English Abstract

全文HTML

--> --> -->

高超声速流动中, 当边界层处于不同流动状态时热流、摩阻等参数会存在巨大差异, 研究由层流到湍流的转捩机理以及合理预测边界层转捩位置对高超声速飞行器热防护设计、飞行器表面流动控制等具有重要的参考意义. 而在真实飞行条件下, 飞行器表面边界层往往表现出强烈的三维性, 此时横流不稳定模态在边界层转捩中可能会占主导地位.
横流是指壁面边界层内部在压力梯度作用下产生的垂直于无黏流方向的速度分量, 由于壁面处和边界层外缘横流速度分量均为0, 故边界层内速度剖面存在拐点, 这是横流不稳定性的来源. 为研究横流不稳定性主导的三维边界层转捩问题, 早在20世纪90年代Kimmel等^[1]便通过计算验证了椭圆锥几何构型提供了横流产生所必需的压力梯度, 且能放大横流不稳定性效应, 可作为理想的实验模型. 美国和澳洲共同开展的HIFiRE-5项目采用的也是长短轴比为2∶1的椭圆锥模型^[2-4].
Choudhari等^[5]以及Paredes和Theofilis^[6]的研究结果表明, 椭圆锥表面的流动可分为3个区域: 短轴附近中心线区域、中心线与前缘线之间的区域以及前缘线附近区域. 其中, 短轴附近中心线与前缘线之间是可能由横流不稳定性主导控制转捩的区域, 存在横流定常涡和横流行进波两种横流的不稳定模态以及横流定常涡的二次失稳^[7,8]; 短轴附近中心线区域由于横流效应下流动会从两侧附着线向此处汇聚^[6,9], 边界层厚度会变厚, 并可能产生不稳定的流向涡结构; 前缘附着线附近则主要由第二模态控制^[10].
目前关于横流不稳定性已经有了大量的数值模拟和风洞实验结果, 取得了一系列的研究成果. 对于不可压缩流动^[11-14], 在低噪声的飞行环境中或静风洞中, 横流定常涡占主导地位, 而在噪声环境和传统的风洞中, 则是趋向于横流行进波占主导地位; 横流定常涡通常出现在模型存在定常扰动的条件下, 例如表面的粗糙度等其他稳定的扰动条件, 而横流行进波则是由于自由来流中的噪声和/或扰动而产生的漩涡扰动, 被裹挟在边界层中不断发展而产生的; 横流定常涡的二次失稳是定常横流涡经过线性增长、非线性饱和阶段后发生的, 可以快速演变为湍流结构. 对于可压缩流动, 即流动为超声速或高超声速时, 关于横流不稳定性规律也有比较深入的研究. 数值计算方面, Saric和Reed^[8,15]指出可压缩流动中横流不稳定性规律与不可压缩流动中是相似的. Kimmel等^[16]在马赫8条件下对长短轴比为2∶1的椭圆锥模型横流不稳定性规律进行了数值研究, 发现在椭锥两侧“肩部”附近横流行进波占主导地位, 且当人工引入表面粗糙度时出现了横流定常涡; Dinzl和Candler^[17]利用DNS方法分析了在马赫6条件下, 不同来流单位雷诺数和模型表面粗糙度时横流定常涡的变化规律, 发现与表面粗糙度相比, 扰动波波长对来流单位雷诺数的变化更敏感, 说明自由来流中噪声条件对横流涡的影响更显著; Moyers等^[18]通过耦合非线性抛物线稳定方程与空间双叶方程, 以横流定常涡二次失稳中性点位置来预测转捩位置.
实验研究方面, Berridge等^[19]利用温敏漆 (temperature sensitive paint, TSP)技术在风洞的静音模式和传统噪声模式下观察到了横流定常涡的足迹. 普度大学团队在BM6QT马赫6静风洞^[20-27]中对长短轴比为2∶1的椭圆锥模型进行了针对性的风洞实验, 在静音模式下, 利用油流实验、TSP实验和红外成像技术均测得了横流定常涡的踪迹, 同时在该模式下利用Kulite传感器测得了横流行进波的特征信号, 特征频率大约为45 kHz且随单位雷诺数的升高而增大, 证明了在静音模式下横流定常涡和行进波会同时存在; 在传统噪声模式下, 只在油流实验中观测到了定常涡的踪迹, 在TSP实验和红外像中没有出现, 而且此模式下也没有捕获到横流行进波信号; 之后Juliano等^[28]在波音公司/美国空军科学研究室的马赫6风洞中利用红外成像技术验证了之前TSP结果与红外热成像结果的可靠性. Borg等^[29]还同时在传统TAMU ACE高超声速风洞中进行了同样的实验, 通过与静风洞数据对比研究来流噪声对流场特征的影响规律, 实验表明传统风洞与静风洞噪声模式下模型壁面的压力测试结果是极其相近的, 但是传统风洞中测得的低频特征信号并不能确定是否为横流行进波, 噪声水平的影响规律也无法得到; Hembling等^[30]在美国空军学院马赫6风洞中做了类似的工作, 他们利用红外热成像技术研究不同来流噪声对椭圆锥横流不稳定性的影响, 未观察到横流涡足迹, 但转捩发生位置与在其他风洞中确定横流涡主导转捩时的结果符合, 故推测其转捩机理相同, 且证明了来流噪声会影响转捩位置. Juliano等^[31,32]还通过热电偶数据计算热流并分析确定转捩位置, 得出椭圆锥横流控制区域的转捩对攻角和偏航角变化比较敏感.
目前, 已有的关于椭圆锥模型边界层转捩问题的实验研究成果主要集中在HiFIRE-5项目中长短轴比为2∶1的38.1%缩比椭圆锥模型^[33,34]上, 已经证明了横流定常涡和横流行进波的存在, 并研究了来流噪声水平、表面粗糙度等因素对横流不稳定模态主导转捩的影响, 但仍然存在明显的不足, 比如不同来流条件下横流不稳定模态控制转捩的类型仍存在不确定性, 研究横流模态类型时采用的实验技术单一导致结论的确定性有限, 以及真实飞行条件下攻角和来流雷诺数等重要因素对横流不稳定性控制转捩的影响规律研究欠缺等.
本文实验研究在更接近新型飞行器外形的4∶1钝头椭圆锥上进行, 采用了多种实验方法从定性和定量方面对实验工况下主导转捩的横流不稳定模态类型做了全面的论证, 保证结论的可靠性, 并系统研究了椭圆锥表面横流不稳定性在不同攻角、来流单位雷诺数条件下的变化规律, 可为后期数值模拟与实验研究提供依据和参考.

2

-->

2.1.风洞设备

本文中实验是在国防科技大学自主研制的吹吸式高超声速静风洞(图1)中进行的, 风洞的运行马赫数为6, 喷管出口尺寸为?300 mm. 为降低风洞噪声水平, 风洞稳定段设置有多孔倒锥、阻尼网和消音夹层等整流装置, 位于喷管喉道上游附近的抽吸装置可抽走喉道壁面附近的涡结构, 使边界层保持为层流状态. 抽吸装置开启时为静音模式, 关闭时为噪音模式, 本文实验是在噪声模式下进行的. 同时, 风洞上游的气流加热和保温装置可以实现来流的总温控制, 最高可达600 K; 通过调节总压(最大总压为3 MPa)可实现来流单位雷诺数的变化控制. 目前在该风洞内已经进行了大量的关于边界层转捩问题的实验研究^[35-37].
图 1 高超声速静风洞照片
Figure1. Picture of hypersonic static wind tunnel.

2 -->

2.2.实验模型

本文采用的是长短轴比为4∶1的椭圆锥电木材料模型, 长轴为75 mm, 短轴为18.75 mm, 模型长度为400 mm, 头部为短半径为4.5 mm的半椭球形. 图2为实验模型的示意图.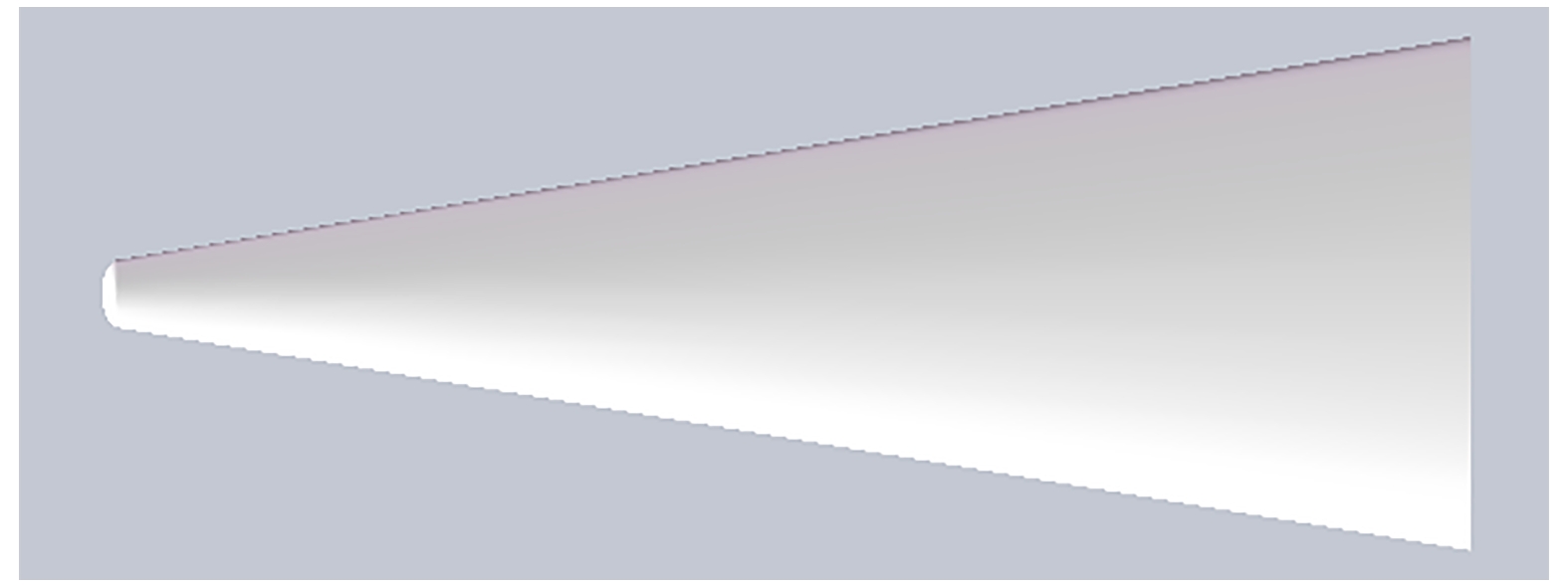
图 2 模型示意图
Figure2. Model diagram.

2 -->

2.3.实验技术

本文综合利用TSP技术、实验室自主开发的高时空分辨率的基于纳米粒子的平面激光散射(nano-tracer-based planar laser scattering, NPLS)技术以及Kulite压力传感器测量以实现对该实验模型边界层转捩规律及机理的多方面数据支持和印证.
3 -->

2.3.1.TSP技术

TSP技术是利用温敏涂料的分子发光特性, 标定并拟合分子发射光强与绝对温度之间的函数关系, 通过相机接收模型表面涂料发射的光强信息来得到模型表面温度的非接触测量手段. 硬件设备包括TSP、光源、滤光片以及相机. 本文选用的TSP在光源作用下, 发射光波长主要分布在400—700 nm范围内, 模型表面底漆上均匀喷涂温敏涂料, 厚度为20 μm, 标定温度范围为5—80 ℃ (278—353 K), 标定曲线^[35]如图3所示, 拟合程度较高. 由拟合曲线得到标定方程: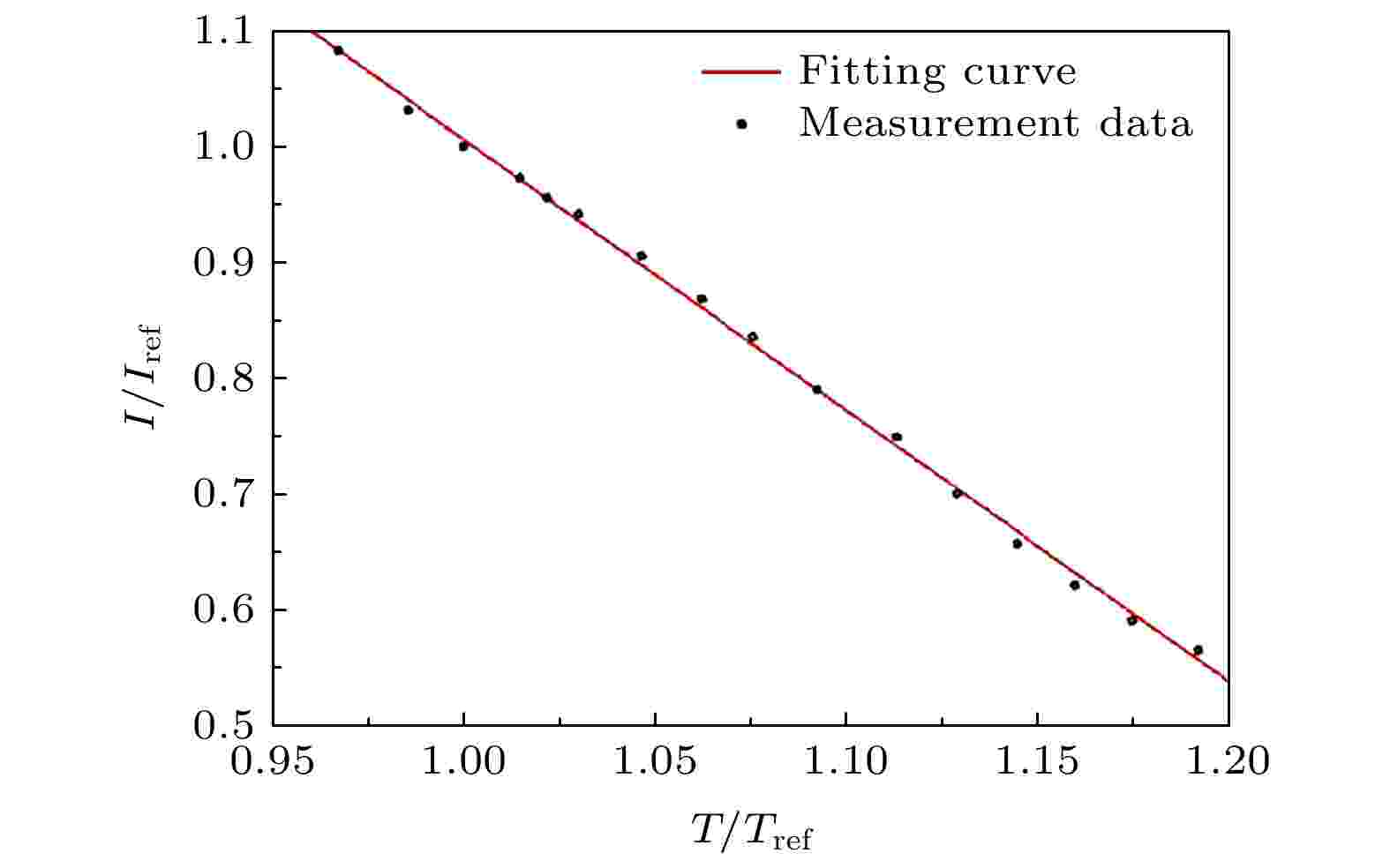

$ \frac{I}{{I}_{\rm{r}\rm{e}\rm{f}}} = - 2.347\frac{T}{{T}_{\rm{r}\rm{e}\rm{f}}} + 3.353 , $

其中I, T分别为模型表面的光强和温度, I_ref, T_ref为参考光强和温度.
图 3 标定曲线
Figure3. Calibration curve.

实验中采用的光源为中心波长为365 nm的LED光源; 滤光片为滤光特性为460 nm长波通的彩色滤光片, 可滤掉波长小于460 nm的光; 相机采用CCD相机, 分辨率为2048 × 2456, 分别采集光源开启前I_light-off、光源开启后I_light-on以及风洞运行时I_wind-on三组图像, 则可得光强比率的计算公式:

$ {I}_{\rm{r}\rm{a}\rm{t}\rm{i}\rm{o}} = \frac{{I}_{\rm{w}\rm{i}\rm{n}\rm{d} \text{-} \rm{o}\rm{n}}-{I}_{\rm{l}\rm{i}\rm{g}\rm{h}\rm{t} \text{-} \rm{o}\rm{f}\rm{f}}}{{I}_{\rm{l}\rm{i}\rm{g}\rm{h}\rm{t} \text{-} \rm{o}\rm{n}} - {I}_{\rm{l}\rm{i}\rm{g}\rm{h}\rm{t} \text{-} \rm{o}\rm{f}\rm{f}}} . $

将(2)式代入方程(1)可算得模型表面的温度分布.
3 -->

2.3.2.NPLS技术

NPLS技术^[36,37]是以传统平面激光散射技术为基础, 创新采用纳米级粒子作为示踪物的高时空分辨率、高信噪比的流动显示技术, 可清楚反映边界层的精细流动结构, 且在时间相关前提下可以定量估算扰动波波长、频率等信息. NPLS测试系统(图4)由ND-YAG激光器、粒子发生器、CCD相机以及同步控制器组成, 工作原理为: 离子发生器产生的纳米粒子与来流在风洞上游均匀混合后经过喷管进入试验段, 在同步控制器作用下, CCD相机与激光器按照既定时序协同工作, 捕获平面激光照亮的粒子形成高分辨率的流动显示图像, 图像记录时间为6 ns, 时间相关图像的时间间隔由激光器发出的两束光的时间间隔决定, 本文中时间相关的两幅图像的时间间隔为5 μs.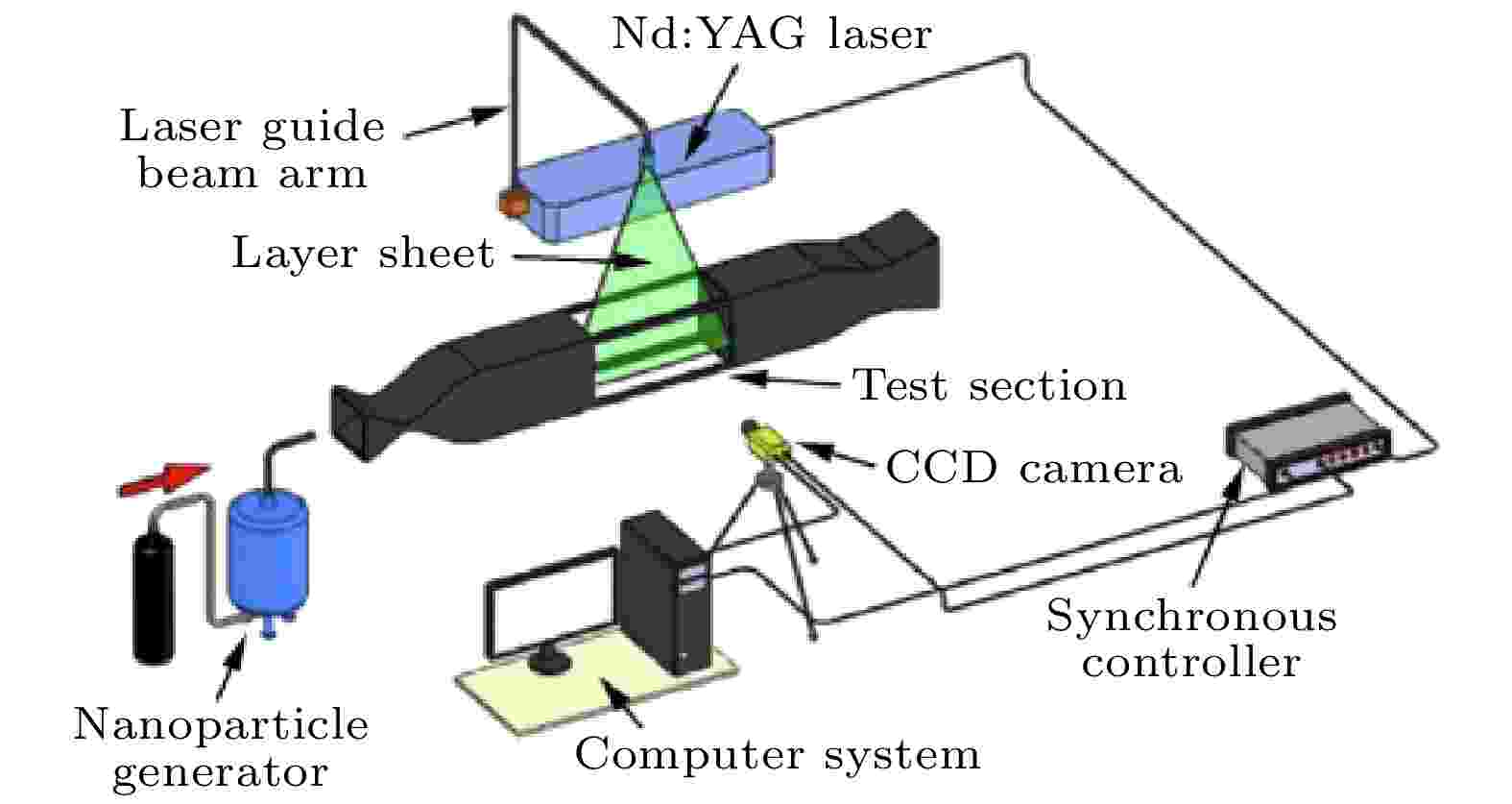
图 4 NPLS技术原理图
Figure4. Schematic diagram of NPLS technique.

3 -->

2.3.3.Kulite传感器测试

压力传感器测量可以捕捉壁面压力信号的主频成分, 以此确定模型边界层内扰动波的特征频率, 这是判断扰动波类型的关键信息. 本文使用的是Kulite压力传感器, 传感器的布置位置是在TSP图像基础上选择关键流动区域而确定的, 测点位置及测点分布见表1和图5.

Sensor	(x, y)/mm	Sensor	(x, y)/mm
1	(360, 0)	2	(360, 12)
3	(360, 24)	4	(360, 36)
5	(360, 48)

表1传感器测点位置
Table1.Sensor measuring point position.

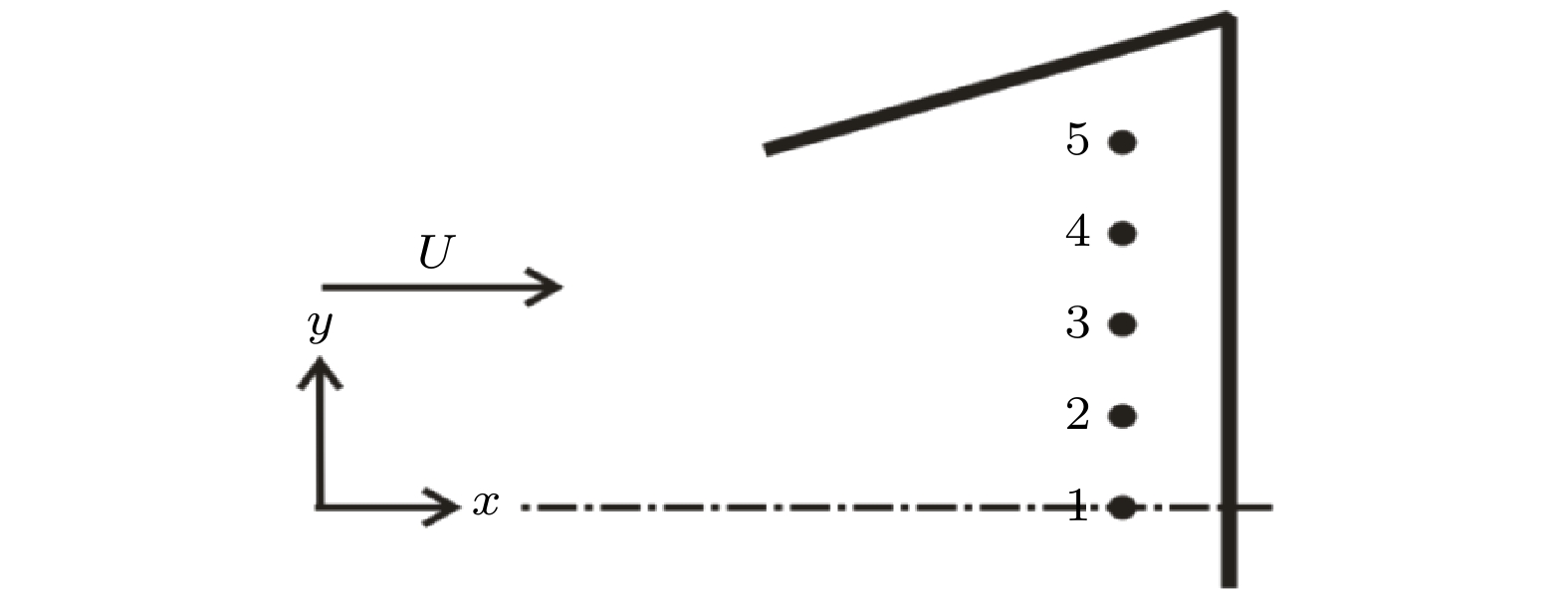图 5 传感器分布示意图
Figure5. Distribution diagram of sensors.

2

-->

3.1.典型工况下边界层转捩机理分析

图6显示的是攻角为0°, 来流单位雷诺数为1.3 × 10⁷ m^–1时模型表面的温升分布云图. 模型两边极高温的区域为前缘线影响的区域, 中心线的低温区域为短轴附近中心线影响的区域, 前缘线与中心线之间的区域为本文研究的重点区域, 在此区域内发生的边界层转捩是由横流不稳定性主导的. 从图6的云图可以看出: 在流向210—320 mm左右的范围内, 靠近前缘线附近为黄色的高温区域, 靠近中心线附近出现一片低温区域, 但比中心线的温度要高, 这是由于模型表面边界层受到高超声速气流绕过钝头细长体模型时在模型表面形成的熵层的影响. 在320—400 mm左右的范围内, 温度突然陡升, 出现了沿中心线对称分布的两片类似三角形的高温区域, 该区域在模型尾部的展向宽度大约为30 mm, 两侧温度比类三角形高温区域要低. 与长短轴比为2∶1的椭圆锥模型在噪声条件下的实验结果相似, 长短轴比为4∶1的光滑椭圆锥模型表面的高温区域中未出现明显的条带状结构, 故推测模型表面不存在横流定常涡.
图 6 温升分布云图(0°, Re = 1.3 × 10⁷/m)
Figure6. Contour of temperature rise distribution (0°, Re = 1.3 × 10⁷/m).

为确定类三角形高温区域的形成原因, 利用NPLS技术沿图6中虚线位置拍摄模型表面的边界层流动状态, 得到了时间相关的两幅边界层精细流动结构的图像(图7), 图像下方灰色楔形区域为模型壁面区域, 白色亮线是由激光打到壁面处产生的散射光引起的, 壁面上方灰度值最大的流动结构为边界层, 其余为主流区域; 图像分辨率为0.147 mm/pixels, 两幅图片的时间间隔为5 μs.
图 7 时间相关的NPLS图像
Figure7. NPLS images with time correlation.

从图7可以看出: 在220 mm以前的范围内, 此时属于前缘线区域的影响范畴, 由于该范围内边界层厚度太小被壁面散射光遮住所以几乎观察不到边界层; 在220—320 mm的范围内, 起初可以隐约看到层流边界层, 随流向方向发展边界层厚度逐渐变大, 说明边界层内部可能出现了扰动; 在320 mm左右处可以观察到明显的大尺度的扰动波结构, 且靠近模型尾部的扰动波的幅值是最大的, 但还没有出现破碎结构, 尚处于边界层转捩的早期阶段. 同样地, 沿图6中虚线位置提取TSP图像的温升曲线(图8), 根据温升变化的趋势可判断, 沿虚线位置上, 模型表面的温度是从x = 325 mm左右的位置开始出现陡升, 这与NPLS图像中扰动波结构出现的位置是符合的, 可以说明类三角形高温区域的出现是由边界层转捩引起的, 但未完全转捩, 处于转捩早期的过渡时期, 转捩阵面的形状呈沿中心线对称的两个类似三角形形状. 由于中心线与前缘线之间的区域是由横流不稳定性占主导, 且从NPLS图像中可以看出扰动波是非定常结构, 所以该区域内边界层转捩应该是由横流的行进波控制的.
图 8 温升曲线
Figure8. Temperature rise curve.

由于时间相关的两幅图像在微秒级的时间间隔内, 边界层流动结构发生的变化是极其微小的, 甚至可以忽略, 故可以用来估算扰动波结构的频率信息. 取图7两幅图像中标记的扰动波结构, 通过图像分辨率、像素信息与实际尺寸之间的对应关系, 可以算得扰动波的波长$ \lambda \approx 31.12\rm{m}\rm{m} $, 且在5 μs的时间间隔内扰动波行进的距离$\Delta x = 3.23\;\rm{m}\rm{m}$, 利用平均速度代替瞬时速度可知扰动波行进速度的计算公式为$ c = \Delta x/\Delta t $, 再由频率的计算公式$ f = c/\lambda $, 可推得该扰动波的频率可以表示为$f = $$ {\Delta }x/({\Delta }t\cdot \lambda )\approx 20.79{\rm{ }}{\rm{k}}{\rm{H}}{\rm{z}}$.
图9所示的是利用Welch方法对攻角为0°、来流单位雷诺数为1.3 × 10⁷ m^–1时Kulite传感器测得的风洞稳定运行时3 s内的压力数据进行计算得到的功率谱结果和传感器底噪功率谱结果. 由底噪结果可知, 传感器本身存在尖锐的电信号, 与流动结构无关, 功率谱曲线覆盖全部的频率无主频信号, 说明传感器是正常工作的. 根据图9结果可以看出: 在57和88 kHz左右出现的尖锐的峰值信号为电信号, 并非流动结构引起; 位于中心线上的测点1和位于转捩阵面外缘到中心线范围内的测点2均存在4 kHz左右的主频信号; 测点3—5则属于横流控制区域类三角形转捩阵面的范围内, 可以观察到3个测点处均出现了明显的能量峰值, 测点3在17 kHz左右, 测点4在21 kHz左右, 而测点5出现在19 kHz左右, 根据传感器的布置位置, 测点5的位置最接近于虚线位置, 且特征信号的频率与NPLS图像估算得来的扰动波的频率基本符合, 所以我们可以判断, 横流控制区域内出现的类三角形的边界层转捩区域是由横流的行进波占主导控制的, 行进波的特征频率大概在20 kHz左右, 且转捩区域内还处于由层流到湍流的过渡阶段, 出现大尺度的扰动波结构, 但未出现破碎结构以及湍流结构.
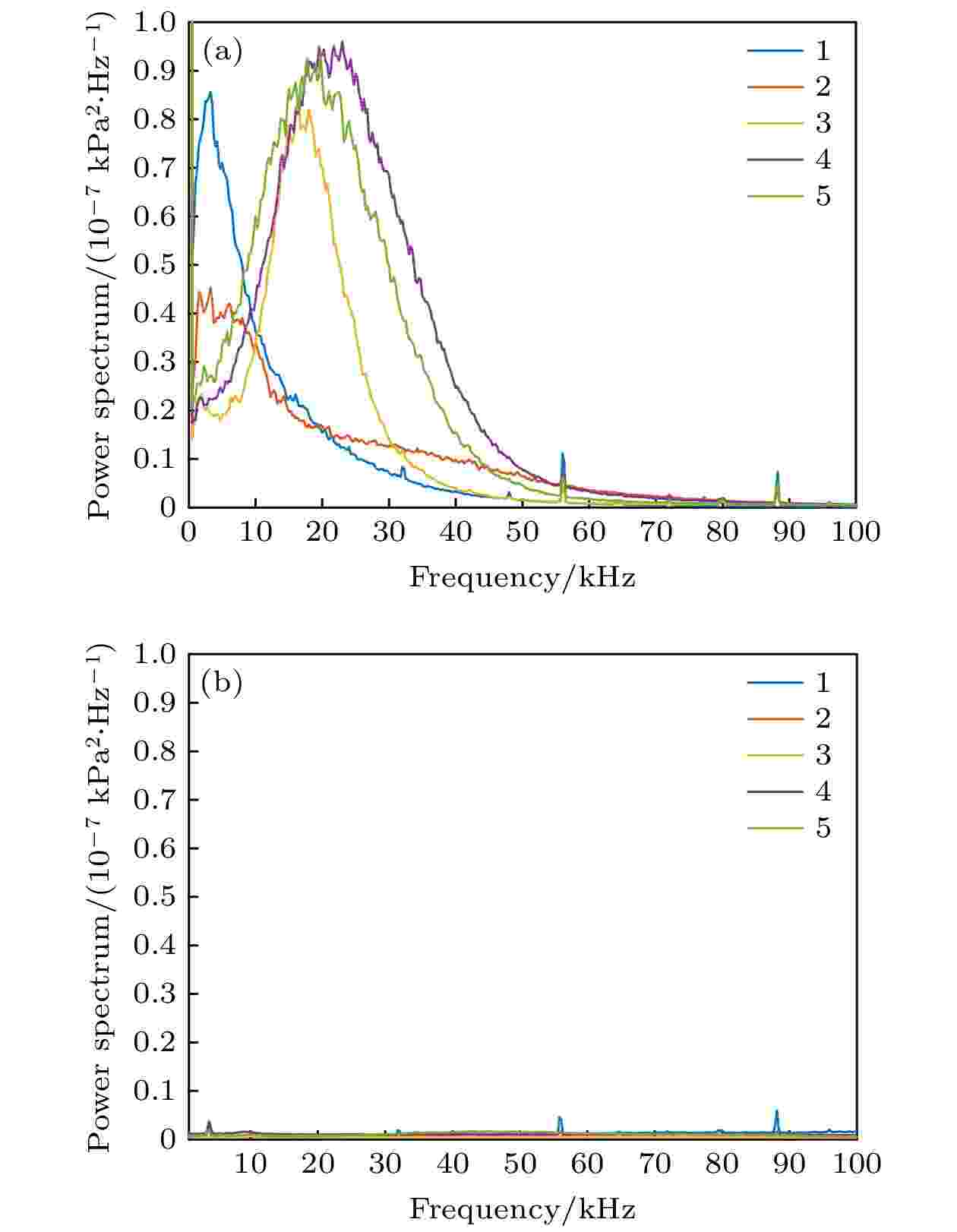图 9 功率谱计算结果 (0°, Re = 1.3 × 10⁷/m)　(a) 风洞运行时; (b) 底噪
Figure9. Power spectrum calculation results (0°, Re = 1.3 × 10⁷/m): (a) During wind tunnel operation; (b) noise of background.

2 -->

3.2.来流雷诺数对转捩的影响

单位雷诺数表征的是惯性力与黏性力的比值. 在高超声速条件下, 来流单位雷诺数是影响壁面附近边界层稳定性的重要因素之一. 从一般意义上来讲, 在高雷诺数的条件下, 惯性力远远大于黏性力, 此时黏性力无法维持边界层稳定的层流状态, 边界层就会发生转捩现象. 为研究来流单位雷诺数对椭圆锥边界层转捩的影响规律, 图10给出了0°攻角时不同来流单位雷诺数下椭圆锥表面的TSP实验结果, 雷诺数的变化范围为7 × 10⁶—1.3×10⁷ m^–1.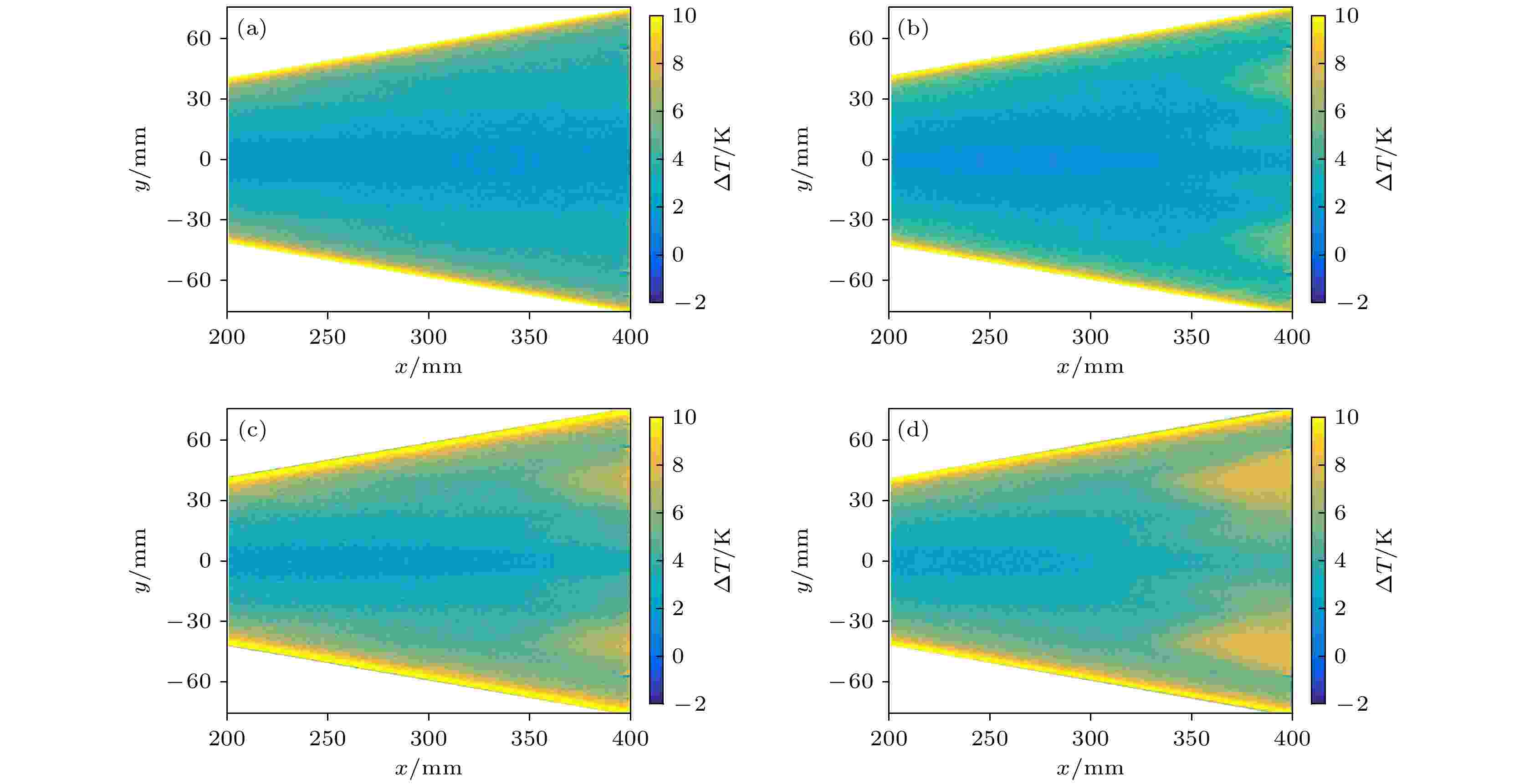
图 10 0°攻角不同雷诺数条件下TSP图像　(a)${Re}_{\rm{\infty }} = 7\times {10}^{6}\;{\rm{m}}^{-1}$; (b)$ {Re}_{\rm{\infty }} = 9\times {10}^{6}\;{\rm{m}}^{-1} $; (c)$ {Re}_{\rm{\infty }} = 1.1\times {10}^{7}\;{\rm{m}}^{-1} $; (d)$ {Re}_{\rm{\infty }} = 1.3\times {10}^{7}\;{\rm{m}}^{-1} $
Figure10. TSP images of angle of attack of 0° at different Reynolds numbers: (a)$ {Re}_{\rm{\infty }} = 7\times {10}^{6}\;{\rm{m}}^{-1} $; (b)$ {Re}_{\rm{\infty }} = 9\times {10}^{6}\;{\rm{m}}^{-1} $; (c)$ {Re}_{\rm{\infty }} = 1.1\times \;{10}^{7}{\rm{m}}^{-1} $; (d)$ {Re}_{\rm{\infty }} = 1.3\times {10}^{7}\;{\rm{m}}^{-1} $.

图10对比了不同来流雷诺数条件下模型表面横流影响区域温度分布的变化, 可以观察到, 在此攻角条件下, 类三角形转捩区域尖部的y坐标是大致相同的, 为更清楚地反映转捩阵面前缘的起始位置, 与图6虚线位置对应提取了不同雷诺数时的温升曲线, 结果如图11所示. 综合温升云图与温升曲线可以判断, 当雷诺数为7 × 10⁶ m^–1时, 温度分布比较均匀, 未出现高温区域, 温升曲线整体接近于水平, 未出现明显的温度陡升的点, 判断此时边界层尚处于稳定的层流状态; 当雷诺数为9 × 10⁶ m^–1时, 在靠近模型尾部开始出现独立的高温区域, 边界层开始转捩, 由温升曲线可知转捩阵面的最前缘位于x = 350 mm左右, 同时在靠近中心线两侧出现了对称分布的细长的高温区, 可能是由横流不稳定模态与中心线流向涡结构的相互作用引起的, 具体原因还需要进一步研究; 当雷诺数为1.1 × 10⁷ m^–1时, 转捩阵面内温升比雷诺数为9 × 10⁶ m^–1时要高, 从温升曲线中可以印证, 且此时转捩阵面最前缘略微提前, 出现在x = 340 mm左右, 中心线两侧的高温区未发生明显变化; 当雷诺数升高到1.3 × 10⁷ m^–1时, 转捩阵面内温度继续升高, 转捩阵面明显前移, 前缘出现在x = 325左右, 中心线两侧的高温区展向宽度增大, 与三角形转捩阵面连接在一起; 综上来讲, 椭圆锥边界层转捩受雷诺数的影响符合雷诺数影响转捩的一般规律, 临界转捩雷诺数在7 × 10⁶ m^–1到9 × 10⁶ m^–1, 边界层由层流开始向湍流过渡, 继续增大雷诺数时, 转捩阵面最前缘前移, 转捩提前, 这是由于横流不稳定性的本质属于拐点不稳定性, 而黏性在高超声速条件下对边界层起稳定作用, 雷诺数增大, 黏性力相对减小, 导致边界层转捩提前.
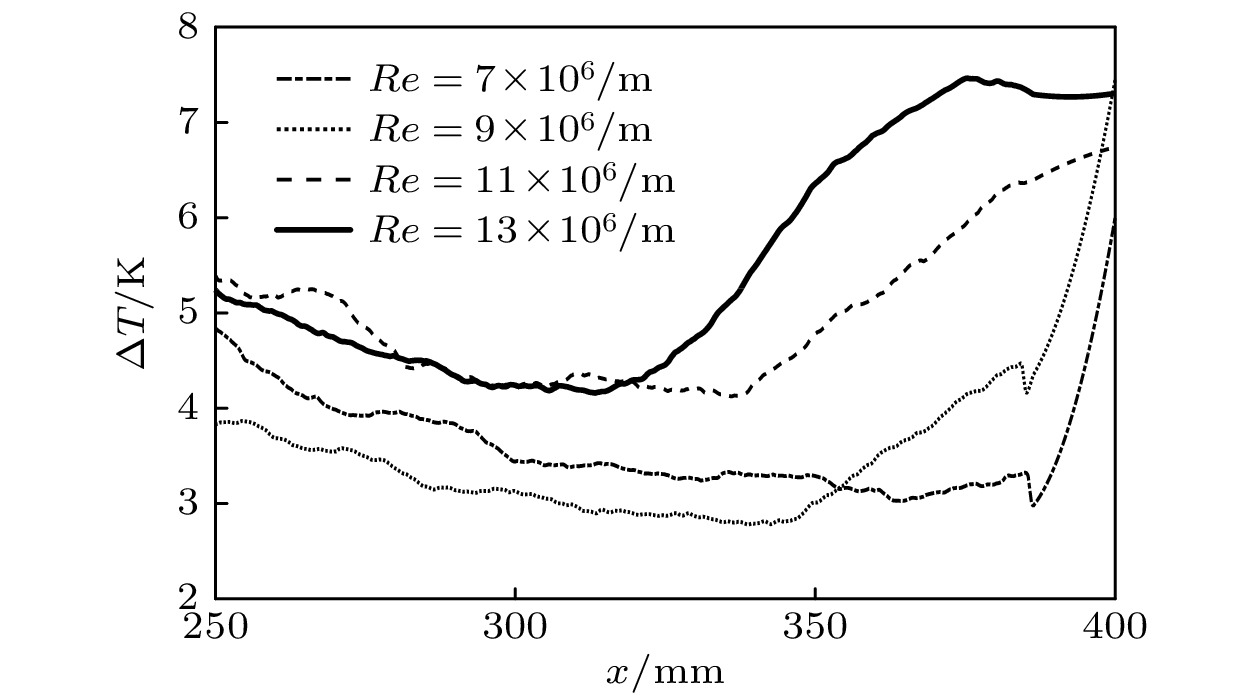图 11 不同雷诺数条件下温升曲线
Figure11. Temperature rise curves at different Reynolds numbers.

为研究转捩开始出现时扰动波特征频率的变化规律, 图12给出了0°攻角时不同来流单位雷诺数下Kulite压力测试计算得到的功率谱结果, 雷诺数的变化范围为7 × 10⁶ m^–1—1.3 × 10⁷ m^–1.
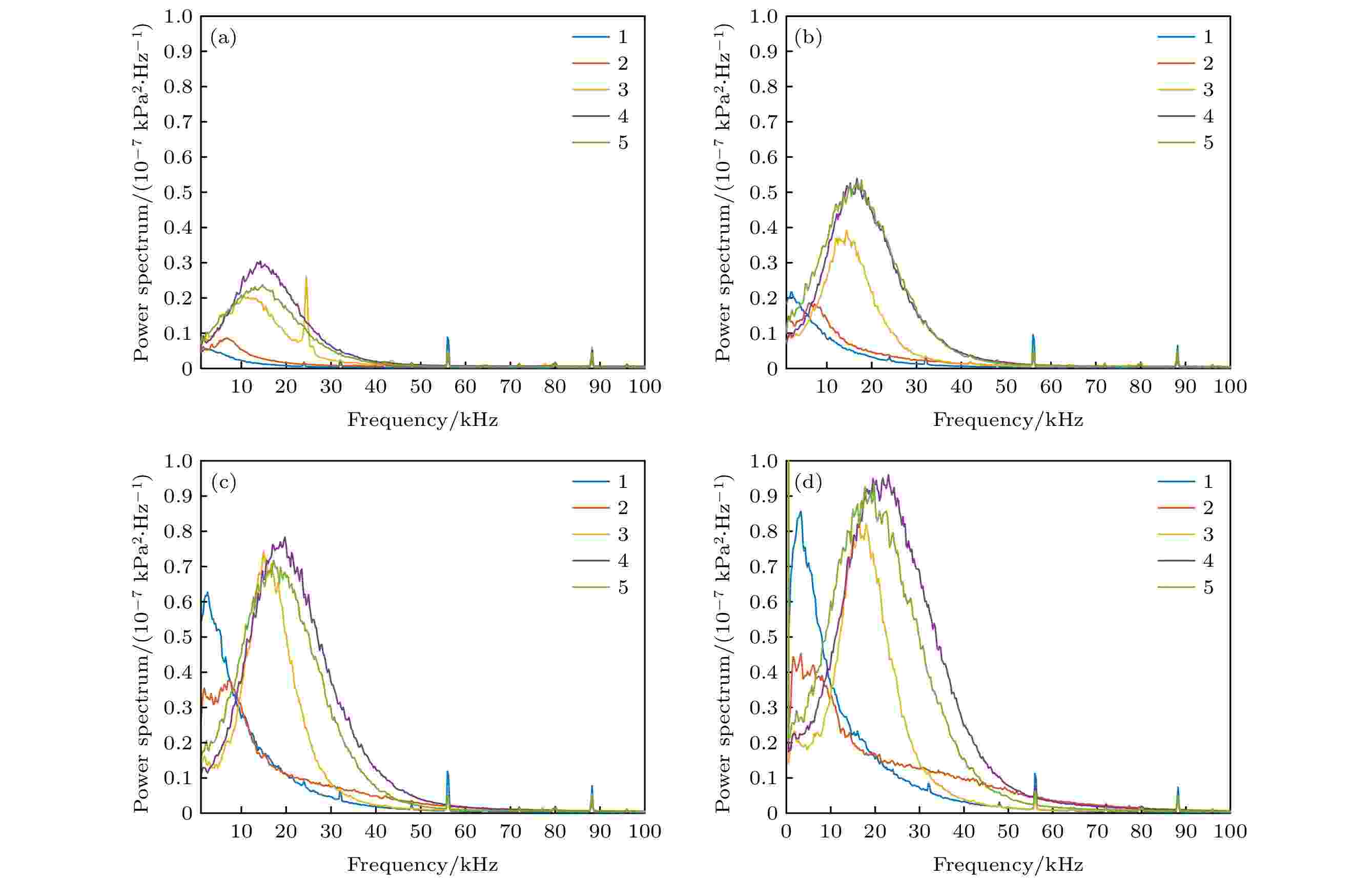图 12 0°攻角、不同雷诺数条件下功率谱结果　(a)$ {Re}_{\rm{\infty }} = 7\times {10}^{6}\;{\rm{m}}^{-1} $; (b)$ {Re}_{\rm{\infty }} = 9\times {10}^{6}\;{\rm{m}}^{-1} $; (c)$ {Re}_{\rm{\infty }} = 1.1\times {10}^{7}\;{\rm{m}}^{-1} $; (d)$ {Re}_{\rm{\infty }} = 1.3\times {10}^{7}\;{\rm{m}}^{-1} $
Figure12. Power spectrum calculation results of angle of attack of 0° at different Reynolds numbers: (a)$ {Re}_{\rm{\infty }} = 7\times {10}^{6}\;{\rm{m}}^{-1} $; (b)$ {Re}_{\rm{\infty }} = 9\times {10}^{6}\;{\rm{m}}^{-1} $; (c)$ {Re}_{\rm{\infty }} = 1.1\times {10}^{7}\;{\rm{m}}^{-1} $; (d)$ {Re}_{\rm{\infty }} = 1.3\times {10}^{7}\;{\rm{m}}^{-1}$

从测点的布置和TSP图像的温度分布可以看出, 测点1和测点2对应于中心线以及中心线旁的区域, 测点3—5在可能出现转捩的区域内. 从功率谱结果可以看出, 测点1和测点2处的峰值信号出现的位置均在10 kHz以内, 当雷诺数为7 × 10⁶ m^–1和9 × 10⁶ m^–1时, 测点2处峰值信号的频率比中心线要高, 随着雷诺数的增大, 测点2处峰值信号特征频率减小至与测点1相同, 但能量比测点1要低, 测点1处峰值信号的能量随雷诺数增大是逐渐增大的, 说明中心线附近的横流区域流动发生了变化, 可能与中心线流向涡结构之间发生了模态间的相互作用; 测点3—5处峰值信号的频率集中在10—20 kHz之间, 能量最高的扰动波信号出现在测点4和测点5附近, 处于最有可能出现边界层转捩的区域, 随着雷诺数的增大, 测点3处的特征信号频率从10 kHz逐渐增加到17 kHz左右, 且幅值也是逐渐增大的, 测点4和测点5处由15 kHz增加并稳定在20 kHz左右, 特征信号的幅值随雷诺数增大也是逐渐增大的, 可以判断该区域内主导边界层转捩的横流行进波的频率在20 kHz左右, 而横流模态频率与幅值随雷诺数增大的原因可能是来流噪声和维持可压缩流动边界层稳定性的黏性力减小共同造成的.
2 -->

3.3.攻角对转捩的影响

在真实的飞行条件下, 飞行器的飞行姿态往往都是带有攻角或者偏航角的, 攻角的变化可能会引起飞行器表面压力梯度的变化, 进而对边界层转捩产生影响. 对于椭圆锥模型而言, 模型表面的压力梯度方向是由两侧指向中间, 在迎风面, 当攻角增大时模型表面中心线附近区域的压力会增大, 使得中心线与两侧的压力梯度减小, 对边界层转捩造成影响.
为研究明确攻角对椭圆锥边界层转捩的影响规律, 利用TSP技术分别测试了当雷诺数为1.1 × 10⁷ m^–1和1.3 × 10⁷ m^–1时不同攻角条件下模型迎风面的温度分布状态, 实验结果如图13和图14所示.
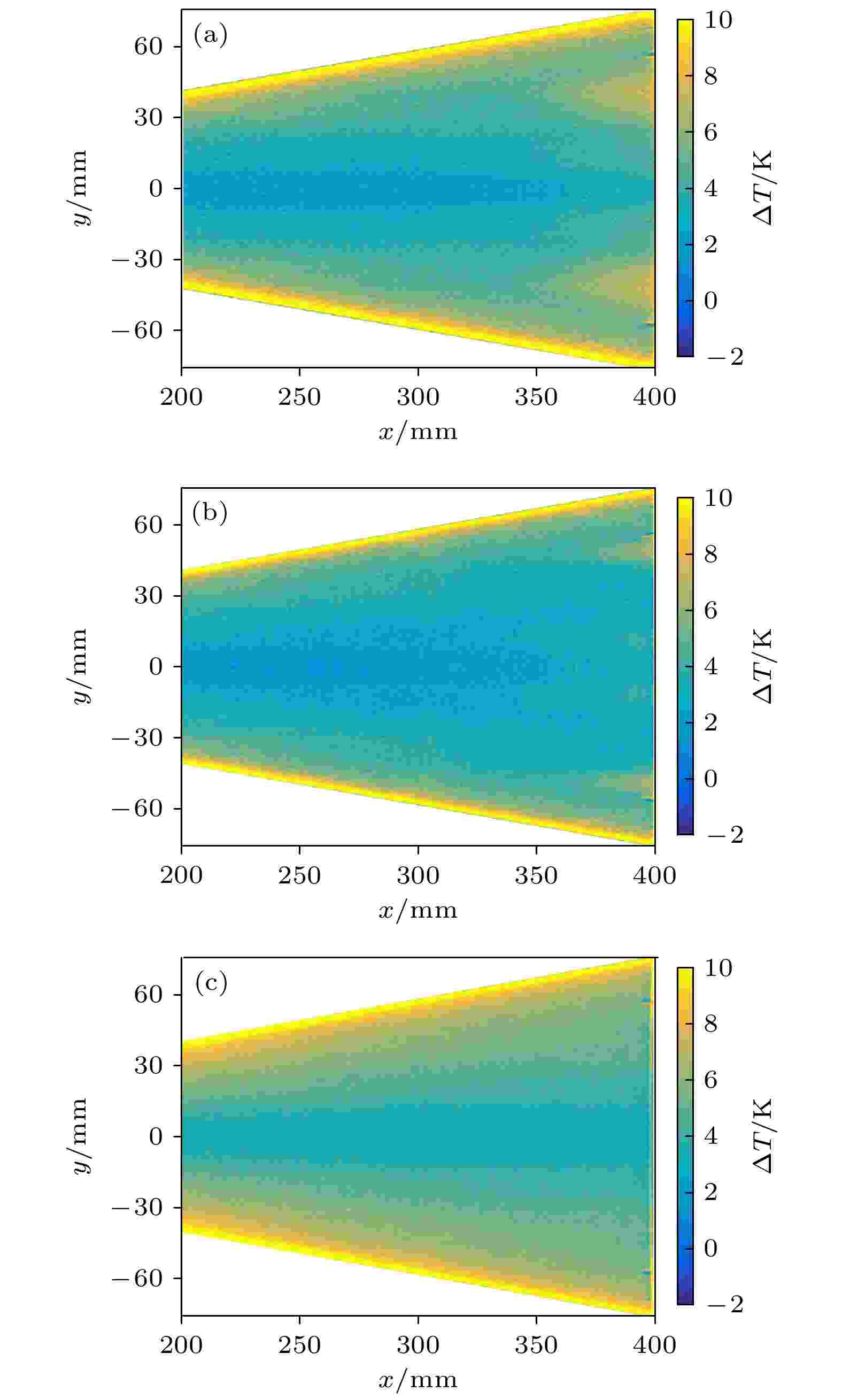图 13 不同攻角TSP图像(${Re}_{\rm{\infty }} = 11\times {10}^{6}\;{\rm{m}}^{-1}$)　(a) 0°; (b) 2°; (c) 5°
Figure13. TSP images at different angles of attack (${Re}_{\rm{\infty }} = $$ 11\times {10}^{6}\;{\rm{m}}^{-1}$) : (a) 0°; (b) 2°; (c) 5°.

图 14 不同攻角TSP图像(${Re}_{\rm{\infty }} = 13\times {10}^{6}\;{\rm{m}}^{-1}$)　(a) 0°; (b) 2°; (c) 5°
Figure14. TSP images at different attack angles (${Re}_{\rm{\infty }} = $$ 13\times {10}^{6}\;{\rm{m}}^{-1}$): (a) 0°; (b) 2°; (c) 5°.

对比图13和图14可以看出, 在不同的来流雷诺数条件下, 攻角对模型表面边界层的转捩影响规律是相同的. 当攻角从0°增加到2°时, 中心线区域两侧细长的高温区未发生明显变化, 说明此处的高温区域是相对独立的, 与转捩阵面内的高温区域关系不大, 不随转捩阵面的变化而变化; 但攻角增大时, 类似三角形的转捩阵面变化很大, 转捩阵面前缘位置明显推迟, 且展向宽度明显减小, 转捩区域距离中心线更远了, 这与模型表面压力梯度的变化是对应的, 说明压力梯度变小导致横流效应减弱, 边界层转捩位置推迟且转捩区域缩小; 当攻角增大到5°时, 模型表面的温度分布比较均匀, 无边界层转捩迹象.
为研究攻角改变时模型表面边界层内扰动波频率的变化规律, 图15和图16给出了与TSP实验状态对应的Kulite压力测试计算得到的功率谱结果.
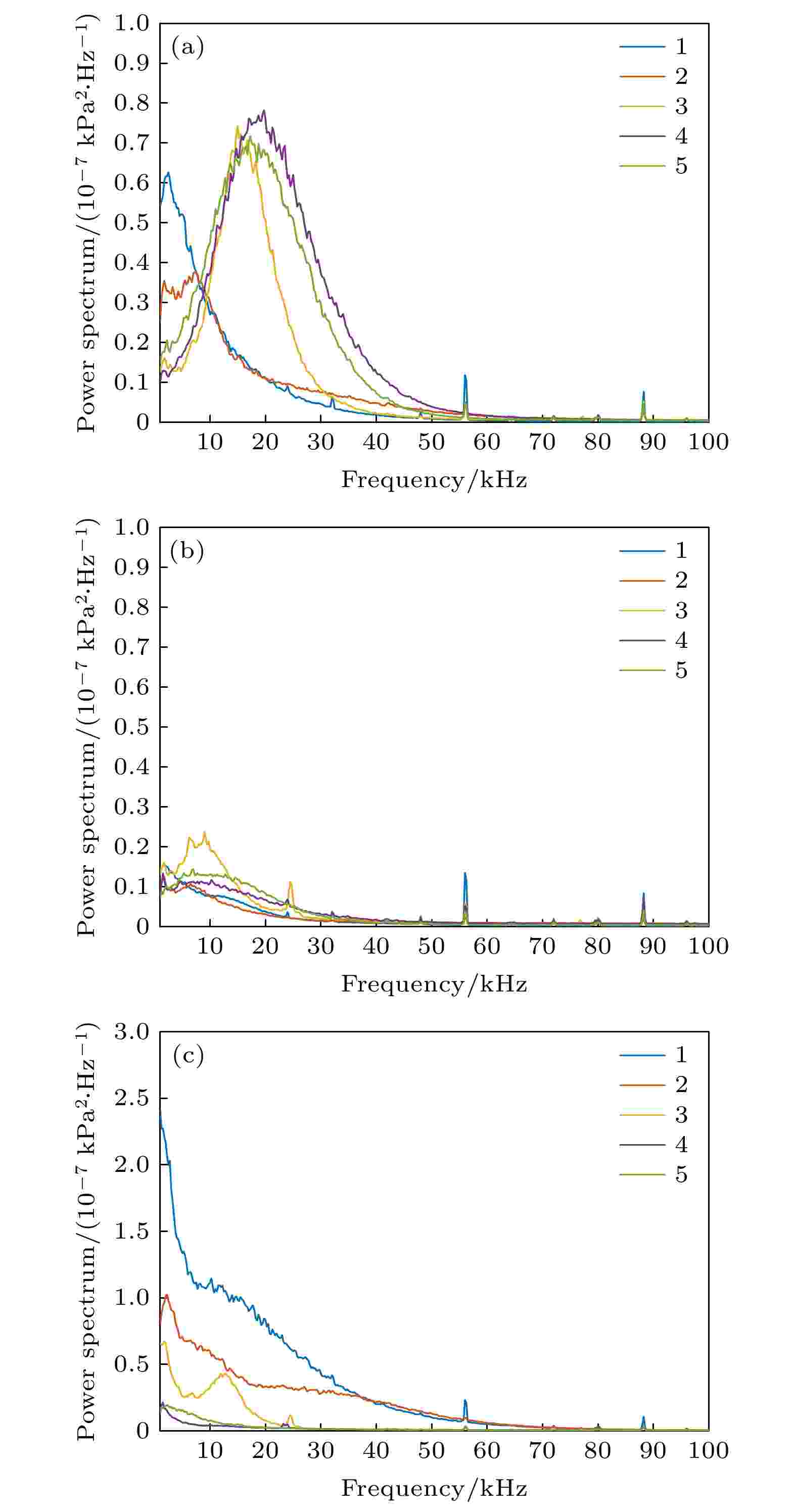图 15 不同攻角功率谱结果(${Re}_{\rm{\infty }} = 11\times {10}^{6}\;{\rm{m}}^{-1}$)　(a) 0°; (b) 2°; (c) 5°
Figure15. Power spectrum calculation results at different angles of attack (${Re}_{\rm{\infty }} = 11\times {10}^{6}\;{\rm{m}}^{-1}$) : (a) 0°; (b) 2°; (c) 5°.

图 16 不同攻角功率谱结果(${Re}_{\rm{\infty }} = 13\times {10}^{6}\;{\rm{m}}^{-1}$)　(a) 0°; (b) 2°; (c) 5°
Figure16. Power spectrum calculation results at different angles of attack (${Re}_{\rm{\infty }} = 13\times {10}^{6}\;{\rm{m}}^{-1}$) : (a) 0°; (b) 2°; (c) 5°.

从功率谱计算结果可以看出, 在一定攻角范围内测点1和测点2处峰值信号均在10 kHz以内, 且频率保持一致, 随攻角增大幅值减小, 当攻角增大至5°时不再有比较明显的峰值信号, 功率谱曲线类似于湍流的频率曲线; 对于测点3—5, 当雷诺数为1.1 × 10⁷ m^–1时, 攻角从0°增加到2°, 只有测点3处存在明显的峰值信号, 且特征信号的频率和幅值均减小, 测点4和测点5未出现明显的峰值信号, 只有频率为10 kHz左右的主频成分, 原因是攻角为2°时两测点不在转捩区域内, 攻角增大到5°时, 测点3处仍存在峰值信号, 频率为13 kHz左右, 测点4和测点5处主频成分消失; 当雷诺数为1.3 × 10⁷ m^–1时, 攻角从0°增加到2°, 测点3和测点5处存在峰值信号, 其中测点3处特征信号的频率和幅值均减小, 测点5频率变化不大但幅值明显减小, 说明此时控制转捩的行进波能量减弱, 测点4未出现明显的主频成分, 原因是攻角为2°时测点4不在转捩区域内, 攻角增大到5°时, 测点3处仍存在峰值信号, 频率和幅值进一步减小, 在10 kHz左右, 测点4和测点5处峰值信号和主频成分均消失.
综上而言, 当雷诺数增大时, 中心线处扰动波的频率变化不大, 中心线与转捩区之间的范围内, 始终存在着频率为10—15 kHz的扰动波信号, 说明攻角增大时, 中心线与前缘线中间区域的横流效应不会完全消失, 横流的行进波始终存在但无法引起转捩, 而对于起主导作用的20 kHz左右的行进波, 随攻角的增大行进波的能量也会减弱.

本文基于TSP技术、NPLS技术以及Kulite压力测试的实验结果, 综合分析了长短轴比为4∶1的椭圆锥表面横流不稳定控制转捩的机理, 得到了来流单位雷诺数以及攻角对边界层转捩的影响规律. 结果表明, 在噪声模式下, 对于长短轴比为4∶1的钝头椭圆锥, 中心线与前缘线之间的区域是由横流的行进波占主导的, 未观察到横流定常涡的足迹, 行进波的特征频率频率大约为20 kHz, 转捩阵面为沿中心线对称分布的两个类似三角形的形状; 当雷诺数增大时, 转捩阵面前缘前移, 边界层转捩位置提前, 行进波的频率和幅值均增大; 在一定的攻角范围内, 当攻角增大时, 迎风面转捩阵面前缘位置推迟且转捩阵面的展向宽度减小, 这与模型表面压力梯度减小有关, 引起转捩的行进波的频率变化不大但扰动波的能量会减小; 当攻角继续增大时, 转捩阵面会消失, 但此时模型表面仍存在横流效应, 但已不能控制和引起边界层转捩.