摘要:磁电电压可调电感器(ME-VTI)是基于磁电效应实现电场对电感的调控. 与其他可调电感器相比, 具有能耗低、体积小、可调性大且连续等特点. 而以往对ME-VTI的研究主要针对结构和磁致伸缩材料, 致使电感器制备工艺复杂或可调性提高不大. 本文通过构建理论模型, 着眼于压电材料场致应变对电感可调性的影响. 采用磁电复合材料Metglas/PMN-PT单晶/Metglas作为磁芯制备ME-VTI. 在1 kHz时可调性高达680%, 相当于选用Metglas/PZT/Metglas磁芯的2.4倍. 前者品质因子达到15.6, 相对于后者提高了2.8倍. 本文提出的基于PMN-PT单晶的ME-VTI为器件集成化、小型化的发展提供了新的思路, 在电力电子领域有重要的应用前景.
关键词: 可调电感器/
磁电效应/
场致应变/
压电单晶

English Abstract

全文HTML

--> --> -->

电感器作为最基本的电路元件, 有着调压、滤波、振荡等作用^[1], 在通信和电子等重要领域不可或缺. 一直以来, 器件的多功能化、集成化、小型化是科技发展的迫切需求. 如图1(a)所示, 可调电感器有望取代电路中繁多的电感器和电容器, 从而减少电路元件的数量, 促进器件小型化的发展. 例如, 传统的负载点转换器为了实现高效率、高功率密度和低噪声, 需要高性能的电感和大量的输出电容. 而基于可调电感器的负载点转换器, 稳态时电感大, 负载瞬态时电感小, 从而增加了电流的转化率和大大减少电容器的数量. 目前对电感调控的方法主要有离散型、金属屏蔽型、磁芯调节型和线圈耦合型等, 但是面临着制造复杂、体积较大、功耗高、可调性小等各类问题^[2-4].
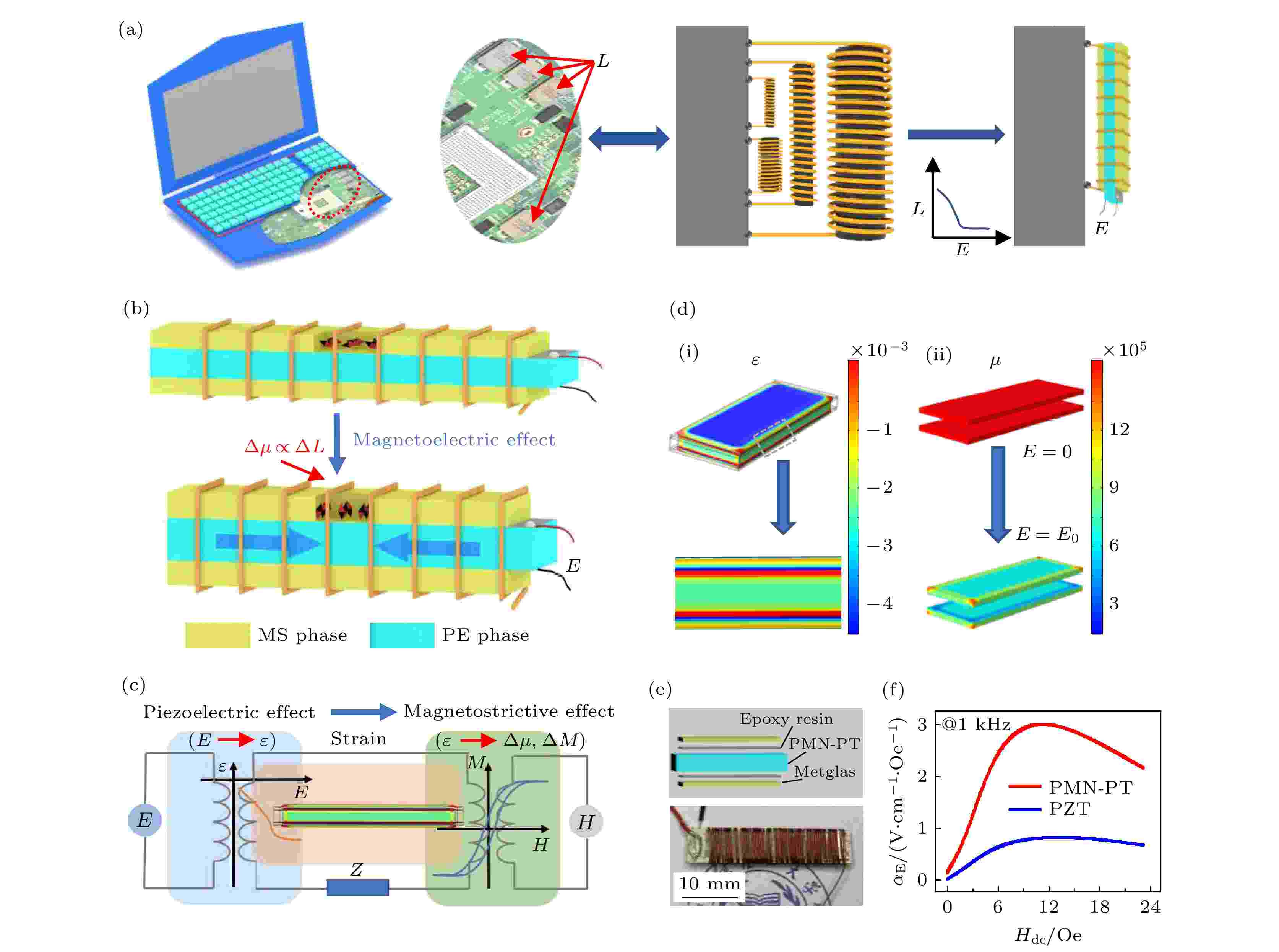图 1 磁电电压可调电感器　(a) 应用示意图; (b) 结构示意图; (c) 逆磁电效应原理图; (d) (i)和(ii) 分别为电场作用时应变和磁导率的变化图; (e) 实物图; (f) PMN-PT基和PZT基磁电系数随偏置磁场的变化
Figure1. Magnetoelectric voltage tunable inductor (ME-VTI): (a) Potential application and (b) structure of ME-VTI; (c) principle of inverse magnetoelectric effect; (d) the variation of (i) strain and (ii) permeability under electric field; (e) photo for a ME-VTI; (f) the ME voltage coefficient of the Metglas/PMN-PT/Metglas and Metglas/PZT/Metglas.

近年来, 磁电电压可调电感器成为研究的热点, 由磁致伸缩材料和压电材料组成的磁电复合材料作为磁芯, 通过电场调控磁导率, 进而达到调控电感的目的^[5-7]. 利用这种方法可以减低能耗, 缩减体积, 且具有较大的可调性^[8,9]. Lou等^[10]利用复合多铁性材料Metglas (FeSiB 合金箔)/PZT (锆钛酸铅)/Metglas作为磁芯, 通过电场可以实现低频下电感量450%的调节. Liu等^[11]利用复合多铁性材料PZT/MnZn铁氧体/PZT作为环形铁芯, 通过电场调控, 可以实现电感量56.6%的调节. 而Yan等^[1]利用复合多铁性材料PZT/NiZnCu-CoFe₂O₄铁氧体/PZT作为环形铁芯, 实现电场对电感的调控. Geng等^[12-15]和Ma 等^[16]采用相场模拟和第一性原理对电感的可调性给出合理的解释.
然而, 以往的研究报道主要从优化磁芯结构和改良磁致伸缩材料两个方面入手提高可调性, 其磁芯压电相主要选用PZT陶瓷, 这造成电感制备工艺复杂(如环形结构和烧结工艺等)和可调性提高不大等问题. 本文采用性能优异的[110]切型PMN-PT单晶(铌镁酸铅-钛酸铅)作为磁芯的压电相, 制备了结构简单且可调性大的条形磁电电压可调电感器(ME-VTI). PMN-PT单晶具有超高的压电响应(d₃₁ > 1400 pC/N)和机电耦合系数(k₃₁ > 90%), 并且具有比传统PZT陶瓷高出10倍以上的场致应变^[17-19].
除此之外, 准静态下PMN-PT基磁电复合材料的磁电系数α_E大于PZT基的. 如图1(f)所示, 在1 kHz时, PMN-PT基的α_E为3 V·cm^–1·Oe^–1 (1 Oe = 10³/(4π) A/m), 相当于PZT基的3倍.
本文采用磁电复合材料Metglas/PMN-PT单晶/Metglas作磁芯, 设计了1个条形电压可调电感器, 具有高达680%的可调性. 为了提高电感可调性, 以往从减少初始磁各向异性(包括磁晶各向异性和形状各向异性)和提高初始磁导率的角度入手, 如优化结构、改善磁性材料等, 而本文从提高应力或应变诱导的各向异性的角度出发, 达到提高电感可调性的目的.

2

-->

2.1.ME-VTI的工作原理

磁电效应分为正磁电效应和逆磁电效应, 前者施加磁场H导致电极化P的出现, 后者施加电场E导致磁化M的出现^[20]. 正磁电效应主要应用在磁场传感器、能量收集器、电流传感器和生物医学组件, 而逆磁电效应主要用在存储器、可调器件、天线等^[21-26]. 磁电电压可调电感器的结构如图1(b)所示, 可调原理基于逆磁电效应, 即电场引起磁化状态的改变, 它是压电效应和磁致伸缩效应的乘积作用^[27], 其原理如图1(c)所示. 作为电感磁芯的压电相受到电场作用发生形变, 以应变为媒介传递到磁致伸缩相, 磁致伸缩相发生应变使得其内部磁畴发生运动, 最终导致磁导率的变化, 电感随之改变. 压电相受到电场作用时, 磁电复合材料的应变分布如图1(d)-(i)所示, 磁致伸缩相发生明显的应变. 压电相施加电场前后磁致伸缩相磁导率的变化, 结果如图1(d)-(ii)所示, 磁导率因受到应力或应变而发生改变, 因此电感可调本质上是磁导率的可调.
2 -->

2.2.ME- VTI的理论模型

均匀的弹性电介质状态可以用一些参变量来表征, 考虑以应力T和电场E为独立变量(压电体在工作过程中不可避免地要发热, 难以维持等温条件, 但热交换通常可忽略, 即满足绝热条件), 特征函数吉布斯自由能及其微分形式为

$ \begin{split} &G=U-{T}_{i}{S}_{i}-{E}_{m}{D}_{m}\text{ }\text{, }\\ &\text{d}G=-{S}_{i}\text{d}{T}_{i}-{D}_{m}\text{d}{E}_{m}\text{ }\text{.}\\ &i=1\text{—}6\text{, }\;m=1\text{—}3. \end{split}$

应变S和电位移D是关于应力T和电场E的函数, 在零应力和零电场附近, 利用(1)式泰勒展开保留一次项:

$\begin{split}& {S_i} = - \frac{{{\partial ^2}G}}{{\partial {T_i}\partial {T_j}}}{T_j} - \frac{{{\partial ^2}G}}{{\partial {T_i}\partial {E_m}}}{E_m} \text{, } \\&{D_m} = - \frac{{{\partial ^2}G}}{{\partial {E_m}\partial {E_n}}}{E_n} - \frac{{{\partial ^2}G}}{{\partial {E_m}\partial {T_i}}}{T_i}{\text{ }}{\text{.}} \end{split}$

此外,

$ {S_i} = \frac{{\partial {S_i}}}{{\partial {T_j}}}{T_j} + \frac{{\partial {S_i}}}{{\partial {E_m}}}{E_m} \text{, } \;{D_m} = \frac{{\partial {D_m}}}{{\partial {T_i}}}{T_i} + \frac{{\partial {D_m}}}{{\partial {E_n}}}{E_n}{\text{ }}{\text{.}} $

对比(2)式和(3)式, 引入:

$ \begin{split}-\dfrac{{\partial }^{2}G}{\partial {T}_{i}\partial {E}_{m}}=\;&-\dfrac{{\partial }^{2}G}{\partial {E}_{m}\partial {T}_{i}}=\dfrac{\partial {S}_{i}}{\partial {E}_{m}}=\dfrac{\partial {D}_{m}}{\partial {T}_{i}}={d}_{mi}\text{ }\text{, }\\ -\dfrac{{\partial }^{2}G}{\partial {T}_{i}\partial {T}_{j}}=\;&\dfrac{\partial {S}_{i}}{\partial {T}_{j}}={s}_{ij}^{E}\text{, }~\;-\dfrac{{\partial }^{2}G}{\partial {E}_{m}\partial {E}_{n}}=\dfrac{\partial {D}_{m}}{\partial {E}_{n}}={\varepsilon }_{mn}^{T}\text{ }\text{.}\end{split} $

因此,

$ {S_i} = s_{ij}^E{T_j} + {d_{mi}}{E_m},\;{D_m} = {d_{mi}}{T_i} + \varepsilon _{mn}^T{E_n} \text{, } $

其中s_ij为弹性柔顺常数, ε_mn为电容率, d_mi为压电常数. (5)式是以应力T和电场E为独立变量的弹性电介质线性状态方程, 由(4)式可以看出, 对特征函数的二次泰勒展开可以在线性范围内表示电介质. 而本文利用压电材料沿长度方向应变, 压电材料应变^pS₁及应力张量的纵向分量^pT₁为

$ \begin{split}{}^{\text{p}}S{}_{1}=\;&{}^{\text{p}}s{}_{11}^{E}{}^{\text{p}}T{}_{1}+{d}_{31}E\text{ }\text{, }\\ {}^{\text{p}}T{}_{1}=\;&\dfrac{1}{{}^{p}s{}_{11}^{E}}{}^{\text{p}}S{}_{1}-\dfrac{{d}_{31}}{{}^{\text{p}}s{}_{11}^{E}}E\text{ }\text{.}\end{split} $

2-2型的磁电复合材料, 基于逆磁电效应而言, 磁致伸缩相的变形受压电相的变形所致, 故磁致伸缩相的应变^mS₁及应力张量的纵向分量^mT₁分别为

$ \begin{split}{}^{\text{m}}S{}_{1}=\;&k{}^{\text{p}}S{}_{1}\text{ }\text{, }\\ {}^{\text{m}}T{}_{1}=\;&{}^{\text{m}}Y{}^{\text{m}}S{}_{1}=k{}^{\text{m}}Y{}^{\text{p}}S{}_{1}\text{ },\end{split} $

其中k为应变传递因子(界面耦合因子), 与胶水的选择和厚度, 材料的选择等因素有关; ^mY为磁致伸缩相的杨氏模量.
磁致伸缩相和压电相的体积分数^mv和^pv分别为

$ {}^{\text{m}}\nu = {{}^{\text{m}}t}/{t}\text{, }~~~\;{}^{\text{p}}\nu = {{}^{\text{p}}t}/{t}\text{ }\text{, } $

其中^mt, ^pt和t分别为磁致伸缩相的厚度、压电相的厚度和两相的总厚度.
结合(6)—(8)式能够得到, ME复合材料总应力张量的纵向分量T₁为

$ \begin{split}{T}_{1}=\;&{}^{\text{m}}\nu {}^{\text{m}}T{}_{1}+{}^{\text{p}}\nu {}^{\text{p}}T{}_{1}=Y{}^{\text{p}}S{}_{1}-\dfrac{{}^{\text{p}}\nu {d}_{31}}{{}^{p}s{}_{11}^{E}}E\text{ }\text{, }\\ Y=\;&\dfrac{{}^{\text{p}}\nu }{{}^{\text{p}}s{}_{11}^{E}}+k{}^{\text{m}}\nu {}^{\text{m}}Y,\end{split} $

其中Y为磁致伸缩相束缚下压电材料的杨氏模量. 对于自由状态ME复合材料的边界条件T₁ = 0, 故由(7)式和(9)式可知, 压电相应变^pS₁和磁致伸缩相的应力^mT₁分别为

$ \begin{split}{}^{\text{p}}S{}_{1}=\;&\dfrac{{}^{\text{p}}\nu {d}_{31}}{Y{}^{\text{p}}s{}_{11}^{E}}E \text{, }~~ {}^{\text{m}}T{}_{1}= \dfrac{k{}^{\text{m}}Y{}^{\text{p}}\nu {d}_{31}}{Y{}^{\text{p}}s{}_{11}^{E}}E \text{.}\end{split} $

磁致伸缩相的相对磁导率μ_r定义为

$ \begin{split}{\mu }_{\text{r}}=\;&1+\dfrac{{\mu }_{0}{M}_{\text{s}}^{2}}{2\left|n{K}_{0}+{K}_{\sigma }\right|}\text{ }\text{, }~~{K}_{\sigma }= \frac{3}{2}{\lambda }_{\text{s}}{}^{\text{m}}T{}_{1}\text{ }\text{, }\end{split} $

式中, μ₀为真空磁导率, M_s为饱和磁化强度, K₀为初始磁各向异性(包括磁晶各向异性和形状各向异性), K_σ为应力诱导磁各向异性(应力各向异性), n为符号因子取±1 (与K₀的符号有关), λ_s为饱和磁致伸缩系数. 考虑到电感线圈受匝数、面积、气隙间距等多因素的影响, 为了方便研究磁导率对电感的影响, 因此定义电感L为

$ \begin{split}L= {\mu }_{\text{r}}G\text{ }\text{, }~~ G= {{L}_{0}}/{{\mu }_{\text{r}0}}\text{ }\text{, }\end{split} $

其中参数G为比例因子, 与线圈匝数, 面积等因素有关, 其物理意义为磁导率为1时的电感值; L₀和μ_r0是零电场时的电感和磁导率.
结合(10)—(12)式得到电感L为

$ \begin{split}L=\;&\dfrac{{L}_{0}}{{\mu }_{\text{r}0}}\left(1+\dfrac{{\mu }_{0}{M}_{\text{s}}^{2}}{\left|2n{K}_{0}+3CE\right|}\right)\text{ }\text{, }\\ C=\;&\dfrac{k{\lambda }_{\text{s}}{}^{\text{m}}Y{}^{\text{p}}\nu {d}_{31}}{Y{}^{\text{p}}s{}_{11}^{E}}\text{ }\text{, }\end{split} $

其中C为常数, 由压电材料和磁性材料的参数、压电材料体积比、应变传递因子决定. 而对应的磁电电压电感器可调性γ可近似为

$ \gamma = \dfrac{{{L_0} - {L_{\text{E}}}}}{{{L_{\text{E}}}}} = \dfrac{{3k{\lambda _s}{}^{\text{m}}Y{}^{\text{p}}\nu {d_{31}}}}{{2n{K_0}Y{}^{\text{p}}s_{11}^E}}E{\text{ }}{\text{.}} $

基于理论模型, 本文采用场致应变较大的压电材料PMN-PT单晶和初始磁各向异性较小的磁致伸缩材料Metglas, 最终实现电感可调性的增加.

2

-->

3.1.实验材料

实验所用Metglas购自Vacuumscheltze GmbH & Co. KG, Germany; PMN-PT单晶由上海硅酸盐研究所提供, 通过改进的Bridgman技术从熔体中生长; PZT陶瓷购自中国宏声声学电子器材有限公司; 黏合剂采用美国采购的west systerm双组分环氧树脂105&206型.
2 -->

3.2.ME-VTI的制备

ME-VTI的制作主要分两步, 具体为:
1) 磁芯的制备. 选用PMN-PT单晶和PZT陶瓷的尺寸为28 mm × 6 mm × 0.6 mm, Metglas的尺寸为24 mm × 6 mm × 0.025 mm. 按一定比例配制黏合剂, PMN-PT和PZT上下表面各沾一层Metglas. 将三明治结构的磁电复合材料常温固化24 h, 固化后, PMN-PT和PZT上下表面各引一根导线.
2)线圈的制备. 选用铜线直径φ = 0.2 mm. 根据上述磁芯尺寸, 围绕磁芯紧密缠绕约50圈线圈.
2 -->

3.3.表征方法

通过中国爱伏特电子科技有限公司AFT-0951型动态应变仪测量压电材料的场致应变, 使用美国Agilent公司 4294A型阻抗分析仪进行可调电感器电感的测试, 使用美国Keithley仪器公司2410型电源为材料提供可调电场.

2

-->

4.1.压电材料场致应变对比

图2(a)-(i)对比几种PZT陶瓷和PMN-PT单晶的场致应变, PMN-PT的场致应变远大于PZT. 对于PMN-PT单晶的场致应变可以划分为3个阶段. 阶段I: 当电场E < 10 kV/cm时, PMN-PT单晶应变随着电场增加而线性增加; 阶段II: 当电场E增加至10—12 kV/cm时, 应变突增至0.36%; 阶段III: 当电场E > 12 kV/cm, 单晶应变又随着电场增加而线性增加, 且Δε/ΔE小于阶段I. PMN-PT单晶场致应变之所以有3个阶段, 原因如图2(a)-(ii)所示. 阶段I: 初始态PMN-PT单晶为三方相(R), 有8个等价的随机分布的自发极化方向$ \langle 111\rangle $, 沿[110]方向加电场, 铁电畴发生翻转, 最终形成“2R”工程畴结构^[28], 此阶段应变主要源于电畴翻转; 阶段II: 当[110]方向电场进一步增大, 原本的三方相晶格在电场作用下发生R -M_B -O相变^[29], 此时应变主要源于场致相变; 阶段III: 在大电场下, PMN-PT单晶为正交相, 且正交相自发极化方向沿$ \langle 110 \rangle $方向, 与外电场方向平行, 因此形成了“1O”的单畴结构^[28], 此时应变主要来源于本征压电晶格畸变. 考虑到压电相上下表面附着磁相后场致应变可能会被束缚, 因此针对研究所需PZT和PMN-PT进行磁电复合后场致应变分析. 如图2(b)所示, PZT的场致应变曲线复合前后几乎没有改变, 而PMN-PT单晶的场致应变复合后呈线性趋势增加, 整体变为复合前的1/3, 且仍大于PZT复合的场致应变.
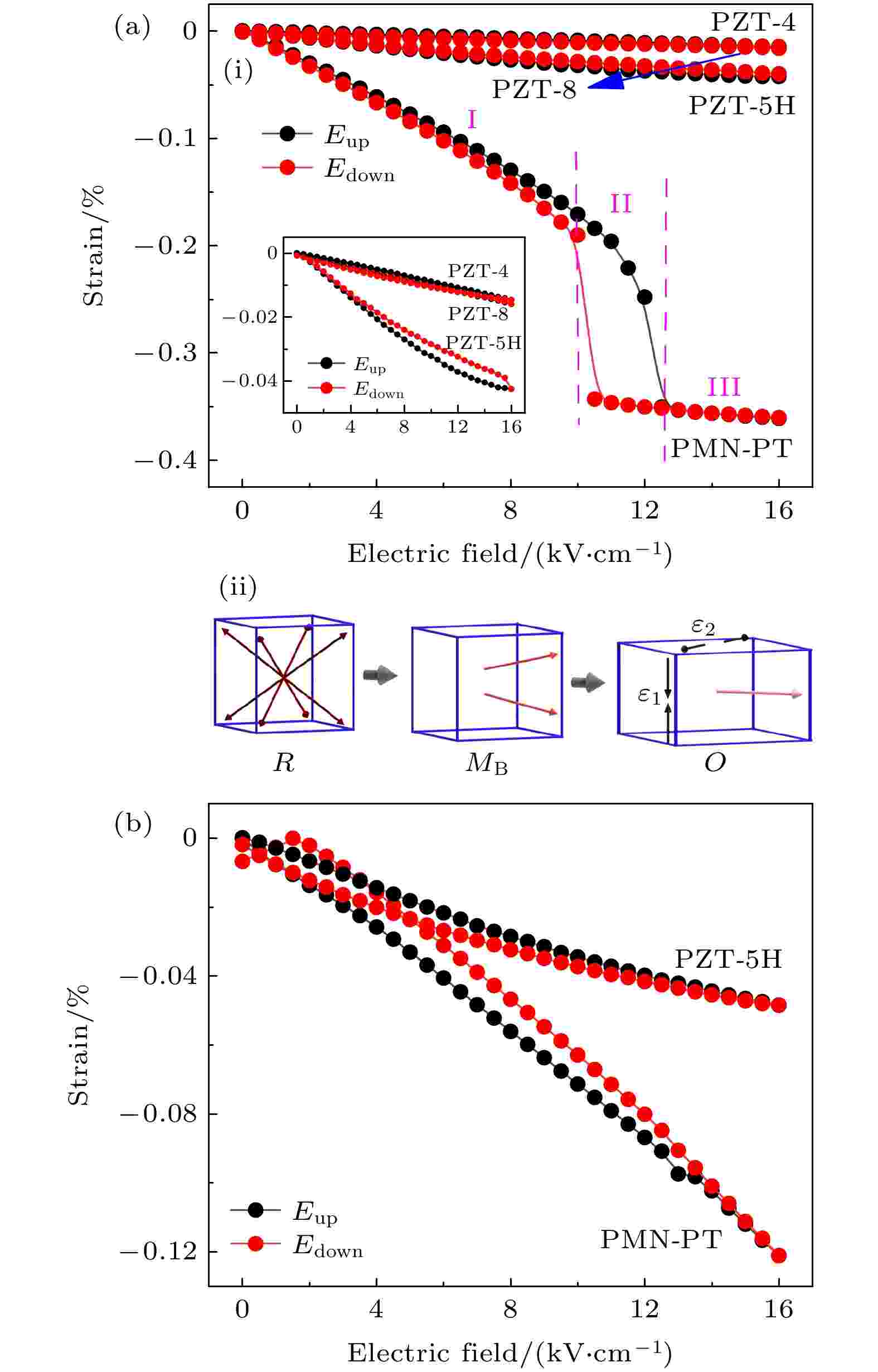图 2 (a) (i)和(ii) 分别为PZT及PMN-PT的场致应变图和PMN-PT的相变示意图; (b) Metglas束缚时PZT和PMN-PT的场致应变图
Figure2. (a) (i) Electric-field induced strain of PZT and PMN-PT and (ii) the phase transition of PMN-PT; (b) the electric-field induced strain of PZT and PMN-PT based ME composites.

2 -->

4.2.可调性分析

图3(a)—(c)展示了不同电场下PZT基和PMN-PT基ME-VTI的电感频谱图. 较高频率下, PZT基的电感比PMN-PT基的衰减得更快, 二者在高频下降的原因是涡流损耗. 高频下磁芯为了抵挡外部交流磁场, 内部会产生涡流, 而Metglas具有较小的电阻率, 导致较大电流, 因此有较大的涡流损耗. 图3(d)—(f)展示不同电场下PZT基和PMN-PT基ME-VTI的可调性频谱图. 较低频率时, PMN-PT基电感相比于PZT基, 随电场的增加电感下降得更快. 较高频率时, PMN-PT基电感可调性稳定性较好. 如图3(g)和图3(h)所示, 在频率为1 kHz时, PMN-PT基电感可调性达到680%, 相当于PZT基电感的3倍. 原因是PMN-PT单晶的应变远大于PZT, 对磁性材料磁畴的翻转影响更大. 可调性起初增加缓慢, 因为电场导致的应力或应变较小, 磁畴只在面内转动; 电场超过临界电场, 电场导致的应变增大, 磁畴面外转动占主导因素.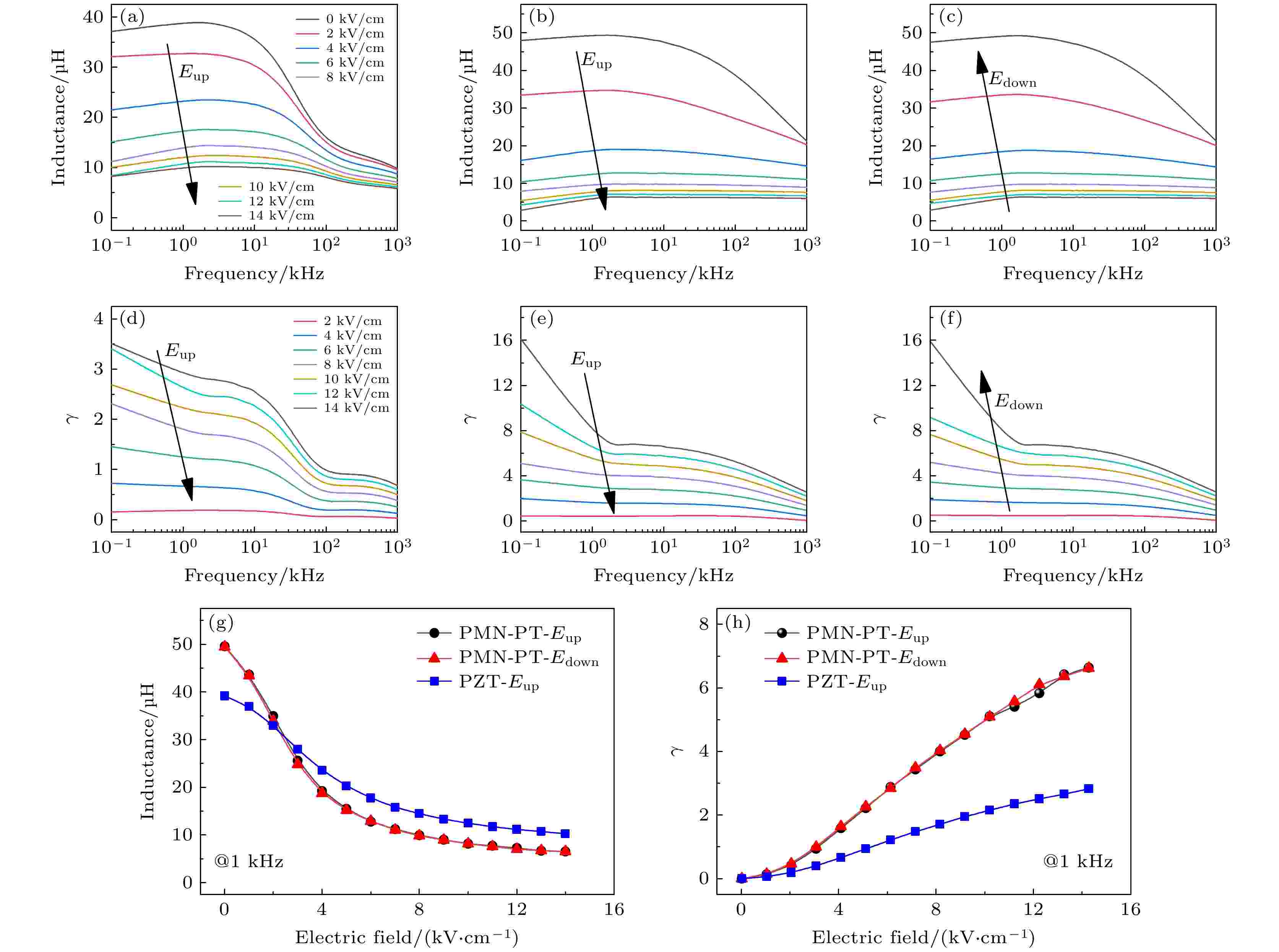
图 3 (a)?(c)和(d)?(f) 分别为磁电电压可调电感器PZT基 (E-field up)、PMN-PT基(E-field up)、PMN-PT基 (E-field down)的电感频谱图和可调性频谱图; (g) 1 kHz时直流电场对PZT基和PMN-PT基电感的影响; (h) 1 kHz时PZT基和PMN-PT基的电感可调性
Figure3. (a)?(c) Inductance and (d)?(f) tunable spectra of PZT based (E-field up), PMN-PT based (E-field up) and PMN-PT based (E-field down) ME-VTI, respectively; (g) inductance of PZT based and PMN-PT based ME-VTI as a function of the applied dc voltage at 1 kHz; (h) tunability γ of PZT based and PMN-PT based ME-VTI at 1 kHz.

2 -->

4.3.品质因子分析

图4(a)—(c)代表不同电场下PZT基和PMN-PT基ME-VTI的品质因子频谱图. 品质因子体现电感储能的优劣. PMN-PT基电感品质因子明显高于PZT基, 并随电场增加峰值右移且增加. 两个体系的品质因子在频率较高时, 随着电场的增加品质因子均增加, 原因是磁导率的降低导致趋肤深度增加, 电阻降低, 因此涡流损耗减少. 而PMN-PT基电感品质因子的峰值之所以会右移, 与应力导致磁致伸缩材料磁导率的降低有关, 因此也可以利用电场实现对铁磁共振频率的调控.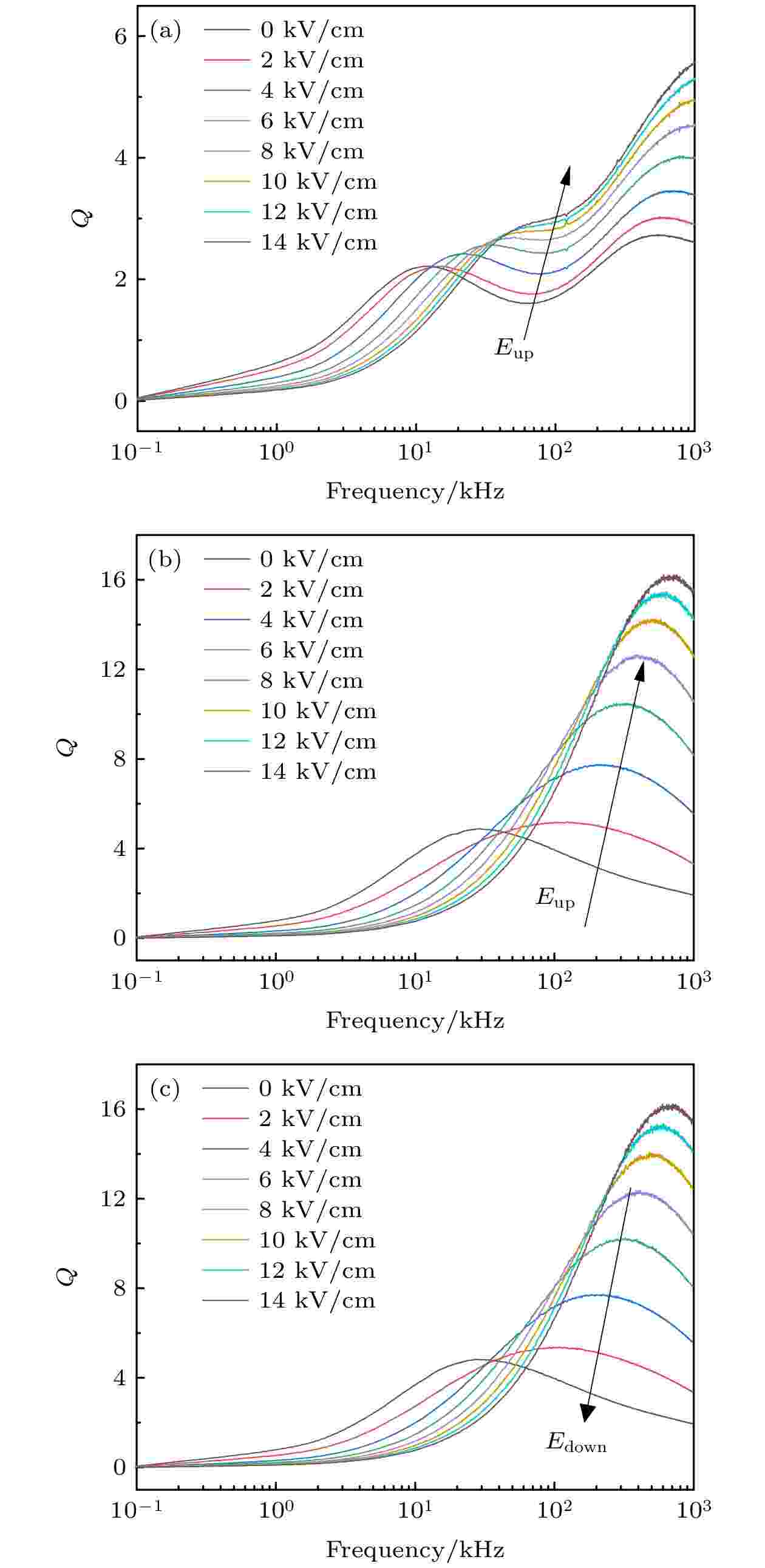
图 4 (a)?(c) 磁电电压可调电感器PZT基(E-field up)、PMN-PT基(E-field up)、PMN-PT基 (E-field down)的品质因子频谱图
Figure4. (a)?(c) Quality factor spectra of PZT based (E-field up), PMN-PT based (E-field up), and PMN-PT based (E-field down) ME-VTI.

2

-->

5.1.理论分析

根据实验数据及以往的研究报道^[30], Metglas的饱和磁致伸缩系数为27 × 10^–6, 杨氏模量为110 GPa, 初始磁各向异性约为700 J/m³. PZT和PMN-PT的弹性柔顺常数分别为16.5 × 10^–12 m²/N和112 × 10^–12 m²/N, 压电常数d₃₁分别为–274 × 10^–12 C/N和–1883 × 10^–12 C/N. 实验中采用的压电材料和磁致伸缩材料体积比分别为0.9231和0.0769. 根据初始磁各向异性的符号及实验数据电感随电场减小, 可知符号因子n为–1. 由图2分析, PZT基和PMN-PT基的应变传递因子k分别取1和0.7. 结合前述推导的(13)式, 如图5所示, 通过拟合PZT基和PMN-PT基电场对电感的调控, 可以看出理论与实验数据趋势较为一致, 其中微弱的偏离与磁畴和材料微观结构的不均匀性、胶水造成的应力松弛等因素有关.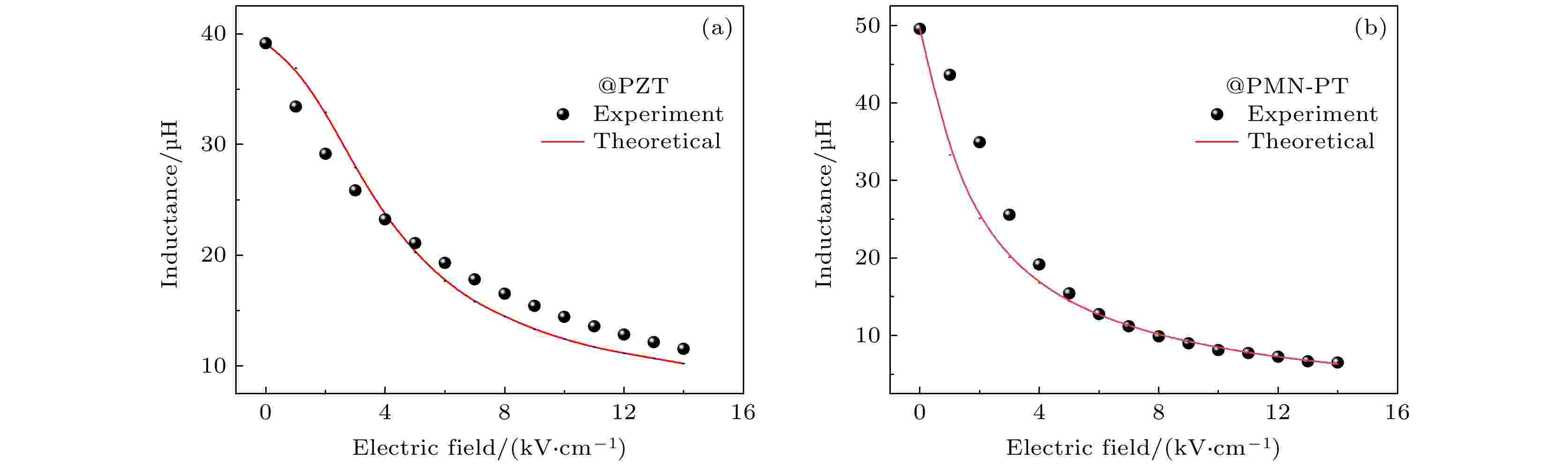
图 5 (a) PZT基和 (b) PMN-PT基电场对电感的调控, 黑色的点代表实验数据, 红色的线代表理论曲线.
Figure5. Variation of (a) PZT based and (b) PMN-PT based inductance under electric field, respectively. The black dots represent the experimental data, and the red line represents the theoretical curve.

2 -->

5.2.有限元模拟分析

图6(a)展示了不同频率下PMN-PT基ME-VTI的可调性, 各频率下随电场的增加可调性均增加. 图6(c)和图6(d)对磁性材料的应力和磁导率进行有限元分析, 可以看出应力导致磁导率降低, 而磁导率又直接影响电感的变化, 模拟结果与图6(b)中的实验结果一致.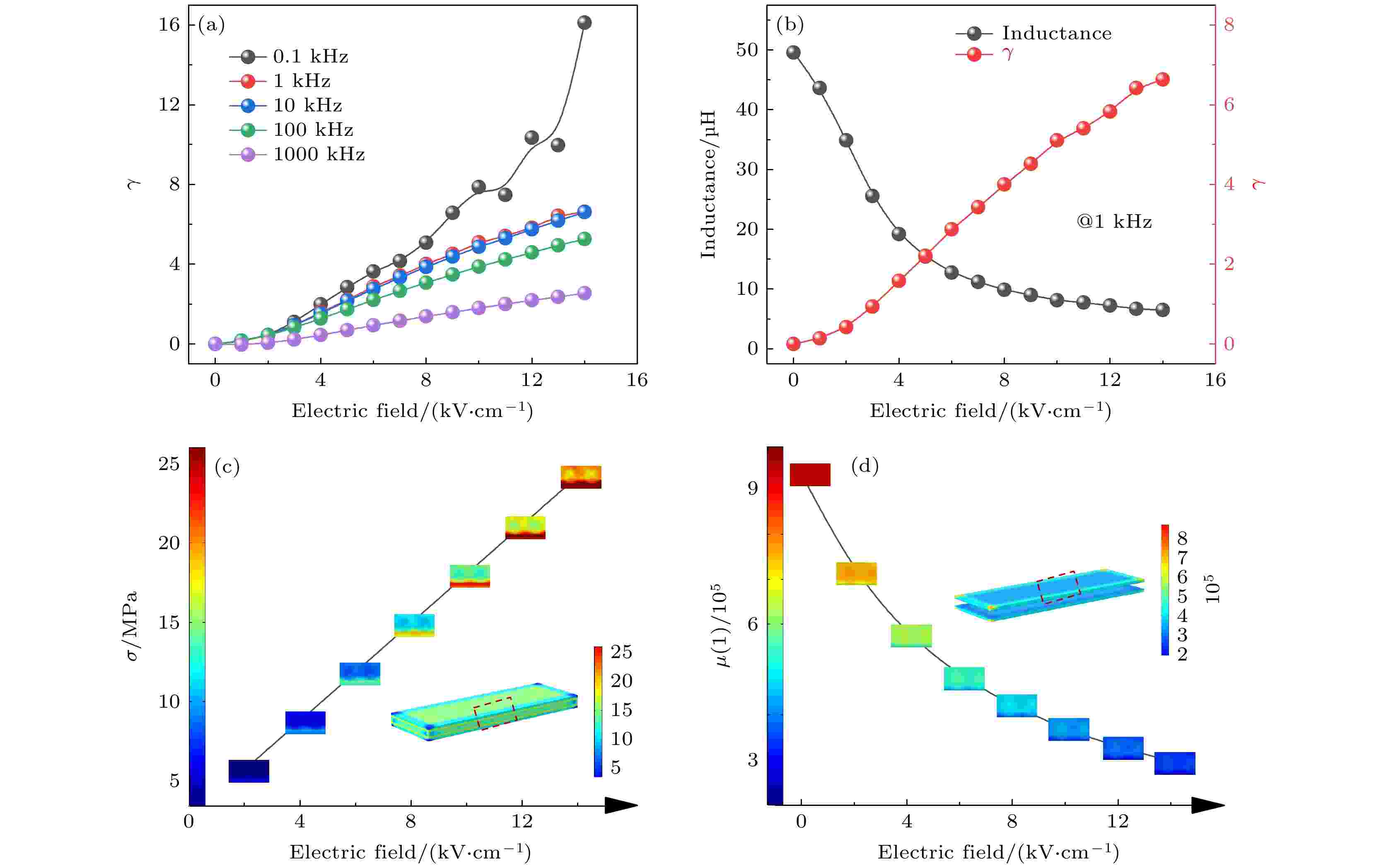
图 6 (a) 各频率下PMN-PT基电压可调电感器电场对可调性的影响; (b) 1 kHz下PMN-PT基电压可调电感器电场对电感和可调性的影响; (c), (d) 分别为电场对应力和磁导率影响的模拟图
Figure6. Influence of electric field of PMN-PT based ME-VTI on (a) tunability at various frequencies; (b) influence of electric field of PMN-PT based ME-VTI on inductance and tunability at 1 kHz; simulation of electric field dependent (c) stress and (d) permeability, respectively.

本文通过构建理论模型, 着眼于压电材料场致应变对电感可调性的影响, 分别采用同尺寸Metglas/PMN-PT/Metglas磁电复合材料和Metglas/ PZT/Metglas磁电复合材料作为磁芯制备了ME-VTI. 由于PMN-PT基的场致应变大于PZT基, 所制得的电感器1 kHz时可调性达到680%, 为PZT基电感的2.4倍. 前者的品质因子达到15.6, 相对于后者提高2.8倍. 基于PMN-PT单晶的ME-VTI和其他类型的可调电感器相比, 具有功耗低, 体积小, 可调性大等优势, 未来在集成化、小型化、多功能化的电子领域有着重要的应用前景.