摘要: 能带理论是凝聚态物理的基石之一, 其应用范围已延伸至许多其他物理领域. 近年来, 众多非厄米物理问题要求将能带理论推广至非厄米体系. 人们在非厄米拓扑体系的研究中发现, 这一推广需要修改能带理论的若干基本概念. 非厄米趋肤效应(non-Hermitian skin effect)这一普遍的非厄米现象导致了布洛赫能带图像的失效以及常规体边对应关系的破坏. 在能谱计算与拓扑不变量定义中, 通常的布里渊区概念需要代之以广义布里渊区(generalized Brillouin zone). 非厄米体系的一系列独特现象可以在广义布里渊区下得到精确刻画. 基于广义布里渊区的非厄米能带理论成功描述并预言了非厄米系统的大量新颖现象. 因其相对布洛赫图像的偏离, 这一理论被称为非布洛赫能带理论(non-Bloch band theory). 本文梳理了广义布里渊区和非布洛赫能带理论的主要概念, 并简要介绍了该理论在非厄米体边对应原理、格林函数、波包动力学、手征衰减和非布洛赫宇称-时间对称性等方面的应用.
关键词: 广义布里渊区 /
非厄米趋肤效应 /
非布洛赫能带理论 /
非厄米能带理论 English Abstract Generalized Brillouin zone and non-Hermitian band theory Hu Yu-Min Song Fei Wang Zhong Institute for Advanced Study, Tsinghua University, Beijing 100084, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 12125405)Received Date: 14 October 2021Accepted Date: 29 October 2021Available Online: 04 November 2021Published Online: 05 December 2021Abstract: The energy band theory is one of the cornerstones of condensed matter physics. It also has wide applications in other branches of physics. Recently, a number of questions from non-Hermitian physics call for a generalization of energy band theory to non-Hermitian systems. In the study of non-Hermitian topological states, it has been found that such a generalization necessitates redefinitions of certain fundamental concepts of band theory. In particular, the non-Hermitian skin effect (NHSE) causes the breakdown of Bloch-band picture and conventional bulk-boundary correspondence. To calculate the energy spectra and define topological invariants, the standard Brillouin zone gives way to the generalized Brillouin zone (GBZ). Many intriguing non-Hermitian phenomena, including the non-Hermitian skin effect, can be precisely characterized in terms of the generalized Brillouin zone. The non-Hermitian band theory based on the concept of generalized Brillouin zone, now generally known as the non-Bloch band theory, has successfully described and predicted a number of novel non-Hermitian phenomena. The present article provides a brief introduction to the main concepts of non-Bloch band theory, and its applications in the non-Hermitian bulk-boundary correspondence, Green’s functions, wave dynamics, chiral damping, and non-Bloch parity-time symmetry.Keywords: generalized Brillouin zone /non-Hermitian skin effect /non-Bloch band theory /non-Hermitian band theory 全文HTML --> --> --> 1.引 言 在量子力学中, 厄米哈密顿量$ ({{H}} = {{H}}^\dagger) $ 通常描述了封闭量子系统的幺正演化. 然而, 这是一种非常理想的情况. 实际上, 很多物理系统与环境之间的耦合不可忽略, 这些耦合使得物质和能量在系统与环境之间交换, 而这些交换过程无法被系统自身的厄米哈密顿量所准确描述. 为了描述系统与环境的耦合, 一种方法是将系统和环境放在一起视为一个封闭大系统, 并试图用整个封闭系统的厄米哈密顿量来刻画其演化. 这种方法实际运用起来通常十分困难. 封闭大系统的自由度时常远大于我们关心的物理系统; 与之相应, 其哈密顿量也非常复杂. 一个更为可行的做法是聚焦于所关心的物理系统自身的自由度, 将其作为一个开放体系(open system). 相应地, 其时间演化不能由一个厄米的哈密顿量来生成, 需要采用非厄米的哈密顿量(或非幺正的时间演化算符). 对于经典波体系, 类似的方案也行之有效.[1 -3 ] :$ {{ \rho }} $ 代表系统的密度矩阵; $ {{H}} $ 表示系统幺正演化的哈密顿量; $ {{L}}_\mu $ 是描述系统与环境之间耦合导致的量子跃迁(quantum jump)的Lindblad耗散算符, 其表明环境的影响将使得系统偏离自身的幺正演化. (1 )式可简记为 $ \dfrac{{\rm d}{{\rho}}(t)}{{\rm d} t} = {\cal{L}} {{\rho}} (t) $ , 其中$\cal{L}$ 通常称为Liouvillian超算符.$ {{ \rho}}(t) $ 的演化的线性微分方程. 如果将密度矩阵$ {{\rho}} (t) =\displaystyle\sum\nolimits_{ij} {{\rho}} {(t)_{ij}}\left| i \right\rangle \left\langle j \right| $ 视作一个态矢量$| {\tilde {{\rho}} (t)} \rangle = $ $ \displaystyle\sum\nolimits_{ij} {{ \rho }} {(t)_{ij}}| i \rangle \otimes | j \rangle$ , 其演化由Liouvillian超算符$ \cal{L} $ 在$ \{ \left| i \right\rangle \otimes \left| j \right\rangle \} $ 这组基下的矩阵形式所描述, 即$ {\partial _t}\left| {\tilde {{\rho}} (t)} \right\rangle = \tilde {\cal L}\left| {\tilde {{\rho}} (t)} \right\rangle $ , 其中$ \tilde{\cal{L}} $ 为$ {{H}}_{\text{eff}} = {{H}}-{\rm i} \displaystyle\sum_{\mu}{{L}}_{\mu}^{\dagger} {{L}}_{\mu} $ , 方程(1 )可表达为$ {{H}}_{\text{eff}} $ 作用下的非幺正演化, 而最后一项代表了环境耦合带来的量子跃迁.$ \left| \psi \right\rangle $ 出发, 在较短的时间内波函数将沿着非厄米有效哈密顿量$ {{H}}_{\text{eff}} $ 进行演化: $ \partial_t \left| \psi \right\rangle = -{\rm i}{{H}}_{\text{eff}} \left| \psi \right\rangle $ . 其有一定的概率在某一时刻$ t $ 发生量子跃迁, 得到一个新的态: $ \left| {\psi (t)} \right\rangle \to {{{L}}_\mu }\left| {\psi (t)} \right\rangle $ . 随后这个态将继续在$ {{H}}_{\text{eff}} $ 的作用下进行演化, 直到下一次量子跃迁发生. 这个过程定义了量子态$ \left| \psi \right\rangle $ 在非厄米有效哈密顿量和量子跃迁共同作用下的一条量子轨迹(quantum trajectory)[4 ] . 实验上, 可以使测量仪器对发生量子跃迁与否作出响应, 从而根据测量结果来筛选某条指定的量子轨迹, 这对应了实验测量中的后选择(post selection). 由于密度矩阵可以视作许多纯态在经典概率下的叠加, 所以对所有可能的量子轨迹进行加权求和可得到密度矩阵在Lindblad量子主方程下的演化.$ \cal{L} $ 和$ {{H}}_{\text{eff}} $ , $ {{H}}_{\text{eff}} $ 描述了后选择下波函数的时间演化, 而$ \cal{L} $ 描述了密度矩阵(无须后选择)的时间演化.[5 -8 ] . 除此之外, 非厄米物理在光学或力学等经典波系统中也发挥着重要作用. 例如, 麦克斯韦方程可以写成和薛定谔方程类似的数学形式, 而在光子晶体系统中, 介质对光的吸收或者光向系统外界的辐射使得这一方程包含非厄米项. 适当调控光学系统的性质可使其呈现出丰富的非厄米物理现象, 如光子拓扑绝缘体中的拓扑激光[9 ,10 ] 和光子能带中连接奇异点(exceptional point)的体费米弧(bulk Fermi arc)[11 ] .[12 ,13 ] .[14 -17 ] . 这些拓扑结构体现为拓扑不变量, 一般定义在布里渊区(Brillouin zone, BZ)上. 例如, 刻画量子霍尔效应的陈数(Chern number)定义为布洛赫波函数的Berry曲率在布里渊区上的积分. 拓扑能带理论基于拓扑不变量和对称性对不同维度的拓扑系统进行分类, 为拓扑材料的研究提供了一个理论框架[16 ] . 其中, 拓扑物态的一条中心原理是“体边对应”(bulk-boundary correspondence), 该原理表明周期边界条件(periodic boundary condition, PBC)下的布洛赫波函数所蕴含的拓扑不变量与开放边界条件(open boundary condition, OBC)下受到拓扑保护的边界态数目之间有着一一对应的关系. 拓扑保护的边界态具有新颖的物理性质. 与偶然出现的边界态不同, 拓扑边界态具有很强的稳定性, 不会被边界上的无序或杂质破坏. 除了科学意义本身, 拓扑态的独特物理性质也具有重要的应用前景.[18 ] .[19 -25 ] . 不同于厄米系统, 具有平移对称性的非厄米系统的一个重要性质是其周期边界条件和开放边界条件下的本征态可以非常不同. 在厄米系统中, 开放边界条件下的本征态是周期边界条件下的布洛赫波(即周期调制的平面波)的线性叠加; 而在非厄米系统中, 开放边界条件下的本征态通常以指数衰减的形式局域在系统的边界附近, 这一现象被命名为“非厄米趋肤效应”[19 ] . 这一效应意味着布洛赫波图像的失效, 也使得非厄米系统的性质对边界条件十分敏感.[19 ,26 ] . 这一理论修改了传统能带理论的若干基本概念, 如布里渊区被广义布里渊区(generalized Brillouin zone, GBZ)所取代. 相应地, 拓扑不变量的定义域也从布里渊区变为广义布里渊区. 这些拓扑不变量被称为非布洛赫拓扑不变量(non-Bloch topological invariants), 它们对边界态的性质给出准确的预言. 非布洛赫拓扑不变量与拓扑边界态的精确对应关系被称为非布洛赫体边对应(non-Bloch bulk-boundary correspondence)[19 ] .2 节首先介绍非厄米趋肤效应和广义布里渊区这两个基本概念; 随后讨论广义布里渊区的基本性质. 第3 节将讨论非厄米能带理论的若干应用, 包括非厄米体边对应、非厄米格林函数、波包动力学、手征衰减(chiral damping)、非布洛赫宇称-时间对称性(non-Bloch parity-time symmetry, or non-Bloch PT symmetry)等现象. 第4 节是一个简短总结. 随着相关研究的不断深入, 非厄米能带理论可能会在越来越多的物理系统中得到应用, 其基础理论也将进一步发展完善. 由于篇幅所限, 本文未能覆盖本方向的所有重要进展, 感兴趣的读者可进一步阅读文中列出的参考文献.2.广义布里渊区与Non-Bloch能带理论 22.1.非厄米趋肤效应 2.1.非厄米趋肤效应 为了引入非厄米能带理论, 首先回顾厄米系统的布洛赫能带理论. 布洛赫定理表明, 具有平移对称性的厄米系统在周期边界条件下的本征态是被布洛赫波函数调制的平面波 $\left\langle {x|n, k} \right\rangle = $ $ {u_{n, k}}(x){{\rm e}^{{\rm i}kx}}$ , 其中实数$ k $ 是位于第一布里渊区的准动量, $ n $ 表示能带指标, $ u_{n, k}(x) = u_{n, k}(x+a) $ 是周期性的布洛赫波函数. 在这里, $ a $ 表示晶格常数. 这些本征态所对应的本征值被记为$ E_n(k) $ , 它们表征了系统的能带结构.$ {\rm{\delta}} {{H}} $ . 如果以周期边界条件下的本征态$ \left\{ {\left| {n, k} \right\rangle } \right\}$ 作为基矢, 该边界项将使得不同的本征态$ \left\{ {\left| {n, k} \right\rangle } \right\} $ 之间存在散射, 其散射矩阵元$ \left\langle {k, n|{\rm{\delta}} {{H}}|k', n'} \right\rangle \sim |{\rm{\delta}} {{H}}|/L $ , 其中$ |{\rm{\delta}} {{H}}| $ 表示边界项的大小而$ L $ 表示系统的长度. 因为$ {\left| {\left\langle {x|n, k} \right\rangle } \right|^2} \sim 1/L$ 且$ {\rm{ \delta}} {{H}} $ 只会局域地影响边界附近的波函数, 所以散射矩阵元正比于$ 1/L $ .$ L\to\infty $ 下, 上述边界项的散射矩阵元趋于零, 其对能谱的影响可以忽略. 因此, 在开放边界条件下, 厄米系统的连续能谱仍由$ E_n(k) $ 给出. 系统的本征态是上述调制平面波的线性叠加, 其在布洛赫波基矢下的展开系数则由边界条件的细节决定.[19 ,27 ] $d_{x} = t_{1}+t_{2} \cos k,\; d_{y} = t_{2} \sin k$ . 图1(a) 给出了它的实空间哈密顿量. $ t_1 $ 和$ t_2 $ 分别表示原胞内和原胞之间的跃迁, $ \gamma $ 代表非厄米项. 非厄米SSH模型有着新奇的拓扑性质, 相关内容将在第3.1 节讨论. 本节主要讨论非厄米SSH模型在不同边界条件下能谱和波函数的行为, 以引出non-Bloch能带理论.图 1 (a) 非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中$|\psi(x)|^2=|\psi_A(x)|^2+|\psi_B(x)|^2$ , 链长$L=40$ ; (c) 非厄米SSH 模型在周期边界条件(黑色虚线)和开放边界条件(蓝色实线)下的能谱; (d) 非厄米SSH 模型的广义布里渊区(蓝色实线), 虚线为布里渊区. 参数值: $t_1=2.5,\; t_2=1,\; \gamma=4/3$ [19 ] Figure1. (a) Sketch of non-Hermitian SSH model; (b) eigenstate profiles under open boundary condition, $|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ and $L=40$ ; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (blue solid lines); (d) generalized Brillouin zone (blue solid line) and Brillouin zone (black dashed line). Parameters: $t_1=2.5,\; t_2= $ $ 1, \gamma=4/3$ [19 ] .$ {{\sigma}}_z{{H}}(k){{\sigma}}_z = $ $ -{{H}}(k) $ 使得其能谱以$ (E, -E) $ 的形式成对出现. 在周期边界条件下, 非厄米SSH模型$ {{H}}_{\text{PBC}} $ 的能谱是上述布洛赫哈密顿量的本征值 $E_{\pm}(k) = $ $ \pm\sqrt{d_x^2+(d_y+{\rm{i}}\gamma/2)^2}$ , 其在复平面上形成闭合的圈(如图1(c) ). 当$ t_1 = t_2\pm\gamma/2 $ ($ t_1 = -t_2\pm\gamma/2 $ ) 时, 系统的能谱在$ k = \pi $ ($ k = 0 $ ) 关闭能隙.$ {{H}}_{\text{OBC}} $ 的能谱与周期边界条件的情况有着显著的区别(图1(c) ). 为了理解这种区别, 可以利用相似变换求出其在开放边界条件下的能谱[19 ] . 假设波函数$ \left| \psi \right\rangle = (\psi_{1, A}, \psi_{1, B}, \psi_{2, A}, \psi_{2, B}, \cdots, \psi_{L, A}, \psi_{L, B})^{\rm{T}} $ 是哈密顿量的本征态, 满足定态薛定谔方程$ {{H}}_{\text{OBC}}\left| \psi \right\rangle = E\left| \psi \right\rangle $ . 开放边界条件下, 方程$ {{H}}_{\text{OBC}}\left| \psi \right\rangle = $ $ E\left| \psi \right\rangle $ 等价于$ \bar {{H}}_{\text{OBC}}\left| {\bar \psi} \right\rangle = E\left| {\bar \psi} \right\rangle $ , 其中$ \left| {\bar \psi} \right\rangle = {{S}}^{-1}\left| \psi \right\rangle $ 且$ \bar {{H}}_{\text{OBC}} = {{S}}^{-1}{{H}}_{\text{OBC}}{{S}} $ . 选取相似变换矩阵$ {{S}} $ 为一个对角矩阵, 其对角元为$\{1, r, r, r^2, r^2, \cdots, r^{L-1}, $ $ r^{L-1}, r^L\}$ , 其中$ r = \sqrt{|(t_1-\gamma/2)/(t_1+\gamma/2)|} $ . 当$ |t_1 | > |\gamma/2 | $ 时, $ \bar {{H}}_{\text{OBC}} $ 变成了标准的厄米SSH 模型, 其跃迁项变为$ \bar t_1 = \sqrt{(t_1-\gamma/2)(t_1+\gamma/2)}, \ \bar t_2 = t_2 $ . 作为一个厄米的哈密顿量, 其体态能谱不再依赖于边界条件, 其OBC能谱可以通过PBC能谱给出, 而PBC能谱可以通过动量空间的哈密顿量得到:$ |t_1 | > |\gamma/2 | $ 的条件下它的能谱是实数. 由于相似变换不改变能谱, $ \bar{{{H}}}(k) $ 的本征值也给出了相似变换前非厄米SSH模型$ {{H}}_{\text{OBC}} $ 在开放边界条件下的能谱. 此时, 能隙关闭的位置在$ \bar t_1 = \pm\bar t_2 $ , 即$ t_{1} = \pm \sqrt{t_{2}^{2}+(\gamma / 2)^{2}} $ [19 ] . 这与周期边界条件下非厄米SSH模型$ {{ H}}_{\text{PBC}} $ 能隙关闭的位置$ t_1 = \pm t_2\pm\gamma/2 $ 有着显著的区别. 第3.1 节将要说明这种区别意味着基于布洛赫哈密顿量的传统体边对应将在非厄米系统中失效.$ {{H}}_{\text{OBC}} $ 变成一个厄米模型, 这个方法并不适用于周期边界条件下的非厄米SSH模型$ {{H}}_{\text{PBC}} $ . 考虑到$ {{H}}_{\text{PBC}} = {{H}}_{\text{OBC}}+{\rm{\delta}} {{H}} $ , 其中$ {\rm{\delta}} {{H}} = {t_2}(\left| {L, B} \right\rangle \left\langle {1, A} \right| + \left| {1, A} \right\rangle \left\langle {L, B} \right|) $ 表示周期边界条件下两个边界之间的跃迁, $ L $ 表示系统的长度, 上述相似变换使得$ {{S}}^{-1}{{H}}_{\text{PBC}}{{S}} = \bar{{ H}}_{\text{OBC}}+ {{S}}^{-1}{\rm{\delta}}{{ H}}{{S}} $ . 此时, $ {{{S}}^{ - 1}}{\rm{\delta}} {{HS}} = {t_2}{r^{ - L}}| {L, B} \rangle \langle {1, A} | + {t_2}{r^L}| {1, A} \rangle \langle {L, B} | $ 是一个随着系统长度$ L $ 增大而指数增大的修正. 周期边界条件下的非厄米SSH模型$ {{H}}_{\text{PBC}} $ 在相似变换后与厄米SSH模型$ \bar {{H}}_{\text{OBC}} $ 相差一个指数大的非厄米边界项, 这与厄米系统中正比于$ 1/L $ 的边界扰动有着显著区别, $ {\rm{\delta}}{{ H}} $ 不再能看成微扰. 这个指数大的边界项正是相似变换解法在周期边界条件下失效的原因, 也导致了$ {{H}}_{\text{PBC}} $ 和$ {{H}}_{\text{OBC}} $ 拥有截然不同的性质. 这表明非厄米系统对边界条件异常敏感.$ \bar {{H}}_{\text{OBC}} $ 的体态波函数$ \left| {\bar\psi_l} \right\rangle $ 在空间中是延展的平面波. 因此, 非厄米SSH模型$ {{H}}_{\text{OBC}} $ 的体态波函数$ \left|{\psi_l} \right\rangle = {{S}} \left| {\bar\psi_l} \right\rangle $ 将以指数衰减的形式局域在系统的边界(图1(b) ). 这意味着通常的平面波中的布洛赫相位因子$ {\rm{e}}^{{\rm{i}}k} $ 变成了$ \beta\equiv r{\rm{e}}^{{\rm{i}}k} $ . 这等价于波矢$ k $ 变为复数: $ k\to k-{\rm{i}}\ln r $ . 这种体态波函数局域在系统边界的现象被称为“非厄米趋肤效应”[19 ] .[19 ] . 定义哈密顿量$ {{H}}(\beta)\equiv $ $ {{H}}(k\to-{\rm{i}}\ln\beta) $ , 或者$ {{H}}(\beta)\equiv {{H}}(k)|_{{\rm{e}}^{{\rm{i}}k}\rightarrow\beta} $ . 通常的布里渊区就是单位圆$ |\beta| = 1 $ , 在单位圆上, $ {{H}}(\beta) $ 给出了非厄米SSH 模型在周期边界条件下的本征能量(图1(c) ). 按照上面的分析, 如果将波矢$ k $ 变为复数$ k\to k-{\rm{i}}\ln r $ , 即$ |\beta| = r $ , 哈密顿量$ {{H}}(\beta) $ 将给出开放边界条件下的能谱(图1(c) ). 实际上, $ |\beta| = r $ 所确定的复平面上的圆定义了非厄米SSH 模型的广义布里渊区(图1(d) ), 它有别于传统的布里渊区($ |\beta| = 1 $ ), 在非厄米系统中扮演着厄米系统里布里渊区的角色. 当$ \beta $ 在广义布里渊区上移动时, $ {{H}}(\beta) $ 的本征值和$ |\beta|^x $ 分别给出了实空间的能谱和具有非厄米趋肤效应的波函数[19 ] .[23 -25 ,28 -43 ] . 它体现了非厄米系统对边界条件的敏感性. 这种敏感性使得系统波函数在周期边界条件下和开放边界条件下呈现出截然不同的行为.2.2.广义布里渊区 -->2.2.广义布里渊区 从非厄米SSH模型的例子可以看到, 非厄米系统在开放边界条件下可呈现出非厄米趋肤效应, 其能谱和波函数由广义布里渊区给出. 在非厄米系统中, 广义布里渊区扮演着厄米情况下布里渊区的角色, 它决定了非厄米系统中诸多独特的行为. 因此, 我们需要更加仔细地研究广义布里渊区的普遍定义与计算方法.2.2.1.非厄米SSH模型的广义布里渊区 -->2.2.1.非厄米SSH模型的广义布里渊区 为了得到广义布里渊区, 需要考察边界条件的重要作用. 例如, 对于图1(a) 所示的非厄米SSH模型, 可以通过边界条件解析地求出其开放边界条件下的能谱[19 ] . 假设系统长度为$ L $ , 在开放边界条件下, 这个模型的实空间薛定谔方程为$\left| \psi \right\rangle = \displaystyle\sum\nolimits_j| {\phi^{(j)}} \rangle$ , 其中$ j $ 为独立的波函数分量指标, $ \left| {\phi^{(j)}} \right\rangle $ 为指数函数形式(暂时省略$ j $ 指标): $ \left(\phi_{x, A}, \phi_{x, B}\right) = \beta^{x}\left(\phi_{A}, \phi_{B}\right) $ , 他们满足:$ B = t_1^2+t_2^2-\gamma^2/4-E^2 $ . 这两个根满足 $\beta_1\beta_2 = $ $ \dfrac{t_{1}-\gamma / 2}{t_{1}+\gamma / 2}$ . 存在两个根意味着上述波函数指标$ j = 1, $ $ 2 $ , 其子格点上的波函数分量满足:9 )式的两个方程在方程(8 ) 的联系下是等价的. 特征方程的两个根表明系统中存在两个独立传播的指数形式波函数, 它们将以一定的形式线性叠加, 以满足相应的边界条件. 因此, 实空间波函数的一般形式可表达为8 )和方程(9 ), 上述波函数有两个独立的参量, 它们的取值将由边界条件给出. 系统的边界条件为$ L\to\infty $ )下, (12 )式的左右两边均指数依赖于$ L $ . 因此(12 )式成立的条件为$ |\beta_1 | = |\beta_2 | $ . 如若不然, 设$ |\beta_1 | > |\beta_2 | $ , 则当$ L $ 很大时方程右侧的$ \beta_{2}^{L+1} $ 项可以忽略, 方程退化为$\beta_{1}^{L+1}(t_{1}-\gamma / 2+ t_{2} \beta_{2}) = 0$ , 意味着$t_{1}-\gamma / 2+ t_{2} \beta_{2} $ $ = 0$ 或者$ \beta_{1} = 0 $ , 无法给出数量正比于$ L $ 的解来. 结合$\beta_1\beta_2 = (t_1-\gamma/2)/(t_1+ $ $ \gamma/2)$ , 可以得到:$ r $ 的广义布里渊区(图1(d) ), 与相似变换所得的结果一致. 满足这个方程的能量$ E $ 将构成该模型在开放边界条件下的能谱(图1(c) ).$ \beta_1^x, \beta_2^x $ , 其线性叠加$\psi(x)\sim C_1\beta_1^x+ $ $ C_2\beta_2^x$ 需要满足系统在左右两端的边界条件. 如图2 所示, 开放边界条件$ \psi(x < 1) = 0 = \psi(x > L) $ 要求两个指数形式的波函数在边界附近相互抵消, 形成驻波. 因此, 在$ x = 1 $ 附近$ C_1\beta_1 $ 和$ C_2\beta_2 $ 处于同一数量级, 而在$ x = L $ 附近$ C_1\beta_1^L $ 和$ C_2\beta_2^L $ 也处于同一数量级. 由此可得, 边界条件的约束使得$ |\beta_1 | = |\beta_2 | $ , 从而能够叠加出实空间的本征态波函数.图 2 非厄米体系在开放边界条件下形成以指数衰减的方式局域在边界的“驻波”, 此驻波由$\beta_1$ 波和$\beta_2$ 波叠加而成Figure2. An eigenstate wavefunction under open boundary condition, which is a superposition of the $\beta_1$ wave and $\beta_2$ wave.$ \beta $ 根, 所以此时边界条件的应用将会复杂一些. 对于这些一般情况, 是否能得到普遍的广义布里渊区方程?图3(a) 表示具有远程跃迁项$ t_3 $ 的非厄米SSH模型, 其布洛赫哈密顿量为[19 ] 图 3 (a) 具有远程跃迁项$t_3$ 的非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中$|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ , $L=40$ ; (c) 周期边界条件(黑色虚线)和开放边界条件(蓝色实线, 通过广义布里渊区计算)下的能谱, 橙色圆点代表直接对角化实空间哈密顿量所得的$L=40$ 系统在开放边界条件下的能谱; (d) 广义布里渊区(蓝色实线)和辅助广义布里渊区(灰色实线), 参数取值: $t_1=1.1,\; t_2=1,\; t_3=0.2,\; \gamma=4/3$ [19 ] Figure3. (a) Sketch of non-Hermitian SSH model with $t_3$ being the third nearest neighbor hopping term; (b) eigenstate profiles under open boundary condition with $|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ and $L=40$ ; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (blue solid lines, calculated from the generalized Brillouin zone). Orange points are eigenenergies from directly diagonalizing the real-space Hamiltonian of an open chain with $L=40$ ; (d) generalized Brillouin zone (blue solid line) and auxiliary generalized Brillouin zone (gray solid line). Parameters: $t_1=1.1 , \;t_2=1, $ $ t_3=0.2, \;\gamma=4/3$ [19 ] .$ d_{x} = t_{1}+(t_{2}+t_3) \cos k, \; d_{y} = (t_{2}-t_3)\sin k $ . 这个模型在开放边界条件下仍具有非厄米趋肤效应(图3(b) ), 但是该模型的特征方程有4个根, 此时无法判断是哪些根应该满足上述$ |\beta| $ 模相等的条件, 这个模型也无法相似变换为一个厄米模型. 而且可以发现, 其广义布里渊区不再是一个圆(图3(d) ). 为了描述一般的非厄米系统, 需要更加普遍地定义广义布里渊区.2.2.2.一般模型的广义布里渊区 -->2.2.2.一般模型的广义布里渊区 本节将讨论一般模型的广义布里渊区的定义. 为了简便, 首先讨论一维单带非厄米模型的广义布里渊区, 随后再推广到多带模型. 考虑一般的一维单带模型, 其布洛赫哈密顿量记为$h(k) = $ $ \displaystyle\sum\nolimits_{n = -m}^mt_n{\rm{e}}^{{\rm{i}}kn}$ , $ m $ 表示格点模型的最大跃迁范围; $ 2 m+1 $ 个不同格点之间的跃迁振幅$ t_{-m}, \cdots, t_m $ 均在复数域上取值; 实数$ k\in[-\pi, \pi] $ . 将单位圆上的相位因子$ {\rm{e}}^{{\rm{i}}k} $ 替换为一般复数$ \beta $ , $ {\rm{e}}^{{\rm{i}}k}\to\beta $ , 可定义一个洛朗多项式:$ x $ 的取值为整数, $ \hat {{a}}_x $ 表示该处的粒子湮灭算符.$ \psi(x) = \left\langle {x|\psi } \right\rangle = C\beta^x $ , 其中$ C $ 是与格点坐标$ x $ 无关的常数. 给定复数能量$ E $ , 实空间薛定谔方程$ {{H}}\left| \psi \right\rangle = E\left| \psi \right\rangle $ 将给出如下限制:17 )式被称为系统的特征方程. 其表明对于能量为$ E $ 的模式, 只有满足$ \psi(x)\sim\beta_n (E)^x $ 这种形式的空间波函数才能在系统中存在, 其中$ \beta_n(E) $ 是方程(17 )的$ 2 m $ 个根之一. 按照根的模长可将它们排序为$ |\beta_1(E)|\leqslant|\beta_2(E)|\leqslant\cdots\leqslant|\beta_{2 m}(E)| $ .17 ), 其所对应的本征波函数还需要满足系统的边界条件. 例如, 周期边界条件要求$ \psi(x) = $ $ \psi(x+L) $ , 其中$ L $ 为周期系统的长度. 这种边界条件要求特征方程至少存在一个根$ \beta_n(E) $ 使得$ \beta_n^L = 1 $ . 在热力学极限下, 这个条件变为$ |\beta_n(E)| = 1 $ , 亦即特征方程存在一个根$ \beta_n(E) = {\rm{e}}^{{\rm{i}}k} $ , $ k $ 为实数. 因此, 周期边界条件下的能谱为$ E(k) = h({\rm{e}}^{{\rm{i}}k}) $ .$\psi(x < 1) = 0= $ $ \psi(x > L)$ . 这种边界条件要求$ 2 m $ 个指数形式的波函数的线性组合$\psi(x) = \displaystyle\sum\nolimits_{n = 1}^{2 m}C_n\beta_n^x$ 需要在系统的左右两端相互抵消, 从而形成“驻波”. 类似图2 的分析可以发现, 为了满足系统左右两端的开放边界条件, 要求对于某一个指数变化的$ C_i\beta_i^x $ , 存在一个与之对应的$ C_j\beta_j^x $ , 使得它们在$ x = 1, L $ 附近有相同的数量级. 这个条件要求存在一对特征方程的根$ \beta_{i, j} $ , 它们满足[19 ] :$ E $ 才有可能在开放边界条件下形成驻波. 在这个方程中, $i,\; j\in\{1,\; 2,\; \cdots,\; 2 m\}$ . 那么, 是不是所有满足这个方程的能量都是系统在开放边界条件下的本征值呢?更加仔细地研究边界条件可以发现(见第2.3 节), 如下方程将描述开放边界条件下的能谱和波函数[19 ,26 ] :19 )说明特征方程(17 ) 的中间两个根所对应的波函数构成了开放边界条件下的“驻波”. 满足方程(19 )的能量$ E $ 定义了开放边界条件下非厄米系统的能谱$ E_{\text{OBC}} $ . 此时, 当$ E\in\{E_{\text{OBC}}\} $ 时, 系统的波函数具有如下形式: $ |\psi(x)|\sim|\beta_m(E)|^x $ . 当$ |\beta_m(E)|\ne1 $ 时, 波函数以指数衰减的形式局域在边界, 呈现非厄米趋肤效应.$ E\in\{E_{\text{OBC}}\} $ 时, 它的两个根$\beta_m(E), $ $ \beta_{m+1}(E)$ 在复平面上形成一个有别于单位圆的围绕原点的圈(图1(d) 和图3(d) ). 这个由所有满足条件的$ \beta_m(E), \beta_{m+1}(E) $ 所构成的集合被称为广义布里渊区[19 ,26 ] . 当$ \beta $ 在广义布里渊区上移动时, 由特征方程给出的$ E(\beta) $ 代表了热力学极限下开放边界条件下的连续能谱. 因此, 方程(19 )被称为广义布里渊区方程.$ |\beta_m(E)| = $ $ |\beta_{m+1}(E)| = 1 $ , 广义布里渊区始终是单位圆, 即传统的布里渊区$ \beta = {\rm{e}}^{{\rm{i}}k} $ ($ k $ 为实数). 此时, 非厄米能带理论回到了厄米情形时的布洛赫能带理论. 广义布里渊区之于非厄米系统, 发挥着类似于布里渊区之于厄米系统的作用. 值得补充说明的是, 广义布里渊区的应用范围并不限于最常见的开放边界条件, 对于其他类型的边界条件, 如畴壁(domain wall)边界条件同样适用 [44 ] .2.3.广义布里渊区方程的推导 -->2.3.广义布里渊区方程的推导 本节将通过全面考察边界条件来严格推导广义布里渊区方程(19 ), 并提供一种广义布里渊区的简便计算方法. 跳过本节并不影响读者理解后续物理内容.15 )所描述的一维单带非厄米模型, 在开放边界条件下, 假设能量为$ E $ 的本征态波函数为$\psi(x) = \displaystyle\sum\nolimits_{n = 1}^{2 m}C_n\beta_n^x$ , 其中$ \beta_n $ 是特征方程$h(\beta)- E = 0$ 的根而$ C_n $ 是依赖于边界条件的$ 2 m $ 个待定系数. 当$ 1\ll x\ll L $ 时, 容易验证这个波函数满足薛定谔方程:20 )式的形式. 系统的左右边界各包含$ m $ 个边界方程. 这$ 2 m $ 个方程将被用来确定开放边界条件下本征态$ \psi(x) $ 的具体形式. 在左边界$ x = 1 $ 附近的$ m $ 个方程具有如下形式:$ j = 1, \;2, \;\cdots, \;m $ . 这个条件等价于$\psi(-m) = $ $ \psi(-m+1) = \cdots = \psi(-1) = 0$ . 同理在右边界$ x = L $ 附近的$ m $ 个方程有如下形式:$ j = 1, \;2, \;\cdots,\; m $ . 这个条件等价于 $\psi(L+m) = $ $ \psi(L\;+\;m\;-\;1) \;= \;\cdots = \psi(L+1) = 0$ . 将$\psi(x) = $ $ \displaystyle\sum\nolimits_{n = 1}^{2 m}C_n\beta_n^x$ 代入(21 )式和(22 )式所述的$ 2 m $ 个边界方程, 可以得到$ 2 m $ 个关于待定系数$ C_n $ 的方程, 它们具有如下结构:$ j = 1,\; 2, \;\cdots,\; m $ . (23 )式中$ g_{j, l} $ 和$ g_{j+m, l} $ 是$2 m\times $ $ 2 m$ 个由系统参数$ t_{-m}, \;\cdots, \;t_m $ 和本征能量$ E $ 所确定的与系统长度$ L $ 无关的系数. 这$ 2 m $ 个线性方程具有非零解的条件为其系数矩阵的行列式等于零, 即[26 ] $ |\beta_1 |\leqslant\cdots\leqslant|\beta_{2 m}| $ , 所以在热力学极限$ (L\to\infty) $ 下, (24 )式左边(记为LHS)的主导项为$ A_1, A_2 $ 是和$ L $ 无关的常数. 在热力学极限下, $0 = $ $ \text{LHS} = \beta_{2 m}^L\beta_{2 m-1}^L\cdots\beta_{m+2}^L(A_1\beta_{m+1}^L +A_2\beta_{m}^L)+\cdots,$ 即$ A_1\beta_{m+1}^L +A_2\beta_{m}^L = 0 $ . 由此可得$\left({\beta_{m}}/{\beta_{m+1}}\right)^L = $ $ -{A_1}/{A_2}$ . 如果$ |\beta_m/\beta_{m+1}|\neq 1 $ , 这个等式左边随着$ L $ 增长而指数增长或衰减, 而右边不依赖于$ L $ . 因此在热力学极限下这个方程成立的条件是$ |\beta_m/\beta_{m+1}| = 1 $ , 即[19 ,26 ] 19 )给出的广义布里渊区方程.$ {{H}}(k) $ 是一个$ q\times q $ 的矩阵(如方程(4 )), 其中$ q $ 为能带的个数, 同样假设不同原胞之间最远的跃迁距离为$ m $ , 此时的特征方程可定义为$ {{H}}(\beta)\equiv {{H}}(k\to-{\rm{i}}\ln\beta) $ , 而$ \mathbb{I} $ 是$ q\times q $ 单位阵. 一般情况下, 上述特征方程有$ 2 mq $ 个根, 将其按照$ |\beta_1 |\leqslant\cdots\leqslant|\beta_{2 mq}| $ 的顺序排列. 在多带模型中, 开放边界条件的左边界和右边界各有$ mq $ 个边界方程. 类似的方法可以给出多带的广义布里渊区方程:图1(a) 的非厄米SSH模型可直接计算其广义布里渊区. 延拓方程(4 )的哈密顿量至复平面, $ {{H}}(\beta)\equiv {{H}}(k\to-{\rm{i}}\ln \beta) $ , 非厄米SSH模型的特征方程$ \det({{H}}(\beta)-E\mathbb{I}) = 0 $ 如方程(8 )所示. 根据韦达定理, 这个方程的两个根满足$\beta_1\beta_2 = \dfrac{t_{1}-\gamma / 2}{t_{1}+\gamma / 2}$ . 于是, 根据广义布里渊区的定义可得$|\beta_1(E)| = |\beta_2(E)| = r \equiv \sqrt{\left| \dfrac{t_{1}-\gamma / 2}{t_{1}+\gamma / 2}\right|}$ , 即方程(13 ). 这说明非厄米SSH模型的广义布里渊区是复平面上半径为$ r $ 的圆(图1(d) ), 与相似变换的分析和解析求解的结果一致.图3(a) 所示具有远程跃迁项$ t_3 $ 的非厄米SSH模型, 将方程(14 )的布洛赫哈密顿量$ {{H}}(k) $ 延拓为$ {{H}}(\beta)\equiv {{H}}(k\to-{\rm{i}}\ln \beta) $ , 可得其特征方程为29 )式的右边记为$ g(\beta) $ , 它是一个关于$ \beta $ 的多项式. 特征方程$E^2 = g(\beta)$ 有4个根$|\beta_1(E)|\leqslant |\beta_2(E)|\leqslant $ $ |\beta_3(E)|\leqslant|\beta_4(E)|$ . 考虑到方程(19 )要求存在模相等的两个根, 假设这两个根为$ \beta $ 和$ \beta {\rm{e}}^{{\rm{i}}\theta} $ , 其中$ \theta\in[0, 2\pi] $ . 这两个根对应相同的能量, 由此可得:$ E^2 $ 可得关于$ \beta $ 的多项式方程[26 ] :$ \theta = [0, 2\pi] $ , 可以求出$ \beta(\theta) $ , 然后根据方程(30 )得出相应的$ E $ , 考察$ \beta $ 和$ \beta {\rm{e}}^{{\rm{i}}\theta} $ 是否为特征方程的中间两根$ \beta_2(E) $ 和$ \beta_3(E) $ (对于一般模型, 是$ \beta_m(E) $ 和$ \beta_{m+1}(E) $ ). 若是, 则$ \beta $ 和$ \beta {\rm{e}}^{{\rm{i}}\theta} $ 属于广义布里渊区. 改变$ \theta $ , 这些解的集合构成了该模型的广义布里渊区(图3(d) 中蓝色实线). 注意到此时的广义布里渊区不再是圆. 这表明在开放边界条件下, 具有远程跃迁项的非厄米SSH 模型无法通过相似变换变为一个厄米模型. 通过广义布里渊区可以求得系统在开放边界条件下的能谱(图3(c) 中蓝色实线), 其结果与在一条有限长的链上直接对角化实空间哈密顿量所得的能谱一致(图3(c) 中橙色圆点). 注意到系统在开放边界条件下存在零能的拓扑边界态, 其能量并非由广义布里渊区给出. 这说明广义布里渊区只提供体态的连续能谱, 与厄米系统中布里渊区的角色一致.$ f(\beta, E) = $ $ \det({{H}}(\beta)-E\mathbb{I}) = 0 $ 是一个关于$ E $ 和$ \beta $ 的多项式方程, 可表达为$ q $ 为能带个数而$ m $ 为原胞间最远的跃迁距离. 这个方程不一定能化简成类似于方程(30 )那样的$ p_1(E) = p_2(\beta) $ 形式, 其中$ p_1, p_2 $ 表示任意的多项式. 因此, 无法简单地消去能量$ E $ 得到关于$ \beta $ 的方程$ p_2(\beta) = p_2(\beta {\rm{e}}^{{\rm{i}}\theta}) $ .[45 ] .$ \tilde\beta = \beta {\rm{e}}^{{\rm{i}}\theta} $ , 其中$ \theta\in[0, 2\pi] $ . 此时$ \beta $ 和$ \beta{\rm{ e}}^{{\rm{i}}\theta} $ 均为特征方程的根:$ \theta $ , 将有两个关于$ E $ 和$ \beta $ 的多项式方程, 利用结式的定义可以直接消除能量$ E $ , 得到一个关于$ \beta $ 和$ {\rm{e}}^{{\rm{i}}\theta} $ 的代数方程$ R(\beta, {\rm{e}}^{{\rm{i}}\theta}) = 0 $ [45 ] . 对任意$ \theta\in[0, 2\pi] $ , 这个方程给出的根同时满足$f(\beta, E) = $ $ f(\beta {\rm{e}}^{{\rm{i}}\theta}, E) = 0$ , 因此它们是方程(18 )的解. 这些解所构成的$ \beta $ 集合被称为辅助广义布里渊区[45 ] . 从这些根中选出满足条件$ |\beta_{mq}(E)| = |\beta_{mq+1}(E)| $ 的根即可得到广义布里渊区, 进而得到开放边界条件下的能谱和波函数.图3(d) 中的灰色实线即为具有远程$ t_3 $ 跃迁项的非厄米SSH模型的辅助广义布里渊区$ |\beta_{1}(E)| = $ $ |\beta_{2}(E)| $ ; $ |\beta_{3}(E)| = |\beta_{4}(E)| $ 对应的辅助广义布里渊区则超出了本图的展示范围.[46 -48 ] . 考虑如下双带非厄米模型:$h_\alpha(\beta) = (t_\alpha-\gamma_\alpha)\beta^{-1}+ $ $ V_\alpha+(t_\alpha+\gamma_\alpha)\beta$ , 且$ \alpha = a, b $ 表示两个单带非厄米Hatano-Nelson模型[49 ,50 ] . 这两个单带模型之间的耦合由参数$ \delta $ 控制.$ \delta = 0 $ )时, 这个系统的特征方程$ (E-h_a(\beta))(E-h_b(\beta)) = 0 $ 可分解为两个独立的方程: $ E-h_a(\beta) = 0 $ 和$ E-h_b(\beta) = $ $ 0 $ . 它们分别对应两个单带模型的特征方程, 其广义布里渊区是两个圆. 这两个圆的半径分别为$ |\beta_\alpha| = \sqrt{\left|\dfrac{t_\alpha-\gamma_\alpha}{t_\alpha+\gamma_\alpha}\right|} $ , 其中$ \alpha = a, b $ . 由此可求得其开放边界条件下的能谱是纯实的.$ \delta\ne0 $ )时, 两条链自身不同的趋肤模(假设$ |\beta_a|\ne|\beta_b| $ )将被耦合在一起, 使得系统的广义布里渊区偏离两个独立的圆. 此时的特征方程$(E-h_a(\beta))(E- h_b(\beta)) = $ $ \delta^2$ 不再能分解为两个独立的单带特征方程. 这个方程有4个根$ |\beta_1(E)|\leqslant\cdots\leqslant|\beta_4(E)| $ . 考察边界条件可以发现此时的广义布里渊区方程为$|\beta_2(E)| = $ $ |\beta_3(E)|$ . 这个模型的广义布里渊区将分布在上述两个圆形广义布里渊区之间的区域[46 ] . 在热力学极限下, 这个广义布里渊区给出的能谱是复数的.$ \delta\to 0 $ )也会使得系统的能谱与$ \delta = 0 $ 的情况不再相同, 能谱从$ \delta = 0 $ 变为非零时将发生不连续的突变. 这一现象被称为临界非厄米趋肤效应. 值得指出, 辅助广义布里渊区在引入微小的$ \delta $ 时相对于$ \delta = 0 $ 并不发生突变, 广义布里渊区的突变来自于模长排序: 只有中间两个根入选广义布里渊区.$ L $ . 固定耦合强度$ \delta $ , 在$ L $ 较小时, 系统的能谱是纯实的. 这意味着此时不同链的趋肤模之间的耦合较小. 当$ L $ 超过某个临界值$ L_{\rm{c}} $ 时, 系统的能谱将随着$ L $ 的增大逐渐从纯实数能谱过渡到热力学极限下广义布里渊区给出的复数能谱. 其复数能谱中拥有最大虚部的本征值对应的波函数在空间中的分布随着$ L $ 的变化会呈现出标度不变的性质[46 ,47 ] .2.4.环绕数和非厄米趋肤效应 -->2.4.环绕数和非厄米趋肤效应 图1 和图3 两个模型均具有非对称的跃迁项, 其原胞内向左跃迁的振幅$ t_1+\gamma/2 $ 比向右跃迁的振幅$ t_1-\gamma/2 $ 大. 直观看来, 这一非对称性导致了其在开放边界条件下的波函数呈现出局域在系统左侧边界的非厄米趋肤效应. 这是否说明具有非厄米趋肤效应的波函数在空间中局域的方向取决于非对称跃迁项中较大的那个方向呢?事实证明, 上述粗略的图像是不准确的.图4(a) 所示的具有非对称次近邻跃迁的一维单带非厄米模型, 其哈密顿量为[51 ,52 ] 图 4 (a) 具有非对称次近邻跃迁的非厄米模型示意图; (b) 开放边界条件下系统本征态的空间分布, 其中链长$L= $ $ 100$ , 蓝色表示波函数局域在左边, 红色表示波函数局域在右边; (c) 周期边界条件(虚线)和开放边界条件(实线)下的能谱, $E_a=-3+0.1 {\rm{i}}$ (黄点)和$E_b=4+0.1 {\rm{i}}$ (绿点)为两个能量参照点; (d) 广义布里渊区(红蓝实线), 辅助广义布里渊区$|\beta_1(E)|=|\beta_2(E)|$ (灰色实线), 和布里渊区(黑色虚线), $|\beta_3(E)|=|\beta_4(E)|$ 对应的辅助广义布里渊区在图示区域以外, 黄点和绿点分别为$E_a=h(\beta)$ 和$E_b=h(\beta)$ 的前3个零点$\beta_{1, 2, 3}$ . 参数取值: $t_1 = 2,\; t_2 = 0.3, \;\gamma= 0.3, $ $ \kappa=0$ [51 ,52 ] Figure4. (a) Sketch of a single-band non-Hermitian model with asymmetric next-nearest-neighbor hoppings; (b) eigenstate profiles under open boundary condition when $L=100$ . Blue/red eigenstates are localized at the left/right side; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (red and blue solid lines), $E_a=-3+0.1 {\rm{i}}$ (yellow point) and $E_b=4+0.1{\rm{ i}}$ (green point) are two reference points; (d) generalized Brillouin zone (red and blue solid line), auxiliary generalized Brillouin zone $|\beta_1(E)|=|\beta_2(E)|$ (gray solid line), and Brillouin zone (black dashed line). Auxiliary generalized Brillouin zone $|\beta_3(E)|=|\beta_4(E)|$ is out of the plot. Yellow and green points are the zeros of $h(\beta)-E_a$ and $h(\beta)-E_b$ , respectively. Parameters: $t_1 = 2, \;t_2 = 0.3, $ $ \gamma= 0.3, \;\kappa=0$ [51 ,52 ] .图4(c) ). 这意味着该模型在开放边界条件下具有非厄米趋肤效应(图4(b) ). 这个模型的特征方程$ h(\beta)-E = 0 $ 是一个关于$ \beta $ 的4次方程. 可以仿照2.3 节的方法求解其广义布里渊区. 对于不同的$ \theta\in[0, 2\pi] $ , 求解$ h(\beta) = h(\beta {\rm{e}}^{{\rm{i}}\theta}) $ 可得一系列$ \beta_\theta $ 和$ E(\beta_\theta) $ . 它们满足方程(18 ): $|\beta_{i}(E)| = $ $ |\beta_{i+1}(E)|$ , 其中$ i = 1, 2, 3 $ . 从中选出满足方程(19 ) 的根即可得广义布里渊区. 图4(d) 中的蓝色和红色实线分别表示位于单位圆内侧和外侧的广义布里渊区$ |\beta_{2}(E)| = |\beta_{3}(E)| $ , 可由其求得开放边界条件下的能谱(图4(c) 中的红色和蓝色实线). 图4(d) 中的灰色实线为辅助广义布里渊区$ |\beta_{1}(E)| = |\beta_{2}(E)| $ . 辅助广义布里渊区$ |\beta_{3}(E)| = |\beta_{4}(E)| $ 超出了本图的展示范围.[53 ] , 已经在声学实验中观察到[43 ] . 在一定条件下, 这类系统存在频率依赖的单向放大, 即不同频率的信号将分别向左或向右放大(见第3.2 节)[51 ] .图1(c) , 图3(c) , 图4(c) ). 从图4(c) 可以看出, 开放边界条件下的能谱被周期边界条件下的能谱所环绕, 且环绕的方向和开放边界条件下能谱对应的波函数局域的方向相关. 为了刻画这种关联性, 引入能谱围绕一个参考能量$ E_0 $ 的环绕数(winding number)[52 ,54 -57 ] :$ \arg $ 表示复数的幅角且$ \cal{C} $ 为积分围道. 考虑到$ h(\beta)-E_0 $ 是关于$ \beta $ 的洛朗多项式, (35 )式等价于$ N_{\text{zeros}}(N_{\text{poles}}) $ 是积分围道$ \cal{C} $ 内$ h(\beta)-E_0 $ 的零点数(极点数).$ \cal{C} $ 选为传统的布里渊区, $ w_{\text{BZ}}(E_{0}) $ 表示周期边界条件下的能谱环绕$ E_0 $ 的次数. 这个环绕数所定义的点能隙拓扑(point-gap topology)是非厄米系统独有的现象. 在厄米系统中, 不论何种边界条件, 系统的能谱都是实轴上的若干条线段. 此时对于任何不在能谱上的参考点$ E_0 $ , 其能谱的环绕数均为零. 但是, 非厄米系统在周期边界条件下的能谱形成环状结构, 环内的参照点对应的环绕数$ w_{\text{BZ}}(E_{0})\ne0 $ .图4(c) 所示, 在由方程(34 )所描述的单带非厄米模型中, 能量参考点$ E_a $ 和$ E_b $ 对应的周期边界条件下的能谱的环绕数分别为$ w_{\text{BZ}}( E_{a}) = +1 $ 和$ w_{\text{BZ}}( E_{b}) = -1 $ . 而这个模型的特征多项式$ h(\beta)-E $ 在原点处是一个二阶极点, 即$ N_{\text{poles}} = 2 $ . 因此, 非零的环绕数表明参考点$ E_a $ /$ E_b $ 在布里渊区内有3/1 个零点, 如图4(d) 中黄点/绿点所示.$ \cal{C} $ 选为广义布里渊区, 任何参考能量$E_0\notin\{E_{{\rm{OBC}}}\}$ 均不被开放边界条件下的能谱所环绕[52 ,54 ] , 即$ N_{\text{zeros}} = N_{\text{poles}} $ . 这个关系可以通过一种极限情况来理解. 假设一般的洛朗多项式$ h(\beta)-E_0 $ 可分解为$ |\beta_1(E_0)|\leqslant\cdots\leqslant|\beta_{2 m}(E_0)| $ 为$ h(\beta)-E_0 $ 的零点. 这个多项式在原点处是一个$ m $ 阶的极点, 即$ N_{\text{poles}} = m $ . 根据数学形式$h(\beta) = $ $ \displaystyle\sum\nolimits_{n = -m}^mt_n\beta^n$ , 当 $ |E_0 | \to \infty $ 时, $ h(\beta)-E_0 = 0 $ 在$ |\beta| \to 0 $ 和$ |\beta| \to \infty $ 附近各有$ m $ 个零点. 在这种情况下, 广义布里渊区包围了在$ |\beta|\to0 $ 附近的$ m $ 个零点$\beta_1(E_0),\; \cdots, $ $ \;\beta_{m}(E_0)$ , 即$ N_{\text{zeros}} = N_{\text{poles}} $ , 可得$ w_{\text{GBZ}}(E_0) = 0 $ . 将$ E_0 $ 从无穷远处连续地拉回, 只要能量$ E_0 $ 不穿过开放边界条件下的能谱, $ \beta_m(E_0) $ 和$ \beta_{m+1}(E_0) $ 总不会到达广义布里渊区, 作为拓扑不变量的环绕数$ w_{\text{GBZ}}(E_0) $ 在整个过程中始终保持不变.$ E_0\notin\{E_{\text{OBC}}\} $ 时, 总能找到一条连续的路径将$ E_0 $ 在不经过开放边界条件下的能谱的情况下移动到无穷远处. 因此, 广义布里渊区内总是包含着$\beta_1(E_0), \;\cdots, \; \beta_{m}(E_0)$ 这$ m $ 个零点, 即$ N_{\text{zeros}} = m $ . 由此可得到方程(37 ).$ E_0 $ 在从内部移动到无穷远处的过程中穿过开放边界条件下的能谱时, $ \beta_{m}(E_0) $ 和$ \beta_{m+1}(E_0) $ 的次序将发生交换, 它们将分别移出或移入广义布里渊区. 因此, 广义布里渊区内始终包含着$ \beta_1(E_0),\; \cdots, \;\beta_{m}(E_0) $ 这$ m $ 个零点, 即$ w_{\text{GBZ}}(E_0) = $ $ 0 $ . 这一事实被表述为一个严格的定理, 其完整证明请参阅文献[52 ].34 )所描述的模型中, 图4(c) 中能量参考点$ E_a $ 和$ E_b $ 对应的开放边界条件下的能谱的环绕数均为零. 参考点$ E_a $ /$ E_b $ 在广义布里渊区内有2个零点, 如图4(d) 中黄点/绿点所示.$ E_0 $ 处在周期边界条件下的环状能谱内部时, $ w_{\text{GBZ}}(E_{0}) = 0 $ 但$ w_{\text{BZ}}(E_{0})\ne0 $ . 这说明布里渊区和广义布里渊区不再重合. 广义布里渊区上的点不再是单位模长, 其对应的开放边界条件下实空间本征态波函数将局域在系统的边界, 呈现非厄米趋肤效应. 如果选取开放边界条件下的一个本征能量作为参考点$ E_0 $ , $ w_{\text{BZ}}(E_{0}) $ 的正负号将决定$ E_0 $ 所对应的本征态局域在体系的左侧边界或右侧边界(图4 ). 因此, 周期边界条件下的能谱的非零环绕数符号和开放边界条件下的非厄米趋肤效应有着一一对应的关系[52 ,54 ] . 进一步研究发现, 周期能谱非零环绕数的具体数值也对应于量子化的物理响应[58 ] .[59 ] . 需要指出的是, 高维的非厄米趋肤效应尚有许多问题有待理解.3.非厄米能带理论的应用 广义布里渊区概念与non-Bloch能带理论为一大类非厄米物理问题提供了出发点, 激发了丰富的研究进展. 本节将讨论非厄米能带理论在体边对应、格林函数、波包动力学、手征衰减和非布洛赫PT对称性等方面的应用.3.1.非厄米拓扑系统的体边对应 3.1.非厄米拓扑系统的体边对应 Non-Bloch能带理论最初提出是为了回答非厄米系统的体边对应问题. 在厄米系统中, 周期边界条件下的布洛赫哈密顿量所蕴含的拓扑不变量与开放边界条件下拓扑保护的边界态之间存在着对应关系[14 -17 ] . 但是, 在非厄米系统中, 布洛赫哈密顿量的能谱及其所对应的调制平面波形式的波函数与开放边界条件下的能谱及波函数有着显著的区别. 这意味着非厄米布洛赫哈密顿量的拓扑性质无法预言开放边界条件下边界态的行为. 实际上, 基于布洛赫能带理论的拓扑不变量在发生改变时, 一般并不对应开放边界条件下边界态数目的变化[19 ] .图1(a) 所示的非厄米SSH模型(方程(4 )). 图3(a) 所示具有远程跃迁项的非厄米SSH模型(方程(14 ))的拓扑性质拥有类似的结论. 前面已经提到, 非厄米SSH 模型在周期边界条件和开放边界条件下的能谱有着显著的区别. 在改变系统参数时, 开放边界条件下边界态出现的位置($ t_1 = \pm\sqrt{t_2^2+(\gamma/2)^2} $ )并不对应周期边界条件下能隙关闭的位置($ t_1 = \pm t_2\pm\gamma/2 $ ), 而是对应开放边界条件下能隙关闭的位置, 如图5(a) 所示. 因此, 为了刻画非厄米系统的体边对应, 需要采用non-Bloch能带理论.图 5 (a) 非厄米SSH模型在开放边界条件下的能谱模长$|E|$ 随着参数$t_1$ 的变化, 红色实线表示拓扑零模边界态, 链长$L=40$ ; (b) Non-Bloch拓扑不变量随着$t_1$ 的变化, 参数取值: $t_2=1,\; \gamma=4/3$ [19 ] Figure5. (a) Absolute values of open-boundary eigenenergies $|E|$ for the non-Hermitian SSH model. Red solid line represents the topological edge zero modes. The chain length $L=40$ . (b) Non-Bloch topological invariant calculated from Eq.(42 ). Parameters: $t_2=1, \;\gamma=4/3$ [19 ] .$ \beta $ 复平面上, 非厄米SSH模型的哈密顿量可以写作:$ {{ \sigma}}_\pm = ({{\sigma}}_x\pm {\rm{i}}{{\sigma}}_y)/2 $ , $ \beta = r{\rm{e}}^{{\rm{i}}\tilde k} $ . 在这里, $r = $ $ \sqrt{|(t_1-\gamma/2)/(t_1+\gamma/2)|}$ 是广义布里渊区的半径而$ \tilde k\in[0, 2\pi] $ 是实参数. 当$ \beta $ 沿着广义布里渊区变化时, 上述$ {{H}}(\beta) $ 的本征值给出了开放边界条件下非厄米系统的连续谱, 其能隙闭合的相变点对应$ t_1 = \pm\sqrt{t_2^2+(\gamma/2)^2} $ .$ {{H}}(\beta) $ 的本征值和本征态如下:$ \left| {{u_{{\rm{R, L}}}}} \right\rangle $ 分别表示$ {{H}}(\beta) $ 的右矢和左矢. 非厄米SSH模型的手征对称性使得$ \left| {{{\tilde u}_{{\rm{R, L}}}}} \right\rangle = {{\sigma}}_z\left| {{u_{{\rm{R, L}}}}} \right\rangle $ 是能量为$ -E(\beta) $ 的右矢和左矢. 他们满足如下归一关系: $ \left\langle {{u_{\rm{L}}}|{u_{\rm{R}}}} \right\rangle = \left\langle {{u_{\rm{L}}}|{{\tilde u}_{\rm{R}}}} \right\rangle = 1 $ , $\left\langle {{u_{\rm{L}}}|{{\tilde u}_{\rm{R}}}} \right\rangle = \left\langle {{{\tilde u}_{\rm{L}}}|{u_{\rm{R}}}} \right\rangle = 0$ . 由此可以定义${{{{Q}} }}$ 矩阵:${{ \sigma}}_z{{{{Q}}}}{{\sigma}}_z = -{{{{Q}}}}$ 使得它有如下反对角形式:[19 ] :图5(b) 所示, 这个基于广义布里渊区的non-Bloch拓扑不变量刻画了开放边界条件下非厄米SSH模型的边界零模态的数目, 准确描述了非厄米系统的体边对应.[24 ,28 ] 、拓扑电路[23 ] 、光学网格系统[25 ] 、拓扑超材料[29 ] 等. 这些实验结果清楚地观测到非厄米趋肤效应, 并显示了基于广义布里渊区的non-Bloch能带理论准确地描述了非厄米系统的体边对应.[44 ] . 非厄米趋肤效应和non-Bloch体边对应在高维系统中也发挥着重要作用. 在二维非厄米陈绝缘体中可以定义non-Bloch陈数, 它准确预言了非厄米陈绝缘体的手征边界态的数目[20 ] . 值得指出, 这里的non-Bloch陈数是在连续极限下计算的, 二维或更高维度的non-Bloch拓扑不变量的高效、普适的计算方法还有待发展. 高维非厄米系统还存在着更丰富的非厄米趋肤效应, 如高阶非厄米趋肤效应, 以及其他丰富的非厄米拓扑相[13 ,60 -68 ] .3.2.非厄米格林函数 -->3.2.非厄米格林函数 非厄米系统中另一类重要的物理量是非厄米格林函数. 格林函数在物理学的很多领域都扮演着十分重要的角色, 它描述了系统对于外界小扰动的线性响应. 因此, 研究非厄米格林函数可以帮助理解非厄米系统的响应和动力学性质.图4(a) 所示的具有非对称次近邻跃迁的一维单带非厄米系统, 其频率空间中的格林函数定义为$ H $ 为实空间哈密顿量. 数值计算表明, 开放边界条件下的格林函数${\rm{ G}}_{L1}(\omega)$ 和${\rm{ G}}_{1 L}(\omega)$ 对于系统长度$ L $ 的依赖关系呈现出如图6 所示的指数变化的行为[51 ] :图 6 (a) 方程(34 )所描述的非厄米模型在开放边界条件下的非厄米格林函数$|G_{L1}|$ 和$|G_{1 L}|$ , 实线是利用广义布里渊区计算的理论值; (b) $L=80$ 时的$|G_{40, j}|$ , 蓝线表示根据广义布里渊区公式计算的理论值. 参数取值: $t_1 = t_2 = 1, $ $ \gamma = 4/3, \;\kappa = -0.8, \;\omega = -1.7$ [51 ] Figure6. (a) Non-Hermitian Green’s functions $|G_{L1}|$ and $|G_{1 L}|$ for the non-Hermitian model in Eq. (34 ) under open boundary condition. Solid lines are calculated from the generalized Brillouin zone. (b) $|G_{40, j}|$ for $L=80$ . The blue lines are the results from the generalized-Brillouin-zone-based formula. Parameters: $t_1 = t_2 = 1,\; \gamma = 4/3, \;\kappa = $ $ -0.8, \;\omega = -1.7$ [51 ] .$ \alpha_{\rightarrow} > 1 $ ($ \alpha_{\leftarrow} > 1 $ )时系统对边界上输入信号的响应会呈现出向右(左)放大的特征.[51 ] :$ i > j $ 的情况. 因为广义布里渊区是复平面上绕原点的一个闭合回路, 所以留数定理表明(45 )式等于广义布里渊区内所有极点的留数之和. 为了计算广义布里渊区内的留数, 需要考虑$ \omega-h(\beta) = 0 $ 在广义布里渊区内的零点, 如图7(a) 和图7(e) 所示. 第2.4 节证明广义布里渊区包含$ m $ 个零点$ \beta_1(\omega), \;\cdots,\; \beta_{m}(\omega) $ . 因此, 当$ i\gg j $ 时, 上述格林函数的渐进行为如下:图 7 (a) 布里渊区(蓝色虚线)和广义布里渊区(红色实线). $\beta_{1, 2, 3}$ 是方程$h(\beta)=\omega$ 在$\kappa=-0.1, \;\omega=4$ 时的根($\beta_4$ 在展示范围之外). $\beta_2$ 位于广义布里渊区和布里渊区之间. (b) $|\beta_2 |$ 随着$\omega, \kappa$ 的变化. (c) $\alpha_\rightarrow$ 随着$\omega, \kappa$ 的变化. (d) $|\beta_2 |$ 和$\alpha_\rightarrow$ 沿着图(c)中虚线$\kappa=-0.1$ 的变化. (e) 和图(a)的区别是$\omega=-3$ , 此时$\beta_3$ 位于广义布里渊区和布里渊区之间. (f) $|\beta_3 |^{-1}$ . (g) $\alpha_\leftarrow$ . (h) $|\beta_3 |^{-1}$ 和$\alpha_\leftarrow$ 沿着图(g)中虚线$\kappa=-0.1$ 的变化. 参数取值: $ t_1 = 2, \;t_2 = 0.3,\; \gamma= 0.3$ [51 ] Figure7. (a) Brillouin zone (blue dashed line) and generalized Brillouin zone (red solid line). $\beta_{1, 2, 3}$ are the roots of $h(\beta)=\omega$ with $\kappa=-0.1, \;\omega=4$ ($\beta_4$ is out of this plot). $\beta_2$ lies between the Brillouin zone and generalized Brillouin zone. (b) $|\beta_2 |$ as a function of $\omega, \;\kappa$ . (c) Numerical $\alpha_\rightarrow$ as a function of $\omega, \;\kappa$ . (d) $|\beta_2 |$ and $\alpha_\rightarrow$ along the dashed cut $\kappa=-0.1$ in panel (c). (e) The same as panel (a) except that $\omega=-3$ . $\beta_3$ lies between the Brillouin zone and generalized Brillouin zone. (f) $|\beta_3 |^{-1}$ . (g) $\alpha_\leftarrow$ . (h) $|\beta_3 |^{-1}$ and $\alpha_\leftarrow$ along the dashed cut $\kappa=-0.1$ in panel (g). Parameters: $ t_1 = 2,\; t_2 = 0.3,\; \gamma= 0.3$ [51 ] .$ i\ll j $ 时, 格林函数的渐进行为如下:图7 所示, 数值计算所得的指数$ \alpha_{\rightarrow}, \alpha_{\leftarrow} $ 和代数方程$\omega-h(\beta) = 0$ 的中间两个零点$ \beta_{m}(\omega), \beta_{m+1}(\omega) $ 符合得很好, 即$ \alpha_{\rightarrow} > 1 $ 或$ \alpha_{\leftarrow} > 1 $ )时, $ \beta_{m}(\omega) $ 或$ \beta_{m+1}(\omega) $ 位于广义布里渊区和布里渊区之间的区域, 如图7(a) 和图7(e) 所示. 值得一提的是, 在目前这个模型里单向放大具有频率依赖性, 即某些频率区间系统会向右放大(图7(a) —图7(d) ), 而另一些频率区间里系统会向左放大(图7(e) —图7(h) ). 这一性质有望应用于将滤波器件与放大器件合二为一.$ \beta_{m}(\omega) $ 和$ \beta_{m+1}(\omega) $ 应为代数方程$ \det(\omega\mathbb{I}-h(\beta)) = $ $ 0 $ 的中间两个零点[51 ] .[58 ] .3.3.非厄米波包动力学 -->3.3.非厄米波包动力学 Non-Bloch能带理论不仅可用于计算开放边界条件下频率空间的格林函数, 还可用于研究非厄米系统在时域上的动力学性质.[69 ] 研究发现, 系统内部波包演化动力学在长时间极限下的Lyapunov 指数能够由广义布里渊区来刻画. 有趣的是, 波包动力学所给出的Lyapunov指数与边界条件无关. 不论是周期边界条件还是开放边界条件, Lyapunov指数都与广义布里渊区上的鞍点有关. 这一现象为实验探测非厄米趋肤效应提供了新的思路.$ x_0 $ 处的$ \delta $ 函数$\psi (x, t = 0) = $ $ \left\langle {x|{x_0}} \right\rangle = {\delta _{x, {x_0}}}$ . 这个波包将在非厄米哈密顿量$ {{H}} $ 的作用下进行演化, $ t $ 时刻的波函数为 $\psi (x, t) = $ $ \left\langle {x|{{\rm{e}}^{ - {\rm{i}}Ht}}|{x_0}} \right\rangle$ . 在周期边界条件下, 该式可以用布洛赫波函数展开:$ h(k) $ 是$ {{H}} $ 对应的布洛赫哈密顿量而$ h(\beta)\equiv $ $ h(k\to-{\rm{i}}\ln\beta) $ 是其向$ \beta $ 复平面的延拓. 通过(49 )式可以看出, 被积函数仅在$ \beta = 0 $ 处有一个本性极点. 这说明积分围道可以在不经过原点的情况下从布里渊区移动到别的围道, 如这个非厄米哈密顿量所对应的广义布里渊区. 因此, 在布里渊区或广义布里渊区上积分会给出同样的$ \psi(x, t) $ , 即周期边界条件和开放边界条件下的波包动力学有着相同的行为. 这要求演化时间$ t $ 远小于波包到达系统边界的时间, 否则波包的行为将受到边界的影响而产生差异. 可以证明, 热力学极限下的时域格林函数$ {\rm{G}}(x, x', t) = \left\langle {x|{{\rm{e}}^{ -{\rm{ i}}Ht}}|x'} \right\rangle $ 在$ t $ 较小时与系统的边界条件无关[70 ] .$ \psi(x, t) $ 中依然蕴含着广义布里渊区的信息. 沿着漂移速度$ v $ 所确定的坐标$ x = x_0+ vt $ 可定义波包演化的Lyapunov指数$ \max(\lambda_v) = \operatorname{Im}(E_m) $ , 其中取得极大值时的漂移速度$ v_m = \left[{{\rm{d}} E(k)}/{{\rm{d}}k}\right]_{E_m} $ . 如果系统在开放边界条件下具有非厄米趋肤效应, 可以证明$ v = 0 $ 一定不是Lyapunov指数的极大值点, 即$ \lambda_0 < $ $ \max(\lambda_v) $ [69 ] . 这说明非厄米趋肤效应会显著影响系统内部的波包动力学.$ \psi(x_0, t) $ 在长时间极限下的行为:$E(\beta_{\rm{s}})$ 为某一个鞍点处的能量, 即$\left.\dfrac{\partial E(\beta)}{\partial \beta}\right|_{\beta = \beta_{\rm{s}}} = $ $ 0$ . (50 )式表明, 在长时间极限下$ v = 0 $ 的Lyapunov指数$\lambda_0 = \operatorname{Im}[E(\beta_{\rm{s}})]$ 是某一个鞍点能量的虚部.图8(a) ), 对应的$\beta_{\rm{s}}$ 一定处在广义布里渊区上[69 ] . 如果有多个鞍点, 虚部最大的鞍点将决定波包的长时间演化. 由此可知, 出发位置波函数振幅的长时间演化行为将由开放边界条件下能谱的末端能量的虚部决定, 因此与广义布里渊区而不是布里渊区相联系. 虽然波包演化一直处于体内(远离边界), 这一结论仍然成立.图 8 (a) 周期边界条件(黑色虚线)和开放边界条件(红色实线)下的能谱, 蓝点代表鞍点$\dfrac{\partial E(\beta)}{\partial \beta}=0$ ; (b) 波包初始位置波函数振幅$|\psi(x_0, t)|$ 随时间的演化. 参数取值: $t_1= 1, $ $ t_2=1,\; \gamma=1.5,\; \kappa=-1.2$ Figure8. (a) Energy spectrums under periodic boundary condition (black dashed line) and open boundary condition (red solid line). Blue points are the saddle points satisfying $\dfrac{\partial E(\beta)}{\partial \beta}=0$ . (b) Time evolution of wavefunction amplitude $|\psi(x_0, t)|$ at the initial location $x_0$ . Parameters: $t_1=1, $ $ t_2=1, \;\gamma=1.5, \;\kappa=-1.2$ .$ \lambda_0 < \max(\lambda_v) $ . 由于上述过程与边界条件无关, 因此即使在周期边界条件下, 系统仍能体现非厄米趋肤效应和广义布里渊区的性质[69 ] .图4(a) 的一维单带模型, 在一条足够长的链($ L = 1000 $ )的中部$ (x_0 = 500) $ 放入一个初态波包$ \psi(x, 0) = \delta_{x, x_0} $ . 在一定的参数下, 随着波包的演化, $ \psi(x_0, t) $ 会呈现出图8(b) 所示的指数衰减的行为$ |\psi(x_0, t)|\sim {\rm{e}}^{-0.293 t} $ . 这个指数非常接近开放边界条件下能谱$ E_\text{OBC} $ 末端的虚部, 即鞍点$ E_{\rm{s}} $ 的虚部$ \operatorname{Im}(E_{\rm{s}}) = -0.279 $ (图8(a) ), 与周期边界条件下能谱的最大虚部无关.[71 ,72 ] , 例如它可以给出淬火动力学中的拓扑不变量[28 ,73 ] .3.4.开放量子体系的Liouvillian能隙与手征衰减 -->3.4.开放量子体系的Liouvillian能隙与手征衰减 上一个例子表明, 非厄米系统的动力学性质受到non-Bloch能带性质的深刻影响. 在引言部分提到, 开放量子体系的Liouvillian超算符可以视为作用在密度矩阵上的有效非厄米哈密顿量, 决定了密度矩阵的时间演化. 一个自然的问题是, Liouvillian作为一个非厄米算子是否可以出现非厄米趋肤效应? 其物理后果是什么? 是否可以在non-Bloch能带理论下描写?$ {{ \rho}} $ 代表系统的密度矩阵, $ {{H}} $ 表示系统幺正演化的哈密顿量, $ {{L}}_\mu $ 是描述系统与环境之间的耦合导致的量子跃迁. 研究发现, Liouvillian超算符也能展现非厄米趋肤效应, 且这种效应会显著地影响系统在长时间下的动力学行为. 在一大类开放量子系统中, 长时间极限下的量子态在周期边界条件下以代数衰减的方式趋近于稳态, 而在开放边界条件下以指数衰减的方式趋近于稳态[74 ] .图9(a) 所示的开放费米子系统, 其哈密顿量$ {{H}} = \displaystyle \sum\nolimits_{ij}h_{ij}{\hat{c}}_i^\dagger {\hat{c}}_j $ 选为SSH模型[27 ] :图 9 开放量子系统中的Liouvillian能隙与手征衰减 (a) 具有耗散的开放SSH模型. (b) 衰减矩阵$ {{X}} $ 的本征值. 蓝色代表周期边界条件, 红色代表开放边界条件. A 和B ($t_1\leqslant t_2$ )在周期边界条件下的Liouvillian能隙为零而C 和D ($t_1> t_2$ )非零. A , B , C , D 4种情况在开放边界条件下的Liouvillian能隙均不为零. 4种情况的参数取值见图(c). (c) 平均粒子数偏离值$\tilde n(t)$ 在周期边界条件下的演化. A 和B 表现为缓慢的代数衰减, 而C 和D 为指数衰减. (d) 每个格点上的费米子数偏离$\tilde n_x(t)$ 在周期边界条件(左)和开放边界条件(右)下的演化. (e) 不同长度系统中平均费米子数偏离$\tilde n(t)$ 在周期边界条件(实线)和开放边界条件(虚线)下的演化. (f) 费米子数偏离$\tilde n_x(t)$ 在开放边界条件(虚线)下的演化. (d)—(f)的参数为$t_1=t_2=1,\; \gamma_g=\gamma_l=0.2$ . (c)—(f) 中所有演化过程的初态均为全占据态$\prod_{x, s}\hat{c}_{x, s}^\dagger \left| 0 \right\rangle$ [74 ] Figure9. Liouvillian gap and chiral damping in an open quantum system with non-Hermitian skin effect: (a) Sketch of the SSH Hamiltonian $ {{H}} $ with additional single-particle gain and loss. (b) Eigenenergies of damping matrix $ {{X}} $ . Blue: periodic boundary condition. Red: open boundary condition. The Liouvillian gap under periodic boundary condition is zero for A and B ($t_1\leqslant t_2$ ), while it is nonzero for C and D ($t_1>t_2$ ). Parameter values are shown in panel (c). (c) Time evolution of the fermion number deviation from the steady-state value, $\tilde n(t)$ , of a periodic-boundary chain. The damping is algebraic for A , B and exponential for C , D . (d) Time evolution of site-resolved fermion number deviation from the steady-state values, $\tilde n_x(t)$ , for the periodic boundary condition (left) and open boundary condition (right). (e) Time evolution of $\tilde n(t)$ under periodic boundary conditions (solid curve) and open boundary conditions (dashed curves) for different chain length $L$ . (f) Time evolution of $\tilde n_x(t)$ for an open-boundary chain at different $x$ . Parameters in (d)–(f): $t_1=t_2=1, \;\gamma_g=\gamma_l=0.2$ . The initial state in (c)–(f) is $\prod_{x, s}\hat{c}_{x, s}^\dagger \left| 0 \right\rangle$ [74 ] .$ {\hat{c}}_{xA}, {\hat{c}}_{xB} $ 是格点上的费米子湮灭算符. 为描述体系与环境的粒子交换, 考虑两种原胞内的耗散算符$ {{L}}_{\mu}^{{\rm{l}}} = \displaystyle \sum\nolimits_{i} D_{\mu i}^{{\rm{l}}}\hat{c}_{i} $ 和$ {{L}}_{\mu}^{{\rm{g}}} = \displaystyle \sum\nolimits_{i} D_{\mu i}^{{\rm{g}}} \hat{c}_{i}^\dagger $ , 其具体形式取为$ \varDelta_{ij}(t) = $ $ \operatorname{Tr}[{\hat{c}}_i^\dagger {\hat{c}}_j{{\rho}}(t)] $ 满足如下演化方程[74 ] :$ {{X }}={\rm{ i}}{{h}}^{\rm{T}}-({{M}}_{\rm{l}}^{\rm{T}}+{{M}}_{\rm{g}}) $ , 且$\alpha = {\rm{g}}, {\rm{l}}$ . 在长时间极限下, 上式会演化到稳态的关联函数$\varDelta_{\rm{s}} = \lim_{t\to\infty}\varDelta(t)$ , 它满足$ {{X}} \varDelta_{\rm{s}}+\varDelta_{\rm{s}} {{X}}^{\dagger}+ $ $ 2 {{M}}_{g} = 0 $ . 现考虑系统趋向稳态的过程, 则$ \tilde\varDelta(t) = $ $ \varDelta(t)-\varDelta_{\rm{s}} $ 的演化方程为$ {{X}} $ 矩阵在动量空间有如下形式:$\gamma\equiv\gamma_{\rm{g}}+\gamma_{\rm{l}}$ . 这个矩阵等价于图1(a) 中的非厄米SSH 模型. 在周期边界条件下, 由$ {{X}} $ 矩阵所确定的Liouvillian能隙$ \varLambda $ 在$t_1\leqslant t_2$ 时等于零, 如图9(b) 中的A , B 所示; 而$ t_1 > t_2 $ 时$ \varLambda\ne0 $ , 如图9(b) 中的C , D 所示.$\prod_{x, s}\hat{c}_{x, s}^\dagger \left| 0 \right\rangle$ 的时间演化, 定义相对稳态的平均粒子数偏离$n_x(t) = \varDelta_{xA, xA}(t)+\varDelta_{xB, xB}(t)$ . 数值模拟发现, 当$t_1\leqslant t_2$ 时, $ \tilde n(t) $ 在周期边界条件下呈代数衰减, 如图9(c) 中的A , B 所示.$ {{X}} $ 具有非厄米趋肤效应. 这使得它的能谱不再是周期边界条件下的能谱. 此时能谱的Liouvillian能隙$ \varLambda \ne0 $ (图9(b) ). 因此, $ \tilde n(t) $ 在长时间极限下会呈指数衰减. 图9(e) 的数值模拟显示系统的平均粒子数在进入指数衰减之前, 会有一段时间呈现周期边界条件时的代数衰减的行为. 且这一行为持续的时间长度正比于体系的尺度$ L $ .$ \tilde n_x(t) = n_x(t)-n_x(\infty) $ 的演化. 周期边界条件下它们都呈现出缓慢的代数衰减的行为. 然而, 在开放边界条件下, $ \tilde n_x(t) $ 先经历一段代数衰减的区域再进入指数衰减. 这个转变从系统的一侧边界$ x = 0 $ 附近开始, 渐渐向系统的另一侧传播. 系统不同位置发生转变的时间正比于该处到边界的距离, 从而形成一个波前, 如图9(f) 所示[74 ] . 这种现象被称为手征衰减(chiral damping), 如图9(d) 所示. 它起源于$ {{X}} $ 矩阵的非厄米趋肤效应. 如果$ {{X}} $ 矩阵在开放边界条件下没有非厄米趋肤效应, 那么粒子数的演化在不同边界条件下有着相似的行为.[75 -78 ] .3.5.非布洛赫PT对称性 -->3.5.非布洛赫PT对称性 宇称-时间对称性(PT对称性)在非厄米系统中扮演着重要的角色. 依赖于非厄米参数的取值, 一个具有PT 对称性的系统可以拥有纯实数或者复数能谱, 这二者之间的转变称为PT对称性破缺[79 -83 ] . 对于一个空间周期性体系, 如果系统没有非厄米趋肤效应, 传统的布洛赫能带理论表明PT对称性破缺发生于布里渊区上的奇异点.[52 ,54 ] , 周期边界条件下的能谱环绕非零面积, 因此不可能为纯实数, 也就不会发生PT 对称性破缺; 然而, 开放边界条件下的能谱可以是实数的. 非厄米趋肤效应使得开放边界条件下能谱为实数的现象被称为非布洛赫PT 对称性(non-Bloch parity-time symmetry). 值得指出的是, 开放边界条件是物理上更自然的边界条件, 也是实验中通常采用的边界条件.3.5.1.一维量子行走系统的非布洛赫PT对称性 -->3.5.1.一维量子行走系统的非布洛赫PT对称性 前面给出的例子里其实已经出现了非布洛赫PT对称性. 如, 图1(a) 描述的非厄米SSH模型满足广义的PT对称性$ {{H}} = {{H}}^* $ . 这种对称性是PT对称性的一般推广, 它保证了哈密顿量在一组合适的基下是一个实矩阵. 在一定的参数区间内该哈密顿量在开放边界条件下的能谱是实数(如图1(c) ), 而在周期边界条件下它的能谱始终是复数. 图3(a) 所示模型具有同样的对称性$ {{H}} = {{H}}^* $ , 当参数取值为图3(c) 时, 非布洛赫PT对称性发生了破缺, 其开放边界条件下的能谱拥有复的本征值.3.3 节讨论过的波包动力学, 在一维单光子量子行走实验中可以观测到这种来自非厄米趋肤效应和广义布里渊区的非布洛赫PT对称性及其破缺[69 ,84 ,85 ] $ \left| {\psi (t)} \right\rangle = {{{U}}^t}\left| {\psi (0)} \right\rangle $ , 其中$t = 0, 1, $ $ 2, \cdots$ , 这可以视为初态$ \left| {\psi (0)} \right\rangle $ 在由$ {{U}} = {\rm{e}}^{-{\rm{i}}{{H}}_{\text{eff}}} $ 定义的有效哈密顿量$ {{H}}_{\text{eff}} $ 的作用下进行演化. 具体实现方式有很多可能, 实际的量子行走实验采用了如下的非幺正算符[85 ] :${\left| 0 \right\rangle } $ 或者$ {\left| 1 \right\rangle } $ , $ {{ \sigma}}_z $ 的两个本征态)沿着一维晶格向不同方向转移. 在每个格点上, 还有旋转算符$ {{S}}_{1, 2} $ 和$ {{M}} $ 的共同作用下, 演化算符$ {{U}} $ 在实空间出现非厄米趋肤效应. 如果考虑两个一维系统首尾相连形成畴壁, 两侧的物理参数分别为$ \theta^{\rm{R}}_{1, 2} $ 和$ \theta^{\rm{L}}_{1, 2} $ , $ {{U}} $ 的本征态会局域在畴壁上[44 ,85 ] . 在这个体系中可以研究非布洛赫PT对称性. 将演化算符$ {{U }} $ 变换到动量空间$ {{U}}(k) $ 并定义${{U}}(\beta) \equiv {{U}} (k \to - {\rm{i}}\ln \beta)$ , 可以求得演化算符的广义布里渊区. 考虑$ \beta $ 在广义布里渊区上取值, 计算发现, 当$ |\cos\theta_2^{{\rm{R(L)}}}| > |\tanh\gamma| $ 时, $ {{U}}(\beta) $ 有如下$ \eta $ -赝幺正性(η -pseudo-unitarity)[85 ] :$\eta = \displaystyle \sum\nolimits_n {\left| {{\xi _n}} \right\rangle \left\langle {{\xi _n}} \right|}$ , 其中$ {\left| {{\xi _n}} \right\rangle } $ 是$ {{ U}}(\beta) $ 的左本征态. 这个方程等价于有效非厄米哈密顿量$ {{ H}}_{\text{eff}} $ 具有$ \eta $ -赝厄米性(η -pseudo-Hermiticity):$ {{H}}_{\text{eff}} $ 的本征值($ {{U}} $ 对应的准能谱)是纯实的或者互为复共轭. 从物理效果来看, 在PT对称的区域和PT对称破缺的区域, 初态波包具有截然不同的演化行为, 可以用第3.3 节中非厄米波包动力学的方法来探测系统的PT对称性[69 ,85 ] .图10 所示, 随着系统参数的改变, 周期边界条件下的能谱始终是复数的, 而开放边界条件下的能谱会经历从实数到复数的相变. 图10 给出了非厄米系统在开放边界条件下的非布洛赫PT对称性及其破缺过程, 破缺点被称为非布洛赫奇异点(non-Bloch exceptional point)[85 ] . 在这个具体系统中, 非布洛赫PT对称性发生破缺的参数条件是$ |\cos\theta_2^{{\rm{R(L)}}}| = |\tanh\gamma| $ . 这与周期边界条件下的情况有着本质区别. 在周期边界条件下, 该参数附近的能谱始终为复数, 未发生任何相变.图 10 一维量子行走系统的准能谱虚部$\operatorname{Im}(E)$ 随着$\theta^{{\rm{R}}}_2$ 的变化. 其他参数为$\theta^{\rm{R}}_1=0.5625\pi,\; \theta^{\rm{L}}_1=-0.0625\pi,\; \gamma=0.2746$ (a) $\theta^{\rm{L}}_2= $ $ 0.75\pi$ ; (b) $\theta^{\rm{L}}_2=-0.9735\pi$ . 蓝色实线和灰色实线分别代表开放边界条件下的非布洛赫能谱和周期边界条件下的布洛赫能谱[85 ] Figure10. Imaginary part of quasienergies $\operatorname{Im}(E)$ versus $\theta^{{\rm{R}}}_2$ for the experimentally realized one-dimensional quantum walk. Parameter values: $\theta^{\rm{R}}_1=0.5625\pi,\; \theta^{\rm{L}}_1=-0.0625\pi, \;\gamma=0.2746$ : (a) $\theta^{\rm{L}}_2=0.75\pi$ ; (b) $\theta^{\rm{L}}_2=-0.9735\pi$ . Blue and gray lines represent quasi-energies under open boundary condition and periodic boundary condition, respectively[85 ] .3.5.2.高维系统的非布洛赫PT 对称性 -->3.5.2.高维系统的非布洛赫PT 对称性 最近的理论研究发现, 非布洛赫PT对称性对于空间维数有着出乎意料的依赖性[86 ] . 分别考虑4个不同体系在开放边界条件下的非布洛赫PT对称性的相图, 他们的布洛赫哈密顿量分别如下:图11(a) 表示一维单带模型图 11 不同系统在开放边界条件下复数能量数目占比$P$ (a), (e) 长度为$L$ 的链上的$ {{H}}_{1 {\rm{D}}} $ , 其中$t=1,\; s=0.15$ ; (b), (f) $L\times L$ 的正方形上的$ {{H}}_{2 {\rm{D}}}^{\text{skin}} $ , 其中$t=1,\; s=0.3$ ; (c), (g) $L\times L$ 的正方形上的$ {{H}}_{2 {\rm{D}}}^{\text{no skin}} $ , 其中$m=0.5, \;t=0.2, \;\varDelta=0$ ; (d), (h) $L\times L\times L$ 的正方体上的$ {{H}}_{3 {\rm{D}}} $ , 其中$t=1,\; s=0.5$ . (d)中边界格点上有随机势$V=\displaystyle \sum\nolimits_{\boldsymbol{r}\in\text{Boundary}}w(\boldsymbol{r}) \left| {\boldsymbol{r}} \right\rangle \left\langle {\boldsymbol{r}} \right|$ , 其中$w(\boldsymbol{r})$ 在$[-W/2, W/2]$ 中均匀分布且$W=0.7$ . 能量虚部的绝对值$|\operatorname{Im}(E)|>10^{-10}$ 即被视为复数能量[86 ] Figure11. Complex eigenenergies proportion $P$ for four different systems under open boundary condition: (a), (e) $ {{H}}_{1 {\rm{D}}} $ on a length-$L$ chain with $t=1,\; s=0.15$ ; (b), (f) $ {{H}}_{2 {\rm{D}}}^{\text{skin}} $ on $L\times L$ squares with $t=1,\; s=0.3$ ; (c), (g) $ {{H}}_{2 {\rm{D}}}^{\text{no skin}} $ on $L\times L$ squares with $m=0.5, \;t=0.2,\; \varDelta=0$ ; (d), (h) $ {{H}}_{3 {\rm{D}}} $ on $L\times L\times L$ cubes with $t=1,\; s=0.5$ . For (d), there is an on-site random potential $V=\displaystyle \sum\nolimits_{\mathbf{r}\in\text{Boundary}}w(\boldsymbol{r}) \left| {\boldsymbol{r}} \right\rangle \left\langle {\boldsymbol{r}} \right|$ on boundary sites where $w(\boldsymbol{r})$ is uniformly distributed in $[-W/2, W/2]$ with $W=0.7$ . Numerically, a complex energy holds a nonzero imaginary part if $|\operatorname{Im}(E)|>10^{-10}$ [86 ] .图11(b) 表示二维单带模型图11(c) 表示二维双带模型图11(d) 表示三维单带模型$ {{H}}_{1 {\rm{D}}}, \ {{H}}_{2{\rm{ D}}}^{\text{skin}}, \ {{H}}_{3 {\rm{D}}} $ 在开放边界条件下具有非厄米趋肤效应, 而$ {{H}}_{2 {\rm{D}}}^{\text{no skin}} $ 没有这一效应. 可以利用复数能量本征值数目$ N_{\rm{c}} $ 占能量本征值总数$ N $ 的比例$ P = N_{\rm{c}}/N $ 来刻画这些模型的PT对称性特征, 得到的结果如图11(e) —图11(h) 所示.图11(e) 所示. 但是, 在二维或更高维的系统中, 当体系的尺寸增大时, 非布洛赫PT对称性破缺的阈值会趋近于零, 如图11(f) 和图11(h) 所示. 即使是一个无穷小的非厄米项, 在体系足够大的时候也会使得系统的大部分本征能量变为复数[86 ] .图11(g) 所示. 与非布洛赫PT对称破缺的维度依赖性不同, 布洛赫PT对称破缺在一维和高维一般均有非零阈值.4.结 语 本文简要介绍了广义布里渊区的non-Bloch能带理论的基本概念, 并讨论了该理论在若干非厄米系统中的应用. 可以看到, 虽然最初提出广义布里渊区是为了理解非厄米拓扑态的体边对应, 但是这一概念的应用范围并不限于拓扑性质. 它可以用于研究非厄米能带结构、格林函数、动力学、PT对称性等诸多方面的物理性质.[54 ,87 -96 ] . 如, 如果系统存在互易性${\cal{T}}h(\beta)^{\rm{T}}{\cal{T}}^{-1} = h(\beta^{-1})$ , 其中幺正算符$\cal{T}$ 满足${\cal{T T}}^* = -1$ , 系统在开放边界条件下会呈现出$ \mathbb{Z}_2 $ 非厄米趋肤效应($ \mathbb{Z}_2 $ non-Hermitian skin effect), 即一个本征能量对应两个分别局域在系统两侧边界的简并的本征态[54 ,87 ,90 ] . 在具有BCS 配对的玻色子系统中(例如很多magnon系统中), 玻色型Bogoliubov准粒子的动力学由一个非厄米矩阵所控制, 因此可以用非厄米能带理论来描述[91 ,92 ,94 ] .[97 -106 ] 、非厄米晶体缺陷[107 -110 ] 、非厄米相互作用系统[111 -117 ] 及非厄米量子场论[118 ,119 ] 等. 
























































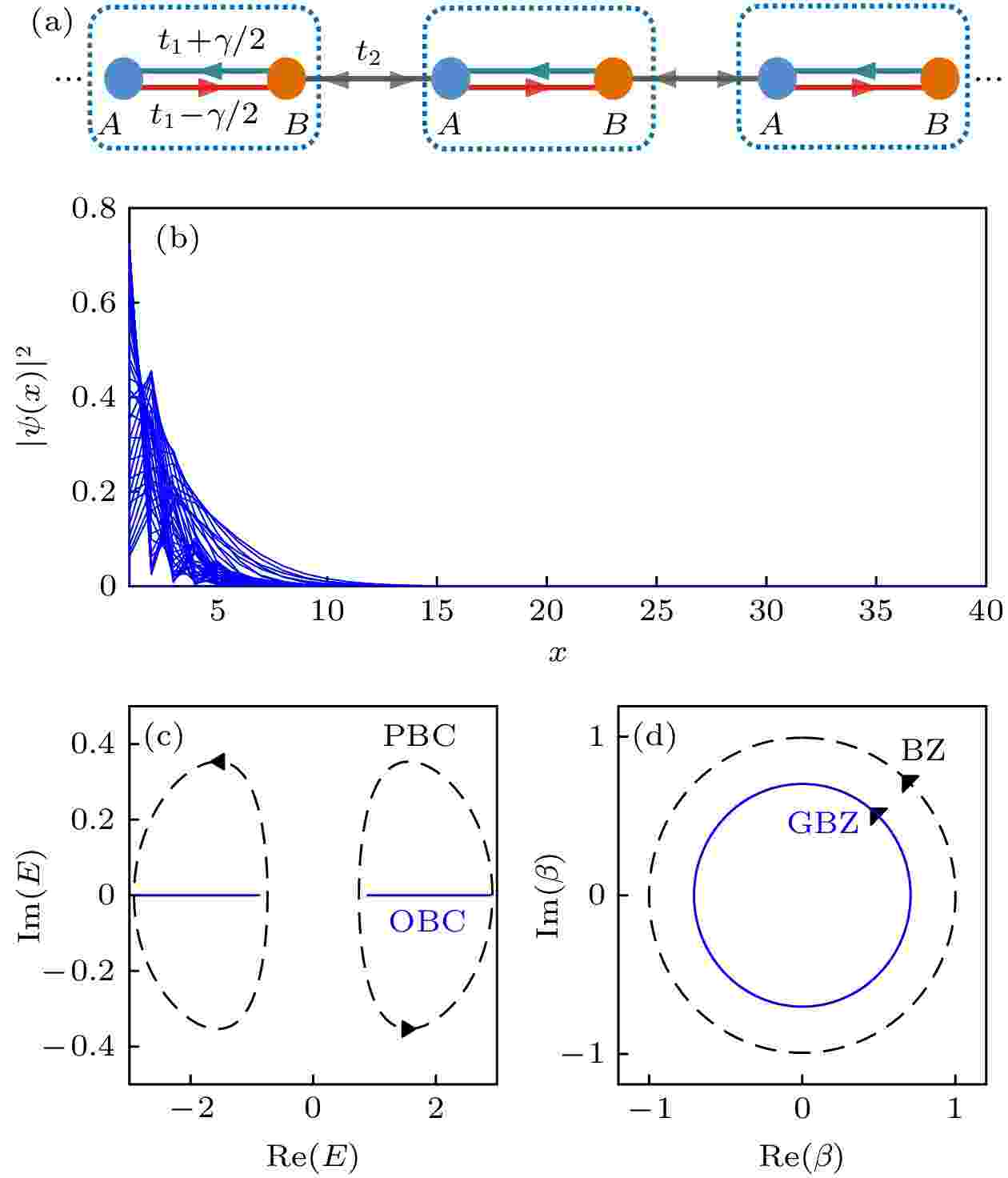 图 1 (a) 非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中
图 1 (a) 非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中












































































































































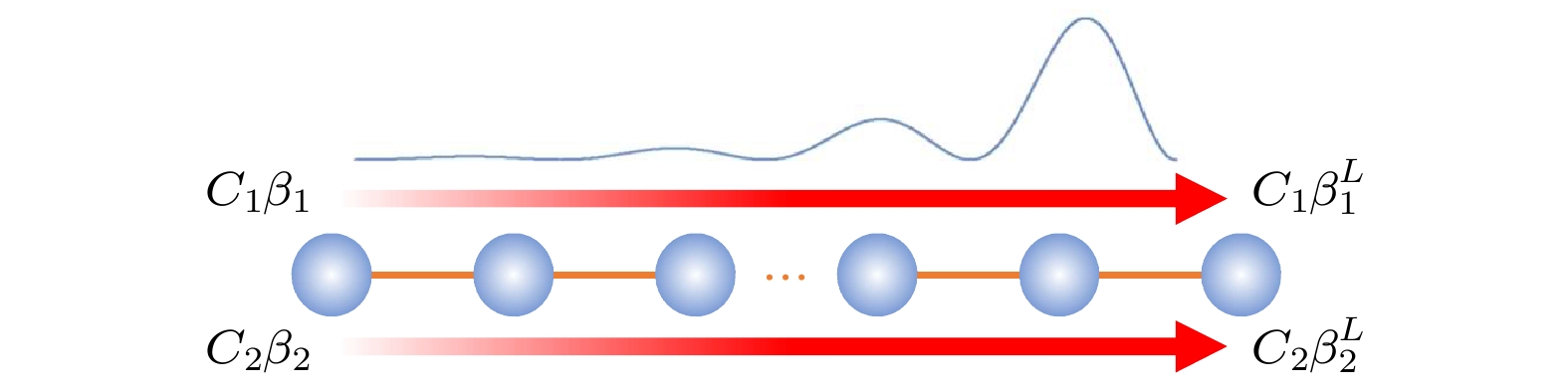 图 2 非厄米体系在开放边界条件下形成以指数衰减的方式局域在边界的“驻波”, 此驻波由
图 2 非厄米体系在开放边界条件下形成以指数衰减的方式局域在边界的“驻波”, 此驻波由





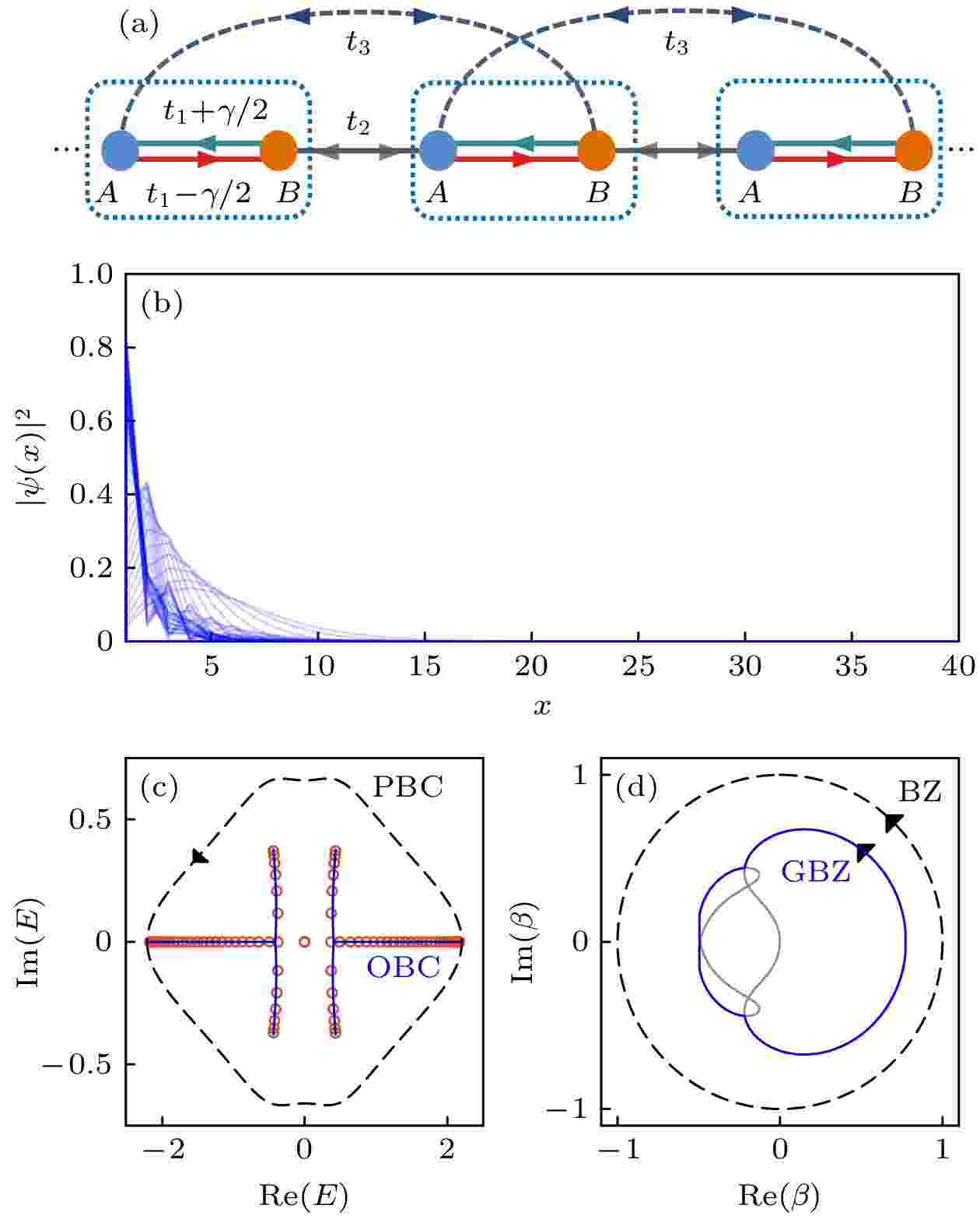 图 3 (a) 具有远程跃迁项
图 3 (a) 具有远程跃迁项

















































































































































































































































































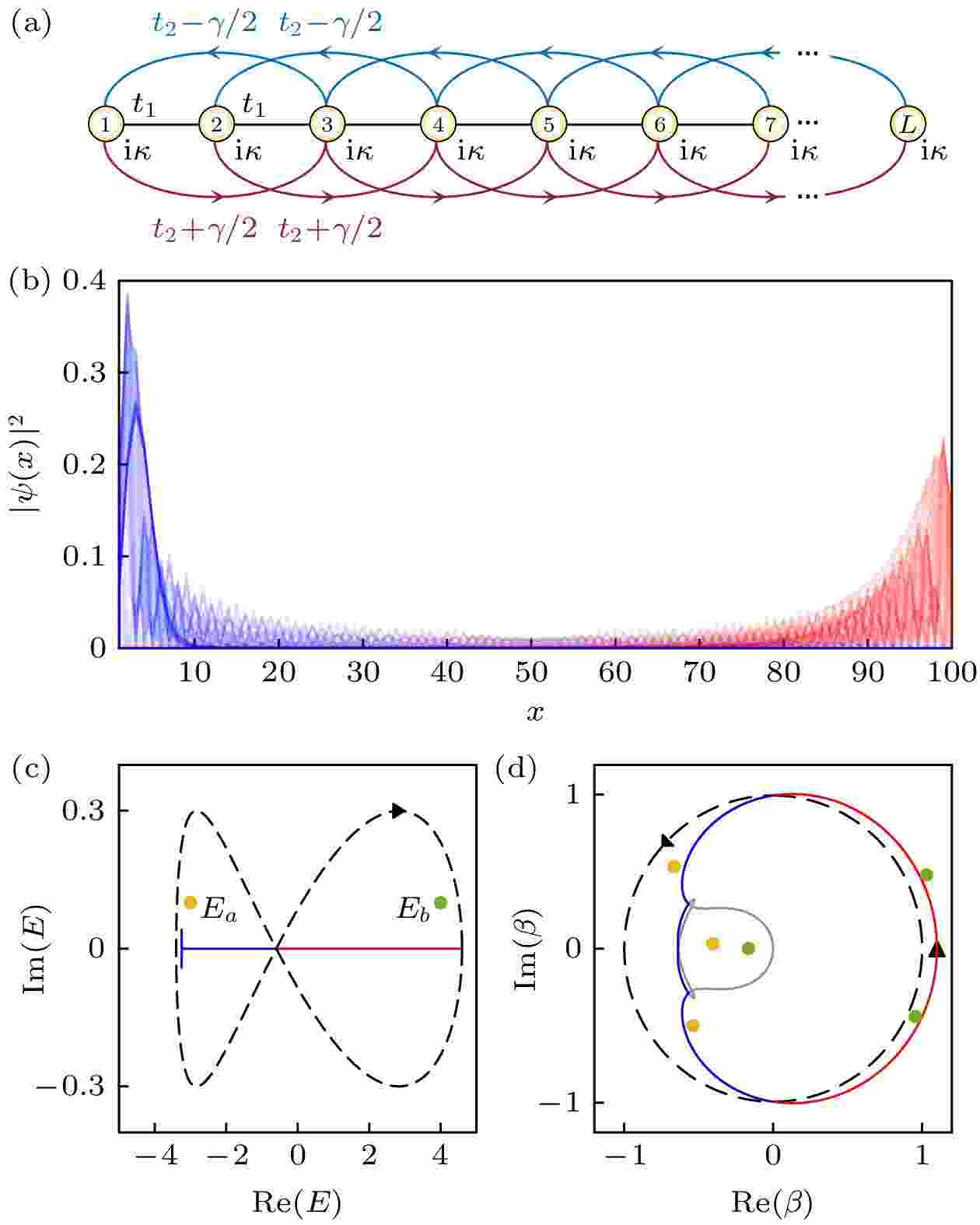 图 4 (a) 具有非对称次近邻跃迁的非厄米模型示意图; (b) 开放边界条件下系统本征态的空间分布, 其中链长
图 4 (a) 具有非对称次近邻跃迁的非厄米模型示意图; (b) 开放边界条件下系统本征态的空间分布, 其中链长






























































































































 图 5 (a) 非厄米SSH模型在开放边界条件下的能谱模长
图 5 (a) 非厄米SSH模型在开放边界条件下的能谱模长































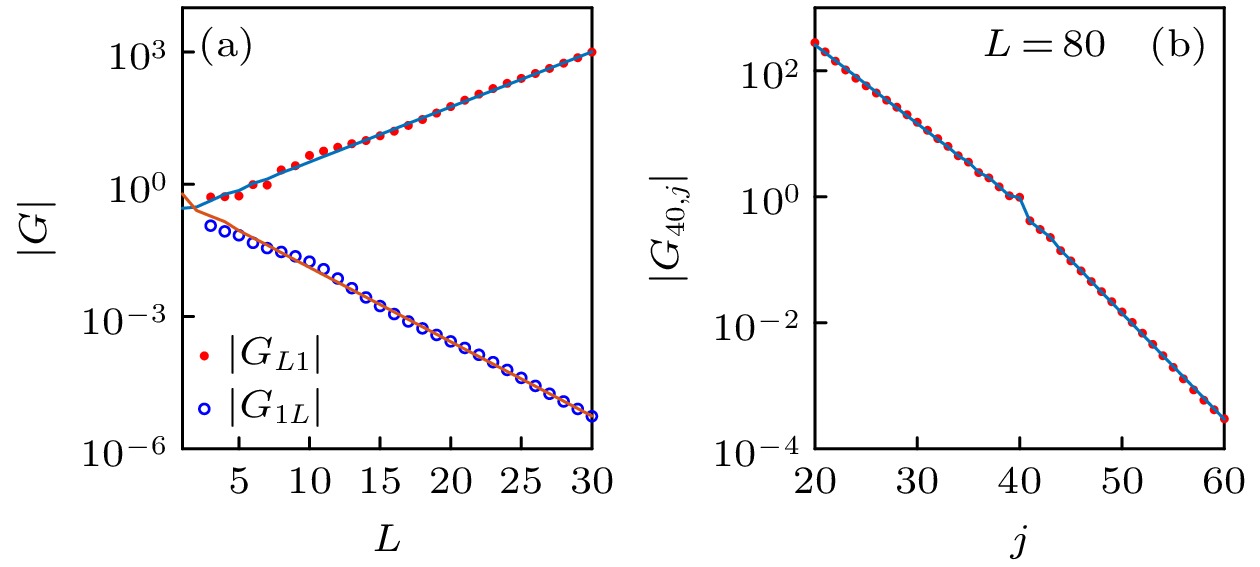 图 6 (a) 方程(34)所描述的非厄米模型在开放边界条件下的非厄米格林函数
图 6 (a) 方程(34)所描述的非厄米模型在开放边界条件下的非厄米格林函数


















 图 7 (a) 布里渊区(蓝色虚线)和广义布里渊区(红色实线).
图 7 (a) 布里渊区(蓝色虚线)和广义布里渊区(红色实线). 














































































































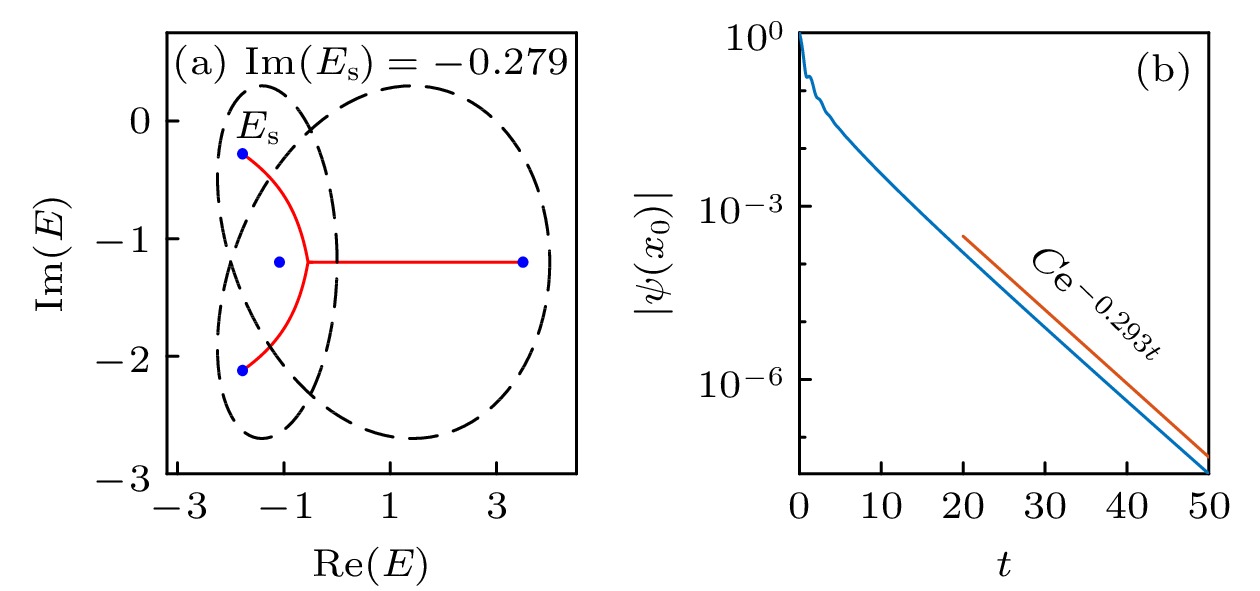 图 8 (a) 周期边界条件(黑色虚线)和开放边界条件(红色实线)下的能谱, 蓝点代表鞍点
图 8 (a) 周期边界条件(黑色虚线)和开放边界条件(红色实线)下的能谱, 蓝点代表鞍点





















 图 9 开放量子系统中的Liouvillian能隙与手征衰减 (a) 具有耗散的开放SSH模型. (b) 衰减矩阵
图 9 开放量子系统中的Liouvillian能隙与手征衰减 (a) 具有耗散的开放SSH模型. (b) 衰减矩阵


































































































 图 10 一维量子行走系统的准能谱虚部
图 10 一维量子行走系统的准能谱虚部










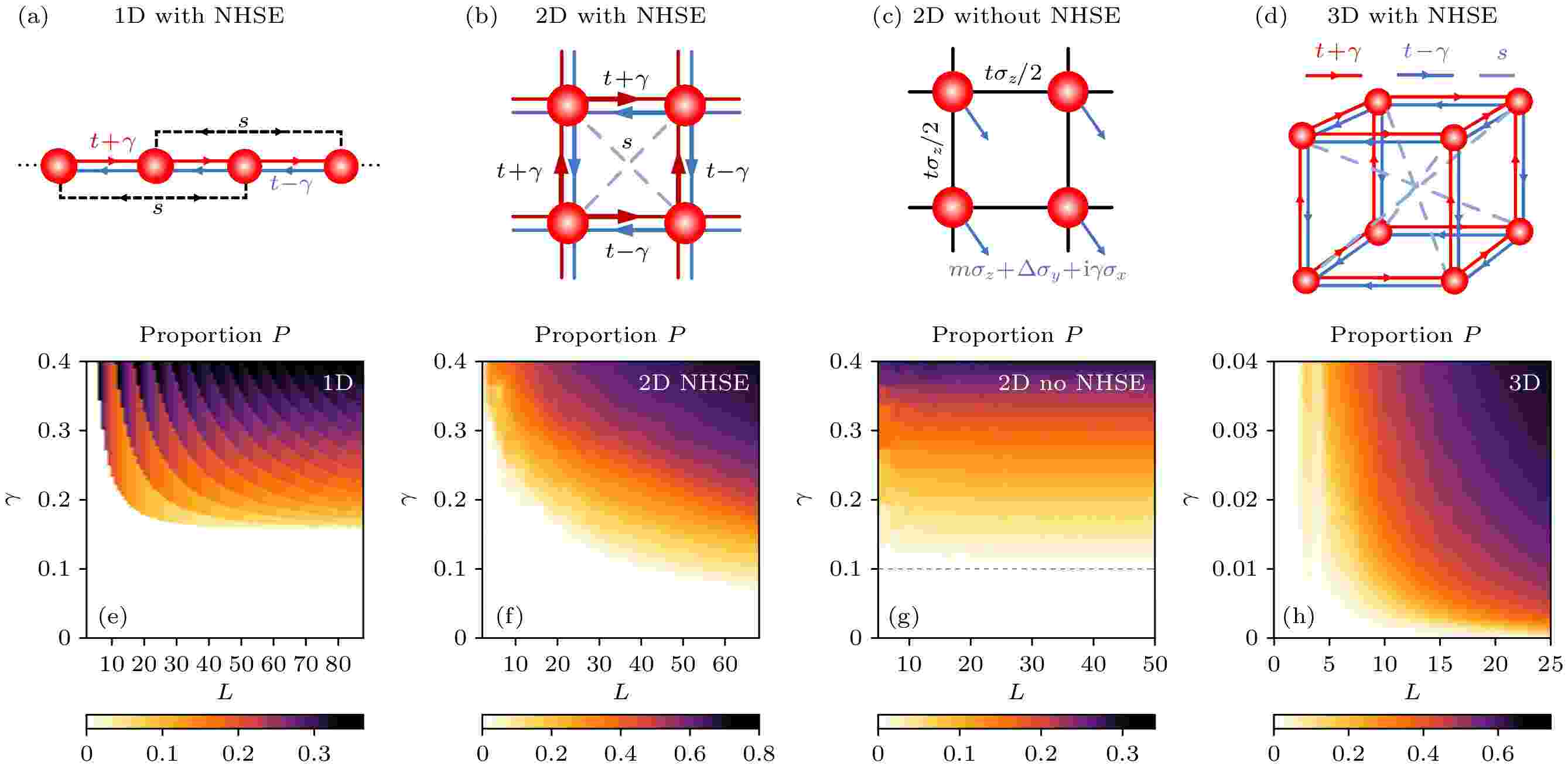 图 11 不同系统在开放边界条件下复数能量数目占比
图 11 不同系统在开放边界条件下复数能量数目占比



















































