摘要:非平衡量子关联体系是近年来受到广泛关注的一类新型量子系统, 其研究对象不局限于某一特定的物理分支, 而是涉及凝聚态物理、原子分子物理和量子光学、量子调控与量子计算、非平衡统计物理等诸多现代物理学的前沿领域. 这些不同体系中涌现出来的非平衡量子关联现象, 既融合了各自体系的不同特征, 又展现出普适的一般规律. 由于其新颖性和复杂性, 这类系统中存在大量未知的基本物理问题和新奇的物理现象, 是当前量子科学理论研究的难点和重点. 同时, 由于量子技术的飞速发展, 理解这类复杂系统对于以量子计算和量子调控为代表的新一代量子科学技术的发展具有重要的现实意义. 本文简要总结了近年来本课题组在非平衡量子多体物理方面的几个代表性工作, 着重讨论了与时间相关的对称性(破缺)导致的新的非平衡量子物态, 准粒子及其中的动力学普适行为.
关键词: 非平衡量子物态/
时间维度效应/
自发对称破缺

English Abstract

全文HTML

--> --> -->

物理世界是由相互作用的多粒子系统组成的. 根据构成其基本粒子的特征尺度(如特征长度、能量等)不同, 物理世界可以划分为一系列不同层级, 每一层级都会涌现出自己特有的物理规律和新的物理概念. 对相互作用的多粒子体系, 其复杂的集体行为往往是由简单的物理规律通过相互作用产生的结果, 因此很难根据更“基本”层级的物理规律做简单外推得以理解. 这类现象称为“演生现象”. 在凝聚态和统计物理中, 常见的演生现象包括自发对称破缺、准粒子与元激发、普适类等^[1].
量子多体物理研究关联量子体系中涌现出的大量粒子的集体行为, 在量子材料、量子计算和精密测量等前沿领域中发挥着重要的作用. 在传统的固体电子材料中, 量子多体物理的研究对象多为处于热力学平衡态(热力学性质)或近平衡态(输运性质)的系统, 而对远离热力学平衡态的性质较少涉及. 近十年来, 由于量子调控技术和测量手段的飞速发展, 在凝聚态物理、超冷原子、固态量子信息等领域中涌现出大量新型的人造量子多体系统, 例如非平衡超导^[2]和磁性系统^[3]、周期驱动的拓扑物质^[4,5]、时间晶体^[6]等. 在这些系统中, 人们不仅可以通过量子调控手段(如激光泵浦^[7]、超快电磁激励等)将量子多体系统激发到远离热力学平衡态的高激发态上, 同时还可以利用最新发展的实验手段(如时间分辨光电子谱^[8], 超快激光光谱学^[9])来实时观测系统的动力学演化过程. 在光晶格中的超冷原子实验系统中, 人们可以通过含时地改变光晶格的相关参数, 例如随时间突然地^[10-13]或线性地^[14], 或周期地^[15-19]改变光势阱的深度, 将这类量子多体系统驱动到远离平衡态的状态. 由于其独特的性质, 这类新型量子关联体系会演生出一些与传统平衡态多体系统完全不同的新现象与新物理, 产生许多亟待解决的物理问题, 急需发展新的有效理论与研究方法. 同时, 这类问题的研究对关联电子输运、量子计算和量子调控等领域的发展有着十分重要的现实意义.
时间是物理学中的基本维度, 在相对论框架下, 时间维度与空间维度在数学上具有等价性. 然而在传统凝聚态物理的研究中, 时间维度所扮演的重要性远远不及空间维度, 在多数情况下, 其仅出现在对处于热力学平衡态系统动力学性质的测量中. 例如, 在输运实验中, 通过对系统外加小的扰动(例如电场), 通过测量系统对于微扰的响应, 利用平衡态系统的涨落耗散定理(线性响应理论), 得到系统在近平衡态下的输运性质(电导率). 在这一过程中, 系统的动力学行为(在微扰下的弛豫动力学), 尽管在实验上具有及其重要的意义, 仅仅是作为一种平衡态/近平衡态物理框架下的探测手段, 其本质还是反映系统平衡态的物理性质. 但是, 当外界的扰动足够强以至让系统远离热力学平衡态/近平衡态时, 线性响应理论中响应函数和关联函数之间的线性关系往往不再适用, 同时这类远离平衡态的系统也会演生出丰富的新现象与新的物理规律. 作为与平衡态物理的核心区别之一, 时间维度作为刻画非平衡物态及其动力学相变的一个基本维度, 在非平衡物理中扮演着至关重要的角色.
对称性自发破缺和普适类是现代物理学中的核心概念. 在凝聚态物理中, 人们通过空间对称群的自发破缺来刻画不同的物相, 并运用普适类来对不同相之间的转变进行分类. 在远离平衡的系统中, 时间维度的加入为这两个基本概念赋予了新的内涵: 与时间相关的对称性及其自发破缺为寻找新的(非平衡)物态提供了新的机遇与挑战. 同时, 将普适类的概念推广到动力学系统, 即研究系统在演化的过程中展现的时间上的普适行为, 不仅拓展了相变理论的研究范畴, 更为非平衡物态的刻画和普适性质的研究奠定了基础. 最后, 由于其内禀的量子关联性, 非平衡量子关联系统的复杂度远远超过经典非平衡系统, 其中量子涨落与非平衡条件的交互作用可能产生出非平衡经典系统和平衡态量子系统中都不存在的新奇宏观量子现象, 极大地拓展了非平衡物理与量子多体物理的研究范畴.
本综述简要总结了近年来本课题组在非平衡量子多体物理方面的几个代表性工作, 着重讨论与时间相关的对称性(破缺)导致的新的非平衡量子物态、准粒子及其中的动力学普适行为. 第2节讨论由于时间平移不变性自发破缺导致的一类典型的非平衡物态: 时间晶体中的瞬子激发行为^[20]. 另外, 讨论了将这一概念推广到虚数时间, 导致的一类新的物态: 温度晶体^[21]. 第3节着重介绍时间反演不变性在宏观层面的自发破缺所导致的一个重要结果: 对于一个对称保护的拓扑体系, 其在微观层面上由时间反演不变性保护的拓扑边缘态耦合上环境之后, 变得不再稳定^[22]. 第4节讨论开放量子系统中弛豫动力学中的动力学普适类, 重点讨论了对称性、相互作用、无序与噪声共同作用下产生的动力学普适行为^[23]. 第5节讨论非平衡量子多体系统中的自发对称破缺的动力学演化框架下的新机制以及由此产生的新奇量子多体态^[24].

时间晶体这一概念于2012年由诺贝尔奖得主Wilczek教授^[6]提出. 在特定条件下, 某些系统可能在时间上形成结构进而自发破坏时间平移不变性. 类比空间上连续的平移对称性自发破缺形成晶体, 这类特殊的物态被称为“时间晶体”. 尽管这一新奇的物态随后被证明不可能出现在热力学平衡态的系统中^[25], 人们随即将这一概念推广到非平衡态: 对一个周期驱动的系统, 如果其物理量的周期是驱动周期T的整数倍, 则这类非平衡物态自发破坏了系统哈密顿量在时间轴上的分立平移对称性(在时间平移t → t+T变换下哈密顿量不变, 而系统的状态发生变化), 故而被称为分立时间晶体(或Floquet时间晶体^[26,27]). 这一概念被提出后, 很快为实验所证实^[28,29]. 时间晶体作为一类典型非平衡量子物质, 受到广泛的关注. 但是作为一种新的物态, 其很多基本的物理性质, 尤其是其针对外界扰动的响应与稳定性问题, 目前并不清楚. 针对这些问题, 我们进行了系统的研究, 取得了一系列结果, 为研究这类新型非平衡量子物态的分类、稳定性及其临界行为奠定了基础.
2

-->

2.1.分立时间晶体中的瞬子激发

自发对称破缺与元激发是凝聚态物理学的两个核心概念: 根据各种不同的对称性及其自发破缺, 人们可以对物质的宏观物相进行分类; 通过对系统元激发的测量, 人们可以从实验中得到物相的各种性质. 在平衡态物理中, 这两个基本概念之间具有深刻的联系: 系统基态的自发对称破缺不仅可以决定低能激发态中元激发的拓扑结构, 也可以决定其能谱及动力学性质. 例如, 在一维聚乙炔电荷密度波态中, 系统的晶格分立平移不变性自发被破缺. 这种基态的Z₂平移不变性的自发破缺决定了其元激发态为位于能隙中心的局域的孤子态, 这种孤子态在空间上分隔了两个简并的电荷密度波态, 并携带分数电荷^[30].
另一方面, 在非平衡物理的框架下, 自发对称破缺这一基本概念被赋予了新的内涵: 其背后的物理机制不再是能量(自由能)最小化, 而是不同动力学模式失稳-竞争-再平衡的结果. 与平衡态系统的一个显著不同是, 对非平衡系统, 自发对称破缺不仅可以发生在空间维度, 也可以发生在时间维度. 具有时间平移不变性的自发对称破缺的物态被称为时间晶体. 对于这类新型的非平衡物态, 一个基本的科学问题是, 其元激发是否还有良好的定义? 如果有, 如何实现并刻画这类激发? 它与系统的对称性(破缺)的关系如何?
针对这些问题, 我们通过类比平衡态系统中Z₂自发对称破缺导致的孤子激发, 提出一个严格可解的时间晶体模型^[20]:

$ \bar H(t) = - J\sum\limits_i {[b_i^\dagger } {b_{i + 1}} + {\rm{h.c}}] + \dfrac{{V(t)}}{L}\sum\limits_{ij} {{{( - 1)}^{i - j}}{n_i}} {n_j}, $

其中, $b_i^\dagger(b_i)$为一维光晶格上硬核玻色子的产生(湮灭算符), n_i为格点i上的粒子密度算符, L为系统尺寸, V(t)为外加的含时(周期)驱动. 硬核玻色子之间的相互作用为一个无穷长程的相互作用, 其强度不随空间距离衰减. 由于这一无穷长程相互作用的性质, 平均场近似在热力学极限下是严格的. 我们引入电荷密度波序参量:

$ m(t) = \left\langle {\psi (t)} \right|\dfrac{1}{L}{( - 1)^i}{n_i}\left| {\psi (t)} \right\rangle \text{, } $

这时系统哈密顿量约化为

$ \bar H(t) = - J\sum\limits_i {[b_i^\dagger } {b_{i + 1}} + {\rm{h.c}}] + m(t)V(t)\sum\limits_i {{{( - 1)}^i}{n_i}} , $

其中序参量m(t)在时间演化的过程中自洽求得. 我们发现该模型在特定条件下, 会展现出分立时间晶体态 (m(t)的周期为V(t)周期的2倍, 见图1(a)).
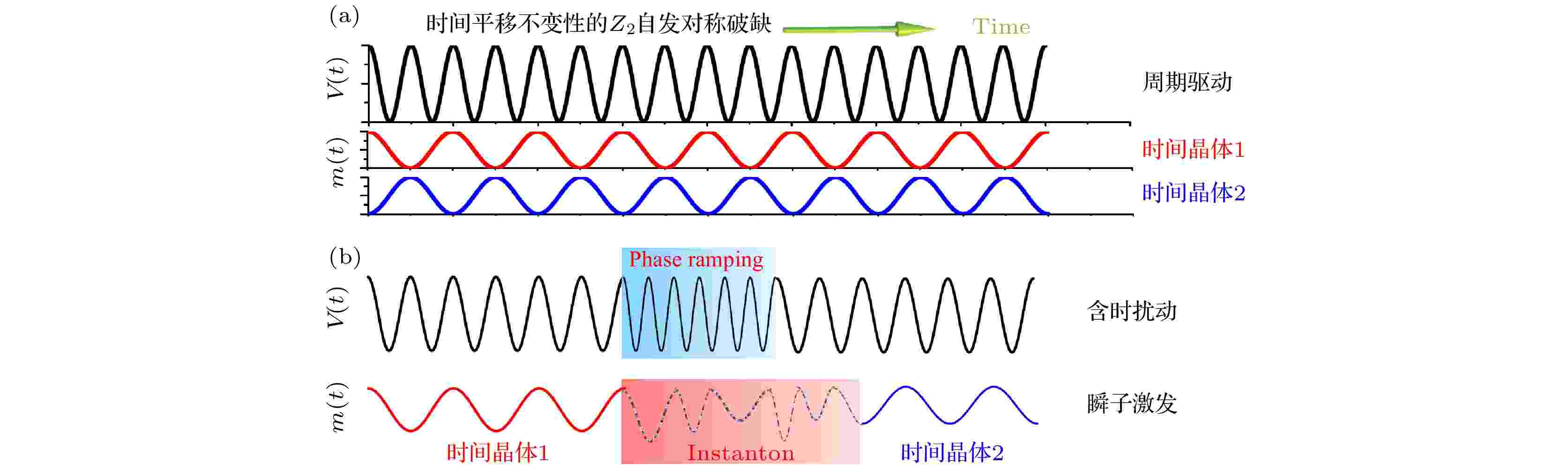图 1 (a) 分立时间晶体态的示意图; (b) 通过含时扰动局部破坏周期驱动的周期性, 导致时间晶体瞬子激发(不同简并时间晶体之间的隧穿)
Figure1. Schematic diagram of (a) a period doubling dynamics in the presence of periodical driving and two degenerate TC phases and (b) the phase ramping protocol in our model and an instanton-like excitation induced by it.

为了研究其对外界(含时)扰动的响应(激发), 我们在一段时间内人为破坏外界驱动的周期性 (这一扰动可以看作在一个周期内, 暂时地增加或减少驱动周期频率). 在分立的时间晶体中, 时间平移不变性的Z₂自发破缺导致了两个“简并”的时间晶体态, 通过对系统施加含时扰动, 我们发现时间晶体对于高频扰动几乎免疫, 但是当扰动频率低于一个临界值时, 系统在时间演化过程中可以从一个简并的时间晶体态“隧穿”到另一个时间晶体态(见图1(b)), 这两个宏观“简并”量子态之间的隧穿类似于量子力学中双势阱系统中的瞬子隧穿效应. 另外, 在临界频率附近, 系统的隧穿时间呈幂指数发散, 这一现象类似于动力学临界系统中的临界慢化现象. 这一研究首次揭示了时间晶体中的瞬子激发, 为研究这类新型非平衡量子物态的分类、稳定性及其临界行为奠定了基础.
2 -->

2.2.虚数时间轴上的时间平移对称性自发破缺: 温度晶体

晶体是在空间具有周期对称性的物质形态. 人类对晶体的探索可以追溯到有文字记载以前. 近代量子凝聚态物理学研究发现, 这种物态通常是在降低温度时, 从连续态(比如流体)通过对称性自发破缺而形成. 不同的对称破缺方式对应各种奇妙的空间群, 从而产生丰富多彩类型的晶体结构. 2012年, Wilczek把晶体的概念推广到了时间维度, 提出量子时间晶体.
温度是热力学中的一个基本概念. 量子力学中的路径积分方法揭示了两个重要的物理概念—温度和时间—之间的深刻联系. 一个温度为T = 1/β的量子系综的配分函数在形式上等价于一个量子动力学系统在(欧几里得空间)虚时间τ∈[0, β] 上的传播子(见图2(a)). 一般来说, 热力学系统的物理可观察量既可以随温度单调上升或下降, 也可能出现非单调的行为, 即物理量的温度依赖曲线出现一个或者多个峰, 这些峰的位置往往对应某些重要的物理现象(例如反常或相变). 基于时间与温度的二象性, 一个基本的探索性问题是, 量子力学是否允许虚时间晶体的存在, 从而在宏观尺度发现“温度”晶体? 换而言之, 能否找到一种物理系统, 其某些性质可以随温度的变化(周期)振荡?
图 2 (a)虚时间晶体在2+1维欧几里得时空中一种典型的时空构型的示意图; (b) 其物理性质随温度振荡
Figure2. (a) A typical world-line configurations of iTC in a (2+1)D Euclidean space; (b) the (inverse) temperature dependence of the CDW order parameter in the iTC phase.

针对以上两个问题, 我们运用量子蒙特卡罗方法, 在一类开放系统中找到了这样一类新型的量子物态^[21]. 考虑一个一维硬核玻色子模型:

$ {H_{\text{S}}} = - J\sum\limits_i {[b_i^\dagger } {b_{i + 1}} + {\rm{h.c}}]. $

假设该模型每个点上耦合一个量子环境. 当量子系统中的粒子与环境耦合时, 环境会诱导出粒子之间的有效相互作用. 一般来说, 这类相互作用具有“延迟性”: 某一时刻的粒子会与之后另一时刻的粒子发生作用, 这一虚时间上的延迟相互作用可以用如下有效(将环境自由度积掉)作用量描述:

$ {S_{\text{R}}} = - \int\nolimits_0^\beta {{\text{d}}\tau } \int\nolimits_0^\beta {{\text{d}}\tau '} {n_i}(\tau )D(\tau - \tau '){n_i}(\tau '), $

其中$D(\tau - \tau ')$代表延迟相互作用随时间间隔的函数. 对某些特定的量子环境, 其诱导出的延迟相互作用随着“延迟时间”具有非单调行为(在某些时间范围内为吸引相互作用, 另一些范围为排斥). 例如, 考虑如下延迟相互作用:

$ D(\tau - \tau ') = \alpha {{\text{e}}^{ - {\omega _{\text{d}}}|\tau - \tau '|}}\cos [2{\text{π }}{\omega _{\text{c}}}(\tau - \tau ')]\text{, } $

这一相互作用可以通过积掉一个(有效的)非厄密的量子环境得到^[31].
通过与传统晶体中的相互作用做类比, 我们发现这类环境诱导的延迟相互作用会导致(虚)时间方向上的结晶行为. 由于虚时间和温度的对应关系, 这类虚时间晶体的物理性质在一定范围内会随温度(周期)振荡(见图2(b)). 另一方面, 当温度降到零温时, 系统的基态会展现出奇异的物理性质, 即一个不可压缩的超流体. 这一零温态不同于目前已知的所有玻色子系统基态, 它源自环境诱导的延迟相互作用和多体系统内部的量子涨落之间的竞争, 反映了开放量子系统中不同于传统封闭量子多体系统的奇异特性.

如何在对多个量子比特进行相干操作的同时, 降低环境对于量子系统的影响一直是量子计算领域的一个核心挑战. 拓扑量子计算因其能极高地容忍局域微扰造成的错误, 成为实现这一目标的一种可能的方案. 作为拓扑量子计算的物理基础, 拓扑量子物态因其潜在的应用价值, 一直是凝聚态物理研究的前沿课题^[32]. 近年来, 以拓扑绝缘体为代表的一类新型拓扑态受到广泛的关注. 不同于传统的拓扑物态(例如量子霍尔效应), 这类物质的拓扑性质只对满足特定对称性的微扰保持稳定, 因此被称为“对称保护的拓扑态(SPT)”^[33]. 例如, 在拓扑绝缘体中^[34], 其边缘上的量子化自旋流被时间反演对称性所保护, 而对于破坏时间反演的微扰(例如外磁场)并不稳定. 一般认为, 环境对量子系统的影响可以看成某种局域的微扰, 如果环境本身以及系统和环境的耦合均不破坏相应的对称性, 则系统的拓扑性质不会受到环境的干扰, 这也是当前拓扑量子计算的理论基础.
然而, 相比于自然界中的其他对称性, 时间反演这一对称性的特殊性在于, 其不仅可以被显式地破坏(例如外加磁场), 也会在宏观层面上自发破缺: 即宏观世界的时间的不可逆性(热力学第二定律). 因此, 研究时间反演在宏观层面的自发破缺对拓扑物态, 尤其是环境对于受到时间反演对称性保护的拓扑物态的影响, 不仅拓展人们对于拓扑物态理解, 同时对于拓扑量子计算领域具有重要的现实意义^[35].
针对这一问题, 我们利用密度矩阵重整化群方法系统地研究了环境对对称性保护的拓扑系统的影响. 考虑一个开放系统, 其总(系统+环境)的哈密顿量为:

$ {H_{{\text{tot}}}} = {H_{\text{s}}} + {H_{\text{b}}} + {H_{{\text{sb}}}} \text{, } $

其中H_s为系统哈密顿量, H_b为环境哈密顿量, H_sb为系统环境耦合哈密顿量. 为了研究方便, 我们考虑系统为一个对称保护的拓扑自旋链, 环境也为一条量子自旋链, 系统和环境在两条链的端点相连(见图4).
图 4 量子多体系统在无序、噪声、相互作用、对称性等因素共同作用下产生普适的弛豫动力学行为
Figure4. Schematic of a open quantum many-body system and its universal dynamics induced by the interplay between disorder, noise, interaction and symmetry.

取H_s为一个自旋为1的量子自旋链(Affleck-Kennedy-Lieb-Tasaki (AKLT)模型^[36]:

$ {H_{\text{s}}} = \sum\limits_i {\Big[{S_i} \cdot {S_{i + 1}}} + \frac{1}{3}{({S_i} \cdot {S_{i + 1}})^2}\Big] \text{, } $

该模型的基态是一个典型的对称保护拓扑态, 即在开边界条件下, 这一自旋为1的自旋链两端会有两个自由的自旋为1/2的边缘态, 这些边缘态受到时间反演、空间反演、$Z^*_2Z $等对称性的保护^[37], 即只要外加微扰不破坏所有这些对称性, 边缘态就不被破坏, 由边缘态决定的基态简并度也会被保护. 下面我们要考虑当系统和环境耦合后, 环境对于对称保护的边缘态的影响, 及其与对称性的关系.
为了考虑环境对于这类对称保护的边缘态的影响, 我们考虑了不同系统环境, 以及系统-环境耦合形式(见图3). 系统-环境耦合的一般形式可以写为:
图 3 一条对称保护的拓扑量子态(AKLT态)通过不同的方式, 耦合上不同量子环境的示意图
Figure3. Schematic of the symmetry-protected topological systems (AKLT state) coupled to different quantum baths via various SB couplings.

$ {H_{{\text{sb}}}} = \sum\nolimits_\alpha {{A^\alpha } \otimes {B^\alpha }} \text{, } $

其中$ {A^\alpha } $为系统算符, $ {B^\alpha } $为环境算符. 我们着重关注时间反演对称性, 即考虑系统和环境哈密顿量都具有时间反演不变性, 同时系统和环境耦合也保持时间反演. 不仅如此, 系统-环境耦合中系统算符$ {A^\alpha } $和环境算符$ {B^\alpha } $各自都保持时间反演不变, 即对这个复合系统来说, 时间反演对称性在所有的微观层次都不被破坏.
我们的研究结果显示, 时间反演这一对称性在拓扑性质保护上具有脆弱性, 即使在上述情况下(时间反演对称性在所有微观层面都被保持), 拓扑系统中由时间反演对称性保护的拓扑边缘态也会被破坏. 其本质原因是因为时间反演对称的特殊性: 在开放系统中, 当我们将环境自由度积掉, 得到只含系统自由度的有效运动方程时, 时间反演对称性可以自发破坏, 从而不再能保护相应的拓扑边缘态. 与之相对应的, 如果边缘态有其他(幺正)对称性保护(例如$Z^*_2Z_2 $ 对称性), 在开放系统中, 边缘态仍然被保护. 这一发现将目前对于对称性保护的拓扑态的研究推广到开放系统, 并对当前基于时间反演对称保护的拓扑物态(例如拓扑绝缘体)的潜在应用提出了挑战^[38].

普适类是现代物理学的一个基本概念. 人们发现不同的临界系统可能展现出某些普适的性质, 这些性质往往与系统的大部分细节无关, 而仅仅被少数关键因素, 如系统的维数、对称性等所决定. 通过对这些普适性质的刻画(临界指数), 人们可以将自然界的连续相变分成有若干普适类. 21世纪70年代, Hohenberg和Halperin等^[39]将这一概念推广到动力学系统, 提出了动力学普适类的概念: 对于临界系统, 其动力学性质(如弛豫时间等)也可以表现出普适行为, 这些行为往往比静态物理量(如关联函数)的普适类更加复杂. 同时, 这类普适动力现象甚至不局限于近平衡系统的相变点附近, 在远离平衡的系统中也能被观察到(如Kardar-Papisi-Zhang普适类^[40]), 目前已经成为非平衡统计物理研究的重要方向.
相比于经典非平衡系统, 量子多体系统中的动力学行为往往更为复杂, 也更加有趣. 由于量子关联系统内在的复杂性, 目前没有一般性的方法来研究这类系统的动力学性质. 因此, 远离平衡态的量子多体系统中是否存在普适的动力学行为一直是该领域的一个基本问题. 我们运用密度矩阵重整化群方法, 研究了一类具有噪声的一维量子多体系统中的弛豫动力学问题^[23]. 考虑一个无序的各项异性的量子自旋链:

$\begin{split} {H_{\text{s}}} =& \sum\limits_i {[(J + \delta )S_i^x} S_{i + 1}^x + (J - \delta )S_i^yS_{i + 1}^y \\&+ {J_z}S_i^zS_{i + 1}^z + h_i^zS_i^z] , \end{split}$

其中$ h_i^z \in [ - \Delta , \Delta ] $之间均匀分布的随机数, 代表无序外场; δ为各项异性参量, 当δ = 0时, 系统具有U(1)对称性. 另外我们在每个自旋上耦合一个z方向的白噪声磁场, 见图4.
可以发现, 尽管噪声会最终将这一多体系统驱动到温度无穷高的稳态, 但是在这一平庸状态附近的弛豫动力学可能展现出非平庸的普适性质. 在这类开放的量子多体系统中, 无序、量子涨落、对称性以及噪声等因素的交互作用会导致丰富的弛豫动力学行为: 在系统具有连续的U(1)对称性时(δ = 0), 随着无序强度的增加, 系统会经历一个从普适的代数弛豫到压缩指数弛豫(stretched exponential)的动力学相变. 当U(1)对称性被破坏后, 系统马上会恢复常规的指数弛豫行为. 一个关键的发现是, 在这一过程中, 这一动力学系统的对称性对于决定系统的长时间的弛豫行为起到了决定性作用. 通过hydrogen dynamics和有效场论的分析, 我们为这一数值发现提供了理论解释. 同时, 这一理论结果与当前超冷原子领域中多体局域化与开放量子系统的实验密切相关^[41,42].

自发对称破缺是现代物理学的一个基本概念. 在平衡态物理中, 在低温下系统通过自发破缺哈密顿量的对称性, 达到能量(自由能)更低且更稳定的有序态. 在非平衡系统中, 外界的能量输入和耗散会驱使系统远离热力学平衡态, 在这一过程中具有不同对称性的非平衡模式往往会自发涌现. 在非平衡物理的框架下, 自发对称破缺这一基本概念被赋予了新的内涵: 其背后的物理机制不再是能量(自由能)最小化, 而是在外界非平衡条件的驱动下, 初始的均匀模式失稳, 不均匀的涨落模式被放大, 同时不同时空模式之间通过竞争与相互作用达到再平衡, 最终赢得竞争的模式决定系统稳态的对称性^[43]. 非平衡稳态中的模式形成与自发对称破缺已经成为经典非平衡统计物理研究的重要前沿课题.
相比于经典非平衡系统, 由于量子关联系统内在的复杂性, 量子多体系统中的动力学行为往往更为复杂, 也更加有趣. 除了常规的模式形成和对称破缺态(例如条纹相), 量子涨落可能恢复被破缺的对称性, 产生出奇异量子多体态, 这类非平衡量子物态既不同于经典非平衡系统中的模式形成, 也和常规量子多体态(如自旋液体)有本质区别. 探索远离平衡的量子多体系统中的自发对称破缺与奇异量子多体态的形成机制对人们理解这类新型量子物质具有重要意义.
我们研究了一类具有驱动-耗散相互作用的玻色系统中的非平衡稳态^[24]. 这一系统的哈密顿量为

$ \begin{split}H =\; & - J\sum\limits_{\left\langle {ij} \right\rangle } {[b_i^\dagger } {b_j} + {\rm{h.c}}] \\& + \sum\limits_i {\Big[ - \upsilon {n_i} + \dfrac{U}{2}} {n_i}({n_i} + 1)\Big] \\&+ \sum\limits_i {\Delta (b_i^{\dagger 2} + b_i^2} ) .\\[-10pt]\end{split} $

与传统Bose-Hubb模型不同, 这一模型中我们引入了玻色子的对产生和对湮灭项, 在特定条件下, 这些项会导致玻色系统失稳, 从而外界驱动将这一系统驱动到远离平衡态.
可以发现, 在非平衡稳态中这一玻色系统会展现出某些类似费米子系统的性质: “费米面”在这一过程中扮演了重要的角色. 最终在“费米面”附近的动量模式赢得竞争, 导致玻色子倾向于凝聚在“费米面”附近的动量上. 在一般情况下, 费米面附近的动量模式之间相互散射, 最终一对具有相反动量的动量模式赢得竞争. 玻色子凝聚在这一对动量上, 在实空间出现具有条纹相的不均匀稳态结构(见图5(a), 图5(b)). 但是在一种特殊情况下, 费米面特殊的“嵌套”结构使得动量模式间可能的散射通道数目极大增加, 这种情况下所有“费米面”上的动量模式都被玻色子占据, 在实空间形成一种密度均匀分布的稳态. 这类凝聚在“封闭线”上而不是“分立点”上的玻色-爱因斯坦凝聚体是一种奇异的量子多体态(见图5(c), 图5(d)), 可能帮助人们理解阻挫量子磁性、高温超导系统等强关联系统中涌现的奇异量子物态. 此外, 这一驱动-耗散玻色子模型与当前基于超导比特的量子计算实验平台具有密切联系, 这一工作揭示了这一平台不仅在量子计算方面具有重要的实际价值, 其本身作为一种新型的人造量子系统, 也可以被用于探索非平衡量子关联系统中的基本物理规律.
图 5 耗散-驱动玻色-赫伯特模型的非平衡稳态中涌现的条纹相 (a), (b) 和奇异玻色液体态(c), (d)
Figure5. The stripe phase (a), (b) and the exotic bose liquid (c), (d) emerging from the steady state of a dissipative-driven Bose Hubbard model.

由于非平衡和量子关联带来的双重复杂性, 这类非平衡量子关联系统目前没有成熟和普适的处理方法, 往往是多种方法综合运用(见图6). 在很多情况下, 可以从平均场近似出发, 抓出非平衡系统中对称破缺态的基本物理, 同时对于某些特定系统(例如BEC系统), 可以采取准经典近似, 将其运动方程约化为经典非线性方程进行处理^[44]. 为了超越平均场并探讨量子涨落扮演的关键作用, 对于一维系统, 通过对现有数值(例如密度矩阵重整化群^[45])和解析(例如玻色化^[46])方法的推广来研究具体模型, 同时结合某些严格可解模型进行结果比对. 对高维系统, 目前没有适用的数值方法. 如何将现有量子多体方法推广来处理高维非平衡问题将是当前这一领域数值计算中的关键难点. 从解析的角度, 利用Schwinger-Keldysh路径积分技术发展有效场论^[47], 并通过微扰展开逐级考虑量子修正. 通过这一系列数值和解析方法相结合, 可能建立适用于非平衡量子关联系统的数值方法和理论框架.
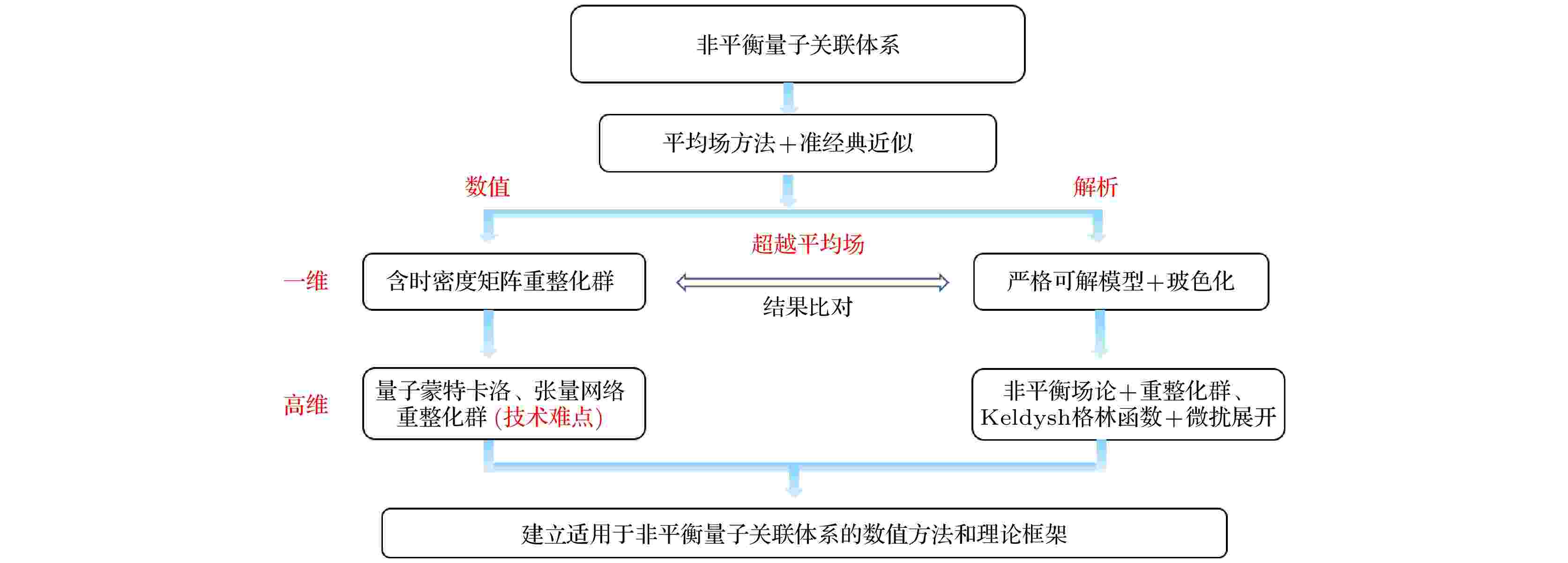图 6 当前处理非平衡量子关联系统的部分解析与数值方法
Figure6. A review of current analytical and numerical methods to deal with non-equilibrium quantum many-body systems.

研究方法中的难点和关键技术是发展适用于高维非平衡量子关联系统的数值方法. 对量子蒙特卡罗方法, 一般认为其只适用于处理热力学平衡态的系统. 在之前的工作中, 我们注意到蒙特卡罗方法的本质是根据特定分布函数进行重要性抽样. 对于热力学平衡态系统, 这一分布函数为玻尔兹曼函数, 而对于非平衡系统, 一般没有普适的分布函数, 需要针对具体问题具体分析. 对于某些特殊的非平衡量子多体系统, 可以找到其非平衡稳态满足的分布函数, 然后根据这一分布函数利用蒙特卡罗方法进行重要性抽样, 同时还要保证抽样过程中不出现严重的“负符号”问题. 这样的特例十分罕见但的确存在^[48], 这些特殊模型对于人们理解非平衡量子关联系统的许多一般性质十分重要. 另一方面, 利用密度矩阵或张量网络重整化群等方法处理非平衡问题面临的重要挑战之一是, 大部分量子系统的纠缠度会随时间迅速增长, 使得这类方法只适用于研究短时间内的动力学行为. 这一困难对于具有短程纠缠的非平衡系统(例如多体局域化系统, 强耗散量子多体系统等)并不十分严重, 这使得我们有可能将这类方法推广到二维系统. 最近动力学平均场方面的研究取得进展, 非平衡动力学平均场方法可能被用来研究更高维相互作用费米子系统的时间演化问题^[49].

非平衡量子关联系统是一个崭新的研究领域, 其中有大量的未解之谜. 由于其具有强关联和非平衡的双重困难, 人们对这一系统的认知极其有限. 在这类系统中, 以往很多基于平衡态热力学的基本物理量(如温度、自由能等)往往不再有良好的定义. 另外, 很多重要的物理概念(如拓扑序、自发对称破缺、普适类)在非平衡物理的框架下可能被赋予新的内涵. 更为重要的是, 这类系统中时间维度的引入以及与其密切相关的对称性和对称性破缺可能演生出传统平衡态量子多体系统中不存在的新的物理概念和物理规律. 同时, 非平衡量子关联体系的研究范围不局限于某一特定的物理分支, 而是涉及凝聚态物理、原子分子物理和量子光学、量子信息与量子计算、非平衡统计物理等诸多现代物理学的前沿领域. 这些不同体系中涌现出来的非平衡量子关联现象, 既融合了各自体系的不同特征, 又展现出普适的一般规律. 我们期待未来不同学科的物理思想和研究方法在这一领域交叉融合, 碰撞出更为绚丽的火花.
感谢王孝群老师、刘文胜老师卓有成效的合作和一直以来的帮助. 感谢李伟、万源、王磊、陈宇、任杰、Navarrete-Benlloch、王子健、岳明锡、杨晓琴、李乔伊、黄易珍等老师和同学在上述工作中的合作和有益的讨论.